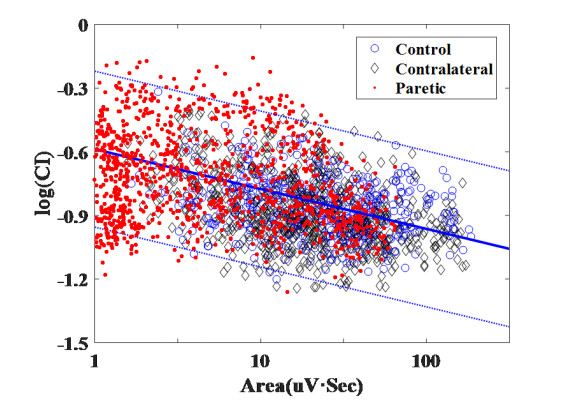
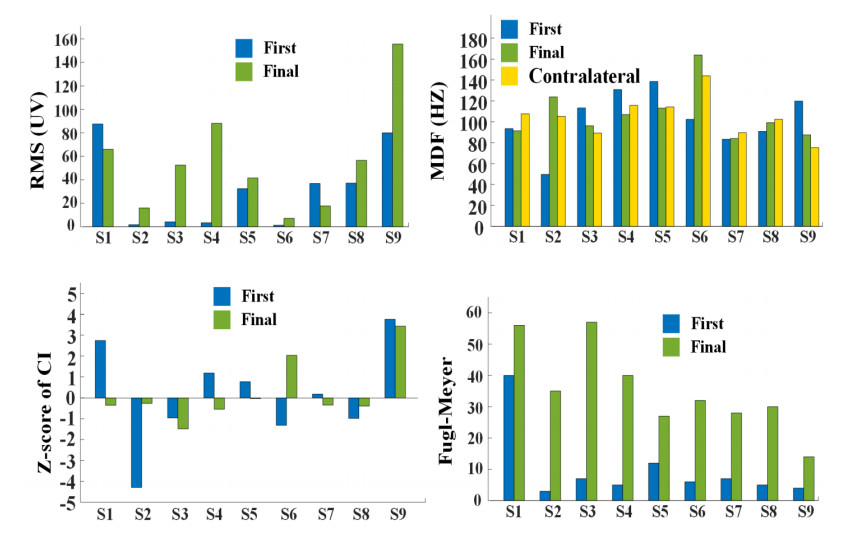
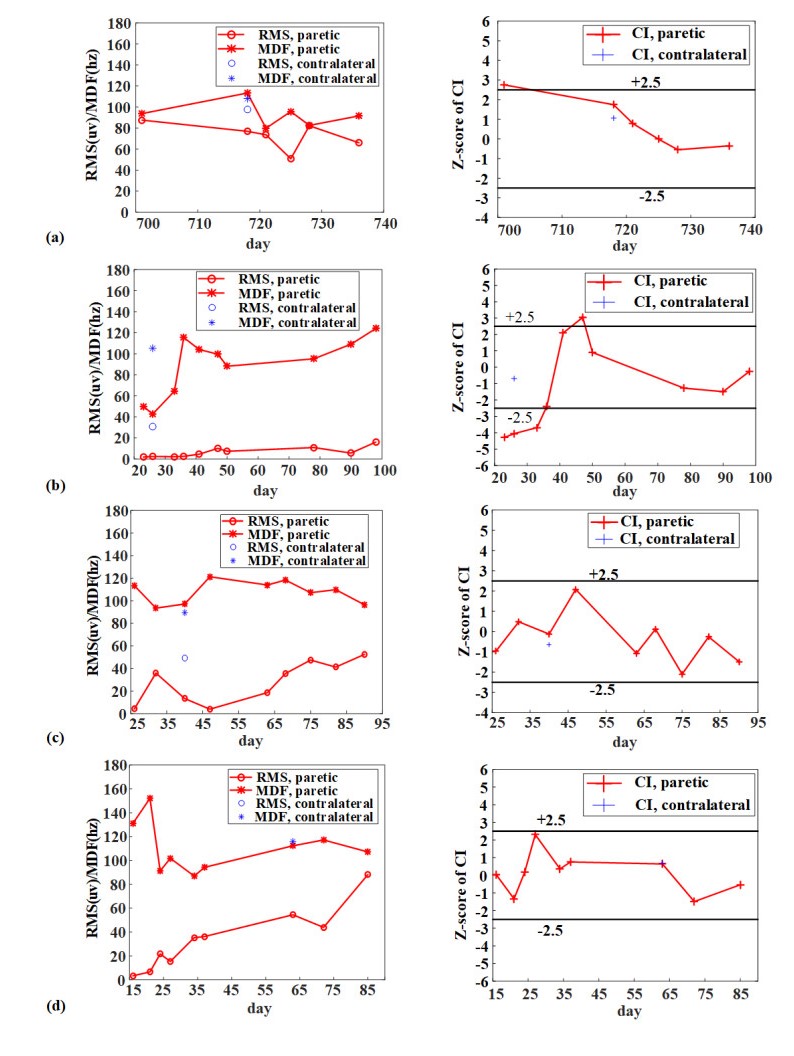
Complex neuromuscular changes have been reported to occur in paretic muscles following stroke, but whether and how they can recover under rehabilitation therapy remain unclear. A tracking analysis protocol needs to be designed involving multiple sessions of surface electromyography (sEMG) examinations during the rehabilitation procedure. Following such a protocol, this pilot study is aimed to monitor paretic muscle changes using three sEMG indicators namely clustering index (CI), root mean square (RMS) and medium frequency (MDF). Initially, a single sEMG examination was performed on the abductor pollicis brevis (APB) muscle on both sides of 23 subjects with stroke and one side of 18 healthy control subjects. With these data to establish CI diagnostic criterion, the paretic muscles of all subjects with stroke showed a very board CI distribution pattern from abnormally low values through normality to abnormally high values. Afterwards, 9 out of 23 subjects with stroke had their paretic muscles examined at least twice before and after the treatment. Almost all paretic muscles had an increase of the RMS, a change of the MDF approaching to the value of the contralateral muscle, and a change of the CI returning to its normal range after common rehabilitation treatments. Finally, 4 of the 9 subjects with stroke participated into repeated examinations of their paretic muscles. The combined use of three indicators helped to reveal specific neuromuscular processes contributing to recovery of paretic muscles, due to their complementary diagnostic powers. Furthermore, neuromuscular processes were found to vary across subjects in type, order and timing during rehabilitation. In conclusion, given the 4 cases following the tracking analysis protocol, this pilot study preliminarily demonstrates usability of three sEMG indicators as tools for examining and monitoring stroke rehabilitation procedure in terms of improvements of paretic muscle changes. All the revealed complex neuromuscular processes imply the necessity of applying sEMG examinations in monitoring rehabilitation procedure, with the potential of offering important guidelines for designing better and individualized protocols toward improved stroke rehabilitation.
1.
Introduction
Nowadays, rolling bearings are the key components widely used in various types of rotating machinery, such as motors, gearboxes, machine tools, etc. Due to adverse working environment, frequent external load and performance degradation, the inner race, outer race and ball of rolling bearing easily suffer from wear, spalling, crack, etc. [1,2,3]. In engineering practice, the faults are random, concurrent, secondary and hidden, which unavoidably leads to the occurrence of compound fault [4]. If effective measures are not taken in time, bearing compound fault may cause machinery idle and even more serious accidents [5,6]. Therefore, the accurate diagnosis of bearing compound fault is of great significance.
However, compared with single fault diagnosis, rolling bearing compound fault diagnosis faces greater difficulties. Firstly, the compound fault signal is not a simple linear sum of single fault signals. The mutual interference and counteraction among different frequency components make the vibration signal more complex and the fault features weaker [7]. Secondly, the sophisticated transmission path seriously attenuates the energy of fault impulse components in the vibration signal collected by sensor, which further weakens the fault features. And they are easily buried in strong environmental noise [8]. Thirdly, the compound fault signal shows obvious nonlinearity and non-stationarity. The mutual coupling and modulation among different type faults make it a great challenge to extract and decouple compound fault features, which easily leads to missed diagnosis and misdiagnosis [9].
In recent years, scholars have proposed many compound fault diagnosis methods for rotating machinery, such as model-based methods [10,11,12], data-driven methods [13,14,15] and signal-based methods [16,17,18]. However, model-based methods require numerous hypotheses, so the established models deviate from the entities, making it difficult to achieve accurate diagnosis. Data-based methods need a large amount of fault data for training, which restricts their using range. Therefore, signal-based compound fault diagnosis methods are paid attention to in this article. Among them, deconvolution-based methods are widely studied in recent years, which deconvolute periodic impulse components from the acquired fault signals to realize compound fault diagnosis [19]. Mcdonald et al. [20] proposed the maximum correlated kurtosis deconvolution (MCKD) method and achieved good results in gear fault diagnosis. But MCKD has many preset parameters, the selection of which determines the fault separation effect. To overcome the above problem, Tang et al. [21] used the cuckoo search algorithm to adaptively select the filter length and shift number in MCKD, and the improved method successfully identified the compound fault of rolling bearing. Nevertheless, the period in MCKD must be set to an integer, otherwise it needs to be resampled and rounded. The filter parameters are calculated in an iterative way, and the obtained filter is just the local optimal solution not always global optimization [22]. Subsequently, aiming at the shortcomings of MCKD, Mcdonald et al. [23] presented a novel deconvolution algorithm named multipoint optimal minimum entropy deconvolution adjusted (MOMEDA), which has aroused many scholars' extensive concern [24,25]. MOMEDA introduces the target vector to define the positions and weights of impulses, and the fault-related periods are identified through the multipoint kurtosis (MKurt) spectrum. MOMEDA can not only set non-integer period but also find the optimal filter without the complicated iterative procedure, avoiding the resampling process [26]. However, MOMEDA does not perform well under strong noise interference. When weak compound fault occurs in rolling bearing, the fault features are very faint, and the fault-related impulses are easily submerged by noise, the rotating frequency of shaft and other interference, which are difficult to be identified. If MOMEDA is directly applied to analyze the vibration signal, the fault periods in the MKurt spectrum will be interfered by various irrelevant components, which will lead to the inaccurate identification of fault periods and further misdiagnosis. Therefore, it is necessary to preprocess the weak compound fault signal before applying MOMEDA to reduce the noise interference.
The Autogram algorithm is a new effective signal denoising technology [27]. It uses maximal overlap discrete wavelet packet transform, unbiased autocorrelation and kurtosis to effectively detect the resonance frequency band submerged in random noise, thus achieving noise reduction and feature extraction of fault signal. Zheng et al. [28] applied Autogram on the fluid pressure signal of hydraulic pump and achieved accurate diagnosis. Wang et al. [29] improved Autogram with maximum envelope to adaptively divide the frequency bands, and then symplectic geometry mode decomposition was performed to diagnose the gear faults. Nevertheless, mere kurtosis index may lead to inaccurate selection of resonance frequency band with strong impulse noise or high repetition rate transient.
Based on the above discussion, a novel weak compound fault diagnosis method for rolling bearing based on improved Autogram and MOMEDA is proposed in this article. Firstly, the improved Autogram can effectively detect the optimal resonance frequency band, thus realizing the denoising of weak compound fault signal. Secondly, MOMEDA is performed to deconvolute the denoised signal, which adaptively obtains the fault periods and decouples the compound fault features. The effectiveness of the proposed method is verified with the simulated signal and experimental datasets of rolling bearings.
The main structure of this article is as follows. Section 2 shows the theory and implementation procedure of the proposed method. Section 3 and Section 4 explain the method's validation with different data, which illustrates its effectiveness and superiority. Finally, the conclusions are drawn in Section 5.
2.
Methods
2.1. Improved Autogram
The Autogram algorithm aims at finding the optimal resonance frequency band that contains abundant fault information. It is selected by comparing the kurtosis of unbiased autocorrelation for decomposition signal's square envelope. Unbiased autocorrelation is given as [27]
where X represents the square envelope of signal, and N is the length of signal.
The traditional kurtosis formula is modified in Autogram to quantize the impulsiveness of signal
The frequency band of the component corresponding to the maximum kurtosis is selected as the optimal resonance frequency band. As a result, the noise interference is reduced. Autogram overcomes the drawback of subjective judgment. However, the effectiveness of kurtosis index decreases with strong impulse noise or high repetition rate transient. The component selection based on kurtosis alone may lead to inaccurate selection.
There are some other effective indexes to evaluate fault features, such as Gini index [30], Hoyer measure [31], multi-scale permutation entropy (MPE) [32], etc. The MPE, a method to detect the randomness and dynamic mutation in time series, can be used to monitor the state of mechanical equipment. MPE first processes the raw time series through coarse graining, and then calculates the permutation entropy at different scales. The specific calculation steps are as follows [33]:
{xi}={x1,x2,⋯,xN} is the raw time series, and the length of {xi} is N. The new coarse-grained series is as follows
where s is the scale factor.
When s = 1, the coarse-grained series is the raw time series, and the result is single-scale permutation entropy. When s > 1, the raw time series is segmented into s coarse-grained series, and the length of each coarse-grained series is N/s. Then the permutation entropy of each coarse-grained series is calculated. The function expression of MPE is constructed as
where m and λ represent the embedding dimension and time delay of permutation entropy, respectively.
To replace the kurtosis index in Autogram, a comprehensive index Z is constructed with kurtosis and MPE
where K represents kurtosis, and M is the average of MPE.
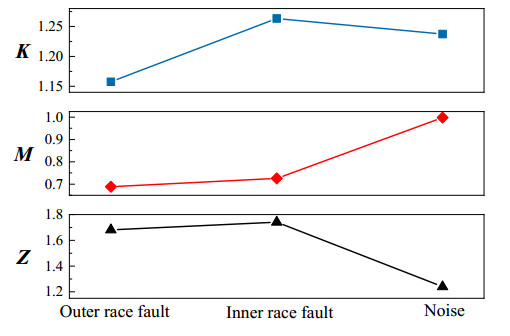
The comprehensive index Z not only takes the impulsiveness and sparsity of signal into consideration, but also can detect the randomness and dynamic mutation. The larger comprehensive index Z, the more fault information contained in the component. The performance of comprehensive index Z is investigated using the simulated signal constructed in Section 3 which is composed of the outer race and inner race fault signals of bearing and strong noise. Figure 1 displays the kurtosis, MPE and comprehensive index values of the three signal components. It is obvious that the kurtosis value of outer race fault signal is smaller than that of noise, so new index is needed. The MPE and comprehensive index Z both have better performance in fault identification. Therefore, comprehensive index Z is suitable for the selection of the optimal resonance frequency band in Autogram.
2.2. MOMEDA
The theory of MOMEDA algorithm is as follows [23]:
The vibration signal collected from the sensor is
where y is the impulse signal generated by fault. h is the response of surroundings and transmission path. e is the noise interference.
The purpose of MOMEDA is to find an optimal FIR filter f in a non-iterative way. Then the input impulse signal y is recovered from the output vibration signal x through f
The Multi D-Norm is introduced in MOMEDA, which is defined as
where t is the vector that defines the positions and weights of target impulses to be deconvolved. So the problem of finding the optimal filter is transformed into calculating the maximum value of Multi D-Norm
The optimal solution is expressed by normalization. And the signal impulses are located and separated through target vector t. Solving Eq (9) is equivalent to computing the derivative of filter coefficients
According to [23], the following equation is known
Mk is expressed as
Therefore, Eq (10) turns to
Eq (13) is simplified as
With the derivative equal to 0, Eq (11) is written as
Eq (15) is simplified as
Since y=XT0f and assuming autocorrelation inverse matrix (X0XT0)−1X0t exists
Considering that the multiples of f are also the solutions of Eq (17), the multiples of filter f=(X0XT0)−1X0t are the solutions of MOMEDA. Therefore, the optimal filter and output solution of MOMEDA are simplified as
Substituting Eq (18) and Eq (19) into y=XT0f, the raw impulse signal is recovered.
To accurately extract the fault features, MKurt is introduced to determine the fault period
When MKurt reaches a peak, the corresponding sampling number is the fault period T, maybe its multiple or factor.
2.3. Implementation procedure of the proposed method
When weak compound fault occurs in rolling bearing, the faint fault features suffer from serious noise interference, making it a great challenge to extract fault information from the raw signal. And different type faults are coupled together, which may cause low accuracy of fault diagnosis and missed diagnosis. To address the problems, a weak compound fault diagnosis method for rolling bearing based on improved Autogram and MOMEDA is proposed in this article. The vibration signal of bearing is preliminarily denoised through improved Autogram at first. And then the filtered signal obtained from the previous step is deconvoluted by MOMEDA to decouple the features of compound fault. The complete process of the proposed method is shown in Figure 2, and the specific steps are as follows:
(1) Perform improved Autogram on the vibration signal of weak compound fault, and find the resonance frequency band corresponding to the largest comprehensive index.
(2) Construct a band-pass filter according to the selected resonance frequency band, and filter the compound fault signal.
(3) Perform MKurt analysis on the filtered signal to identify the fault periods.
(4) Perform MOMEDA on the filtered signal with different deconvoluted periods, and solve the optimal filters to recovery the impulse signals. So the compound fault is decoupled.
(5) Perform square envelope analysis on the separated deconvoluted signals, and judge the bearing faults according to the fault characteristic frequencies in the spectrums. Therefore, the diagnosis of rolling bearing weak compound fault is realized.
3.
Simulation analysis
To verify the feature decoupling effect of the proposed method, a bearing weak compound fault signal model with inner race and outer race is constructed by numerical simulation
where g = 0.1 represents the damping coefficient. The parameters of source signals s1(t) and s2(t) are as follows: the natural frequencies fn are set to 3000 and 5000 Hz, respectively. The fault characteristic frequencies f = 1/T of outer race and inner race are 73 and 207 Hz. The sampling frequency fs is set to 25600 Hz, and a sample in a 0.5 s time horizon is analyzed. A = [0.8147, 0.9058] is a randomly generated matrix. To simulate weak compound fault, n(t) is the incorporated strong Gaussian white noise with -6 dB signal-to-noise ratio.
The time-domain waveforms and their corresponding square envelope spectrums of the simulated bearing weak compound fault signals are represented in Figure 3. Figure 3(e) is composed of Figure 3(a), (c) and strong noise. It can be found from Figure 3(e) that the signal is dominated by noise, and the periodic impulse components cannot be identified. Only the inner race fault characteristic frequency and its double frequency appear in Figure 3(f), but they have low amplitudes with serious noise interference. The feature of outer race fault is completely submerged in noise, making it difficult to be extracted. Therefore, only the inner race fault can be diagnosed somewhat by conventional square envelope spectrum analysis, while the outer race fault is missed diagnosed.
Figure 4 is the analysis result of simulated signal through improved Autogram. The color represents the value of comprehensive index, and the largest index is 4.04. The center frequency and bandwidth of the corresponding resonance frequency band are 2800 and 800 Hz, respectively. Then the simulated signal is band-pass filtered according to the obtained center frequency and bandwidth.
To identify the fault periods, MKurt analysis is performed on the obtained filtered signal, and the MKurt spectrum is shown in Figure 5. It is evident that To = 351 along with its half can be identified clearly, which is very close to the theoretical value of outer race fault period To = fs/fo = 350.68. Similarly, Ti = 124 along with its half and double appear in Figure 4, approaching the theoretical value of inner race fault period Ti = fs/fi = 123.67. Therefore, the compound fault signal contains the impulse components with the above two periods.
The deconvoluted period is set to 351 at first. The filtered signal is deconvoluted by MOMEDA, and the time-domain waveform and square envelope spectrum of the deconvoluted signal are shown in Figure 6. The periodic impulse component is very obvious in Figure 6(a) with excellent denoising effect. From Figure 6(b) we can observe that the background noise is significantly reduced. The outer race fault characteristic frequency fo and its frequency multiplication components are dominant in the square envelope spectrum. Thus the outer race fault is diagnosed effectively. Then the deconvoluted period is adjusted to 124. Figure 7 illustrates the deconvoluted result after performing MOMEDA on the filtered signal. Seen from Figure 7(a), the impulse component is distinct and regular. The spectral lines in Figure 7(b) are quite clear, and obvious spectral peaks appear at the inner race fault characteristic frequency fi and its double frequency. So the inner race fault is judged out. In view of above, the proposed method can effectively decouple the features of weak compound fault, thus realizing compound fault diagnosis.
To highlight the superiority of the proposed method, a contrastive analysis is performed with a prevalent compound fault diagnosis method, the parameter-adaptive variational mode decomposition (VMD) [34]. The simulated signal is decomposed into two IMFs by parameter-adaptive VMD, and their time-domain waveforms and corresponding square envelope spectrums are displayed in Figure 8. We can find that the inner race fault characteristic frequency fi and its double frequency appear in IMF2, but there are many interference frequencies in the square envelope spectrum compared with Figure 7(b). And no outer race fault features can be identified in IMF1 and IMF2, which is prone to missed diagnosis. The result proves the advantages of the proposed method in weak compound fault diagnosis.
4.
Experimental verification
4.1. Description of datasets
To further verify the feasibility and applicability of the proposed method, the XJTU-SY bearing datasets are adopted for analysis, which are more close to the faults in practical application [35]. The testbed of rolling bearings is displayed in Figure 9. It is mainly composed of an AC motor, a motor speed controller, a support shaft, support bearings, a hydraulic loading system and the tested bearing. Two accelerometers are horizontally and vertically installed on the tested bearing through magnet bases. During the experiment, the sampling frequency is set to 25.6 kHz. The sampling interval is 1 min, and each sampling time is 1.28 s. The XJTU-SY bearing datasets contain the whole life vibration signals of bearings under different working conditions, including single faults and compound faults. In order to study the weak compound fault of bearing, the forward portion of vibration signals with weak fault features is selected for analysis. Bearing 1_5 and Bearing 3_2 are chosen as the research objects, for compound fault with inner race and outer race and compound fault with inner race, outer race and ball occur in them, respectively. The faults of different components are shown in Figure 10.
According to the bearing parameters, different fault characteristic frequencies are calculated as
where fi, fo and fb represent the fault characteristic frequencies of inner race, outer race and ball, respectively. Z is the number of balls. d the ball diameter, and D is the bearing mean diameter. α is the contact angle. N represents the rotating speed. The fault characteristic frequencies can be obtained in Table 1.
4.2. Experimental data analysis
4.2.1. Compound fault with inner race and outer race
A sample from the forward portion of Bearing 1_5 dataset (the 23rd sample of the horizontal vibration signal) is randomly selected for analysis. Figure 11 illustrates the time-domain waveform and square envelope spectrum of the compound fault signal with inner race and outer race acquired by the accelerometer. Seen from Figure 11(a), no obvious periodic impulse component appears due to the noise interference and transmission attenuation. In Figure 11(b), the spectral peak appears at the rotating frequency, but the fault characteristic frequencies of inner race and outer race cannot be identified.
The sample is analyzed by improved Autogram, and the result is displayed in Figure 12. The largest comprehensive index is 5.01. And the center frequency and bandwidth of the corresponding resonance frequency band are 1400 and 400 Hz. Then the sample is band-pass filtered according to the obtained center frequency and bandwidth.
Figure 13 displays the MKurt spectrum of filtered signal, from which the fault periods can be identified. It can be noticed that Ti = 155.1 along with its half and double can be clearly identified, which is relatively close to the theoretical value of inner race fault period Ti = fs/fi = 148.76. In addition, To = 233.8 along with its half, 1.5 times and double are evidently observed. It is basically consistent with the theoretical value of outer race fault period To = fs/fo = 237.24. So the fault periods of compound fault are successfully determined.
The filtered signal is further processed through MOMEDA with the fault periods determined by the MKurt spectrum. Figure 14 and Figure 15 illustrate the time-domain waveforms and square envelope spectrums of the deconvoluted signals. It can be found that the time-domain waveforms display obvious periodic impulse features. The inner race fault characteristic frequency fi and its double frequency are clearly identified without interference component, as illustrated in Figure 14(b). Similarly, it can be found from Figure 15(b) that the outer race fault characteristic frequency fo and its first 4 multiples are dominant in the square envelope spectrum. Therefore, the results demonstrate that the compound fault with inner race and outer race occurs in Bearing 1_5, which is consistent with the actual circumstance.
From the above analysis, we can find that there is a certain gap between the inner race fault period Ti = 155.1 determined by the MKurt spectrum and its theoretical value 148.76. For the purpose of verifying the accuracy of the fault period determined by the MKurt spectrum, the theoretical value of fault period is directly inserted into MOMEDA without MKurt analysis, and the result is displayed in Figure 16. We can observe that the periodic impulse component is still hidden in the time-domain waveform, and the inner race fault characteristic frequency cannot be effectively extracted from the corresponding square envelope spectrum, which illustrates the superiority of proposed method.
Figure 17 displays the result of compound fault signal decomposed by parameter-adaptive VMD. Although the time-domain waveforms exhibit impulse features, only a few fault features are extracted from the square envelope spectrums. The outer race fault characteristic frequency fo can be identified in IMF2, but it has a low amplitude and its frequency multiplication components are still submerged in noise. All IMFs are severely interfered by the rotating frequency fr and its multiples, and the inner race fault feature cannot be found. Therefore, the parameter-adaptive VMD cannot diagnose the weak compound fault of rolling bearing effectively, which further shows the effectiveness and meliority of the proposed method.
4.2.2. Compound fault with inner race, outer race and ball
Figure 18 shows the time-domain waveform and square envelope spectrum of a randomly selected sample from the forward portion of Bearing 3_2 dataset (the 842nd sample of the horizontal vibration signal). According to Figure 18(a), the signal components are complex, and the periodic impulse component is masked by noise. There are many irrelevant interference frequencies in Figure 18(b), but the fault characteristic frequencies of inner race, outer race and ball cannot be found.
The result of improved Autogram is shown in Figure 19. The largest comprehensive index is 16.49. And the center frequency and bandwidth of the corresponding resonance frequency band are 2800 and 800 Hz. Then the sample is band-pass filtered according to the parameters.
To determine the fault periods effectively, the MKurt analysis is employed to process the filtered signal. From the MKurt spectrum given in Figure 20, we can observe that Ti = 133 along with its half and double, To = 207.4 along with its half and Tb = 307.5 along with its quarter and half can be clearly recognized. They are very close to the theoretical values of inner race, outer race and ball fault periods 130.16,207.59 and 309.69, respectively. Therefore, there exist the above three fault periods in the compound fault signal.
The deconvoluted periods are set to 133,207.4 and 307.5, respectively. Figure 21–23 delineate the time-domain waveforms and square envelope spectrums of the deconvoluted signals after MOMEDA process. From the time-domain waveforms we can notice that the periodic impulses are significantly enhanced, and the noise interference is effectively suppressed. The inner race fault characteristic frequency fi and its double frequency are dominant in the square envelope spectrum given in Figure 21(b), and there exist no interference frequencies. Therefore, the inner race fault component in the compound fault signal is effectively revealed. From Figure 22(b) we can find that the outer race fault characteristic frequency fo has a low amplitude, but its double frequency is clearly identified. So the outer race fault can be diagnosed. The ball fault characteristic frequency fb and its abundant multiple components are the main frequency components, and the spectral lines are very distinct, as displayed in Figure 23(b). Therefore, the ball fault is judged out. In conclusion, the proposed method can effectively decouple the compound fault with inner race, outer race and ball of Bearing 3_2.
To further verify the superiority of proposed method, the raw vibration signal is directly processed by MOMEDA without improved Autogram. From the MKurt spectrum displayed in Figure 24, we can notice that the fault periods of inner race, outer race and ball can be recognized, but some obvious interference spectral peaks appear at 161.4,215.1,322.5, etc., which is easy to cause poor identification of fault periods and misdiagnosis. In contrast, the spectral lines in Figure 20 are clearer, and the fault periods are accurately identified. The analysis results conclude that the proposed method has an advantage over MOMEDA in weak compound fault diagnosis. Furthermore, when parameter-adaptive VMD is performed to decompose the compound fault signal, the outer race fault cannot be effectively diagnosed. The results are similar to those in Subsection 4.2.1, which are not described here due to the limited extent.
5.
Conclusions
To solve the problem of rolling bearing weak compound fault features intercoupling and suffering from serious noise interference, a novel weak compound fault diagnosis method based on improved Autogram and MOMEDA is proposed in this article. The MOMEDA algorithm is an effective compound fault separation method, but its effect is susceptible to strong noise. So the raw weak compound fault signal needs to be preprocessed. The improved Autogram algorithm obtains the resonance frequency band induced by weak compound fault according to a new comprehensive index constructed with kurtosis and MPE. Then the vibration signal is preliminarily denoised through band-pass filter. Furthermore, the fault periods are adaptively determined by MKurt analysis, and MOMEDA obtains the deconvoluted signals with different periods, which realizes weak compound fault diagnosis. The simulated signal of rolling bearing weak compound fault and the experimental signals from XJTU-SY Bearing Datasets are used to verify the proposed method, and the results show that the weak compound faults are accurately diagnosed. Compared with the parameter-adaptive VMD algorithm, the proposed method has better performance in fault decoupling, which verifies its effectiveness and superiority.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: