1. Introduction
Over the last two decades, the rate of urbanisation on a global scale has been explosive, increasing from 12% in 1990 [1] to over 50% in 2011 [2]. This meteoric rise has generally emerged from high population growth [3] and rural to urban migration, both of which have been rapid in developing countries due to inadequate planning guidelines and the pursuit of economic development [4]. Of the world's developing countries, those within Asia are experiencing the highest rate of urban growth [2]. In particular, Dhaka Megacity, Bangladesh, is one of the fastest growing cities in the world [5,6].
The population in Dhaka Megacity (hereafter Dhaka) has increased from 2.3 million in 1975 [7] to approximately 15.4 million in 2011 [2]. Failure to manage urban growth has led to a significant decline in urban green space over this time, with natural surfaces rapidly being converted into impervious ones [8,9]. Extensive removal of natural surfaces modifies heat retention, its dispersion and evaporative and transvaporative rates [10], which in-turn modifies local climate, air flow and atmosphere [11,12]. Combined, these factors can create an urban heat island (UHI) effect, where urban atmospheric and surface temperatures become significantly warmer than its natural surrounds [11,13].
UHIs have a profound impact on human well-being due to temperature driven increases in infectious diseases [14,15] and have potential to contribute to increasing dengue fever [16] and typhoid fever [17] risk in Dhaka. Considering that Dhaka has been found to have experienced significant urban green space and floodplain removal over the last several decades due to urban development [5,9,18] and its influence on UHI formation, it is vital that modification to Dhaka's urban thermal environment over a multi-decadal period is better understood.
Traditional urban thermal environmental studies are based on the collection of air temperature readings at multiple locations between urban and rural landscapes from weather stations [19], mobile thermometers [20] or both [21]. These approaches are somewhat limited in developing cities where weather stations are unavailable or infrequent [22], such as in Dhaka. Remotely sensed (RS) imagery can be an alternative source for studying urban thermal environments via the analysis of land surface temperature—LST. Through LST, the surface urban heat island (SUHI) effect can be studied, and based on strong relationships observed between near surface air temperature and LST, is considered a reliable indicator of atmospheric UHIs [23,24]. Imagery acquired from the Landsat series of satellites have been the most commonly used medium for assessing changes to urban thermal environments arising from land-use/land-cover (LULC) modification [25,26,27].
Two common approaches to investigate the relationship between LULC and LST are recognised [24]. One approach utilises information recorded from multispectral sensors to determine and compare LST of various LULC types over multiple dates [28]. The other approach is to extract biophysical parameters that quantitatively represent various LULC types from multispectral imagery through the use of indices or classification routines, and utilise these parameters to model LST [24]. Common indices and classification routines include: the Normalised Difference Vegetation Index (NDVI) to highlight vegetated surfaces [29]; the Normalised Difference Built-up Index (NDBI) for urban built-up surfaces [30]; the Modified Normalised Difference Water Index (MNDWI) for water body detection [24]; and linear spectral mixture analysis (LSMA) [31].
LSMA has seen increased use in urban thermal studies due to its ability to consider the mixed-pixel problem inherent in multispectral imagery [32]. This process separates multispectral image pixels into multiple ‘fraction' images that represent the relative abundance of materials captured in multispectral imagery based on its spectral characteristics [33,34]. Fraction images in this approach include the Green Vegetation Fraction - GVF and Impervious Surface Area—ISA fraction [32]. Here, we extend on this approach by applying it to multi-date Landsat imagery.
This study uses multi-date Landsat imagery (1990-2000-2011) to explore the consequences of rapid LULC modification resulting from rapid urbanisation on LST in Dhaka. Specifically, we aim to: (a) calculate LST for all three dates and compare it to contemporaneously mapped LULC; and (b) calculate biophysical parameters using index-based and linear spectral unmixing (fraction based) and assess their utility for LST modelling. We hypothesise that the greatest change in LST will be coincident to areas that have been converted into impervious surfaces as a consequence of rapid urbanisation and that fraction-based imagery will provide superior results, relative to an index-based approach, due to its ability to unmix land-covers from pixels.
2. Study area
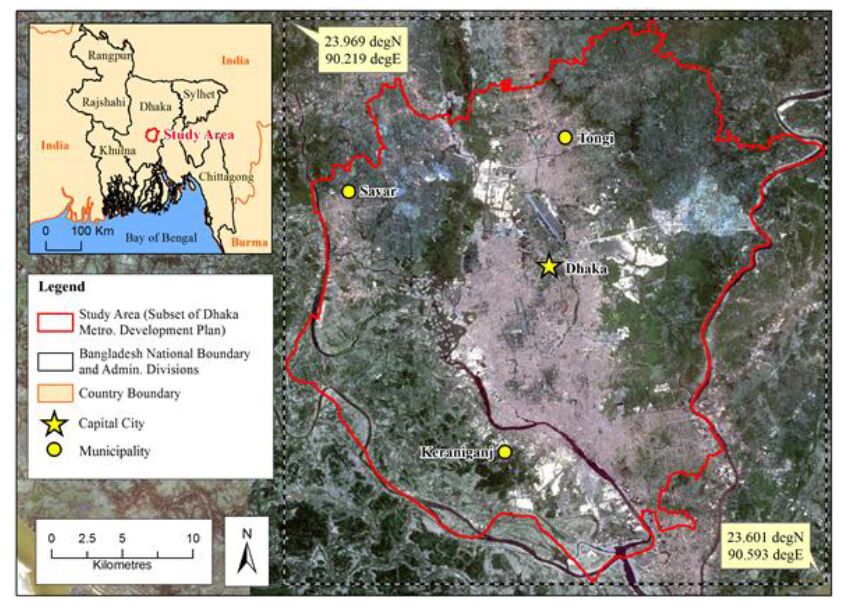
The study area is focused on Dhaka, Bangladesh (Figure 1). The broad Dhaka metropolitan extent is commonly referred to as Dhaka Megacity (DM), which is based on population number as defined by the Bangladesh Bureau of Statistics (BBS) in 1991. As access to urban planning and development spatial data is limited in Bangladesh, the official entirety of the DM could not be considered. Instead, a bounding polygon that includes a subset of both the DM and Dhaka Metropolitan Development Plan (DMDP) planning area zone (as defined by the City Development Authority, RAJUK) was used. Inclusion of the DMDP extended the DM study area extent along its east and southeast boundary only—the north, south and west DMDP extent falls entirely within the DM [9]. The study area covers an area of approximately 87,400 ha, and comprises the Tongi, Savar and Keraniganj municipalities in the northern, western and southern areas of the study area, respectively (Figure 1).
Dhaka is situated on the eastern banks of the Buriganga River and lower reaches of the Ganges Delta on flat low-lying land close to sea level [8]. It experiences a humid, hot and wet subtropical climate with an annual mean temperature of 26.1 °C [35]. Three broad seasons are recognised; a cool and dry winter from November to February, a hot and dry summer from March to May, and a rainy monsoon season from June to October [9,36].
3. Materials
3.1. Image selection and pre-processing
Three Landsat 5 TM (Thematic Mapper) images captured on 7 January 1990 at 10:00 AM Bangladesh Time (BDT) (late winter), 8 March 2000 at 10:30 AM BDT (early summer), and 4 April 2011 10:30AM BDT (peak summer) were acquired from the Geo-Informatics and Space Technology Development Agency (GISTDA), Thailand. As the study area is on the boundary of two Landsat Rows, two scenes were acquired for each year, located at row/path 137/43 (northern scene) and 137/44 (southern scene). All bands have a spatial resolution of 30 m except for band 6 - thermal infrared (TIR) with a resolution of 120 m. All Landsat images were provided at Level 1G, which are corrected for radiometric geometrical distortions.
3.1.1. Geometrical correction
All Landsat scenes were subjected to further geometrical correction using 75 ground control points (GCPs) taken from topographic maps of 1990 to register each scene to the Bangladesh Transverse Mercator (BTM) system [37]. The selected GCPs were well dispersed throughout scenes and resulted in a root-mean-square-error (RMSE) of <0.5 of a pixel using a first-order polynomial and nearest-neighbour resampling.
3.1.2. Calibration and atmospheric correction
The raw digital numbers (DNs) for each Landsat 5 image (bands 1-5,7) were first converted to at-sensor spectral radiance by applying the calibration coefficients (gains and bias) specified by Chander and Markham [38] and Chander et al. [39]. This process used an image-based radiometric correction [40] to minimise radiometric differences between images and was applied using the COST model in IDRISI Selva [41] via the following formula:
where Ls represents at-sensor spectral radiance in Watts * m−2 * sr−1 * µm−1, gain and bias are conversion coefficients, and DN is the digital number [40]. The COST model then removed atmospheric effects arising from changes in surface reflectance [39,40] using various atmospheric parameters including image capture date (in GMT) and sun elevation angles obtained from Landsat header files, and DN haze values derived from blackbody pixels and band wavelengths.
This process was undertaken to ensure the cosine effect of different solar zenith angles due to time differences between image capture, exo-atmospheric solar irradiance differences due to aerosols and dust particles, and variation arising from sun-to-earth distance differences were corrected [38,39,41]. COST achieves this with the following formula:
|
ρ λ =π∗L λ ∗d2ESUN λ ∗cosθs
|
(2)
|
where ρλ represents unit-less planetary reflectance, Lλ is spectral radiance, d2 is earth-sun distance in astronomical units squared, and ESUNλ is mean solar exo-atmospheric irradiances.
Finally, the pairs of Landsat scenes were mosaicked into a single image for each study year and clipped to the study area boundary. The resulting atmospherically corrected images were used to derive biophysical parameters. Calibration and correction of Landsat 5 TIR imagery (band 6) during LST calculation is outlined in Section 4.1.
3.2. Land-use/Land-cover
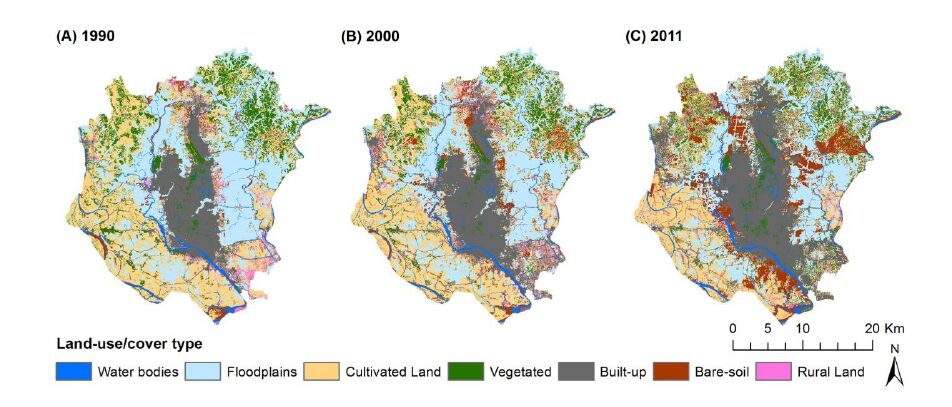
LULC images for 1990, 2000 and 2011 are shown in Figure 2. These images were provided by Dewan and Corner [9], who developed several LULC images of the study area with classes based on a modified Anderson Level 1 Scheme [42] and derived via a hybrid classification technique as outlined by [43]. Subsequentaccuracy assessment performed by Dewan and Corner [9] indicated an overall accuracy of 88%, 90% and 95% for the 1990, 2000 and 2011 LULC images, respectively. Preliminary assessment of the LULC images suggest that built-up and bare-soil surfaces are located predominately within Dhaka's central urban core and have expanded to the north and south over the study period. Floodplains almost completely surround the central urban core on all sides. It is from the close proximity of these floodplains that Dhaka experiences considerable flooding during rainy season periods [5] and highly fertile soils [44].
4. Methods
4.1. Calculation of LST
Several methods exist for deriving LST from the Landsat 5 TIR band (band 6), including the mono-window routine (45) and single-channel algorithm (46). These methods require ancillary atmospheric information and parameters over the study area during satellite overpass to compensate for atmospheric differences between Landsat images. As atmospheric information was unavailable for all Landsat image capture dates, an alternative image-based approach was employed to derive LST based on 47, 48 and 49.
First, the DN of each TIR band was converted to spectral radiance (Ls) derived using Equation 1 [40] and then transformed to at-sensor brightness temperature (Ts) through the inverted Planck's law(Equation 3) using calibration constants obtained from Chander et al. [39]:
where Ts is the effective at-sensor brightness temperature in Kelvin (K), Ls is the spectral radiance at the sensor's aperture in Watts * m−2 * sr−1 * µm−1, and K1 and K2 are calibration constants. For Landsat 5 TM satellite, K1 = 607.76 Watts * m−2 * sr−1 * µm−1 and K2 = 1260.56 K, respectively.
Secondly, the derived Ts images were then corrected for spectral emissivity [50] using the NDVI Threshold Method proposed by Sobrino et al. [51]. This method was chosen as it is considered appropriate for the estimation of emissivity for Landsat TM data as multiple thermal bands and night-time images are not required, unlike other methods such as temperature and emissivity separation (TES) and thermal infrared spectral indices (TISI) [27]. Furthermore, use in LST studies has proven successful [52,53].
The NDVI threshold method obtains the emissivity values from an NDVI image by considering three different cases, based on fixed thresholds: soil pixels (NDVI < 0.2), pixels of dense vegetation (NDVI > 0.5) and pixels with mixed soil and vegetation (0.2 ≤ NDVI ≤ 0.5). To convert NDVI values into land surface emissivity, the emissivity coefficient (ε) was set to 0.96 for soil pixels (ε = εS λ) and 0.99 for dense vegetation pixels (ε = εV λ + Cλ= 0.985 + 0.005) based on Artis and Carnahan [50], Nichol [54] and Sobrino et al. [55]. The emissivity coefficient for mixed soil and vegetation pixels wascalculated using Equation 4 [55] where Pvege is the vegetation fraction obtained according to Equation 5 [56] and the cavity effect (C λ), which accounts for effects of rough or heterogeneous surfaces, was calculated using Equation 6 with a geometrical factor (F') set to 0.55 after Sobrino et al. [57].
|
ε=εVλ∗Pvege+εSλ∗(1 Pvege)+Cλ
|
(4)
|
|
Pvege=(NDVI − NDVIsoilNDVIvege − NDVIsoil)2
|
(5)
|
|
Cλ=(1 −εSλ)∗εVλ∗(F)∗(1Pvege)
|
(6)
|
In addition, a value of 0.955 was used for surface water emissivity and all major water-bodies were masked out of the Landsat imagery, as water can influence the accuracy of the process [58].
Lastly, land surface temperature (LST) was retrieved from the Ts imagery and atmospherically corrected emissivity data. This used a method proposed by Artis and Carnahan [50], which is suited to studies that lack ancillary atmospheric parameters [32,47,49]:
|
LST=Ts1 + ( λ σ TBhc)ln ε
|
(7)
|
where Ts is the derived brightness temperature, λ is the effective wavelength (11.475 μm for Landsat TM band 6), σ is Boltzmann constant (1.38 × 10−23 J/K), h is Planck's constant (6.626 × 10−34 Js), c is velocity of light in a vacuum (2.998 × 10−8 m/s), and ε is the atmospherically corrected emissivity value. As the LST images represent different years and seasons, LST images were finally normalised using the method suggested by Carlson and Arthur [59].
4.2. Calculation of biophysical parameters
4.2.1. Index-based approach
The use of index-based biophysical parameters in LST analysis and modelling can provide important insight into the heat mitigation or enhancement characteristics of various land surfaces [60,61]. Indices used in this study include NDVI to highlight densely vegetated surfaces [62], the NDBI (normalised difference built-up index) as an indicator of built-up urban surfaces and bare-soil [30], and the MNDWI (modified normalised difference water index) as an indicator of water-bodies and rivers [63]. The NDVI, NDBI and MNDWI indices (Equation 8-10, respectively) were calculated using ArcMap 10.1 [64].
|
NDVI=RNIR−RREDRNIR+RRED
|
(8)
|
|
NDBI=RMIR−RNIRRMIR+RNIR
|
(9)
|
|
MNDWI=RGREEN−RMIRRGREEN+RMIR
|
(10)
|
where RNIR is the reflectance in the near-infrared band (TM band 4), RRED and RGREEN are the reflectance in red and green bands (TM band 3 and 2, respectively), and RMIR is the reflectance in the middle infrared band (TM band 5).
4.2.2. Linear spectral mixture analysis
An alternative to index-based biophysical parameters is linear spectral mixture analysis (LSMA), which is able to unmix the components within a pixel [65]. LMSA was used to derive the green-vegetation fraction (GVF), which is similar to NDVI and estimates the fraction of green vegetation within each pixel. The impervious surface abundance (ISA) fraction, which is similar to the NDBI, estimates the fraction of built-up or bare-soil surfaces per pixel. LSMA was completed in two main stages using ENVI 4.8 software [66].
Stage 1: Water-body masking and image normalisation
Pixels representing water are typically masked-out prior to undertaking LSMA as these pixels add unnecessary endmember spectra into the spectral range [32]. A unique mask was created from the water class of each LULC map. Wu [67] indicates that it is beneficial to reduce brightness variability within each fraction image to reduce the number of endmembers representing each component, thus reducing redundant information whilst retaining useful information for separating vegetation, impervious surface and soil fractions. To achieve this, the Normalised Spectral Mixture Analysis (NSMA) method [67] was implemented for each Landsat scene. The NSMA method uses the following equations based on Wu [67]:
where Ŕb is the normalised reflectance for Landsat 5 TM band b in a pixel, Rb is the original reflectance for Landsat 5 TM band b, μ is the average reflectance for that pixel, and N is the total number of Landsat 5 TM bands (i.e., 6 bands for Landsat TM).
Stage 2: Minimum noise fraction transform, pixel purity index and n-dimensional visualisation
Landsat image dimensionality was reduced to remove unnecessary noise from image bands by using the Minimum Noise Fraction (MNF) transform. The MNF comprises of two standard principal component (PC) transforms, which provide an output composed of uncorrelated MNF components that are used to assist in the endmember selection process [68]. We used the first four components in LSMA as the other components were comprised of noise. Following this, pure-pixel endmembers were identified by refining the MNF components and mixed pixels via a Pixel Purity Index (PPI) algorithm [69,70]. The endmembers trialed for each Landsat scene included: vegetation, soil, and impervious surface.
After selection of endmembers, the constrained least-squares solution (Equation 13) was applied to unmix the MNF components identified earlier in which the residual eb is minimized:
|
ˊ Rb= Σmi=1˙fiˊ Ri,b +eb
|
(13)
|
where ˙fi is the fraction of endmember i, Σmi=1˙fi = 1 and ˙fi = ≥0; ˊ Ri,b is the normalised reflectance of endmember i in band b for that pixel; m is the number of endmembers; and eb is the residual or band error. Additionally, the constrained least-squares solution assumes (Equation 14):
This approach unmixed the selected MNF components into Green Vegetation Fraction (GVF), Impervious Surface Area (ISA), and soil abundance fraction images, and a summary of root-mean-square-error (RMSE) statistics was produced (Table 1).
Table 1. Summary of root-mean-square-error (RMSE) statistics derived from linear spectral mixture analysis for combinations of three (vegetation, soil, impervious surface) endmembers for each study year.
| RMSE |
1990 |
2000 |
2011
|
| Minimum |
0.00 |
0.00 |
0.01
|
| Maximum |
0.23 |
0.34 |
0.29
|
| Mean |
0.11 |
0.17 |
0.21
|
4.3. Temporal comparison of LULC to LST
Spatial relationships, patterns and distributions between LULC classes and LST over the study period were visualised and explored by overlaying each LST images over their corresponding LULC classes map using ArcMap 10.1. The mean LST of each LULC type for each year was obtained using Zonal Statistics. Significant differences (α = 0.05) between the LST means of each LULC class across years were then determined using Tukey's Honestly Significant Different test [71] to explore potential changes to Dhaka's urban thermal environment over the study period. Image differencing was undertaken on LULC class maps to generate change maps for the periods: 1990-2000, 2000-2011, and 1990-2011, which were then linked to LST images as tables to explore influence of LULC change on LST.
Variation in LST is the result of several factors including LULC change, time of the day, and seasonality [11,72]. All acquired Landsat images used in analysis were captured at the same approximate time (10:00 AM Bangladesh local time) due to the sun-synchronous orbit [73], avoiding acquistion time issues. To correct for differences in seasonality, the normalisation method developed by Zhou and Wang [24] was utilised to correct seasonal differences in LST whilst retaining differences in LULC type. This approach compares the mean LST of each LULC type across each image using the following equations (Equation 15-17):
where dTij is the temperature difference between LULC type j in the first comparison year (Ya) and LULC type i in the second comparison year (Yb); ΔTi is the temperature difference for the same LULC type i between two comparison years; dTn is the normalised temperature by subtracting dTij − ΔTi.
4.4. Comparison of LST and biophysical parameters
Relationships were examined between LST images and biophysical parameters at 1000 samples distributed randomly over the entire study area. Samples were generated using a stratified random sampling design, where 148 random samples were randomly generated for each of the LULC strata. The strength of the relationship between biophysical parameters and LST was examined using univariate regression via SPSS Statistics software [74]. Fisher's r to z transformation [75] was used to identify if the correlation between LST and LMSA were significantly different to the index-based parameters (i.e., NDVI vs GVF; NDBI vs ISA).
5. Results
5.1. Temporal comparison of LULC to LST
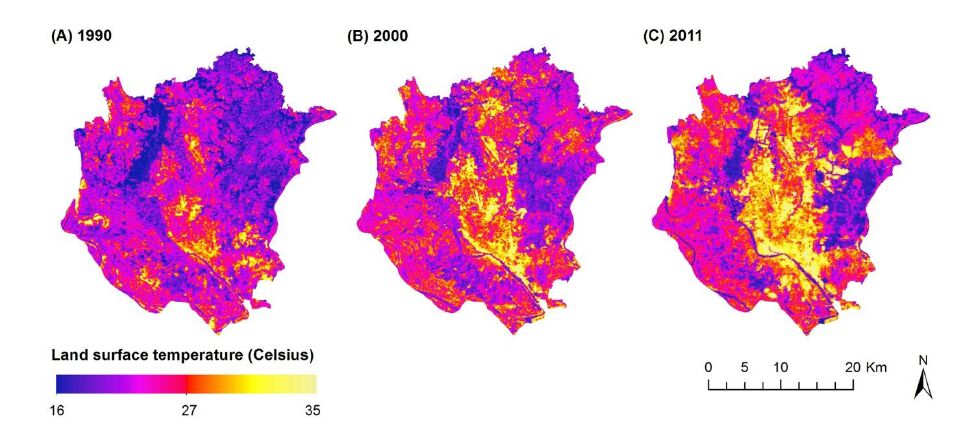
High LST areas were observed to be associated with built-up and bare-soil LULC classes, based on a visual comparison between Figure 2 and Figure 3. In contrast, areas of lower LST are associated with floodplains, cultivated land and vegetation. Figure 3 indicates that surface temperature is increasing in both magnitude and spatial distribution over time.
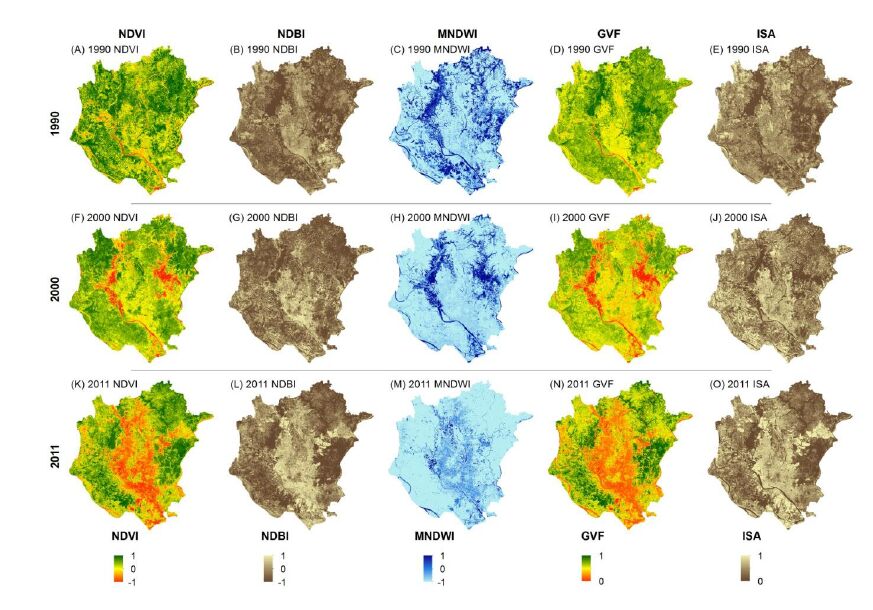
Locations with high NDVI and GVF values (Figure 4), and thus densely vegetated, declined significantly over the study period, particularly in Dhaka's central urban core (Figure 4). In contrast, locations with high NDBI and ISA values increased, indicating urban development over the study period. Locations with high MNDWI values declined on floodplain areas over the study period. These trends, in particular decreasing vegetated surfaces due to conversion into impervious surfaces, have been noted in Dhaka in similar studies [76,77].
Built-up, bare-soil and cultivated LULC types consistently exhibited the highest mean LST, which increased significantly at each temporal data point studied (Table 2). In contrast, water-bodies consistently exhibited the lowest temperatures each year and did not significantly change throughout the study period when using normalised LST imagery. Floodplains and vegetated land maintained low LST and did not change significantly between 2000 and 2011 (Table 2). Comparison of each year indicated that the mean LST of each LULC type continually increased over the study period and these changes were significant between years for built-up areas, bare-soil, cultivated and rural classes, with the greatest mean increases occurring in the built-up and bare-soil classes. Comparison between water LULC types using normalised and non-normalised LST images was undertaken to explore the influence of seasonality on surface temperature. While water LST is considerably consistent and not significantly different across study years, water temperature based off non-normalised imagery increases considerably across years and present LST means that are significantly different.
Table 2. Mean land surface temperature showing the variability of each land-use/land-cover over the study period.
| LULC Type |
Land Surface Temperature (°C)
|
|
1990 |
2000 |
2011 |
All Years
|
| Meana |
SDb |
Mean |
SD |
Mean |
SD |
Mean
|
| Built-up |
21.18a |
1.03 |
25.36b |
1.03 |
27.69c |
1.38 |
24.74
|
| Bare-soil |
20.79a |
1.31 |
24.86b |
1.07 |
27.38c |
1.51 |
24.34
|
| Cultivated |
20.56a |
1.05 |
24.32b |
0.67 |
25.76c |
0.99 |
23.55
|
| Rural |
20.47a |
1.01 |
24.25b |
0.67 |
25.85c |
1.04 |
23.52
|
| Vegetated |
19.12a |
0.85 |
23.15b |
0.57 |
24.11b |
1.03 |
22.13
|
| Floodplain |
19.01a |
1.06 |
23.24b |
0.81 |
23.74b |
1.11 |
22.00
|
| Water (N LSTc) |
18.24a |
0.91 |
18.53a |
0.71 |
18.91a |
1.46 |
18.56
|
| Water (Non-N LSTd) |
18.56a |
1.03 |
23.09b |
0.93 |
24.47c |
0.75 |
22.04
|
a Different subscripts represent significantly different LST means (α = 0.05) between years for land-use/land-cover type;
b SD = Standard Deviation
c N LST = Normalised land surface temperature
d Non-N LST = Non-normalised land surface temperature. |
Influence of LULC type on LST modification was explored by subtracting LST values for each LULC type for the periods 1990 to 2000 and 2000 to 2011 (Table 3). This was undertaken for both normalised and non-normalised LST images as a consideration for potential seasonal differences between LULC types. Investigation of normalised LST for the two periods indicates that LST increased markedly when natural LULC types were converted into built-up and bare-soil. Not surprisingly, water-bodies exhibited the highest LST increase when converted into built-up areas, with an average increase of ca. 2 °C (Table 3). Similarly, mean LST for vegetated surfaces and floodplains increased by an average of ca. 1.2 °C and 1.6 °C, respectively, when converted into impervious surfaces (Table 3). These temperature increases align with similar studies, which have noted an LST increase over 2 °C following the conversion of vegetated surfaces into impervious or bare-soil following urban developments over several decades in similar climates [78,79].
Table 3. Influence of land-use/cover change on non-normalised and normalised land surface temperature for 1990-2000 and 2000-2011 comparison periods. No LULC occurred in classes with the same label.
| Land-use/cover Type |
Land Surface Temperature (°C)
|
|
Comparison Period
|
|
1990-2000 |
2000-2011
|
| Converted |
Non-Norm. |
Non-Norm. |
Norm. |
Non-Norm. |
Non-Norm. |
Norm.
|
| From |
To |
dTa |
dT (SDb) |
dTc |
dT |
dT (SD) |
dT
|
| Water |
Water |
4.53 |
4.2 |
0.28 |
1.38 |
3 |
0.3
|
| Floodplain |
3.74 |
2.5 |
0.5 |
0.71 |
4.1 |
0.79
|
| Culti. land |
4.32 |
2.5 |
0.96 |
2.23 |
3.8 |
0.81
|
| Vegetated |
4.04 |
1 |
0.59 |
2.33 |
0.7 |
0.49
|
| Built-up |
5.36 |
0.0 |
2.18 |
4.78 |
2.2 |
2.03
|
| Bare-soil |
4.66 |
2.2 |
1.59 |
3.66 |
0.4 |
1.13
|
| Rural |
4.25 |
0.3 |
0.47 |
2.33 |
4.2 |
0.28
|
| Floodplain |
Water |
5.03 |
0.2 |
0.5 |
2.17 |
1.5 |
0.79
|
| Floodplain |
4.24 |
1.8 |
0.0 |
1.5 |
0.7 |
0.0
|
| Culti. land |
4.82 |
3.4 |
1.06 |
3.02 |
0.5 |
0.57
|
| Vegetated |
4.54 |
0.8 |
0.59 |
3.11 |
3.1 |
0.3
|
| Built-up |
5.86 |
2.3 |
1.68 |
4.95 |
0.5 |
1.62
|
| Bare-soil |
5.16 |
2.2 |
1.09 |
4.44 |
4.8 |
0.92
|
| Rural |
4.75 |
0.9 |
0.97 |
3.11 |
2.4 |
0.51
|
| Cultivated Land |
Water |
3.97 |
3 |
−0.96 |
1.59 |
2.7 |
−0.81
|
| Floodplain |
3.18 |
3.3 |
−1.06 |
0.93 |
2.2 |
−0.57
|
| Culti. land |
3.76 |
2.4 |
0.0 |
2.44 |
1.2 |
0.0
|
| Vegetated |
3.49 |
3.9 |
−0.46 |
2.54 |
3.1 |
−0.27
|
| Built-up |
4.8 |
2 |
0.63 |
4.37 |
3.2 |
1.05
|
| Bare-soil |
4.1 |
0.8 |
0.03 |
3.87 |
2.1 |
0.34
|
| Rural |
3.69 |
4.1 |
−0.09 |
2.54 |
4.9 |
−0.07
|
| Vegetated |
Water |
4.44 |
0.4 |
0.59 |
1.86 |
1 |
0.49
|
| Floodplain |
3.65 |
1.2 |
−0.59 |
1.2 |
2.7 |
−0.3
|
| Culti. land |
4.22 |
0.8 |
0.46 |
2.72 |
0.4 |
0.27
|
| Vegetated |
3.95 |
3 |
0.0 |
2.81 |
3.8 |
0.0
|
| Built-up |
5.27 |
2.3 |
1.09 |
4.64 |
1.5 |
1.32
|
| Bare-soil |
4.57 |
2.8 |
0.75 |
4.14 |
1.1 |
0.62
|
| Rural |
4.15 |
1.5 |
0.37 |
2.81 |
3.3 |
0.21
|
| Built-up |
Water |
3.35 |
1.9 |
−2.18 |
0.55 |
3.8 |
−2.03
|
| Floodplain |
2.56 |
0.2 |
−1.68 |
−0.12 |
4.8 |
−1.62
|
| Culti. land |
3.13 |
2.3 |
−0.63 |
1.4 |
0.8 |
−1.05
|
| Vegetated |
2.86 |
2.8 |
−1.09 |
1.49 |
0.4 |
−1.32
|
| Built-up |
4.18 |
3.5 |
0.0 |
3.33 |
1.4 |
0.0
|
| Bare-soil |
3.48 |
2 |
−0.59 |
2.82 |
0.3 |
−0.7
|
| Rural |
3.06 |
3.2 |
−0.72 |
1.49 |
0.5 |
−1.11
|
| Bare-soil |
Water |
3.94 |
3.5 |
−1.59 |
1.25 |
1.6 |
−1.13
|
| Floodplain |
3.15 |
2.4 |
−1.09 |
0.58 |
3.2 |
−0.92
|
| Culti. land |
3.73 |
1.1 |
−0.03 |
2.1 |
2.1 |
−0.34
|
| Vegetated |
3.45 |
2.9 |
−0.75 |
2.2 |
3 |
−0.62
|
| Built-up |
4.77 |
1.3 |
0.59 |
4.03 |
3.8 |
0.7
|
| Bare-soil |
4.07 |
4.6 |
0.0 |
3.53 |
1.1 |
0.0
|
| Rural |
3.66 |
1.9 |
−0.12 |
2.2 |
1.4 |
−0.41
|
| Rural |
Water |
4.06 |
1.2 |
−0.47 |
1.66 |
2.3 |
0.28
|
| Floodplain |
3.27 |
1.5 |
−0.97 |
0.99 |
3.3 |
−0.51
|
| Culti. land |
3.85 |
4.2 |
0.09 |
2.51 |
0.3 |
0.07
|
| Vegetated |
3.58 |
4.4 |
−0.37 |
2.61 |
3 |
−0.21
|
| Built-up |
4.89 |
0.3 |
0.72 |
4.44 |
2.5 |
1.11
|
| Bare-soil |
4.19 |
3.5 |
0.12 |
3.94 |
0.8 |
0.41
|
| Rural |
3.78 |
2.2 |
0.0 |
2.61 |
1.9 |
0.0
|
a Non-norm. dT = Non-normalised land surface temperature difference;
b Norm. dT = Normalised land surface temperature difference;
c SD = Standard Deviation. |
The LST of cultivated land resulted in only minor change when converted into built-up and bare-soil for both comparison periods. Likewise, temperature differences between built-up and bare-soil were minimal (Table 3).
Considering that the greatest LST change appears to be associated with natural areas being converted into impervious surfaces, built-up and bare-soil classes were merged to further explore the spatial correspondence between LST and LULC change due to urbanisation. Floodplains, cultivated land and vegetation were not included due to seasonal influence. Comparison between each of the time periods indicates that impervious surfaces have expanded on to surrounding LULC types such as floodplains, water-bodies and cultivated land (Figure 5). Likewise, urban expansion appears to be moving from the urban core in north, north-east, north-west, east, and south-east directions.
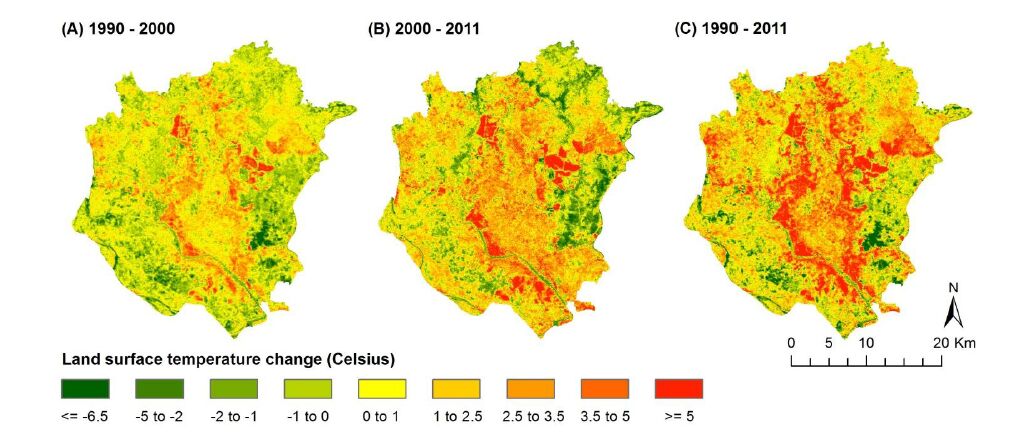
Differences in LST were calculated and visualised for the comparison periods in order to inspect the influence of urban development on LST change (Figure 6). Differences in LST across study periods were also calculated and visualised to assess LST changes as a result of LULC modification (Figure 6). The thermal environment of Dhaka matched these cover changes across each comparison period, with significant expansion of LST into areas that were floodplains and rural land that have changed into impervious, built-up, areas (cf. Figure 5 and Figure 6).
5.2. Comparison of LST and biophysical parameters
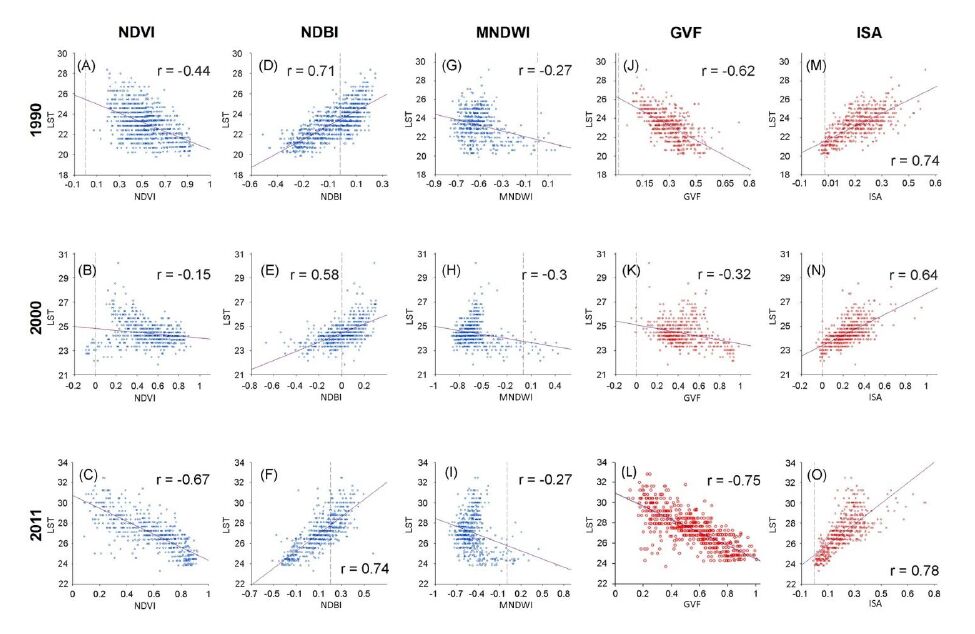
The strength of the correlation between NDVI/GVF and LST varied considerably between years (Figure 7), although it was persistently negative, reflecting the inverse relationship often observed between dense vegetation and LST. In contrast, the correlation between NDBI/ISA and LST was positive, strong, and relatively stable throughout the study period highlighting LST increases in tandem with impervious surfaces (Figure 7) These trends, particularly those between vegetation, impervious surfaces and LST, have been highlighted in similar studies [12,60]. The MNDWI consistently had a weak negative correlation with LST for the study period (Figure 7 G, H, I), indicating the resistance of water-bodies to increases in LST.
Comparison of the correlation coefficients between the fraction-based approach (GVF) and the index-based approach (NDVI) for detecting greenness identified that the GVF was a better predictor of LST than the NDVI. However, differences were only significant in 1990 (Table 4). Likewise, the ISA fraction-based approach had consistently higher correlation with LST than the NDBI for all time periods, although differences were not significant at α = 0.05 (Table 4). Within techniques, the NDBI was significantly more correlated to LST than NDVI (1990-2000) and the ISA outcompeted the GVF (Table 4).
Table 4. Significant differences between the corresponding index-based and fraction-based approaches (i.e., NDVI vs GVF; NDBI vs ISA).
|
NDVI vs GVF1 |
NDBI vs ISA |
NDVI vs NDBI |
GVF vs ISA
|
| 1990 |
0.04 |
0.33 |
<0.05 |
0.06
|
| 2000 |
0.10 |
0.25 |
<0.05 |
<0.05
|
| 2011 |
0.13 |
0.25 |
0.17 |
0.31
|
| 1p-values < 0.05 identify significant differences between approaches. |
6. Discussion
Dhaka's urban thermal environment has been significantly modified over the last several decades as a result of LULC change from rapid urbanisation. Built-up and bare-soil surfaces associated with urban growth have rapidly replaced pre-existing natural surfaces including vegetation, floodplains and water-bodies. On-going conversion has modified the thermal environment of the area, as indicated by increases in the magnitude and spatial distribution of LST over the study period. Our findings are based on Landsat imagery acquired at three temporal data points (1990, 2000, 2011). Our selection criteria required cloud-free imagery close to anniversary dates. Ideally, additional images should be employed to study the changes through time more finely [80] and closer to anniversary dates. However, we note that greater temporal resolution was severely impeded by an almost ubiquitous presence of cloud cover in the Landsat scenes visualised. Unfortunately, this is a problem in studies exploring urban thermal environments situated in tropical or sub-tropical regions of the world, a problem which has restricted numerous studies to small image sets in analysis of LST change across wide temporal and seasonal ranges [32,47,81,82].
6.1. Temporal comparison of LULC to LST
The highest mean LST in each study year were the built-up and bare-soil surfaces, which shared similar mean LST across study years likely due to similarity in albedo [25,83]. The mean LST of both surfaces continually increased over the study period, and the mean LST of natural surfaces such as water-bodies, floodplains and vegetation increased significantly when converted into these impervious surfaces. The higher mean temperature of these surfaces is likely due to the ability of impervious surfaces to retain solar heat [84]. Further, the removal of natural surfaces such as floodplains and vegetation to make way for these surfaces likely modified the surface energy balance and reduced evapotranspiration, resulting in an increase in the sensible heat flux and a reduction in latent heat flux [85] as well as modification to the heat storage and conductivity charactistics of the original surfaces [86].
Natural surfaces such as vegetation, cultivated land and floodplains exhibited moderate LST increases across the study period, possibly as a result of seasonal variation. Floodplains become highly inundated during certain periods of heavy rain [9], altering the thermal characteristics of the surface. The presence of prominent crop vegetation, extensive harvest activity between January and March [87], and moisture stress from pre-monsoonal drought [44,88] also results in fluctuations in land surface temperatures at different times of the year. The mean LST of water-bodies maintained a consistent temperature of approximately 19 °C across the study period, likely due to the consistently high thermal inertia of water surfaces [89]. Water-bodies only maintained consistent temperatures after seasonal variation was normalized across the study period. Without normalisation, water-body surface temperature increased and was significantly different across the study period, highlighting strong seasonal influence across our restricted, non-normalised Landsat image set.
A reduction of water-bodies and vegetated areas, which typically mitigate high surface temperatures due to differing albedos and heat storage capacity [1,90], are also likely to have contributed to an increase in the LST. Regardless, as a result of several decades of rapid urbanisation in Dhaka, impervious surfaces have expanded considerably. Considering that impervious materials such as concrete maintain a high thermal inertia and conductivity [25], high heat storage capacity [86] and can increase surface reflections and reduce wind dispersal in an urban area [91], the rapid development of these surfaces and the removal of natural surfaces has led to postively trending LSTs in Dhaka.
These findings reflect the results of similar studies in comparable subtropical or monsoonal climates. For instance, Xu et al. [92] investigated the influence of LULC change on LST of the subtropical Quanzhou region of south-eastern China over two decades using Landsat imagery. They found that LULC change had led to rapid urban expansion, causing natural surfaces to be converted into impervious surfaces, resulting in an urban heat island (UHI) effect. It was found through multivariate statistics that built-up surfaces contributed greatly to LST increase. Likewise, Weng [93], explored the influence of LULC change on LST in the subtropical Zhujiang Delta, China over a decade. Weng [93] found that land development raised surface radiant temperature by approximately 10°C and found that this change indirectly reduced the biomass of the Zhujiang Delta. LST increases were highly correlated to urban expansion, particularly to the development of major roads. Importantly, simulated forecasts in Dhaka to 2029 indicate continued and rapid increases in LST [76] and reinforce both the negative influence of unmanaged urban growth on LST and the importance of maintaining natural surfaces.
Our results are strongly dependent on the accuracy of the land cover derivatives used over the three time periods, which were noted as having overall accuracies between 88 and 95%. Hence, we assume that, like Dewan and Corner [94], green space has been rapidly converted to predominantly impervious surfaces over the entire study period. However, this is in contrast to Raja [77] and Raja and Neema [95], who explored LULC change and LST in Dhaka across the period 1989-2010 and determined that vegetated and other natural surfaces actually increased in area over time (i.e., in 2010).
Almost equally consistent across these studies, are noted issues pertaining to seasonal influence on LST. Raja [77] and Raja and Neema [95] indicate unexpected area increases in some LULC types and decline in mean LST within their most recent study year (2010) may potentially be related to seasonal variations. Similarly, Dewan and Corner [94] attributed season to inflated mean LST of built-up surfaces in some years. Here we have applied and statistically validated the correction proposed by Zhou and Wang [24] for seasonal differences, avoiding these possible influences thus enabling more confident acquisition of non-anniversary date, cloud-free imagery in Dhaka. We encourage similar validation be carried out in other study areas.
Similarly, Ahmed et al. [76] indicated that reliance on a limited set of index-based parameters potentially reduced LST model strength when predicting LST dynamics in Dhaka and suggested improvements could be made using improved, or more, biophysical parameters. Based on our findings, use of LSMA-derived parameters offer stronger correlations with LST than traditional index-based parameters, and may therefore improve model strength. Furthermore, the continued advancement in modern satellites spectral resolution (e.g., Landsat 8, Sentinel 2), coupled with LSMA, could be applied to extract far more surface materials from imagery than index-based techniques, improving LULC maps and correlations with LST [96].
6.2. Comparison of LST and biophysical parameters
Univariate statistics indicated that the use of LSMA-derived biophysical parameters (GVF and ISA) were more highly correlated to LST than their index-based equivalents (NDVI and NDBI). This is particularly evident when comparing NDVI to GVF, and differences were most pronounced in 1990. NDBI was a stronger predictor of LST than NDVI, which has previously been reported [12] and is due to the comparatively low seasonal influence on impervious surfaces [97,98]. Similarly, ISA was a stronger predictor than GVF.
Despite the improvements that the LSMA method can provide for deriving accurate biophysical parameters and LST modelling, it is important to note that the user should make some considerations prior to use. First, the LSMA approach is a highly iterative and particularly elaborate process. This makes it prone to more human error when compared to the index-based approach. The requirement of expert knowledge is also a key factor in deriving accurate fraction images, limiting the use of this process to specialists. Furthermore, deriving urban impervious surface fraction imagery is highly prone to the ‘mixed pixel problem' due to high pixel variability associated with built-up surfaces [99]. This makes the selection of accurate endmembers both difficult and time consuming during the process. To this end, it is reasonable to suggest that studies utilising LSMA to derive biophysical parameters should also derive NDVI or NDBI and compare to the results of LSMA to assess accuracy.
7. Conclusion
The increase in unmanaged urbanisation in Dhaka and its immediate surroundings has led to a continuous increase in LST as vegetation and floodplains are converted into either bare-soil or built-up surfaces. Two index-based biophysical parameters (NDVI and NDBI) were compared with two LSMA-based parameters or fraction surfaces (GVF and ISA). NDBI indicated a strong relationship with LST due to its heat retaining capacities. However, the LSMA parameters yielded stronger relationships with LST than the corresponding index-based parameters, particularly for vegetation (GVR>NDVI).
Acknowledgements
We are extremely grateful for the comments of two anonymous reviewers, which significantly helped to improve this paper.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: