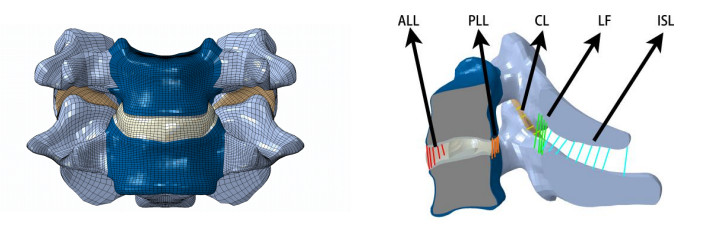
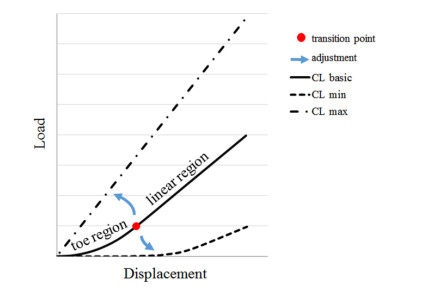
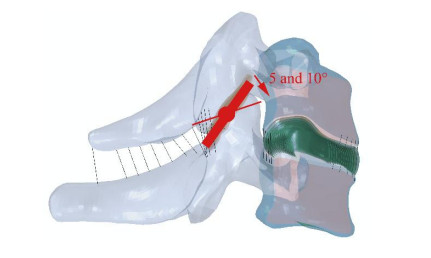
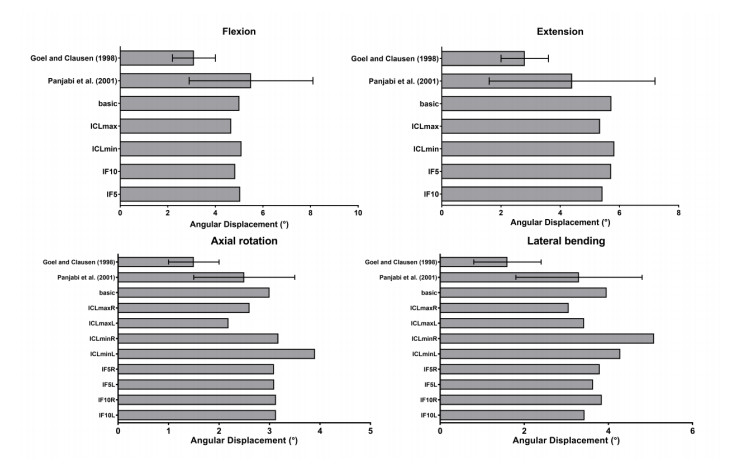
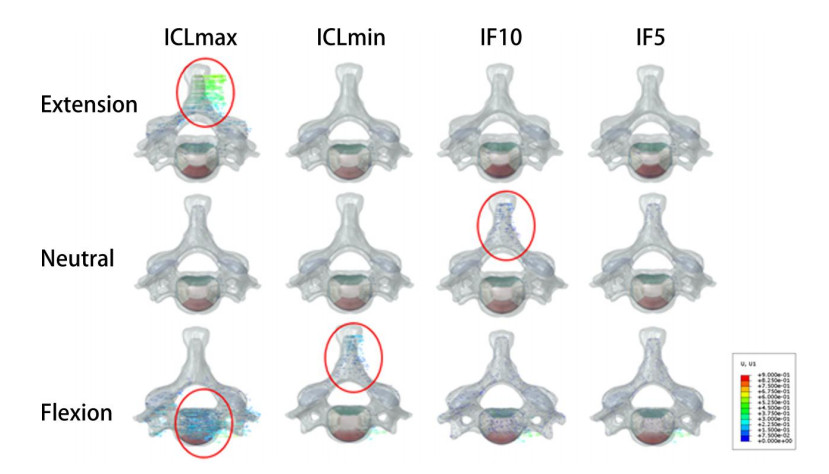
It has been demonstrated that articular facet degeneration can cause local strain alterations and induce neck pain. This study aims to quantify the biomechanical effects of normal and degenerated C5–C6 articular facets, and evaluate the correlation of mechanical strain between healthy and degenerated spine. A 3-dimensional finite element (FE) model of the C5–C6 cervical spine was developed [Model 0 (M0)]. The asymmetric models of C5–C6 bilateral articular facet joint were established separately to mimic articular facet joint degeneration. The capsule ligament stiffness of C5–C6 unilateral facet joint was altered with minimum and maximum threshold to simulate capsule ligaments' lesion and calcification [Model 1 (M1) and Model 2 (M2), respectively]. Besides, the cervical C5–C6 unilateral articular facet joint direction was changed by 5° and 10° forward to imitate the moderate joint hyperplasia and severe osteophyte (Model 3 and Model 4 respectively). M1 increased the rotation range of ipsilateral side (left), while M2 reduced, and both had limited effect on the contralateral side (right). The angle increased in Model 3 (M3) (61°) and Model 4 (M4) (55°) comparing to M0 during the axial rotation, and the angle of M4 was larger. M3 and M4 increased the nucleus pulposus pressure with and without controlled angular displacement during axial rotation. The pressure of nucleus pulpous increased during M1 rotating to the abnormal side but decreased when rotating to the other side, but the results of M2 were opposite. The capsule ligament stiffness made an impact on segmental mobility and vertebral spatial position, and the sagittal angle of articular facet joint exerted an influence on disc pressure distribution.
1.
Introduction
Sanda is a combat sport derived from Wushu, where two competitors face off on a designated area, employing striking techniques (i.e., punches and kicks) and grappling methods (i.e., projections and wrestling) to secure victory in the fight. To succeed on the international stage, an athlete must use a variety of physical, technical, and mental attributes. Therefore, training optimization is crucial, encompassing various performance factors, including physiological, psychological, sociological, genetic, muscular, metabolic, biomechanical, etc.
Limited research has been conducted in the field of Sanda biomechanics [1]–[4], with existing studies primarily focusing on specific parameters of performance capacity. Biomechanics, defined as the study of physics and mechanical systems in human movement, aims to identify the cognitive mechanisms that initiate and organize movement, the parameters of the produced movement, and the forces and constraints that act upon it [5].
However, few studies [6]–[8] have investigated how combat sports percussionists' abilities are affected by the development of physical qualities, such as speed and strength. In combat sports, most previous research [9]–[14] has focused on studying mechanical, physiological, and motor aspects individually, rather than examining their interaction and impact on striking performance.
In Sanda, multiple techniques are permitted, including punches, kicks, sweeping, seizures, and projections, all of which must be executed with sufficient force to be recognized by the referees. The distribution of scores depends on the technique employed; kicks to the body and head offer greater significance than punches delivered to the same regions. The execution of sweeping and projections gives the highest number of points when the fighter is in a standing position. Additionally, exiting from the combat zone, as well as counts and warnings issued to the opponent, contribute to the accumulation of points. Thus, kicks are considered the most challenging essential elements in combat. Conversely, they are regarded as a crucial element to employ in the pursuit of maximizing points during the competition.
According to Le Camus and Le Camus [15] and the Sanda International Competition Arbitration Rules [16], two points are awarded to the fighter who performed a clean kick to the trunk, making kicks an essential component to earn maximum points during the fight.
To be considered valid by referees, Sanda strikes must be executed with sufficient power, precise form, and a clearly defined height. Achieving such technical precision requires a high velocity of execution, which in turn necessitates a significant level of strength to accelerate and propel one's own body effectively. Furthermore, a high degree of motor automatism and gestural coordination is essential. Consequently, strength, speed, flexibility, and coordination emerge as key determinants of Sanda performance. As noted by Ouddak [17], motor coordination is the ability to execute precise and intentional gestures with speed (i.e., speed of execution), efficiency (i.e., achieving the goal), and reliability (i.e., high reproduction rate).
In this context, controlling gestures effectively is essential [15], asserts that gesture control involved executing movements in stages and managing each phase individually. Regarding Sanda performance, this idea highlights the importance of precise motor control [18]–[20]. Although limited research exists on Sanda [21],[22], it is comparable to other combat sports in terms of its technical aspects, including kick boxing [23], Taekwondo [24], Karate [25], and Muay-Thai and Jiu-Jitsu [26].
Despite some regulatory differences, particularly regarding kicks, the most frequently used techniques in Sanda are the front kick (i.e., Dan Tui), the side kick (i.e., Ce Chuai Tui), and the roundhouse kick (i.e., Pian Tui). Each of these kicks plays a crucial role in scoring and executing strategic moves effectively. Indeed, the roundhouse kick, a key skills of Sanda athletes, is characterized by powerful impact and is one of the most frequently used and effective technique in competition [27]. However, few studies [28],[29] regarding this turning kick exist. Therefore, the roundhouse could be the fastest, strongest, and most effective kick among Sanda athletes [30].
In this respect, we propose to study the qualities of strength, speed, and effectiveness of three kicks in Sanda in the present research. Our primary focus will be the kinematic analysis of these factors to determine the best kick. The purpose of this study is to examine three Sanda kick techniques, the roundhouse kick (RK), the front kick (FK), and the side kick (SK), through kinetic and kinematic analysis. These three techniques are known as Pian Tui, Dan Tui, and Ce Chuai Tui, respectively, in Wushu nomenclature. We hypothesized that the RK exhibits the optimal execution of speed and force, making it the most effective kick.
2.
Materials and methods
2.1. Participants
G*Power software (Version 3.1, University of Dusseldorf, Germany [31]) was used to compute an a priori power analysis with a type I error of 0.05 and 90% statistical power. The research revealed that at least 19 participants are needed to detect a significant moderate effect size (f = 0.31, d = 0.62 and critical F = 3.259) for both kinetic variables (such as force, power, inertia, and momentum) and kinematic variables (i.e., velocity, joint angles, and segment angles) [32],[33].
Nineteen Tunisian senior national team Sanda players volunteered to participate in this study. Of them, fourteen were male (age 21.79 ± 2.33 years; height 1.74 ± 6.25 m; body mass 70.06 ± 11.28 kg; training average 20 h/week; experience 10.36 ± 4.75 years of practice) and five were female (age 22.40 ± 3.36 years; height 1.63 ± 7.40 m; body mass 60.94 ± 7.37 kg; training average 20 h/week; experience 7.40 ± 2.70 years of practice). The subjects had no neurological, muscular, or tendon injuries, and they were in excellent health.
2.1.1. Ethics approval of research
After receiving comprehensive information about the study's protocols, methodologies, advantages, and potential hazards, each participant signed a permission form indicating their agreement to participate in the research. The National Observatory of Sport's Ethical Committee authorized the trial, which was carried out in accordance with the Declaration of Helsinki (ONS/UR/18JS01).
2.2. Experimental design and procedures
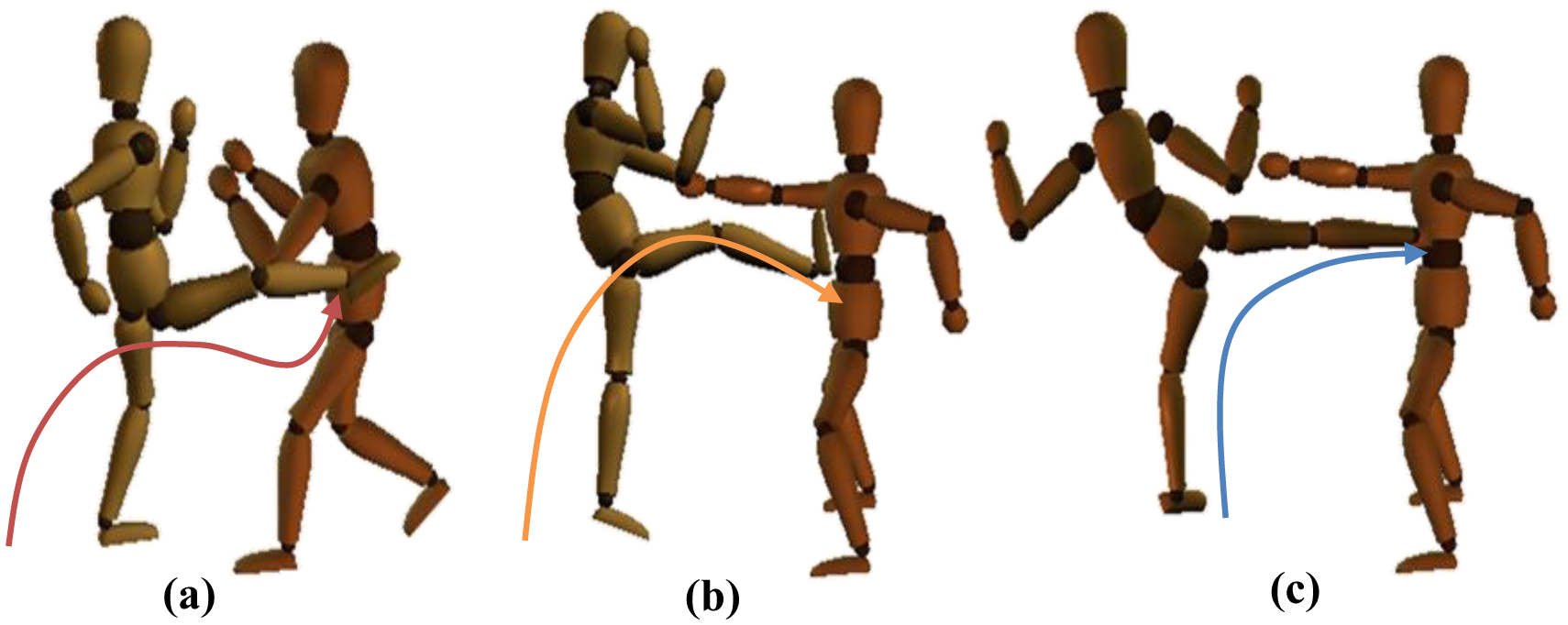
This is a 2D kinematic analysis of three types of Sanda foot strikes, namely the RK (Figure 1a), FK (Figure 1b), and SK (Figure 1c), to study the variation in strength, speed, and power indices when performed on a punching bag. The experimental session began with each participant doing a 10-minute warm-up that comprised lower-limb and trunk stretching exercises.
Before testing, participants were be familiarized with the equipment and the experimental protocol. Throughout the experiment, standardized instructions were delivered to the subjects, and verbal encouragement were provided to encourage them to achieve their best performances.
The participant placed themselves on the mat in front of the two cameras (e.g., one from the front and the other from the side 3m from the bag), carrying 20 low-mass retro-reflective markers stuck to their body. The dominant leg was tested at each test. The expert placed themself in front of a punching bag and performed each type of foot strike three times in a randomized manner (e.g., RK, FK, and SK) with a 30-second recovery between repetitions and two minutes between strike types for each session (e.g., 3 sessions, over 3 days from 2 PM to 4 PM) (Figure 2).
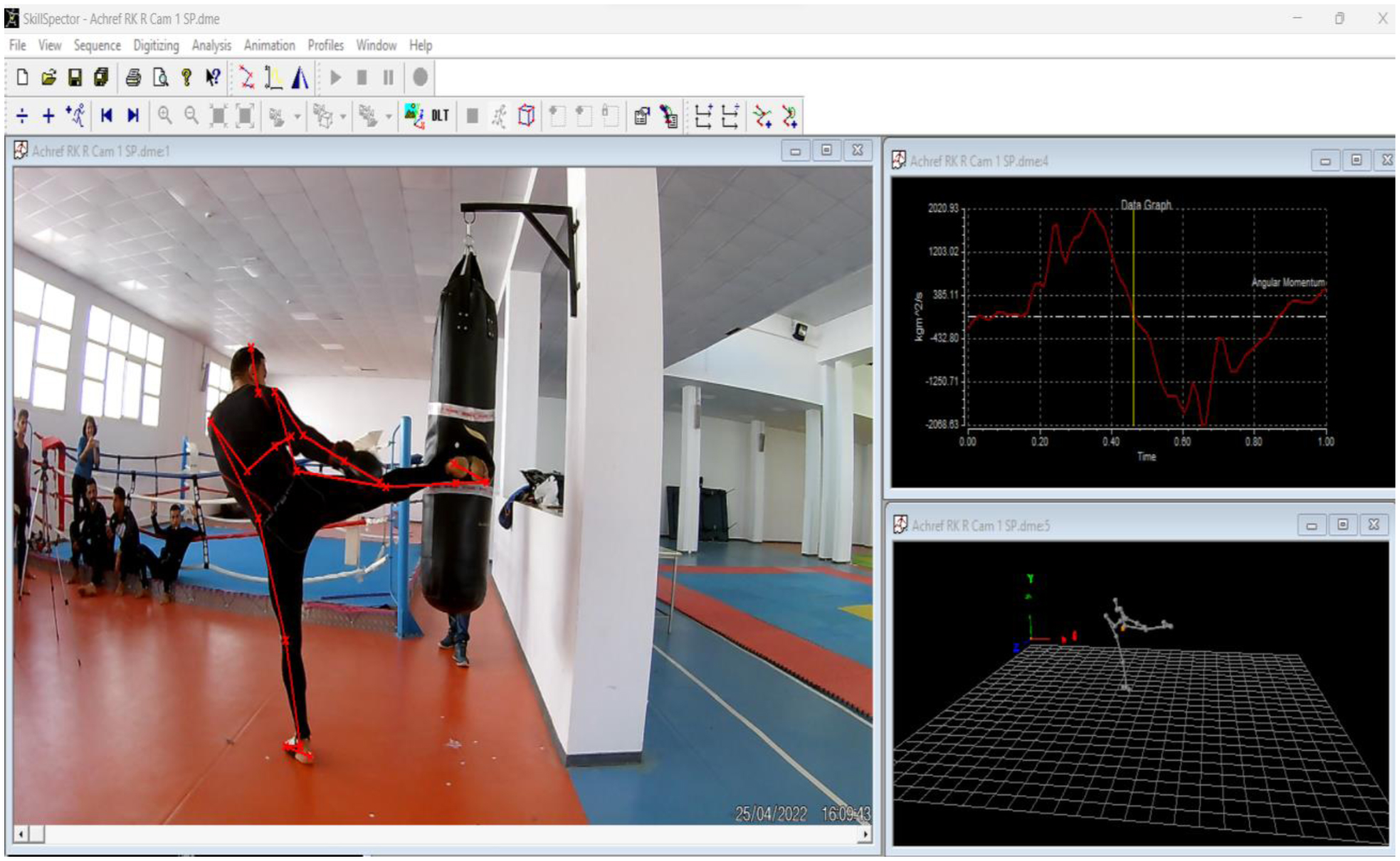
Before the test, each expert performed each kick three times on the punching bag, trying to calibrate their evolution to perform the kicks on a very specific point marked on the punching bag. The kinematic data were then captured using two cameras ACME Sports & Action Camera (VR301 4K; full HD; f / 2.2 lens; 120Hz). The video decoding will be done using the free software Virtual Dub version 1.10.4 [34]. Digitalization of data using free software SkillSpector® (Geeware, Version 1.3.2, Svendborg, Denmark. Copyright© 2007, [35]–[37]), (Figure 3).
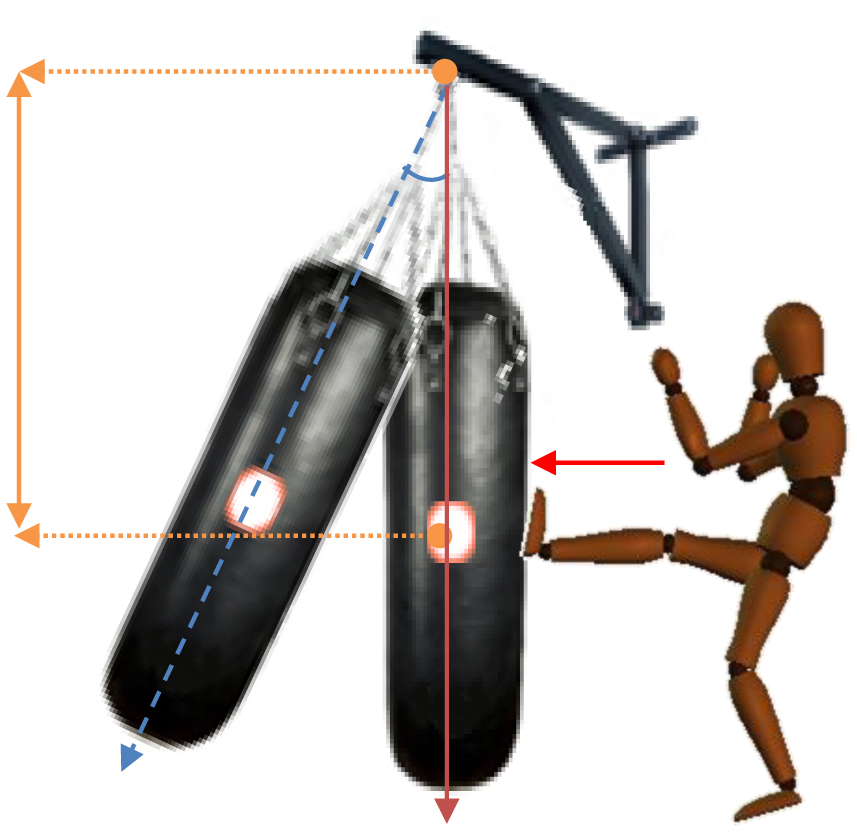
The biomechanical model adopted was Hanavan [38], as updated by de Leva [39]. This basic model consists of 20 points and 14 segments distributed throughout the body. Curious Labs, Inc. Poser® 4.0.3 created 3D Kinograms and constructions of important key positions. The calculation of force through inverse dynamics used the formula of Harnois and Lavoie [40] (equation 1a and 1b; Figure 4).
Where I is the inertia, F is the striking force, m is the mass of the punching bag, L is the length of the punching bag, d is the length between the hanging point and the centre of mass of the punching bag, θ is the rotating angle of the punching bag, T is the contact time with the punching bag, and t is the time of movement of the punching bag.
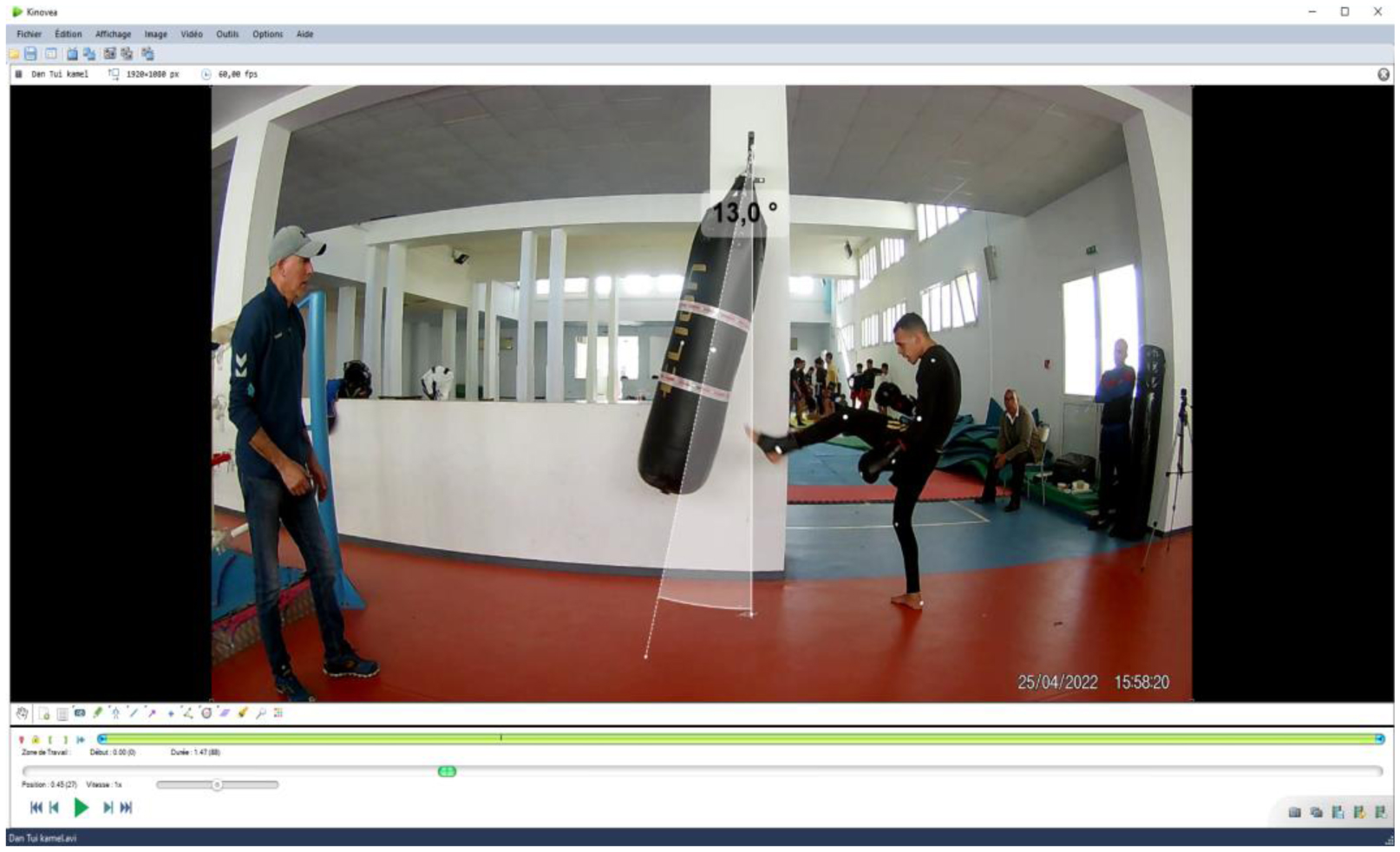
The calculation of the angle and the distance of the punching bag displacement was carried out by the free software Kinovea [version 0.8.15, Copyright© 2006–2011, [41] (Figure 5).
2.3. Statistical analysis
As part of the statistical study, the data analysis was carried out using the SPSS 25 package (SPSS, Chicago, IL, USA). Standard deviation (SD) and 95% confidence intervals (95% CI) are used to report data. G*POWER software was used to calculate effect size (d) (Faul et al., 2009). For the purpose of interpreting d, the following scale was employed: < 0.2 (trivial), 0.2–0.6 (small), 0.6–1.2 (moderate), 1.2–2.0 (large), and > 2.0 (very large) [42],[43]. To ensure that residuals (errors) are normally distributed, the Shapiro-Wilk test was conducted. Results indicated that all residuals were normally distributed. Therefore, repeated measures ANOVA was employed to examine the varied kicks in Sanda Wushu (i.e., RK, FK, and SK). The sphericity assumption was verified using Mauchly's test. The Greenhouse-Geisser correction was applied when sphericity was violated. Additionally, the data was visually checked for potential outliers using boxplots. Also, pairwise comparison was conducted using the Bonferroni test. Furthermore, the usual error of measurement (TEM), which is reported as the coefficient of variation (CV), and the intraclass correlation coefficient (ICC) were used to assess the absolute and relative reliability of kicking forces (i.e., in RK, FK, and SK). The smallest worthwhile change (SWC) was estimated by multiplying the between-subject SD by 0.2 (SWC0.2), showing the typical minor effect [42]. The test's ability to identify a change was classified as “good,” “OK,” or “marginal” depending on whether the TEM was below, similar to, or higher than SWC0.2, respectively [44]. The least detectable change (MDC95%), the 95% confidence interval for the difference in score between paired observations, was calculated as MDC95% = TEM 1.96 √ 2 [45]. In addition, to facilitate the estimation of the kicking force, estimated by inverse dynamics analysis, linear regression equations (i.e., stepwise regression) were derived to predict the kicking force through the kinetic measurement. The criterion of significance was fixed at p < 0.05.
3.
Results
The absolute and relative reliability of kicking force assessed using inverse dynamics for RK, FK, and SK were very high (Table 1).
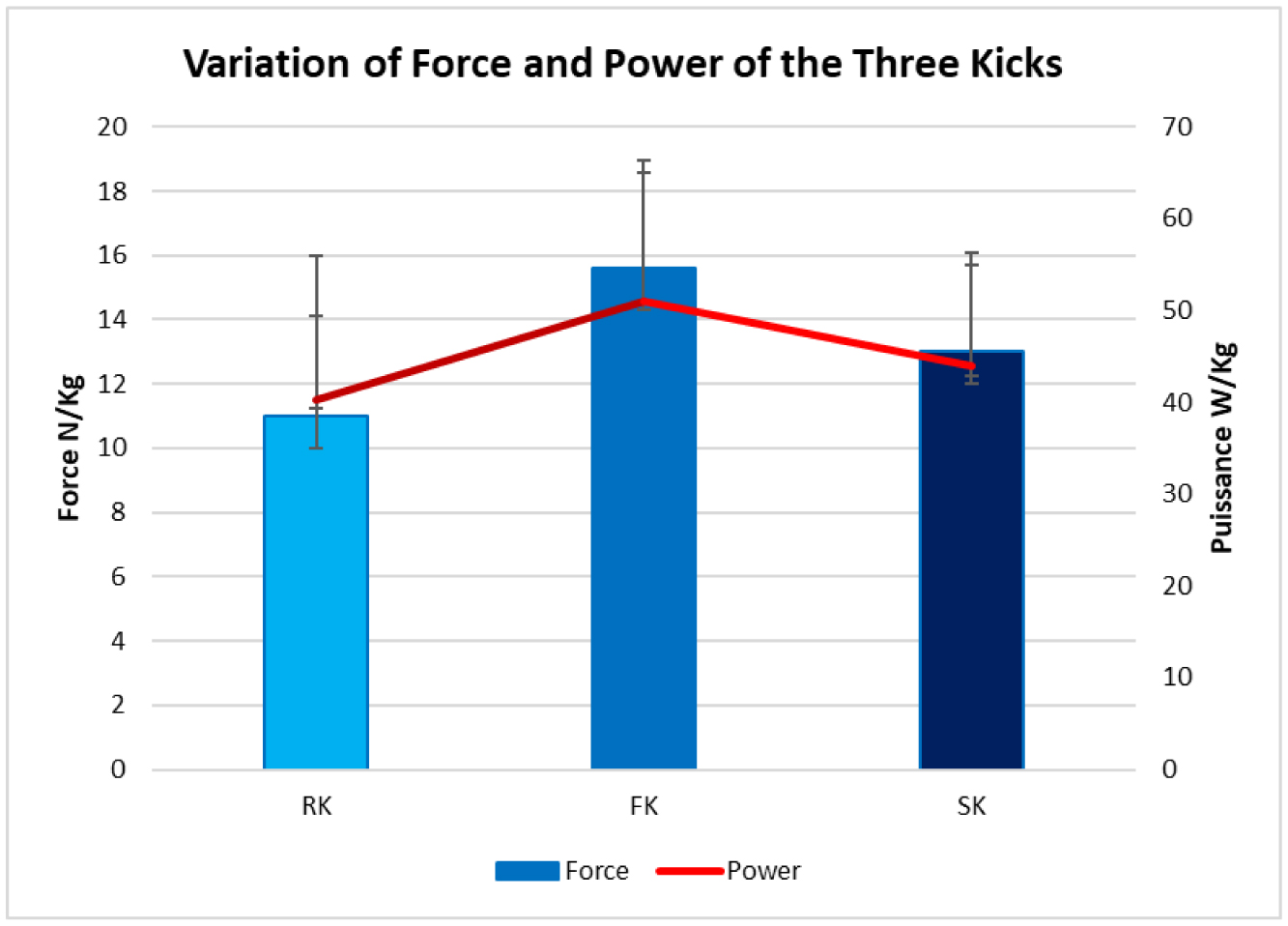
The outcomes of the repeated measures in Table 2 show that ANOVA demonstrated a significant difference in all kinetic parameters. Figure 6 provides a visual representation of the variation in power and force for the three kicking techniques. Table 3 presents the results of pairwise comparisons between the kicking techniques (i.e., RK, FK, and SK).
ANOVA testing showed that the sphericity is assumed for all variables and revealed significant differences in force, linear moment, and inertia (p < 0.001). Additionally, there was a significant difference in power (p < 0.01) and angular moment (p < 0.050). However, when comparing the kicking techniques pairwise, a highly significant difference was observed in force and inertia between the three kicks (RK vs. FK, RK vs. SK, and FK vs. SK). Regarding linear momentum, a significant difference was found between RK vs. FK and RK vs. SK. Lastly, a significant difference was shown in power and angular moment only between RK vs. FK.
Also, the results of the repeated measures ANOVA showed that the sphericity is assumed for most linear kinematic variables except vertical, horizontal, and total velocity of the toe, and horizontal velocity of the ankle. In these cases, Greenhouse-Geisser correction was used. In addition, ANOVA testing revealed significant differences in most linear kinematic parameters, except for execution time, COM horizontal velocity, ankle horizontal and total velocity, and hip vertical velocity (Table 4). Table 5 provides pairwise comparisons between the kicking techniques (i.e., RK, FK, and SK).
The tabulated data reveals notable variations in several variables, such as impact time (Imptime), COM displacement (dxCOM and dyCOM), COM velocity (VyCOM and VtCOM), toe velocity (VxTo, VyTo, VtTo), ankle velocity (VyAk) and acceleration (AxAk, AyAk, AtAk), knee velocity (VxKn, VyKn, VtKn), and hip velocity (VxHp, VtHp).
In the same way, repeated measures ANOVA results demonstrate that the sphericity is assumed for most angular kinematic variables except angular velocity of ankle, knee, hip, calf, and thigh. In these cases, the Greenhouse-Geisser correction was applied. Also, ANOVA testing showed significant differences in all angular kinematic parameters (refer to Table 6). A Bonferroni pairwise comparison between kicking techniques (i.e., RK, FK, and SK) is presented in Table 7.
The following is an explanation of angular kinematics parameters that show a highly significant difference for various joint angles and angular velocities. These parameters include the angle of knee (AngKn), hip (AngHp), calf (AngCf), thigh (AngTg), and angular velocity of the ankle (AngVAk), knee (AngVKn), hip (AngVHp), calf (AngVCf), thigh (AngVTg), and foot sole (AngVFs).
To facilitate the estimation of the kicking force, estimated by inverse dynamics analysis, linear regression equations (i.e., stepwise regression) were derived to predict the kicking force, through the kinetic variables, for the three Sanda Wushu kicks (i.e., RK, FK, and SK) (Equation 2a, 2b, and 2d).
4.
Discussion
The purpose of this study was to investigate the kinetic and kinematic parameters of three distinct Sanda kick methods (i.e., RK, FK and SK), which are referred to as Pian Tui, Dan Tui, and Ce Chuai Tui, respectively, in Wushu terminology. A total of 19 Sanda players (i.e., 14 males and 5 females) from Tunisia's senior national team participated in this study.
The main findings of this study indicated that the force measured via inverse dynamics was reproducible and reliable, independent of the kicking technique employed (i.e., RK, FK, or SK). The results clearly showed that the FK generated the highest absolute force compared to the other two techniques (i.e., RK and SK). Sanda athletes demonstrated an average force of 15.618 ± 3.337 N/kg for the FK, while the RK recorded 11.008 ± 3.106 N/kg, and the SK showed 13.021 ± 2.702 N/kg. Additionally, the FK demonstrated the highest peak power, achieving 51.030 ± 13.996 W/kg, while the RK and SK showed lower peak power values of 40.272 ± 15.613 W/kg and 43.899 ± 12.416 W/kg, respectively. The results demonstrate that the FK generated 42% more force than the RK (p < 0.01) and 20% more force than the SK, underscoring its superior power and effectiveness in Sanda kicking techniques.
These results align with those of VagnerCleatherOlah et al. [46] who showed that the FK impact force was significantly higher than the RK, reinforcing our findings. The FK produced 47% (p < 0.01), 92% (p < 0.01), and 120% (p < 0.01) more force in novice, sub-elite, and elite groups, respectively, indicating significant gains in impact force across skill levels in our research. These findings further support the concept that the FK is particularly effective at generating high-impact kicks.
Beyond technique, the effectiveness of the FK is not solely dependent on technique but also on the strength of specific muscle groups. According to VagnerCleatherKubový et al. [47] variations in static and dynamic strength of the lower extremity's external rotators influence kicking performance, with differences observed across experience levels. This highlights the importance of muscular conditioning and biomechanical optimization in mastering the FK, reinforcing the need for targeted training programs to enhance both velocity and overall striking efficiency.
On the other hand, there were not significant variations in the strength of the internal rotators, extensors, or hip flexors. The results suggest that the strength of the external rotators is the primary factor that determines the capacity to maintain hip speed and orientation during a powerful kick.
According to other studies [8],[48], the force produced during a kick may also be influenced by variables such the angular velocity of the knee and the isokinetic strength of the hip flexors and extensors . In order to optimize impact power from longer distances, combat athletes should concentrate on maximizing knee extension angular velocity during the precontact phase [34].
In addition, this study emphasizes the significance of LM, AM, and MI in understanding the biomechanics of kicking techniques in martial arts. Also, our analysis revealed significant variations in both linear and angular kinematics, highlighting their essential role in kick execution. The results indicated a highly significant variation in LM and MI (p < 0.001), as well as a significant variation in AM (p < 0.01). These results align with recent research by HarionoRahayu and Ndayisenga [49] who highlighted the importance of maintaining a slightly bent front knee. They noted that excessive knee flexion could compromise stability and increase body inertia, leading to decreased overall kicking efficiency.
Furthermore, the research of Wasik and Shan [50] indicated that the MI of the upper body plays a role in foot take-off, while the arms improve rotational force. The arms enhance movement during the sweeping motion by drawing the rebounding leg behind, consequently optimizing the technique's execution.
In a related study, Sidthilaw [51] demonstrated that the typical swinging angle for a kick ranges between 10° and 25°. Additionally, regardless of whether the bag was heavier or lighter, it generated sufficient acceleration to be accurately measured above background noise. Notably, the bag's weight also contributed significantly to MI, effectively simulating the response of a human body upon impact. Furthermore, he emphasized the crucial role of the arms movement in kick execution. To optimize the force generated by the kick, there must be a compensatory motion to counterbalance the AM produced by the rotating leg. This interplay between limb coordination and momentum regulation plays a pivotal role in enhancing kicking efficiency and overall striking performance.
In terms of linear kinematics including impact time, displacement, velocity, and acceleration, our study identified significant variations across these parameters. A comparison of the average velocity among the three kicking techniques revealed distinct differences in the kick velocity (i.e., SKs 3.835 ± 0.497 m/s, FKs 5.503 ± 0.906 m/s, and RKs at 7.042 ± 1.196 m/s). These findings indicate that the RK is the fastest among the three techniques, highlighting its classification as a high-velocity kick.
With regard to linear kinematics, the findings of VagnerCleatherOlah et al. [46], demonstrated that the maximum foot velocity of the RK was significantly higher than that of the FK, with a 44% increase (p < 0.01) in the sub-elite group and a 48% increase (p < 0.01) in the elite group. The authors suggest that the RK possesses an inherent capacity for rapid execution, aligning with FalcoLandeoMenescardi et al. [52] indicating that circular kicks generate greater foot velocity at impact than linear kicks due to the rotation of segments in different planes. From a tactical standpoint, increased kicking velocity offers a significant advantage, since it can interrupt the opponent's defensive reaction and improve striking effectiveness. Consequently, the velocity of execution serves as a key indicator of a kick's efficiency. This study explored this characteristic by examining three different kicking techniques and evaluating velocity variations across different joint actions. So, velocity is essential in the kicking techniques used in martial arts, with kinematics being a critical element in performance evaluation. The execution of an FK may vary depending on the practitioner's skill and tactical objectives. Previous investigations by Wąsik and Shan [50] have established that FK velocity is influenced by several biomechanical parameters, such as knee velocity, kick duration, and foot take-off time.
A higher maximal knee velocity is significantly correlated to higher FK velocity (r = 0.92). Furthermore, the total kick duration and foot take-off time demonstrate moderate correlations with FK velocity, with a correlation value of 0.73 and −0.61, respectively. The findings suggest that evaluating the kinematics of the ankle, knee, and hip can effectively evaluate performance levels. Notably, elite fighters typically exhibit greater peak knee angular velocity compared to their less experienced competitors. Our study determined that the mean maximum velocity of the FK was 5.503 ± 0.906 m/s. In comparison, research conducted by FeldMcNair and Wilk [53], on FK velocity among karate practitioners (without specifying the karate style) reported a velocity range of 9.9 to 14.4 m/s. These discrepancies suggest that kick velocity can vary significantly based on factors such as technical execution, training background, and biomechanical efficiency.
Considering the biomechanical characteristics of elite practitioners, VagnerCleatherKubový et al. [47] cautiously recommend aiming for a maximum hip velocity exceeding 2.2 m/s, which is substantially higher than the 1.04 m/s recorded in our study. This significant difference highlights how important it is to improve hip mechanics to improve kicking performance, especially in highly skilled athletes.
Regarding the velocity of the RK, numerous studies [46],[54],[55] have utilized a training shield as the target for measurement. In our study, the mean velocity of the RK was recorded at 7.042 ± 1.196 m/s. Comparatively, Hsieh Huaang and Huang [56] reported a maximum foot velocity ranging between 13.2 and 14.4 m/s. Similarly, research by Gavagan and Sayers [57] recorded a velocity of 14.66 m/s, while AandahlHeimburg and Tillaar [58] observed peak velocities reaching 17.35 m/s. These variations highlight the potential influence of measurement methods, training intensity, and biomechanical factors on RK execution speed across different studies. In the case of the SK, our study recorded a velocity of 3.835 ± 0.497 m/s. In contrast, research by FeldMcNair and Wilk [53] on karate athletes reported SK velocities ranging from 9.9–14.4 m/s. Similarly, a study by Pieter and Pieter [30], on elite American Taekwondo athletes found SK velocities between 5.20 and 6.87 m/s, with an average maximum velocity of 5.347 m/s. These findings highlight a notable disparity between the velocities achieved by Taekwondo and Karate practitioners. The differences may be attributed to variations in technical execution, training methodologies, and biomechanical strategies specific to each martial art. This suggests that the mechanics of the SK can vary significantly depending on the discipline, ultimately influencing its speed and effectiveness in combat scenarios.
In our study, the final ankle velocity during the execution of the RK was recorded at 3.6 ± 0.8 m/s. However, findings from Sidthilaw [51] indicate that impact velocity varies depending on the kicking height. Specifically, low-level kicks reached an impact velocity of 6.9 ± 0.8 m/s, mid-level kicks recorded 7.1 ± 1.1 m/s, and high-level kicks measured 6.8 ± 1.2 m/s. Additionally, the maximum ankle velocity was reported as 10.2 ± 0.5 m/s for low-level kicks, 10.3 ± 0.6 m/s for mid-level kicks, and 10.0 ± 0.8 m/s for high-level kicks. It is noteworthy that these values remain lower than the maximum foot velocity (11.0–11.3 m/s) recorded for three types of Taekwondo FKs in the study by Park [59]. These variations suggest that differences in kicking technique, biomechanics, and martial arts discipline may significantly influence velocity outputs at both the ankle and foot levels.
By our study, the analysis of knee velocity across the three kicking techniques revealed that the SK exhibited the highest velocity at 1.77 ± 0.6 m/s, closely followed by the FK at 1.67 ± 0.4 m/s. In contrast, the RK demonstrated the lowest knee velocity at 0.98 ± 0.4 m/s. These findings contrast with those of VagnerCleatherOlah et al. [46], who reported significantly higher knee velocities for the RK (6.73 ± 0.56 m/s) compared to the FK (5.32 ± 0.62 m/s) during middle-level kicks. This discrepancy may be attributed to differences in experimental protocols, participant skill levels, or methodological approaches.
In a related study, Siddhartha and Krishnendu [2] reported a knee velocity of 5.25 m/s for the SK at the medium level, while Wąsik [60] observed a knee velocity of 3.04 ± 0.79 m/s for the same technique. When compared to the findings of Vagner et al., these results suggest that the SK generally exhibits lower knee velocities, which contrasts with our observations. However, our analysis of hip velocity across the three kicks revealed that the FK achieved the highest velocity at 1.04 ± 0.2 m/s, followed by the SK (0.67 ± 0.2 m/s) and the RK (0.4 ± 0.2 m/s). These findings are consistent with those of VagnerCleatherOlah et al. [46] who also reported higher hip velocities for the FK (2.4 ± 0.49 m/s) compared to the RK (2.36 ± 0.31 m/s). This alignment underscores the importance of hip kinematics in differentiating the biomechanical profiles of these kicking techniques.
Another critical kinematic parameter is the impact time, defined as the duration of contact between the striking foot and the target. In our study, the shortest impact time was recorded for the RK at 0.07 ± 0.01 s, followed by the SK at 0.10 ± 0.02 s and the FK at 0.11 ± 0.02 s. These findings are consistent with previous research. For instance EstevanAlvarezFalco et al. [58] reported an impact time of 0.02 ± 0.0001 s for the RK, while VagnerCleatherKubový et al. [47] observed an impact time of 0.166 ± 0.063 s for the FK, further validating our results.
Additionally, angular velocity plays a pivotal role in determining the effectiveness of a kick. The speed of execution is a crucial factor, as it often exceeds the opponent's reaction time. Kicking speed is influenced by several variables, including acceleration, linear velocity, and the angular velocity of the hip and knee [61],[62], These factors collectively contribute to the overall efficiency and force generation of the kick.
In terms of maximum angular velocity, the RK exhibited the highest value for the knee at 40.14 rad/s, highlighting the critical role of knee movement and extension in generating speed and power during this technique. Conversely, the FK demonstrated a higher maximum angular velocity for hip extension (13.76 rad/s) compared to the RK. These findings align with the work of VagnerStastnyCleather et al. [8] who emphasized the significance of hip movement in executing the FK with both speed and efficiency. This suggests that hip kinematics significantly influence kicking speed and interaction forces, underscoring the need for sub-elite athletes to prioritize hip movement training to enhance performance.
Further supporting these observations, Sidthilaw [51], reported angular velocities (AngV) of 12.6 ± 3.9 rad/s, 11.8 ± 1.9 rad/s, and 12.1 ± 2.8 rad/s for low-, middle-, and high-level kicks, respectively. The angular velocity of the knee at impact was measured at 7.1 ± 1.5 rad/s, 7.7 ± 3.6 rad/s, and 9.5 ± 3.0 rad/s for the same kick levels. Additionally, VagnerCleatherKubový et al. [47] demonstrated that synchronizing hip acceleration with knee speed accounted for 59% of the variability in maximum force, leading to an increase in the knee's angular velocity. These findings collectively emphasize the interplay between hip and knee kinematics in optimizing kicking performance. The ankle angle is a critical factor influencing the effectiveness of a kick. In our study, the average ankle angle was measured at 133°. This finding aligns with Nakayama [63] who emphasized the importance of proper foot angulation for accurate technique execution and target impact, particularly involving the plantar region of the metatarsus phalangeal.
Similarly, PortelaBarbosaCavazzotto et al. [64], identified an optimal ankle angle of 130° approximately for efficient kicks, with non-impact kicks achieving satisfactory results at an average angle of 134°. It is important to note that the kinematic effects on the target may vary depending on the skill level of the athletes [65],[66]. Which is why our study focused exclusively on elite competitors.
Further analysis of existing literature suggests that athletes should prioritize increasing the speed at which the knee approaches the target to maximize foot velocity during kicks [61]. Additionally, research into optimal kicking mechanics such as the placement of the supporting leg, the flexion angles of the hip and knee, and the coordination of joint movements could provide valuable insights into enhancing foot speed and overall kicking performance.
The FK is typically executed with the rear leg from a guard stance. As described by Singh [67] the knee is lifted to form an angle of approximately 90° between the thigh and calf, a position referred to as the chamber. The leg is then extended to strike the target while maintaining the elevated knee position. Similarly, the SK is often performed with the rear leg, beginning with the knee raised to a 90° angle between the thigh and knee.
In contrast, Sidthilaw [51] demonstrated that during the RK, the angular velocities of the thigh and shank are positively correlated until the knee angle reaches 90°. Beyond this point, the angular velocity of the thigh decreases, while the shank's angular velocity continues to increase, reaching its maximum at the moment of foot contact with the target.
Even though the publications on kick biomechanics provide insightful information, it's critical to recognize the limitations of this research. In the first hand, the study's potential to have missed pertinent research due to certain criteria, such as linguistic restrictions or differences in nomenclature between FKs, RKs, and SKs, is one of its weaknesses. This could introduce bias and limit how far the results can be applied. Additionally, while front, side, and roundhouse kicks were the focus of this study, martial arts and combat sports employ a variety of kicks. It would be interesting to study/analyse and/or compare other kicking techniques in Sanda Wushu.
Nonetheless, although these kinematic variations are well documented, their exact impact on the efficacy and striking force of the FK remains largely unexplored. A further investigation is needed to determine how variations in kinematic parameters influence the general performance and tactical efficiency of the FK in combat situations.
On the other hand, this study conducted basic kinetic analyses; however, the exact mechanism linking muscle forces to kick forces is still not well understood. Future studies could enhance our understanding of this relationship through using musculoskeletal modeling, enabling a more thorough investigation of the biomechanical roles of individual muscles in kicking motions.
Additionally, the analysis system utilized in this study is semi-automatic. This approach provides valuable insights; however, future research may gain from the implementation of real-time analysis systems that incorporate force sensors. These systems would allow for a more accurate evaluation of muscle activation patterns and their direct influence on kick forces. Integrating real-time force measurements with musculoskeletal models allows researchers to more accurately characterize the coordination and efficiency of technical gestures.
To sum up, musculoskeletal modeling offers a valuable approach to understanding the complex interplay between muscle forces and kick dynamics. Integrating this method with real-time data collection could enhance future research, providing a deeper insight into the biomechanical and neuromuscular factors that affect kicking performance. This method will strengthen the evidence supporting training and performance optimization while also advancing our knowledge of kick biomechanics.
5.
Conclusions
In summary, this study provides valuable insights into the biomechanical differences between the FK, SK, and RK in terms of impact force, peak velocity, and maximum angular velocity. These findings enhance our understanding of the kinematic and kinetic factors that influence the efficiency and effectiveness of these techniques in Sanda.
The results and subsequent discussion highlight that the FK stands out as the most effective kick due to its optimal balance of force production and execution speed. By analyzing the kinematic and kinetic parameters of these techniques in elite athletes, we can better evaluate and refine technical movements in Sanda and other combat sports.
Key recommendations for training include focusing on knee speed during the FK and knee extension rate during the RK to minimize kick execution time. Additionally, athletes should prioritize performance-based exercises that enhance core stability and hip mobility, as these factors significantly contribute to increasing hip angular velocity and overall kicking performance.
A comprehensive analysis of the three kicking techniques suggests that evaluating movement patterns and employing time-motion analysis can lead to improved technical execution. Future research should explore additional parameters across various Sanda techniques to further identify factors that can optimize performance and inform evidence-based training strategies.
Use of AI tools declaration
The writers of this article affirm that they did not create it using artificial intelligence (AI) methods.









 DownLoad:
DownLoad: