|
[1]
|
Y. X. Bai, Research on ground collapse mechanism of shield tunnelling in saturated sandy pebble stratum and corresponding measures, Southwest Jiaotong University, 2012.
|
|
[2]
|
J. Z. Huang and G. Y. Xu, Study on the constitutive model of sandy pebble soil, Proceedings of China-Europe Conference on Geotechnical Engineering, Springer, Cham, (2018), 26–30.
|
|
[3]
|
J. Z. Huang, G. Y. Xu, Y. Wang, et al., Equivalent deformation modulus of sandy pebble soil-Mathematical derivation and numerical simulation. Math. Biosci. Eng., 16 (2019), 2756–2774.
|
|
[4]
|
M. Hu, Numerical method to study the physical and mechanical characteristics of sandy pebble soil and the response caused by shield tunneling, South China University of Technology, 2014.
|
|
[5]
|
C. He, Y. C. Jiang, Y. Fang, et al., Impact of shield tunneling on adjacent pile foundation in sandy cobble strata. Adv. Struct. Eng. 8 (2013), 1457–1467.
|
|
[6]
|
C. He, K. Feng and Y. Fang, Surface settlement caused by twin-parallel shield tunnelling in sandy cobble strata, J. Zhejiang Univ.-SCI A, 11 (2012), 858–869.
|
|
[7]
|
M. N. Wang, L. H. Wei, J. F. Lu, et al., Study of face stability of cobble-soil shield tunnelling at Chengdu metro, Rock Soil Mech., 1 (2011), 99–105.
|
|
[8]
|
C. L. Li, Method for calculating loosening earth pressure during construction of shield tunnels, Chin. J. Geotech. Eng., 9 (2014), 1714–1720.
|
|
[9]
|
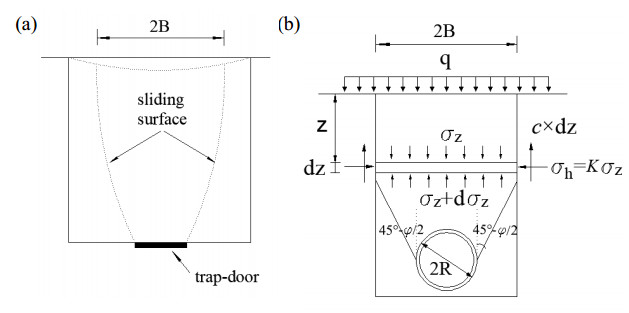
K. Terzaghi, Stress distribution in dry and in saturated sand above a yielding trap-door, Proceedings of First International Conference on Soil Mechanics and Foundation Engineering. Cambridge, Massachusetts, (1936), 307–311.
|
|
[10]
|
S. Z. Chen and C. X. Xu, Analysis and consideration of two ground pressure theories, Hydraulic Sci. Technol., 3 (2001), 22–24.
|
|
[11]
|
J. Wu, S. M. Liao and D. Zhang, Loosening zone and earth pressure around tunnels in sandy soils based on ellipsoid theory of particle flows, Chin. J. Geotech. Eng., 35 (2013), 714–721.
|
|
[12]
|
Q. M. Gong, R. L. Zhang, S. H. Zhou, et al., Method for calculating loosening earth pressure around tunnels based on ellipsoid theory of particle flows, Chin. J. Geotech. Eng., 39 (2017), 99–105.
|
|
[13]
|
R. L. Handy, The arch in soil arching. J. Geotech. Eng., 111 (1985), 302–317.
|
|
[14]
|
Y. R. Zheng and C. Y. Qiu, On the limitations of Protodyakonov's pressure arch theory, Mod. Tunnel Technol., 53 (2016), 1–8.
|
|
[15]
|
K. Terzaghi, Theoretical soil mechanics, New York: Wiley, 1943.
|
|
[16]
|
Y. C. Jiang, Y. Fang, C. He, et al., Study on delayed settlement formation induced by shield tunneling in sandy cobble strata, Chin. J. Undergr. Space Eng., 11 (2015), 171–177+265.
|
|
[17]
|
Y. C. Jiang, Study on the soil disturbance mechanism of shield tunnelling in sandy cobble stratum, Southwest Jiaotong University, 2014.
|
|
[18]
|
Y. X. Bai, T. Y. Qi, Y. D. Li, et al., Prediction for surface collapse deformation of shield construction based on LSSVM, Chin. J. Rock Mech. Eng., 32 (2013), 3666–3674.
|
|
[19]
|
J. Du, Z. R. Mei and Y. Z. Chen, Study of failure calculation of tunnel face based on drawing ellipsoid theory, Tunnel Constr., 38 (2018), 1497–1504.
|
|
[20]
|
B. H. Brady and E. T. Brown, Rock mechanics for underground mining, 3rd ed. New York: Kluwer Academic Publishers, (2005), 454–463.
|
|
[21]
|
B. H. Brady and E. T. Brown, Rock mechanics: for underground mining. Springer science & business media, 2013
|
|
[22]
|
J. P. Guo, D. Liu and R. F. Li, Reconstruction of moving transition equation for ellipsoid drawing theory, Met. Min., 10 (2015), 37–40.
|
|
[23]
|
R. Kvapil, Sublevel caving. SME mining engineering handbook, 2nd ed. New York: Soc. Min. Engrs., AIME, (1992), 1789–1814.
|
|
[24]
|
R. F. Li, Several main problems of ellipsoid drawing theory: The necessity of establishing quasi-ellipsoid drawing theory, China Molybdenum Industry, 5 (1994), 39–43.
|
|
[25]
|
J. P. Giroud, R. Bonaparte, J. F. Beech, et al., Design of soil layer-geosynthetic systems overlying voids, Geotext. Geomembr., 9 (1990), 11–50.
|
|
[26]
|
W. Zhu, X. C. Zhong and R. Jia, Simulation on relaxation effect of vertical earth pressure for shield tunnels by particle flow code, Chin. J. Geotech. Eng., 30 (2008), 750–754.
|
|
[27]
|
C. J. Lee, K. H. Chiang, C. M. Kuo, Ground movement and tunnel stability when tunneling in sand ground, J. Chin. Inst. Eng., 27 (2004), 1021–1032.
|
|
[28]
|
P. J. Lou and Y. Xu, Discussion on Method for calculating loosening earth pressure during construction of shield tunnels, Chin. J. Geotech. Eng., 37 (2015), 1353–1354.
|
|
[29]
|
C. L. Li, Reply to discussion on Method for calculating loosening earth pressure during construction of shield tunnels, Chin. J. Geotech. Eng., 37 (2015), 1355–1356.
|
|
[30]
|
A. Marston, The theory of external loads on closed conduits in the light of the latest experiments, Iowa: Iowa Engineering Experiment Station, 1930.
|
|
[31]
|
R. X. Chen, B. Zhu, Y. M. Chen, et al., Modified Terzaghi loozening earth pressure based on theory of main stress axes rotation, Rock Soil Mech., 31 (2010), 1402–1406.
|











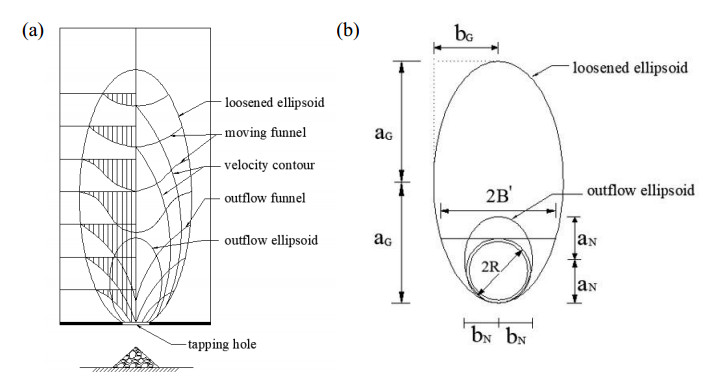
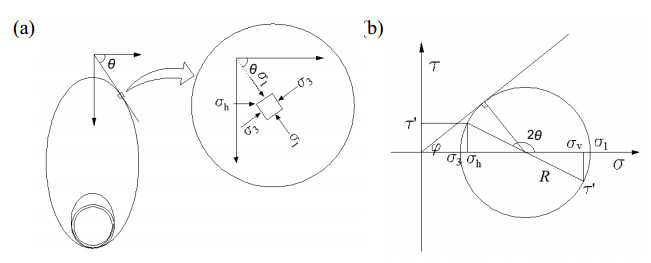
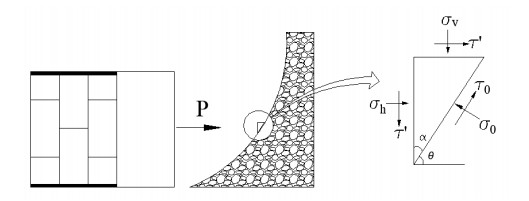
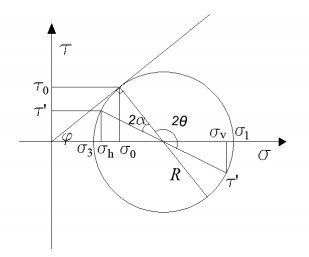


 DownLoad:
DownLoad: