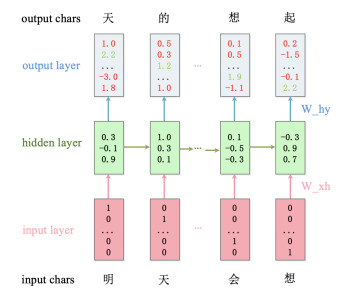
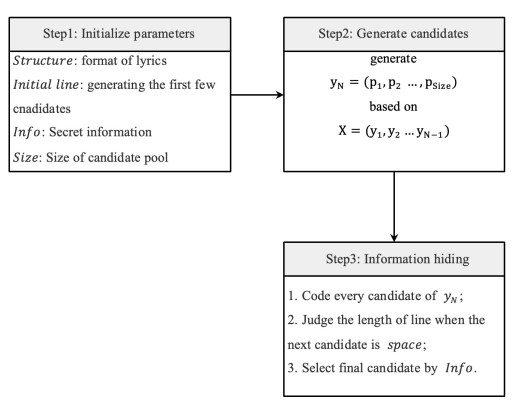
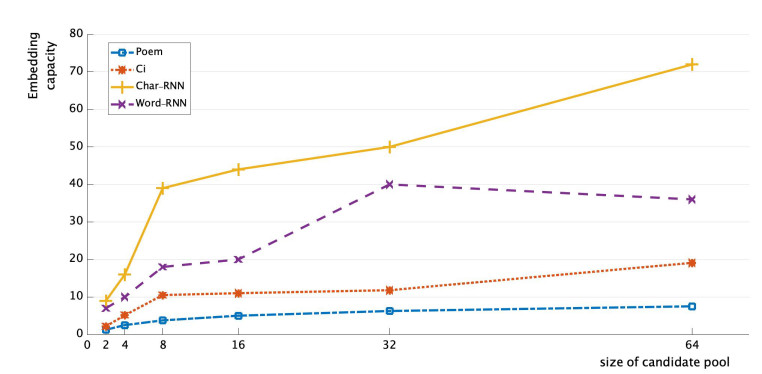We present a Recurrent Neural Network (RNN) Encoder-Decoder model to generate Chinese pop music lyrics to hide secret information. In particular, on a given initial line of a lyric, we use the LSTM model to generate the next Chinese character or word to form a new line. In so doing, we generate the entire lyric from what has been generated so far. Using common lyric formats and rhymes we extracted, we generate lyrics embedded with secret information to meet the visual and pronunciation requirements. We carry out experiments and theoretical analysis, and show that lyrics generated by our method offer higher embedding capacities for steganography, which also look more natural than the existing steganography methods based on text generations.
1.
Introduction
Predator-prey relationship exists throughout nature, for example, lions and gazelles, birds and insects, lynx and snowshoe hare, etc. In contrast with random diffusion, prey-taxis describes an active movement behavior of predators towards the zones of higher prey density, and is one of critical reasons why distribution of predators and prey in a region may display heterogeneity or aggregation. The first classical prey-taxis predator-prey model may be trace back to Kareiva and Odell [1] (cf. the Eqs (40), (51), (56), (57) therein) where on the population level they explored a predator-prey interaction between the ladybug beetle Coccinella septempunctata and the golden aphid Uroleucon nigrotuberculatum. This model is generally represented by
where u and w refer to population density of predators and prey respectively, d(w) is the predators' random motility function, χ(u,w) in the prey-taxis term −∇(uχ(u,w)∇w) measures sensitivity of the prey-taxis per unit strength of the gradient ∇w, and dw is random diffusion rate of the prey population. Interspecific and intraspecific interactions between the predators and prey are denoted by
More precisely, γuF(u,w) (resp. wf(w)) may characterize birth or arrival (immigration) of the predators (resp. of the prey), h(u) (resp. g(u,w)) refers to death or departure (emigration) of the predators (resp. of the prey). Thus one may take g(u,w)=uF(u,w) if the death or departures of prey is predominantly caused by predation. As summarized in the Eqs (1.4)–(1.7) of [2], there are numerous forms of functional response function F(u,w) such as Beddington-DeAngelis type (cf. [3,4]), prey dependent form, and ratio dependent forms (cf. [5]). Allee's effect and logistic growth rate function f(w) are frequently-used in the literature. Later we will specify some of them for our purpose.
As a model to account for evolution process of two species inhabiting an isolated environment (thus often coupled with zero-Neumann boundary condition), system (1.1) covers a considerable number of predator-prey relationships of direct prey-taxis effect. We below review several impressive results according to typical assumptions on χ(u,w) since these may greatly govern the existence of global solutions and dynamics behavior of the system.
On the one hand, when χ(u,w) is a constant small enough, Wu et al. [2] proved global existence and boundedness of solutions in Ω⊂Rn(n≥1) under some generic conditions on F,h and f. This smallness may be removed in some cases. To be precise, Jin and Wang [6] obtained the global boundedness and stability of the classical solution with respect to Rosenzweig–MacArthur (F of Holling II and f of logistic) type in Ω⊂R2; For ratio-dependent F and logistic f, Cai et al. [7] established the global existence as well as uniform-in-time boundedness of classical solutions in Ω⊂Rn(n≥1).
On the other hand, when χ(u,w) is density-dependent (i.e., non-constant) and χ(u,w)=χ(u) in particular, one inference is that there is a maximal density of the predators due to volume-filling effect or prevention of overcrowding (cf. [8]). This hypothesis indicates that there is a truncation on the prey-taxis sensitivity χ(u). With this view in mind, Ainseba et al. [9] obtained the existence of weak solutions by Schauder fixed-point theorem and its uniqueness via duality technique, in addition to attaining pattern formation; Tao [10] derived the existence of global-in-time classical solutions in Ω⊂Rn(1≤n≤3); He and Zheng [11] further obtained the global existence of solution with uniform-in-time bound; The existence of non-constant steady states was studied in [12,13] via bifurcation theory and index degree theory. Another viewpoint is that the truncation above may be removed when χ(u,w)=χ(w), partly because uniform-in-time boundedness of w is essentially ensured by the w-equation in Eq (1.1). For example, Jin and Wang [14] showed the global existence and uniqueness of bounded classical solution in Ω⊂R2 when 0≤χ(w)∈C2([0,+∞)).
Note that if there is no consideration of spatial diffusion and prey-taxis effect (i.e., dw=0,d(w)=0 and χ(u,w)=0), then studies on pure ODE systems of predator-prey relationship can be seen in [15,16,17,18,19] and the references therein.
Different from the aforementioned direct search for prey, some predators might start with perceiving chemical signals released by prey, for instance smell of blood or pheromone (trace pheromone, aggregation pheromone, etc.), and then hunt for the prey by tracking such signals, the process of which is called an indirect prey-taxis in this paper. Similar to a role of direct prey-taxis in promoting the heterogeneity of ecosystems, strong indirect prey-taxis may also cause spatial heterogeneity (cf. [20]) without considering predator's reproduction, mortality, and random diffusion of the prey. Later Tyutyunov et al. proposed another more general model (cf. [21]) which reads
where u=u(t,x) and w=w(t,x) represent population density of predators and prey at position x∈Ω⊂Rn(n≥1) and time t∈(0,+∞) severally; v=v(t,x) is concentration of chemicals released by prey which are secreted at a constant rate β>0, decay in a fixed rate σ>0, and diffuse with a constant diffusivity dv>0. The (−d(v)∇u+uχ(v)∇v) is called the predators' flux density, d(v) is the predators' random-motility function, and uχ(v)∇v means that predators move towards the increasing gradient of the chemical density at an average speed of χ(v)∇v with χ(v) measuring indirect prey-taxis sensitivity per unit strength of the gradient ∇v. In this way the advection term −∇⋅(uχ(v)∇v) is viewed as indirect prey-taxis effect of predators.
Some generic assumptions on d(v),χ(v),f(w) and F(w) can be summarized as follow. One may suppose that
so ∇⋅(d(v)∇u−χ(v)u∇v)=Δ(d(v)u) and then d′(v)<0 may indicate that predators will slow down their diffusion when encountering prey signals. This is the well-known "density-suppressed" effect and for further details we refer readers to [22,23,24,25,26] and the references therein. The per capita growth rate of prey population in absence of predators is denoted by f(w) which satisfies
and thus allows logistic type, i.e., f(w)=r(1−wK) with r,K>0. The prey-only dependent functional response function F(w) is often assumed to fulfill
which consequently incorporates:
System (1.2) may cover some reaction-diffusion systems used to describe the dynamics amongst the bacterial cell density, concentration of acyl-homoserine lactone, and nutrient density (cf. [22]). In addition, if χ(v)=0 and dv and dw are density-dependent as well, then Eq (1.2) can be used to describe the interactions among uninfected cells, free viruses produced by infected cells, and infected cells (cf. [27]). In this paper we will understand it in the view of indirect predator-prey relationship. Firstly, when χ(v) and d(v) are supposed to be constants and Ω⊂R1, Tyutyunov et al. [21] studied pattern formation condition on stationary states of Eq (1.2) with zero-Neumann boundary condition. Their numerical analysis illustrated that non-trivial homogeneous stationary state of the model becomes unstable with respect to small perturbation caused by increasing prey-taxis strength; Zuo and Song [28] obtained some interesting dynamical behaviors including stability and double-Hopf bifurcation results; Secondly, if χ(v) and d(v) are constants and Ω⊂Rn(n≥1), Yoon and Ahn [29] derived the unique global-in-time classical solution to the system (1.2) with functional response functions involving Beddington-DeAngelis type, and showed asymptotic stability of both prey-only and coexistence steady states. They found that prey-taxis is an essential factor in generating patterns. Thirdly, when d(v) is a positive constant but χ(v) is density dependent, Wang and Wang [30] investigated global existence and boundedness of the unique classical solution as well as the asymptotic stabilities of nonnegative and spatial homogeneous equilibria as Ω⊂Rn(n≥1).
In this fashion a question arises: what will happen if both χ(v) and d(v) are density-dependent? Correlative conclusions remain unknown, to the best of our knowledge. This motivates us in this paper to focus on
where Ω⊂Rn(n≥1) is a bounded domain with smooth boundary ∂Ω, →n is the unit outer normal vector towards ∂Ω, ℓ≥0, and dw,γ,θ>0.
Motivated by the above discussion, we have studied in this work the global existence of classical solution of Eq (1.4) and its global asymptotical stability. Before specifying our main results, several notations need to be explained. Let X be a metric space. We denote by Cm+1−(X) the set of functions with their k-times (0≤k≤m,k,m∈N) derivatives being Lipschitz continuous in X. Note that the k-times derivatives are Lipschitz continuous if (k+1)-times derivatives are bounded in X.
To ensure the existence of solutions to Eqs (1.2) and (1.4), the real-valued functions d(v),χ(v),f(w), and F(w) should satisfy that
(H1) d(v),χ(v)∈C1+1−([0,+∞)) and for v∈[0,+∞), χ(v)≥0, d(v)>0 and d′(v)≤0;
(H2) f∈C1+1−([0,+∞)) and there exists a constant K>0 such that f(K)=0 and f(w)<0 for all w>K and f(w)>0 for w∈(0,K);
(H3) F(w)∈C1+1−([0,+∞)) and there is a constant CF>0 such that 0≤F(w)≤CF|w|. Moreover, F′(w)>0 for all w∈[0,+∞).
Thus (H2) allows logistic f(w) and all F(w) in Eq (1.3) support (H3).
2.
Main results
Note that our results are applicable to Eq (1.2) since system (1.4) can reduce to Eq (1.2) when ℓ=0. We first derive the existence of global-in-time classical solution to Eq (1.4).
Theorem 2.1. Let Ω⊂Rn(n≥1) be a bounded domain with smooth boundary ∂Ω. Under the hypotheses (H1)–(H3), if (u0,v0,w0)∈C2(¯Ω,R3) with u0,v0,w0≥0(≢0) and fulfills 0-order compatibility condition (i.e. ∇u0|∂Ω=∇v0|∂Ω=∇w0|∂Ω=0), then the problem Eq (1.4) has a unique nonnegative (resp. positive) classical solution on [0,∞) (resp. on (0,∞)) satisfying
Furthermore, there is an constant C>0 independent of t such that
where 0<w(t,x)≤max{K,‖w0‖L∞(Ω)} for all (t,x)∈(0,+∞)×Ω.
We next investigate the asymptotic behaviors of such a classical solution. Suppose that Eq (1.4) has a constant steady state denoted by (uc,vc,wc), then
If in addition each component of (uc,vc,wc) is nonnegative, three possible constant steady states may be formulated as follow:
● extinction state: if uc=0 and wc=0 then (uc,vc,wc)=(0,0,0);
● exclusion (prey-only) state: if uc=0 but wc>0 then wc=K and (uc,vc,wc)=(0,βKσ,K);
● coexistence state: uc,wc>0 thus vc=βwcσ>0,uc=wcf(wc)F(wc) and γF(wc)=θ+ℓuc. Denote by (u∗,v∗,w∗) this positive constant solution.
To construct appropriate Lyapunov functions we desire, we have to impose that
(H4) for any w∈[0,+∞), φ(w):=wf(w)F(w) is continuously differentiable, φ′(w)<0 and 0<φ(0)=limw→0+φ(w) exists.
This is not very stringent and can be achieved if f(w)=r(1−wK) and F(w) is Holling type I or II with 0<K≤c in Eq (1.3).
After these preparations, we can formulate our second result as below.
Theorem 2.2. Suppose that (u,v,w) is a global classical solution to the system (1.4) fulfilling (H1)–(H4). Let K be defined in (H2).
1) If γF(K)≤θ, then the prey-only state (0,βKσ,K) exists and is globally asymptotic stable. Furthermore, if γF(K)<θ, there are constants ˆc1,ˆc2,T0>0 such that
2) If the coexistence steady state (u∗,v∗,w∗) exists and
with K2 from Remark 3.2 and C1:=max{K,‖w0‖L∞(Ω)}, then (u∗,v∗,w∗) is globally asymptotic stable. Moreover, there are constants ˉc1,ˉc2,T1>0 such that
Note that there is no γF(K)>θ (biologically interpreted as "strong predation") assumed in 2) of Theorem 2.2 since it has been ensured by the existence of the coexistence steady state along with (H2) and (H3). In fact, (H2) and (H3) imply 0<w∗<K and then γF(K)>γF(w∗)=θ+ℓu∗≥θ by F′(w)>0 in (H3). Also, Eq (2.4) might be simplified by specific f and F, for example:
Corollary 2.3. If f(w)=r(1−wK) and F(w)=wc+w with 0<K<c then the coexistence steady state exits and Eq (2.4) becomes
with K2 from Remark 3.2. Then the asymptotic stability above-mentioned remains unchanged.
The content of this paper is organized as follows. We shall prove the global existence of the classical solution to system (1.4) in Section 3. For this classical solution, we will show in Section 4 its global asymptotic stability associated with two constant steady states. Finally in Section 5 we intend to derive linear instability criterion of the steady states and to do some numerical simulations from which one may see how density-dependent prey-taxis and predators' diffusion can influence on resulting patterns.
3.
Global existence of the classical solution
We shall apply the celebrated results developed by H. Amann [31,32] to derive local and global existence of classical solution to Eq (1.4). The conclusions and proofs can be applied to Eq (1.2) after slight modifications.
3.1. Local existence
Lemma 3.1 (Local existence and uniqueness). Let Ω⊂Rn(n≥1) be a bounded open domain. If (H1)–(H3) hold, (u0,v0,w0)∈C2(Ω,R3) with u0,v0,w0≥0(≢0), then there exists Tmax∈(0,+∞] depending on (u0,v0,w0) such that the problem Eq (1.4) has a unique nonnegative (resp. positive) classical solution on [0,Tmax) (resp. (0,Tmax)) satisfying
Proof. Note that we first strengthen the conditions in (H1)−(H3) by replacing the interval [0,+∞) with R. Finally we will see the obtained results still make sense without this enhancement. For clarity, we reformulate Eq (1.4) as
where for x∈Ω and t≥0, w=(u,v,w)τ and w0=(u0,v0,w0)τ∈R3 (τ denoting transposition) are two vector-valued functions, ∇w=(∇u,∇v,∇w)τ,
It is easy to see that d(v)>0 for v∈R by (H1). Then along with dv,dw>0, all ordering principal minor determinants of A(x) are positive, which implies that A(x) is positively definite for all x∈R3. Thus we know for all t>0,x∈Ω, wt−∇⋅(A(w)∇w) is Petrowskii parabolic (cf. Eq (50) in [33]) and ∇⋅(A(w)∇w) is normally elliptic (cf. p.16 or Theorem 4.4 in [31]) with separated divergence form. Moreover, ∇⋅(A(w)∇w) coupled with the boundary condition in Eq (3.2) is normally elliptic as well.
By (H1) all elements of A(x) are in C1+1−(R) (functions and their first derivatives being Lipschitz continuous on R). Similarly the regularity conditions in (H2) and (H3) show every component of Ψ(w) is C1+1−(R3). In terms of Theorem 7.3-(ii), Theorem 9.2, and Corollary 9.3 of H. Amann [31], we know that given w0∈W2p(Ω,R3) with p>n and p≥2, there exist a Tmax∈(0,+∞] relating to w0 and 0<2ϵ<min{2−n/p,1} such that Eq (1.4) has a unique (cf. the Corollary 9.3) maximal classical solution on [0,Tmax)×Ω satisfying
for every compact subinterval J′ of (0,Tmax), where B(X,Y) (resp. Cm(X,Y)) denotes the set of all bounded mappings (resp. all m-th continuously differentiable functions) from X to Y, and Cm+ι(X,Y) is the set of all mappings from X to Y which up to their m-th derivatives are ι- Hölder continuous on X with ι∈(0,1) and m∈N. Moreover, if w0∈C2(Ω,R3), then by Theorem 1 of [32] we know that the Eq (3.2) has a unique maximal classical solution
As a result, Eq (3.3) implies Eq (3.1).
Then we may find this unique local classical solution is nonnegative on [0,Tmax). Indeed, we may first rewrite the u-equation in Eq (1.4) as
By the regularity Eq (3.3), v,w in u-equation can be treated as known functions at present. Then within any [0,T]⊂[0,Tmax) one can apply comparison principle of linear parabolic equations to such a equation coupled with ∇u⋅→n=0 and u0(x)≥0(≢0). Thus we derive u≥0 in [0,Tmax)×Ω and u>0 in (0,Tmax)×Ω. Similarly, one may acquire that v,w>0 in (0,Tmax)×Ω, and v,w≥0 in [0,Tmax)×Ω. Therefore, R in (H1)−(H3) as supposed at the very beginning of this proof can be replaced by [0,+∞). This completes the proof.
By Theorem 1 of [32], it suffices to verify that ‖(u,v,w)(t,⋅)‖Hsp(Ω)≤C(T)<+∞ for any t∈(0,T)⊂(0,Tmax), p>n and p≥2 as well as some s satisfying 1<s<min{1+1p,2−np}, in order to extend such a local unique classical solution to a global one. To make this extendability criteria easier to verify (i.e., to weaken this Hsp-topology, the Bessel potential space), we resort to Theorem 5.2 of [32] at the cost of imposing an extra condition on the initial value. This can be formulated in the following lemma.
Lemma 3.2. Suppose that (u0,v0,w0)∈C2(¯Ω,R3) additionally fulfills 0-order compatibility condition (i.e., ∇u0|∂Ω=∇v0|∂Ω=∇w0|∂Ω=0). Then the above local classical solution is global if
3.2. L∞ estimate on w(t,x),v(t,x) and u(t,x)
Lemma 3.3. Under the conditions in Lemma 3.1, it holds that
where K is from (H2) and is independent of Tmax.
Proof. One may use comparison principle to prove this result and more details can be seen in Lemma 2.2 of [6].
Remark 3.1. Under the conditions in Lemma 3.1, if (u,v,w) is a nonnegative classical solution to Eq (1.4) on (0,Tmax)×Ω, then
where C is a positive constant and independent of Tmax.
It is easy to see that the solution to v-equation of Eq (1.4) can be formally expressed via heat semigroup theory with zero-Neumann boundary condition. Precisely, the estimation on v(t,x) follows from Lemma 1 of Kowalczyk and Szymańska [34] as below.
Lemma 3.4. Assume that Ω⊂Rn(n≥1), v0(x)∈W1∞(Ω) and
Then for every t∈(0,Tmax), the classical solution v(t,x) of the v-equation in Eq (1.4) satisfies
Here C and C are positive constants and independent of Tmax.
In conjunction with Lemma 3.3 we thus have the following W1∞ estimate on v(t,x).
Remark 3.2. There exists a constant K2>0 independent of Tmax such that if v0∈W1∞(Ω), then ‖v(t,⋅)‖W1∞(Ω)≤K2 for all t∈(0,Tmax).
The next lemma is to show L∞ estimate on u(t,x).
Lemma 3.5. Let (H1)–(H3) hold. Suppose that (u,v,w) is the solution of Eq (1.4) obtained in Lemma 3.1. Then there exists a positive constant ˜C independent of Tmax such that
Proof. Here we adopt Moser's iteration method. Indeed, we assume t∈(0,T)⊂(0,Tmax) with 0<T<Tmax. Multiplying the first equation in Eq (1.4) by up−1(p≥1) and integrating the result with respect to x in Ω may yield
Lemma 3.1 shows u(t,x),v(t,x),w(t,x)>0 for all (t,x)∈(0,Tmax)×Ω. In addition, Remark 3.2 concludes that ‖∇v‖L∞(Ω)≤‖v(t,⋅)‖W1∞(Ω)≤K2 (independent of Tmax). Thus (H1) implies d(v)≥d(K2)=:c0 and |χ(v)|≤max0<v≤K2χ(v)=:c1. By 0≤F(w)≤CFw in (H3) we then may obtain
Applying Cauchy's inequality to the first term may lead us to
Hence
Below by setting p≥2 and due to up−2|∇u|2=|up2−1∇u|2=|2p∇up2|2=4p2|∇up2|2, we have
with C1=max{K,‖w0‖L∞(Ω)}. So it remains to consider: (I) θ−CFC1γ>0 and (II) θ−CFC1γ≤0. For the case (I), one may have
and for the case (II),
To conduct Moser's iteration, we use Gagliardo-Nirenberg interpolation to decompose the right-hand ∫Ωup into ∫Ω|up2| and ∫Ω|∇up2|2 so that the latter one can be cancelled if its coefficient is set appropriately.
Indeed, by Gagliardo-Nirenberg interpolation inequality and Young's inequality with parameter η>0 and with index 1α and 11−α one may have
with α=1q−121n+1q−12∈(0,1) as 1≤q<2. Then associated with Eq (3.5), by taking q=s=1 in Eq (3.7) we may infer that α=12n+1, α1−α=n2, and
where we have taken η=2c20p2c2(c1K2)2 and c4=(c3+c2(c1K2√c2)n(√2c0)n)⋅(c1K2)22c0. Therefore, we derive
In regard to Eq (3.6), taking q=s=1 in Eq (3.7) again will produce that
where we have set η=(p−1)c0p2c2(CFC1γ+θ) and c5=(c3+(c2√CFC1γ+θ)n(√c0)n)⋅(CFC1γ+θ). Hence Eqs (3.8) and (3.9) jointly show that
with c6=c4+c5.
To sum up, by letting κ:=θ−CFC1γ>0 in case (I) or κ:=θ>0 in case (II), there is a constant c7:=max{c4,c6} which is independent of p, such that
on (0,T)⊂(0,Tmax). Notice that the rightmost term above is unrelated to time variable t. Then solving this inequality with respect to t on (0,T)⊂(0,Tmax) gives
This indicates
with ˜F(p):=max{‖u0‖L∞(Ω),supt∈[0,T)(∫Ωup(t,x)dx)1p}. Denoting c8=|Ω|+c7κ+1 and setting p=2i,i=1,2,3,⋯, then we have
and ˜F(1)={‖u0‖L∞(Ω),supt∈[0,T)∫Ωu(t,x)dx}≤{‖u0‖L∞(Ω),C} where C is from Eq (3.4) and thus is independent of i,Tmax and T. Finally, letting i→+∞ concludes that for all t∈(0,T)⊂(0,Tmax),
Hence such an estimate holds for all t∈(0,Tmax) due to T arbitrarily in (0,Tmax). This completes the proof.
Remark 3.3. By rewriting the third component in Eq (1.4) as
with R=w+wf(w)−uF(w), then one may apply Lemma 3.4 to this equation after a rescaling. Since in view of Lemma 3.3 and Lemma 3.5, one may infer that
with constants C,C independent of Tmax. It follows that
if w0(x)∈W1∞(Ω) where constant C is independent of Tmax.
This remark is useful to prove asymptotic stability in the next section.
3.3. Proof of Theorem 2.1
Proof. Lemma 3.1 has shown the existence of local unique classical solution to Eq (1.4). The extendability standard of such a classical solution in Lemma 3.2 can be satisfied by Lemma 3.3, Lemma 3.5, and Remark 3.2. So one can obtain the global existence of unique classical solution to Eq (1.4), and the regularity Eq (2.1). Finally the estimate Eq (2.2) holds for all t>0 by Remark 3.2, Lemma 3.5 and Remark 3.3.
4.
Global asymptotic stability
In the last section we have proved that system (1.4) possesses a unique global-in-time classical solution under (H1)–(H3). In this section we concentrate on its longtime behaviors if (H4) holds in addition. To this end, we introduce the following two basic lemmas.
Lemma 4.1. If F fulfills condition (H3), then a function
is nonnegative and convex. Furthermore, if z→κ then
This lemma can be proved by doing Talyor's expansion of ζ(z) with respect to z up to its second order derivative at z=κ (ζ(κ)=ζ′(κ)=0). One may refer to Lemma 4.1 in [6] for more details.
We below summarize limit property of a dynamic system (cf. Chap.4 in [35]) that we will use later. Given a dynamic system (nonlinear semigroup) {S(t):t≥0} on a complete metric space (M,‖⋅‖). Then for a real-valued continuous function L(x), x∈M, we say L(x) is a Lyapunov function of this dynamic system if for all t≥0,x∈M and δ∈R,
For any x∈M, Γ(x):={S(t)x:t≥0} denotes the trajectory through x. In particular, we call x is an equilibrium point of the dynamic system if Γ(x)={x}.
Lemma 4.2. Let E:={x∈M:dL(S(t)x)dt=0}. Denote by Z:={x∈E:S(t)x∈Efor allt≥0} the largest invariant subset of E. For some x0∈M, if the trajectory Γ(x0)={S(t)x0:t≥0} is contained in a compact set of M, then there are two properties for the ω-limit set Vω(x0) of Γ(x0) (or x0) as:
(i) Vω(x0)⊂Z;
(ii) S(t)x0→Z as t→∞,
where Vω(x0):={limk→+∞S(tk)x0∈M:∃tk>0,limk→+∞tk=+∞}=⋂τ≥0¯{S(t)x0:t≥τ}.
Additionally if all y∈E are equilibria and all elements of E are isolated from each other, then Vω(x0) consists of equilibria and contains only one element.
Lemma 4.1 may help us to construct Lyapunov functions we need. Lemma 4.2 indicates that one may apply Lemma 4.2 to corresponding Lyapunov functions, in order to investigate the global asymptotic stability of the prey–only state (0,βKσ,K) and the coexistence state (u∗,v∗,w∗). Indeed, Theorem 2.1 means that system (1.4) has the unique global-in-time classical solution (u,v,w)∈C2(¯Ω,R3) which is continuous to its initial value (u0,v0,w0)=:u0(x)∈C2(¯Ω,R3). This indicates that system (1.4) can generate a dynamic system on C2(¯Ω,R3), still denoted by {S(t):t≥0}, such that S(t)u0:=u(t,x;u0(x)):=(u(t,x;u0(x)),v(t,x;v0(x)),w(t,x;w0(x)))∈C2(¯Ω,R3), and S(0) is an identity, i.e., S(0)u0(x)=u0(x) for any u0(x)∈C2(¯Ω,R3). Then {S(t)u0:t≥0} is a trajectory through u0(x) which can be contained in a compact subset of C2(¯Ω,R3) by Eq (2.2) and one estimation similar to the Eqs (46) and (48) in Theorem 4.1 of [36]. The (0,βKσ,K) and (u∗,v∗,w∗) can be viewed as two equilibria of this dynamic system.
In addition, (H2) and (H4) indicate that F′(w)>0 and −φ′(w)>0 are continuous on [0,C] for any C>0. Thus
exists and is strictly positive.
With these preparations at hand, we below prove 1) of the Theorem 2.2.
4.1. Asymptotical stability of prey-only steady state
Lemma 4.3. Let (H1)−(H4) hold and (u,v,w) be a globally classical solution of Eq (1.4) obtained in Theorem 2.1. Then the prey–only state (0,βKσ,K) is globally asymptotic stable provided that F(K)≤θγ. Furthermore, if F(K)<θγ, there are constants ˉc1,ˉc2,T0>0 such that for t>T0>0
Proof. We may construct a function for t>0 that
where (u,v,w) is the classical solution to Eq (1.4) and the constant M>0 is to be determined after Eq (4.5).
Next we show that L1 is a Lyapunov function, i.e., dL1dt≤0 for all (u,v,w) solving Eq (1.4). Indeed, under the zero-Neumann boundary condition in Eq (1.4), one has
Moreover,
and from f(K)=0 in (H2) we may derive that
where φ(w)=wf(w)F(w), wi is between w and K, i=1,2, in addition to
On the other hand, by βwc=σvc and wc=K, one may infer that
and using the Young's inequality with ε will yield
for any ε>0,Mβ>0.
Then by using the assumption F(K)≤θγ, setting 0<ε≤2σβ, and by invoking the estimates from Eqs (4.3) and (4.4) one may update Eq (4.3) that
In light of Lemma 3.3 we know 0<w1,w2≤C1 with C1=max{K,‖w0‖L∞(Ω)}. Hence making use of Eq (4.2) and taking
will conclude that dL1dt≤0.
For each t>0, we let
Here H1(u,v,w):=uγ+M2(v−βKσ)2+ζ(w) is a convex function of (u,v,w) in view of Lemma 4.1 with κ=K. H1(u,v,w) has no more than one minimum point, so does L1(t) in the sense of (u, v, w). The equation \frac{\mathrm{d}\mathcal{L}_{1}(t)}{\mathrm{d}t} = 0 thus has at most one solution in the sense of (u, v, w) , which implies that \frac{\mathrm{d}\mathcal{L}_{1}(t)}{\mathrm{d}t} = 0 if and only if (u, v, w) = (0, \frac{\beta K}{\sigma}, K). Then Lemma 4.2 concludes that the solution of Eq (1.4) which is bounded will approach (0, \frac{\beta K}{\sigma}, K) as t\rightarrow \infty. In other words, (0, \frac{\beta K}{\sigma}, K) is globally asymptotic stable.
We can further ascertain the corresponding convergent rate. Due to F(K) < \frac{\theta}{\gamma} , the first inequality in Eq (4.5), and Lemma 4.1, there exists a constant \hat{c}_1 > 0 such that
Solving this inequality shows
where the constant \hat{c}_2 > 0 depends only on \mathcal{L}_{1}(0). Lemma 4.1 also signifies that there is a T_1 > 0 such that
which means
with \hat{c}_3 = 3\max\big\{\hat{c}_2\gamma, \, \, \big(\frac{2\hat{c}_2}{M})^{1/2}, \, \, \big(\frac{4F(K)\hat{c}_2}{F'(K)}\big)^{1/2}\big\}.
We next may strengthen this convergence rate. Since (u, v, w) is a classical solution to Eq (1.4), then by Eq (2.2) there exists a constant \hat{c}_4 > 0 such that \| u\|_{L_{\infty}(\Omega)}, \|\nabla v\|_{L_{\infty}(\Omega)}, \|\nabla w\|_{L_{\infty}(\Omega)} \leq \hat{c}_4 when t > T_1 > 0. Similar to the estimation of Eqs (46) and (48) in Theorem 4.1 of [36] and by semigroup theory and L^p - L^q estimate, there exist \hat{c}_4' > 0 and \epsilon \in (0, 1) such that \|w(t, \cdot)\|_{C^{2+\epsilon}(\bar{\Omega})}, \|v(t, \cdot)\|_{C^{2+\epsilon}(\bar{\Omega})} \leq \hat{c}_4' for all t > T_1' > 0 . Denote {T}_0 = \max\{T_{1}, T_1'\}. One can apply the Theorem 7.2 or 7.4 in Chap.V of [37] to the first equation of Eq (1.4) which can be rewritten as u_t -d(v)\Delta u + b(t, x, u, \nabla u) = 0 with
Then there exits another constant, still denoted by \hat{c}_4, such that \|\nabla u\|_{L_{\infty}(\Omega)}\leq \hat{c}_4 for all t > T_0.
An application of Gagliardo–Nirenberg interpolation inequality may yield that for all t > T_0 ,
where \hat{c}_6: = \hat{c}_5 (\hat{c}_{4}^{\frac{n}{n+1}}\, \hat{c}_{3}^{\frac{1}{n+1}} +\hat{c}_{3}), \, \hat{c}_8: = \hat{c}_7 (\hat{c}_{4}^{\frac{n}{n+2}}\hat{c}_{3}^{\frac{2}{n+2}}+\hat{c}_{3}), and \hat{c}_{10}: = \hat{c}_9 (\hat{c}_{4}^{\frac{n}{n+2}}\hat{c}_{3}^{\frac{2}{n+2}} +\hat{c}_{3}). Therefore,
with \hat{c}_{11}: = \hat{c}_6+ \hat{c}_8+ \hat{c}_{10}. This completes the proof.
4.2. Asymptotical stability of coexistence steady state
As is shown in Eq (2.3), the positive coexistence state (u_{*}, v_{*}, w_{*}) should satisfy
We are now in a position to prove part 2) of the Theorem 2.2.
Lemma 4.4. Let (H1)-(H4) hold and (u, v, w) be the global classical solution of Eq (1.4) obtained in Theorem 2.1. If the coexistence steady state (u_{*}, v_{*}, w_{*}) exists and
with K_2 from Remark 3.2 and C_1 = \max \big\{K, \|w_0\|_{L_{\infty}(\Omega)} \big\} and \varphi(w) = \frac{wf(w)}{F(w)}, then the (u_{*}, v_{*}, w_{*}) is globally asymptotic stable. Moreover, there are three constants \tilde{c}_1, \tilde{c}_2, T_1 > 0 such that
Proof. We may construct the following function for t > 0 that
where (u, v, w) is the global classical solution of Eq (1.4) and M > 0 is a constant to be determined in Eq (4.9). Similar to Lemma 4.3, we first verify \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t}\leq 0 . Replacing u_t, v_t, w_t in the following equality may yield
For the terms above involving \nabla u and \nabla v and for u\neq 0, one may notice that
where \tau refers to transpose and
is positive semi-definite when
Here 0 < v(t, x) < \mathcal{C}_1 for all t > 0 and all x\in \Omega, owning to Remark 3.2 and the regularity Eq (2.1) in Theorem 2.1. In terms of u_* = \frac{w_{*}f(w_{*})}{F(w_{*})} one may obtain that
where \varphi(w) = \frac{wf(w)}{F(w)}, \tilde{w}_i lies between w and w_{*}, i = 1, 2. In light of \ell u_* +\theta = \gamma F(w_{*}), we have
Note that (v - v_{*})(\beta w -\sigma v) = \beta (v - v_{*})(w- w_{*}) - \sigma (v - v_{*})^2 by v_{*} = \frac{\beta w_{*}}{\sigma} . One can derive from Young's inequality that
for 0\leq \frac{\beta\varepsilon}{2}\leq \sigma or 0 < \varepsilon\leq \frac{2\sigma}{\beta}. Consequently, we know
Lemma 3.3 shows 0 < \tilde{w}_1, \tilde{w}_2\leq C_1 with C_1 = \max \big\{K, \|w_0\|_{L_{\infty}(\Omega)} \big\} . Thus by Eq (4.2) we can set
Then Eq (4.6) implies there exists a M > 0 such that both Eqs (4.8) and (4.9) hold, which means \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t}\leq 0.
Next we claim that \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t} = 0 will lead to (u, v, w) = (u_{*}, v_{*}, w_{*}). In fact,
and \mathcal{H}_{2}(u, v, w) = \frac{1}{\gamma}\big(u -u_{*}-u_{*}\ln\frac{u}{u_{*}}\big) +\frac{M}{2}(v- v_{*})^2 +\int_{w_{*}}^{w}\frac{F(\eta)-F(w_{*})}{F(\eta)} \, \mathrm{d}\eta is a nonnegative convex function of (u, v, w) based on Lemma 4.1, the expansion Eq (4.10), and on Eq (4.11) as below. So the equation \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t} = 0 has at most one minimum point in the sense of (u, v, w). Together with (u, v, w) = (u_{*}, v_{*}, w_{*}) leading to \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t} = 0, thus we may infer that the equation \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t} = 0 indicates (u, v, w) = (u_{*}, v_{*}, w_{*}), which concludes that \frac{\mathrm{d}\mathcal{L}_2(t)}{\mathrm{d}t} = 0 if and only if (u, v, w) = (u_{*}, v_{*}, w_{*}). Then by Lemma 4.2 the solution (u, v, w) of Eq (1.4) which is bounded will converges to (u_{*}, v_{*}, w_{*}) as t\rightarrow \infty. In other words, (u_{*}, v_{*}, w_{*}) is globally asymptotic stable.
We can further acquire its the convergent rate. Indeed, letting \kappa = w_{*} in Lemma 4.1 means
with \tilde{w} lying between w and w_{*}. Furthermore, denoting \rho(u) = u -u_{*}-u_{*}\ln\frac{u}{u_{*}} and doing its Taylor expansion at u = u_{*} may show
where \tilde{u} lies between u and u_{*}. Lemma 3.5 and the regularity Eq (2.1) jointly show that there exists a \tilde{T}_{1} > 0 such that 0 < \delta \leq u\leq \mathcal{C}_2 < \infty as t > \tilde{T}_{1} , which means \frac{u_{*}}{2\mathcal{C}_{2}^2} \leq \frac{u_{*}}{2\tilde{u}^2} \leq \frac{u_{*}}{2\delta^2}. Again observing the derivations from Eqs (4.7) to (4.9), there is a constant \tilde{c}_0 > 0 such that
Analogous to the corresponding parts in proving Lemma 4.3, there exist two constants \tilde{c}_1, \tilde{c}_2 > 0 and T_1\geq \tilde{T}_1 > 0 such that
5.
Linear instability and patterns
The previous sections involve that there exists the unique global classical solution to Eq (1.4) and it may approach its steady states exponentially under suitable conditions. However, there is no discussion of instability on its steady states. To figure this out, we below shall analyse linear instability of these constant steady states and then numerically explore the impact of density-dependent d(v) and \chi(v) on the patterns.
5.1. Linear instability
Proposition 5.1. Assume that (u_c, v_c, w_c) is the constant steady state of the system (1.4). Then the (u_c, v_c, w_c) is linearly instable if there exists at least one \lambda_j in Eq (5.4) having strictly positive real part (viz. one of Eqs (5.5)–(5.7) holds) ; It is linearly stable if all the real parts of \lambda_j are strictly negative.
Proof. We first linearize the system (1.4) at (u_{c}, v_{c}, w_{c}) as
where \tilde{\mathbf{w}}: = (u-u_{c}, v-v_{c}, w-w_{c})^{\tau},
In order to obtain the eigenvalues (denoted by \{\lambda_{j}\}_{j = 0}^{\infty} ) of the linear operator \mathbf{B} , we invoke the following eigenvalue problem:
the eigenvalues \{\mu_{j}\}_{j = 0}^{\infty} of which, without counting the finite multiplicities, can be formulated as
Then to \{\mu_{j}\}_{j = 0}^{\infty} the corresponding eigenfunctions, denoted by \{\phi_{j}(x)\}_{j = 0}^{\infty} in L^{2}(\Omega) , constitute an orthonormal basis of L^{2}(\Omega). Plus \frac{\partial \tilde{\mathbf{w}} }{\partial t} = \frac{\partial \mathbf{w} }{\partial t}, we thus can formulate a general solution \tilde{\mathbf{w}} to Eq (5.1) (note \frac{\partial \tilde{\mathbf{w}}}{\partial t} = \mathbf{B}\tilde{\mathbf{w}} = \lambda \tilde{\mathbf{w}} ) in the form of components (in particular spatial parts in L^{2}(\Omega) ) as
where u_{j}, v_{j}, w_{j} are constants for all j . Note that if there is a j such that u_{j} = v_{j} = w_{j} = 0 , one may automatically remove the corresponding terms in Eq (5.2). In this fashion we have
which is equivalent to
or the eigenpolynomial
where I is a 3\times 3 unit matrix and other real-valued coefficients are:
Denote \mathbf{p} = a_2-\frac{{a_1}^2}{3} , \mathbf{q} = \frac{2{a_1}^3}{27}-\frac{a_1a_2}{3}+a_3, \vartheta = e^{\mathbf{i}\frac{2\pi}{3}} = -\frac{1}{2}+\frac{\sqrt{3}}{2}\mathbf{i} with \mathbf{i} = \sqrt{-1} , and \Xi = \frac{\mathbf{q}^2}{4}+ \frac{\mathbf{p}^3}{27}. Then by Cardano's formula for every j one can specify three roots of Eq (5.4) as:
Consequently, we may identify the linear instability by requiring one of the real parts of these roots to be strictly positive in the following cases:
● When \Xi > 0 , one may readily see that \frac{-\mathbf{q}}{2}\pm\sqrt{\Xi}\in \mathbb{R} and thus \lambda_{j}^{(1)} is real and \lambda_{j}^{(2)} , \lambda_{j}^{(3)} are complex numbers. So we require
with \Lambda: = \sqrt[3]{\frac{-\mathbf{q}}{2}+\sqrt{\Xi}} +\sqrt[3]{\frac{-\mathbf{q}}{2}-\sqrt{\Xi}} ;
● When \Xi = 0 then \lambda_{j}^{(1)} , \lambda_{j}^{(2)} and \lambda_{j}^{(3)} are real (by \vartheta+\vartheta^2 = -1 ) and \lambda_{j}^{(2)} = \lambda_{j}^{(3)} . Then we demand
with \Lambda_0: = \sqrt[3]{\frac{-\mathbf{q}}{2}} ;
● When \Xi < 0 , \lambda_{j}^{(1)} , \lambda_{j}^{(2)} , and \lambda_{j}^{(3)} are real but different from each other. So we need
This completes the proof.
Note that Proposition 5.1 does not concisely show how the density-dependent d(v) and \chi(v) directly affect the patterns. So we next resort to numerical simulations with parameters taken hypothetically. The units of these parameters can be inferred from pp.252–262 of [1].
5.2. Numerical simulation in one-dimensional case
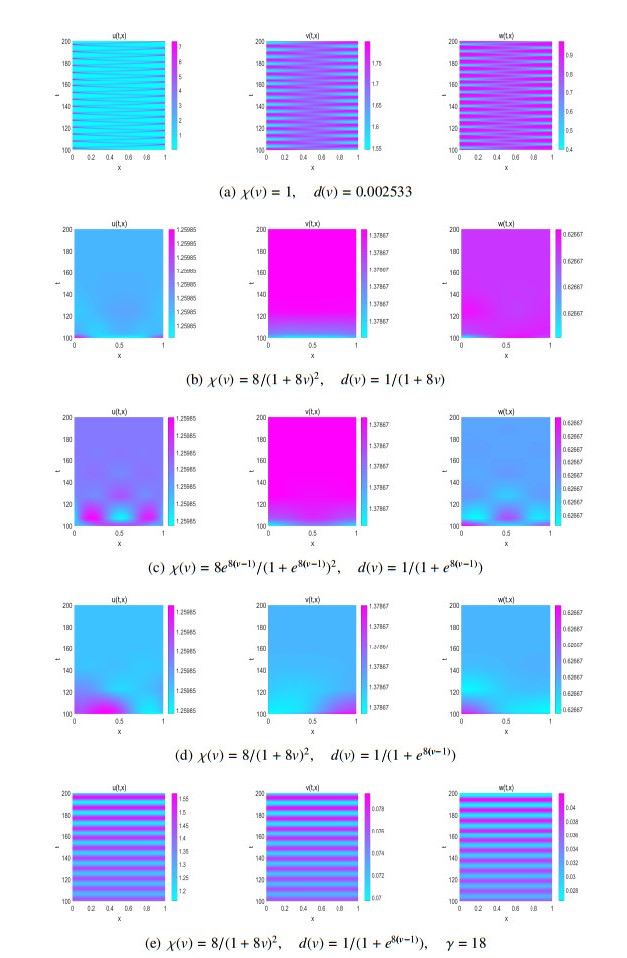
When motility function d(v) and prey-taxis sensitivity function \chi(v) are constants, one may find (cf. [21]) that the coexistence state of spatial one-dimensional model (1.2) (i.e., Eq (1.4) with \ell = 0 ) becomes unstable regarding small perturbation (by increasing prey-taxis coefficient). In this subsection, we shall show that some density-dependent d(v) and \chi(v) can stabilize such a stationary state but this stabilization effect can be weakened by enhancement of conversion rate.
To show this difference, we remain unchanged some parameters and functions taken in [21], except for d(v) , \chi(v) and conversion rate \gamma . Specifically, the growth rate function of prey is \Theta -logistic type
and the functional response function is Ivlev type
Let \Omega = (0, L) and take other parameters in Table 1. Thus we derive from Eq (2.3) (with \ell = 0 ) that (u_*, v_*, w_*)\approx(1.2599, 1.3787, 0.6267) . In addition, we set initial value as u_0(x) = u_*+0.01\cdot\cos(\pi x), v_0(x) = v_*+0.01\cdot\sin(\pi x), w_0(x) = w_*+0.01\cdot\cos(\pi x).
When d(v) = 0.002533 and \chi(v) = 1 , one can still derive the patterns (cf. (a) in Figure 1) that are analogous to the first row of Figure 7 in [21]. However, if we replace them by density-dependent forms such as d(v) = \frac{1}{1+e^{8v-1}} or \frac{1}{1+8v} , things will become different.
Precisely, it is not difficult to see from (a) to (d) in Figure 1 that some density-dependent d(v) and \chi(v) of exponential or algebraic form may flatten, or we say stabilize, the pattern bifurcating from the coexistence steady state (u_*, v_*, w_*) under small perturbations. However, this effect might be suppressed by increasing conversion rate. For example, after resetting conversion rate \gamma , approximate time-periodic patterns can appear, like the change from (d) to (e) in Figure 1. In addition, by enhancing \gamma in Figure 1(b), (c) (for instance, by letting \gamma = 26 ), the system may produce patterns like Figure 1(d) as well.
5.3. Numerical simulation in two-dimensional case
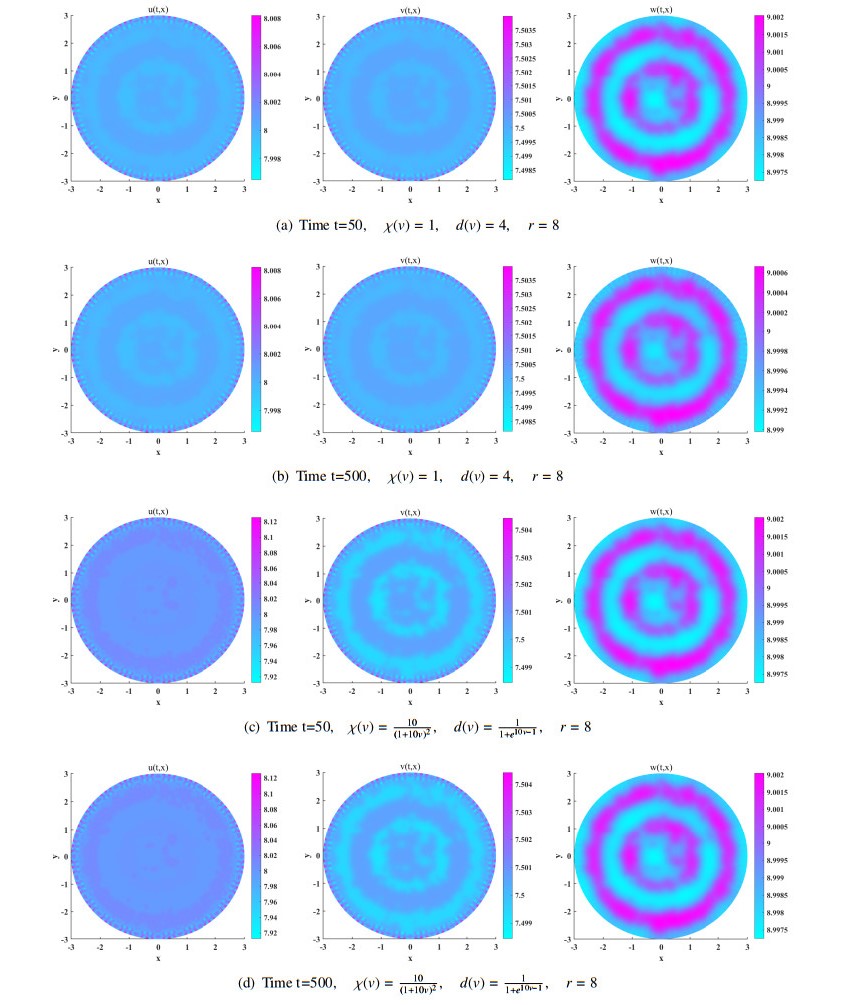
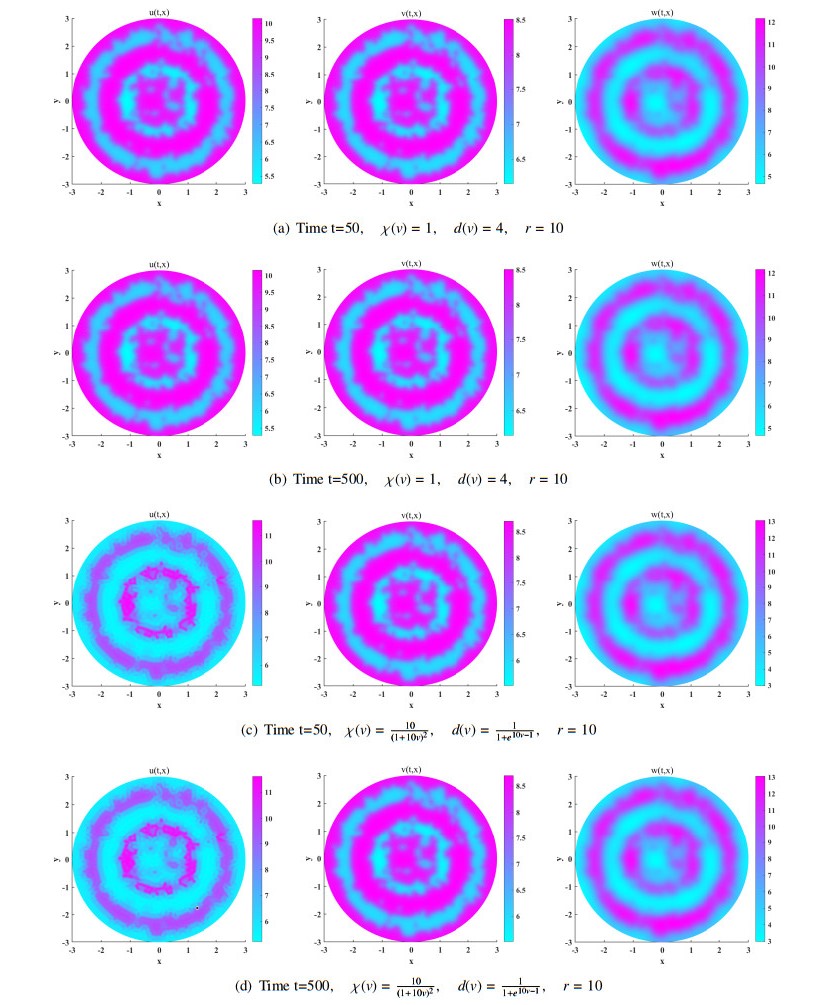
An individual-based modelling method to simulate one population whose individuals undergo density-dependent movement in 2-dimensional spatial domain can be see in [38]. For two populations spatially in a 2-dimensional disc, i.e., one predator and one prey considered in the system (1.4) with \ell > 0 , some density-dependent d(v) and \chi(v) may help to change the spatial distribution similarity which exists in non-density-dependent case between predators and signals of prey.
We herein set the growth rate function of prey as
and take the functional response function to be the Holling type II
together with different values of r and different forms of d(v) and \chi(v) specified below Figures 2 and 3. Without loss of generality, we may adopt initial values as
where Q(x, y) = \cos\pi x + \cos\pi y, (x, y)\in \mathcal{B}_3(\mathbf{0}) –a circle with radius 3 and centre at the origin, (u_c, v_c, w_c) may equal to (0, 0, 0), (0, \frac{\beta K}{\sigma}, K) or (u_{*}, v_*, w_{*}) , the last of which exists as \gamma r > \theta, u_{*} = w_{*} = \frac{K(\gamma r-\theta)}{K\ell +\gamma r} and v_{*} = \frac{K\beta(\gamma r-\theta)}{\sigma(K\ell +\gamma r)}. Other specific parameters are given in Table 2.
Figures 2 and 3 present the spatial distribution of predator, chemicals released by prey and of prey, in a circular domain at time t = 50 and t = 500 . We may observe that:
\rm(i) non-constant steady states exist since the corresponding patterns have few changes from time t = 50 to t = 500. Parameter r seems important in producing more abundant patterns after other parameters are fixed, for example (a) and (b) in Figure 2 and that in Figure 3, or (c) and (d) in Figure 2 and that in Figure 3;
\rm(ii) if d(v) and \chi(v) are constants, spatial distribution of predators and chemoattractant are very similar; The density-dependent decays of d(v) and \chi(v) may lower the similarities, but the extent may be effected by other parameters, like r in f .
5.4. Biological explanation of the simulations
System (1.4) describes a spatiotemporal evolution process of an isolated ecosystem within a domain \Omega , which includes two populations i.e., one predator and one prey. The most arresting feature in Eq (1.4) is that the predators may search for the prey as their food, mainly through chemoattractants released by the prey, since some factors including natural camouflage, the environment of the prey, range of visibility of the predators, etc., result in many difficulties for the predators in finding the prey directly. So the chemoattractants usually have diffused relatively far from the prey before they are perceived by the predators. Here u(x, t) , v(x, t) , and w(x, t) refer to population density of the predators, concentration of the chemical signals, and population density of the prey, respectively. The system being isolated means that there might be negligible quantities of the predators, the prey, and the prey signals crossing the boundary of \Omega , compared with overwhelming majorities of them (the predators, the prey, and the prey signals) within \Omega . Other organisms living in \Omega are not taken into consideration in the Eq (1.4).
Theorem 2.1 states that the system (1.4) has a global-in-time classical solution which is continuous to its initial value, when (H1)–(H3) are satisfied. As a result, for given initial densities u_{0}(x), v_{0}(x) and w_{0}(x) , one can predict by the unique classical solution of Eq (1.4) the density of the predators, the prey signals and the prey, at any time 0 < t < \infty and any spatial position x\in\Omega . The obtained L_{\infty} bound in Theorem 2.1 signifies that there is a maximal density for all three of them.
Theorem 2.2 illustrates that in some cases (if (H4) holds), the spatial distributions of the predators, the prey signals, and the prey in \Omega may be approximately homogeneous as the time goes by. This is, as it should be, a much ideal case, but at least the large-time behavior of such a solution indicates a trend through which one can foresee whether this ecosystem can evolve into exclusion state (prey being extinct in \Omega ) or coexistence state over time. So this tendency which can be viewed as an early warning, makes significantly biological sense to protect the biodiversity and ecological balance in the domain \Omega .
For simplicity, in regard to numerical simulations we only list the patterns which bifurcate from coexistence steady state in Subsections 5.2 and 5.3 (the case of exclusion state is similar). In Subsection 5.2, (a) of Figure 1 recovers the pattern corresponding to the point A in Figure 7 obtained in [21] with d(v) and \chi(v) being constants, which is the starting point of our simulations. Then in (b) and (c) of Figure 1, we set \chi(v) = -d'(v) with d(v) satisfying algebraic decay and exponential decay respectively. Finally in Figure 1 (d) and (e) we remove the relation \chi(v) = -d'(v) and take \chi(v) and d(v) to be algebraic and exponential decay severally. From this process we see that random motility function d(v) and indirect prey-taxis sensitivity \chi(v) , being density-dependent form, may help the spatial distribution (of the predators, the prey signals, and the prey) to be approximately homogeneous. Because one may observe that the spatial distributions of Figure 1 (b)–(e) become more even than that of Figuere 1 (a), although the approximate time-periodic pattern may appear when the conversation rate \gamma is increased.
All simulations in Subsection 5.2 are spatial 1-dimensional case, which matter in theory. What will happen in spatial 2-dimensional case makes more realistic sense, which is the aim of Subsection 5.3. Firstly, we see the spatial distribution of high density for both the prey signals and the prey, either in Figures 2 or 3, stagger a little bit each other (instead of being overlap) in position (this point can also be seen in Figure 1 but it is not so distinct). This is consistent with the feature of indirect prey-taxis that signals of the prey have diffused a distance far from the prey before they are captured by the predators. Secondly, when \chi(v) and d(v) are constants (cf. (a), (b) in Figures 2 and 3), we find that the spatial distribution of the predators and of the prey signals are highly similar, since the predators conduct the signals-based (indirect prey-taxis) foraging strategy to search for the prey. However, the \chi(v) and d(v) in density-dependent form (cf. (c), (d) in Figures 2 and 3) may lower similarity of spatial distribution between the predators and the prey chemicals. Finally, increasing the value of r (from f(w) ) in Figure 2 may yield Figure 3 from which one may infer that some parameters in Eq (1.4), like r , are important to produce abundant patterns.
Acknowledgments
The author is very grateful to Prof. Zhi-An Wang and to the anonymous reviewers of this paper for their valuable suggestions and insightful comments which improve the exposition of this paper deeply and greatly. The author would like to thank The Hong Kong Polytechnic University for supporting publication expenses of this article.
Conflict of interest
The author declared no conflicts of interest in this paper.









 DownLoad:
DownLoad: