Exploring the dynamics of a tritrophic food chain model with multiple gestation periods

1.   Introduction

Time delays are ubiquitous in all biological situations, as species require some time in order to complete various biological activities such as digestion, gestation, maturation, incubation, etc. Also, the present growth of species may be affected by the past generations through delay mechanism ^[1,2]. Introduction of time delay may change qualitatively the dynamical behaviors of a predator-prey interaction model, therefore, it is important to investigate the dynamical properties of a predator-prey model with time delays in both theoretical research and practical applications. One of the interesting observation of inclusion of time delay is the appearance of oscillatory behaviour in single species models ^[3,4]. Time delay can produce chaotic oscillations even in simple predator-prey models ^[5,6]. The introduction of time delay leads to rich dynamical behaviors such as periodic orbits, stability switching, chaotic dynamics, and multiple stable coexistence through the different bifurcation routes ^[7]. Mathematical models incorporating the time delays are widely discussed in the books of MacDonald ^[8], Kuang ^[3] and Cushing ^[9].

Recently, the impact of multiple delays on the dynamics of ecological systems has caught the attention of many researchers. In particular, Gakkhar and Singh ^[5] have studied the predator-prey model with Holling type Ⅱ response function and discrete delays. They have observed that the stable species coexistence undergoes Hopf-bifurcation for the critical value of delay and a further increase in delay beyond the Hopf-bifurcation leads the system dynamics to the chaotic state. Also in two neuron system with multiple delays, Song et al. ^[10,11] have obtained stability switching, multiple stable coexistence of two resting states, two anti-symmetric periodic activity with period three, one self-symmetric periodic activity with period one, one quasiperiodic spiking and chaotic behavior. Jiang et al. ^[12] have considered the Phytoplankton-Zooplankton model with Holling Ⅲ functional response and discrete delay. They have shown that the oscillations can be prevented by adjusting the magnitude of delay. Song et al. ^[13] have discussed the food chain system with multiple digestion delays and predicted that the multiple delays can generate and suppress the higher order limit cycles and chaos. Lotka-Volterra food chain system with two discrete delays has been investigated by Cui and Yan ^[14]. They have determined the linear stability, Hopf-bifurcation, direction and stability of bifurcating period solutions by considering the sum of two delays as a bifurcating parameter. Jiang and Wang ^[15] have investigated the predator-prey model with three delays and discussed the delay induced destabilization and stability analysis of periodic solutions. Further, Ghosh et al. ^[16] have studied the stability and bifurcation analysis of an eco-epidemiology model with multiple delays. Three species Leslie-Gower type food chain model with resource digestion delay and consumer digestion delay is analyzed by Guo et al. ^[17]. It has been noted that the multiple delays lead to the stability switching, generate or terminate the recurrent bloom and help control the species population to the stable coexistence.

Delay induced destabilization is a common finding. A lot of work has been done with the objective to find the critical value of the delay parameter at which system bifurcates from its stable state and starts showing the oscillatory behaviour ^{[18,19,20,21,22,23]}. However, Sen et al. ^[24] have provided the necessary and sufficient conditions for stability of interior equilibria in a ratio-dependent predator-prey model with Allee effect and maturation delay. Stabilizing effect of maturation delay in a ratio-dependent predator-prey model with Allee effect is investigated by Banerjee and Takeuchi ^[25]. Wang and Jiang ^[26] have demonstrated that different values of delay can induce or eradicate chaotic dynamics in the predator-prey system with dormancy in predator. Motivated by these research work, we have asked the following research questions in the current manuscript:

(ⅰ) How do multiple gestation delays affect the stable and oscillatory coexistence of species? Do several delays behave in a similar fashion?

(ⅱ) Is it possible to obtain some parameter sets so that stable coexistence of species is not affected by the introduction of delays?

(ⅲ) Is it possible to obtain various complex dynamical behaviors such as higher order limit cycles and chaos? If yes, what is the impact of delays on these complex dynamical structures?

For ecological forecasting, it is necessary to understand the predator-prey linkage in food chain or web systems. Different functional and numerical responses are used for modeling the trophic interactions and they are one of the most important components in the study of interacting populations. In most of the studies, population dynamics is modeled with the help of monotonic response functions (Holling type Ⅰ, Ⅱ, Ⅲ). Observational and experimental results show that these types of response functions are not appropriate for modeling the situations with group defence and inhibitory effects ^[27]. More suitable in these situations is Holling type Ⅳ functional response ^[28,29]. In their experiment of uptake of phenol by pure culture of Pseudomonas putida growing on phenol in continuous culture, Sokol and Howell ^[30] proposed the simplified form of Monod-Haldane functional response as $p(x) = \frac{m x}{a+x^2}$. They obtained that fits better fits to the experimental data and simple as involving only two parameters. Edwards ^[31], Boon and Laudelout ^[32], Xiao and Ruan ^[27] suggested that this type of functional response takes place at the microbial level: when the nutrient concentration attains a high value, an inhibitory effect on the specific growth rate may occur. Recently, Ali et al. ^[33,34] proposed a three species food chain system with Sokol-Howell functional response. They have studied the boundedness, local and global stability of the system. Dynamical behavior is also explored by using the numerical simulations. Explosive instabilities in three species food chain model with this functional response have been investigated by Parshad et al. ^[35]. A three species Rosenzweig-MacArthur food chain model with this functional response has been investigated by Ali et al. ^[36].

In the current work, we have studied a food chain model with multiple gestation delays. As assimilation of prey into the predator biomass is a complex phenomenon and completed through various bio-physiological activities, which require time, therefore, time lags in predators gestation process have been considered. Effect of gestation delay in the system of interacting populations is studied by many researchers ^{[18,19,20,22,23,37,38,39]}. Patra et al. ^[40] have analyzed the effect of discrete delay in a three species food chain model with ratio-dependent type functional response. Pal et al. ^[41] have studied the tritrophic food chain model with gestation delay, where species interacts with Holling type II response function. Here, gestation delays are incorporated in the model using the Wangersky-Cunningham delay formulation ^[42]. The conventional way of delay formulation has been extensively studied in literature ^[5,24,40,43]. In recent years, Wangersky-Cunningham delay formulation is used prominently due to its clear biological explanation ^{[19,24,25,41]}.

The organization of paper is as follows. Formulation of the model is given in section 2. In section 3, positive invariance, boundedness, equilibria and stability analysis have been discussed. Local stability analysis and Hopf-bifurcation about the interior equilibrium point for all possible cases to incorporate gestation delays have been derived in section 4. Numerical simulation results have been presented in section 5. Finally, discussion and conclusion are given in the last section.

2.   Formulation of the mathematical model

The model has been developed under the following assumptions.

$(1)$ The behavior of whole community arises due to the coupling of three types of interacting populations: prey $X(t)$, intermediate predator $Y(t)$ and top predator $Z(t)$.

$(2)$ Prey population grows logistically with intrinsic growth rate $r$ and carrying capacity $K$. Thus, per capita growth rate of prey in the absence of predator is given by $r\left(1-\frac{X(t)}{K}\right)$.

$(3)$ Intermediate and top predators consume their sole food (prey and intermediate predator respectively) according to Sokol-Howell functional response.

$(4)$ In the absence of their only foods intermediate and top predators die out with their natural death rates.

$(5)$ Consumption of prey by the predator is not an instantaneous process. However, predator requires some period of time to convert the prey density into itself due to gestation.

Under the above assumptions, interactions between the species are modeled by the following system of DDEs:

All the parameters $r, \; K, \; \omega, \; a_1, \; b, \; \omega_1,$ $\; \omega_2, \; a_2, \; c, \; \omega_3, \; T_1$ and $T_2$ are positive and brief description about these parameters is given in Table 1.

Model (2.1) involves 12 parameters, which complicates the system analysis. Thus, to reduce the complexity of model (2.1), we non-dimensionalize it by using the following transformations:

Then model (2.1) is reduced in the following dimensionless form:

All the variables and parameters of dimensionless system (2.2) are positive. We denote by $C$ the Banach space of continues functions $\phi:[-\tau, 0]\rightarrow\mathfrak{R}^3$ with norm

The initial conditions are given as

For biological reasons, it is assumed that

By the fundamental theorem of differential equations ^[44], there exists a unique solution $(x(t), \; y(t), \; z(t))$ of the model (2.2) with initial conditions (2.3).

3.   Preliminaries

In this section, we present some basic results such as positive invariance, boundedness of the solutions, equilibria analysis and characteristic equation of model (2.2).

3.1.   Positive invariance

It is important to discuss the positivity of solutions of model (2.2) as they represent the populations of prey, intermediate predator and top predator at any time. In the biological sense, positivity makes sure that population never becomes negative and always survives in the finite time. We have established the positivity through the following theorem.

Theorem 3.1. Every solution of the system (2.2) with initial conditions (2.3) is positive.

Proof. The model (2.2) with the initial conditions (2.3) can be written in the following form:

The model (2.2) becomes

with $W(\theta) = (\phi_1(\theta), \phi_2(\theta), \phi_3(\theta))\in C_{+} \; \; \text{and}\; \; \phi_1(0), \phi_2(0), \phi_3(0) > 0.$ It is easy to check in system (3.2) that whenever choosing $W(\theta) \in \mathfrak{R}_{+}^3$ such that $x = y = z = 0,$ then

with $w_1(t) = x(t), \; w_2(t) = y(t), \; w_3(t) = z(t)$. Using the lemma 4 given in ^[45], any solution of (3.2) with $W(\theta)\in C_{+}$ saying $W(t) = W(t, W(\theta))$, is such that $W(t)\in \mathfrak{R}_{+}^3$ for all $t\geq0.$ Hence the solution of the system (3.2) exists in the region $\mathfrak{R}_{+}^3$ and all solutions remain nonnegative for all $t > 0.$ Therefore, the positive orthant $\mathfrak{R}_{+}^3$ is an invariant region.

3.2.   Boundedness

Theorem 3.2. Let $(x(t), y(t), z(t))$ be any positive solution of the model (2.2), then there exists a time $\widetilde{T} > 0$, such that $0 \leq x(t) \leq M_{1}, \; 0 \leq y(t) \leq M_{2} \;$ and $0 \leq z(t) \leq M_{3}\;$ for $t > \widetilde{T},$ where $M_{1} = 1, \; M_{2}$ = $\frac{\omega_6}{4 \omega_5}, \; M_{3} = \frac{\omega_{6}\omega_9(\omega_5-\delta)}{4\omega_5 \delta},$ $\delta$ is any positive constant satisfying $\delta < \min\{\omega_5, \omega_8\}$.

Proof. From the positive invariance theorem, we have $x(t)\geq 0$, $y(t)\geq 0$ and $z(t)\geq 0$. Therefore, we only need to show that $x(t)\leq M_1, \; y(t)\leq M_2$ and $z(t)\leq M_3$. From the prey equation, we obtain that

thus

therefore,

Now, we construct a new function

By differentiating $\sigma(t)$ with respect to time $t,$ we obtain

And by using the positivity of solutions, we get

Then adding $\omega_5 \sigma(t)$ on the both side of above inequality, we get

Since, $\max\{{x(t-\tau_1)(1-x(t-\tau_1))}\} = \frac{1}{4}$, implies,

Therefore, by using the lemma (2) given in ^[46], we obtain

If $\widetilde{T}_1 = 0$, then

therefore

i.e.

thus,

Again for boundedness of $z(t)$, we construct another function

By differentiating above equation with respect to time $t$, we have

Now, by using system (2.2), we obtain

And by adding $\delta \gamma(t)$ on the both side of above inequality, where $\delta < \text{min}\{\omega_5, \omega_8\},$ we obtain

Then using the boundedness of $x(t)$, we obtain

Therefore, from lemma 2 given in ^[46], we have

If $\widetilde{T_2} = 0,$ then,

Therefore

where

Thus

3.3.   Equilibria analysis

Steady state solutions are obtained analytically by putting $\dot{x} = 0, \; \dot{y} = 0$ and $\dot{z} = 0$, which are independent of time delays $\tau_1$ and $\tau_2$. The model has four equilibrium points.

(ⅰ) Trivial equilibrium point $P_{0}(0, 0, 0)$ always exists.

(ⅱ) Predators free axial equilibrium point $P_{1}(1, 0, 0)$ exists.

(ⅲ) Top predator free planar equilibrium point $P_{2}(\bar{x}, \bar{y}, 0),$ where $\bar{y} = (1-\bar{x})(\bar{x}^2+\omega_4)$, and $\bar{x}$ is a solution of the equation

which has positive solution $\bar{x}$ if

Notice that $\bar{y} > 0$ iff $\bar{x} < 1$.

Following we discuss the existence conditions of $P_2$ for three cases.

(a)

(b)

(c)

(ⅳ) Positive coexistence equilibrium point $P_3(x^*, y^*, z^*)$ exists provided

where $y^* = \frac{\omega_{9}\pm\sqrt{\omega_{9}^{2}-4\omega_{8}^2\omega_{7}}}{2\omega_8}$, $z^* = (y^*{^2}+\omega_7)(-\omega_5+\frac{\omega_6x^*}{x^*{^2}+\omega_4}),$ and $x^*$ is the positive root of following equation

Let $f(x^*) = {x^*}{^3}-x^*{^2}+\omega_4x^*+y^*-\omega_4$, then $f(0) = (y^*-\omega_4)$, $f(0) < 0$ if $y^* < \omega_4 \;$, i.e. $\; \omega_4\omega_{9} < \omega_8(\omega_{7}+\omega_{4}^2)$ and $f(1) = y^* > 0.$ Since $f(0)f(1) < 0$, by intermediate value theorem, Eq. (3.6) has a positive root lies in (0, 1) when

Positive equilibrium point $P_3(x^*, y^*, z^*)$ exists if the conditions (3.5) and (3.7) hold.

In the absence of both delays, the general variational matrix of model (2.2) at any arbitrary point $(x, y, z)$ is given by

The behaviour of equilibrium points is summarized as follows.

(ⅰ) Eigenvalues of variational matrix at $P_0(0, 0, 0)$ are $1, \; -\omega_5, \; -\omega_8$. Therefore, $P_0$ is a saddle point having unstable manifold along $x$-direction and stable manifold along $y$ and $z$-direction.

(ⅱ) Eigenvalues of variational matrix at $P_1(1, 0, 0)$ are $-1, \; -\omega_5+\frac{\omega_6}{1+\omega_4}, \; -\omega_8$. Therefore, $P_1$ is locally asymptotically stable (LAS) provided $\frac{\omega_6}{1+\omega_4} < \omega_5.$

(ⅲ) At $P_2(\bar{x}, \bar{y}, 0)$, the variational matrix becomes

$A$ is stable iff

Define $f(x) = \omega_5 x^2-\omega_6 x+\omega_4\omega_5$. Then we have $f(\bar{x}) = 0,$ and

Since $f(\sqrt{\omega_4}) = 2\omega_4\omega_5-\omega_6\sqrt{\omega_4}\leq0$, we have $\bar{x}_{-} < \sqrt{\omega_4} < \bar{x}_{+}$. Hence by (3.9), $P_{2}^{+} = (\bar{x}_{+}, \bar{y}_{+}, 0)$ is always unstable. From (3.10), we have $\omega_8\bar{y}^2-\omega_9\bar{y}+\omega_7\omega_8 > 0$. Hence $\bar{y} > 0$ if $\omega_9^2 < 4\omega_7\omega_8^2$. That is, (3.10) is satisfied if there exists no $P_3(x^*, y^*, z^*)$.

Now let's consider the case where no $P_3$ exists. For this case, (3.10) is satisfied for any $\bar{y} > 0$ and (3.9) is satisfied for $\bar{x}_{-}$. Since $\bar{y}_{-} = (1-\bar{x}_{-})(\bar{x}_{-}^2+\omega_4)$, we have

(a) When $\omega_4 > 1/3$, (3.12) is satisfied for any $\bar{x}_{-}\geq0$. Hence, $P_{2}^{-}$ is LAS when $\omega_4 > 1/3$ and no $P_{3}$ exists.

(b) When $\omega_4 < 1/3$,

where $\bar{x}_{-} = \frac{\omega_6-\sqrt{\omega_6^2-4\omega_4\omega_5^2}}{2\omega_5}$.

Hence $P_{2}^{-}$ is LAS when $\omega_4 < 1/3$ and no $P_{3}$ exists and (3.13) is satisfied.

4.   Local stability analysis and Hopf-bifurcation

In this section, we discuss the effect of discrete delays on the dynamics of model (2.2).

At $P_0$, characteristic equation is

There are one positive root $\lambda_1 = 1$ and two negative roots $\lambda_2 = -\omega_5, \; \lambda_3 = -\omega_8$, which are independent of $\tau_1$ and $\tau_2$. Hence $P_0$ is unstable for any $\tau_1\geq0$ and $\tau_2\geq0$.

At $P_1$, characteristic equation is

There are one root $\lambda_1 = -\omega_5+\frac{\omega_6}{1+\omega_4}e^{-\lambda\tau_1}$ and two negative roots $\lambda_2 = -1, \; \lambda_3 = -\omega_8$.

Following we consider the equation

If $\tau_1 = 0$, then $\lambda_1 = -\omega_5+\frac{\omega_6}{1+\omega_4}$. It shows that $P_1$ is LAS when $\frac{\omega_6}{1+\omega_4} < \omega_5$. If $\tau_1 > 0$, let us suppose that $\lambda_1 = i\omega \, (\omega > 0)$ is a pure imaginary root of equation (4.1). Separating the real and imaginary parts, we have

Squaring and adding both sides of above equations lead to the following equation

This shows that $P_1$ is LAS for any $\tau_1, \tau_2\geq 0$ if $\frac{\omega_6}{1+\omega_4} < \omega_5$.

If $\frac{\omega_6}{1+\omega_4} > \omega_5$, then equation (4.3) has one positive root $\omega_1^{-} = \frac{\sqrt{(\omega_6+\omega_5(1+\omega_4))(\omega_6-\omega_5(1+\omega_4))}}{1+\omega_4}.$

Solving equation (4.2) for $\tau_1$ yields

The minimum value of $\tau_1^{(j)}$ is renamed as

Then, we have the following theorem.

Theorem 4.1. (ⅰ) $P_0$ is unstable for any $\tau_1\geq0$ and $\tau_2\geq0$.

(ⅱ) $P_1$ is LAS for any $\tau_1, \tau_2\geq 0$ if $\frac{\omega_6}{1+\omega_4} < \omega_5$.

(ⅲ) $P_1$ is LAS for $0\leq \tau_1 < \tau_1^{-}$ and any $\tau_2\geq0$ if $\frac{\omega_6}{1+\omega_4} > \omega_5$, where $\tau_1^{-}$ is given by (4.5). Furthermore, model (2.2) undergoes Hopf-bifurcation to periodic solutions at $P_1$ when $\tau_1 = \tau_1^-$.

For $P_2$, we consider two cases.

Case a: $\tau_1 > 0, \; \tau_2 = 0$.

At $P_2$, characteristic equation is

where

One characteristic root is $\lambda_1 = -\omega_8+\frac{\omega_9\bar{y}}{\bar{y}^2+\omega_7}$. It is easy to show that $\lambda_1 < 0$ for any $\tau_1\geq0$ and $\tau_2\geq0$ if and only if $\frac{\omega_9\bar{y}}{\bar{y}^2+\omega_7} < \omega_8$.

Following we consider the equation

Let $i\omega\; (\omega > 0)$ be a root of equation (4.7), then we have

Simplifying and equating real and imaginary part of equation (4.8), we get

Squaring and adding equations (4.9) and (4.10) we get

where

We define

$G_0(0) = q_0 = (e_{11}+d_{22})^2-(e_{11}e_{22}-e_{12}e_{21})^2$, $G_1(\infty) = \infty$.

Let

then $G_0(0) < 0$ and $G_0(\infty) = \infty$. Thus, equation (4.31) has at least one positive root. Without loss of generality, we assume that it has finite number of positive roots saying $\omega_1, \; \omega_2, \; \omega_3, \cdots, \omega_N$. For every fixed $\omega_k, \; k = 1, \; 2, \; 3, \cdots, N$, there exist a sequence $\{\tau_{10}^{k, j}\mid \; j = 0, 1, 2, \cdots\}$, where

Let

Case b: $\tau_1 = 0, \; \tau_2 > 0$.

At $P_2$, characteristic equation is

where $h_1 = \frac{\bar{y}(\omega_4-\bar{x}{^2})}{(\bar{x}^2+\omega_4)^2}+2\bar{x}-1 > 0$ if the condition (3.8) is satisfied, $h_2 = \frac{\bar{x}}{{\bar{x}}^2+\omega_4}\frac{\omega_6(1-\bar{x})(\omega_4-\bar{x}^2)}{{\bar{x}}^2+\omega_4} > 0$ if the condition (3.9) is satisfied. Hence the equation $\lambda^2+h_1\lambda+h_2 = 0$ have two negative roots if and only if the conditions (3.8) and (3.9) are satisfied. Following we consider the equation

Following a similar analysis of $P_1$, we obtain the critical value

where $\omega_2^{-} = \frac{\sqrt{(\omega_9\bar{y}+\omega_8(\bar{y}^2+\omega_7))(\omega_9\bar{y}-\omega_8(\bar{y}^2+\omega_7))}}{\bar{y}^2+\omega_7}$. The minimum value of $\tau_2^{(j)}$ is renamed as

Then, we have the following theorem.

Theorem 4.2. (ⅰ) Suppose that $\tau_1 > 0, \; \tau_2 = 0$ and $\frac{\omega_9\bar{y}}{\bar{y}^2+\omega_7} < \omega_8$ are satisfied. Then $P_2(\bar{x}, \bar{y}, 0)$ is LAS for $\tau_{1} < \tau^*_{10}$ and unstable for $\tau_{1} > \tau^*_{10}$. Further, the system (2.2) undergoes the Hopf-bifurcation about $P_2$ when $\tau_{1} = \tau^*_{10}$.

(ⅱ) Suppose that $\tau_1 = 0, \; \tau_2 > 0$, the conditions (3.8) and (3.9) are satisfied. Then $P_2(\bar{x}, \bar{y}, 0)$ is LAS for any $\tau_2 > 0$ if $\frac{\omega_9\bar{y}}{\bar{y}^2+\omega_7} < \omega_8$. And $P_2(\bar{x}, \bar{y}, 0)$ is LAS for $\tau_2 < \tau_2^{-}$ if $\frac{\omega_9\bar{y}}{\bar{y}^2+\omega_7} > \omega_8$, where $\tau_2^{-}$ is given by (4.19). Furthermore, model (2.2) undergoes Hopf-bifurcation to periodic solutions at $P_2$ when $\tau_2 = \tau_2^-$.

Next we obtain the characteristic equation of model (2.2) about interior equilibrium point $P_3(x^*, y^*, z^*)$ by linearizing the model (2.2). Let $\bar{x}(t) = x(t)-x^*, \; \bar{y}(t) = y(t)-y^*, \; \bar{z}(t) = z(t)-z^*$ be the perturbed variables about $P_3(x^*, y^*, z^*)$. Then the linearized form of model (2.2) is given by (bar signed are dropped for simplicity)

where

and $\alpha = x^*{^2}+\omega_4, \; \beta = y^*{^2}+\omega_7$.

Thus, the characteristic equation of the linearized system is given by

where $I_3$ is an identity matrix of order 3.

Furthermore, equation (4.20) can be rewritten as the simplified form,

where

Now we discuss the following cases.

Case Ⅰ: $\tau_1 = 0 = \tau_2$.

In this case, equation (4.21) becomes

where $F_{12} = B_2+C_2+D_2, \; F_{11} = B_1+C_1+D_1+E_1, \; F_{10} = B_0+C_0+D_0+E_0$. Therefore, by Routh-Hurwitz criterion, $P_3 = (x^*, y^*, z^*)$ is LAS in the absence of delay if

Straight forward calculation shows that $F_{12} > 0$, if

$F_{10} > 0$, if

$(F_{12}F_{11}-F_{10}) > 0, \;$ if

and

Based on the above analysis, we have constructed the following theorem for stability of model (2.2) about $E^*(x^*, y^*, z^*)$ in the absence of delay.

Theorem 4.3. Suppose that the interior equilibrium point $P_3(x^*, y^*, z^*)$ exists. Then, $P_3$ is LAS provided the conditions (4.23)–(4.26) hold.

Case Ⅱ: $\tau_1 > 0, \; \tau_2 = 0$.

In this case, equation (4.21) becomes

Let $i\omega\; (\omega > 0)$ be a root of equation (4.27), then we have

Simplifying and equating real and imaginary part of equation (4.28), we get

Squaring and adding equations (4.29) and (4.30) we get

where

We define

Then $G_1(0) = r_1 = (B_0+D_0)^2-(C_0+E_0)^2$, $G_1(\infty) = \infty$.

Let

then $G_1(0) < 0$ and $G_1(\infty) = \infty$. Thus, equation (4.31) has at least one positive root. Without loss of generality, we assume that it has finite number of positive roots saying $\omega_1, \; \omega_2, \; \omega_3, \cdots, \omega_N$. For every fixed $\omega_k, \; k = 1, \; 2, \; 3, \cdots, N$, there exist a sequence $\{\tau_{1}^{k, j}\mid \; j = 0, 1, 2, \cdots\}$, where

Let

By differentiating the equation (4.27) with respect to $\tau_{1}$, we have the following transversality condition

provided $L_1(\omega_k)S_1(\omega_k)+R_1(\omega_k)T_1(\omega_k) > 0$, where

Then, we have the following theorem.

Theorem 4.4. Suppose that $\tau_1 > 0, \; \tau_2 = 0$ and conditions (4.23)–(4.26) are satisfied. Then the interior equilibrium point $P_3(x^*, y^*, z^*)$ is LAS for $\tau_1 < \tau^*_{1}$ and unstable for $\tau_1 > \tau^*_{1}$. Further, the system (2.2) undergoes the Hopf-bifurcation about $P_3(x^*, y^*, z^*)$ when $\tau_1 = \tau^*_{1}$.

Case Ⅲ: $\tau_{1}\in(0, \; \tau^*_{1}), \; \; \tau_{2} > 0$.

In this case, we assume that $\tau_1$ is arbitrarily fixed within the stable interval $(0, \tau_1^*)$, while consider $\tau_2$ as free parameter. Let $i\omega$ ($\omega > 0$) be a root of equation (4.21), then we have

Simplifying and equating real and imaginary part, we obtain

Squaring and adding above equations (4.37) and (4.38), we obtain

where

Following the same analysis as in Case Ⅱ, equation (4.39) has finite number of positive roots, saying $\omega_1, \omega_2, \omega_3, \cdots, \omega_N$, when

For every fixed $\omega_k, \; k = 1, \; 2, \; 3, \cdots, N$, there exist a sequence $\{\widetilde{\tau}_{2}^{k, j}\mid \; j = 0, 1, 2, \cdots\}$, where

where

Let

And assuming that

Then, we have the following theorem.

Theorem 4.5. Suppose that conditions (4.23)–(4.26) are satisfied and $\tau_{1}\in(0, \; \tau^*_{1})$. Then the coexisting equilibrium point $P_3(x^*, y^*, z^*)$ is LAS when $\tau_2 < \widetilde{\tau}_{2}^*$ and it is unstable when $\tau_{2} > \widetilde{\tau}_{2}^*$. Moreover, Hopf-bifurcation occurs when $\tau_{2} = \widetilde{\tau}_{2}^*.$

Case Ⅳ: $\tau_1 = 0, \; \tau_2 > 0$.

From the equation (4.21), we have

Let $i\omega\; (\omega > 0)$ be a root of equation (4.44), then we have

Equating real and imaginary part of equation (4.45), we obtain

Squaring and adding both equations of system (4.46), we obtain

where

Now, similarly as in the Case Ⅱ, we define

$G_2(0) = r_2 = (B_0+C_0)^2-(D_0+E_0)^2\;$ and $\; G_{2}(\infty) = \infty$.

Let

Then $G_2(0) < 0$ and $G_2(\infty) > 0$, thus equation (4.47) has atleast one positive root. Without loss of generality, we have assume that it has finite number of positive roots say $\omega_1, \omega_2, \omega_3, \cdots, \omega_N$. For every $\omega_k, \; k = 1, 2, 3, \cdots, N$, there exists a sequence $\{\tau_{2}^{k, j}\mid \; j = 0, 1, 2, \cdots\}$, where

Let

Differentiating the equation (4.44) with respect to $\tau_2$, we have the following transversality condition

provided $L_2(\omega_k)S_2(\omega_k)+R_2(\omega_k)T_2(\omega_k) > 0$, where

Then, we have the following theorem.

Theorem 4.6. Suppose that $\tau_1 = 0, \tau_2 > 0$ and conditions (4.23)–(4.26) are satisfied. Then the equilibrium point $P_3$ is LAS for $\tau_2 < \tau_2^*$ and unstable for $\tau_2 > \tau_2^*$. Further, the system (2.2) undergoes the Hopf-bifurcation around $P_3(x^*, y^*, z^*)$ when $\tau_2 = \tau_2^*$.

Case Ⅴ: $\tau_2\in(0, \; \tau_2^*)$, $\tau_1 > 0$.

In this case, we fix $\tau_2$ at some value from its stability range $(0, \; \tau_2^*)$ and choose $\tau_1$ as free parameter, by the similar procedure used in Case Ⅲ. Stability results are summarized in the following theorem.

Theorem 4.7. Suppose that the parameters of model (2.2) are such that conditions (4.23)- (4.26) are satisfied, $\tau_{2}\in(0, \; \tau_2^*)$ and condition $(B_0+D_0)^2 < (E_0+C_0)^2$ also holds. Then the coexisting equilibrium point $P_3$ is LAS, when $\tau_1 \in (0, \; \widetilde{\tau}_1^*)$ and it is unstable when $\tau_1 > \widetilde{\tau}_1^*$. Moreover, Hopf-bifurcation occurs when $\tau_1 = \widetilde{\tau}_1^*,$ where

with

and where

5.   Numerical experiment results

In this section, analytical findings and the various dynamics of model (2.2) have been illustrated with the help of numerical examples. In the following, we present three examples corresponding to stable positive equilibrium, limit cycles and chaos of the non-delay model, and we show how time delays influence the non-delay model.

Example 1. Taking $\omega_4 = 1.4, \; \; \omega_5 = 0.22, \; \; \omega_6 = 0.8, \; \; \omega_7 = 2.29, \; \; \omega_8 = 0.09, \; \; \omega_9 = 0.6$ in the model (2.2), yields the following system:

Initial densities of species are taken as $(x_0, y_0, z_0)$ $= (0.3, 0.3, 0.3)$. Simulations are carried out in the non-delay system by Matlab. Unique positive interior equilibrium point is obtained as $P_3 = (0.825453, 0.363298, 0.235593)$. Here we have taken all numerical numbers with 6 digits after decimal to unify the results obtained from Mathematica.

Now, for system (5.1) we have verified all five cases with the help of numerical simulations.

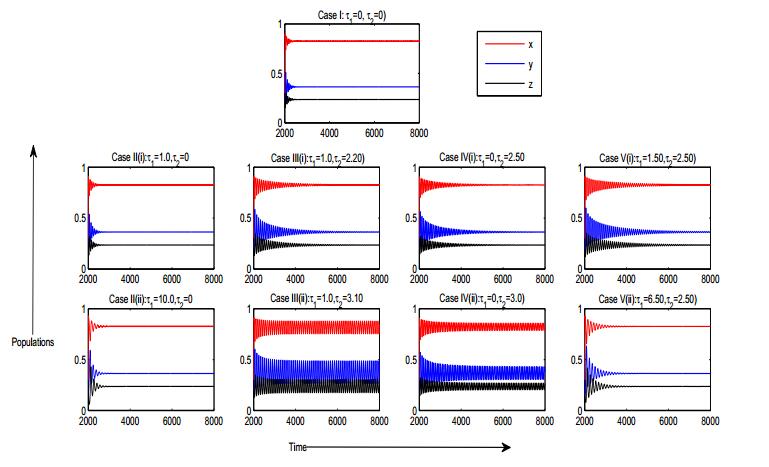
(ⅰ) Case Ⅰ ($\tau_1 = \tau_2 = 0$): $F_{12} = 0.700569 > 0, \; F_{10} = 0.005547 > 0$ and $F_{12}F_{11}-F_{10} = 0.008031 > 0$. Thus, all the conditions of Case Ⅰ are satisfied. Numerical simulation results show that the interior equilibrium point, $P_3 = (0.825453, 0.363298, 0.235593)$ is LAS (see Figure 1 (Case Ⅰ: $\tau_1 = \tau_2 = 0$)).

(ⅱ) Case Ⅱ ($\tau_1 > 0, \tau_2 = 0$): Conditional stability condition (4.33) is not satisfied, as $(B_0+D_0)^2-(C_0+E_0)^2 = 0.000031 > 0$. We have not obtained any positive root of equation (4.31). Thus, we are not able to find any value of $\tau_1$, where system experiences Hopf-bifurcation. System is LAS for all $\tau_1 > 0$ (see Figure 1 (Case Ⅱ(ⅰ): $\tau_1 = 1.0, \; \tau_2 = 0$ and Case Ⅱ(ⅱ): $\tau_1 = 10.0, \; \tau_2 = 0$)).

(Ⅲ) Case Ⅲ ($\tau_1 \in (0, \tau_1^*), \tau_2 > 0$): As in Case Ⅱ, system not bifurcates for any value of $\tau_1$, thus all values of $\tau_1$ comes in its stability range. $(B_0+C_0)^2-(E_0+D_0)^2 = -0.000019 < 0$, so conditional stability condition (4.40) is satisfied. In particular, we have taken $\tau_1 = 1.0$, for this value of $\tau_1$, $\omega = 0.069338$ and critical value of $\tau_2$ is obtained as $\widetilde{\tau_2}^* = 3.0405$. System is LAS for $\tau_2 = 2.2 < \widetilde{\tau_2} = 3.0405$ and unstable for $\tau_2 = 3.1 > \widetilde{\tau_2}^* = 3.0404$. Hopf-bifurcation occurs at $\widetilde{\tau_2}^* = 3.0404$ (see Figure 1 (Case Ⅲ(ⅰ): $\tau_1 = 1.0, \; \tau_2 = 2.20$ and Case Ⅲ(ⅱ):$\tau_1 = 1.0, \; \tau_2^* = 3.10$)).

(ⅳ) Case Ⅳ ($\tau_1 = 0, \tau_2 > 0$): $(B_0+C_0)^2-(D_0+E_0)^2 = -0.000019 < 0$, thus conditional stability condition (4.48) is satisfied. Critical value of $\tau_2$ for $\omega = 0.0794052$ is obtained as $\tau_2^* = 2.88823$.

thus transversality condition is also satisfied at $\tau_2^* = 2.88823$. System is LAS for $\tau_2 = 2.5 < \tau_2^* = 2.88823$ and shows oscillations for $\tau_2 = 3.0 > \tau_2^* = 2.88823$ (see Figure 1 (Case Ⅳ(ⅰ): $\tau_1 = 0, \tau_2 = 2.50$ and Case Ⅳ(ⅱ): $\tau_1 = 0, \tau_2 = 3.0$)). Hopf-bifurcation occurs at critical value of $\tau_2 = \tau_2^* = 2.88823$.

(ⅴ) Case Ⅴ ($\tau_1 > 0, \tau_2 \in (0, \tau_2^*)$): In this case, for $\tau_2 = 2.5$ from its stability range $(0, \; 2.88823)$, conditional stability condition is not satisfied as $(B_0+D_0)^2-(E_0+C_0)^2 = 0.000031 > 0$. Also we have not get any critical value of $\tau_1$, in the stability range of $\tau_2$. Thus, system not bifurcates for any value of $\tau_1$ in the stability range of $\tau_2$. System is LAS for all $\tau_1\geq 0$, $\tau_2 \in (0, 2.88823)$ (see Figure 1 Case Ⅴ(ⅰ): $\tau_1 = 1.50, \tau_2 = 2.50$, V(ⅱ) $\tau_1 = 6.50, \tau_2 = 2.50$).

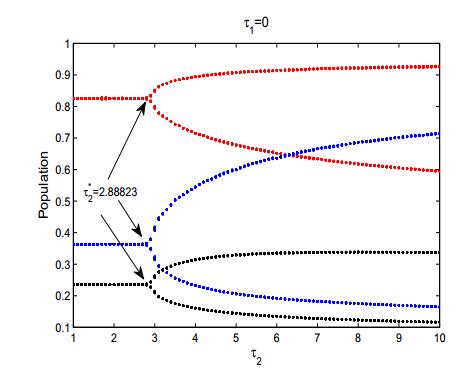
Bifurcation diagram with respect to $\tau_2$ keeping $\tau_1 = 0$ is shown in Figure 2. This illustrates that the bifurcation occurs at critical value of $\tau_2^* = 2.88823$, and below this value system (5.1) is stable and above this value system (5.1) shows oscillatory behaviour.

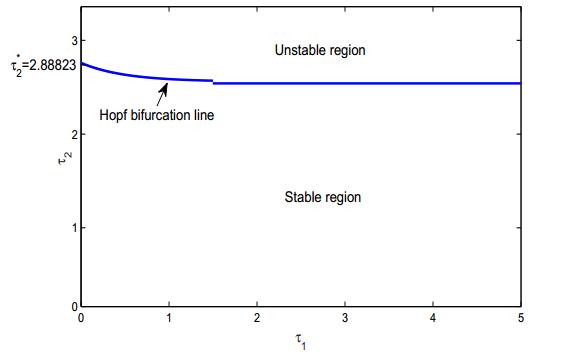
The two dimensional bifurcation diagram for the system (5.1) in $\tau_1-\tau_2$ plane has been presented in Figure 3. In this figure, the blue line denotes Hopf-bifurcation line i.e., at any point $(\tau_1, \tau_2)$ on this blue line, system experiences Hopf-bifurcation. The regions which lie below and above this line are stability and instability regions, respectively. For $\tau_2 < \tau_2^* = 2.88823$, system (5.1) remains stable for all $\tau_1\geq 0$ and for $\tau_2 > \tau_2^* = 2.88823$, system (5.1) becomes unstable for all values of $\tau_1\geq 0$. Here, we have only one critical value $\tau_2^*$, below which the system is stable and above which system becomes unstable and it remains unstable, thus the system does not exhibit stability switching ^[47] with further increase in values of delay parameters.

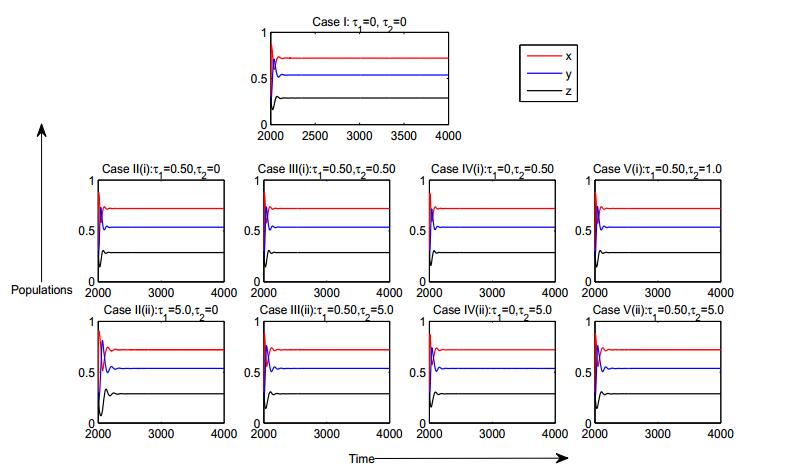
Further, in the numerical Example 1, we have taken $\omega_7 = 3.29$, i.e. slightly increase the value of $\omega_7$ (protection provided by environment to the middle predator). Coexistence equilibrium point is obtained as $P_3 = (0.720293, 0.536708, 0.287340)$. Then, in the absence of delay, system in Example 1 is LAS (see Figure 4 (Case Ⅰ)). We have numerically discussed all the Cases (Ⅱ-Ⅴ) for different values of $\tau_1$, $\tau_2$ and observed that system remains stable (see Figure 4 (Case Ⅱ-Ⅴ)). Thus, for sufficiently high value of environmental protection to the intermediate predator, system remains stable around coexistence equilibrium point and not bifurcates for any value of $\tau_1 \; \text{and} \; \tau_2$ (gestation delays for middle and top predators respectively). Detail description of all the Cases (I-V) is given in Table 2.

Example 2. Consider the following model with a new parameter set

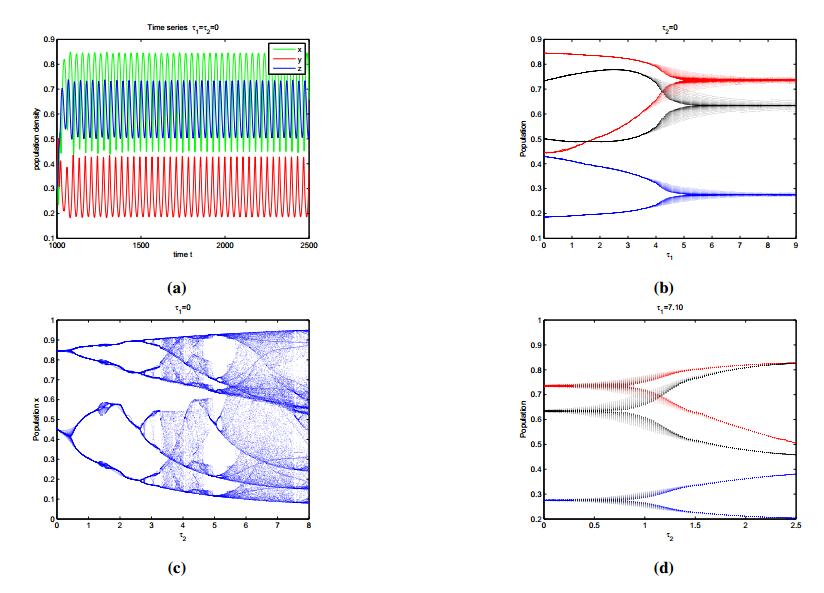
Note that parameter values of system (4.6) are the same as those of system (5.1), except for $\omega_4$ and $\omega_7$. That is, the protection provided by the environment to the prey and intermediate predator is decreased in Example 2. Dynamics of the original system (2.2) have been explored with the help of Example 2. It is observed that system (4.6) shows the limit cycle behaviour in the absence of delay (see Figure 5(a)). Now, we have investigated the effect of both delays $\tau_1$ and $\tau_2$ individually on the dynamics of system (4.6). It is clear from the Figure 5(b), when $\tau_1$ crosses the value ${\tau}^{*}_{1} = 4.85$ for $\tau_2 = 0$, system (4.6) becomes stable and remains stable for $\tau_1 > {\tau}^{*}_{1} = 4.85$, $\tau_2 = 0$. Thus, oscillatory behaviour of coexisting equilibrium point is settled down to the stable dynamics. Again, effect of delay $\tau_2$ for $\tau_1 = 0$, is determined by the Figure 5(c), which shows that increasing value of $\tau_2$ makes the system dynamics chaotic through the period doubling sequences. The combined effect of both the gestation delay $\tau_1$ and $\tau_2$ on the system dynamics is given in the Figure 5(d). Figure 5(d) is plotted at $\tau_1 = 7.1$ (value of $\tau_1$ at which system (4.6) is stable in the absence of $\tau_2$) while taking $\tau_2$ as bifurcating parameter. It is observed that the stable coexistence of species is lost by increasing the value of $\tau_2$ and oscillatory coexistence is obtained for higher value of $\tau_2$.

Example 3. Again, consider the following example with new set of parameter values

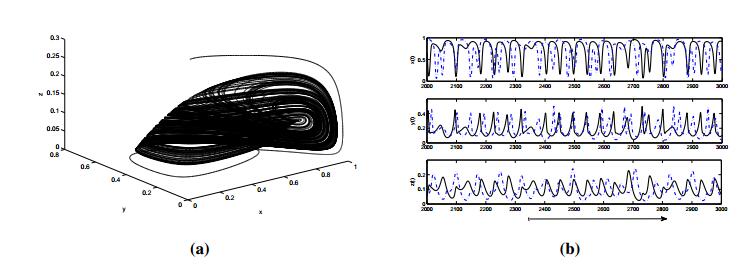
Chaotic behaviour of model (2.2) is illustrated with the help of Example 3. To determine the chaotic behaviour of system, we have plotted the 3D phase portrait of the system. A chaotic attractor is obtained around which system tends to evolve for wide variety of initial conditions and for given sufficient time (see Figure 6(a)). Sensitivity on initial condition (SIC) test is one of the most intuitive tool to check the chaotic behaviour. SIC test tells that if the trajectories owning the slightly different initial conditions grow until their differences become as large as the signal then this ensures the existence of chaotic dynamics in the system. SIC test is given by Figure 6(b).

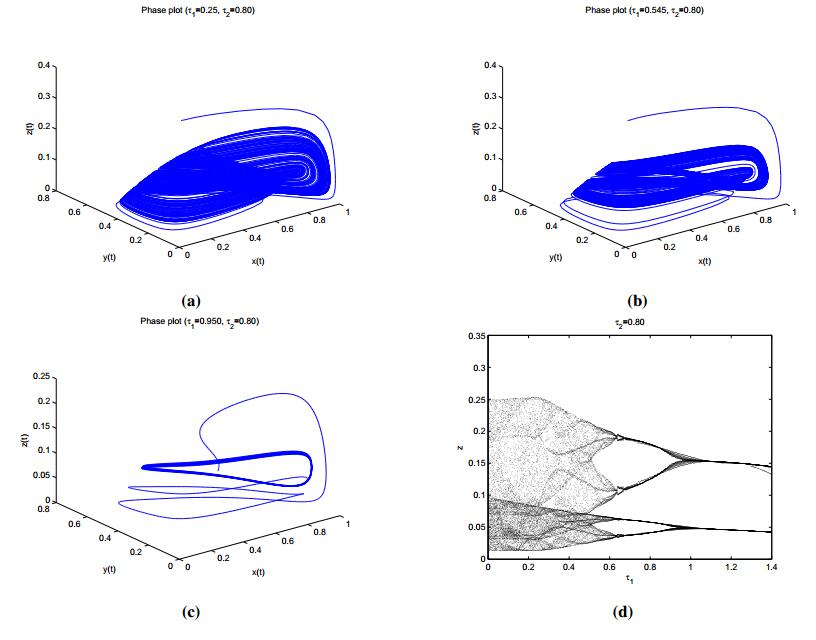
To describe the effect of gestation delay $\tau_1$ and $\tau_2$ on the chaotic dynamics of system, bifurcation diagram for $x$ as a function of $\tau_1$ keeping $\tau_2 = 0.8$ is given by Figure 7(d), which shows that the period halving Hopf-bifurcation phenomenon. Therefore, increase in the value of $\tau_1$ leads to the stable limit cycle dynamics through sequence of chaotic dynamics and different order limit cycles (see Figure 7(a)–(c)).

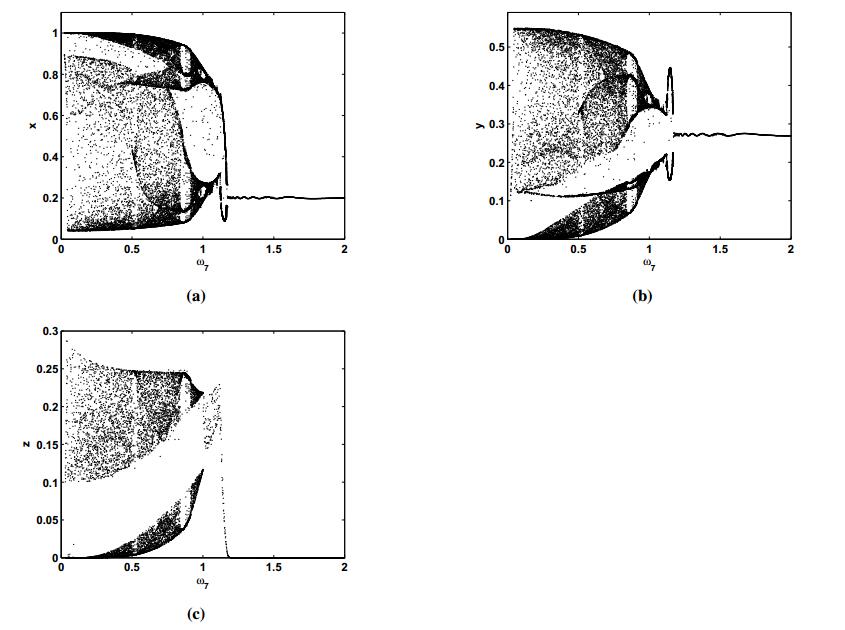
Bifurcation diagrams of the species $x, \; y, \; z$ are also presented taking $\omega_7$ as bifurcating parameter for system (5.4) in the absence of delay. Period halving Hopf-bifurcation phenomenon is observed. It is clear from the bifurcation figure that, for higher value of $\omega_7$, i.e., protection provided by environment to the intermediate predator, species $x, y$ will survive and remain stable, moreover species $z$ will extinct (see Figure 8).

6.   Discussion and Conclusion

Empirical results supporting the existence of chaos in real ecological systems are very rare. McCann et al. ^[48] suggested that it might be due to weak links of species, which may provide stability to these systems. In addition, it is difficult to obtain the accurate data on intrinsic role of species interactions due to measurement error, weather fluctuation, and seasonal disturbances. Experimental demonstrations of chaos in a three species food chain system of ciliate Tetrahymena pyriformis, rod-shaped Pedobacter and coccus Brevundimonas were given by Becks et al. ^[49] and Becks and Arndt ^[50]. In contrast to experimental evidences, chaotic behavior can be observed in interacting population model of species predation, competition, etc. ^{[46,51,52,53]}.

In this work, we have examined a three species food chain system with nonmonotonic functional response. The system is highly nonlinear and applicable for modeling the large variety of natural systems. Gestation delays are incorporated in the system for more realistic consideration. Various interesting dynamical conclusions have been drawn. Stability properties of the system about the equilibrium points are discussed for both delayed and non-delayed systems. Boundedness, positive invariance and conditions for stability of the system are derived. Hopf-bifurcation analysis is discussed for all possible combinations of time delays $\tau_1$ and $\tau_2$. Extensive numerical simulations are performed to validate the analytical findings and to explore the various complex dynamical structures.

From numerical simulation results, we have observed that gestation delay $\tau_1$ has stabilizing effect on the model dynamics (see Figure 5(b)), which is rare as signature feature of time delay is destabilization ^[18,22,41]. Recently, stabilizing effect of maturation time delay has been discussed by Banerjee and Takeuchi ^[25]. However, increasing the value of time delay $\tau_2$ makes the model dynamics chaotic (see Figure 5(c)). Thus, gestation delay for the top predator, $\tau_2$ has a destabilizing effect on the model dynamics. We have obtained the critical value of $\tau_2^* = 2.88823$, below which system shows stable dynamics and above this value system starts showing oscillations through Hopf-bifurcation. Hopf-bifurcation diagram for species $x$, $y$ and $z$, taking $\omega_7$ as bifurcating parameter are also plotted for the non-delayed system. Main findings of our work can be summarized as follows:

(ⅰ) New periodic activities are induced in the stable dynamics of the system due to the incorporation of GDTP, $\tau_2$ and periodic activities are suppressed due to the introduction of GDMP, $\tau_1$.

(ⅱ) Numerically, it has been explained that for the sufficiently high value of $\omega_7$ (environmental protection to intermediate predator), if the system is stable about coexisting equilibrium point in the absence of delay then it will remain stable for all possible combination of $\tau_1$ and $\tau_2.$

(ⅲ) Existence of chaotic dynamics in the system has been observed which is confirmed by the SIC test. Effect of gestation delays $\tau_1$ and $\tau_2$ on the chaotic dynamics is studied with the help of bifurcation diagram and phase portrait.

Acknowledgments

This work was partially supported by the Science & Engineering Research Board (SERB), DST, Govt. of India under grant No. MTR/2017/000301 (to R.K.U.), the Japan Society for the Promotion of Science (JSPS) through the "Grant-in-Aid 26400211 (to Y.T.)".

Conflict of interest

The author declares no conflicts of interest in this paper.