Polymorphisms in the ANKS1B gene are associated with cancer, obesity and type 2 diabetes

1.   Introduction

Graph theory was introduced by Leonhard Euler for obtaining solution of the mathematical problem named "Seven Bridge of Königsberg" in 1736 ^[4]. The practices of the theory are used in the solution of many complex problems of modern life. Topology is an important branch of mathematics because of its contribution to the other branches of mathematics. Recently, the topology has been used as the appropriate frame for all sets connected by relations. Because rough sets and graphs are also based relational combinations, the topological structures of rough sets ^[2] and relation between rough sets and graphs are studied by some researchers ^[5,6,8].

An interesting research topic in graph theory is to study graph theory by means of topology. Some researches have created topologies from graphs using various methods. In 2013, M. Amiri et. al. have created a topology using vertices of an undirected graph ^[3]. In 2018, K.A. Abdu and A. Kılıçman have investigated the topologies generated by directed graphs ^[1].

In this paper, we aim at studying to create a topological space by using a simple undirected graph without isolated vertices. We present some properties of the topology that we create by using such graphs. We show that a topology can be generated by every simple undirected graph without isolated vertices. Moreover, we examine the topologies generated by using certain graphs. We define an equivalence relation on the set of the graphs with same vertices set. Finally, we give necessary and sufficient condition for continuity and openness of functions defined from one graph to another by using the topologies generated by these graphs. As a result of this, we present condition for the topological spaces generated by two different graphs to be homeomorphic.

2.   Preliminaries

In this section, some fundamental definitions and theorems related to the graph theory, approximation spaces and topological spaces used in the work are presented.

Definition 1. ^[4] A graph is an ordered pair of $ (U(G), E(G)) $, where $ U(G) $ is set of vertices, $ E(G) $ is set of edges linking to any unordered pair of vertices of $ G $. If $ e $ is an edge linking to the vertices $ u $ and $ v $, then it is said $ e $ links to vertices $ u $ and $ v $. $ u $ and $ v $ called as ends of $ e $. Moreover, it is said that these vertices are adjacent. A set of pairwise non-adjacent vertices of a graph is called an independent set. If the set of edges and vertices of a graph are finite, this graph is a finite graph. An edge whose ends are only one vertice is called a loop. An edge with distinct ends is a link.

Definition 2. ^[4] A graph is called simple graph, if there is at most one edge linking to arbitrary two vertices of the graph and it has not a loop.

Definition 3. ^[4] Let $ G = (U, E) $ be a graph. If vertices set $ U $ can divided into two subsets $ A $ and $ B $ so that each edge of $ G $ has one end in $ A $ and one end in $ B $, $ G $ is called bipartite graph. In other words, a graph $ G $ is bipartite iff vertices set $ U $ of $ G $ can divided into two independent sets.

Definition 4. ^[4] A walk is a sequence of finite number of adjacent vertices such that $ v_{0}e_{1}v_{1}e_{2}v_{2}...e_{k}v_{k} $ in a graph $ G = (U, E) $. A walk that each edge and vertice is used at most one time is called a path.

Definition 5. ^[4] A cycle is a path with the same starting and ending point and it is denoted with $ C_{n}. $

Theorem 1. ^[7] Let $ X $ be a nonempty set and $ \beta $ be a class of subsets of $ X $. If following conditions are satisfied, the collection $ \beta $ is a base just for one topology.

1. $ X = \bigcup_{B\in \beta }B $

2. For $ B_{1}\in \beta $ and $ B_{2}\in \beta $, the set $ B_{1}\cap B_{2} $ is union of some set belonging to $ \beta $.

3.   A topological space induced by a simple undirected graph

Definition 6. Let $ G = (U, E) $ be a graph. Then the set of vertices becoming adjacent to a vertice $ u $ is called adjacency of $ u $ and it is denoted $ A_{G}(u) $. Minimal adjacency of $ u $ is defined as

Theorem 2. Let $ G = (U, E) $ be a simple undirected graph without isolated vertices. Then the class $ \beta _{G} = \{[u]_{G}:u\in U\} $ is a base for a topology on $ U $.

Proof. Firstly, we shall show that $ \bigcup_{u\in U}\left[u\right] _{G} = U $. From definition of $ [u]_{G} $, $ u\in \lbrack u]_{G} $ is obtained for every $ u\in U. $ Since the graph $ G $ is a graph without isolated vertices, the class $ \{[u]_{G}:u\in U\} $ covers to the set $ U $. That is,

Secondly, we shall show that there exists $ V\subseteq U $ such that $ \left[u \right] _{G}\cap \left[v\right] _{G} = \bigcup_{w\in V\subseteq U}\left[w \right] _{G} $, for every $ \left[u\right] _{G} $, $ \left[v\right] _{G}\in \beta _{G} $. Let $ \left[u\right] _{G}, \left[v\right] _{G}\in \beta _{G} $. Then $ \left[u\right] _{G}\cap \left[v\right] _{G} = \emptyset $ or $ \left[u\right] _{G}\cap \left[v\right] _{G}\neq \emptyset $. If $ \left[u \right] _{G}\cap \left[v\right] _{G} = \emptyset $, it is seen that $ \left[u \right] _{G}\cap \left[v\right] _{G} = \bigcup_{w\in \emptyset }\left[w \right] _{G} $ since $ \bigcup_{w\in \emptyset }\left[w\right] _{G} = \emptyset $. If $ \left[u\right] _{G}\cap \left[v\right] _{G}\neq \emptyset $, there exists at least one $ w\in U $ such that $ w\in \left[u\right] _{G}\cap \left[v\right] _{G} $. Then $ w $ belongs to both $ \left[u\right] _{G} $ and $ \left[v \right] _{G} $. Since $ w\in \left[u\right] _{G} $, it is seen that $ w\in A_{G}(t) $, for all $ t\in U $ such that $ u\in A_{G}(t) $. Similarly, since $ w\in \left[v\right] _{G} $, it is seen that $ w\in A_{G}(t^{\prime }) $, for all $ t^{\prime }\in U $ such that $ v\in A_{G}(t^{\prime }) $.

Hence, $ \ w\in A_{G}(t) $ and $ w\in A_{G}(t^{\prime })\Rightarrow w\in A_{G}(t)\cap A_{G}(t^{\prime }) $

Then it is obtained that

On the other hand,

Then it is obtained that

Therefore, the following equation is obtained from (3.1) and (3.2):

Consequently, $ \beta _{G} $ is a base for a topology on $ U $.

Corollary 1. Each simple undirected graph without isolated vertices creates a topology on vertices set of the graph.

Definition 7. Let $ G = (U, E) $ be a simple undirected graph without isolated vertices. Then the topology generated by $ \beta _{G} = \{[u]_{G}:u\in U\} $ is called the topology generated by the graph $ G $. This topology is in the form of:

Here, the class of closed sets of this topology is in the form of:

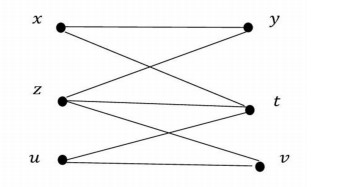
Example 1. The graph whose vertices set is $ U = \{x, y, z, t, u, v\} $ is given in Figure 1.

Figure 1.  The Graph $ G $.

DownLoad: Full-Size Img PowerPoint

The minimal adjacencies of each vertice are as follows:

Thus,

and

$ \tau _{G} $ is topology generated by $ G $. The class of closed sets of this topology is

Class of both open and closed sets is as follows:

Here, it is seen that both open and closed sets different from $ U $ and $ \emptyset $ are $ \{x, z, u\} $ and $ \{y, t, v\} $. Moreover, the graph $ G $ is bipartite and these sets are independent sets whose intersection is $ \emptyset $ and union is $ U $.

Theorem 3. Let $ K_{A, B} = (U, E) $ be a complete bipartite graph. Then the topology generated by $ K_{A, B} $ is a quasi-discrete topology.

Proof. Since $ K_{A, B} $ is a bipartite graph, $ A\cap B = \emptyset $ and $ A\cup B = U $. For every $ x\in U $, $ x\in A $ or $ x\in B $. Let $ x\in A $. Since $ K_{A, B} $ is a complete bipartite graph, we have $ A_{K_{A, B}}(x) = B $ and $ \left[x\right] _{K_{A, B}} = A $. Let $ x\in B $. Then we have $ A_{K_{A, B}}(x) = A $ and $ \left[x \right] _{K_{A, B}} = B $. Hence, the base of the topology generated by $ K_{A, B} $ is as follows:

Therefore, the topology generated by $ K_{A, B} $ is as follows:

$ \tau _{K_{A, B}} $ is a quasi-discrete topology on $ U $.

Theorem 4. Let $ K_{n} = (U, E) $ be a complete graph, where $ U = \{v_{1}, v_{2}, ..., v_{n}\} $. Then the topology generated by $ K_{n} $ is discrete topology on $ U $.

Proof. The minimal neighborhoods of vertices set $ U = \{v_{1}, v_{2}, ..., v_{n}\} $ are as follows respectively:

Therefore,

and the topology generated by $ K_{n} $ is as follows:

It is seen that $ \tau _{K_{n}} $ is discrete topology on $ U $.

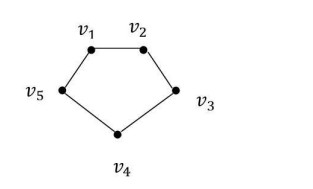
Example 2. Let us investigate the topological space generated by $ C_{5} $ given Figure 2 whose vertices set is $ U = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}\} $.

Figure 2.  The Graph $ C_{5} $.

DownLoad: Full-Size Img PowerPoint

The adjacencies of the vertices of the cycle $ C_{5} $ are as follows:

The minimal adjacencies of the vertices of the cycle $ C_{5} $ are as follows:

Thus,

The class $ \beta _{C_{5}} $ is a base for the discrete topology on $ U $. Thus, the topological space generated by this graph is discrete topological space on $ U $.

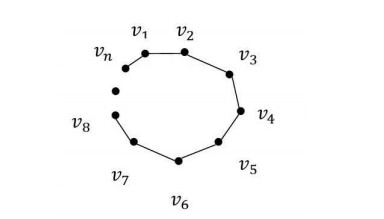
Theorem 5. Let $ C_{n} = (U, E) $ be a cycle whose vertices set is $ U = \{v_{1}, v_{2}, ..., v_{n}\} $, where $ n\geq 3 $ $ (n\neq 4) $. Then the topological space generated by the cycle $ C_{n} = (U, E) $ is a discrete topological space.

Proof. The graph $ C_{n} $ is as in Figure 3.

Figure 3.  The Graph $ C_{n} $.

DownLoad: Full-Size Img PowerPoint

The adjacencies of the vertices of the cycle $ C_{n} $ are as follows:

The minimal adjacencies of the vertices of the cycle $ C_{n} $ are as follows:

Thus, we have

The class $ \beta _{C_{n}} $ is a base for discrete topology on $ U $. Thus, it is seen that the topological space generated by the graph $ C_{n} $ is the discrete topological space on $ U $.

When we assume $ n = 4 $, the graph $ C_{4} $ is a complete bipartite graph. The topological space generated the graph $ C_{4} $ whose vertices set is $ U = \{v_{1}, v_{2}, v_{3}, v_{4}\} $ is $ \tau _{C_{4}} = \{U, \emptyset, \{v_{1}, v_{4}\}, \{v_{2}, v_{3}\}\} $. This topology is not discrete topology, but it is quasi-discrete topology.

Remark 1. Two different graph $ G $ and $ G^{\prime } $with same vertices set can create the same topology. It is seen clearly that although the graphs $ K_{n} $ and $ C_{n} $ with same vertices set is different these graphs create same topology.

Theorem 6. Let $ G $ be set of all simple undirected graphs whose vertices set is $ U = \{v_{1}, v_{2}, ..., v_{n}\} $ without isolated vertices. The relation $ \sim $ defined on $ G $ as "$ G_{1}\sim G_{2}\Leftrightarrow \tau _{G_{1}} = \tau _{G_{2}} $" is a equivalence relation.

Proof. ⅰ) Since $ \tau _{G_{1}} = \tau _{G_{1}}, G_{1}\sim G_{1} $

ⅱ) Let $ G_{1}\sim G_{2} $.From definition "$ \sim ", $ it is seen that $ \tau _{G_{1}} = \tau _{G_{2}} $. Since $ \tau _{G_{2}} = \tau _{G_{1}, } $ we obtain that $ G_{2}\sim G_{1}. $

ⅲ) Let $ G_{1}\sim G_{2} $ and $ G_{2}\sim G_{3}. $ Then it is seen that $ \tau _{G_{1}} = \tau _{G_{2}} $and $ \tau _{G_{2}} = \tau _{G_{3}} $. Thus, we obtain that $ \tau _{G_{1}} = \tau _{G_{3}\text{.}} $ Consequently, we obtain that $ G_{1}\sim G_{3}. $

Since $ G $ is symmetric, transitive and reflexive, it is an equivalence relation.

Theorem 7. Let $ G = (U, E) $ and $ G^{\prime } = (U^{\prime }, E^{\prime }) $\ be two graphs without isolated vertices. Let $ \tau _{G} $ and $ \tau _{G^{\prime }} $ be the topologies generated by $ G $ and $ G^{\prime } $ respectively and $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be a function. Then $ f $ is continuous iff for every $ u\in U $,

Proof. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be a continuous function. Then $ \beta _{G} = \{\left[u\right] _{G}:u\in U\} $ and $ \beta _{G^{\prime }} = \{\left[u^{\prime }\right] _{G^{\prime }}:u^{\prime }\in U^{\prime }\} $ are bases of topologies $ \tau _{G} $ and $ \tau _{G^{\prime }} $, respectively. Since $ f $ is continuous, there is $ B\in \beta _{G} $ such that $ f(B)\subseteq \left[f(u)\right] _{G^{\prime }} $ for every $ u\in U $. $ \left[u\right] _{G} $ is the minimal element containing $ u $ of $ \beta _{G} $. Thus, it is obtained that

Conversely, let $ f(\left[u\right] _{G})\subseteq \left[f(u)\right] _{G^{\prime }} $ for every $ u\in U $. It is seen that $ \left[f(u)\right] _{G^{\prime }}\in \beta _{G_{f(v)}^{\prime }} $, for every $ u\in U $. Since $ f(\left[u\right] _{G})\subseteq \left[f(u)\right] _{G^{\prime }} $ and $ \left[u\right] _{G}\in \beta _{G_{v}} $, the function $ f $ is a continuous function.

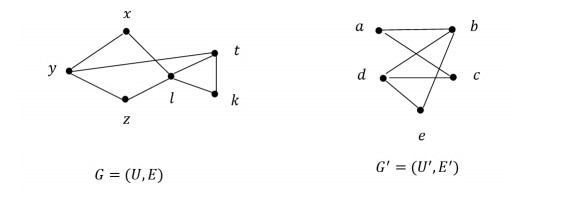
Example 3. Let us investigate the graphs $ G = (U, E) $ and $ G^{\prime } = (U^{\prime }, E^{\prime }) $ is given in Figure 4. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be a function defined by

Figure 4.  The Graphs $ G $ and $ G^{\prime } $.

DownLoad: Full-Size Img PowerPoint

The minimal adjacencies of vertices of $ G $ are follows:

The minimal adjacencies of vertices of $ G^{\prime } $ are as follows:

It is seen that $ f(\left[v\right] _{G})\subseteq \left[f(v)\right] _{G^{\prime }} $, for every $ v\in U $. Therefore, $ f $ is a continuous function.

Corollary 2. Let $ f:(U, \tau _{K_{n}})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be arbitrary function, where $ K_{n} = (U, E) $ is a complete graph and $ G^{\prime } = (U^{\prime }, E^{\prime }) $ is arbitrary graph. Then $ f $ is continuous function.

Theorem 8. Let $ G = (U, E) $ and $ G^{\prime } = (U^{\prime }, E^{\prime }) $ be two simple undirected graphs without isolated vertice and $ \tau _{G} $ and $ \tau _{G^{\prime }} $ the topologies generated by this graphs, respectively. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be a function. Then $ f $ is open function iff for every $ u\in U, $

Proof. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be an open function. Then $ f(\left[u\right] _{G}) $ is an open subset of $ U^{\prime } $ for every $ \left[u\right] _{G}\in \beta _{G} $. It is obtained that

Therefore, we have

Conversely, Let $ \left[f(u)\right] _{G^{\prime }}\subseteq f(\left[u\right] _{G}) $, for every $ u\in U $. It is seen that for every $ u\in U $,

Thus, $ f(\left[u\right] _{G}) $ is an open subset of $ U^{\prime } $. Consequently, we can say $ f $ is an open function.

From above theorem, it is seen that an open function may not continuous and a continuous function may also not be open. Now we give a necessary and sufficient condition for a function to be continuous and open.

Theorem 9. Let $ G = (U, E) $ and $ G^{\prime } = (U^{\prime }, E^{\prime }) $ be simple undirected two graphs without isolated vertices and $ \tau _{G} $ and $ \tau _{G^{\prime }} $ the topologies generated by this graphs, respectively. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $ be a function. Then $ f $ is a open and continuous function iff for every $ u\in U, $

Proof. It is clearly seen from Theorem 3.6 and Theorem 3.7.

Corollary 3. Let $ G = (U, E) $ and $ G^{\prime } = (U^{\prime }, E^{\prime }) $ be simple undirected two graphs without isolated vertice and $ \tau _{G} $ and $ \tau _{G^{\prime }} $the topologies generated by this graphs, respectively. Let $ f:(U, \tau _{G})\rightarrow (U^{\prime }, \tau _{G^{\prime }}) $\ be a function. Then $ f $ is a homeomorphism iff $ f $ is a bijection that for every $ u\in U, $

4.   Conclusions

In this paper it is shown that topologies can be generated by simple undirected graphs without isolated vertices. It is studied topologies generated by certain graphs. Therefore, it is seen that there is a topology generated by every simple undirected graph without isolated vertices. Properties proved by these generated topologies are presented. An equivalence of the graphs with same vertices set is defined. Finally, necessary and sufficient condition is given for continuity and openness of a function defined to another graph from one graph. This enables us to determine whether these topological spaces is homeomorphic without needing to find the topological spaces generated by two graphs.

Acknowledgement

The first author would like to thank TUBITAK (The Scientific and Technological Research Council of Turkey) for their financial supports during her PhD studies.

Conflict of interest

The authors declare that they have no competing interest.