Numerical evaluation of ablation zone under different tip temperatures during radiofrequency ablation

1.   Introduction

Radiofrequency ablation (RFA) has become a promising minimally invasive technique for treating hepatocellular carcinoma (HCC) and metastatic liver cancer ^[1,2], especially for treating tumors with 3 cm or smaller in diameter. An RFA device involves a radiofrequency (RF) power generator, an RF applicator, and a ground pad. The RF applicator consists of an RF electrode, an aperture component, and an insulation component. The ground pad is often placed on the patient's back or thigh during an RFA procedure. The alternating current (approximately 300–500 kHz) is delivered from the RF generator through the electrode inserted into the target tissue and can lead to resistive or Joule heating ^[3,4]. The RFA device and the patient constitute a closed-loop electrical circuit. There are three types of RFA devices: power-controlled type, impedance-controlled type, and temperature-controlled type ^[5]. At present, temperature-controlled RFA devices are widely used to ablate liver tumors. RF power is applied to retain the tip temperature at a preset value ^[6].

The major limitation associated with RFA is the small sizes of ablation zones, causing incomplete tumor ablation ^[7]. A tumor-free safety margin was one of the most significant factors influencing the local tumor recurrence (LTR) rate after RFA treatments ^[8]. A post-ablation safety margin over 0.5 cm could reduce the LTR of liver cancer ^[6]. To reduce the risk of LTR, treatment planning is crucial for RFA, which involves the modelling of the ablative margin and the ablation volume during RFA. The finite element method (FEM) has been proposed for modelling the RFA-induced ablation volume changes. Zhang et al. ^[9] investigated the correlation between the ablation zone and the tissue size in pulsed RFA (PRFA). It was shown that the half-square PRFA could acquire a larger ablation zone compared with the half-sine PRFA. Nagarajan et al. ^[10] investigated the relationship between the wavelength, averaged liver tissue absorption coefficient, reduced scattering coefficient, and the tissue damage in thermal ablation of ex vivo porcine liver tissues. A curve function was derived. However, the major limitation is that the liver absorption coefficient and the scattering coefficient at higher temperatures are not accurately measured. At present, the issue how to quantify the ablation zones remains unresolved.

For a successful RFA treatment planning, the AM dimensions and the ablation volumes should be efficiently and accurately evaluated. In this study, the changes of the ablative margins with time at four tip temperatures in temperature-controlled RFA were analyzed. The characterization forms of the ablation volumes over time for different tip temperatures were derived.

2.   Materials and method

2.1.   Ex vivo porcine liver experiments

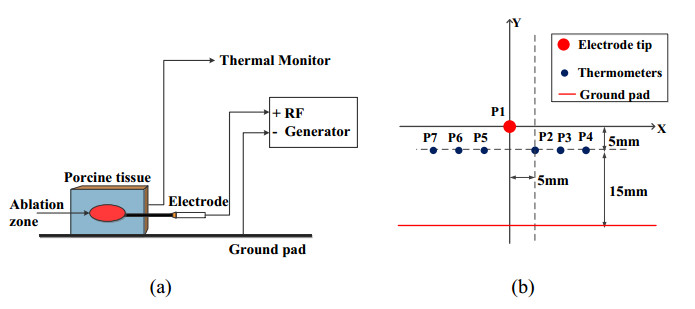
The experimental system consisted of a temperature-controlled RFA device (RFA-I; Blade Co., Ltd., Beijing, China) with a single-needle electrode (RFA0115), a multiple data acquisition device (34970A; Agilent Technologies Inc., Santa Clara, CA, USA), a ground pad and ex vivo porcine livers. The RFA-I device had a frequency of 330 kHz, with four tip temperatures (80, 85, 90, and 95 ℃). The tip temperature of 90 ℃ was commonly used in the temperature-controlled RFA for liver tissues ^[11,12,13]. Therefore, these four tip temperatures were all tested in this study. The data acquisition device was utilized to measure the temperature changes in real time. The RF electrode and the thermometers were horizontally inserted into the ex vivo porcine liver, as shown in Figure 1 (a). The plan view of the positions of the RF electrode and thermometers are shown in Figure 1 (b).

Figure 1.  Experimental setup: (a) the schematic diagram for ex vivo porcine liver RFA, (b) the plan view of the positions of the RF electrode and thermometers.

DownLoad: Full-Size Img PowerPoint

2.2.   Temperature-controlled RFA model

2.2.1.   Geometric modelling

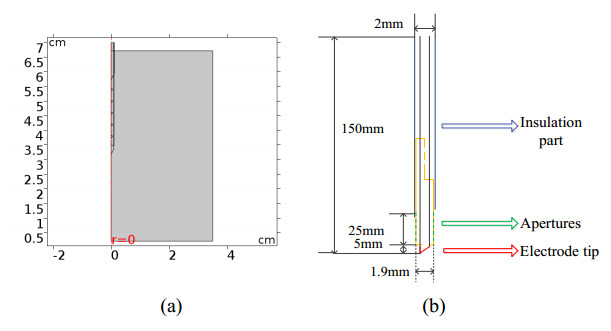
Generally, the diffusion equation is solved numerically by FEM, which offers advantages in speed and flexibility ^[14]. In the numerical simulation study, COMSOL Multiphysics software (COMSOL Inc., Palo Alto, CA, USA) was employed to carry out the FEM modelling of temperature-controlled RFA. To improve the computational efficiency of the FEM model, a two-dimensional axisymmetric RFA numerical model was built in this study. The RF single-needle electrode was disposed as the axis of symmetry. As shown in Figure 2 (a), the RF electrode tip lies at the point (0 mm, 32.5 mm), and the width and height of the tissue are 35 and 65 mm, respectively. Figure 2 (b) shows the structure of the RF electrode, consisting of insulation part, apertures and electrode tip.

Figure 2.  Numerical simulation of RFA: (a) geometric model, (b) the structure of the RF electrode.

DownLoad: Full-Size Img PowerPoint

2.2.2.   Mathematical modelling

A coupled electromagnetic field-heat transfer field modeling approach was employed in the RFA simulation. Combining these two fields, we can predict the temperature distributions within the tissue. For the electromagnetic field, the applied voltage can be computed by using the generalized Laplace equation:

where $\sigma (T)$ is the electrical conductivity (S/m) and $U$ is the electric potential (V). The heat generated within the tissue by RF electrical current, ${Q_{hs}}$, can be determined by

For the thermal field during RFA, the Pennes bio-heat transfer equation was used in this study to achieve the heat-transfer modelling of blood perfused tissue and the biological metabolic activity ^{[15,16,17,18]}:

where $T$ and ${T_b}$ are the temperatures of tissue and blood (℃), respectively; $t$ is the ablation time (s); $\rho$ and ${\rho _b}$ are the densities of tissue and blood, respectively (kg/m³); $c$ and ${c_b}$ are the specific heat capacities of tissue and blood, respectively (J/(kg∙K); $k$ is the thermal conductivity of tissue (W/(m∙K); ${\omega _b}$ is the volume blood perfusion rate (s^-1); ${Q_m}$ is the metabolic heat generation rate (W/m³) and usually can be neglected; ${Q_{hs}}$ is the heat generated by the RF electrical current and can be computed by Equation (2.2) (W/m³).

Early studies indicated that the electrical conductivity and the thermal conductivity of tissues would change with temperature in the clinical RFA therapy ^[9]. Therefore, in this study, the temperature-dependent functions were selected for $\sigma$ and $k$ parameters of both liver tumor and healthy liver tissue to enhance the prediction accuracy of the temperature distribution simulation model. In the FEM model of liver RFA, the thermal and electrical properties of ex vivo livers are listed in Table 1.

Table 1.  Thermal and electrical properties of ex vivo liver tissue.

Properties	Temperature dependence	Values
$\rho$(kg/m3)	$\rho = {\rho _0}$	1079
$c$(J/(kg∙K)	$c = {c_0}$	3540
$\sigma$(S/m)	$\sigma (T) = (1 + 0.02(T - {T_{ref}})){\sigma _{ref}}, \;T < 100\;^\circ {\text{C}}$	${\sigma _{ref}} = 0.2, \;{T_{ref}} = 20\;^\circ {\text{C}}$
$k$(W/(m∙K)	$k(T) = {k_{ref}} + 0.0013(T - {T_{ref}}), \;T < 100\;^\circ {\text{C}}$	${k_{ref}} = 0.52, \;{T_{ref}} = 20\;^\circ {\text{C}}$

---

 | Show Table

DownLoad: CSV

2.2.3.   Numerical simulation setup

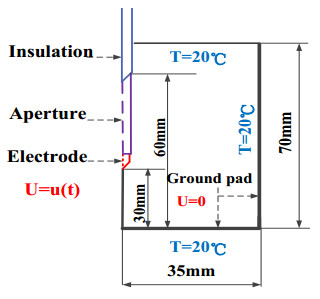
To solve the simulation model of RFA, the boundary conditions and the initial conditions of the FEM model were specified. For the current field, the single-electrode tip was regarded as the voltage source, and the boundary of the liver tissue was set as the ground. As far as the bio-heat transfer physical field was concerned, the initial and boundary temperatures and the tissue blood perfusion rate were set at 20 ℃ and 0 s^-1, respectively, for consistency with the ex vivo experiments. The electrical boundary and thermal boundary conditions of single-electrode tip and ex vivo porcine liver in the temperature-controlled RFA numerical model are shown in Figure 3. Table 2 shows the thermal and electrical properties of the RF single-electrode.

Figure 3.  Boundary conditions of the geometric model.

DownLoad: Full-Size Img PowerPoint

Table 2.  Thermal and electrical properties of RF single-electrode.

Elements	$\sigma$(S/m)	$k$(W/(m∙K)	$\rho$(kg/m3)
Electrode	1e8	18	6450
Apertures	4e6	71	21500
Insulation	1e-5	0.026	70

---

 | Show Table

DownLoad: CSV

In this study, the triangle meshing algorithm was used in the FEM model due to the convenient and provable mathematical properties. To examine the mesh convergence, the meshes of the model were set at coarse level (3582 elements), medium level (5146 elements), and fine level (5306 elements), respectively. To further improve the accuracy of simulation temperature and the computational efficiency of the model, the optimized meshes involved two kinds of resolution levels. The eletrode tip was modelled by fine meshed, the insulation part and the apertures of electrode were modelled by medium meshes, and the porcine tissue was modelled by medium meshes. The whole model had 36 vertex elements, 714 boundary elements, 5146 elements, and 20963 degrees of freedom. The simulation results showed that this kind of triangle meshes had better convergence and could be solved in 34 s.

A variable RF voltage source was controlled by a proportional-integral (PI) controller so that the tip temperature would maintain at a preset value. RF voltage was computed by

where $U$ is the voltage applied on the RF single-electrode tip; ${K_P}$ and ${K_I}$ are the proportional and integral coefficient, respectively, and are determined based upon the preset tip temperature through a trial-and-error procedure ^[20]. In this study, ${K_P}$ and ${K_I}$ are assumed to be 0.17 and 0.0045, respectively.

2.2.4.   Ablation volume assessment

Thermal isoeffective dose (TID) model, Arrhenius model and isothermal contour (IT) have been employed to assess the ablation volume after RFA ^[7]. The TID model is derived from the Arrhenius model and is only used to assess the tissue death caused by lower temperatures (43–50 ℃). Many studies estimate tissue damages in the RFA numerical model using the Arrhenius model ^[21,22,23]:

where $\Omega \;(t)$ is the degree of the tissue death, $A$is the frequency factor (s^-1), $R$ is the universal gas constant (8.314 J∙mol^-1K^-1), and $T(\tau )$ is the heating temperature (K).

The 50–60 ℃ isotherm contour (IT50-60) was also employed to calculate ablation volumes in RFA ^{[24,25,26,27]}. However, some researches demonstrated that IT50 might overestimate the size of ablation volumes. IT54 was often regarded as the reasonable isotherm of irreversible damage during RFA treatment ^[12]. The degree of tissue damage is quantified by IT54 and can be computed as

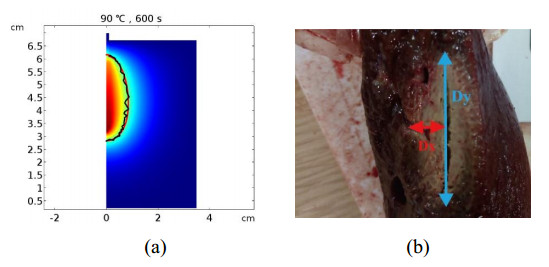
In Figure 4 (a), the smooth red curve indicates the damage zone assessed by the IT54 method, and the rough black curve is the evaluation result from the Arrhenius model. It can be seen that the thermal coagulation zone based on the Arrhenius model has a good consistency with IT54. Thus, we utilized IT54 as a metric for comparing ablation zone boundaries predicted by numerical simulations. According to the gross pathology of the RFA-induced thermal lesion of ex vivo liver in Figure 4 (b), the ablation zone can be divided into four zones: the carbonization zone around the electrode tip, the pale lesion zone, the congestive zone, and the unheated normal liver tissue. In Figure 4 (b), ${D_y}$ denotes the longitudinal diameter of the ablation zone, and ${D_x}$ represents the transverse radius of the ablation zone.

Figure 4.  The sectional results of the ablation zone: (a) ablation zones assessed by the IT54 method (smooth red curve) and the Arrhenius model (rough black curve), (b) gross pathology of ablated ex vivo porcine liver.

DownLoad: Full-Size Img PowerPoint

2.3.   Characterization of AM based on the growth model of transverse and longitudinal diameter

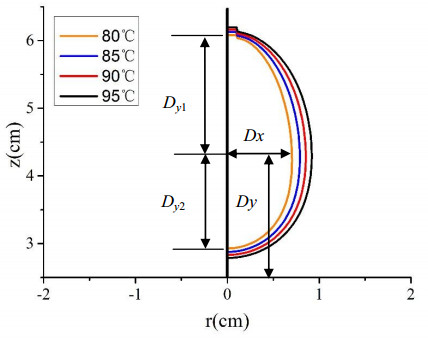
Overestimating the expected shape and size of the ablation zone can result in failure of local tumor control. IT54 at different tip temperatures from FEM model of RFA are shown in Figure 5. It can be observed that the AM is more similar to the water drop shape when the tip temperature was set at 80 ℃. To depict the AM changing with time more properly, the longitudinal diameter of the ablation zone was divided into ${D_{y1}}$ and ${D_{y2}}$. According to the values of the characteristic lengths (${D_{y1}}$ and ${D_{y2}}$) obtained by the numerical simulations, it was found that these lengths varying with ablation time ($t$ > 150 s) at different tip temperatures could be computed as follows:

Figure 5.  The ablation boundary of IT54 in FEM model.

DownLoad: Full-Size Img PowerPoint

where ${D_i}$ represents ${D_x}$, ${D_{y1}}$ and ${D_{y2}}$, respectively; ${c_1}$, ${c_2}$ and ${c_3}$ are regression coefficients.

Equation (2.7) shows that ${D_x}$, ${D_{y1}}$ and ${D_{y2}}$ non-linearly increase with the ablation time. The larger the transverse and longitudinal diameters of the ablation zone are, the larger the AM is. Because the variation of the AM is closely related to the characteristic lengths, we built the growth model of AM based upon the values of transverse and longitudinal diameters. The AM data at the end of RFA (t = 600 s) were obtained by using the numerical model. The AM was described as follows:

The shape and size of the AM would gradually expand over time. However, in Equation (2.8), the proposed model merely described the AM shape at the end of RFA. To investigate the dynamic changes of AM with ablation time during temperature-controlled RFA, variation coefficients (${\alpha _1}$, ${\alpha _2}$, ${\beta _1}$ and ${\beta _2}$) were introduced into Equation (2.8). Therefore, the AM changing with time during temperature-controlled RFA could be described by

2.4.   Relationship between ablation volumes and ablation time at different tip temperatures

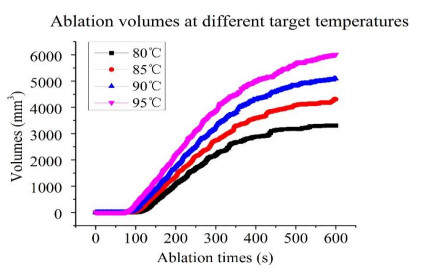
According to the data of the computational model, the ablation volumes at different preset values during RFA were analyzed. The ablation volumes at four tip temperatures exhibit a similar trend over time (Figure 6). The tissue has a low center temperature at the beginning of the temperature-controlled RFA, and the ablation zone has gradually developed after about 70 s ablation, as indicated in Figure 6. In this study, the volume data (Table 3) of temperature-controlled RFA was acquired by solving Equation (2.6), and the volume function was fitted by 1Stopt software (7D-Soft High Technology, Inc., Beijing, China). The volume model can be calculated by

Figure 6.  Variations of ablation volumes over time at different target temperatures.

DownLoad: Full-Size Img PowerPoint

Table 3.  Ablation volumes (mm³) at different preset tip values.

t(s)	$V({T_{set}} = 80\;^\circ {\text{C}})$	$V({T_{set}} = 85\;^\circ {\text{C}})$	$V({T_{set}} = 90\;^\circ {\text{C}})$	$V({T_{set}} = 95\;^\circ {\text{C}})$
150	415.7	653.8	893.8	1173.6
200	1058.9	1362.4	1743.6	2161.1
250	1674.2	2132	2536.6	3083.9
300	2189.6	2740.1	3284	3834.1
350	2661.6	3292.9	3803.8	4489.5
400	2876	3593.3	4295.6	5000.3
450	3132.1	3875.2	4591.5	5260.3
500	3179.1	4085.4	4813.5	5658.8
550	3293.2	4136	4981.3	5835.5
600	3306.5	4310	5090.8	6012.4

---

 | Show Table

DownLoad: CSV

where ${V_i}$ represents the ablation volume; $i$ takes 80, 85, 90, and 95 ℃, respectively; ${c_1}$, ${c_2}$, ${c_3}$ and ${c_4}$ represent function coefficients.

3.   Results

3.1.   Validation of the temperature-controlled RFA numerical model

A total of 12 ex vivo porcine liver samples (n = 3 for each of the four tip temperatures) were used and the size of each liver sample was approximately 70×70×40 mm³. In Table 4, it was found that there was a good agreement on ablation zone sizes between the numerical model and the ex vivo porcine liver experiments. There were acceptable discrepancies on the transverse and longitudinal diameters of the ablation zone between the ex vivo experiments and FEM models at the end of ablation (t = 600 s). The discrepancy may come from inaccurate evaluation of ablation zone sizes. Overall, the proposed FEM model has a better accuracy to predict ablation zone sizes.

Table 4.  Comparisons of the transverse and longitudinal diameters of the ablation zone obtained from the FEM models and ex vivo porcine liver experiments.

Target Temperature	Half of transverse diameter Dx (mm)		Longitudinal diameter Dy (mm)
	Ex vivo*	FEM	Ex vivo*	FEM
80 ℃	6.25 ± 0.3	7.05	29.3 ± 1.5	31.56
85 ℃	6.50 ± 0.8	7.90	31.3 ± 1.2	32.51
90 ℃	7.65 ± 0.6	8.55	33.2 ± 3.6	33.33
95 ℃	8.50 ± 0.5	9.19	34.0 ± 10	34.11
*Results of the ex vivo porcine liver experiments were given as mean ± standard deviation.

---

 | Show Table

DownLoad: CSV

3.2.   Characterization of AM based on the growth model of transverse and longitudinal diameters

When the tip temperatures are taken as different preset values (80, 85, 90, and 95 ℃), the results of the characteristic lengths (${D_x}$, ${D_{y1}}$, and ${D_{y2}}$) could be acquired by solving the FEM model. Substituting the above results into Equation (2.7), the coefficients of the characteristic lengths growth model can be obtained, as shown in Table 5. The correlation coefficients (${R^2}$) of prediction data and simulation results were all greater than 0.95. It is demonstrated that the prediction model has a good reliability.

Table 5.  Correlation coefficients of characteristic lengths.

		${c_1}$	${c_2}$	${c_3}$	R2*
80 ℃	Dx(mm)	0.82851	−228.927	−1.18125	0.9980
	Dy1 (mm)	0.94280	12.46742	−0.41346	0.9666
	Dy2(mm)	1.51848	−1190.96	−1.36653	0.9791
85 ℃	Dx(mm)	1.02059	−55.44892	−0.86038	0.9987
	Dy1 (mm)	−3.67090	8.78543	−0.07177	0.9633
	Dy2(mm)	1.66457	−216.91	−1.03306	0.9786
90 ℃	Dx(mm)	1.10417	−52.77189	−0.83942	0.9988
	Dy1 (mm)	4.37371	−0.66816	0.20841	0.9698
	Dy2(mm)	2.16516	−38.81296	−0.63381	0.9858
95 ℃	Dx(mm)	1.20012	−44.30765	−0.79151	0.9997
	Dy1 (mm)	1.30378	20.51249	−0.55363	0.9530
	Dy2(mm)	1.75060	−543.33	−1.20729	0.9756
* ${R^2}$represents the square of the correlation coefficient.

---

 | Show Table

DownLoad: CSV

For instance, when the preset value of the electrode tip is 90 ℃, the characteristic length growth model of ablation zone can be obtained from Equation (2.7) and Table 5, and can be expressed as follows:

The sizes of ablation zones increased with ablation time. At the last stage of RFA, the growth rates of characteristic lengths were declining. When the tip temperatures were set at 80, 85, 90, and 95 ℃, the data of AM (t = 600 s) could be received by FEM model of RFA. Based on the above results and Equation (2.8), the coefficients of AM prediction model were obtained (Tables 6 and 7). All the ${R^2}$ values were greater than 0.92, indicating the high precision of the proposed AM prediction model. To obtain the results of AM at different ablation times, the variation coefficients (${\alpha _1}$, ${\alpha _2}$, ${\beta _1}$ and ${\beta _2}$) were introduced into Equation (2.8). ${\alpha _1}$, ${\alpha _2}$, ${\beta _1}$ and ${\beta _2}$ can be described as

Table 6.  Correlation coefficients of F1(x), t = 600 s.

	${c_1}$	${c_2}$	${c_3}$	${c_4}$	${R^2}$*
80 ℃	3.28042	-1.83373	0.69982	-2.13926	0.9206
85 ℃	3.19238	-1.51302	0.58961	-1.17663	0.9850
90 ℃	3.33907	-1.19719	0.11529	-0.44639	0.9998
95 ℃	3.23823	-0.99572	0.04486	-0.31572	0.9589

---

 | Show Table

DownLoad: CSV

Table 7.  Correlation coefficients of F2(x), t = 600 s.

	${c_1}$	${c_2}$	${c_3}$	${c_4}$	${R^2}$*
80 ℃	2.27220	-2.21882	-0.21987	1.27316	0.9969
85 ℃	2.15501	-1.81214	-0.02759	0.58058	0.9981
90 ℃	1.90836	-1.56529	0.04312	0.32386	0.9988
95 ℃	1.88225	-1.35413	-0.01681	0.25887	0.9975

---

 | Show Table

DownLoad: CSV

In Equation (3.2), when t is 600 s, the values of ${\alpha _1}$, ${\alpha _2}$, ${\beta _1}$ and ${\beta _2}$ are 1.

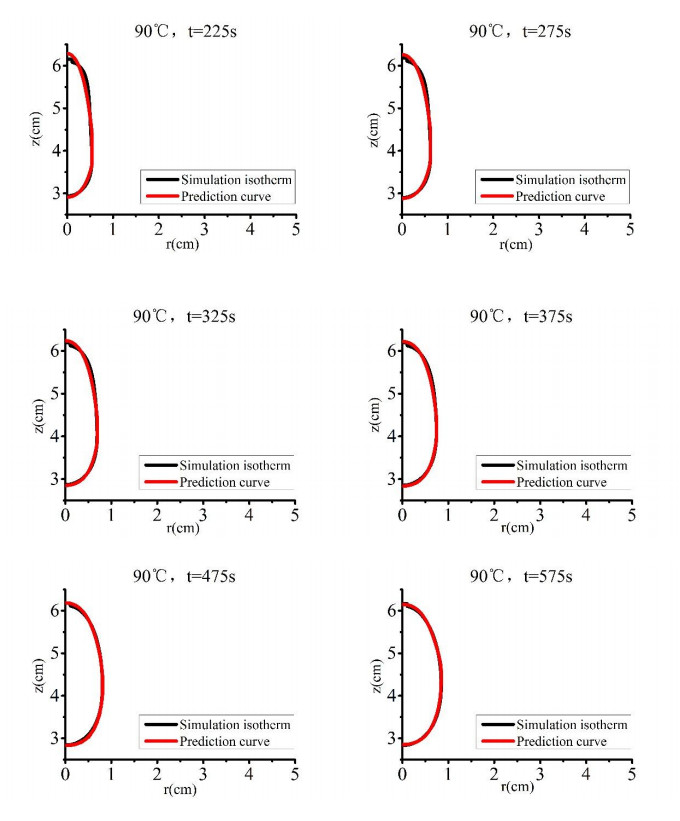
To demonstrate the validity of the AM model, we compared the fitted values with FEM simulation values. When the tip temperature is 90 ℃, the AM prediction model can be obtained from Equations (2.9), (3.1), and (3.2), and can be depicted as

The simulations and predictions of AM results at different ablation times were compared in Figure 8. It was demonstrated that the results of AM model had a good consistency with FEM model. When t is 225, 275, 325, 375, 475, and 575 s, the mean square errors of predictions for AM were 1.21, 0.33, 0.62, 0.27, 0.32, and 0.19 mm, respectively.

Figure 8.  Comparisons of simulation and prediction results for AM.

DownLoad: Full-Size Img PowerPoint

3.3.   Relationship between ablation volumes and ablation time at different tip temperatures

The ablation volumes can be obtained by the FEM model when the tip temperatures are set at different temperatures. Substituting the volume simulation results at different preset values into Equation (2.10) can derive the coefficients of the ablation volume model, as shown in Table 8.

Table 8.  The ablation volume model during temperature-controlled RFA.

Temperature	${c_1}$	${c_2}$	${c_3}$	${c_4}$	Time Constraint (s)	${R^2}$*
80 ℃	$- 1.3 \times {10^{ - 5}}$	-0.002	13.67	-1424	$t$$\geqslant$94 s	0.9958
85 ℃	$- 8.2 \times {10^{ - 6}}$	-0.009	18.15	-1766	$t$$\geqslant$82 s	0.9979
90 ℃	$- 7 \times {10^{ - 6}}$	-0.012	21.56	-1973	$t$$\geqslant$76 s	0.9990
95 ℃	$- 9.6 \times {10^{ - 7}}$	-0.022	26.77	-2254	$t$$\geqslant$73 s	0.9989

---

 | Show Table

DownLoad: CSV

At the beginning of temperature-controlled RFA, the center temperature of the single-electrode tip rapidly rises to the preset temperature. As ablation time goes on, the tissue starts to coagulate. There are some differences for the coagulation time at different preset temperatures. Considering this phenomenon, the time constraints (t) was introduced into the ablation volume model, as listed in Table 8. In each case, the correlation coefficient of numerical simulations and curve fitting results is greater than 0.99. The proposed ablation volume model can effectively predict ablation volume during temperature-controlled RFA. When the tip temperature is 90 ℃, the ablation volume model can be expressed as:

where t is the ablation time (s).

4.   Discussion

Compared with surgical resection, RFA has the characteristics of cost-effectiveness and well-tolerance for the treatment of liver tumors that are less than 3 cm in diameter ^[28,29]. However, previous studies reported that the liver tumor was prone to recur due to incomplete ablation in RFA procedure ^[16]. Therefore, accurate preoperative assessment of the shape and size of the ablation zone can effectively prevent tumor recurrence after RFA. Numerical models of the RFA treatments have become a powerful tool for forecasting the temperature profiles and damage volumes within the target tissue. The purpose of this study was to investigate the shape and size of ablation zone changing with ablation time at different tip temperatures (i.e., 80, 85, 90 and 95 ℃) during temperature-controlled RFA.

A two-dimensional simulation model of liver RFA with single-electrode was built in this study. To achieve a constant center temperature of single-electrode in RFA procedure, a closed-loop PI controller was used in the FEM model. Twelve RFA experiments of ex vivo porcine livers were performed to validate the effectiveness of the FEM model for temperature-controlled RFA. Non-linear dynamic growth models of the characteristic lengths were built by using 1Stopt software to depict the variations of the transverse and longitudinal diameters. It could be found from the characteristic growth models that the transverse and longitudinal diameters of the ablation zones increased with the ablation time, and the longitudinal diameter of the ablation zone along the direction of the RF electrode was often greater than the transverse diameter. These findings are in good agreement with the characteristics of transverse and longitudinal diameters of the ablation zones obtained from the ex vivo animal experiments. Wang et al. ^[30] proposed a neural network-based system to evaluate the ablation lesion depth in real time. All training data (n = 72) were successfully obtained by power-controlled RFA within ex vivo animal tissue experiments (pork loin and belly). The results demonstrated that the accuracy of NN trained to estimate the size of ablation lesion depth was approximately 93%. Compared with our growth model, the prediction model by Wang et al. ^[30] required more experimental data to train the model and the constructing process was rather complex.

The novelty of this study was to employ the growth characteristics of the transverse and longitudinal diameters of the ablation zones, and propose a prediction model of the ablation boundaries based on the characteristic length growth model. Ablation zones of different applicator types were usually identified as simple ellipsoids. However, in practice, the simplified ellipsoid is merely a rough estimation of the ablation zone ^[31]. The shape of the ablation zone is not a regular ellipsoid when the target temperature is low. In view of the characteristics of the ablation zone, the boundary of the ablation zone was divided into two parts. When the temperature of the single-electrode tip took different values, the accuracy of the ablation zone boundary could be ensured. By calculating the mean square error of the AM simulation results and the AM fitting results, the effectiveness of the AM prediction model was verified. Some scholars have applied the CT image of the patient's liver to assess the ablation ranges. Jiang et al. ^[8] investigated the quantitative evaluation of AM after RFA procedure and the correlation between AM and local tumor volume changes with a 3D reconstruction technique. The 3D reconstruction technique is an accurate method for evaluating the AM before RFA treatment. However, the 3D reconstruction process usually takes about 30 minutes and the efficiency is relatively low.

For the success of RFA, the ablation volume needs to completely cover the tumor tissue and retain a safety margin with 5-10 mm ^[32]. In this paper, an attempt was made to investigate the relationship between ablation volumes and ablation time during RFA using an ex vivo porcine liver model. It has been found that there is a polynomial relationship between the ablation volume and the ablation time at different preset values. The prediction model of ablation volumes demonstrated that the higher the pre-set value of the electrode tip was, the larger the ablation volume would be. The ablation volume increased with the ablation time when the pre-set value of the electrode was a constant. In a FEM study by Singh et al. ^[33], it was found that the size of ablation volume in different tissues (liver, lung, kidney, and breast) was associated with preset target temperature during temperature-controlled RFA. According to the results of numerical simulations in different tissues for different values of tip temperatures, they have obtained a non-linear volume model. Compared with our ex vivo porcine liver experiments, Singh used tissue-mimicking phantom gel and monopolar multi-tine electrode to conduct experiments. It is well known that the thermophysical parameters of tissue-mimicking phantom gel and liver tissues are different.

The AM prediction model and the ablation volume model were proposed in this paper. These models can effectively forecast the ablation volume sizes and the shape of ablation zone boundaries under different tip temperatures and different ablation time. However, there are some limitations in this study. (1) The FEM models were built only based on the homogeneous tissue without considering tumor properties, which would allow a direct comparison with the ex vivo porcine liver experiment studies. (2) The effects of blood perfusion rates have not been considered in the FEM model of ex vivo liver RFA. Compared with RFA experiment results of in vivo porcine livers, ex vivo RFA may produce larger ablation zones because the blood perfusion has been neglected. However, the proposed novel prediction method of ablation zone sizes in this study could be useful for investigating the relationship between the tip temperature and the ablation zone size. (3) Further, the large blood vessel has been neglected in this study. Thus, the proposed prediction models of the AM and the ablation volume will not be suitable if there is a large blood vessel nearby the target tissue. To solve these limitations, three-dimensional (3D) reconstruction of liver tissue will be achieved by the patient's liver CT image, and a correlation study of ablation volume with time will be performed based on this 3D model in the future work.

5.   Conclusion

Accurately estimating the shape and size of the tissue coagulation zone during RFA procedure is able to markedly improve the therapeutic effect of RFA, while minimizing unnecessary damage to the surrounding normal tissues and critical structures. The aim of this study is to investigate the characterization method of the AM and the ablation volume with ablation time during temperature-controlled RFA. Two conclusions can be drawn from the present study:

(1) A non-linear dynamic growth model of the characteristic lengths of the ablation zone over time was derived. Based on the growth model of the characteristic lengths of the ablation zone, the function of the AM was proposed.

(2) Based on the FEM model of single-electrode temperature-controlled RFA, the non-linear function of the ablation volume with time at different preset tip temperatures was built.

Acknowledgments

The authors would like to thank the anonymous reviewers for their constructive comments and suggestions. This work was funded by Beijing Natural Science Foundation [Grant No. 7174279] and National Natural Science Foundation of China [Grant Nos. 71661167001, 61801312 and 61871005].

Conflict of interest

We declare that the authors have no competing interests that might be perceived to affect the results and or discussion reported in this paper.