Abbreviations:
ER, endoplasmic reticulum; [Ca2+]i, cytosolic calcium concentration; ATPase, adenosine 5'-triphosphatase; PMCA, plasma membrane Ca2+-ATPase; SERCA, sarcoplasmic/endoplasmic reticulum Ca2+-ATPase; SPCA, secretory pathway Ca2+-ATPase; HACS, high affinity calcium system; VGCC, voltage gated calcium channels; LACS, low affinity calcium system; NALCN, calcium/sodium leak channels, non-selective; TRP, transient receptor potential; MCU, mitochondrial calcium uniporter; HSR, hypotonic shock responsive system; GIC, glucose-induced system; CaMKs, Ca2+/calmodulin dependent kinases; CAX, Ca2+/H+ exchanger; FLC, flavin carriers; PKD, polycystic kidney disease; FAD, flavin adenine dinucleotide; TRPML, TRP-like mucolipins; TRPP, TRP-like polycystin; mPTP, mitochondrial permeability transition pore; UPR, unfolded proteins response.
1. Introduction
Genetically treatable eukaryotes present the extraordinary opportunity to dissect the properties of calcium homeostasis and calcium signaling in eukaryotic cells as well as to understand the calcium-related pathological processes in human diseases. Saccharomyces cerevisiae proved to be an ideal organism in which to study calcium signaling related proteins associated with diseases [1,2], using yeast as a in vivo test tube either to study molecular properties of heterologous calcium transporting proteins [3] or to screen for drugs that can compensate for ion channel malfunction [1]. Nevertheless, the evident, relevant difference between yeast and mammals is the lack of redundancy of multiple isoforms in yeast and the existence of more complex systems in mammalian cells [3].
As in all eukaryotic cells, the basal level of cytosolic calcium ([Ca2+]i) is maintained in fungi in a range from 50 to 200 nM against a high gradient across the membrane [4,5]. Differently than in mammalian cells, whose primary store for calcium is the ER compartment [6], fungi store large amounts of calcium mainly in their peculiar organelle, the vacuole. The vacuole contains up to 95% of total cellular Ca2+, which is mostly immobilized as polyphosphate salt in yeast [7]. Indeed, Ca2+ vacuolar sequestration is the fungal physiological equivalent of detoxification by excretion into the extracellular space.
The greater redundancy of Ca2+-permeable channels, cation/proton exchangers and P-ATPases in filamentous fungi (between 28 putative proteins from A. clavatus and 34 from A. oryzae) compared to that of S. cerevisiae (19 proteins) is likely related to a more complex cellular organization and filamentous growth form [8,9]. All the calcium transporters families hereafter described are present in filamentous fungi, often with several proteins (see Table 1 for an overview). In filamentous fungi, there is evidence for the involvement of calcium in the cell cycle, sporulation, spore germination, hyphal tip growth, hyphal orientation, hyphal branching and circadian rhythms [9].
Table 1.Calcium transporters in the indicated fungi.
| Calcium transporters family | Mammalian homologuous | S. cerevisiae | Candida spp. | N. crassa | Aspergillus | Cryptococcus |
| family | protein | | | | spp. | spp. |
| Ca2+ pumps | PMCA | | Pmc1 | Pmc1 | Nca-2, Nca-3 | PmcA, PmcB, PmcC | XP_570160, XP_568029 |
| SERCA | | - | - | Nca-1 | XP_663347, XP_680733 | Eca1, XP_572412 |
| SPCA | | Pmr1 | Pmr1 | Pmr | Pmr1 | XP_568029 |
| | ATP13A1 | Spf1/Cod1 | Spf1 | XP_958407 | XP_660750 | XP_568028 |
| Ca2+/H+ exchangers | - | | Vcx1 | Vcx1 | Cax, XP_962297, XP_011394181 | VcxA | Vcx1 |
| - | | Vnx1 | XP_719429 | XP_963351 | XP_664590 | XP_569752 |
| | TMEM165 | Gdt1 | XP_712922 | XP_964855 | XP_662418 | XP_571162 |
| HACS | VGCC | α1 subunit | Cch1 | Cch1 | Cch-1 | CchA | Cch1 |
| | γ subunit | Ecm7 | Ecm7 | - | - | - |
| partial similarity to NALCN | | Mid1 | Mid1 | Mid-1 | MidA | XP_569171 |
| LACS | | | ? | | | | |
| PMP22/claudin | | Fig1 | Fig1 | Fig-1 | FigA | Fig1 |
| TRP-like | TRP | | Yvc1 | Yvc1 | Yvc-1 | Yvc1 | Yvc1 |
| | | Flc1, Flc2, Flc3, Yor365c | Cfp1, Cfp2, Cfp3 | Calcium-related spray protein, XP_964688, XP_963745 | (see Figure 3) | (see Figure 3) |
| MCU | | MCU | - | - | XP_959658 | XP_751795 | XP_566527 |
| | MICU1 | - | - | XP_961607 | XP_748987, XP_682054 | XP_569565 |
PMCA, plasma membrane Ca2+-ATPase; SERCA, sarcoplasmic/endoplasmic reticulum Ca2+-ATPase; SPCA, secretory pathway Ca2+-ATPase; HACS, high affinity calcium system; VGCC, voltage gated calcium channels; LACS, low affinity calcium system; NALCN, calcium/sodium leak channels, non-selective; TRP, transient receptor potential; MCU, mitochondrial calcium uniporter. LACS pore forming subunits have not been identified yet. For fungal species where no homologs have been characterized up to now, NCBI accession numbers of BLAST search best hits obtained by GenomeNet (Kyoto University Bioinformatics Center, http://www.genome.jp/tools/blast/) were reported, albeit representing hypothetical proteins.
2. Calcium active transport in fungi
Vacuolar Ca2+ uptake has been thoroughly studied in yeast [10]: like in plants, two mechanisms are active for this purpose, a primary energized Ca2+-ATPase pathway and a secondary energized Ca2+-exchanger pathway, both working in recovering basal Ca2+ level in the cytosol after a stimulus-induced Ca2+ burst, so contributing to calcium signaling shaping, to conferring high Ca2+ concentration tolerance, and to feeding Ca2+ to the intracellular stores.
2.1. Ca2+-ATPases
Ca2+-ATPases are high affinity P-type ATPases [11] present in bacteria, archaea and eukarya [12], that can efficiently tackle the smallest changes in cytosolic Ca2+. Three types of Ca2+-ATPase are present in animals: the sarcoplasmic/endoplasmic reticulum Ca2+-ATPase (SERCA) [13], the secretory pathway Ca2+-ATPase (SPCA) [14], and the plasma membrane Ca2+-ATPase (PMCA) [15], only found in eukaryotes. Though structurally similar, there are clear distinctions between each type as far as pump transport kinetic and regulatory characteristics are concerned.
Genes encoding vacuolar Ca2+-ATPases have been identified in a variety of fungal and plant species, most closely related to PMCA-type pumps. PMCAs possess a cytosolic autoinhibitory domain at the C-terminus which is relieved by binding of calmodulin (CaM) [16].
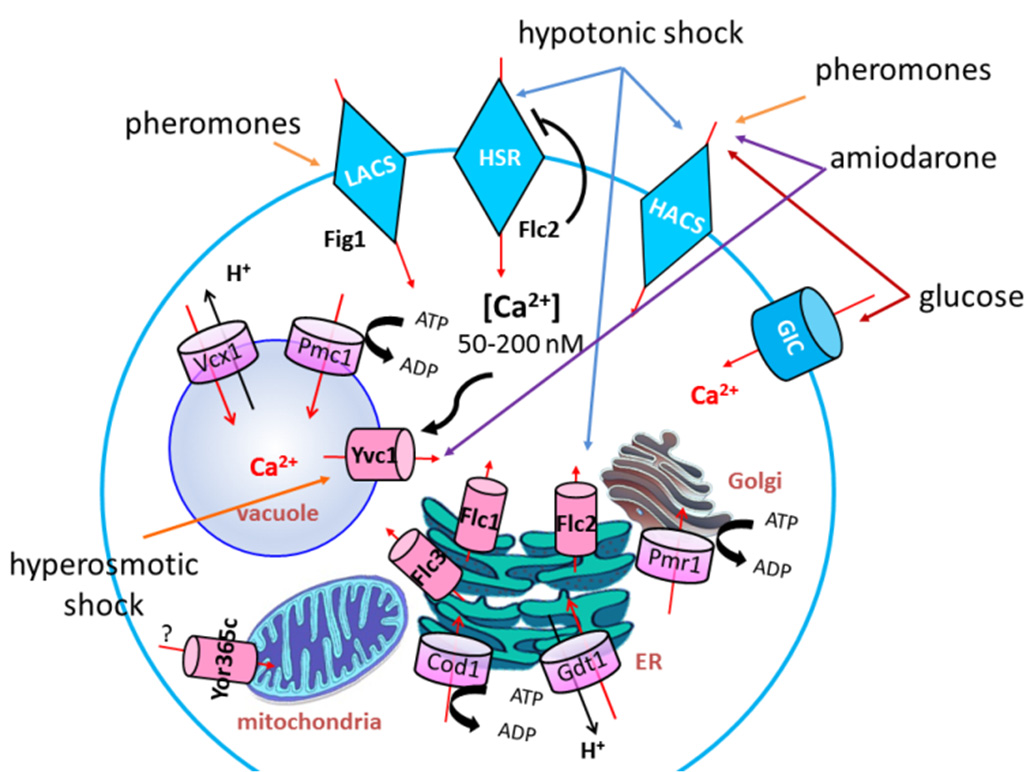
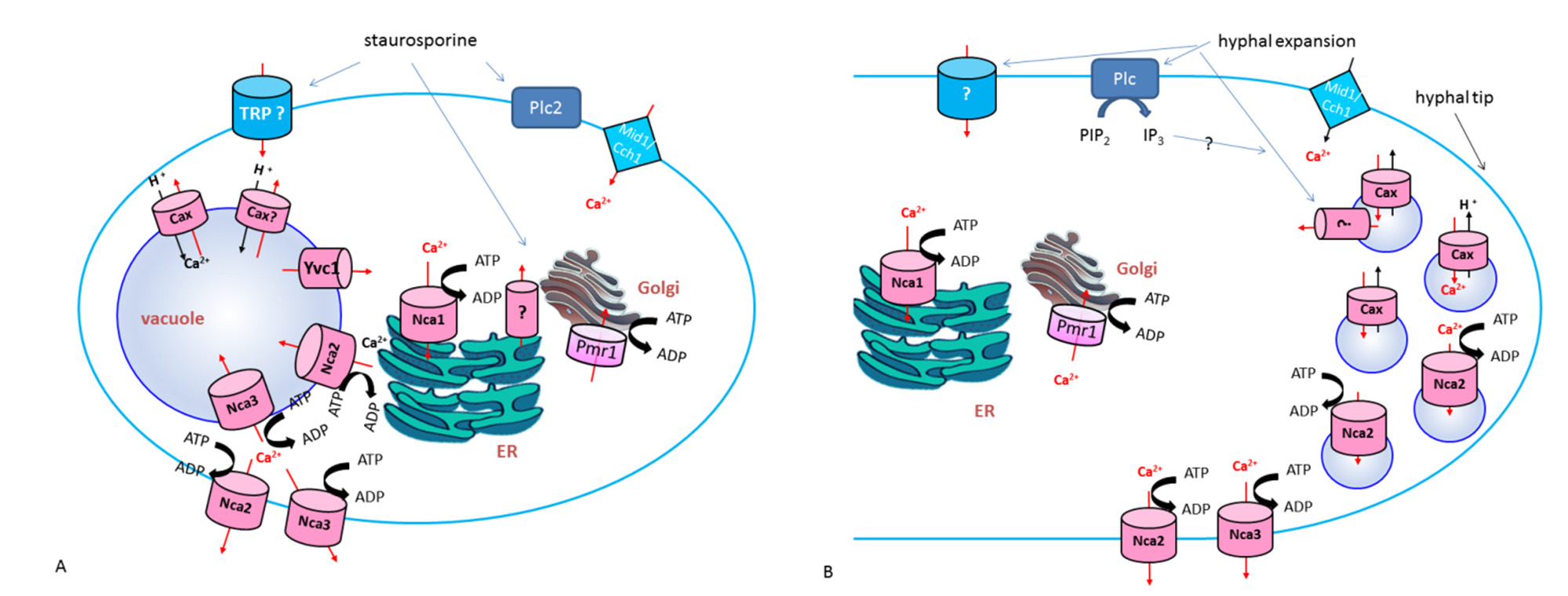
The vacuolar S. cerevisiae Ca2+-ATPase Pmc1 was the first PMCA to be isolated, two decades ago [17], albeit not in the plasma membrane but in the vacuolar membrane, as common in other fungi and protozoans (see Figure 1). For example, two Ca2+-ATPases from N. crassa (NCA-2 and NCA-3) are expressed at the vacuole, although they can also localize at the plasma membrane (see Figure 2) [18,19].
Yeast Pmc1 protein lacks domains involved in regulation by calmodulin and acidic phospholipids, which are typical of the mammalian members of this family. Interestingly, Pmc1 is actually itself regulated by Ca2+, but at the transcriptional level [20,21].
The Δnca2 strain cannot grow in high concentrations of calcium ions, and it accumulates Ca2+ to excessively high levels, differently than pmc1Δ strain of S. cerevisiae [22]. Again, very high Ca2+ concentrations (e.g. 700 mM) are very toxic to pmcAΔ pmcBΔ double mutants in Aspergillus nidulans, which is considered a model fungus for filamentous fungi [23]. Three PMC1 calcium transporter homologues in Aspergillus fumigatus, the most important aerial fungal pathogen of human beings, were shown to be involved in calcium and manganese metabolism, but only PmcA influenced virulence [24]. Recently deletion of pmrA and/or pmcA were reported to produce defects in growth, morphogenesis and cell wall integrity in A. nidulans [25].
SERCA family members are described in many eukaryotes, regulating Ca2+ levels in the ER lumen, including animals, plants, protists, and some fungi. In fact, whereas no SERCA family members have been identified in budding yeast and related ascomycetes, SERCA-type Ca2+ pumps were identified in the ER and the nuclear envelope [19] in N. crassa, encoded by NCA-1 gene (see Figure 2), in the encapsulated yeast and human pathogenic dimorphic yeast Cryptococcus neoformans, encoded by ECA1 gene [26] and in the related basidiomycete plant-pathogenic fungus Ustilago maydis [27]. ECA1 is involved in tolerance to multiple stresses. While the growth phenotypes of the U. maydis and C. neoformans eca1 mutants are very similar, in U. maydis eca1 mutants a defective cell morphology is clearly related to overactive Ca2+/calmodulin dependent kinases (CaMKs) affecting microtubules organization (see below), while many of the C. neoformans eca1 phenotypes would derive from impaired ER function in protein processing.
In contrast, the first member of the SPCA subfamily in fungi to be identified was Pmr1 (plasma membrane ATPase related pump), in budding yeast [28], localized in the Golgi membranes and endoplasmic reticulum (ER) [29], where it pumps Ca2+ (and Mn2+) to the lumen (see Figure 1) [30], which is very important particularly in the ER [31] for the appropriate folding and processing of proteins during transport through the secretory pathway [32]. Although double mutants lacking both Pmr1 and the vacuolar membrane Ca2+-ATPase Pmc1 are inviable irrespective of Ca2+ concentration, triple mutants also defective in the Ca2+-binding subunit of calcineurin, Cnb1, are viable but require exogenous Ca2+ for growth [22].
Members of the SPCA family of Ca2+-ATPases have recently been found in all higher organisms [11]. Inadequate Ca2+ uptake into acidic Ca2+ stores is known to impair the functionality both of the organelles and of the cytosolic Ca2+ homeostasis system in human cells. For example, mutation of secretory pathway Ca2+-ATPase isoform 1 (SPCA1), the human orthologue of yeast PMR1, causes Hailey-Hailey disease, a rare autosomal dominant skin disorder, which is accompanied by an increase of the [Ca2+]i and a reduction in the Golgi luminal Ca2+ concentration [33,34].
S. cerevisiae additionally contains a type V, P-type ATPase, Cod1/Spf1, localized to the ER, which can contribute to regulating cytosolic Ca2+ levels [35,36] and is required for Golgi protein glycosylation activity [37]. The spf1Δmutant shows disrupted cellular calcium homeostasis, causing increased transcription of calcium-regulated genes that becomes dramatic when paired with disruption of the Golgi apparatus-localized Ca2+ pump Pmr1. Roles for Spf1 in the maintenance of cellular calcium homeostasis, ER stress responses, hyphal development, biofilm formation and virulence were also suggested in C. albicans [38,39]. Spf1 and its orthologues were suggested to play a unique role in the functioning of the ER in a broad range of metazoans. Actually, Spf1 has recently been reported to have a role in regulating ergosterol [40] and Mn2+ content in ER compartment [41].
2.2. Ca2+/H+ exchangers
Differently from Ca2+-ATPases, Ca2+ exchangers are low affinity but high capacity Ca2+ transporters and can efficiently transport Ca2+ ions following a large burst of cytosolic Ca2+ [42]. They derive energy for the transport by the counter exchange of another cation, either Na+, as for the animal Na+/Ca2+ exchanger, or H+, as for the yeast or plant Ca2+/H+ exchanger. Indeed, the strong acidification of yeast vacuoles through a V-type H+-ATPase provide a large proton gradient which can be efficiently exploited in Ca2+ uptake [7].
CAX (Ca2+/H+ exchanger) genes [43], in addition to plants and fungi, are present in prokaryotes, invertebrates and lower vertebrates (e.g. fish and amphibians), but not yet identified in higher animals [44].
The yeast vacuolar Ca2+/H+ exchanger encoding gene VCX1 was recovered in a screen for suppressors of calcium-sensitive phenotype of pmc1 mutant exposed to high calcium [17]; later, Vcx1 protein was biochemically characterized [42,45] as a high capacity transporter but with a lower affinity for Ca2+ compared to the Ca2+ pump Pmc1, suitable to rapidly sequester Ca2+ into the vacuole when [Ca2+]i is high [42,46]. Vcx1 structure has recently been determined, as first within the CAX family [47]. Opposite to Pmc1, whose expression is activated by calcineurin, Vcx1 is inhibited by calcineurin [17,45] probably post-translationally [48], likely to prevent oversequestration of Ca2+ into the vacuole.
Ca2+/H+ exchange activity appears to be a conserved pathway for vacuolar Ca2+ sequestering in fungi. Vacuolar CAX proteins have been identified and characterized in various fungal species [8,18,49,50]. In contrast to S. cerevisiae Vcx1, the expression of the Ca2+/H+ exchanger gene VcxA from A. nidulans and A. fumigatus is stimulated rather than repressed by calcineurin and its Ca2+-induced expression is dependent on the Crz1 orthologue CrzA [49] (described in Section 4). However, orthologues from other fungi such as C. neoformans are also negatively regulated by calcineurin [50], making difficult to draw a general scheme.
Gdt1 belongs to a well conserved‘uncharacterized Protein Family 0016’of membrane proteins, with characteristics similar to the Ca2+/cation exchanger superfamily. Moreover, properties leading to selectivity for calcium ions in the sequences of Gdt1 and TMEM165 suggest they could be CAXs [51]. In yeast, the gdt1Δsensitivity to high concentrations of Ca2+ worsens in the gdt1Δpmr1Δmutant. Gdt1 is localized in the cis-and medial-Golgi apparatus, as Pmr1, and both contribute to Ca2+ supply to the Golgi apparatus [52]. In humans, defects in the Gdt1 homologous human protein TMEM165 are known to cause a subtype of congenital disorders of glycosylation [53].
Despite the homology of S. cerevisiae Vnx1 with other members of the CAX (calcium exchanger) family of transporters, Vnx1 was initially reported as unable to mediate Ca2+ transport but showing a low affinity Na+/H+ and K+/H+ anti-porter activity [54] and was only later further characterized as a proper CAX member [55].
Finally, a Ca2+/H+ exchange system was recently hypothesized in yeast plasma membrane, based on a calcium transport driven by the proton-motive force generated by the plasma membrane H+-ATPase registered in functionally inverted (inside-out) plasma membrane vesicles [56].
3. Calcium passive transport in fungi
3.1. High Affinity Calcium System (HACS)
Identification of several protein(s) involved in calcium influx in yeast cells was achieved taking advantage of genetic approaches. The first such system to be identified was a plasma membrane complex known as HACS (High Affinity Calcium System), composed of Cch1, a protein homologous to mammalian voltage-dependent calcium channels α-1 subunit [57], and Mid1 protein, a“stretch-activated”calcium channel [58]. Recently, Ecm7, a member of the PMP-22/EMP/MP20/Claudin superfamily of transmembrane proteins that includes γ-subunits of voltage-gated calcium channels, was identified as another subunit of HACS [59,60].
To date, the predicted homologues of Cch1 and Mid1 have been identified in many fungi, including ascomycetes and basidiomycota fungi [1], the saprophytes S. pombe [61], N. crassa [62] and A. nidulans [63], animal pathogenic fungi C. albicans [64] and C. neoformans [65], and plant pathogenic fungi Gibberella zeae [66,67], Claviceps purpurea [68] and Uromyces appendiculatus [69].
Fully functional in synthetic media, these channels are activated in budding yeast under the most diverse conditions, such as stimulation by pheromones [4,70], hypotonic shock [71], salt and environmental stress [72,73], depletion of calcium from internal stores [74], hypotonic shock [71,75], ethanol stress [76], glucose refeeding [77,78,79], membrane depolarization [59,80], cold stress [73] and fungicides treatment [81]. On the contrary, in cells growing in rich media, HACS system is inhibited by calcineurin (a Ca2+/calmodulin-dependent phosphatase, see below), probably by dephosphorylation [82,83]. In filamentous fungi, HACS mutants show heterogeneous phenotypes across species, including growth and calcium homeostasis defects for most species [62,66,67,68,84].
As mammalian VGCCs, Cch1 homologues in fungi typically contain positive residues (although reduced in number) in the voltage sensing (S4) domains [57,85,86], suggesting that HACS may directly sense membrane depolarization, although there is no direct evidence; nonetheless, sudden dissipation of the transmembrane H+ gradient led to rapid activation of HACS in S. cerevisiae [59,80] and C. albicans [87]. Moreover, the addition of protonophore (depolarizing) compounds, like CCCP, also stimulates calcium uptake in S. cerevisiae [88,89,90]. Recent evidence suggests that Kch1 and Kch2 K+ transporters activate HACS and downstream components of the essential calcium signaling pathway in S. cerevisiae cells during the response to mating pheromones, likely inducing partial depolarization of the plasma membrane [91,92].
Mid1 homologues belong to a fungal specific family of calcium channels.In S. cerevisiae Mid1 has been reported as having 4 hydrophobic domains, which are necessary for localization to the membrane [58], and 2 cysteine-rich regions (C1 and C2) toward the C-terminus hypothesized to act in protein binding [93,94], essential in yeast [93], and recently shown to be closely related to a similar domain in calcium/sodium leak channels (NALCN) [95,96].
In the filamentous fungus C. neoformans Mid1 contains a modulatory region in its C-terminal tail that functions as a direct modulatory region for Cch1 channel [86], but is not conserved in other fungi.
In fungi, Cch1 and Mid1 mutants are affected by significant reduction in calcium uptake [1], but, differently than in S. cerevisiae, in the filamentous fungus N. crassa the mid1 mutant can mate [62].
These predicted calcium channel proteins are also involved in virulence in pathogenic fungi [65,68,97,98]. The pathogenic yeast C. albicans also carries one homolog of Kch1/Kch2, and homozygous knockout mutants were deficient in the activation of HACS during the responses to tunicamycin. However, the Kch1 homolog was not necessary for HACS activation or cell survival in response to several clinical antifungals that target the ER or cell wall. Thus, Kch1-family proteins represent a conserved linkage between HACS and only certain classes of ER stress in these yeasts [92].
In different filamentous fungi species, HACS mutants show both shared and variable phenotypes, including reduced vegetative growth and defects in calcium homeostasis for most species [62,66,67,68]. Both similar (for example slowed vegetative growth and calcium homeostasis lesions) and divergent (reduced ascospore discharge and abnormal ascospore morphology in F. graminearum vs. altered hyphal electrophysiology in N. crassa) phenotypes are observed [62], likely resulting from lineage-specific adaptation and concomitant expansion of calcium signaling components.
The Cch1-Mid1 channel represents the only high-affinity Ca2+ channel in the plasma membrane of fungal cells; Cryptococci (the pathogenic yeast form of the filamentous fungi in the genus Filobasidiella) cannot survive in low-Ca2+ environments in the absence of HACS [86]. In Neurospora crassa, Mid1 impacts conidiation and hyphal turgor, but it does not have any effect on mating, which is different from the case in S. cerevisiae [62]. In A. nidulans, MidA plays important roles in conidiation, hyphal polarity, and cell wall integrity [63]. Calcium signaling involving HACS components has been reported to play a role in hyphal growth, sporulation, and fruiting body function in the filamentous fungus Fusarium graminearum (sexual-stage Gibberella zeae), a pathogen of wheat and barley. The deletion of CCH1, MID1, or both resulted in reduced vegetative growth rate, conidiation and ascospore development. External calcium addition rescued all phenotypes, at least partially, except for the abnormal ascospore development seen in strains lacking Mid1 [66,67]. All the A. fumigatusΔcchA, ΔmidA, andΔyvcA strains demonstrated attenuated virulence in a neutropenic murine model of invasive pulmonary aspergillosis, suggesting a role for these genes not only in calcium homeostasis but also in virulence [99].
3.2. Low Affinity Calcium System (LACS)
Further experimental evidence supports the existence of a different, yet not fully characterized, system of calcium influx with lower affinity, involving the Fig 1 protein, a member of PMP22/claudin superfamily [100,101], acting at the late stage of the yeast mating process in S. cerevisiae cells growing in rich media [102] and named LACS (Low Affinity Calcium System). Orthologues of FIG 1 are also present in the genomes of fission yeast, Candida and filamentous fungi [9,100,101,103].
In mammals, claudin superfamily members are involved in several processes such as membrane-membrane interactions, cytoskeletal attachment, signaling, and vesicle trafficking [104,105].
Fig 1 is involved in calcium influx and membrane fusion during the mating of S. cerevisiae and C. albicans, although, in this last, mating was not impaired in fig 1 mutants. Its expression level is increased upon exposure to mating pheromone. Although Fig 1 is involved in calcium uptake during cell fusion in yeasts, its lack of homology to any known ion influx channel suggests that it may act indirectly on calcium influx [100]. Furthermore, pheromone-induced cell death is dependent on FIG 1 but independent of its calcium uptake activity in yeasts [106].
In C. albicans, Fig 1 plays a role in hyphal suppression in some environments and in hyphal tip growth reorientation upon contact with a ridge [107].
Fig 1 homologs are involved in sexual development in filamentous fungi such as Fusarium graminearum, A. nidulans and N. crassa, and vegetative growth and macroconidium (i.e. the larger asexual reproductive spore) production in F. graminearum and A. nidulans, but not in N. crassa [101,103].During vegetative growth, A. nidulans FigA acts mainly as a calcium uptake system component, while in asexual and sexual development, it works as a regulator of differentiation: in a figA deletion mutant, adding extracellular Ca2+ was able to rescue the hyphal growth defects but could not restore asexual and sexual reproduction [103]. In fact, in higher fungi, multicellular hyphae are compartmentalized by the formation of septa, but a small pore is retained to enable communication between adjacent hyphal compartments. The location of FigA at the center of hyphal septum in A. nidulans (probably around the pore) indicates it may also confer selective permeation properties that allow proper solutes to pass between cells. Thus, the hitherto known functions of FIG1 in fungi also seem to involve signal transduction and membrane-membrane interactions.
3.3. TRP-like calcium channels
Transient receptor potential (TRP) channels are found among mammals, flies, worms, ciliates, Chlamydomonas, and yeasts, but not in plants-for a review see [108,109]. These channels probably work as tetramers of six transmembrane domains (TMs) proteins. Sequence similarities are restricted to some short sequence motifs mainly in TM5, TM6, and adjacent domains. In the yeast genome, there is one gene for long known to encode a TRP-like canonical sequence, forming the calcium channel in the vacuolar membrane Yvc1, for Yeast Vacuolar Conductance 1 [110,111,112], spanning the short amino acid sequence motif within TM6, 448VILLNILIALY458, which is conserved in the corresponding TM6 of most mammalian TRPs [113]. Yvc1 is a calcium activated calcium channel, which could also be strongly stimulated by other cations such as manganese, magnesium (Tisi R, unpublished results) and zinc [77]. In its C-terminus, Yvc1 contains a cluster of four acidic residues (573DDDD576), which may be important for Ca2+-dependent regulation of channel activity through direct Ca2+ binding [114].
Yvc1 mediates the hyperosmolarity induced Ca2+ release [111]. Mechanical activation of Yvc1 upon vacuole shrinking caused by a hyperosmotic shift occurs regardless of Ca2+ concentration and is apparently independent of its known Ca2+ activation: the deformation of the vacuolar membrane is likely the direct cause of opening of the Yvc1 channel to release vacuolar Ca2+ [112,115]. Furthermore, recent results suggest that Yvc1 calcium channel is an important component of the signal transduction pathway activated in response to glucose addition leading to a raise in [Ca2+]i and the activation of plasma membrane H+-ATPase [116].
In Candida albicans as well, the yvc1Δ/Δ mutant displayed difficulty in stress response, but also in morphogenesis and virulence, suggesting a key role of Yvc1 in hyphal polarized growth and re-orientation to host signals in this pathogenic yeast [117].
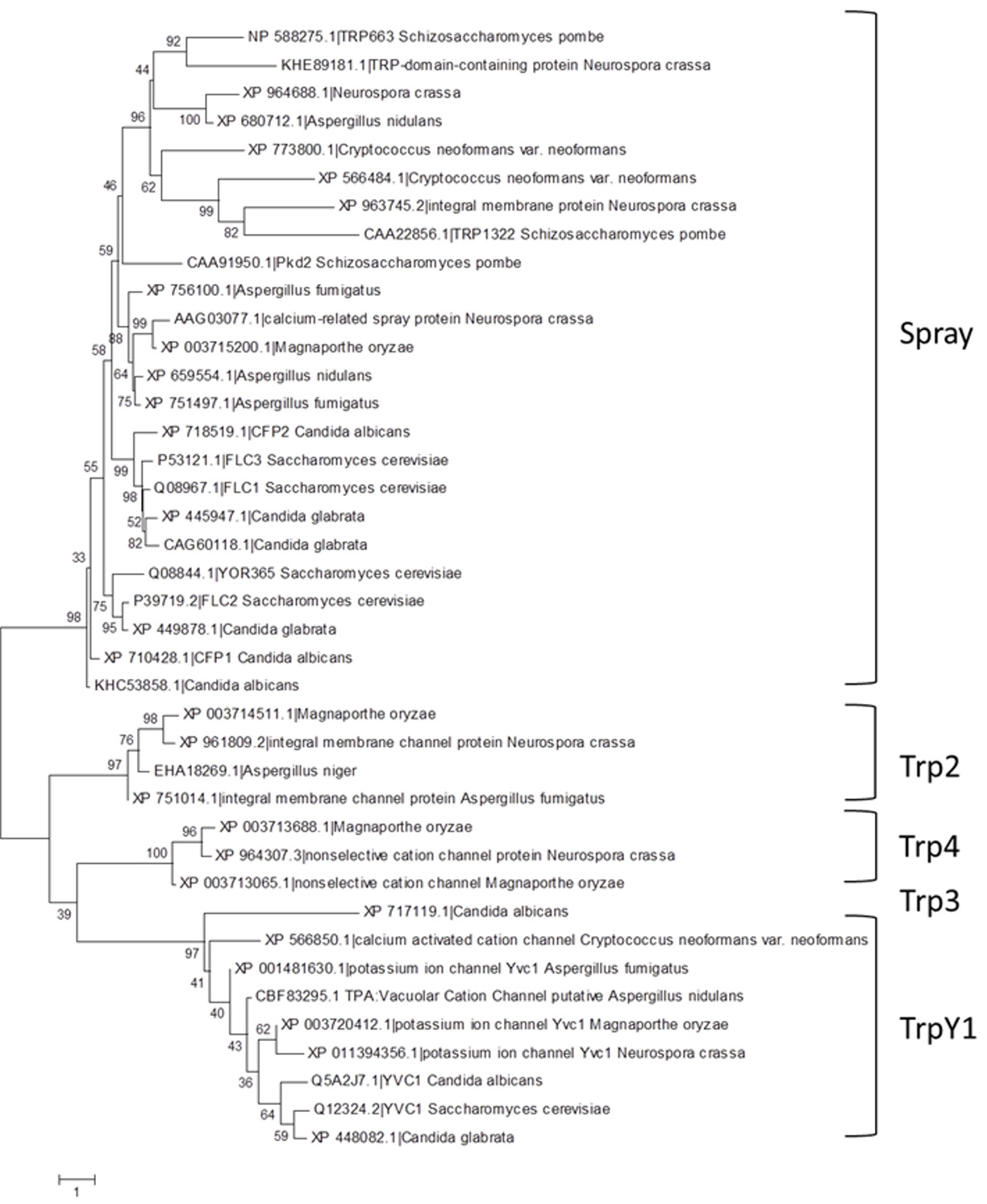
Though the only canonical TRP channel so far widely accepted in fungi is Yvc1/TrpY1 [8], nonetheless a few proteins were recently proposed as putative homologs of the mammalian TRP channels in pathogenic fungi, organized in three distinct groups, termed TrpY1-like (the largest group), Trp2 and Trp3 [118]. Trp3 homologs are mainly found in Candida spp. and are absent in Neurospora, Aspergillus or Cryptococcus spp.
More members of TrpY1 and Trp2 subfamilies were found in public database with the BLAST alignment tool [119] and their phylogenetic relationship were reconstructed taking advantage of multiple sequence alignment by Guidance2 software (http://guidance.tau.ac.il/ver2/) and M-coffee (http://tcoffee.vital-it.ch/apps/tcoffee/index.html) software. The resulting tree identifies a novel group of fungal TRP channels that we describe as Trp4 (see Figure 3). Many fungal homologues of Yvc1 channel subunits contain highly acidic regions in their C-terminal domains, which are similar to the acidic region involved in activation of Yvc1 by Ca2+ [114], while there are fewer acidic residues in the Trp2 homologues and very few in the Trp3 homologues [118]. Trp4 homologues have shorter tails than Trp2 homologues, similarly to TrpY1 subfamily members, but with very few acidic residues, similarly to Trp3 homologues.
Recently, in N. crassa, programmed-cell-death-inducing treatment with staurosporine was reported to trigger both Ca2+ uptake from the extracellular medium, by a novel fungal influx system resembling a TRP channel, and an IP3-mediated release of organelle-stored Ca2+ [120], causing a defined change in cytosolic free Ca2+ dynamics and distinct Ca2+ signatures. Phospholipase C Plc2 was identified as a pivotal player during cell death, hyphal development and triggering of the characteristic staurosporine-induced Ca2+ signature. The TRP Ca2+ uptake system seems to be more active in the absence of Cch1. Consistently, lack of Cch1 and Mid1 renders S. cerevisiae and C. neoformans cells very sensitive to ER stress caused by tunicamycin or azole drugs [59,121,122].
Mammalian cells swell when facing hypo-osmotic shock, which induces an increase in [Ca2+]i [123] mediated by some members of the TRP channel family, including plasma membrane-localized TRPV4 [124] and TRPM7 [125]. Whereas it is widely accepted that mammalian and bacterial cell volume regulation is governed by ion channels and transporters in the plasma membrane [123,126], in budding yeast hypo-osmotic shock also involves a release of calcium from internal stores [71,75,127]. In fact, this calcium release likely originates from the secretory compartments and involve a family of putative ion transporters [75], named Flc (for Flavin Carriers) proteins since they were formerly proposed as required for importing FAD into the endoplasmic reticulum [128]. Conversely, a member of this family, Flc2, was also previously proposed as a homolog of a TRP-like polycystic-kidney-disease (PKD)-related calcium channel identified in S. pombe [129,130]. S. pombe pkd2 is essential for cellular viability, and appears to be a key signaling component in the regulation of cell shape and cell wall synthesis through an interaction with a Rho1-GTPase in the plasma membrane [129]. As with human PKD2, the fission yeast Pkd2 protein is localized mainly to Golgi and, to a lesser extent, to plasma membrane when endogenously expressed, similarly to FLC proteins in budding yeast [128]. Consistent with the observed hyper-sensitivity to Calcofluor white stain in the flc2Δstrain, Flc2 was also previously reported to be regulated by the cell wall biogenesis and maintenance pathway through Rlm1, an important cell integrity maintenance factor. Moreover, disruption of FLC2 gene confers hyper-activation of the cell wall integrity MAPK cascade, suggesting a role in cell wall maintenance as previously suggested for the fission yeast homolog.
Perturbation in cytosolic resting calcium concentration and hyper-activation of calcineurin in flc1-deficient exponentially growing cells suggest a role for this transporter in calcium homeostasis in yeast [75].
The FLC genes represent a conserved fungal gene family of integral membrane proteins, spanning a TRP-like domain. The S. cerevisiae genome contains three homologues of C. albicans FLC1/CFP2, i.e. YPL221W, YAL053W, and YGL139W, which exhibited 48, 36, and 47% amino acid identity to CaFLC1 and were designated FLC1, FLC2, and FLC3, respectively. Moreover, the uncharacterized ORF YOR365C exhibits slightly less homology to C. albicans FLC1 (28% identity) but higher similarity to FLC2 than FLC1 or FLC3. Hsiang and Baillie [137] recently identified YOR365C and the FLC gene family as one of 17“core fungal”genes that are represented in all fungal species but not in prokaryotes or nonfungal eukaryotes. Members of this family were identified in several pathological and non-pathological fungi (see Figure 3), formerly identified either as members of a calcium-related spray proteins family or as similar to a putative FAD transporter in budding yeast. The paradigm of this family is the Neurospora crassa calcium-related spray protein [138], the previously mentioned ER-localized calcium channel regulating thigmotropism, i.e. the ability of this organism to respond to a topographical stimulus by altering the axis of growth of the hyphae [139].
Sequence alignment revealed that fungal spray proteins are more similar to the TRPML (for mucolipin) branch of TRP channels, actually the most closely related to TRPP (for polycystin) class of calcium transporters [75]. Three isoforms are present in vertebrates (TRPML1-3) which mostly reside in membranes of organelles of the endolysosomal system such as early and late endosomes, recycling endosomes, lysosomes, or lysosome-related organelles [140,141]. TRPML1 is a calcium and iron permeable intracellular channel in lysosomes, and thus the loss of function impairs endosomal/lysosomal function and autophagy [140], leading to mucolipidosis type IV disease, an autosomal-recessive neurodegenerative lysosomal storage disorder. A single TRPML homologue has been characterized in protostomes such as round worms [142] and flies [143]. TRPML has also been identified in the slime mold Dictyostelium, where it localizes to“post lysosomes”, the equivalent to secretory lysosomes in animal cells [143]. The biophysical properties and the activation mechanism of TRPMLs are still unclear, though Ca2+ permeability is established [141] and TRPMLs have been proposed as targets for PI(3, 5)P2 [144].
Furthermore, two Spray homologues in S. pombe, Trp1322 and again Pkd2, were shown to mediate the cytoplasmic Ca2+ rise caused by the extracellularly added CaCl2 [145]. Interestingly, the overexpression of another Spray member, TRP663, which showed the most significant plasma membrane localization, failed to elicit any increase in the cytosolic Ca2+ level, suggesting a specific role in calcium stress response for the former two TRP channels, likely involving also calcium release from intracellular stores.
3.4. Mitochondrial calcium channels
In several organisms mitochondria were proved to undergo an inner membrane permeability increase, the permeability transition (PT), due to opening of the mitochondrial PT pore (mPTP), a high conductance channel which requires mitochondrial F1/FO ATP synthase as an important component [146] which can be activated in vitro by oxidative stress, with properties similar to the permeability transition pore of mammals [147].
In mammalian mitochondria, another calcium transporter was identified, the mitochondrial Ca2+ uniporter (MCU) [148,149], which was found to be involved in metabolism, apoptosis and cell signaling [150]. Although no homologues of MCU were found in S. cerevisiae, which tallies with the lack of effect of ruthenium red on mitochondrial Ca2+-uptake in S. cerevisiae [151], nonetheless homologues of MCU were found in some pathogenic fungi such as Aspergillus spp. and Cryptococcus spp. andin about 40% of all sequenced fungal genomes [118], although phylogenetically distinct from plant and animal MCU homologues. Genes encoding homologues of MCU may have been lost in several independent events in different phyla of fungi [118].
MCU activity is modulated by an EF-hands containing Ca2+-sensing subunit MICU1 [150], also present in Aspergillus spp. and Cryptococcus spp. but apparently absent in Candida spp. and S. cerevisiae [118], confirming that this mitochondrial Ca2+-uptake pathway is present in some pathogenic fungi but not in S. cerevisiae [118,148,149].
3.5. Other calcium channels
Surprisingly, bacterial mechanosensitive channel MscS homologues, designated Msy1 and Msy2, were reported to be involved in hypo-osmotic shock response in the fission yeast S. pombe [152]. The msy1− msy2− mutant cannot survive upon hypo-osmotic shock, but this cell death is not caused by cell rupture and is enhanced by the influx of extracellular calcium. Single-cell Ca2+ imaging shows that cell swelling is followed by a cytoplasmic Ca2+ increase upon hypo-osmotic shock and the msy1− msy2− mutant exhibits an abnormally large cytoplasmic Ca2+ increase. Moreover, hypo-osmotic-shocked msy1− msy2− cells have two abnormally enlarged vacuoles and cracks between the outer and inner nuclear membranes [152,153]. The fungal MscS homologues are more closely conserved than those of plants, algae and bacteria. Differently than in bacteria, Msy1 and Msy2 are not localized in plasma membrane but in organellar membranes: Msy1 is localized mainly in the perinuclear ER and Msy2 in the cortical ER [152]. Homologues of Msy1 were found in the genomes of a wide range of ascomycetes and basidiomycetes, but not in the Saccharomyces cerevisiae genome, which instead contains another as-yet-unidentified mechanosensitive channel in the plasma membrane [154].
The existence of at least two additional high affinity systems in S. cerevisiae, the GIC (for Glucose Induced Calcium) and the hypotonic shock responsive (HSR) transporters were reported [75,77].
In contrast to HACS system, both the GIC transporter, involved in calcium influx upon glucose refeeding, and the plasma membrane localized HSR are not functional in the absence of a functional calcineurin [75,77] but GIC functionality does not require Crz1 activity (Tisi R., unpublished results), while HSR functionality inhibition is due to HACS hyperactivity in a calcineurin-deficient strain [75]. GIC transporter is sensitive to magnesium, as was also expected according to predictions by calcium homeostasis modeling [2,74] and to gadolinium. Its pharmacological behavior is peculiar, since it is sensitive to nifedipine but not to verapamil [77], whereas both inhibit L-type voltage-dependent calcium channels [155]. This behavior suggests that this hypothetical carrier might belong to a novel class of calcium channels, as confirmed by Saccharomyces cerevisiae genome analysis, showing no more uncharacterized proteins evidently homologous to the up to date known calcium channels [118]. Conversely, hypotonic shock-induced plasma membrane HSR transporter is not sensitive to nifedipine or gadolinium, while it is partially inhibited by verapamil (Tisi R, unpublished results), suggesting that the GIC pore forming subunits belongs to a distinct family than HSR composing subunits.
C. albicans RCH1 (regulator of Ca2+ homoeostasis 1) encodes a plasma membrane protein comprising ten transmembrane domains, similar to human SLC10A7 (solute carrier family 10 member 7). Deletion of RCH1 confers hypersensitivity to high concentrations of extracellular Ca2+ and tolerance to azoles and Li+, which phenocopies the deletion of C. albicans PMC1, encoding the vacuolar Ca2+ pump, suggesting Rch1 may be involved in the regulation of calcium homeostasis as a negative regulator of the Ca2+ influx in C. albicans cells [156] as well as in S. cerevisiae, where it is transcriptionally regulated by calcium/calcineurin signaling through the sole CDRE element in its promoter [157].
4. Calmodulin/calcineurin calcium effector module in fungi
4.1. Calmodulin
Calmodulin and calcineurin share largely conserved functions among pathogenic fungi and model fungi [158]. In eukaryotic organisms, generally, calcium binds to calmodulin (CaM), a small protein having four EF-hand (helix-loop-helix) motifs, which are characteristic of a large family of calcium-binding proteins [159]. The peculiarity of S. cerevisiae CaM (encoded by CMD1 gene) is the loss of Ca2+ binding in the fourth EF-hand motif [160]. Increase of intracellular Ca2+ availability leads to Ca2+ binding to calmodulin, triggering a conformational change that allows the Ca2+/CaM complex to activate target proteins.
Calmodulin signaling, mainly through calcineurin phosphatase, is involved in a plethora of processes in fungi, including regulation of growth, differentiation, stress response, mating, budding, as well as in determining tolerance to antifungal drugs [161,162,163,164]. Most of these components have been first identified and characterized in the budding yeast Saccharomyces cerevisiae but appear to be widely conserved in fungi [118,165].
Calmodulin gene is essential for viability, as well as its ability to bind calcium in most organisms [166,167,168]; conversely, in budding yeast only Ca2+-independent functions of calmodulin are essential for growth [169,170]. For instance, Cmd1 has a constitutive Ca2+-independent role in autophagy [171]. Moreover, in addition to calcineurin, yeast calmodulin has at least 11 additional targets [172,173]. The calcineurin-independent roles of calmodulin in pathogenic fungi are less understood, but would impinge on stress responses and morphogenetic transitions. The calmodulin gene was shown to be essential for infection in different human or plant pathogens [174,175,176]. Data about the functions of calmodulin are unfortunately even rarer in C. neoformans. Expression of a calmodulin-independent calcineurin mutant did not suppress the growth defect of the cam1tsmutant at 37°C, indicating that calmodulin performs Ca2+-and calcineurin-independent and-dependent roles in controlling C. neoformans morphogenesis and high-temperature growth [177].
Nonetheless, calcineurin protein phosphatase and calcium/calmodulin-dependent protein kinases (Cmk1 and Cmk2) are the main targets of the Ca2+/CaM complex, at least during stress responses [165,178,179].
4.2. Calcineurin
Consistently, calcineurin is not essential for budding yeast growth in normal laboratorial conditions, whereas it is required for survival in diverse stress conditions, such as exposure to high cation concentrations, cell wall stress, prolonged exposure to mating pheromone, and even illumination, mainly for its role in controlling ion transporters and cell-wall biosynthesis gene expression [180,181,182,183,184,185,186,187,188].
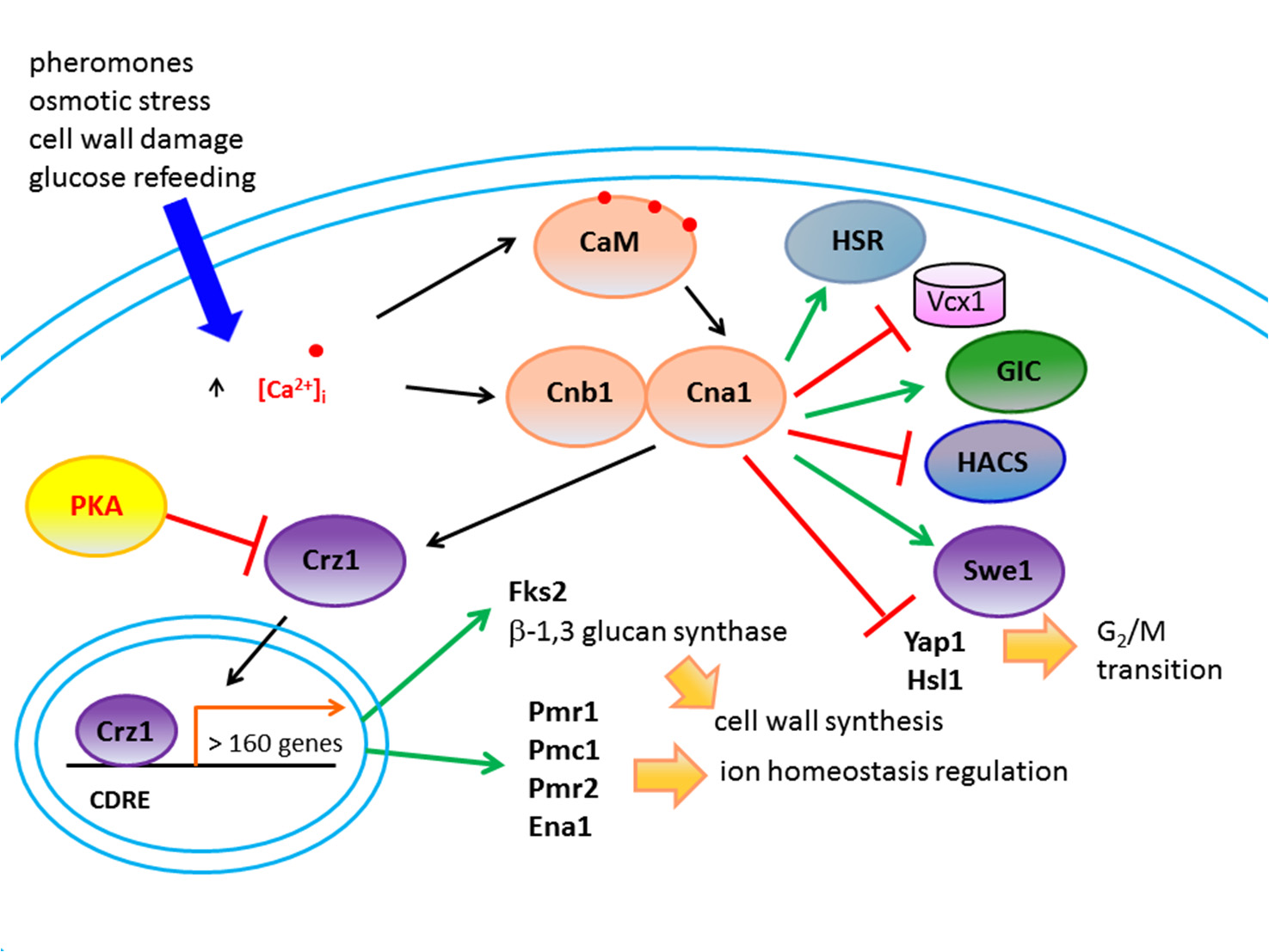
In fact, calcineurin is primarily involved in calcium homeostasis, as, as said, it regulates the activity of diverse calcium transporters on the plasma membrane [75,77,82], it inhibits the activity of the vacuolar antiporter Vcx1 and, by allowing Crz1 transcription factor translocation into the nucleus, induces the expression of more than one hundred genes [20,189,190,191,192] including not only those encoding Pmc1 and Pmr1 Ca2+-ATPases [17,22,30,48,193,194], but also genes encoding a Na+/Li+ transporter (ENA1 alias PMR2), and FKS2 gene, encoding for a β-1, 3 glucan synthetase involved in cell-wall synthesis [20,21,195] (see Figure 4). Unlike in S. cerevisiae, in the non-conventional yeast Torulaspora delbrueckii calcineurin is required for both Ca2+ and Mn2+ tolerance, but the calcineurin-Crz1 pathway has no apparent role in Na+ homoeostasis [196]. In the case of Candida or Cryptococcus neoformans, calcineurin has been shown to be involved in drug tolerance, hyphal growth and virulence [197,198].
In filamentous fungi, calcineurin is important for cell cycle progression, hyphal branching, stress adaptation, sclerotial development and formation of the infectious appressorium in a plant pathogen [199,200,201,202,203,204]. In Aspergillus, the calcineurin complex (CnaA and CnaB) localizes at both the hyphal tips and septa to direct proper hyphal growth and regular septum formation [205,206]. Again, in A. oryzae, depletion of calcineurin mRNA causes a marked reduction of growth in stressful conditions [199].
Additionally, yeast calcineurin is involved in G2 cell-cycle regulation [207] in association with the Mpk1 MAP kinase cascade (see section below).
4.3. Calcineurin-responsive zinc finger (Crz1) transcription factor
Crz1 transcription factor, first identified as a calcineurin target in the yeast S. cerevisiae [20], is a distant homolog of the mammalian nuclear factor of activated T cells (NFAT). In mammalian cells, NFAT is activated by calcineurin to regulate many cellular processes including T cell activation, neuron differentiation, heart development, fertilization, memory and muscle contraction [208].
Crz1 orthologues have hitherto been identified in various lower eukaryotes; sometimes different names have been assigned to the orthologues, such as Prz1 in S. pombe [209], or CrzA in Aspergillus fumigatus and A. nidulans [49,203,210]. Crz1 orthologues can possess from one to four C2H2 zinc finger DNA binding motifs [211], recognizing 24-bp regions, named CDREs (calcineurin-dependent response elements) [20], with consensus GNGGC(G/T)CA [192], identified in target genes elicited by high throughput approach [211].
Crz1 and its orthologues are generally involved in metal ion resistance, and development, which preferentially correlates with cell wall integrity preservation [211], although which metal ion and what kind of stress stimuli they respond to seem to be species specific. Developmental defects (in hyphal morphology or conidiation) have been described for Crz1 defective mutants in Aspergillus species [49,203,210], M. grisea and M. oryzae [212,213], C. neoformans [214,215,216], and for different Candida species [197,217,218,219,220]. Further defects ofΔcrz1 mutants have been found during growth at alkaline pH [49,210] and at elevated temperature [210,219], as well as in resistance to ethanol [221], H2O2 [222], and caffeine [223]. It has been shown in C. neoformans that Crz1 is involved in biofilm formation [216]. Interestingly, the A. fumigatus CrzA is necessary in a murine infection model, similarly to calcineurin [203,204,210], while the C. neoformans Δcrz1 mutant exhibited attenuated virulence [214].
Several regulators of Crz1 orthologues were recently identified. The casein kinase I homologues Hrr25, beyond PKA, phosphorylates Crz1 in S. cerevisiae [224,225], counteracting the entry of the protein into the nucleus. In S. pombe, phosphorylation of Prz1 could require multiple kinases [226]; actually, fission yeast protein kinase A (Pka1)—in contrast to the S. cerevisiae PKA—does not phosphorylate Prz1 directly [224,226]. Two 14-3-3 proteins, Rad24 and Rad25, bind to phosphorylation sites of Prz1, consequently preventing their dephosphorylation by calcineurin. However, the role of other proposed regulators is not yet clear [226]. A further regulator of Crz1 previously identified in S. cerevisiae is Skn7, which has been proposed to protect Crz1 from degradation [227].
The homolog of casein kinase I CkiA is involved in CrzA phosphorylation in A. nidulans, but, surprisingly, without affecting the nucleocytoplasmatic transport [228].
In addition to the previously mentioned functions, the role of calcineurin in nutrient acquisition has been recently documented. For instance, calcineurin has been linked with the utilization of inorganic phosphate in Aspergillus fumigatus [229]. Moreover, in S. cerevisiae, the activation of Crz1 transcription factor was observed in derepressed cells after glucose refeeding in the presence of extracellular calcium [77]. Many genes required for adaptation to glucose shortage, such as HXT2, HXT7, MDH2, or ALD4, transcriptionally respond to calcium and high pH signaling through Crz1 [230]. Furthermore, Nitrogen Catabolite Repression (NCR) and nitrate induction mechanisms, both regulating nitrate assimilation in Hansenula polymorpha, are controlled by calcineurin nitrogen-dependent calcineurin activation in this yeast [231].
4.4. Other actors in calcium signaling
RCAN (regulator of calcineurin) proteins comprise a family of endogenous calcineurin regulators that are conserved from yeast to human and that are required for normal calcineurin signaling [232]. RCANs were first identified in screens for calcineurin-binding proteins [233] or calcineurin inhibitors [48] in fungi. Mammalian RCANs were discovered by database searches of the human genome for genes homologous to the yeast counterparts [234]. They have complex effects in cells, including both positive and negative contributions to calcineurin signaling, whose precise mechanisms are still unclear. Yeast rcn1 null mutants displayed diminished calcineurin signaling [48]: the stimulatory effect of Rcn1 on calcineurin requires phosphorylation of Rcn1 by Mck1, a GSK3 protein kinase, at Ser113, within the conserved FLISPP motif that is a signature of RCAN proteins [235]. Phosphorylated yeast Rcn1 is targeted for proteasomal degradation by the ubiquitin ligase SCFcdc4 [236,237], suggesting that a relief of calcineurin inhibition following RCAN phosphorylation could account for the observed stimulatory effect of RCAN proteins [237]. Moreover, phosphorylated Rcn1 is itself a substrate of calcineurin [235].
Myristoylation of the calcineurin regulatory subunit is also conserved from yeast to humans [238]; its disruption enhances the Ca2+ sensitivity of phosphatase activation or could also increase substrate affinity leading to an elevated basal activity of non-myristoylated calcineurin. Actually, in yeast, Ca2+ transients impinge on calcineurin subcellular localization, although the majority of calcineurin always localizes to the soluble fraction [239].
Whereas much is known about calcineurin, evidence about the roles played by the 44 Ca2+/CaM-dependent protein kinases [240] in budding yeast cells is limited, although there are some reports suggesting their involvement in the control of cell cycle, in the response of yeast cells to pheromones [184,241] and in general stress resistance [187,242]. A hyperactivated version of cmk1 causes cell cycle arrest accompanied by morphological defects in S. pombe [243], whereas deletion of the cmk2 gene results in hypersensitivity to oxidative stress [244].
CaMKs function in cell wall integrity (CWI) and cellular redox regulation in C. albicans [245]. CAMK1 plays an important role in growth and development of Neurospora [246] and is essential in A. nidulans [247]. Conidial germination (i.e. asexual reproductive spore production) and appressorial formation (i.e. formation of the specialized cell, called appressorium, typical of many fungalplant pathogens, that is used to infecthostplants) were delayed and virulence was attenuated in theΔcmk1 mutants in the rice blast fungus Magnaporthe oryzae [248].
S. pombe Cmk1 is significantly homologous to mammalian CaMK1, including a putative phosphorylation site (Thr192) for CaMKK. The fission yeast Ssp1 kinase, which controls G2/M transition and response to stress or nutrient limitation, was the first, albeit putative, CaMKK proposed in this yeast [249], and recently the Ca2+/CaM-dependent activity of Ssp1 and Cmk1 regulation by Ssp1 in mitotic commitment have been described [250]. Ssp1 has a CaM binding domain (CBD) and associates with 14-3-3 proteins as mammalian CaMKK does. Cmk1 kinase was reported to negatively regulate Prz1 activity, which in turn controls cmk1 gene transcription [251].
5. Calcium signaling pathways in fungi
As said, calcium is involved in many signaling processes in yeasts, participating in the control of different biological processes, such as response to membrane depolarization [88], mating pheromones [4], salt and environmental stresses [72,83,111,162,182,252], hypotonic shock [71,75], nutrient sensing [77,79,89,253,254,255], cell cycle progression [85,256], vacuole fusion [257], and cell integrity response [258]. In N. crassa, Ca2+-signaling is known to be involved in regulating a similar variety of processes such as Ca2+ stress tolerance, the circadian clock, growth, hyphal tip branching, ion transport, sexual development and UV survival [259,260,261,262,263].
The following subsections will analyze calcium signaling cross-talking with other signal transduction pathways. Unless differently specified, data were obtained in budding yeast.
5.1. Cell Wall Integrity (CWI) pathway
Hypotonic conditions [264] not only induce an intracellular calcium pulse, but the MAP kinase Mpk1/Slt2 is reported to be activated in these conditions and by high extracellular calcium concentrations [265]. Mpk1/Slt2 is the main effector of the Cell Wall Integrity (CWI) Pkc1/Slt2 pathway [266].
Cross-talk between the Ca2+ and Pkc mediated pathways has mainly been described in S. cerevisiae and in a few other filamentous fungi. CWI pathway activation results in an inhibition of Hsl1, a negative regulator of Swe1 (a serine/tyrosine dual-specific kinase), resulting in a delay in cell cycle progression mediated by the Clb-Cdc28 complex. Swe1 is also activated in a calcineurin-dependent manner, and cnb1 mutations are synthetically lethal with Pkc1 pathway mutations [258,267].Moreover, the function of the stress-induced β-1, 3-glucan synthase subunit Fks2 in cell wall remodeling during mating is not only dependent on the activity of the Pkc1 pathway, but also on calcineurin [195,268]. In fact, Crz1 induces in parallel to other CWI pathways the FKS2 gene [195,269]. The gene encoding one of the catalytic subunits of calcineurin (CNA1) is essential in strains that lack components of the cell wall integrity MAP kinase pathway [121,258,270]. Again, Ptp2 and Msg5 are key regulatory phosphatases that prevent over-activation of the calcium-induced signaling cascade, under the parallel control of the Slt2 and calcineurin pathways in budding yeast [271]. Genetic analysis suggested that Crz1 is located downstream both of the Slt2 and calcineurin pathway and is possibly the point of convergence between these parallel pathways [272], but this is not observed upon hypo-osmotic shock, where Mpk1 responsive Rlm1-dependent, but not Crz1-dependent, transcription is induced [75]. A genetic interaction between CnaA and PkcA was also reported in the filamentous fungus A. nidulans: calcineurin loss caused a defect in mitochondrial respiration, which was rescued by PkcA overexpression [273]. PkcA is fundamental to the cell wall integrity (CWI) pathway, is essential for viability, and is involved in polarized growth, morphogenesis and apoptosis [274,275,276,277]. Crosstalk between PkcA and the unfolded protein response (UPR) (see below) or other MAP (mitogen-activated protein) kinase cascades has also been observed [278,279].
5.2. Phosphoinositides pathway
It is known that in mammalian cells G proteins can activate PI-specific phospholipase C enzymes (PLCs), which catalyze the hydrolysis of PI-(4, 5)-bisphosphate (PIP2) to diacylglycerol (DAG) and D-myo-inositol-(1, 4, 5)-trisphosphate (IP3). DAG directly activates protein kinase C (PKC), while IP3 triggers release of calcium from intracellular stores via interaction with IP3 receptors in the endoplasmic reticulum (ER). A similar pathway has been time after time hypothesized in fungi, but it is far from being elucidated.
Activation of calcineurin by an increase of cytosolic Ca2+ mediated by G proteins and PLC has been observed in B. cinerea [280]. In contrast, it has been shown that PLC does not activate calcineurin signaling in C. neoformans [281].
In Neurospora crassa, an IP3-dependent increase in cytoplasmic Ca2+ was observed upon activation of one of the four N. crassa novel phospholipase C-δ subtype (PLC-δ) proteins [282,283] by membrane stretch [284,285], which triggers Ca2+ release through a large conductance channel, associated with the vacuolar membrane, and a small conductance channel, associated with endoplasmic reticulum (ER)-and Golgi-derived hyphal tip vesicles, thus maintaining high Ca2+ concentration required for hyphal tip growth [284,285,286] (see Figure 2B). In M. oryzae, the rice blast fungus, the PLC1, PLC2 and PLC3 PI-PLC-δ isoforms play distinct roles in regulating intracellular Ca2+ fluxes essential in fungal development and pathogenicity [287,288]. In C. neoformans, Plc1, again a homologue of the mammalian PI-PLC-δ, supplies the IP3 substrate required for the catalytic activity of the major IP3 kinase, Arg1, which is essential for cellular homeostasis and virulence [281].
In the model yeast S. cerevisiae, a single PLC isoform has similar catalytic activity to the mammalian PLC-δ isoform and is necessary for growth at non permissive temperatures (above 35°C), survival under hyperosmotic stress, and utilization of galactose, raffinose, or glycerol as a carbon source at permissive temperatures [289,290]. Cells deficient in PLC1 also show benomyl sensitivity, alterations in chromatin structure of centromeres, mitotic delay, and a higher frequency of chromosome loss [291]. DAG production upon phospholipase C activity is required for the Rab-and SNARE-dependent homo-typic vacuole fusion [292]. Synthesis of inositol pyrophosphates through activation of Plc1 is required for cell cycle progression after mating pheromone arrest [293].
However, in fungi, the role of the PIP2 breakdown products and the mechanism of Plc1-dependent signaling in initiating calcium influx is still uncertain since no homologs of mammalian IP3 receptors have been identified in fungal genomes [8,283]. A role for yeast TRP channels in response to IP3 generation was recently proposed [116,120]. Besides, a correlation between phosphoinositides and calcium signaling has been suggested [294]. In glucose-starved S. cerevisiae, glucose addition caused Plc1-dependent influx of extracellular calcium [79,295], accompanied by a transient increase in IP3 [296], leading to H+-ATPase activation [294], vacuolar calcium release [116] and induction of mitochondrial Sal1 ATP-Mg/Pi exchange activity resulting in the rapid increase of mitochondrial ATP levels [297]. However, it is unclear as to whether calcium influx is triggered by IP3 or by PIP2 depletion or via direct interaction of Plc1or of a soluble IP3-binding protein with a calcium channel [79,116,296]. Moreover, transient IP3 increase in nitrogen-depleted cells following addition of ammonium sulfate did not trigger any spike in intracellular calcium [298].
Recently, plasma membrane PI(4, 5)P2 was reported to be crucial for yeast invasive growth and this phospholipid was suggested to function upstream of the cAMP-dependent protein kinase A signaling pathway [299].
In yeasts, phosphoinositide specific phospholipases C are also important for yeast response to stress, in addition to their roles in nutrient sensing, growth control and differentiation [300]. In S. cerevisiae, during hyperosmotic shock, calcineurin concentrates in puncta and at sites of polarized growth, due to enhanced binding to and dephosphorylation of the PI(4, 5)P2 phosphatase, synaptojanin/Inp53/Sjl3, which leads to reorganization of PI(4, 5)P2-enriched membrane domains. Upon the shock, Inp53 moves from the trans-Golgi network to cortical actin patches where it likely regulates excess membrane endocytosis process in a conserved response shared by eukaryotic cells [301].
5.3. Unfolded protein response (UPR) pathway
Ca2+ influx through HACS and activation of calcineurin are also required for survival of S. cerevisiae cells exposed to conditions such as exposure to the glycosylation inhibitor tunicamycin, to dithiothreitol, but also to Ca2+ starvation, that stress the endoplasmic reticulum, inducing activation of the unfolded protein response (UPR) signaling pathway [121], which triggers expression of molecular chaperones in order to restore ER and Golgi functionality [302,303]. HACS-dependent Ca2+ uptake activates calcineurin promoting cell survival upon exposure to ER stressors [121,242]; this protection requires a functional stress-responsive Slt2/Mpk1 protein kinase cascade but not classical UPR factors [83,304]. Kch1, the low-affinity K+ transporter is up-regulated in response to several ER stressors and necessary as well for HACS activation [92].
Interestingly, the IRE1 gene, encoding UPR-involved transmembrane protein kinase and nuclease, was first identified as the gene for inositol prototrophy of S. cerevisiae [305], and the HAC1 gene, encoding the unfolded protein response regulator transcription factor, was isolated as a multicopy suppressor gene for the ire1 mutation [306].
Though the essential targets of calcineurin in this process have not yet been identified, activated calcineurin preserves the vacuolar membrane from damages of prolonged ER stress, preventing non-apoptotic cell death [307].
Lack of ER P-ATPase Cod1/Spf1 also, impairing ER function, induces constitutive activation of the UPR pathway, hypersensitivity to tunicamycin, and synthetic lethality with deletion of HAC1 [35]. Furthermore, a link was suggested between the perturbation of the complex sphingolipid metabolism and ER stress-mediated Ca2+-dependent mitochondrial apoptosis in yeast [308]. Sphingolipids are structural components of eukaryotic cell membranes which associate with sterols to form lipid rafts, which act as a platform for sorting proteins and clustering signal transducers [309]. In addition to structural roles, sphingolipid metabolites such as ceramide, long-chain base (LCB) and LCB phosphate (LCB-P) play pivotal roles as signaling molecules in many processes, including cell migration, stress response, survival, apoptosis, senescence, differentiation and endocytosis [310].
5.4. Programmed cell death (PCD) pathway
Disruption of Ca2+ homeostasis is a well-established signal for programmed cell death (PCD) in mammalian cells [311]. Recent evidence supports the hypothesis that unicellular organisms, including S. cerevisiae, also undergo programmed cell death in response to diverse insults, among which prolonged ER stress such as lipid imbalance and misfolded protein accumulation [312,313,314,315,316,317,318]. As in mammalian cells, Ca2+ can influence this process in yeast: as mentioned above, calcineurin-dependent Ca2+ influx in response to ER stress protects against cell death [83], whereas the antifungal agent amiodarone triggers massive Ca2+ flux from external and internal stores, eventually leading to apoptotic-like cell death, especially in calcineurin-deficient strains [319]. The existence of a common PCD pathway in yeast is suggested by the observation that both intracellular Ca2+ elevation and a burst of ROS take place during the yeast PCD induced by amiodarone, Al3+, acetic acid and K+ deprivation [320,321,322,323].
Mitochondria-dependent apoptosis associated with the rise of cytosolic Ca2+ has been reported both in pheromone-and amiodarone-induced cell death [320]. Mitochondria sequester Ca2+ ions, therefore contributing in recovering intracellular Ca2+ levels [324,325]. Ca2+ ions can diffuse readily through the outer membrane of the mitochondria and are then transported through the inner membrane into the mitochondrial cytoplasm through highly selective ion channels and transporters [326]. An increase in mitochondrial Ca2+ levels boosts ATP production which as a consequence increases the concentration of cellular reactive oxygen species (ROS) which can lead to apoptosis [327]. Interestingly, whereas amiodarone-induced Ca2+ influx is required for its toxicity [320,328], Ca2+ influx in response to other stresses plays a prosurvival role, rather than a pro-death role [76,121,329].
Ca2+ homeostasis seems to be necessary for longevity in yeast, as it was suggested in mammalian cells [330]: basal activity of calcineurin is required for maintenance of replicative life span under normal growth conditions. Calcineurin is involved in Cln2 G1 cyclin up-regulation, by a mechanism that is mediated by the degradation of Yap1 oxidative stress responsive transcription factor [331], thus assuring a G2 delay in response to stress [332].
5.5. Other cross-talks with calcineurin
The best-investigated pathways concerning a cross talk with calcineurin besides the cell wall integrity (CWI) pathway are the high osmolarity glycerol (HOG) pathway [333] and the alkaline stress response pathway.
Calcineurin-Crz1antagonizes the HOG pathway by downregulating it [334], however the exact mechanism is not known yet.
In S. cerevisiae and C. albicans, alkaline pH activates the Rim101 signal transduction pathway. In parallel, alkaline pH leads to an increase in the cytosolic Ca2+ concentration, activating the calcineurin-Crz1 signaling pathway [87,270,335]. Whereas Rim101 transcription factor regulates some genes together with Crz1, nonetheless both transcription factors also regulate specific genes under alkaline pH conditions [270,335].
Though it is known that CrzA of A. nidulans can be activated by alkaline pH [228], little more is known about the existence of a crosstalk between calcineurin-Crz1 and alkaline pH signaling in filamentous fungi.
6. Calcium signaling and fungal pathogenicity
It is well known that calcium signaling pathways are required for virulence in several fungal pathogens [336]. Studies in the divergent human pathogenic fungi Candida albicans [337,338,339], Candida glabrata [340,341] and Cryptococcus neoformans [164,342]revealed that calcineurin is critical for virulence; nonetheless, calcineurin functionality is refined through different mechanisms in each fungus, accordingly to the stressful conditions the pathogens face in vivo, such as high temperature, oxidative conditions, osmotic stress, alkaline environments, high temperatures, and starvation. A fungal pathogen will need a robust cell wall and efficient stress response in order to adapt with and resist to adverse conditions during infection.
In recent years, the emergence of fungal resistance has become frequent, partly due to the widespread clinical use of fluconazole, which is effective in prevention and treatment of Candida albicans infections. The limited selection of antifungal drugs for clinical fungal infection therapy has led to a new interest on research of novel antifungal targets that can be targeted by new antifungal drugs [343].
Targeting the calcineurin signaling pathways for therapy against pathogenic fungi is a validated approach [344,345,346]; inhibitors of calcineurin, such as FK506, cyclosporine, and sirolimus can convert fungistats such as tunicamycin, dithiothreitol, and generally ER stressors, to efficient fungicides. Unfortunately, they are commonly used as immunosuppressants since they inhibit conserved calcineurin signal transduction cascades required for T-cell activation [347]. Similarly, calcineurin inhibitors significantly improve lethality of the commonly used azole-class of antifungal drugs, which target sterol biosynthesis in the ER of fungal cells, in a wide array of pathogenic or non-pathogenic fungi [121,162,337,338,348,349,350].
Consistently, Δcrz1 mutants show reduced virulence in several plant and animal pathogenic fungi [197,203,210,212,213,218,219,220,222,340,351,352] but the phenotype is often less dramatic than in calcineurin mutants [20,21,223], suggesting that additional calcineurin targets are relevant for virulence.
6.1. Candida albicans
Candida organisms are generally commensal colonizers of skin and mucosal surfaces; most infections spring from the endogenous flora. Chemotherapeutic regimens can cause severe damage to the intestinal mucosa, allowing Candida spp. commensals to reach the bloodstream [353]. Candida albicans is the leading cause of fungal infections in humans, causing mucosal infections in both immunocompetent and immunocompromised individuals and invasive infections in immunocompromised individuals. Emergence of resistance in C. albicans has been largely seen in patients with advanced acquired immunodeficiency syndrome who undergo low dosage long term treatment with systemic antifungals [354].
C. albicansis capable of switching from yeast-like to filamentous growth in response to several environmental cues, such as elevated temperature, growth in serum, pH changes, and the presence of an extracellular matrix [355,356]. The transition to the filamentous growth form is involved in acquisition of virulence of C. albicans, so that mutants that are unable to grow in the filamentous form are avirulent [357]. Many Candida infections involve the formation of biofilms on implanted devices such as in dwelling catheters, consisting of exopolymeric material matrix-enclosed microcolonies of yeasts, hyphae and pseudohyphae, arranged in a bilayer structure [358,359]. Six transcription regulators control biofilm formation establishing an interconnected transcriptional network, integrating responses to many environmental conditions [360,361,362]. Calcium signaling via calmodulin is involved in triggering filamentous growth as well, since compounds that inhibit calmodulin function can prevent this transition [363], independently of calcineurin [364]. A mutant lacking any calcineurin subunit is avirulent and is unable to colonize and grow in the bloodstream of infected animals [365,366]. Calcineurin is not required for morphogenic transition, but it is critical for survival in serum. Antimicrobial peptides present in serum, which act by disrupting the plasma membrane of microbes, could be responsible for attacking C. albicans; consistent with this hypothesis, azole antifungal drugs that normally act in a fungistatic manner become lethal to C. albicans and other Candida species when calcineurin function is compromised [162,366,367].
6.2. Aspergillus spp.
Aspergillus species (most frequently A. fumigatus) infections are responsible for a high rate of morbidity and mortality in immunodepressed patients, such as patients with malignant blood diseases, or pulmonary diseases (cystic fibrosis, tuberculosis). Long-term azole therapy and the use of azole fungicides in agriculture have increased the number of cases of resistance to the only effective agent that can be used in oral treatments of these fungal infections [368,369,370].
In Aspergilli, small, easily dispersed conidia are the key for dispersal. In A. nidulans, CchA and MidA are required for hyphal polarity establishment, cell wall synthesis, and for conidiation, in low-calcium environmental conditions [371,372]. Nonetheless, only one out of three Pmc1 homologous calcium transporters is required for A. fumigatus infectiveness [24]; surprisingly, aΔmid1 strain was reported to be hypervirulent in a murine infection model [84].
6.3. Cryptococcus neoformans
Cryptococcus neoformansis a human pathogenic yeast (the teleomorph or sexual form is a filamentous fungus in the genus Filobasidiella) that can produce a polysaccharide capsule [373], which allows it to infect immunocompromised patients, causing meningoencephalitis [374,375]. The calcium-calcineurin signaling pathway in Cryptococcus neoformans is fundamental for sensing and adaptation to the human host [98,376,377]. Calcineurin is indeed essential for growth of C. neoformans at temperatures above 35°C and in the presence of increased levels of CO2, alkaline pH, and high concentrations of cations [342,378]. Calcineurin was reported to orchestrate thermal stress responses at mRNA processing sites [379]. Another peculiarity of C. neoformans is that calcineurin is required for filamentous growth in mating, diploid filamentation, and haploid fruiting [380,381]. The relationship between calcineurin and the cell wall integrity protein kinase C-Mpk1 MAP kinase signal transduction pathway, well characterized in S. cerevisiae, has been conserved in C. neoformans, except that in calcineurin-deficient strains the Mpk1/Slt2 MAP kinase pathway is activated [382] and induces expression of the FKS1 gene, encoding the only β-1, 3-glucan synthase in C. neoformans [383], whereas calcineurin and the MAP kinase pathway are both required for the induction of the FKS2 gene in the budding yeast.
The mpk1 mutants are attenuated for virulence but not avirulent, in contrast to calcineurin mutants [382]. The downstream effectors of C. neoformans calcineurin are still poorly characterized, apart from the Crz1 orthologue, previously identified as a protein kinase C target, during starvation, to regulate cell wall integrity; Crz1 is a target of calcineurin under non-starvation conditions, during cell wall stress and growth at high temperature [215]. Recently, Crz1/Sp1 was reported to be required for growth under hypoxic conditions, calcium resistance at 37°C, biofilm formation and azole resistance [216].
7. Conclusion
Though the general scheme of calmodulin/calcineurin signaling pathways in pathogenic fungi is similar to S. cerevisiae (see Figure 4), the lifestyle requirements for a pathogen has shaped specific signaling modules in these organisms, including the more difficult to analyze human fungal pathogens. For instance, in A. nidulans, a novel serine-proline rich region (SPRR) located between two conserved CnaA domains, the CnaB-binding helix and the CaM-binding domain is evolutionarily conserved and unique to filamentous fungi while completely absent in human calcineurin. Mutation of the SPRR serine residues to block phosphorylation led to significant hyphal growth and virulence defects, indicating the requirement of calcineurin phosphorylation at the SPRR for its activity and function [384]. These findings suggest the possibility of exploiting the presence of such unique traits for drug design of novel antifungals efficient against invasive aspergillosis.
The role of calcium channels and pumps in morphogenesis, stress response and virulence in C. albicans has been widely investigated [38,385,386,387]. It was reported that calcium chelators such as ethylene diamine tetra-acetic acid (EDTA) can disrupt C. albicans biofilms, indicating the importance of calcium homeostasis in C. albicans biofilm development [388,389]. For instance, calcium signaling appears essential for expression of some genes (such as ALS3) required for biofilm formation [390].
Moreover, calcium transporters such as Cch1, Eca1 and Vcx1 are involved in C. neoformans virulence [26,50,65,98]. The Mid1 and Cch1 channel in C. neoformans is actually involved in ER stress response [122]. Furthermore, Pmc1 was essential for both the progression of pulmonary infection and brain colonization in mice, emphasizing the crucial role of calcium signaling and transport for cryptococcal pathogenesis [391].
These insights taken together encourage pursuing strategies targeting calcium transporters.
Although the availability of genetic and molecular tools on fungal model organisms has allowed gaining huge knowledge about calcium homeostasis and signaling machinery, often helpful in order to elucidate calcium significance as a second messenger up to multicellular organisms, much is still unknown about calcium signaling not only in filamentous fungi but also in yeasts.
Despite the threat to public health represented by fungal infections such as systemic candidiasis or invasive aspergillosis, most pharmaceutical companies are leaving the area of anti-fungal development due to insufficient returns compared to investments in other classes of drugs.
In the last years, the central role of calcium pathways in yeast adaptation to environmental stress has been assessed, revealing that a novel set of potential targets for anti-fungal therapies awaits to be undercovered, and will deserve further investigation in the future years.
Conflict of interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: