Environmental Kuznets curve hypothesis in a financial development and natural resource extraction context: evidence from Tunisia

1.   Introduction

Symbiosis is an important aspect of ecology ^[1]. In fact, an entire journal, titled Symbiosis, is devoted to the study of symbiotic interactions at all levels ranging from the molecular to the organismic. The precise meaning assigned to the term symbiosis may vary depending on context; a fairly general definition, given in ^[2], is a close physical association between different species, regardless of whether that association is harmful, beneficial or neutral to any of the species involved.

In many cases of interest, the symbiosis is between a host, and one or more types of symbiont living within the host, often in large numbers. Two examples, both relating to humans, are infectious diseases ^[3,4] and gut microbe interactions ^[5]. A harmful symbiont is a pathogen, while a beneficial symbiont is a mutualist. Previous mathematical studies have focused on studying either the pathogen case ^[6] or the mutualist case ^[7,8], however it would be useful to understand, from a unified perspective, how the nature of the host-symbiont relationship affects the range of observed interactions.

To this end, we study a simple two-variable model of host-symbiont interactions with four parameters (described in the next section) that includes both horizontal and vertical transmission of the symbiont, and naturally incorporates both the pathogen and mutualist cases, as well as the intermediate neutral (neither harmful nor beneficial) case, modelled by the symbiont's effect on the host birth rate. As well, we assume recovery is possible; that is, it is possible for the symbiont within a host to die without killing the host. For simplicity, we assume perfect vertical transmission of the symbiont, and distinguish only presence or absence of the symbiont within the host, tracking the population density of both unassociated hosts (those without the symbiont) and associated hosts. A generalization to imperfect vertical transmission is also easily implemented, though we have not considered it here.

A special case of our model appears in ^[9], in which the authors discuss how it is possible, with a mixture of horizontal and vertical transmission, for a pathogen to successfully invade and persist within a host population, and they also give precise conditions for the pathogen to reach full occupation. In their model, only the pathogen case is considered, and recovery from the symbiont does not occur. In addition, the concern is with existence of certain equilibria and so a full description of the dynamics is not given. However, they also consider the case of imperfect transmission which is not covered here. From a different perspective, a model of mutualism ^[7], which is similar though not identical to this model, shows a qualitatively similar nullcline structure in some cases that leads to bistability; interestingly, this similarity is only observed after a change of variables is made in our model, from associated and unassociated host density to total host density and proportion of hosts that are associated.

For our model we are able to obtain a complete description of the dynamics for all values of the four parameters. In all but a single case, every trajectory tends to one of at most three distinct equilibria, ruling out sustained oscillations and reducing the study of the model to the characterization of equilibria. In turn, the number and location of equilibria is closely related to two factors:

● the effect of the symbiont upon the host (pathogen, mutualist or neutral), and

● which of the two is larger: the difference in the birth rate of associated vs. unassociated hosts (which is positive only for mutualists), and the horizontal rate of spread of the symbiont through the host population.

The second quantity is shown to be relevant only after making the above-mentioned change of variables. One way to view it is by how the symbiont allocates resources: is it focused on increasing the host's rate of birth and thus vertical transmission, or is it focused on spreading immediately to existing hosts via horizontal transmission?

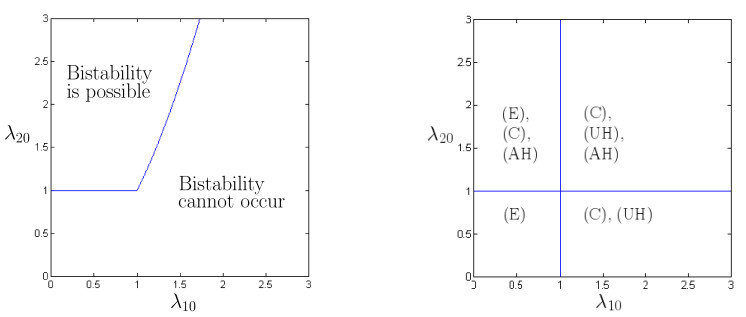
An important finding for this model is that bistability (between host-symbiont coexistence and either host extinction or host survival only) can only occur when the symbiont is a mutualist that is more focused on horizontal transmission than on improving host birth rate (i.e. when the second quantity above is positive), and that in the absence of bistability, all solutions with a positive density of both host and symbiont tend to a unique equilibrium. Moreover, in the absence of bistability the set of qualitative behaviours displayed by the system is insensitive as to whether the symbiont is a pathogen or a mutualist, except in the difference in host density between the host-without-symbiont equilibrium vs. the host-symbiont coexistence equilibrium, when both exist.

The original motivation for making a detailed study of this model was to obtain complementary results for a study of the corresponding stochastic spatial model ^[10]. When working on that paper, a preliminary analysis of the differential equations yielded partial but artifically restrictive results. The reason for this restriction was revealed only after making the change of variables mentioned above, from associated vs. unassociated host density to total host density vs. proportion of hosts that are associated, which made evident the occurrence of bistability, which previously we had thought was not possible. Thus one conclusion of this analysis is that the (biological) perspective of host-symbiont interactions as being a "stacked" system, in which hosts have their own birth-death dynamics, while symbionts within the host population have a similar birth-death dynamics taking place over the host population, is also a useful perspective when analyzing the dynamical system. It is worth noting that the stacked perspective is also used in ^[11] and indeed in our paper ^[10], where it assists in the analysis of the stochastic spatial model by suggesting comparisons with simpler models.

2.   Model derivation and main result

For simplicity, we ignore environmental transmission of the symbiont, and distinguish only presence or absence of the symbiont within the host. Unassociated hosts reproduce at some rate, and all hosts die at some rate which is normalized to 1. Associated hosts can infect unassociated hosts, and can also recover and become unassociated. Moreover, associated hosts reproduce at some possibly different rate from associated hosts. We assume, again for simplicity, perfect vertical transmission of the symbiont, so that offspring of associated parents are always associated. The symbiont is identified as pathogen, mutualist, or neutral by its effect on the host's birth rate.

To derive the differential equations that we study, we begin with a set of $N$ sites each of which can be either empty, occupied by an unassociated host, or occupied by an associated host. Each unassociated host attempts to give birth to an unassociated host onto a site chosen uniformly at random at rate $\lambda_{10}$, being successful if that site is empty. Similarly, each associated host attempts to give birth to an associated host at rate $\lambda_{20}$. Each host dies at rate $1$, while each associated host becomes an unassociated host at rate $\delta$. Each associated host attempts to transmit the symbiont to a randomly chosen site at rate $\lambda_{21}$, being successful if the recipient is an unassociated host. Let $U_0^{(N)}(t), U_1^{(N)}(t), U_2^{(N)}(t)$ denote the number of empty sites, unassociated hosts and associated hosts, respectively. Since $\sum_{i = 0}^2U_i^{(N)}(t) = N$, we find that $(U_1^{(N)}(t), U_2^{(N)}(t))$ is a Markov chain with the following transitions.

If we rescale to proportions $u_i^{(N)}(t) = U_i^{(N)}(t)/N$, then a result of Kurtz ^[12] implies that as $N\to\infty$, on any bounded time interval, sample paths of $(u_1^{(N)}(t), u_2^{(N)}(t))$ converge in probability to solutions of the following pair of equations, which we take as our object of study:

We note of course that the asymptotic behaviour of these equations is, in general, not the same as the above stochastic process. That said, for such models the connections often run deeper than just finite-time convergence; see for example the work of ^[13].

As it turns out, it is more productive to study the total proportion of hosts: $x_1 = u_1+u_2$ and the proportion of hosts that are associated: $x_2 = u_2/x_1$. Letting $\lambda_a = \lambda_{20}- \lambda_{10}$ and $\lambda_b = - \lambda_a + \lambda_{21}$, after a bit of algebra we obtain the system

The coordinate change $u\to x$ is singular at $x_1 = 0$ but note the inverse $u_1 = x_1(1-x_2), \ u_2 = x_1x_2$ is smooth and onto. Thus, every solution of (2.1) is the image of a solution of (2.2), so to understand (2.1) it is enough to study (2.2). In terms of the original description, the host population survives if $\liminf_{t\to\infty} x_1(t) > 0$ and the symbiont survives if $\liminf_{t\to\infty} x_2(t) > 0$. The symbiont takes over if $\lim_{t\to\infty}x_2(t) = 1$. It should be clear that takeover is only possible if $\delta = 0$, and even then only if further conditions are satisfied.

From the form of (2.2) it should be clear that $(x_1, x_2)$ is a more natural choice of variables than $(u_1, u_2)$, since the right-hand sides in (2.2) both factor nicely into density dependent form, with a good deal of symmetry between the two equations. This form is the previously mentioned "stacked" perspective, wherein the total host density, and the prevalence of the symbiont within the host population, are thought to be the best descriptors of the population demographics. The sign of $\lambda_a$ separates the pathogen, neutral and mutualist cases by $\lambda_a < 0, = 0, > 0$ respectively. The sign of $\lambda_b$ determines whether or not a higher host density is beneficial to the spread of the symbiont, measured by the proportion of hosts that are associated – since it depends on $\lambda_{21}$, we say the symbiont is weakly infectious if $\lambda_b < 0$, neutrally infectious if $\lambda_b = 0$ and strongly infectious if $\lambda_b > 0$. Distinguishing various cases according to the sign of $\lambda_a$ and $\lambda_b$ is crucial to making a complete analysis.

We first identify the regions of interest. Define the feasible region $\Lambda = [0, 1]^2$ and let

In addition, let

Except for some corner cases, these are the only candidates for equilibria on the boundary of $\Lambda$.

Define $\lambda_M = \max(\lambda_{10}, \lambda_{20})$ which is an upper bound on the host birth rate. Also define the conditions

(AinvU) stands for "associated invades unassociated", and is relevant iff $\lambda_{10} > 1$, in which case it corresponds to parameter values for which a small introduction of associated hosts in a stable population of unassociated hosts leads to an increase in the proportion of associated hosts. Equivalently, $G_2(p_1 + \epsilon e_2) > 0$ for small $\epsilon > 0$, where $e_2 = (0, 1)$. (UinvA) is analogous, and is relevant iff $\lambda_{20} > 1$ and $\delta = 0$.

The following is the main result of this article. Since the classification is somewhat lengthy we begin with a brief summary. There are four main cases: (E), (UH), (AH), (C), and two exceptional cases: (RS) and (B). In every case except for redundant symbiont (RS), every trajectory in $\Lambda_+$, the interior of the feasible region, tends to one of at most three equilibria, and tends to a unique equilibrium when bistability (B) does not occur. When (RS) and (B) do not occur, the system settles into one of the following four states:

● extinction of both host and symbiont (E),

● survival of host and extinction of symbiont (UH),

● survival of host and complete adoption of the symbiont (AH), which is only possible if $\delta = 0$, and

● survival of host, with stable coexistence of associated and unassociated hosts (C).

Case (RS) is defined precisely as $\lambda_{10} = \lambda_{20} > 1$, $\delta = \lambda_{21} = 0$ and would otherwise correspond to (UH). Case (B) is defined later, under section heading Subcase 5b, in terms of intersections of the nullclines. It falls strictly within the range of parameter values satisfying $\lambda_a > 0$ and $\lambda_b > 0$, that is a strongly infectious, mutualist symbiont, and would otherwise correspond to either (E) or (UH).

Theorem 2.1. The following six cases include all parameter values.

We begin with two exceptional cases.

1. Redundant symbiont (RS). Suppose $\lambda_{10} = \lambda_{20} > 1$ and $\delta = \lambda_a = \lambda_{21} = 0$, which would otherwise correspond to (UH). For all $x \in \Lambda_+$, $\lim_{t\to\infty} \phi_1(t, x) = a_1$ and $t\mapsto \phi_2(t, x)$ is constant.

2. Bistability (B). This occurs for a non-empty set of parameter values satisfying $\min(\lambda_a, \lambda_b) > 0$, $\delta > 0$, that would otherwise correspond to (E) if $\lambda_{10}\le 1$, or to (UH) if $\lambda_{10} > 1$. Moreover, the set of values $(\delta, \lambda_{21})$ that gives (B) is non-empty iff $\lambda_{20} > \max(1, \lambda_{10}^2)$.

There are three subcases: onset (OB), marginal (MB) and non-marginal (NB) bistability. (NB) is an open, contractible set of parameter values and (OB), (MB) are piecewise smooth and on the boundary of (NB). In each subcase there is an interior equilibrium $\bar x \in \Lambda_+$ satisfying $\max(0, a_1) < \bar x_1 < a_2$.

i) Onset of bistability (OB). $\lim_{t\to\infty}\phi(t, x) = \bar x$ for $x \in \Lambda_+$.

ii) Marginal bistability (MB). There is a set $U \subset \Lambda_+$, open in $\Lambda_+$ and not containing $\bar x$, such that

iii) Non-marginal bistability (NB). There are $\bar x \in U_2$, $\bar y \in \Lambda\setminus (U_1\cup U_2)$, with $\max(0, a_1) < \bar y_1 < \bar x_1 < a_2$ and $\max(0, a_3) < \bar y_2 < \bar x_2 < 1$, and disjoint sets $U_1, U_2\subset \Lambda_+$ both open in $\Lambda_+$, with $\Lambda_+\setminus (U_1\cup U_2)$ the stable manifold of $\bar y$, such that

Suppose (RS) and (B) do not hold. Then, there exists $\bar x \in \Lambda$ such that $\lim_{t\to\infty}\phi(t, x) = \bar x$ for all $x \in \Lambda_+$.

Assuming (RS) and (B) do not hold, four cases are possible.

1. Extinction. (E) $\bar x = (0, \max(0, a_3))$, if $\lambda_{10}\le 1$ and $\lambda_{20} \le 1+\delta$.

2. Survival and coexistence of associated and unassociated host. (C)

(a) $\delta > 0$ and either

i. $\lambda_{10}\le 1$ and $\lambda_{20} > 1+\delta$, or

ii. $\lambda_{10} > 1$ and (AinvU) holds, or

(b) $\delta = 0$ and either

i. $\lambda_{10}\le 1$, $\lambda_{20} > 1$ and (UinvA) holds,

ii. $\lambda_{10} > 1$, $\lambda_{20}\le 1$ and (AinvU) holds, or

iii. $\min(\lambda_{10}, \lambda_{20}) > 1$, (AinvU) holds and (UinvA) holds.

3. Survival of unassociated host only. (UH) $\bar x = p_1$ if $\lambda_{10} > 1$ and (AinvU) does not hold.

4. Survival of associated host only. (AH) $\bar x = p_2$ if $\delta = 0$, $\lambda_{20} > 1$ and (UinvA) does not hold.

It is worth noting the behaviour under (OB) is the same as in (C). The reason why we do not include it in (C) is because it occurs for parameter values that would otherwise satisfy either (E) or (UH).

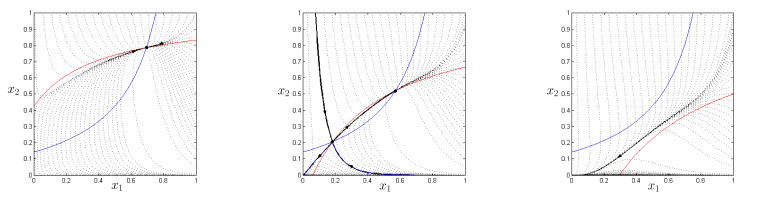
In Figure 2 we show streamlines together with nullclines in a few different cases.

Theorem 2.1 gives a complete picture of the dynamics, with the possible objections that

● the exact parameter ranges for (OB), (MB), and (NB) are not specified, and

● a precise formula for interior equilibria is not given.

In the case of (MB) and interior equilibria this is because they are determined by intersection conditions between curved nullclines on the interior of $\Lambda$. Despite this, in Subcase 5b we give a fairly nice formula for (OB), which leads to the iff condition $\lambda_{20} > \max(1, \lambda_{10}^2)$ for the possibility of bistability given in Theorem 2.1. We also give a satisfying characterization of the values of $(\delta, \lambda_{21})$ such that (NB) occurs.

Before moving onto the proof we unpack somewhat the result of Theorem 2.1, tying it to the original motivation. We begin with (B) since it is the most unusual case. Ignoring (OB) and (MB) since they are boundary cases, when (NB) occurs there are two stable equilibria; the first gives either extinction of the host (if $\lambda_{10} \le 1$) or survival without symbiont (if $\lambda_{10} > 1$), while the second is a coexistence equilibrium at a higher host density. The case $\lambda_{10} \le 1$ is obligate mutualism, as for example with termites and their protozoa ^[14], since neither the host nor the symbiont can survive without the other; this has been previously observed mathematically in, for example, ^[15]. The case $\lambda_{10} > 1$ is facultative mutualism, whereby the host is able to survive without the symbiont, but still benefits from its introduction. We note that, in order for (B) to occur, not only must the symbiont be a mutualist, but because of the condition $\lambda_{20} > \max(1, \lambda_{10}^2)$, the benefit it imparts must be sufficiently high, and quite significant if $\lambda_{10}$ is fairly large. On the other hand, since $\lambda_b = - \lambda_{21}+ \lambda_a$, its tendency $\lambda_{21}$ to spread through the host population must also exceed the benefit $\lambda_a = \lambda_{20}- \lambda_{10}$ that it imparts to the host birth rate. Thus bistability can only occur when we have a very helpful, yet selfish mutualist in the sense that the significant benefit it provides is still exceeded by its rate of spread through the host population. The latter trait can also be viewed as a strategy for survival which is more focused on horizontal transmission than on vertical transmission.

When we have either a pathogen ($\lambda_a < 0$), or a mutualist that does more to aid host survival than to spread itself through the host population ($\lambda_b < 0$), (B) does not occur. In this case there is a single equilibrium attracting all solutions in the interior of the feasible region, which is determined by the location of boundary equilibria (survival of unassociated hosts or associated hosts, in isolation) together with the invasion conditions (AinvU) or (UinvA), and whether or not the recovery rate is zero. In particular, it is straightforward to determine whether we have host extinction (E), survival of unassociated host only (UH), coexistence (C), or survival of associated host only (AH), so we leave it to the reader to inspect each case. This description, of course, bears the exception of the trivial case (RS) that essentially corresponds to two equally viable species that don't interact except in their competition for space.

The remainder of the paper is organized as follows. In Section 3 we recall some basic theory of plane systems of differential equations. In Section 4 we take care of the dynamics on $\Lambda \setminus \Lambda_+$, which consists of invariant lines on the boundary of the feasible region. In Section 5 we study the dynamics on the interior of $\Lambda$, in several steps. We first study special parameter values where (2.2) separates into a simpler form. We then determine boundary equilibria and their stability. Next we study the nullclines, and move on to study the itinerary of trajectories on regions delineated by the nullclines. We then give a sufficient condition to rule out periodic orbits, homoclinic orbits and heteroclinic cycles, using Dulac's criterion. At this point, we have the tools to study the dynamics in the remaining cases where (2.2) does not assume a simple form, and we complete the proof.

3.   Background and definitions

We first recall some basic theory that can be found in ^[16], specialized to the present context. Let $F \in C^1(\mathbb{R}^2, \mathbb{R}^2)$. Corresponding to $F$ there exists a $C^1$ function $\phi:S \to \mathbb{R}^2$ called the flow, defined on an open $S \subset \mathbb{R}\times \mathbb{R}^2$ containing $\{0\}\times \mathbb{R}^2$ and satisfying

In particular, for fixed $x$, $t\mapsto \phi(t, x)$ solves the initial value problem

in an open time interval around $0$. Letting $\tau_+(x) = \sup \{t:(t, x) \in S\}$ and $\tau_-(x) = \inf\{t:(t, x) \in S\}$, if we require that for every $x \in \mathbb{R}^2$,

1. $\tau_-(x) = -\infty$ or $\lim_{t \downarrow \tau_-(x)}\|\phi(t, x)\| = \infty$ and that

2. $\tau_+(x) = \infty$ or $\lim_{t \uparrow \tau_+(x)}\|\phi(t, x)\| = \infty$,

then $\phi$ exists and is the unique function with the stated properties. In particular, for every $x \in \mathbb{R}^2$ the above initial value problem has a unique solution forward and backward in time, to either $\pm t = \infty$ or until it diverges. Given $x \in \mathbb{R}^2,$ the corresponding trajectory $\Gamma$ is defined as

and the sets $\{\Gamma(x):x \in \mathbb{R}^2\}$ form a partition of $\mathbb{R}^2$ into trajectories. We are also interested in the positive semi-trajectory

We say that a set $E \subset \mathbb{R}^2$ is invariant if $x \in E$ implies $\Gamma(x) \subset E$, and forward invariant if $x \in E$ implies $\Gamma^+(x) \subset E$. If $E$ is both bounded and forward invariant, the above implies $\tau^+(x) = \infty$ for every $x \in E$. In this case we are interested in the omega-limit set of points $x \in E$, defined by

and contained in the closure of $E$. Omega-limit sets are known to be closed, connected, invariant, and made up of trajectories, which can be of a few types, including the following. An equilibrium point is a point $x$ such that $F(x) = 0$. A periodic orbit is the positive semi-trajectory of a point $x$ satisfying $\phi(T, x) = x$ for some $T > 0$, and a separatrix cycle is the union of finitely many equilibrium points $p_1, \dots, p_m$ for some $m\ge 1$ and trajectories $\Gamma(x_i), i = 1, \dots, m$ satisfying

A separatrix cycle with $m = 1$ is a homoclinic orbit, and with $m > 1$ is a heteroclinic cycle. It should be clear from the definition that if $\omega(x)$ is a single point, then $\lim_{t\to\infty}\phi(t, x) = \omega(x)$.

4.   Preliminary analysis

We return to (2.2) and begin by studying the dynamics on invariant boundary lines.

Dynamics on $\Lambda\setminus \Lambda_+$. Let $L_1 = \{x_2 = 0\}$, $L_2 = \{x_1 = 0\}$ and $L_3 = \{x_2 = 1\}$, so that

The lines $L_1, L_2$ are invariant, as is $L_3$ if $\delta = 0$. On $L_1$ the equilibria are $p_0$ and $p_1$. Since $G_1 = x_1(\lambda_{10}(1-x_1)-1)$ if $x_2 = 0$, the segment $\{0 < x_1\le 1, \ x_2 = 0\}$ is forward invariant and for $x$ in that segment,

On $L_2$ the equilibria are $p_0$ and $p_3$. Since $G_2 = x_2(\lambda_a (1-x_2)-\delta)$ if $x_1 = 0$, the segment $\{x_1 = 0, \ 0 < x_2 \le 1\}$ is forward invariant and for $x$ in that segment,

On $L_3$, $G_2 = -\delta x_2$, so if $\delta = 0$ that line is invariant and the equilibria are $p_3$ and $p_2$. Since $G_1 = x_1(\lambda_{20}(1-x_1)-1)$ if $x_2 = 1$, the segment $\{0 < x_1\le 1, \ x_2 = 1\}$ is forward invariant and for $x$ in that segment,

Forward invariance of $\Lambda, \Lambda_+$. Note that on the line $\{x_1 = 1\}$, $G_1 = -1 < 0$, and if $\delta > 0$ then $G_2 < 0$ on $\{x_1 > 0, \ x_2 = 1\}$. Therefore $\Lambda$ is forward invariant. This is because every side of $[0, 1]^2$ is either invariant, or else is such that for $x$ on that side, $\phi(t, x) \in (0, 1)^2$ for small enough $t > 0$, which means that trajectories cannot exit $[0, 1]^2$ along any of its four sides. The same is true if we remove any number of invariant lines from $\Lambda$. In particular, $\Lambda_+$ is also forward invariant.

5.   Dynamics on $\Lambda_+$

Next we determine $\omega(x)$ for $x \in \Lambda_+$, proving Theorem 2.1. By forward invariance $\omega(x) \subset \text{Cl}(\Lambda_+) = \Lambda$, where $\text{Cl}$ denotes the closure. The analysis is broken up into five broad cases. In each situation we point out which case in Theorem 2.1 ((RS), (OB), (MB), (NB), (E), (C), (UH), (AH)) applies.

Case 1 – low host birth rate: $\lambda_M = \max\{ \lambda_{10}, \lambda_{20}\} \le 1$ (E). If $x \in \Lambda$ then $G_1 \le x_1(\lambda_M(1-x_1)-1)$.

So, $\lambda_M\le 1$ implies $G_1 \le -x_1^2$ and $\lim_{t\to\infty}\phi_1(t, x) = 0$.

Case 2 – neutral symbiont: $\lambda_M > 1, \ \lambda_a = 0.$ In this case $\lambda_{10} = \lambda_{20} > 1$ and $\lambda_b = \lambda_{21}$, so

Since $\lambda_{10}, \lambda_{20} > 1$, $a_1, a_2 > 0$. Moreover if $x \in \Lambda$ then $\lim_{t\to\infty}\phi_1(t, x) = a_1$. Since $\lambda_{10} = \lambda_{20}$, we have $\lambda_{20}(1-a_1) = \lambda_{10}(1-a_2) = 1$, so (AinvU)$\Leftrightarrow \lambda_{21}a_1 > \delta$ and (UinvA)$\Leftrightarrow \lambda_{21}a_2 > 0 \Leftrightarrow \lambda_{21} > 0$.

If $\delta = \lambda_{21} = 0$ (RS) then $G_2 = 0$, so $t\mapsto\phi_2(t, x)$ is constant.

If $\delta = 0$ and $\lambda_{21} > 0$ (AH) then $G_2 > 0$ for $x_1 > 0$ and $0 < x_2 < 1$, so $\lim_{t\to\infty}\phi_2(t, x) = 1$ for $x\in \Lambda_+$.

If $\delta > 0$ and $\lambda_{21} = 0$ (UH) then $G_2 < 0$ for $x_2 > 0$, so $\lim_{t\to\infty}\phi_2(t, x) = 0 \ \hbox{for} \ x \in \Lambda_+$.

If $\delta, \lambda_{21} > 0$, then using the limiting value of $\phi_1$ we find that

If $\lambda_{21}a_1 \le \delta$ (UH) then $\bar x_2 = 0$ and if $\lambda_{21}a_1 > \delta$ (C) then $0 < \bar x_2 < 1$.

Case 3 – neutrally infectious symbiont: $\lambda_M > 1, \ \lambda_a \ne 0, \ \lambda_b = 0$. In this case $\lambda_{10}\ne \lambda_{20}$ and $\lambda_{10} = \lambda_{20}- \lambda_{21}$. This forces $\lambda_{20} > \lambda_{10}$ so that $\lambda_a > 0$ and $\lambda_{21} > 0$. Multiplying on both sides by $\lambda_{10}$,

which is $\Leftrightarrow \lambda_{10} > 0$ and $\lambda_{21} > \delta$. Multiplying on both sides by $\lambda_{20}$,

so (UinvA) does not hold. We find

so

Then,

Plugging $\bar x_2$ into the equation for $G_1$ we find

In particular, $\phi_1\to 0$ exactly on the condition $\lambda_{10}+ \lambda_a \bar x_2 \le 1$, which

This concludes the easy cases. To treat cases with $\lambda_a, \lambda_b \ne 0$, more effort is required. We will start by studying equilibria on the boundary of $\Lambda_+$, then nullclines on $\Lambda_+$, then itineraries on $\Lambda_+$. Then, we will be ready to consider the remaining cases.

Equilibria on $L$. Let $L = L_1 \cup L_2$ if $\delta > 0$ and $L = L_1\cup L_2 \cup L_3$ if $\delta = 0$, so that $\Lambda_+ = \Lambda \setminus L$. Since $\lambda_a, \lambda_b \ne 0$, $p_0, p_1, p_2, p_3$ are the possible equilibria (eq) on $L$. Letting $a_1 = 1-1/ \lambda_{10}, \ a_2 = 1-1/ \lambda_{20}, \ a_3 = 1-\delta/ \lambda_a$,

1. $p_0 = (0, 0) \in L_1\cap L_2$ is always an eq in $\Lambda$.

2. $p_1 = (a_1, 0) \in L_1$ is an eq in $\Lambda \setminus \{p_0\}$ if $\lambda_{10} > 1$.

3. $p_3 = (0, a_3) \in L_2$ is an eq in $\Lambda \setminus \{p_0\}$ if $\delta < \lambda_a$, and if $\delta = 0$ then $p_3 = (0, 1) \in L_2 \cap L_3$.

4. $p_2 = (a_2, 1) \in L_3$ is an eq in $\Lambda \setminus \{p_3\}$ if $\delta = 0$ and $\lambda_{20} > 1$.

To assess stability we compute the Jacobian matrix $J(x) = (\partial_j G_i(x))_{ij}$.

If $x \in L$ then at least one of $x_1, x_2$ is equal to $0$ or $1$, and $J(x)$ is triangular, so its eigenvalues are equal to its diagonal entries. Straightforward computation shows that

1. $J(p_0)$ has eigenvalues $\lambda_{10}-1$ and $\lambda_a-\delta$,

2. $J(p_1)$ has eigenvalues $1 - \lambda_{10}$ and $J_{22}(p_1)$,

3. $J(p_2)$ has eigenvalues $1- \lambda_{20}$ and $J_{22}(p_2)$ if $\delta = 0$, and

4. $J(p_3)$ has eigenvalues $\lambda_{20}-(1+\delta)$ and $\delta - \lambda_a$.

Since $\lambda_b = - \lambda_a+ \lambda_{21}$, $\lambda_a = \lambda_{20}- \lambda_{10}$, $\lambda_{10}(1-a_1) = 1$ and $1-a_1 = 1/ \lambda_{10}$,

and if $\delta = 0$ then since $- \lambda_a = \lambda_{10}- \lambda_{20}$ and $\lambda_{20}(1-a_2) = 1$,

Using these calculations and the fact that $G_2(x+ \epsilon e_2) = \epsilon G_2(x) + o(\epsilon)$,

ⅰ) $J_{22}(p_1) > 0 \Leftrightarrow$ (AinvU) $\Leftrightarrow$ $G_2 > 0$ just above $p_1$.

ⅱ) $J_{22}(p_2) > 0 \Leftrightarrow$ (UinvA) $\Leftrightarrow$ $G_2 < 0$ just below $p_2$.

Recall the following three types of equilibria $p$:

ⅰ) Attracting: for some $\epsilon > 0$, $|x-p| < \epsilon$ implies $\lim_{t\to\infty}\phi(t, x) = p$.

ⅱ) Saddle point: the stable manifold and unstable manifold

are smooth curves each consisting of $p$ and a pair of trajectories, and the tangent lines to $W_s, W_u$ at $p$ are eigenvectors of $J(p)$ with eigenvalues whose real part is negative, respectively positive.

ⅲ) Repelling: for some $\epsilon > 0$, $|x-p| < \epsilon$ implies $\lim_{t\to-\infty}\phi(t, x) = p$.

Given equilibrium $p$, let $\mu_1, \mu_2$ be the eigenvalues of $J(p)$, and recall that [hartman-grobman]

ⅰ) $p$ is attracting if $(\mu_1), \ (\mu_2) < 0$,

ⅱ) $p$ is a saddle point if $(\mu_1) < 0 < (\mu_2)$, and

ⅲ) $p$ is repelling if $0 < (\mu_1), \ (\mu_2)$.

If one or both of $(\mu_i) = 0$ then $p$ could be of any type, or none.

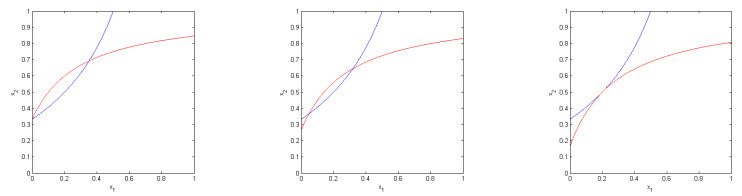
Nullclines.

$\gamma_1$ is a hyperbola with vertical asymptote $x_1 = 1$, so instead let $\gamma_1$ be the branch with $x_1 < 1$.

If $\delta = 0$ then $\gamma_2 = \{x_2 = 1\} \cup \{x_1 = - \lambda_a/ \lambda_b\}$ so instead let $\gamma_2$ be the vertical line $\{x_1 = - \lambda_a/ \lambda_b\}$.

If $\delta > 0$ then $\gamma_2$ is a hyperbola with horizontal asymptote $x_2 = 1$, so instead let $\gamma_2$ be the branch with $x_2 < 1$. Both $\gamma_1$ and $\gamma_2$ intersect each of the invariant lines at most once. The intersection points, and conditions for existence, are

● $\gamma_1\cap \{x_2 = 0\} = p_1$ if $\lambda_{10} > 0$,

● $\gamma_1 \cap \{x_1 = 0\} = r_1 = (0, b_1)$ with $b_1 = (1- \lambda_{10})/ \lambda_a$,

● $\gamma_1 \cap \{x_2 = 1\} = p_2$ if $\lambda_{20} > 0$,

● $\gamma_2 \cap \{x_2 = 0\} = r_2 = (b_2, 0)$ with $b_2 = (\delta- \lambda_a)/ \lambda_b$,

● $\gamma_2 \cap \{x_1 = 0\} = p_3$, and

● $\gamma_2 \cap \{x_2 = 1\} = r_3 = (b_2, 1)$ if $\delta = 0$.

By considering what happens when $x_2 = 0$ and noting that $\{x_1 = 0\}, \gamma_1$ are the only null sets for $G_1$ when $0 \le x_1 \le 1$, it follows that $G_1 > 0$ to the left of $\gamma_1$ in $\Lambda_+$. On the other hand, since $\partial_{x_1}G_2 = \lambda_b x_2(1-x_2)$, if $\lambda_b < 0$ then $G_2 > 0$ to the left of $\gamma_2$, while if $\lambda_b > 0$ then $G_2 > 0$ to the right of $\gamma_2$, in $\Lambda_+$.

If $\lambda_{10} > 1$ then $b_2 = a_1$ marks the boundary between (AinvU) and its complement.

Similarly, if $\lambda_{20} > 1$ and $\delta = 0$ then $b_2 = a_2$ marks the boundary between (UinvA) and its complement.

Also, it's easy to check that $b_1 = a_3$ is equivalent to $\lambda_{20} = 1+\delta$.

It's useful to think of $\gamma_1$ as the graph of the function

and when $\delta > 0$ to think of $\gamma_2$ as the graph of the function

If $\delta = 0$ then $\gamma_1\cap \gamma_2$ has cardinality $0$ or $1$ as $\gamma_1$ has at most one intersection point with any vertical line. If $\delta > 0$ then since the sign of the pairs $(g_1'(x_1), g_1''(x_1))$ and $(g_2'(x_1), g_2''(x_1))$ do not depend on $x_1$ and never coincide (to see this, break up according to $(\hbox{sgn}(\lambda_a), \hbox{sgn}(\lambda_b))$, noting that $\lambda_a+ \lambda_b = \lambda_{21}\ge 0$ implies $(\hbox{sgn}(\lambda_a), \hbox{sgn}(\lambda_b)) \ne (-1, -1)$), $\gamma_1\cap \gamma_2$ has cardinality $0, 1$ or $2$.

Itineraries. Let $G = (G_1, G_2)$ and for a pair $(a, b)$ let $\hbox{sgn}(a, b) = (\hbox{sgn}(a), \hbox{sgn}(b)) \in \{-1, 0, 1\}^2$. For each sign vector $\sigma \in \{-1, 0, 1\}^2$ let

Since all signs are represented, $\{R(\sigma):\sigma \in \{-1, 0, 1\}^2\}$ is a partition of $\Lambda_+$. Note that one or more of these sets could be empty.

● The set $R(0, 0) = \gamma_1 \cap \gamma_2 \cap \Lambda_+$ consists of equilibrium points and has cardinality $0, 1$ or $2$.

● The sets $R(0, 1)\cup R(0, -1) = \gamma_1 \cap \Lambda_+ \setminus \gamma_2$ and $R(1, 0) \cup R(-1, 0) = \gamma_2 \cap \Lambda_+\setminus \gamma_1$, so we refer to the union of all four as $R_\gamma$. Since neither hyperbola has either a horizontal or vertical tangent at any point, while $G$ is horizontal or vertical on each one (or if $\delta = 0$, $\gamma_2$ is vertical while $G$ is horizontal on $\gamma_2$), it follows that on $R_{\gamma}$, $G$ is transverse to the tangent space of $R_\gamma$, so for any $x\in \Lambda_+$, the set of times $\{t:\phi(t, x) \in R_\gamma\}$ is a discrete set.

● The sets $R(\sigma)$ for $\sigma \in \{-1, 1\}^2$ are open subsets of $(0, 1]^2$ that, based on the number of intersection points of $\gamma_1$ and $\gamma_2$, each have at most 2 connected components.

If $x \in (0, 1]^2 \setminus R(0, 0)$ then since $R(0, 0)$ is invariant and $\{t:\phi(t, x) \in R_\gamma\}$ is discrete, there is a (possibly finite) symbolic sequence $I(x) = (\sigma_1, \sigma_2, \dots)$ called the itinerary of $x$, with each $\sigma_i \in \{-1, 1\}^2$, and an increasing sequence of times $t(x) = (t_1, t_2, \dots)$, with $t_0 = 0$, and with $t_i = \infty$ iff $I(x)$ has length $i$, with the property that

Define a directed graph called the sign graph with vertices $\{-1, 1\}^2$ by including each directed edge $(\sigma, \sigma')$ iff there is $x$ such that $(I_i(x), I_{i+1}(x)) = (\sigma, \sigma')$ for some $i\ge 1$. The sign graph is cyclic if there is a sequence of edges $(\sigma_1, \sigma_2), \dots, (\sigma_k, \sigma_1)$, and acyclic if not. Appearance of $(\sigma, \sigma')$ in the sign graph is also represented by $R(\sigma)\to R(\sigma')$. $R(\sigma)$ is absorbing if none of the edges $(\sigma, \cdot)$ appear on the sign graph. An equilibrium point $p \in \text{Cl}(R(\sigma))$ is a sink for $R(\sigma)$ if for some $x \in R(\sigma)$, $I(x) = \sigma$ and $\lim_{t\to\infty}\phi(t, x) = p$. If $p$ is a sink for $R(\sigma)$ then it is a local maximum of $x\mapsto \sigma \cdot x$ on $R(\sigma)$. The following lets us seal the fate of trajectories, when the sign graph is acyclic. The proof is given in the Appendix.

Lemma 5.1. If $I(x)$ is finite and its last entry is $\sigma$ then $\omega(x)$ is a sink for $R(\sigma)$.

In particular, if the sign graph is acyclic then for all $x \in \Lambda_+$, $\omega(x)$ is a sink.

Periodic orbits and cycles. Lemma 1 makes our life easier when the sign graph is acyclic. When the sign graph is cyclic, we will use the following proposition to simplify the analysis.

Proposition 5.1. For each $x \in \Lambda_+$, $\omega(x)$ is either

1. an equilibrium point or

2. contains a separatrix cycle intersecting an equilibrium in $L$.

Proof. There are three steps.

$1.$ Show there are no periodic orbits in $\Lambda$ and no separatrix cycles in $\Lambda_+$.

$2.$ Show that a separatrix cycle intersecting $L$ must intersect an equilibrium in $L$.

$3.$ Invoke a generalized form of the Poincaré-Bendixson theorem.

Step 1. We begin with

Lemma 5.2 (Dulac's criterion). - Suppose we have the planar system

Let $R \subset \mathbb{R}^2$ be a simply connected region in the plane and $B : \mathbb{R}^2 \to \mathbb{R}^2$ be a $C^1$ function (called a Dulac function) such that the divergence of $BF$ is non-zero and has constant sign almost everywhere on $R$. Then, the system $u' = F (u)$ has no periodic orbit and no separatrix cycle on $R$.

Since most proofs of Dulac's criterion only rule out periodic orbits, we include a proof in the appendix.

No periodic orbit or separatrix cycle in $\Lambda_+$. Since the restriction of $x \mapsto (x_1(1-x_2), x_1x_2)$ to $\{0 < x_1 \le 1, \ 0 < x_2 < 1\}$ maps bijectively onto $\{u_1, u_2 > 0, \ u_1+u_2 \le 1\}$, periodic orbits and separatrix cycles are mapped to the same. So, to rule them out on the former set, we find a Dulac function for (2.1) on the latter set. The function $B(u) = 1/(u_1u_2)$ works, since

is strictly negative when $u_1, u_2 > 0$ (at least one of $\lambda_{10}, \lambda_{20}$ is positive).

If $\delta = 0$ the set $\{0 < x_1 \le 1, \ 0 < x_2 < 1\}$ is equal to $\Lambda_+$.

If $\delta > 0$, $\Lambda_+$ includes also the segment $\{0 < x_1 \le 1, \ x_2 = 1\}$. Since $G_2 < 0$ on that segment, any trajectory that intersects it also intersects $\Lambda^c$, so is not contained in $\Lambda$.

No periodic orbit in $L$. If a periodic orbit $C$ intersects $L = \Lambda \setminus \Lambda_+$, it intersects an invariant line on $L$. Since $C$ is a single trajectory, it is a subset of that invariant line. Since $C$ is the continuous injective image of a circle and $L$ is either a pair of orthogonal lines, or two parallel lines and an orthogonal line, this cannot occur.

Step 2. A separatrix cycle is the continuous injective image of a circle. If it intersects $L$, it intersects an invariant line on $L$, so it must contain an equilibrium point on that line. If it did not, it would consist of a single trajectory on that line.

Step 3. This step is a trivial application of the following result.

Theorem 5.1 (Generalized Poincaré-Bendixson Theorem). - Let $E\subset \mathbb{R}^2$ be an open set and $F \in C^1(E, \mathbb{R}^2)$. Suppose the system $x' = F(x)$ has a positive semi-trajectory $\Gamma^+(x)$ contained in a compact set $K \subset E$ with the property that $F(x) = 0$ for at most finitely many $x \in K$. Then, $\omega(x)$ is either

1. an equilibrium point,

2. a periodic orbit, or

3. contains a separatrix cycle.

Proof. This is given by Theorem 2 in Section 3.7 of ^[17], and the comments that follow.

This concludes the proof of Proposition 5.1.

Trajectories. We are now ready to study dynamics in the remaining cases. We break up our analysis according to the sign of $\lambda_a, \lambda_b$. The interested reader will note that Case 3 above can also be covered here using the same methods, although it does not give an explicit formula for the interior equilibrium, when there is one.

Case 4 – pathogen: $\lambda_M > 1$, $\lambda_a < 0$, $\lambda_b\ne 0$. In this case, $\lambda_{10} > \max(1, \lambda_{20})$ and $\lambda_b = - \lambda_a+ \lambda_{21} > 0$, so $a_1 = 1-1/ \lambda_{10} > 0$, $b_2 = (\delta- \lambda_a)/ \lambda_b > 0$ and $G_2 > 0$ to the right of $\gamma_2$. $g_1$ is decreasing and concave, and if $\delta > 0$ then $g_2$ is increasing and concave, while if $\delta = 0$ then $\gamma_2 = \{x_1 = b_2\}$ – in either case $\gamma_2$ lies to the right of $\{x_1 < b_2\}$ so $G_2 < 0$ on this set. Since $G_1 > 0$ near $p_0$ it attracts no points in $\Lambda_+$, and since $p_3 = (0, a_3)$ with $a_3 = 1-\delta/ \lambda_a \ge 1$, if $p_3 \in \Lambda$ then $\delta = 0$, $p_3 = (0, 1)$ and $G_2 < 0$ in a $\Lambda_+$-neighbourhood of $p_3$, which means $p_3$ attracts no points in $\Lambda_+$.

If $b_2 \ge a_1$ then (AinvU) does not hold, which gives (UH). $R(-1, 1) \to R(-1, -1) \to R(1, -1)$ appear from right to left. If $p_2 \in \Lambda$ then since $\lambda_{20} < \lambda_{10}$, $a_2 < a_1\le b_2$ so $G_2 < 0$ in a $\Lambda_+$-neighbourhood of $p_2$. Since the sign graph is acyclic, every solution tends to a sink, and the only candidate is $p_1$.

If $\delta > 0$ and $b_2 < a_1$ (AinvU) which gives (a.ii) of (C), or $\delta = 0$ and $a_2 < b_2 < a_1$ which gives (AinvU) and (UinvA) and thus (b.iii) of (C) if $a_2 > 0$ or (b.ii) of (C) if $a_2\le 0$, then (C) holds. $\gamma_1\cap \gamma_2$ is a unique point $p_4 \in \Lambda_+$ and $p_1$ is a saddle, as is $p_2$ if $\delta = 0$. The sign graph is cyclic, so we use Proposition 1 to conclude that solutions tend to $p_4$ provided no separatrix cycles on $\Lambda$ contain an equilibrium on $L$ – let $C$ denote a possible candidate. Since $p_1$ is a saddle, $W_s(p_1) = \{0 < x_1, \ x_2 = 0\}$ so $p_1 \in C$ implies $p_0 \in C$. Since $p_0$ is a saddle with $W_s(p_0) = \{x_1 = 0, \ x_2 < a_3 = 1-\delta/ \lambda_a\}$, $p_0 \in C$ implies $p_3 \in C$. If $\delta > 0$, $p_3 \notin \Lambda$ so $C$ cannot exist, otherwise $\delta = 0$ and $p_0 \in C$ implies $p_3 = (0, 1)\in C$. If $\lambda_{20} < 1$ then $W_s(p_3) = \{a_2 < x_1, \ x_2 = 1\}$ and $C$ cannot exist. If $\lambda_{20} = 1$ then since $\gamma_2$ does not intersect $p_3$, still $G_2 < 0$ in a $\Lambda_+$-neighbourhood of $p_3$, so $W_s(p_3)$ is disjoint from $\Lambda_+$ which means $W_s(p_3) = \{0 \le x_1, \ x_2 = 1\}$ and $C$ cannot exist. If $\lambda_{20} > 1$ then $p_3$ is repelling, and $C$ cannot exist. If $\delta > 0$ then $p_2 \notin \Lambda$, and if $\delta = 0$ and $p_2 \in \Lambda$ then $p_2$ is a saddle with $W_s(p_2) = \{0 < x_1, \ x_2 = 1\}$, so $p_2 \in C$ implies $p_3 \in C$. Since $p_3$ is repelling, $C$ cannot exist.

If $\delta = 0$ and $b_2 \le a_2 < a_1$ then (AinvU) holds but (UinvA) does not, which gives (AH). $R(1, -1)\to R(1, 1) \to R(-1, 1)$ appear from left to right, and $p_1$ is a saddle. Since the sign graph is acyclic, solutions tend to a sink, and the only candidate is $p_2$.

Case 5 – mutualist: $\lambda_M > 1$, $\lambda_a > 0$, $\lambda_b\ne 0$. In this case $\lambda_{20} > \max(1, \lambda_{10})$ so $a_2 > 0$, and $g_1$ is increasing and convex. Notice that $g_1$ intersects the set $\{x_1 = 0, 0\le x_2 < 1\} \cup \{0\le x_1 < a_2, \ x_2 = 0\}$ at exactly one point, which is $p_1$ if $\lambda_{10} > 1$, $p_0$ if $\lambda_{10} = 1$ and $r_1 = (0, b_1) = (0, (1- \lambda_{10})/ \lambda_a)$ if $\lambda_{10} < 1$.

Subcase 5a – weakly infectious mutualist: $\lambda_b < 0$. If $\delta > 0$ then $g_2$ is decreasing and concave, and recall $\gamma_2\cap \{x_2 = 0\}$ contains only the single point $(b_2, 0)$ with $b_2 = (\delta- \lambda_a)/ \lambda_b$, and $\gamma_2\cap \{x_1 = 0\}$ contains only the single point $p_3 = (0, a_3)$ with $a_3 = 1-\delta/ \lambda_a$. $\gamma_1\cap \gamma_2 \cap \Lambda_+$ contains exactly one point if either $0 < a_1 < b_2$ or $a_1\le 0$ and $a_3 > b_1$, both of which correspond to (C), and otherwise is empty. Notice that

If $\delta = 0$ then $b_2 = - \lambda_a/ \lambda_b > 0$ and $p_3 = (0, 1)$ is a saddle, so attracts no points in $\Lambda_+$. If $a_1 < b_2 < a_2$, which corresponds to (C), then $\gamma_1\cap\gamma_2 \cap \Lambda_+$ contains exactly one point, otherwise $\gamma_1\cap \gamma_2\cap \Lambda_+$ is empty.

If $\delta > 0$ and $\gamma_1\cap \gamma_2\cap \Lambda_+$ is empty then either $a_1 > 0$ and $a_1\ge b_2$ (UH), or $a_1 \le 0$ and $a_3 \le b_1$ which implies $\lambda_{10} \le 1$ and $\lambda_{20} \le 1+\delta$ (E). There are at most three sign regions in $\Lambda$ (two if $b_2 \le 0$): $R(1, 1)\to R(1, -1) \to R(-1, -1)$, appearing in that order from left to right. In case of (UH), $p_0$ is a saddle and $p_1 \in \Lambda$, and in case of (E), $p_0$ is the only equilibrium in $\Lambda$.

If $\gamma_1\cap\gamma_2 \cap \Lambda_+$ is not empty then it is a unique point $p_4 \in \Lambda_+$. If $a_1\le 0$ then $p_0$ is a saddle, otherwise $p_0$ is repelling and $p_1$ is a saddle, and if $\delta = 0$ then $p_2, p_3$ are saddles. A similar argument as before shows there is no periodic orbit or separatrix cycle in $\Lambda$. Thus, all solutions tend to $p_4$.

If $\delta = 0$ and $0 < b_2 \le a_1 < a_2$ (UH), $R(1, 1) \to R(1, -1) \to R(-1, -1)$ appear from left to right. Since $a_1 > 0$, $p_0$ is a saddle and $p_1 \in \Lambda$, while $p_2, p_3$ are saddles, so solutions tend to $p_1$.

If $\delta = 0$ and $a_1 < a_2 \le b_2$ (AH), then $R(-1, -1)\to R(-1, 1) \to R(1, 1)$ appear from right to left, $p_0$ is repelling, and $p_1, p_3$ are saddles, so solutions tend to $p_2$.

Subcase 5b – strongly infectious mutualist: $\lambda_b > 0$. In this case (B) can occur, so we take a moment to define precisely the three conditions in terms of the nullclines:

1. (OB) occurs when $g_1, g_2$ intersect at two points in $\Lambda$, one in $\Lambda_+$ and the other on the subset $\{x_1 = 0, 0\le x_2 \le 1\} \cup \{0 \le x_1 \le 1, x_2 = 0\}$ of the boundary.

2. (MB) occurs when $g_1, g_2$ intersect tangentially at one point in $\Lambda_+$.

3. (NB) occurs when $g_1, g_2$ intersect at two points, both in $\Lambda_+$.

As we go through the various cases we will point out when one of the above might occur; in particular, we'll see that they all occur for values that would otherwise correspond to (E) or (UH). We'll also describe the dynamics in all possible cases. We'll then show that each of (OB), (NB), (MB) does occur, make some effort to characterize them, and show (NB) is simply connected.

If $\delta = 0$ then $G_2 = x_2((\lambda_a + \lambda_bx_1)(1-x_2) > 0$ on $\Lambda_+$, so (AH) holds. $b_1 = - \lambda_a/ \lambda_b < 0$ and $R(-1, 1) \to R(1, 1)$ appear from right to left. Because of the sign of $G_2$, $p_0$ (and $p_1$ if $a_1 > 0$) attract no points, and $p_3 = (0, 1)$ is a saddle. Since the sign graph is acyclic, solutions tend to a sink, and the only candidate is $p_2$.

For the rest we assume $\delta > 0$. $g_2$ is increasing and concave, so $\gamma_2$ intersects the set $\{x_1 = 0, 0 \le x_2 < 1\} \cup \{x_1 \ge 0, x_2 = 0\}$ at exactly one point, which is $p_3 = (0, a_3) = (0, 1-\delta/ \lambda_a)$ if $\delta < \lambda_a$, $p_0 = (0, 0)$ if $\delta = \lambda_a$ and $r_2 = (b_2, 0) = ((\delta- \lambda_a)/ \lambda_b, 0)$ if $\delta > \lambda_a$.

If either $a_1 > \max(b_2, 0)$, or $a_1\le 0$ and $a_3 > \max(b_1, 0)$, then $\gamma_1\cap \gamma_2\cap \Lambda_+$ is a unique point $p_4 \in \Lambda_+$. A similar argument as before shows that all solutions tend to $p_4$. The first option gives $\lambda_{10} > 1$ and (AinvU) so corresponds to (C). For the second option, note that $a_1 \le 0 \Leftrightarrow \lambda_{10}\le 1$ and

so it also corresponds to (C).

If $b_2 = a_1 > 0$ (UH), then $\gamma_1, \gamma_2$ intersect at $p_1$. If $g_1'(a_1) \ge g_2'(a_1)$, then $\gamma_1\cap\gamma_2 \cap \Lambda_+$ is empty, and the sign regions $R(1, -1), R(-1, -1), R(-1, 1)$ appear from left to right with $R(1, -1), R(-1, 1) \to R(-1, -1)$, so the sign graph is acyclic. Since $b_2 > 0$ and $\gamma_2$ is increasing, $a_3 < 0$ so $p_3 \notin \Lambda_+$ and $G_1 > 0$ near $p_0$ so solutions tend to $p_1$. If $g_1'(a_1) < g_2'(a_1)$, which as we'll see corresponds to (OB), then $\gamma_1\cap \gamma_2\cap \Lambda_+$ is a single point $p_4$. All four sign regions now appear, with $R(1, -1), R(-1, 1) \to R(1, 1), R(-1, -1)$. To show all solutions tend to $p_4$ it remains to show that $p_1$ is not a sink for any sign region. $p_1$ is in the closure of $R(1, -1), R(-1, 1)$ and $R(1, 1)$. Since $G_2 > 0$ on $R(-1, 1)$ $p_1$ cannot be a sink, and $p_1$ is a local minimum of $x\mapsto x\cdot(1, 1)$ on $R(1, 1)$, whereas a sink is a local maximum. The only remaining candidate is $R(1, -1)$. $G_2$ has a double root at $p_1$, which can be seen from either the transverse intersection of two $x_2$-nullclines ($\{x_2 = 0\}$ and $\gamma_2$) or by writing $G_2$ as a function of $\tilde x = x-p_1$. Writing $G$ in these coordinates,

and

If a trajectory in $R(1, -1)$ tends to $p_1$ then $\tilde x_1 \to 0^-$ and $\tilde x_2 \to 0^+$. If $\tilde x_1 < 0 < \tilde x_2$ are small in magnitude then by $1^{st}$-order approximation $G_1 \ge c_1(-\tilde x_1+ \tilde x_2) > 0$ for some $c_1 > 0$, and by $2^{nd}$-order approximation, $G_2 \le c_2 \tilde x_1 \tilde x_2 - c_3\tilde x_2^2 < 0$ with $c_3, c_4 > 0$. Writing a solution to (2.2) as $\tilde x_2 = h(\tilde x_1)$,

noting that $0 < -\tilde x_1, x_2 \le -\tilde x_1+x_2$ on the last step. So, given initial value $\tilde x_1(0), \tilde x_2(0)$, the corresponding solution has $h(\tilde x_1) \ge \tilde x_1(0)e^{-c \tilde x_1}$ with $c = (c_2+c_3)/c_1$, so intersects $\{ \tilde x_1 = 0\}$ at a positive value of $\tilde x_2$. Thus no trajectories tend to $p_1$.

If $a_3 = b_1 \ge 0$ (E), then $\gamma_1, \gamma_2$ intersect at $p_3$. If $g_1'(a_3) \ge g_2'(a_3)$, then as above, $\gamma_1\cap\gamma_2\cap \Lambda_+$ is empty and $R(1, -1), R(-1, 1) \to R(-1, -1)$. Since $a_1\le 0$, if $a_3 = 0$ then $p_0$ is the only equilibrium, and if $a_3 > 0$ then $G_2 > 0$ near $p_0$ and $p_1 \notin \Lambda_+$ so solutions tend to $p_3$. If $g_1'(a_3) < g_2'(a_3)$, then $\gamma_1\cap \gamma_2\cap \Lambda_+$ is a single point $p_4$, and $R(1, -1), R(-1, 1) \to R(1, 1), R(-1, -1)$. A similar argument as above shows that $p_3$ attracts no points in $\Lambda_+$ – this time, $G_1$ has a double root, so write a solution as $\tilde x_1 = h(\tilde x_2)$ and perform a similar estimate. This situation corresponds to (OB).

If $0 < a_1 < b_2$ (UH) then $\gamma_1\cap\gamma_2\cap \Lambda_+$ has cardinality $0, 1$ or $2$, with a saddle node bifurcation when the cardinality is $1$.

1. If the cardinality is $0$, then $R(1, -1), R(-1, 1) \to R(-1, -1)$ and solutions tend to $p_1$, similar to the case $g_1'(a_1)\ge g_2'(a_1)$ above.

2. If the cardinality is $1$, then we have (MB). To see this, note that $p_1$ is attracting, and there is a unique interior equilibrium $p_4$. Three sign regions $R(1, -1), R(-1, -1), R(-1, 1)$ appear, with $R(1, -1), R(-1, 1)\to R(-1, -1)$ and $R(-1, -1)$ disconnected by $p_4$ into two components, the lower of which with sink $p_1$ and the upper with sink $p_4$. Since $p_1$ is locally stable it attracts an open neighbourhood $S \ni p_1$ of points in $\Lambda_+$. Since the basin of attraction of $p_1$ is $\bigcup_{t < 0}\phi(t, S)$ it is open in $\Lambda_+$.

3. If the cardinality is $2$, we have (NB). To see this, note that $p_1$ is again attracting, and there are two interior equilibria $p_4, p_5$, letting $p_5$ denote the upper one. All sign regions appear, with $R(1, -1), R(-1, 1) \to R(-1, -1), R(1, 1)$ and $R(-1, -1)$ split in two as before. $p_1$ is the unique sink for the lower part of $R(-1, -1)$, and $p_5$ the unique sink for $R(1, 1)$ and the upper part of $R(-1, -1)$. Since $\gamma_1, \gamma_2$ intersect transversally at $p_4$ and $p_5$ and are the only nullclines through those points, the Jacobian is non-singular so both equilibria are hyperbolic. Since $p_5$ attracts more than a single curve of points it is attracting, and since $p_4$ fails to attract nearby points in $R(-1, -1)$ and $R(1, 1)$ it is not attracting. As argued above, both $p_1$ and $p_5$ have open basins of attraction in $\Lambda_+$. Since $\Lambda_+ \setminus \{p_4\}$ is open in $\Lambda_+$ and connected, it cannot be the combined basins of attraction of $p_1$ and $p_5$ since that would imply a disconnection. The only option is that some points other than $p_4$ tend to $p_4$, so $p_4$ is a saddle and its basin of attraction is its stable manifold, which is a smooth curve.

If $a_1 \le 0$ and $0 < a_3 < b_1$ (E) then $\gamma_1 \cap \gamma_2 \cap \Lambda_+$ has cardinality 0, 1 or 2 as before. Similar observations show that (E), (MB), (NB) occur, respectively.

Properties of (B). We now show that each of (OB), (MB) and (NB) occurs for some parameter values, that (MB) and (OB) lie on the boundary of (NB), and that (NB) is simply connected. For this it is helpful to view the parameter space in terms of the four independent variables $(\lambda_{10}, \lambda_a, \delta, \lambda_b)$, subject to the general constraints $\lambda_{10}, \delta \ge 0$, $\lambda_a \ge - \lambda_{10}$ and $\lambda_b \ge - \lambda_a$. Here, of course, we may assume further that $\delta, \lambda_a, \lambda_b > 0$, since (B) has been ruled out in other cases. We'll let $\bar x$ and $\bar y, \bar x$ denote $\gamma_1\cap \gamma_2 \cap \Lambda$ when its cardinality is, respectively, 1 or 2, with $\bar y < \bar x$ in the elementwise order.

We recall $g_1, g_2$ and their derivatives:

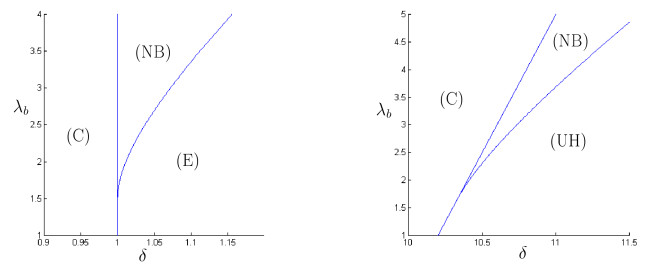
Existence. Our approach is to first characterize (OB), then show a small change in $\delta$ leads to (NB), then show a large enough change in $\delta$ gives (MB). We treat separately the cases $a_1\le 0$ and $a_1 > 0$, beginning with $a_1 \le 0$. To have (OB) we need $g_1(0) = g_2(0)$, i.e., $b_1 = a_3$, and $g_1'(0) < g_2'(0)$. Earlier we showed that $a_3 = b_1 \Leftrightarrow \lambda_{20} = 1+\delta$, that we write as $\delta = \lambda_a+ \lambda_{10}-1$, which requires $\lambda_a+ \lambda_{10} > 1$, i.e., $\lambda_{20} > 1$, since $\delta > 0$ by assumption. If $g_1'(0) < g_2'(0)$ then $\lambda_a^{-1} < \delta \lambda_b/ \lambda_a^2$, so $\lambda_a < \delta \lambda_b$, that we write as $\lambda_b > \lambda_a/\delta$. Thus if $\lambda_{10}\le 1$ and $\lambda_a$ are fixed, (OB) occurs iff $\lambda_a+ \lambda_{10} > 1$, $\lambda_b \in (\lambda_a/(\lambda_a+ \lambda_{10}-1), \infty)$ and $\delta = \lambda_a+ \lambda_{10}-1$, which is a non-empty set of parameters. Take some such choice of parameters, and note that $g_1(0)-g_2(0) = 0$ and $g_1'(0)-g_2'(0) < 0$. Since $g_2$ decreases with $\delta$ while $g_1$ is unchanged, a small increase in $\delta$ then gives (NB). If $\delta$ is increased enough, then $g_2(1) < g_1(0)$ and $\gamma_1\cap\gamma_2\cap \Lambda_+$ is empty, so there is a unique intermediate value of $\delta$ that gives (MB). This is depicted in Figure 3.

If $a_1 > 0$, to have (OB) we need $a_1 = b_2 > 0$ and $g_1'(a_1) < g_2'(b_2)$. The former gives $a_1 = (\delta- \lambda_a)/ \lambda_b$, that we write as $\delta = \lambda_b a_1 + \lambda_a$ noting $a_1$ depends only on $\lambda_{10}$, while the latter gives $\lambda_{10}^2/ \lambda_a < \delta \lambda_b/\delta^2$, or $\delta < \lambda_a \lambda_b/ \lambda_{10}^2$. Plugging in $\delta$ and putting $\lambda_b$ terms to one side gives the condition $\lambda_b(\lambda_a/ \lambda_{10}^2-a_1) > \lambda_a$. Given $\lambda_{10}$ and $\lambda_a$, $\lambda_b$ can be chosen large enough to satisfy this inequality iff

Thus for $a_1 > 0$, (OB) occurs iff $\lambda_a > \lambda_{10}^2- \lambda_{10}$, $\lambda_b \in (\lambda_a/(\lambda_a/ \lambda_{10}^2-a_1), \infty)$ and $\delta = \lambda_ba_1+ \lambda_a$. Again, this is a non-empty set of parameters. As before, we can vary $\delta$ to obtain (NB) and (MB).

A consequence of the above existence arguments is that they specify for which values of $\lambda_{10}$ and $\lambda_a$ bistability can be achieved by appropriate choice of $\delta, \lambda_b$, namely, for $\lambda_{20} > \max(1, \lambda_{10}^2)$. They also show that for any choice of $\lambda_{10}, \lambda_a, \lambda_b$, the set of values of $\delta$ that gives (B) is a bounded set, with (OB) at the lower endpoint, (MB) at the upper endpoint and (NB) in the interior. A slice of the phase portrait is shown in Figure 4.

Geometry. It's clear that (NB) is an open set in parameter space. Define the functions $\tilde \lambda_a = \lambda_{10}+\max(1, \lambda_{10}^2)$ and

Note that both functions are continuous. From the above discussion we obtain functions $\delta^-(\lambda_{10}, \lambda_a, \lambda_b)$ and $\delta^+(\lambda_{10}, \lambda_a, \lambda_b)$ with domain $\lambda_{10}\ge 0$, $\lambda_a > \tilde \lambda_a$ and $\lambda_b > \tilde \lambda_b$ such that (OB), (NB) and (MB) occur iff $(\lambda_{10}, \lambda_a, \lambda_b)$ are in the domain and $\delta = \delta^-$, $\delta^- < \delta < \delta^+$ and $\delta = \delta^+$, respectively. The function $\delta^-$ is given above explicitly, piecewise:

and one easily verifies its continuity. The function $\delta^+$ is not given explicitly, but we can show it is smooth, using the implicit function theorem. (MB) corresponds to a unique $\bar x_1 \in (0, 1)$ such that $g_1(\bar x_1)-g_2(\bar x_1) = g_1'(\bar x_1)-g_2'(\bar x_1) = 0$. We have

where the $'$ indicates $\partial_{x_1}$. At (MB), $g_1(\bar x_1)'-g_2(\bar x_1)' = 0$, moreover $g_1''-g_2'' > 0$ since $g_1-g_2$ is convex. Also, $\partial_\delta(g_1-g_2) = -1/(\lambda_a+ \lambda_bx_1)^2 > 0$ since $\lambda_a > 0$ by assumption. Thus the above matrix is invertible. Since $(g_1-g_2, g_1'-g_2')$ is a smooth function of parameters, and of $x_1$, when $\lambda_a > 0$ and $x_1 \in (0, 1)$, by the implicit function theorem, $(\bar x_1, \delta^+)$ is a smooth function of $(\lambda_{10}, \lambda_a, \lambda_b)$, on the domain of $\delta^+$.

We now show (NB) is a contractible set, via a sequence of homotopies that gives a deformation retraction. Define $\tilde \delta = (\delta^-+\delta^+)/2$, which is continuous, and note that (NB) occurs when $\delta = \tilde\delta$. Notice that $\tilde \lambda_a, \tilde \lambda_b$ and $\tilde \delta$ are functions of $\lambda_{10}$, $\lambda_{10}$ and $\lambda_a$, and $\lambda_{10}, \lambda_a$ and $\lambda_b$ respectively. Define the sequence of homotopies as follows, at each step letting $\tilde \lambda_a, \tilde \lambda_b$ and $\tilde \delta$ take the previous values in the list as their input:

(ⅰ) $H_1 = (\lambda_{10}, \lambda_a, \lambda_b, (1-t)\delta + t \, \tilde \delta)$,

(ⅱ) $H_2 = (\lambda_{10}, \lambda_a, (1-t) \lambda_b + t (\tilde \lambda_b+1), \tilde\delta)$,

(ⅲ) $H_3 = (\lambda_{10}, (1-t) \lambda_a + t(\tilde \lambda_a+1), \tilde \lambda_b+1, \tilde \delta)$,

(ⅳ) $H_4 = ((1-t) \lambda_{10}+t, \tilde \lambda_a+1, \tilde \lambda_b+1, \tilde \delta)$.

Note that $t\in [0, 1]$ is the deformation parameter. In words,

(ⅰ) $H_1$ acts only on $\delta$, centering its value to $\tilde \delta$,

(ⅱ) $H_2$ acts on $\lambda_b$ and $\delta$, centering $\lambda_b$ to $\tilde \lambda_b+1$ while keeping $\delta = \tilde \delta$,

(ⅲ) $H_3$ centers $\lambda_a$ to $\tilde \lambda_a+1$ while keeping $\lambda_b = \tilde \lambda_b+1$ and $\delta = \tilde \delta$ and

(ⅳ) $H_4$ centers $\lambda_{10}$ to $1$ while keeping other parameters centered.

We have already checked the continuity of component functions, and it's clear they keep points in (NB). Applying the $H_i$ in sequence deforms (NB) to the single point with $\lambda_{10} = 1$ and the corresponding values of $\tilde \lambda_a, \tilde \lambda_b$ and $\tilde \delta$.

6.   Discussion and conclusion

In this article we consider a simple differential equation model of host-symbiont dynamics, that includes both vertical and horizontal transmission of the host, as well as recovery (i.e. transition from associated [with symbiont] to unassociated [without symbiont] host). The model naturally incorporates the pathogen, neutral, and mutualist cases through the choice of parameter values, providing a unified setting for the study of all three cases.

Our analysis indicates that the most natural way to view the process is through the total host density (both associated and unassociated) and the proportion of hosts that are associated. Moreover, the two main factors governing the dynamics are (ⅰ) the effect of the symbiont on the host (i.e. whether it is pathogen, neutral or mutualist) and (ⅱ) the difference between the additional birth rate of associated vs. unassociated hosts (which is positive only for mutualists) and the rate of horizontal transmission of the symbiont.

We obtain a complete picture of the model's dynamic phases, as follows. Except for the very special case when the symbiont is completely redundant (neutral, no recovery and no horizontal transmission), populations that initially contain both host and symbiont, and not located at an unstable equilibrium, always settle down to one of at most three equilibria. The limiting equilibrium is unique when the symbiont is either a pathogen, is neutral, or is a mutualist but focuses more on increasing the host birth rate than on horizontal transmission. Bistability (exactly two locally attracting equilibria) can occur when the symbiont is a sufficiently beneficial mutualist that focuses more on horizontal transmission than on increasing the host birth rate. There are three limiting equilibria only in a boundary case at the onset of bistability. When the limiting equilibrium is unique, survival and coexistence are determined by straightforward invasibility conditions, i.e., whether one type can invade the extinction equilibrium (for survival) or the stable equilibrium containing only the other type (for coexistence).

Interestingly, the dynamical behaviour, and in particular the number of stable equilibria, hinges less on whether the symbiont is pathogen or mutualist, and more on whether the symbiont is highly beneficial (increases host birth rate), versus highly infectious (has a high rate of horizontal transmission). Moreover, we have shown that, at least when including only the simple mechanisms considered in this model, stable periodic behaviour is not possible.

Conflict of interest

All authors declare that there is no conflicts of interest in this paper.

Appendix

Proof of Lemma 5.1. For a definite sign vector $\sigma \in \{-1, 1\}^2$ and $\epsilon > 0$ let

noting that $R(\sigma) = \bigcup_{ \epsilon > 0}R(\sigma, \epsilon)$ and $\sigma \cdot G(x) \ge \epsilon \ \hbox{for} \ x \in R(\sigma, \epsilon)$. If $x \in R(\sigma, \epsilon)$ for definite $\sigma$ and letting

$\phi(t, x) \in R(\sigma, \epsilon)$ for $t < \tau(x, \epsilon)$, so using the second fact above,

Since for $y, z \in \Lambda_+$, $|\sigma \cdot y- \sigma \cdot z| \le 2$, it follows that $\tau(x) \le 2/ \epsilon$. Thus, letting $E(\sigma, \epsilon) = \text{Cl} \left(R(\sigma) \setminus R(\sigma, \epsilon) \right)$ and

where $\text{Cl}$ denotes the closure, $E(\sigma)$ consists of equilibrium points in $\text{Cl}(R(\sigma))$. Letting $\tau(x) = \inf\{t:\phi(t, x) \notin R(\sigma)\}$, the only way that $\tau(x) = \infty$ is if for any $\epsilon > 0$, eventually $\phi(t, x) \in E(\sigma, \epsilon)$, which means that $\omega(x) \in E(\sigma)$. Since $\omega(x)$ is connected and (for the cases that remain) the set of equilibrium points in $\Lambda$ is finite, the first claim follows. The second claim follows since acyclic implies itineraries are finite.

Proof of Lemma 5.2. Suppose $\Gamma$ is a periodic orbit or a separatrix cycle, both of which are the image of a circle in $\mathbb{R}^2$, under a piecewise $C^1$ function. Since trajectories do not cross, the image is injective, so let $D$ be the interior of $\Gamma$, whose existence is given by the Jordan curve theorem. By Green's theorem,

where $F = (F_1, F_2)$. First suppose $\Gamma$ is a periodic orbit with solution curve $u(t)$ satisfying $u(T) = u(0)$. Ignoring the orientation, since it only changes the sign, the latter integral can be parametrized with $dx = \dot u_1(s)ds, \ dy = \dot u_2(s)ds$ as

However, $F_2(u(s)) = \dot u_2(s)$ and $F_1(u(s)) = \dot u_1(s)$ so the integrand is identically zero, thus so is the integral, and this contradicts the assumption on $\nabla \cdot (BF)$. Suppose instead that $\Gamma$ is a separatrix cycle and let $u^{(1)}(t), \dots, u^{(m)}(t)$ denote the corresponding heteroclinic solutions. Since solutions are arranged tip-to-tail as described by (3.1), it follows that $\{\dot u^{(i)}(t):t \in \mathbb{R}, i = 1, \dots, m\}$ orients the tangent space for $\Gamma$, so up to its sign, we can parametrize the above contour integral as

and the same observation shows the integral is zero, which is a contradiction.