Fast two dimensional to three dimensional registration of fluoroscopy and CT-scans using Octrees on segmentation maps

1.   Introduction

Ecosystem modeling and analysis is a fascinating and active research field in biology, in which the study of the interaction between predator and prey is a central topic in ecology and evolutionary biology^[1,2]. With the progress of ecological research, the views on how predators interact with the prey and affect the prey population have also changed greatly. Predators have a dual impact on the structure of the ecological system^[3]. On the one hand, predators physically attack and kill the prey^[4], thereby reducing the number of prey. On the other hand, the existence of predators alone can make the prey individual in a state of psychological pressure, resulting in many changes in the behavior of prey species^[5]. This is a common anti-predator response, also known as the 'fear effect', which eventually slows the growth of prey populations^[6].

In attempts to better understand the influence of fear effect on the predator-prey system, scholars developed lots of mathematical models of predator-prey system with fear effect. For example, Wang et al.^[7] investigated the impacts of fear effect on the stability of the system, and obtained that the fear effect can lead to the bifurcation of limit cycle under appropriate parameter values. Further, Wang and Zou et al.^[8] inspired by the experimental work by Zanette and his colleagues^[9], expanded their previous study^[7] by incorporating age structures into prey populations (juvenile and adult stages) and allowing adult prey to adaptively avoid predators. Das and Samanta^[10] investigated the impacts by introducing an exponential form of fear effect into a stochastic predator-prey system when extra meals were offered to predators. Sahoo and Samanta^[11] explored a two-prey and one-predator model by incorporating fear factors into switching mechanisms during prey reproduction and predation. Das et al.^[12] studied a predator-prey model that incorporates fear factors into including birth and mortality in prey populations with a functional Holling type-II response. See references ^{[13,14,15,16]} for more fear factor influences in predator-prey model dynamics.

In addition to the above interactions, the predator-prey system is also disturbed by various external factors, which can cause huge changes in the number of species in the short term. This change is called an impulse in the modeling process, and the impulse differential equation can well describe this change^[17]. Correspondingly, there are two types impulsive control strategies in impulsive differential equations, namely, fixed-time impulse and state-dependent impulse^{[17,18,19,20]}.

State-dependent feedback control methods are commonly represented by impulsive semi-dynamical systems, which can well characterize threshold control strategies. That is, control interventions will only take place when a target species size reaches a preset threshold density. In recent years, state-dependent feedback control has received extensive attention from researchers and has been applied in many fields and sciences, for example, fishery harvesting ^[21,22,23], integral pest management ^[24,25,26], the effects between biological populations^[27,28,29], virus control ^[30,31,32], etc.

In controlling reality biological species, we focus on choosing a proper time to implement the control interventions and designing a practical strategy in proceeding the control. A basic assumption of many existing models is that when the biological population density reaches a fixed threshold, then the control is carried out, which is subject to the above-mentioned state-dependent feedback control. But from a biological point of view, a fixed threshold control policy usually ignores many important aspects in the real world. There are two practical situations: low population density but high rate of change; high population density but low rate of change. In the above two situations, we may not need to trigger the control interventions even though the population density is high, but the growth rate is low. Thus, the threshold policy needs to include both population density and its changing rate, which is actually a nonlinear threshold control strategy. Note that, the nonlinear threshold policy was recently studied in many works^{[17,31,33,34]}, and rich dynamic behaviors were observed in these studies. In the control of biological populations, another assumption in the impulsive model is that the changing rate is proportional to the population density due to the use of control interventions. However, there should definitely be a limitation for this term. Therefore, the saturated form using a nonlinear function can be more realistic. To the best of our knowledge, no study has tried to introduce the nonlinear threshold policy and the nonlinear control function into the predator-prey system with fear effect, and the analysis of the dynamic behaviors remains challenging.

The major goal of this research is to introduce the nonlinear threshold policy and the nonlinear function of the control effect into an impulsive predator-prey system with fear effect, propose a state-dependent impulsive system with nonlinear threshold control, and focus on studying its dynamic behaviors. In Section 2, a predator-prey state-dependent impulsive model with fear effect is proposed, and a ratio-dependent nonlinear action threshold is adopted. In Section 3, the corresponding Poincaré map is constructed by giving the range of impulsive set and phase set, and some fundamental properties of Poincaré map are discussed. In Section 4, the conditions for the existence and stability of order-1 periodic solution are given, and the existence of order-k ($ k \ge 2 $) periodic solutions are discussed. The Section 5 is numerical simulation, which verifies our theoretical results and discusses the effect of fear factors on system dynamics. Finally, the relevant biological significance are discussed and conclusions are given.

2.   Model formulation and preliminaries

In the literature ^[35], the authors considered the impulse control guided by a linear threshold of the density of prey based on a predator-prey model with fear effect, and partially studied the dynamics of the proposed model. In the current study, we extend the model in ^[35] by introducing a nonlinear threshold control policy, taking the combination of the density of prey and its changing rate as the action threshold. The model is given by:

where $ x(t) $ and $ y(t) $ are the sizes of the prey and predator populations, respectively. $ b $, $ d $ and $ c $ represent the birth rate, natural mortality rate, and density-dependent decay rate caused by intraspecific competition for prey, respectively, $ k $ represents the level of fear. $ \frac{{px(t)}}{{1 + wx(t)}} $ indicates the Holling II functional response, $ e $ denotes the ratio of biomass conversion (satisfying the restriction $ 0 < e < p $), $ m $ is the death rate of the predator. The parameters $ {u_1} $, $ {v_1} $ and $ ET $ are all positive constants with $ {u_1} + {v_1} = 1 $.

Another major assumption in existing research is that the prey capture rate is a linear function dependent on population density, and the predator release amount is a positive number. Nevertheless, in real nature, natural resources are finite, and implementing of control policies should be determined by the present size of the population. Both the capture rates of prey and the release amount of predator should be based on population saturation functions. Consequently, we consider the finiteness of natural resources in our model is very meaningful. We apply the following nonlinear impulsive functions relevant to biological population density and capture rate.

that is, when the prey population density reaches the action threshold $ {u_1}x(t) + {v_1}\frac{{dx\left(t \right)}}{{dt}} = ET $, the control measures will be taken to update the number of prey and predator to $ x(t) - \frac{{\delta x{{(t)}^2}}}{{x(t) + \mu }} $ and $ y(t) + \frac{\tau }{{1 + \eta y(t)}} $, respectively. Here, $ \delta $ and $ \mu $ denote maximum capture rates and the half-saturation constant for the prey, $ \tau $ represents the maximum number of predators released, $ \eta $ is the morphological coefficient. The release of predators will not surpass the $ \tau $ due to realistic factors, such as definite resources. For simplicity, we denote $ x({t^ + }) = {x^ + } $ and $ y({t^ + }) = {y^ + } $.

Without the feedback control, the ODE system

With the dynamics of system (2.2) has been investigated in ^[35], and here we beriefly recall its dynamics that are useful in the present research. The two nullclines of system (2.2) are noted by $ {L_1} $ and $ {L_2} $, where

System (2.2) always exists a trivial equilibrium $ O(0, 0) $, which is a saddle point, and a boundary equilibrium $ {E_0}(\frac{{b - d}}{c}, 0) $. When $ (b - d)(ep - mw) < cm $, $ {E_0} $ is stable; when $ (b - d)(ep - mw) > cm $, $ {E_0} $ is unstable. In addition, system (2.2) has an internal equilibrium $ {E^*}({x^*}, {y^*}) $, where

If $ k > {k^*} $, then $ {E^*}({x^*}, {y^*}) $ is a stable focus or node; if $ k < {k^*} $, then $ {E^*}({x^*}, {y^*}) $ is unstable and there exists a unique stable limit cycle, where

3.   The Poincaré map and its properties

In a biological sense, our discussion is limited to the region $ R_ + ^2 = \{ (x, y):x \ge 0, y \ge 0\} $. The impulsive set and phase set become two curves because system (2.1) adopts the action threshold control strategy of prey density and its changing rate. According to $ {u_1}x(t) + {v_1}\frac{{dx\left(t \right)}}{{dt}} = ET $ and the first equation of system (2.1), we can obtain

denoted by $ {L_M} $, where

From $ {x^ + } = x - \frac{{\delta {x^2}}}{{x + \mu }} $, we have

Therefore

where

Let

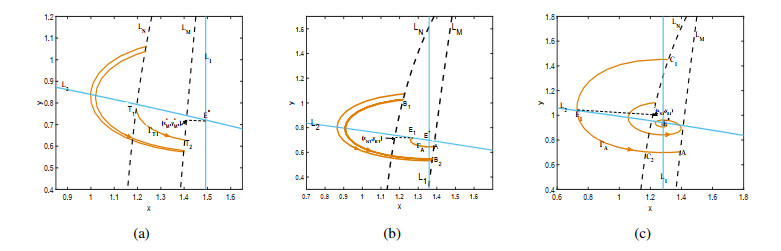
denoted by $ {L_N} $. Next, unless otherwise specified, we always take an initial point $ S_0^ + (x_0^ +, y_0^ +) $ from the curve $ {L_N} $. The trajectory starting from $ {L_N} $ may not reach $ {L_M} $ due to different initial conditions. Now, define the range of the impulsive set and phase set based on the different positions of the trajectories of system (2.1) with the equilibrium point (see Figure 1).

Case (i) $ {x^*} \ge x_M^* $

Let the horizontal coordinate of curve $ {L_M} $ at $ y = {y^*} $ is $ x_M^* $. Since $ {x^*} \ge x_M^* $, there exists a curve $ {\Gamma _{{T_1}}} $ such that the $ {L_N} $ tangent to this cure at the $ {T_1}({x_{{T_1}}}, {y_{{T_1}}}) $. Clearly, the curve $ {\Gamma _{{T_1}}} $ intersects the $ {L_M} $ at point $ {T_2}({x_{{T_2}}}, {y_{{T_2}}}) $ (see Figure 1 (a)). Therefore, we denote the impulsive set and phase set as:

where $ (x, y) $ is a point on the curve $ {L_M} $ and $ ({x^ + }, {y^ + }) $ is a point on the curve $ {L_N} $.

Case (ii) $ {x^*} \le x_M^* $

When $ {x^*} \le x_M^* $, there must have a point $ A({x_A}, {y_A}) $ on impulsive set such that the trajectory $ {\Gamma _A} $ is tangent to $ {L_M} $ at that point and intersects $ {L_2} $ at point $ {E_1}({x_{{E_1}}}, {y_{{E_1}}}) $. Suppose the horizontal coordinate of curve $ {L_N} $ at $ y = {y_{{E_1}}} $ is $ {x_{{N_1}}} $. Therefore, we consider the following two different cases:

(I) $ {x_{{E_1}}} > {x_{{N_1}}} $. If $ {x_{{E_1}}} > {x_{{N_1}}} $, the situation is the same as Case (i), and the trajectory $ {\Gamma _A} $ does not intersect $ {L_N} $. There exists a trajectory $ {\Gamma _{{B_1}}} $ tangent to $ {L_N} $ at point $ {B_1}({x_{{B_1}}}, {y_{{B_1}}}) $, and after a period of time the trajectory $ {\Gamma _{{B_1}}} $ will intersect the impulsive set $ L_M $ at point $ {B_2}({x_{{B_2}}}, {y_{{B_2}}}) $ (see Figure 1 (b)). For this situation, the impulsive set is defined by

and the corresponding range of phase set is defined by

(II) $ {x_{{E_1}}} < {x_{{N_1}}} $. If $ {x_{{E_1}}} < {x_{{N_1}}} $, the curve $ {\Gamma _A} $ intersects the line $ {L_N} $ at points $ {C_1}({x_{{C_1}}}, {y_{{C_1}}}) $ and $ {C_2}({x_{{C_2}}}, {y_{{C_2}}}) $, where $ {y_{{C_1}}} > {y_{{C_2}}} $. In this case, it is easy to observe that none of the solution trajectory from the interior of segment $ \mathop {{C_1}{C_2}}\limits^{\_\_\_\_\_} $ reach the curve $ {L_M} $, that is, it is not affected by the impulsive effect (see Figure 1 (c)). So we define the impulsive set by

and the phase set is

Based on the above discussion, the construction of Poincaré map is given below. Given an initial point $ S_0^ + (x_0^ +, y_0^ +) \in N $, we define the trajectory starting from $ S_0^ + $ as $ \Gamma (t, {t_0}, S_0^ +) = \Gamma (x(t, {t_0}, (x_0^ +, y_0^ +)), y(t, {t_0}, (x_0^ +, y_0^ +)) $. For any $ S_i^ + (x_i^ +, y_i^ +) \in N $, the trajectory from $ S_i^ + $ reaches the $ L_N $ at point $ {S_{i + 1}}({x_{i + 1}}, {y_{i + 1}}) $ in a finite time $ \tilde t $. We express this process as

where $ {y_{i + 1}} = {y^ + }(\tilde t, x_i^ +, y_i^ +) $. From the Cauchy-Lipschitz Theorem we know that $ {y_{i + 1}} $ can only be represented by $ y_i^ + $. Therefore, we have

Consider the scalar differential equation from system (2.1):

The function $ g(x, y) $ is continuously differentiable. Further, we denote $ x_0^ + = X $, $ y_0^ + = Z $, and $ S_0^ + (x_0^ +, y_0^ +) \in N $. Let

here the value of $ x $ is between the $ L_N $ and the $ L_M $. According to (3.2) have

Thus, from Eqs. (3.1) and (3.4), the Poincaré map can be expressed as

Next, we provide some fundamental properties of the Poincaré map $ Q(Z) $ in the following theorem.

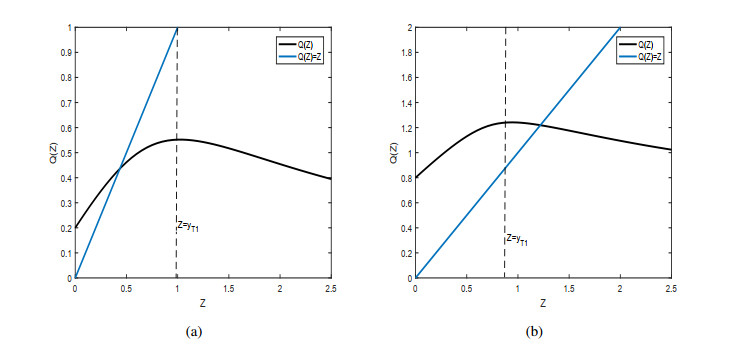
Theorem 3.1. ^[35]Assume $ {x^*} \ge x_M^* $, then the Poincaré map satisfies the following properties (Figure 2):

($ i $) The domain of $ Q(Z) $ is $ [0, + \infty) $. Moreover $ Q(Z) $ is monotonically increasing on $ [0, {y_{{T_1}}}] $ and monotonically decreasing on $ [{y_{{T_1}}}, + \infty) $.

($ ii $) $ Q(Z) $ is continuously differentiable in $ [0, + \infty) $, and has a unique fixed point.

When $ {x^*} \le x_M^* $ and $ {x_{{E_1}}} > {x_{{N_1}}} $, the properties of Poincaré map is similar to Case (i). In what follows, we consider the case where $ {x_{{E_1}}} < {x_{{N_1}}} $.

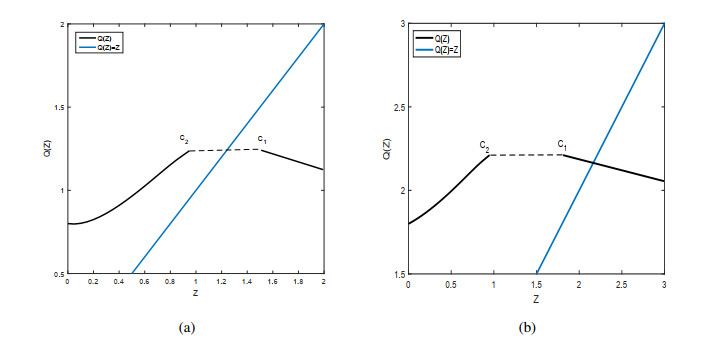
Theorem 3.2. Suppose $ {x^*} \le x_M^* $ and $ {x_{{E_1}}} < {x_{{N_1}}} $. The Poincaré map satisfies (Figure 3):

($ i $) The domain of $ Q(Z) $ is $ (0, {y_{{C_2}}}] \cup [{y_{{C_1}}}, + \infty) $. On $ (0, {y_{{C_2}}}] $ the map $ Q(Z) $ monotonically increases and on $ [{y_{{C_1}}}, + \infty) $ the map $ Q(Z) $ monotonically decreases.

($ ii $) $ Q(Z) $ is continuously differentiable in its domain.

($ iii $) If $ Q({y_{{C_1}}}) > {y_{{C_1}}} $, the map $ Q(Z) $ has a unique fixed point on $ [{y_{{C_1}}}, + \infty) $. If $ Q({y_{{C_2}}}) < {y_{{C_2}}} $, there is no fixed point.

Proof. ($ i $) When $ {x_{{E_1}}} < {x_{{N_1}}} $, we know the trajectory $ {\Gamma _A} $ is tangent to the impulsive set $ {L_M} $ and intersect with the phase set $ {L_N} $ at two points $ C_1 $ and $ C_2 $. For $ \forall S_i^ + (x_i^ +, y_i^ +) \in N $, if $ y_i^ + \in ({y_{{C_2}}}, {y_{{C_1}}}) $, the trajectory starting from the $ S_i^ + $ cannot reach the $ L_M $. Meanwhile, the $ Q(Z) $ is well defined on $ (0, {y_{{C_2}}}] \cup [{y_{{C_1}}}, + \infty) $.

Suppose there are two points $ S_{{k_1}}^ + (x_{{k_1}}^ +, y_{{k_1}}^ +) $ and $ S_{{k_2}}^ + (x_{{k_2}}^ +, y_{{k_2}}^ +) $ on the phase set. If $ y_{{k_1}}^ +, y_{{k_2}}^ + \in (0, {y_{{C_2}}}] $ and $ y_{{k_1}}^ + < y_{{k_2}}^ + $. The trajectory from these two points will reach the impulse set after time $ \tilde t $, i.e., $ \Gamma (\tilde t, x_i^ +, y_i^ +) = \Gamma (\tilde t, {x_{i + 1}}, {y_{i + 1}}) $. Since the uniqueness of the solution we have $ {y_{{k_1} + 1}} < {y_{{k_2} + 1}} $. Hence, according to the expression of Poincaré map $ Q(Z) $, we get $ Q\left({{y_{{k_1} + 1}}} \right) < Q\left({{y_{{k_2} + 1}}} \right) $. So, $ Q(Z) $ is monotonically increasing on $ (0, {y_{{C_2}}}] $.

When $ y_{{k_1}}^ +, y_{{k_2}}^ + \in [{y_{{C_1}}}, + \infty) $ and $ y_{{k_1}}^ + < y_{{k_2}}^ + $. The trajectory starts from point $ y_{{k_1}}^ + $, $ y_{{k_2}}^ + $ cross the nullcline $ L_1 $ and intersects the $ L_N $ at the points $ S_{{k_1}}^{'}(x_{{k_1}}^{'}, y_{{k_1}}^{'}) $ and $ S_{{k_2}}^{'}(x_{{k_2}}^{'}, y_{{k_2}}^{'}) $. We can easily obtain $ y_{{k_1}}^{'} > y_{{k_2}}^{'} $, and from the uniqueness of the solution, we have $ Q\left({y_{{k_1}}^{'}} \right) > Q\left({y_{{k_2}}^{'}} \right) $. So, $ Q(Z) $ is monotonically decreasing on $ [{y_{{C_1}}}, + \infty) $.

($ ii $) From equation (3.2) we can easily determine that $ g(x, y) $ is a continuously differentiable function. Therefore, it follows from the continuity and differentiability theorem for solution of ordinary differential equation that the Poincaré map Q(Z) is also continuously differentiable on $ (0, {y_{{C_2}}}] \cup [{y_{{C_1}}}, + \infty) $.

($ iii $) The curve $ {\Gamma _A} $ from $ C_1 $ reaches the $ L_M $ at point $ A $, and then arrives in $ L_N $ at point $ {A^ + }\left({x_A^ +, y_A^ + } \right) $ through the impulsive effect. If $ Q({y_{{C_1}}}) > {y_{{C_1}}} $, then $ y_A^ + = Q({y_{{C_1}}}) \in [{y_{{C_1}}}, + \infty) $, i.e., $ y_A^ + > {y_{{C_1}}} $. Since $ Q(Z) $ is monotonically decreasing on $ [{y_{{C_1}}}, + \infty) $, then $ Q\left({y_A^ + } \right) < Q\left({{y_{{C_1}}}} \right) = y_A^ + $. By the existence of zeros theorem and the continuous differentiability of $ Q(Z) $, there exists a point $ \tilde y \in ({y_{{C_1}}}, y_A^ +) $ and satisfies $ Q(\tilde y) = \tilde y $, which implies that $ Q(Z) $ has a unique fixed point on $ [{y_{{C_1}}}, + \infty) $.

If $ Q({y_{{C_2}}}) < {y_{{C_2}}} $, for any $ {y_i} \in (0, {y_{{C_2}}}] $, the trajectory from point $ {S_i}({x_i}, {y_i}) $ arrives the $ L_M $ at point $ {S_{i + 1}}({x_{i + 1}}, {y_{i + 1}}) $, then $ {S_{i + 1}}({x_{i + 1}}, {y_{i + 1}}) $ is pulsed to $ S_{_{i + 1}}^ + (x_{_{i + 1}}^ +, y_{_{i + 1}}^ +) $. By knowing the direction of the trajectory of system (2.1), it is easy to infer that $ y_{_{i + 1}}^ + < {y_{i + 1}} < {y_i} $. Therefore, there is no $ {\tilde y_1} \in (0, {y_{{C_2}}}] $ such that $ Q({\tilde y_1}) = {\tilde y_1} $.

4.   Order-k periodic solution

From the discussion in the above section, we explore the existence of an equilibrium point in the system, which implies that there is an order-1 periodic solution to system (2.1). Next, we will explore more properties of order-k $ (k \ge 1) $ periodic solutions.

Theorem 4.1. If $ {x^*} \ge x_M^* $ (Case (i)), system (2.1) has a unique order-1 periodic solution. Furthermore, we can obtain that

($ i $) If $ Q({y_{{T_1}}}) < {y_{{T_1}}} $, the order-1 periodic solution of system (2.1) is globally asymptotically stable;

($ ii $) If $ Q({y_{{T_1}}}) > {y_{{T_1}}} $, then system (2.1) has a globally stable order-1 periodic solution if and only if $ {Q^2}(y_0^ +) > y_0^ + $ for any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $.

Proof. From Eq. (3.2), we have $ y_{i + 1}^ + = \xi (y_i^ +) + \frac{\tau }{{1 + \eta \xi (y_i^ +)}} = Q(y_i^ +) $. Therefore, the trajectory from $ S_0^ + (x_0^ +, y_0^ +) \in N $ reaches the point $ {S_1}({x_1}, {y_1}) $ on the impulsive set after a period of time, and will arrive at point $ S_1^ + (x_1^ +, y_1^ +) \in N $ through the impulsive effect. This process can be defined as $ Q(y_0^ +) = \xi (y_0^ +) + \frac{\tau }{{1 + \eta \xi (y_0^ +)}} = y_1^ + $, repeat the above process can obtain $ Q\left[{Q\left({y_0^ + } \right)} \right] = Q\left({y_1^ + } \right) = y_2^ + = {Q^2}\left({y_0^ + } \right) $, further we have $ {Q^k}\left({y_0^ + } \right) = y_k^ + $.

($ i $) For different value ranges of initial point $ y_0^ + $, we will have the following three situations:

Case $ a $. If $ \tilde y < y_0^ + < {y_{{T_1}}} $, since $ Q({y_{{T_1}}}) < {y_{{T_1}}} $ and $ Q(Z) $ is monotonously increasing on $ [0, {y_{{T_1}}}] $, so we have $ {y_{{T_1}}} > Q\left({{y_{{T_1}}}} \right) > Q\left({y_0^ + } \right) > Q\left({\tilde y} \right) = \tilde y $, $ Q\left({y_0^ + } \right) = y_1^ + < y_0^ + $, further through the similar process we can get

which represents that $ {Q^k}(y_0^ +) $ decreases monotonically and $ \mathop {\lim }\limits_{n \to + \infty } {Q^k}(y_0^ +) = \tilde y $.

Case $ b $. If $ 0 < y_0^ + < \tilde y $, through a similar analysis above, we can obtain $ y_0^ + < Q\left({y_0^ + } \right) = y_1^ + < Q\left({\tilde y} \right) = \tilde y $ and $ Q\left({y_0^ + } \right) < {Q^2}\left({y_0^ + } \right) < Q\left({\tilde y} \right) = \tilde y $, by mathematical induction we have

That is $ {Q^k}(y_0^ +) $ increases monotonically and $ \mathop {\lim }\limits_{n \to + \infty } {Q^k}(y_0^ +) = \tilde y $.

Case $ c $. If $ y_0^ + \in [{y_{{T_1}}}, + \infty) $, since $ Q({y_{{T_1}}}) < {y_{{T_1}}} $ and $ Q(Z) $ is monotonously decreasing on $ [{y_{{T_1}}}, + \infty) $, so according to the properties of $ Q(Z) $ we have $ Q(y_0^ +) < Q({y_{{T_1}}}) < {y_{{T_1}}} $, i.e., $ Q(y_0^ +) < {y_{{T_1}}} $. When $ \tilde y < Q(y_0^ +) < {y_{{T_1}}} $, this is the situation $ a $.; when $ 0 < Q(y_0^ +) < \tilde y $, this is the same as situation $ b $.

In summary, we always can obtain

($ ii $) Sufficient condition: When $ Q({y_{{T_1}}}) > {y_{{T_1}}} $, $ Q(Z) $ has unique fixed point $ \tilde y \in [{y_{{T_1}}}, + \infty) $ by Theorem 3.1 and monotonically decreasing on $ [{y_{{T_1}}}, + \infty) $. Thus, if $ {Q^2}(y_0^ +) > y_0^ + $ for any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $, then have

Further more, we derive that

Thus by the monotone bounded theorem we can get $ \mathop {\lim }\limits_{k \to + \infty } {Q^{2k}}(y_0^ +) = \mathop {\lim }\limits_{k \to + \infty } {Q^{2k + 1}}(y_0^ +) = \tilde y $, then order-1 periodic solution is globally stable.

Necessary condition: Suppose $ \tilde y $ is an order-1 periodic solution of system (2.1), i.e., $ Q(\tilde y) = \tilde y $. Let $ \tilde y_1^ + \in [{y_{{T_1}}}, \tilde y) $ and satisfies $ {Q^2}(\tilde y_1^ +) \le \tilde y_1^ + $. By the global stability of $ \tilde y $ it follows that there exists $ \tilde y_2^ + \in (\tilde y - \varepsilon, \tilde y + \varepsilon) $ such that $ {Q^2}(\tilde y_2^ +) > \tilde y_2^ + $, where $ \varepsilon $ is sufficiently small. It also follows from the continuity of Poincaré map that there must exist a $ {\tilde y^{'}} \in (\tilde y_2^ +, \tilde y_1^ +) $ satisfying $ {Q^2}({\tilde y^{'}}) = {\tilde y^{'}} $, which shows that system (2.1) has an order-2 periodic solution and contradicts the conditions we know. Thus, if there exists a globally stable order-1 periodic solution for system (2.1), then $ {Q^2}(y_0^ +) > y_0^ + $ for any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $.

Theorem 4.2. When $ {x^*} \le x_M^* $ and $ {x_{{E_1}}} < {x_{{N_1}}} $ (Case (ii)(II)), if $ Q({y_{{C_1}}}) > {y_{{C_1}}} $ and $ {Q^2}(y_0^ +) > y_0^ + $ for any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $, then system (2.1) exists an order-1 periodic solution which is globally stable.

Proof. By Theorem 3.2, when $ Q({y_{{C_1}}}) > {y_{{C_1}}} $, we obtain that the Poincaré map $ Q(Z) $ has a unique fixed point on the interval $ [{y_{{C_1}}}, + \infty) $, which implies that system (2.1) has an order-1 periodic solution on the interval $ [{y_{{C_1}}}, + \infty) $.

For any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $, let $ {Q^k}(y_0^ +) = y_k^ + $. Since $ Q(Z) $ that is monotonically decreasing on $ [{y_{{C_1}}}, + \infty) $, then have $ \tilde y < Q\left({y_0^ + } \right) < Q\left({{y_{{C_1}}}} \right) $. If $ {Q^2}(y_0^ +) > y_0^ + $, then $ {y_{{C_1}}} < y_0^ + < y_2^ + < \tilde y < y_1^ + < Q\left({{y_{{C_1}}}} \right) $. By further deduction we can get

Therefore, we have $ \mathop {\lim }\limits_{k \to + \infty } y_{2k}^ + = \mathop {\lim }\limits_{k \to + \infty } y_{2k + 1}^ + = \tilde y $. That is to say the order-1 periodic solution $ Q(\tilde y) = \tilde y $ is globally stable if $ Q({y_{{C_1}}}) > {y_{{C_1}}} $ and $ {Q^2}(y_0^ +) > y_0^ + $ for any $ y_0^ + \in [{y_{{T_1}}}, \tilde y] $.

Theorem 4.3. When $ {x^*} \ge x_M^* $ (Case (i)), if $ Q({y_{{T_1}}}) > {y_{{T_1}}} $ and $ {Q^2}({y_{{T_1}}}) > {y_{{T_1}}} $, then system (2.1) has a stable order-1 or order-2 periodic solution.

Proof. For any initial point $ S_0^ + (x_0^ +, y_0^ +) $ in the phase set, where $ x_0^ +, y_0^ + > 0 $, there exists a positive integer $ k $ such that $ y_k^ + = {Q^k}\left({y_0^ + } \right) $ holds after the pulse. When $ y_0^ + < {y_{{T_1}}} $, it follows from Theorem 3.1 that $ Q(Z) $ has no fixed point in the interval $ [0, {y_{{T_1}}}] $ and is monotonically increasing. Therefore, there exists a integer $ q $ such that $ y_q^ + > {y_{{T_1}}} $ and $ y_{q - 1}^ + < {y_{{T_1}}} $, then can get $ y_q^ + = Q(y_{q - 1}^ +) < Q\left({{y_{{T_1}}}} \right) $, i.e., $ {y_{{T_1}}} < y_q^ + < Q\left({{y_{{T_1}}}} \right) $.

According to $ Q(Z) $ is monotonically decreasing in $ [{y_{{T_1}}}, Q({y_{{T_1}}})] $, we have

Thus we only need to study periodic solutions in interval $ [{y_{{T_1}}}, Q({y_{{T_1}}})] $. Let $ Q\left({y_0^ + } \right) = y_1^ + \ne y_0^ + $ and $ {Q^2}\left({y_0^ + } \right) = y_2^ + \ne y_0^ + $, which means system (2.1) has an order-1 or order-2 periodic solution. Next, we consider the following four circumstances:

(i) If $ {y_{{T_1}}} \le y_2^ + < y_0^ + < y_1^ + \le Q\left({{y_{{T_1}}}} \right) $, from the monotonicity of $ Q(Z) $ we can obtain $ y_3^ + = Q(y_2^ +) > Q(y_0^ +) = y_1^ + > Q(y_1^ +) = y_2^ + $ and $ y_4^ + = Q\left({y_3^ + } \right) < Q(y_1^ +) = y_2^ + < Q(y_2^ +) = y_3^ + $, i.e., $ {y_{{T_1}}} \le y_4^ + < y_2^ + < y_0^ + < y_1^ + < y_3^ + \le Q\left({{y_{{T_1}}}} \right) $. The following relationships are obtained by mathematical induction

(ii) If $ {y_{{T_1}}} \le y_1^ + < y_2^ + < y_0^ + \le Q\left({{y_{{T_1}}}} \right) $, then have $ y_2^ + = Q(y_1^ +) > Q(y_2^ +) = y_3^ + > Q(y_0^ +) = y_1^ + $ and $ y_3^ + = Q(y_2^ +) < y_4^ + = Q(y_3^ +) < Q(y_1^ +) = y_2^ + $, i.e., $ {y_{{T_1}}} \le y_1^ + < y_3^ + < y_4^ + < y_2^ + < y_0^ + \le Q\left({{y_{{T_1}}}} \right) $. Furthermore, we have

(iii) If $ {y_{{T_1}}} \le y_0^ + < y_2^ + < y_1^ + \le Q\left({{y_{{T_1}}}} \right) $, through the similar discussion, we easy to get

(iv) $ {y_{{T_1}}} \le y_1^ + < y_0^ + < y_2^ + \le Q\left({{y_{{T_1}}}} \right) $, after the similar derivation we have

After analysis, for case (i) and case (iv), there exists different values $ {\tilde y_1}, {\tilde y_2} \in ({y_{{T_1}}}, Q({y_{{T_1}}})) $ such that $ \mathop {\lim }\limits_{k \to + \infty } {Q^{2k - 1}}(y_0^ +) = {\tilde y_1} $ and $ \mathop {\lim }\limits_{k \to + \infty } {Q^{2k}}(y_0^ +) = {\tilde y_2} $, where $ {\tilde y_1} \ne {\tilde y_2} $. This means that in both cases there is a stable order-2 periodic solution of system (2.1).

For case(ii) and case (iii), there has $ \tilde y \in ({y_{{T_1}}}, Q({y_{{T_1}}})) $, so that $ \mathop {\lim }\limits_{k \to + \infty } {Q^{2k - 1}}(y_0^ +) = \mathop {\lim }\limits_{k \to + \infty } {Q^{2k}}(y_0^ +) = \tilde y $, i.e., system (2.1) exist a stable order-1 periodic solution.

Theorem 4.4. If $ Q({y_{{T_1}}}) > {y_{{T_1}}} $ and $ {Q^2}({y_{{T_1}}}) > y_{m1}^ + $, where $ y_{m1}^ + = \max \{ {y^ + }, Q\left({{y^ + }} \right) = {y_{{T_1}}}\} $, then system (2.1) has an order-3 periodic solution.

Proof. When $ Q({y_{{T_1}}}) > {y_{{T_1}}} $, the $ Q(Z) $ has a unique fixed point on $ [{y_{{T_1}}}, Q({y_{{T_1}}})] $, i.e., $ Q\left({\tilde y} \right) = \tilde y $, where $ \tilde y \in ({y_{{T_1}}}, Q({y_{{T_1}}})) $. Based on the continuity of $ Q(Z) $, there exist $ y_{m1}^ + \in (0, \tilde y) $ which make $ Q(y_{m1}^ +) = {y_{{T_1}}} $. Let $ G(y) = y - {Q^3}(y) $, then have $ {Q^3}(y_{m1}^ +) = {Q^2}\left({{y_{{T_1}}}} \right) > y_{m1}^ + $ and $ {Q^3}(0) > 0 $, so have $ G(0) < 0 $ and $ G(y_{m1}^ +) > 0 $. Therefore, there is at least one value $ \tilde y \in (0, y_{m1}^ +) $ such that $ G(\tilde y) = 0 $, namely, $ {Q^3}(\tilde y) = \tilde y $, which shows that an order-3 periodic solution of system (2.1) exists.

Remark 4.1. Using the similar proof methods as above, we can show that if $ {Q^{k - 1}}({y_{{T_1}}}) > y_{m1}^ + $, where $ Q(y_{m1}^ +) = {y_{{T_1}}} $, then system (2.1) has an order-k ($ k \ge 2 $) periodic solution.

5.   Numerical simulations

In this subsection, we will design some numerical examples to verify the theoretical results. In addition, the influence of fear factor $ k $ on the dynamics of system (2.1) is also discussed.

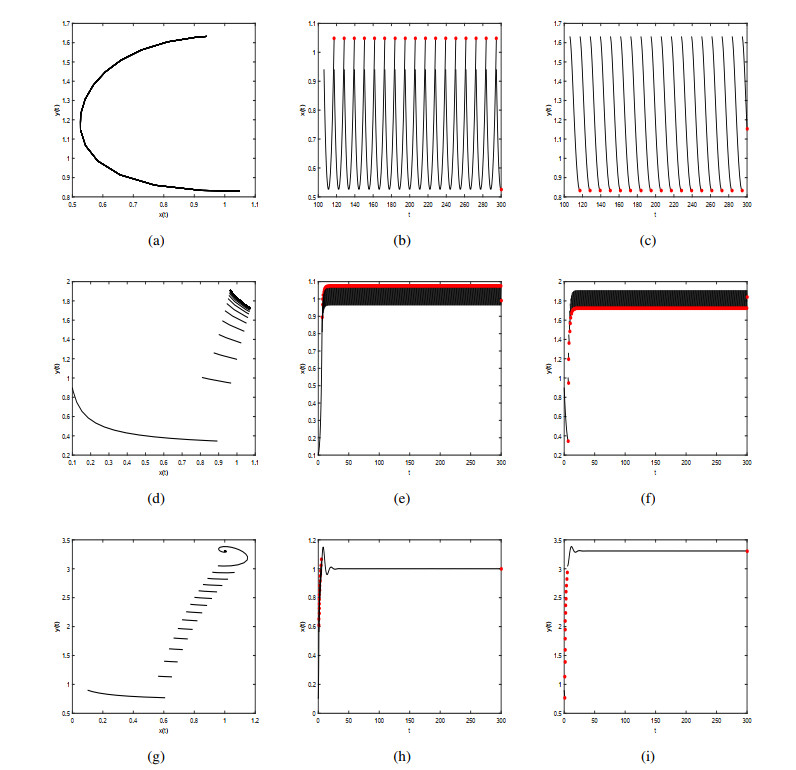
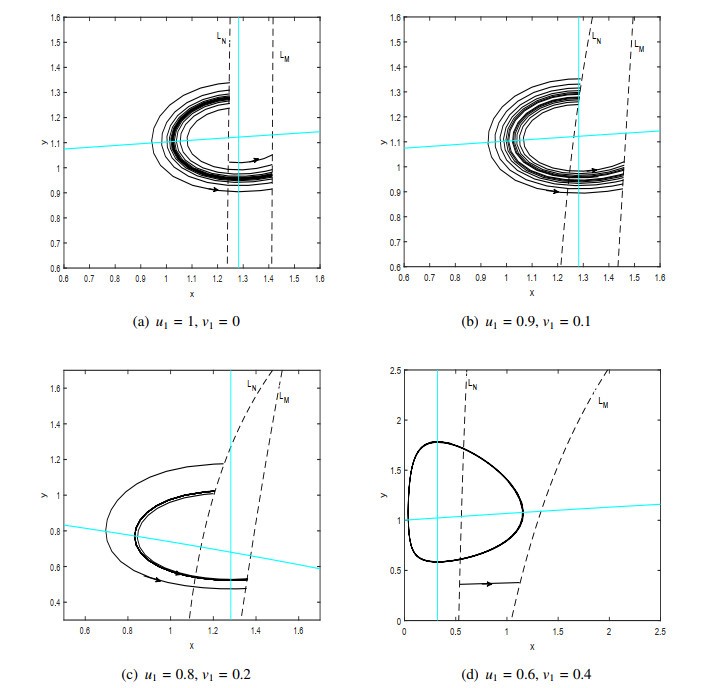
We set the parameters as $ k = 0.04 $, $ d = 0.02 $, $ c = 0.01 $, $ w = 1 $, $ e = 0.44 $, $ m = 0.2 $, $ \delta = 0.2 $, $ \mu = 1 $, $ \tau = 1.8 $, $ \eta = 5 $, $ u_1 = 0.6 $, $ v_1 = 0.4 $, $ ET = 0.7 $. For Case (i), we set $ b = 0.6 $, $ p = 1 $, it can be seen from Theorem 4.1 that when $ {x^*} \ge x_M^* $, system (2.1) has a stable order-1 periodic solution. Observation of Figure 4(a) shows that system (2.1) forms a stable order-1 periodic solution after the impulse. For Case (ii)(II), let $ b = 0.7 $, $ p = 0.5 $, when $ Q({y_{{C_1}}}) > {y_{{C_1}}} $, system (2.1) has a stable order-1 periodic solution, as is illustrated in Figure 4(d). Let $ b = 2.3 $, $ p = 0.5 $, $ w = 0.1 $ and $ k = 0.5 $, when $ Q({y_{{C_1}}}) > {y_{{C_1}}} $, Figure 4(g) indicates that system (2.1) does not have periodic solution, after multiple impulses, the system is stable at the equilibrium $ E^* (0.998, 3.313) $.

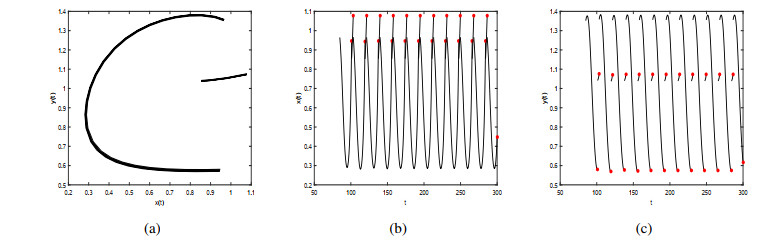
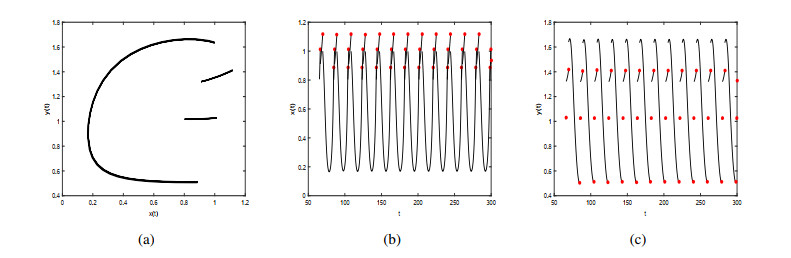
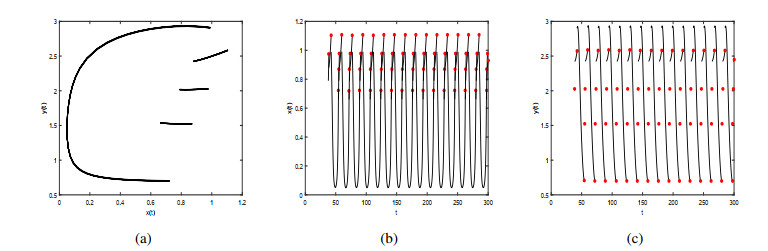
Figure 5(a) shows the trajectory of the order-2 periodic solution of system (2.1). Figure 5(b) and Figure 5(c) are the solutions of the prey and predator corresponding to the order-2 periodic solution, respectively. By observing Figure 5, we can find that the existence of order-2 periodic solution of system (2.1) indicates that reasonable predation behaviour can keep the system in a stable ecological equilibrium. As the parameter $ b $ increases, the existence of the order-1 periodic solution of system (2.1) cannot be guaranteed, for example, when $ b = 0.8 $, system (2.1) has an order-3 periodic solution (Figure 6), and when $ b = 1.4, $ system (2.1) has an order-4 periodic solution (Figure 7).

In the action threshold, when the weighted coefficients $ u_1 = 1 $ and $ v_1 = 0 $, the impulsive set and phase set become two straight lines (Figure 8(a)). This reduces to the linear impulsive systems that have been studied in most previous, in which case the action threshold only depends on the population density of the prey. When changing the weighted coefficients of the action threshold, here $ v_1 \ne 0 $, we can observe that the impulsive set and phase set become two curves and that the curvature of the curves varies with $ u_1 $ and $ v_1 $, see Figure 8. When we use an action threshold control strategy determined by the density of the prey and its rate of change, system (2.1) still has a stable order-1 periodic solution (Figure 8(a)-(c)). On the other hand, if the comprehensive control strategy is more dependent on the change rate of the prey, the control goal can be successfully achieved after a limited number of control measures, making the prey population density is below a given action threshold, as can be seen in Figure 8(d).

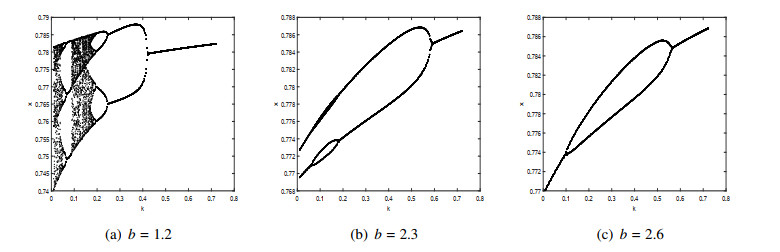
To explore the impact of the fear coefficient $ k $ on the dynamics of system (2.1), we choose $ k $ as the bifurcation parameter and perform a one-dimensional bifurcation analysis on system (2.1). It can be seen from Figure 9 that the internal equilibrium $ E^* $ of system (2.1) is unstable when the parameter set satisfies $ k < k^* $. The bifurcation diagram of $ k $ ($ 0 < k \le 0.8 $) shows that there is a very complex dynamic phenomenon in system (2.1). In particularly, the order-3 periodic solutions exist in the relatively small scope of $ k $ ($ 0.06 < k < 0.08 $), such as Figure 9(a), which further verifies the validity of the results shown in Theorem 4.4. Comparing the bifurcation diagrams at different birth rates $ b $, we conclude that changing $ b $ can significantly alter the dynamics of system (2.1), and an interesting phenomenon is that period doubling and period halving branches occur as $ b $ increases, as shown in Figures 9(b) and 9(c). The island in the middle of Figure 9(b) indicates that the density of prey and predators shows a complex pattern when $ k $ lies in the interval around $ (0.06, 0.19) $.

6.   Conclusion

State-dependent impulsive semi-dynamic systems are among the most discontinuous non-smooth systems and have been investigated in many applications like integrated pest managememt, virus dynamical systems, and diabetes treatment^{[17,36,37,38]}. In the last few years, substantial progress has been made in the study of such systems in terms of analytical techniques, qualitative analysis, and applied research^[39,40]. In particular, with the help of the mathematical tool of Poincaré map, a comprehensive and in-depth branch study of impulsive systems with nonlinear impulsive functions can be carried out, including the existence and global stability analysis of order-k periodic solutions.

In this studies, we establish and analyze a predator-prey state-dependent impulsive model with fear effect. The action threshold of the model depends on the density of the prey and its changing rate, which means that the action threshold depends not only on the density of the prey, but also on the density of the predator. The action threshold contains two weighted quantities $ u_1 $ and $ v_1 $, when the weighted parameter $ v_1 = 0 $, the action threshold will be transformed into $ ET $, previous literatures^{[24,35,37,38]} has carried on the extensive modeling and research.

In comparison with the main results in the literature ^[35], the innovation of our model is the use of action thresholds determined by the density of prey and its changing rate. This leads to the transformation of the impulsive set and phase set into more complex curves, i.e., non-linear impulsive set and phase set, thus developing analytical techniques for the existence and stability of the order-1 periodic solution, including the study of the existence of order-k ($ k \ge 2 $) periodic solutions.

By analysing three different positional relations between the trajectory of system (2.1) and the equilibrium point, the corresponding impulsive set and phase set are obtained (Figure 1). Based on these conditions, the Poincaré map is constructed and using the definition of Poincaré map, the conditions under which order-1 periodic solution and order-2 periodic solution exist for system (2.1) are examined, and the stability of order-1 periodic solution is investigated. The numerical simulation of the order-1 periodic solution also proves our theoretical results, as shown in Figure 4. Further, we also study the existence of order-k ($ k \ge 2 $) periodic solutions and give the conditions that guarantee the existence of such order-k ($ k \ge 2 $) periodic solutions (Figures 5–7).

To further show how the fear coefficient $ k $ affects the dynamics of system (2.1), choosing $ k $ as the bifurcation parameter and fixing the other parameters to those in Figure 7, and the period-doubling bifurcation interspersed with the chaotic window are observed. Therefore, system (2.1) exhibits a sharp transition from a chaotic window to an order-k periodic solutions via a periodic halving bifurcation, and then from an order-k periodic solutions to an order-(k+1) periodic solutions with $ k \ge 2 $ by period-adding bifurcation. In a biological sense, due to the existence of the fear effect, the birth rate of the prey will decrease. When the birth rate $ b $ is small, the fear coefficient $ k $ will make the prey-predator system more complicated. The control methods used in this research are more general and the results obtained are more realistic, as the various factors affecting the population are taken into account in the modelling.

Acknowledgments

The authors would like to thank all the reviewers who participated in the review. Funding will be provided by The National Natural Science Foundation of China (Grant Nos.11961024, 11761031) for the publication of this paper.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Data availability statement

The authors declares that the data supporting the results of this study are available in the article.