Model validation for a noninvasive arterial stenosis detection problem

1.   Introduction

Mosquito-borne diseases such as dengue, yellow fever, and Zika are threatening more than half the world's population. Due to the lack of vaccines, the primary traditional method in control of these mosquito-borne diseases to suppress the mosquito population density by spraying insecticides. However, this method failed to achieve a sustainable effect on keeping mosquito population density below the critical level of epidemic risk. Even worse, heavy applications of pesticides have led to insecticide resistance and environmental pollution. In recent years, releasing sterile mosquitoes has provided an effective and biologically safe control method for eliminating or reducing mosquito populations and thus to control mosquito-borne diseases. In such a method, male mosquitoes are first sterilized using radiological or chemical techniques, and then released into the field to sterilize wild females. A wild female mosquito that mates with a sterile male will either be non-reproductive, or lay eggs that are not hatchable. Repeating releases of sterile mosquitoes could eventually wipe out wild mosquitoes, or, more realistically, suppress the wild mosquito population ^[1,2].

Various mathematical models have been developed to study the interactive dynamics of wild and sterile or Wolbachia-infected mosquitoes, including ordinary differential equation models ^{[3,4,5,6,7,8,9]}, delay differential equation models ^{[10,11,12,13,14]}, partial differential equation models ^{[15,16,17,18]}, and stochastic dynamical equation models ^[19,20], to cite only a few. Recently, Li in ^[7] formulated a simple model with constant release rate of sterile mosquitoes

where $ S_\nu(t) $ and $ S_g(t) $ are the numbers of wild and sterile mosquitoes at time $ t $ respectively, $ a $ is the number of offspring produced per individual female adult per unit of time, $ b $ is the constant release rate of sterile mosquitoes, $ \xi_\nu $ is the carrying capacity parameter such that $ 1-\xi_\nu S_\nu $ describes the effect of density dependence, and $ \mu_1 $ is the death rate of wild or sterile mosquitoes. In (1.1), it was assumed implicitly that the mating of sterile male mosquitoes with wild females has an instant impact on the reproduction such that the model is based on ordinary differential equations without time-delay. It does not incorporate the development or maturation of mosquitoes that undergo four distinct life stages.

Including the maturation process, we let $ \tau $ be the average waiting duration from the eggs to the eclosion of adults in the next generation. We then extend model (1.1) to the following model with time delay

In this new model $ e^{-\mu_{0}\tau} $ is the survival rate of the immature mosquitoes that were born at time $ t-\tau $ and are still alive at the time $ t $, and $ \mu_1, \mu_2 $ are the death rates of wild and sterile mosquitoes, respectively.

The initial condition for (1.2) is given as

where $ t_0\geq \tau $. For convenience, we write

It is well-known that the oscillation phenomena may appear when time delays are included in differential equations, as shown, for example, in recent studies of mosquito population models with time delays ^[10,12]. We aim to offer an accurate description of the oscillation phenomena of (1.2), and study how the oscillatory properties change with respect to the release of sterile mosquitoes. Specifically to our model (1.2)-(1.3), we define the oscillations as follows.

Definition 1.1. Let $ (S_\nu(t), S_g(t)) $ be a non-constant positive solution of (1.2)-(1.3). We say that $ (S_\nu(t), S_g(t)) $ is non-oscillatory about its equilibrium $ (\overline{S_\nu}, \overline{S_g}) $ if $ S_\nu(t)-\overline{S_\nu} $ and $ S_g(t)-\overline{S_g} $ are positive or negative eventually. Otherwise, it is said to be oscillatory about $ (\overline{S_\nu}, \overline{S_g}) $. We say that (1.2) is oscillatory about $ (\overline{S_\nu}, \overline{S_g}) $ if every non-constant solution of (1.2) is oscillatory. Otherwise, (1.2) is said to be non-oscillatory about $ (\overline{S_\nu}, \overline{S_g}) $.

In this paper, we study the oscillatory properties of (1.2). The paper is organized as follows. In Section 2, we establish useful lemmas and find that, (1.2) is oscillatory about the unique non-zero equilibrium when no sterile mosquitoes are released. In Section 3, we determine an oscillation threshold, denoted by $ \hat{b} $, for the constant release rate $ b $ of sterile mosquitoes, such that all non-trivial positive solutions oscillate when $ b < \hat{b} $, and the oscillation disappears when $ b > \hat{b} $. In Section 4, numerical simulations are provided to demonstrate our new findings. Concluding remarks are finally given in Section 5.

2.   Preliminaries

In this section, we first establish useful lemmas that help us to prove the main results of this paper. In addition, we show that every non-trivial solution of (1.2) oscillates with respect to its unique non-zero equilibrium when no sterile mosquitoes are released. We first determine the monotonicity of the following birth-progression function.

Lemma 2.1. Consider the birth-progression function

and let

Then

Proof. We omit the detail of the proof since the result can be obtained by directly taking the derivative of $ g(x, z) $ with respect to $ x $.

We next discuss the boundedness and positivity of solutions of (1.2).

Lemma 2.2. Suppose $ \mu_1 > \xi_\nu g(C^*(m_0), m_0) $. Then system (1.2)-(1.3) has a unique solution $ (S_\nu, S_g) $ which is bounded and positive for all $ t\in [t_0, \infty) $.

Proof. The existence and uniqueness of the solution of (1.2) follows from the standard results in the theory of delay differential equations ^[21]. From the second equation of (1.2), it is easy to see that $ 0 < m_0\le S_g(t)\le M_0 $ for all $ t\geq t_0 $, where $ m_0 $ and $ M_0 $ are defined in (1.4). It remains to verify the positivity and boundedness of $ S_\nu $ in (1.2).

We first confirm that $ S_\nu(t) < 1/\xi_\nu $ holds for all $ t\geq t_0 $ when $ \mu_1 > \xi_\nu g(C^*(m_0), m_0) $. Otherwise, there exists $ t_1 > t_0 $ such that $ S_\nu(t_1) = 1/\xi_\nu $, and $ S_\nu(t) < 1/\xi_\nu $ for all $ t\in [t_0-\tau, t_1) $. Hence $ S_\nu'(t_1)\geq 0 $. However, from (1.4) and the first equation of (1.2), we have

which is a contradiction to $ S_\nu'(t_1)\geq 0 $.

Next, we prove the positivity of $ S_\nu(t) $. If not, there exists $ t_2 > t_0 $ such that $ S_\nu(t_2) = 0 $ and $ 0 < S_\nu(t) < 1/\xi_\nu $ for all $ t\in [t_0-\tau, t_2) $. Hence $ S_\nu'(t_2)\leq 0 $, which contradicts

The proof is complete.

Remark 1. We assume that the condition $ \mu_1 > \xi_\nu g(C^*(m_0), m_0) $ holds throughout the rest of this paper.

Define the intrinsic growth rate of wild mosquito population by

The following lemma clarifies the existence of equilibria of (1.2).

Lemma 2.3. Define

If $ 0 < b < b^* $, then (1.2) has three nonnegative equilibria: $ N_0: = \left(0, \frac{b}{\mu_2}\right) $ and $ N^{\mp} = \left(S_\nu^\mp, \frac{b}{\mu_2}\right) $, where

When $ b = b^* $, (1.2) has two nonnegative equilibria: $ N_0 $ and $ N^*: = \left(\dfrac{r_0-1}{2r_0\xi_\nu}, \dfrac{b}{\mu_2}\right) $; When $ b > b^* $, $ N_0 $ is the only nonnegative equilibrium of (1.2).

We next investigate the oscillation of (1.2) with respect to the unique non-zero equilibrium when $ b = 0 $. In this case, (1.2) becomes

It is clear that $ \lim\limits_{t\rightarrow\infty}S_g(t) = 0 $. Therefore, the oscillation of (2.2) is exactly the same as that of the next equation

which has a unique positive equilibrium $ S_\nu^{(1)} = (r_0-1)/r_0\xi_\nu $.

We now study the oscillation of (2.3) with respect to $ S^{(1)}_\nu $ when $ r_0 > 2 $. Let $ y(t) = S_\nu(t)-S^{(1)}_\nu $. Then instead of considering the oscillation of $ S_\nu(t) $ with respect to $ S^{(1)}_\nu $ in (2.3), we consider the oscillation of $ y(t) $ about $ y(t) = 0 $ for the following equation

where $ q = \mu_1\left(r_0-2\right) > 0 $.

To proceed, we first establish the following three lemmas to reach the conclusion of Theorem 1.

Lemma 2.4. If $ r_0 > 2 $, then every non-oscillatory solution of (2.4) about $ y(t) = 0 $ converges to zero as $ t\to\infty $.

Proof. Let $ y(t) $ be an arbitrary non-oscillatory solution of (2.4) about $ y(t) = 0 $. Then it is positive or negative eventually. It suffices to prove that

(ⅰ) Suppose that $ y(t) $ is eventually positive. Then there exists $ \bar{t_1} > t_0 $ large enough such that $ y(t) > 0 $ for all $ t > \bar{t_1}+\tau $. In the meantime, based on (2.4), we have

Thus $ \lim\limits_{t\to\infty}y(t) = L $ holds and we claim that $ L $ is non-negative. If $ L > 0 $, then

Thus we have $ y'(t)\leq \varrho < 0 $ for sufficiently large $ t $, and hence $ \lim_{t\to\infty}y(t) = -\infty $, which is a contradiction. Therefore, $ \lim_{t\to\infty}y(t) = L = 0 $.

(ⅱ) Suppose that $ y(t) $ is eventually negative. To prove (2.5), we let

It is easy to see that (2.5) is true if and only if $ \underline{y} = 0 $. Otherwise, $ \underline{y} < 0 $. There are only two cases to consider: $ \underline{y} = \overline{y} $, and $ \underline{y} < \overline{y} $.

If $ \underline{y} = \overline{y} < 0 $, then $ \lim_{n\to\infty} y(t) = \underline{y} = \overline{y} $ exists. Taking limits in (2.4) on both sides gives

Notice that $ y(t) $ is bounded, then we derive $ \mu_1 +q +\mu_1 r_0 \xi_\nu \underline{y} = 0 $ and $ \underline{y} = -S_\nu^{(1)} $. Hence there exists a sequence $ \{t_n\} $ large enough such that $ y'(t_n)\le 0 $, $ y(t_n)\to -S_\nu^{(1)} $, and $ y(t_n) = \min\limits_{t\le t_n} y(t) $. Then it follows from (2.4) that

which leads to

and

Solving the inequality above, we obtain $ y(t_n-\tau)\le -S_\nu^{(1)} $, which is a contradiction to $ y(t_n-\tau) > -S_\nu^{(1)} $.

If $ \underline{y} < \overline{y} < 0 $, then there exists a sequence $ \{s_n\} $ large enough such that $ y'(s_n) = 0 $, $ y(s_n)\to \underline{y} $. From (2.4), we have

Notice that $ y(s_n-\tau) $ is bounded in the interval $ (-S_\nu^{(1)}, 0) $. Then there exists a convergent subsequence, denoted by $ \{s_n\} $ again, such that

where $ \underline{y} \le y_1: = \lim_{n\to\infty}y(s_n-\tau) \le \overline{y} $. Hence

and $ y_1\le -S_\nu^{(1)} $. Meanwhile, $ y_1\geq \underline{y} \geq -S_\nu^{(1)} $, thus $ y_1 = \underline{y} = -S_\nu^{(1)} $.

Take $ t^{*} > t_0 $ large enough such that $ y'(t^*) = 0 $, and $ y(t^*) = \min\limits_{t\le t^*} y(t) $. Then it follows from (2.4) that

which yields

and $ y(t^*-\tau)\le -S_\nu^{(1)} $, a contradiction to $ y(t^*-\tau) > -S_\nu^{(1)} $. The proof is complete.

To show the oscillatory behavior of solutions of (2.4) about $ y(t) = 0 $, we linearize (2.4) at $ y(t) = 0 $ which leads to

Based on the results in ^[22], we immediately have the following necessary and sufficient condition for the oscillation of solutions of (2.6) with respect to $ y(t) = 0 $.

Lemma 2.5. ^[22] Every non-trivial solution of (2.6) is oscillatory about $ y(t) = 0 $ if and only if

where $ q = \mu_1(r_0-2) > 0 $.

We then show the equivalence of the oscillations between (2.4) and (2.6) about $ y = 0 $.

Lemma 2.6. Equation (2.4) is oscillatory about $ y = 0 $ if and only if (2.6) is oscillatory about $ y = 0 $.

Proof. Assume that (2.4) is oscillatory about $ y = 0 $. We confirm that (2.6) is also oscillatory about $ y = 0 $. Otherwise, there exists a solution $ y(t) $ of (2.6) that is non-oscillatory about $ y(t) = 0 $. Without loss of generality, suppose that $ y(t) $ is eventually negative. Then there exist $ \delta > 0 $ and $ t_1 > t_0 $ such that $ -\delta < y(t) < 0 $, for all $ t > t_1 $. Let $ Y(t) $ be a solution of (2.4) with the same initial value condition as that of $ y(t) $ in (2.6). Notice that

By the comparison principle, we have $ Y(t)\le y(t) < 0 $, for $ t > t_1 $, which is a contradiction to the assumption that (2.4) is oscillatory about $ y(t) = 0 $.

On the other hand, we show that (2.4) oscillates about $ y = 0 $ if (2.6) oscillates about $ y = 0 $. If not, then there exists a solution $ y_{1}(t) $ of (2.4), which is either eventually positive or eventually negative. There are two cases to consider.

(ⅰ) If $ y_{1}(t) $ is eventually positive, then there exists $ t_2 > t_0 $ such that $ y_{1}(t) > 0 $, for all $ t > t_2 $. Let $ Y_{1}(t) $ be the solution of (2.6) with the same initial condition as that of $ y_{1}(t) $ in (2.3). Again, by the comparison principle, we have $ Y_{1}(t)\geq y_{1}(t) > 0 $, for all $ t > t_2 $, a contradiction to the oscillation of (2.6) about $ y(t) = 0 $.

(ⅱ) If $ y_{1}(t) $ is eventually negative, then there exists $ t_3 > t_0 $ such that $ y_{1}(t-\tau) < 0 $, $ y_{1}(t) < 0 $, for all $ t > t_3 $. From Lemma 4, we have $ \lim_{t\to \infty}y_{1}(t) = 0 $. Since (2.7) holds, there exists a positive constant $ \varepsilon_0 < 1 $ such that

which suggests that the equation

is oscillatory about $ y(t) = 0 $. Moreover, since

there exists $ t_4 > t_3 $ such that

Then

and thus

Let $ \overline{Y}(t) $ be a solution of the equation $ y'(t)+\mu_1y(t)+\varepsilon_{0}q y(t-\tau) = 0 $ with the same initial condition as the solution $ y_{1}(t) $ of (2.4). Then $ \overline{Y}(t) < y_{1}(t) < 0 $ for all $ t > t_4 $, which is a contradiction to the oscillation of the equation

about $ y(t) = 0 $. Therefore, equation (2.4) is oscillatory about $ y = 0 $ if and only if (2.6) is oscillatory about $ y = 0 $. The proof is complete.

We note that the oscillations of $ S_\nu $ about $ S_\nu^{(1)} $ between system (2.2) and (2.3) are exactly the same. Based on Lemmas 2.3, 2.4, and 2.5 above, a sufficient and necessary condition for the oscillations of solutions of equation (2.2) can be summarized as follows.

Theorem 1. If $ r_0 > 2 $, then every non-trivial positive solution of (2.2) is oscillatory about $ S_\nu^{(1)} $ if and only if (2.7) holds.

Remark 2. Theorem 1 provides a sufficient and necessary condition for the oscillations of non-trivial positive solutions about the unique non-zero equilibrium in equation (1.2) when no sterile mosquitoes are released. In fact, from the estimation of parameters of (1.2) in Table 1, we find that (2.7) is always true and so (2.2) is oscillatory about $ S_\nu^{(1)} $, which is consistent with the oscillation phenomenon of the annual abundance of wild mosquitoes in the wild. These results are important for the discussion of the main results in Section 3.

3.   Main results

Given that (1.2) is oscillatory about the unique non-zero equilibrium in the absence of sterile mosquitoes, it becomes interesting to ask how the oscillatory property of (1.2) with the increase of the releases of sterile mosquitoes. Interestingly, we find an oscillation threshold, denoted by $ \hat{b} $, for the release rate of the sterile mosquitoes, and show that this oscillation phenomenon will be maintained when the release rate $ b < \hat{b} $, whereas it will disappear when $ b > \hat{b} $. The result of oscillation threshold is described as follows.

Theorem 2. Let $ \hat{b} $ be the unique solution of

where

Then $ \hat{b} $ is the oscillation threshold of the release rate $ b $, below which the oscillation phenomenon maintain, and above which it will disappear.

Proof. By using the similar argument as that in Theorem 1, we conclude that every non-trivial positive solution of (1.2) is oscillatory about the non-zero equilibrium $ N^+ $ if and only if

The proof is nearly the same as that of Theorem 1, so we omit it.

Next, we claim that $ q(b) $ decreases with the increase of $ b $. It follows from the definition of $ S_\nu^{+} $ in Lemma 2.3 that $ S_\nu^{+}(b) $ is monotonously decreasing. Hence $ 3r_0\xi_\nu S_\nu^{+}-2r_0+1 $ is positive and monotonously decreasing with respect to $ b $. Moreover, By taking derivative, we obtain

thus $ S_\nu^{+}/(\mu_2S_\nu^{+}+b) $ is monotonously decreasing. Consequently, $ q(b) $ is monotonously decreasing.

Notice that (1.2) is oscillatory about $ N^+ $ when $ b = 0 $. According to Theorem 1, we have $ q(0)\tau e^{\mu_1\tau} > 1/e $. Meanwhile, when $ b = b^* $, we have

Thus, there exists unique $ \hat{b}\in(0, b^*) $ such that $ q(\hat{b})\tau e^{\mu_1\tau} = 1/e $. Notice that (1.2) is oscillatory about $ N^+ $ if and only if (3.1) holds, we conclude that system (1.2) is oscillatory about $ N^+ $ when $ 0\le b < \hat{b} $, and non-oscillatory when $ \hat{b}\le b \le b^* $. The proof is complete.

4.   Numerical simulations

In this section, numerical simulations are given to validate the main theoretical results in Section 3.

4.1.   Estimation of parameters

In Table 1 below, we list important parameter values for Aedes albopictus and sterile mosquitoes, most of which are taken from earlier experimental data in the literature ^{[23,24,25,26,27,28,29]}. Since the parameter values are affected by many factors such as temperature and rainfall, we can not determine their exact values but take reasonable estimations of the ranges. Using a similar method for the parameter estimations as in ^[12], we estimate $ \tau\in [16, 66] $. By using the measured half-lives, we have $ \mu_1\approx 0.0277 $ from ^[29], and $ \mu_1\in [0.0231, 0.0693] $ from ^[26], hence the life span of adult mosquitoes is $ T_1 = 1/\mu_1\approx 36.10 $, and $ T_1\in [14.43, 43.29] $. Furthermore, it takes 5 days on average for a female mosquito to lay eggs after the eclosion, and the total number of eggs laid by each female is 120.76 on average ^[26]. Consequently, the egg-laying phase of a female mosquito is $ T_2\in[9.43, 38.29] $, and $ a\in [3.15, 12.81] $. From ^[23,24], we find that sterile mosquitoes will die in about 7 days after releasing to the wild field. Thus we estimate that the death rate of sterile mosquitoes is about 1/7. Besides, according to ^[27], we obtain that the survival probability of the average maturation time of wild mosquitoes is about 0.05. We note that $ \xi_\nu $ is usually proportional to the area size. From simulations, it shows that different values of $ \xi_\nu $ produce similar dynamics, which allows us to take $ \xi_\nu = 0.0025 $ as a representative value.

4.2.   Oscillation threshold

To make the oscillation behavior be clearer, we employ simulation examples with different release rates to testify the result of oscillation threshold given in Theorem 2.

Suppose that the model parameters of (1.2) are given as

All the parameter values in (4.1) are within the estimation ranges given in Table 1. By substituting these parameter values into (2.1), we derive $ b^*\approx 32.143 $. Notice that the oscillation threshold $ \hat{b} $ is the unique solution of the equation $ q(b)\tau e^{\mu_1\tau} = 1/e $, we have $ \hat{b} \approx 21.7754 $.

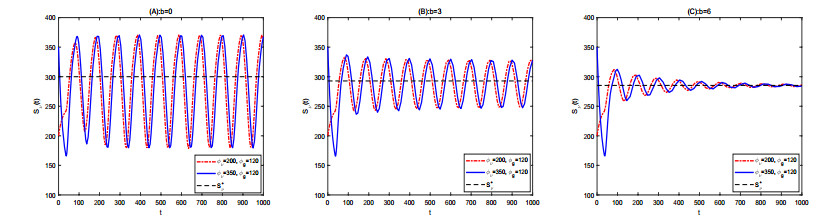
We select three different release rates $ b = 0 $, $ b = 3 $ and $ b = 6 $ from the interval $ [0, \hat{b}) $. For these three cases, the number of wild mosquitoes $ S_\nu(t) $ oscillates around $ S_\nu^+ $, as shown in Figure 1. This testifies the first part of Theorem 2, that is, the non-trivial positive solutions of (1.2) are oscillatory about $ N^+ $ when $ b < \hat{b} $. When $ b = 0 $, there is no sterile mosquitoes released into the wild, the number of mosquitoes oscillates with a larger amplitude, as shown in Figure 1 (A). As the release rate increases, the amplitude is reduced. When $ b = 6 $, the number of mosquitoes oscillates in a narrow range around $ S_\nu^+ $, as shown in Figure 1 (C).

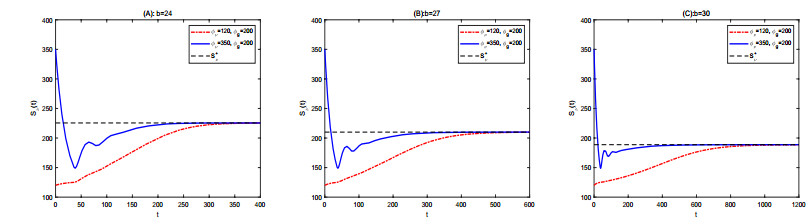
We increase the release rate of sterile mosquitoes further, and let $ \hat{b} < b < b^* $. For instance, we take $ b = 24 $, $ b = 27 $ and $ b = 30 $ separately from the interval $ [\hat{b}, b^*] $. As shown in Figure 2, we find that the number $ S_\nu(t) $ is less than $ S_\nu^+ $, and then gradually increases and approaches to $ S_\nu^+ $. This phenomenon testifies the second part of Theorem 2, that is, the solutions $ (S_\nu, S_g) $ are non-oscillatory about $ N^+ $.

Figure 2 also shows that the wild mosquito population is first suppressed to a low level by releasing sterile mosquitoes with higher rates, then gradually tends to a stable level $ S_\nu^+ $. Figure 1 and 2 both show that the stable level of wild mosquitoes is reduced when the release rate increases from $ 0 $ to $ b^* $.

5.   Concluding remarks

To control the life-threatening mosquito-borne diseases such as dengue, yellow fever, and Zika, one of the biologically safe methods is to release male sterile mosquitoes into the field to suppress the wild mosquito population. We, in this paper, consider the oscillatory properties of a delayed mosquito population suppression model with a constant release rate of sterile mosquitoes. We find that every non-trivial positive solution of the model oscillates with respect to its unique non-zero equilibrium when no sterile mosquitoes are released, i.e., $ b = 0 $. We then study the oscillatory behavior of the model with the releases of sterile mosquitoes, and establish an oscillation threshold, denoted by $ \hat{b} $, for the constant release rate $ b $ of sterile mosquitoes such that the oscillation of solutions maintains when $ b < \hat{b} $, whereas the oscillation disappears when $ b > \hat{b} $. Furthermore, through numerical examples, we show that the amplitudes of the oscillation become smaller and smaller and then the oscillation disappears as release rates of sterile mosquitoes increase. Oscillatory phenomenon is common for solutions of delay differential equations. However, to the best of our knowledge, an establishment of the oscillation threshold which determines the existence or disappearance of solution oscillations is one of the first in the field of mosquito population dynamics.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 11631005), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT-16R16), the Guangzhou Postdoctoral International Training Program Funding Project, the Science and Technology Program of Guangzhou (No. 201707010337) and the Foundation of Yunnan Educational Committee (No. 2017ZDX027). The authors thank Professor Jianshe Yu for his help in improving the original Lemma 2.4.

Conflict of interest

The authors have declared that no competing interests exist.