1. Introduction
Soft materials responsive to external stimuli such as temperature, pH, and electric fields, have attracted considerable attention as soft actuators in the next generation. A magnetic elastomer is a soft material responsive to magnetic fields and consists of polymeric matrixes and magnetic particles. The elastic modulus of magnetic elastomers can be altered by an application of magnetic fields [1,2,3]. So far, we have studied the effect of magnetic fields on the viscoelastic properties for magnetic elastomers and have improved the magnetic-field response [4,5,6].
According to vibration engineering, it has been found that a relative change of the natural frequency Δf/f0 is proportional to a relative change in elastic modulus ΔG'/G'0 as the following [7],
Therefore, it can be found that the natural frequency can be continuously changed by magnetic fields because the elastic modulus can be continuously varied by magnetic fields. Thus, magnetic elastomers are useful for active dampers driven by magnetic fields. Actually, Komatsuzaki et al. have fabricated a dynamic vibration absorber using magnetorheological elastomers that demonstrates the ability of broadband vibration control [8,9]. They reported that the natural frequency shifted from 60 to 250 Hz by an electric current of 3.5 A [8]. Guyen et al. developed a vibration isolator with a frequency shift of ~8 Hz by a magnetic field of 218 mT [10]. Fu et al. have also developed a semiactive/fully active hybrid isolator using magnetorheological elastomer and piezoelectric material. They found that the natural frequency can be shifted by approximately 20 Hz by an exciting current of 1 A for electromagnet [11].
In this study, we report the effect of a magnetic field on the vibration properties for polyurethane and magnetic elastomers with various plasticizer contents and discuss the influence of a magnetic field or plasticizer content on the natural frequency and transmissibility.
2. Materials and method
2.1. Synthesis of polyurethane and magnetic elastomers
Polyurethane elastomers and magnetic elastomers were synthesized by a prepolymer method. Poly(propylene glycol) (Mw = 2000, 3000), prepolymer cross-linked by toluene diisocyanate, a plasticizer (dioctyl phthalate, DOP), and carbonyl iron (CI) particles were mixed by a mechanical mixer for several minutes. Polyurethane elastomers were synthesized by a similar manner without using CI particles. The median diameter of CI particles was 7.0 ± 0.2 μm determined by a particle size analyzer (SALD-2200, Shimadzu). The saturation magnetization for CI particles was evaluated to be 245 emu/g by a SQUID magnetometer (MPMS, Quantum Design). The mixed liquid was poured in a silicon mold and cured in an oven for 20 min at 100 ℃. The weight concentration of DOP was defined by the ratio of DOP to the matrix without magnetic particles; DOP/(DOP + matrix). The weight concentration of magnetic particles (CI-CS) was kept at 70 wt%; CI/(CI + matrix), which corresponds to a volume fraction of 0.23.
2.2. Vibration measurements
Figure 1 demonstrates the photograph of experimental set-up for vibration measurements for polyurethane elastomers and magnetic elastomers. The acceleration was measured by a piezo electric acceleration sensor (P51C, San-ei Instruments Inc.) with varying the frequency from 5 to 300 Hz at room temperature. We measured the frequency spectra of transmissibility for two different samples obtained from different batch, and the averaged value and standard error were indicated. The sample was a cylinder with a diameter of 20 mm and a length of 10 mm. The transmissibility τ was calculated from the following equation,
|
τ=a2a1=√1+(tanδ)2(1−(ff0)2)2+(tanδ)2
|
(2)
|
Here,
a1 and a2 is the acceleration measured by the sensor 1 and sensor 2, respectively; f and f0 is the frequency and natural frequency, respectively; tanδ is the loss factor of elastomers. A cylindrical electromagnet (Fujita Ltd. FSGP-40) with a weight of 300 g was used for generating magnetic fields. The electric potential and electric current was 22.3 V and 0.23 A, respectively, when a magnetic field of 60 mT was applied. Two kinds of weight with masses of 69 g and 224 g were used to clear the effect of mass on the natural frequency or transmittance. The strain was calculated to be 9.4 × 10–3–6.5 × 10–2 for a loading weight of 69 g and 3.9 × 10–2–1.2 × 10–1 for a loading weight of 224 g using the values of storage modulus ( = 3G'). The Payne effect for magnetic elastomers presented here were relatively weak. The onset strain from the linear to nonlinear viscoelastic regime was seen at γ ~ 10–3 at the lowest. Therefore, most of vibration experiment was carried out in the nonlinear viscoelastic regime.
2.3. Dynamic viscoelastic measurements
To clear the viscoelastic properties of polyurethane and magnetic elastomers, the dynamic viscoelastic measurements were carried out using a rheometer (MCR301, Anton Paar) at 20 ℃. The dynamic modulus was measured at a strain of 10–4 (linear viscoelastic regime) and 0.1 (nonlinear viscoelastic regime). The frequency was constant at 1 Hz. An electric current with 0.33 A was used for the rheological measurement which corresponds to a magnetic field of 60 mT. The sample was a disk of 20 mm diameter and 1.5 mm thick.
3. Results and discussion
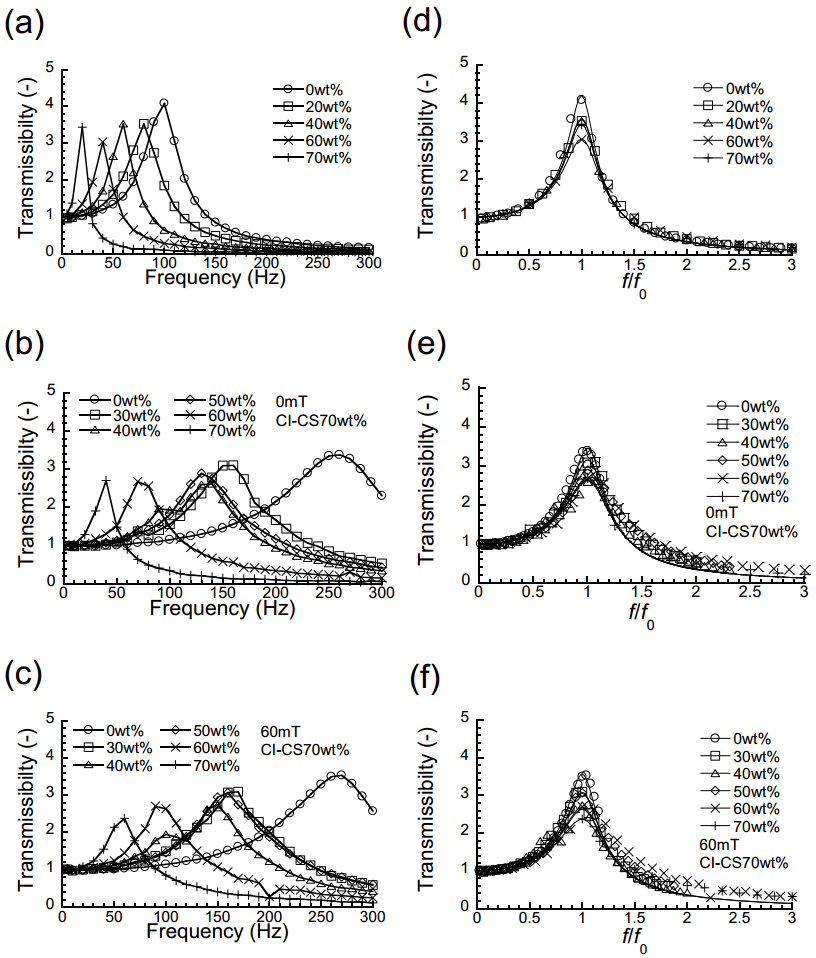
Figure 2a shows the frequency spectra of transmissibility for polyurethane elastomers with various plasticizer contents at 0 mT. The frequency spectra shifted to low frequencies as increasing the plasticizer content. Figure 2b exhibits the frequency spectra of transmissibility at 0 mT for magnetic elastomers with various plasticizer contents. The natural frequency for magnetic elastomers with a plasticizer content of 0 wt% was seen at approximately 250 Hz. As well as polyurethane elastomers, the frequency spectra shifted to low frequencies as increasing the plasticizer content. The frequency shift was much significant compared to that for polyurethane elastomers without magnetic particles. The transmissibility for magnetic elastomers slightly decreased with the plasticizer content. Figure 2c appears the frequency spectra of transmissibility at 60 mT for magnetic elastomers with various plasticizer contents. The frequency spectra for magnetic elastomers at 60 mT were similar to those at 0 mT. Figure 2d shows the frequency spectra of transmissibility normalized by the natural frequency for polyurethane elastomers with various plasticizer contents at 0 mT. The natural frequency is the frequency at which a system tends to oscillate in the absence of any driving or damping force [12,13]. The peaks of transmissibility for magnetic elastomers were wider than those for polyurethane elastomers at both 0 and 60 mT. This means that the loss factor of polyurethane elastomers is higher than those of magnetic elastomers. The loss factor obtained from the fitting by Eq 2 was listed in Table 1. The loss factor for both magnetic elastomer and polyurethane elastomer increased with the plasticizer content. Magnetic elastomers showed high values of loss factor compared to those for polyurethane elastomers. Although the measurement frequency was 1 Hz in dynamic viscoelastic measurement, the storage modulus, loss modulus, and loss factor at low and high strains were listed in Table 2. The storage modulus for both magnetic elastomer and polyurethane elastomer decreased with the plasticizer content, independently of the strain amplitude. The loss factor for magnetic elastomers at a strain of 10–4 was comparable with that for polyurethane elastomers. However, at a strain of 10–1, the loss factor for magnetic elastomers with high plasticizer content was higher than that for polyurethane elastomers, which is similar trend with the loss factor obtained from vibration experiment.
Table 1. Loss factor tanδ determined from transmissibility and rheological measurement for polyurethane and magnetic elastomers.
|
Fitting |
|
Rheometer |
| DOP |
ME2) |
PU3) |
γ = 10–4 |
|
γ = 0.1 |
| (wt%)1) |
ME |
PU |
ME |
PU |
|
0 mT |
60 mT |
0 mT |
60 mT |
0 mT |
60 mT |
| 0 |
0.32 |
0.30 |
0.26 |
|
0.12 |
0.12 |
0.14 |
|
0.17 |
0.17 |
0.22 |
| 20 |
|
|
0.34 |
|
|
0.12 |
|
|
0.19 |
| 30 |
0.34 |
0.33 |
|
0.12 |
0.11 |
|
0.19 |
0.20 |
|
| 40 |
0.40 |
0.38 |
0.34 |
0.10 |
0.10 |
0.12 |
0.16 |
0.17 |
0.13 |
| 50 |
0.37 |
0.33 |
|
0.09 |
0.09 |
|
0.15 |
0.16 |
|
| 60 |
0.42 |
0.40 |
0.37 |
0.13 |
0.12 |
0.10 |
0.18 |
0.20 |
0.09 |
| 70 |
0.42 |
0.47 |
0.29 |
0.10 |
0.08 |
0.10 |
0.14 |
0.16 |
0.10 |
| 1) Plasticizer content, 2) magnetic elastomer, 3) polyurethane elastomer |
Table 2. Storage modulus G' and loss modulus G" determined from rheological measurement for polyurethane and magnetic elastomers.
|
γ = 10–4 |
|
γ = 0.1 |
| DOP |
G' (kPa) |
|
G" (kPa) |
G' (kPa) |
|
G" (kPa) |
| (wt%)1) |
ME2) |
PU3) |
ME |
PU |
ME |
PU |
ME |
PU |
|
0mT |
60mT |
0mT |
60mT |
0mT |
60mT |
0mT |
60mT |
| 0 |
86 |
94 |
27 |
|
10 |
12 |
3.6 |
|
48 |
51 |
19 |
|
8.2 |
8.8 |
4.3 |
| 20 |
|
|
23 |
|
|
2.6 |
|
|
18 |
|
|
3.4 |
| 30 |
55 |
69 |
|
6.7 |
7.7 |
|
37 |
43 |
|
6.9 |
8.4 |
|
| 40 |
58 |
73 |
25 |
5.9 |
7.5 |
2.6 |
36 |
43 |
20 |
5.8 |
7.3 |
2.6 |
| 50 |
44 |
61 |
|
4.0 |
5.9 |
|
33 |
41 |
|
4.9 |
6.5 |
|
| 60 |
19 |
36 |
14 |
2.4 |
4.3 |
1.2 |
16 |
26 |
12 |
2.9 |
5.1 |
1.2 |
| 70 |
19 |
38 |
4.6 |
1.8 |
3.0 |
0.46 |
14 |
24 |
4.5 |
1.9 |
3.8 |
0.46 |
| 1) Plasticizer content, 2) magnetic elastomer, 3) polyurethane elastomer |
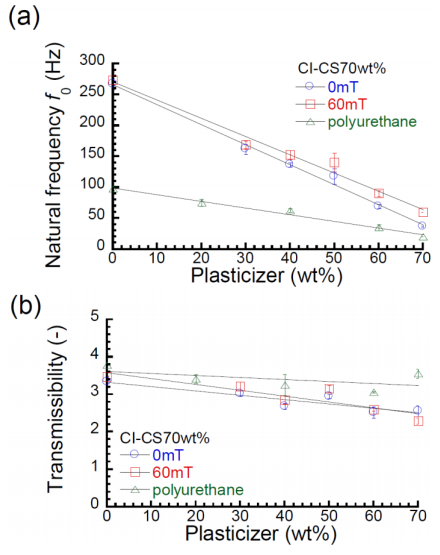
Figure 3a shows the relationship between the natural frequency and plasticizer content for polyurethane and magnetic elastomers. The natural frequency for both polyurethane and magnetic elastomers linearly decreased with the plasticizer content. It was found that the natural frequency for magnetic elastomers is much affected by the plasticizer content than that for polyurethane elastomers. It is because that the variation of the elastic modulus by the plasticizer content for magnetic elastomers is larger than that for polyurethane elastomers. The natural frequencies at 60 mT for magnetic elastomers with high plasticizer content were higher than those at 0 mT, however the magnetic-field effect on the natural frequency was extremely small. Although the mechanism of magnetically tunable vibration by a weak field is unclear, the change in natural frequency would be larger as increasing the magnetic field strength. It has been found that bimodal magnetic elastomers with nonmagnetic particles exhibit giant increase in elastic modulus [14]. Therefore, bimodal magnetic elastomers would be suitable for materials of magnetically tunable vibration driven by weak magnetic fields.
Figure 3b depicts the relationship between the transmissibility and plasticizer content for polyurethane and magnetic elastomers. Magnetic elastomers demonstrated a clear decrease in the transmissibility with increasing the plasticizer content, while polyurethane elastomers exhibited weak dependency compared to magnetic elastomers. There was large difference in the transmissibility between magnetic elastomer and polyurethane elastomer at high plasticizer contents, which is opposite to the behavior of natural frequency shown in Figure 3a.
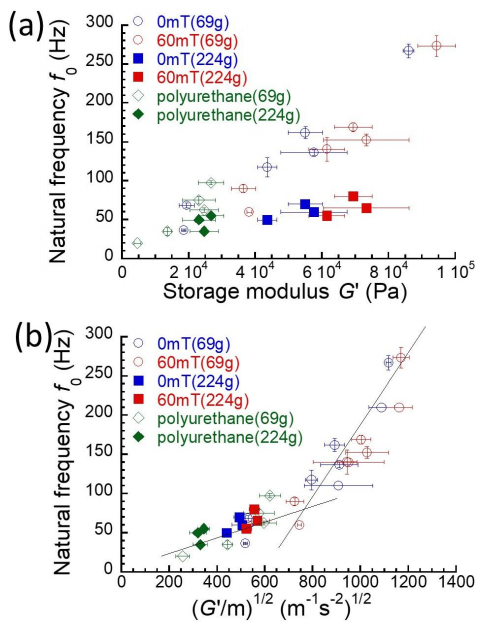
Figure 4a exhibits the relationship between the natural frequency and storage modulus for polyurethane and magnetic elastomers with various plasticizer contents, under different two loads. Under a load of 69 g, the natural frequency for magnetic elastomers increased with the storage modulus independently of the magnetic field. Similarly, the natural frequency for polyurethane elastomers increased with the storage modulus. However, the natural frequency under a load of 224 g for both magnetic and polyurethane elastomers distributed at low frequency region.
Figure 4b shows the relationship between the natural frequency and (G'/m)1/2 for polyurethane and magnetic elastomers with various plasticizer contents. If the vibration observed here is a simple harmonic motion, the natural frequency relates to the elastic modulus G' and mass m as the following relation,
As seen in the plot, the natural frequencies for all elastomers were explained by Eq 3, independently of the loading weight, however, a crossover was observed at around 750 N1/2m–1kg–1/2. This means that the natural frequency is strongly influenced by the viscous component such as loss modulus G" at frequencies below approximately 70 Hz.
4. Conclusions
We investigated the effect of plasticizer content on the vibration absorbing properties for polyurethane and magnetic elastomers. A natural frequency was observed on the frequency spectra at frequencies below 300 Hz for both polyurethane and magnetic elastomers. It was found that the natural frequency depends on both the storage modulus and loading weight. A plot of natural frequency vs. (G'/m)1/2 revealed that the observed vibration can be basically explained by a simple harmonic motion. However, at frequencies below ~70 Hz, it was found that the influence of the viscous component on the natural frequency cannot be neglected. We also investigated the effect of a weak magnetic field on the natural frequency or transmissibility for magnetic elastomers. It was found that magnetic elastomers undergo a small shift in the natural frequency even by a weak magnetic field.
Acknowledgements
This research was partially supported by a grant from the Cooperative Research Program of "Network Joint Research Center for Materials and Devices" (No. 20161257) and TAKEUCHI Scholarship Foundation (No.160005), The UNION TOOL Foundation.
Conflict of interests
The authors declare that there is no conflict of interests.










 DownLoad:
DownLoad: