Emotion, emotion regulation and sleep: An intimate relationship

1.   Introduction

Many physical systems of interest can be described by evolutionary games on graphs within the more general framework of dynamical systems on complex networks ^[2]. For example, opinion dynamics under social network influence ^[3], spread of contagious diseases subject to competition and selection ^[4,5,6], crime dynamics ^[7], bacterial networks ^[8], multi-agent decision-making dynamics ^[9,10], and the emergence of cooperation in networked populations ^{[11,12,13,14,15,16,17,18]}. Among the different interaction mechanisms, the simplest ones can be modeled as two-strategy games ^[19,20,21]. Differently from the standard approaches presented in ^{[11,14,16,17,18]}, where the interactions among players are described as discrete time stochastic processes, the evolutionary games equation on networks (EGN) proposed in ^[1], is a system of ordinary differential equations. More specifically, each of them takes the form of a replicator equation ^[19], ruling the dynamics of any single player in a population of $ N $ individuals arranged on a network, while other standard approaches ^[12,13,15] consider the average dynamics of the whole population. Recently, model reduction and symmetries have been investigated by using the concept of lumpability of graphs ^[22].

Similarly to the standard case, the replicator equation on networks possesses different kinds of steady states: mixed steady states that belong to the interior of the simplex (all players play all strategies with the probability in (0, 1)), pure steady states for which all entries belong to the border of the simplex (all players play all strategies with probability $ 0 $ or $ 1 $), and pure/mixed steady states (where some players play a pure strategy and others play a mixed one. Mixed steady states, hereafter called internal steady states, are particularly important in the EGN because they represent situations where a player assumes hybrid decisions corresponding to partially agree to all available strategies. This includes the case for which some of the strategies are strongly preferred to the others, for example the probability to choose a given strategy can be very close to $ 1 $, although different. As a consequence, the probability to choose all the other strategies will be very close to $ 0 $ since the sum of all strategy components for each player equals $ 1 $. Internal steady states are the most reasonable states for which a group of individuals can be able to agree on a compromised decision.

Moreover, the importance of the internal states mentioned above lies on the fact that they represent situations where different subpopulations may coexist. Thus, studying the attractiveness of these states is connected to the possibility that subetaoups of the players eventually coexist in an asymptotically stable manner ^[1,19,20]. On the contrary, oscillations making the dynamics more interesting will be produced only if we have unstable internal steady states ^[23].

In this paper, we study the feasibility of internal steady states in the EGN proposed in ^[1], by considering different situations, such as, for example, the presence of self-connections in the network. This is particularly relevant for social applications, since self-loops describe well how a player is able to interact also with himself, thus modeling positive or negative feedback on player decisions. We find necessary conditions for the feasibility of internal steady states of EGN. We distinguish the cases of dominant, coordination and anti-coordination payoff matrices of the underlying games. Moreover, we prove sufficient conditions for the feasibility of internal steady states when the graph is complete. Existence and feasibility of internal steady states are relevant for solving control and consensus problems. Controlling dynamical systems over networks in order to drive a population of agents towards a specific steady state has been widely studied ^{[24,25,26,27]}, while the presence of adaptive networks has been tackled in ^[28,29].

In ^[30], the authors developed a new notion: equilibrium interdependence of agents. This investigates how the changes in the parameters impact the equilibrium of the system and how they influence the strategy of other players. In the same direction, we propose a similar approach, where after analyzing the effect of changing some model parameters, we also investigate the effect of modifying the connectivity of players. Therefore, in this work, we prove results concerning how the dynamics of the whole system is influenced by varying the network connectivity of a single node. The problem under investigation connects with the diffusion centrality issue ^[31], whereby the role of the central individuals in a social network is analyzed by observing indirect information flow.

Finally, the effect of link removal from central players is studied theoretically for graphs with no self-edges, while numerical results are proposed to investigate the case of graphs with self-edges. Including self-edges in the model proposed in ^[1] is very promising to study the stability of internal steady states ^[32]. Indeed, it has been shown that stability of certain internal steady states is not possible for graph with no self-edges. Thus, the stability strongly depends on the strength of self-connections as well as on graph topology.

The paper is organized as follows. In Section 2 we illustrate the basics of evolutionary games on networks and in particular on two-strategy game for graphs including self-loops. Section 3 states the necessary conditions for the existence of internal steady states. Some numerical results are provided to analyze the existence of mixed steady states for a generic and heterogeneous scenario. Then, in Section 4 we present sufficient conditions in the case of complete graphs. In Section 5 we tackle the problem of link removal from a player by providing theoretical results for the case of no self-loops, and numerical experiments for the case with self-loops. Finally, in Section 6 we state some conclusions and suggest future developments.

2.   Preliminaries

We start by considering the evolutionary game equation on a network (EGN) introduced in ^[1]:

where $ s $ belongs to a set of strategies $ S = \{1, 2, \ldots, M\} $, $ v $ belongs to a set of vertices $ V = \{1, 2, \ldots, N\} $ and $ x_{v, s} $ is the probability that vertex $ v $ chooses strategy $ s $, $ p^{G}_{v, s} $ is a Von-Neumann Morgenstern utility payoff of player $ v $ using pure strategy $ s $, and $ \phi^G_v $ is the average payoff over the set of strategies available to vertex $ v $.

In this paper we consider a generalization of the model where $ p^{G}_{v, s} $ and $ \phi^G_v $ are both defined by means of player-to-player payoff matrices $ B_{v, u} \in \mathbb{R}^{M \times M} $, such that $ B_{v, u} $ is the payoff matrix used by player $ v $ against player $ u $. As a consequence, the model presented in ^[1] coincides with the special case, whereby $ B_{v, u} = B_{v}, \; \forall u, v \in V $. As usual, $ p^{G}_{v, s} $ and $ \phi^G_v $ depend on the graph $ G $, which in turn is defined by means of an $ N \times N $ adjacency matrix $ A = (a_{v, u}) \in \mathbb{R}^{N \times N}_{\geq 0} $ with $ {(v, u) \in V^{2}} $. More precisely,

and

where $ {\bf e}_{s} $ is the $ s $-th canonical-basis vector of $ \mathbb{R}^{M} $ and $ {\bf x}_{v} = [x_{v, 1} \; x_{v, 2} \; \ldots \; x_{v, M}]^{T} $ is the distribution of pure strategies of player $ v $.

Moreover, we consider graphs with self-loops, i.e., $ a_{v, v} \geq 0 $. In this regard, it is straightforward to consider also self-games described by payoff matrices $ B_{v, v} $, where a player $ v $ plays against itself. For convenience, we define the degree of a node as $ \text{deg}\left({v}\right) = \sum_{u = 1}^{N}a_{v, u} $. Since we are only concerned with graphs without isolated vertices, then $ \sum_{u = 1, u \neq v}^{N}a_{v, u} = \text{deg}\left({v}\right) - a_{v, v} > 0 $. Hence, $ \delta_{v} = {a_{v, v}}/{\text{deg}\left({v}\right)} $, which is the relative self-connectivity (i.e., how strong is the self-connection with respect to the sum of all connection weights) is such that $ 0 \leq \delta_{v} < 1 $.

Since for every $ v $ the constraint $ x_{v, 1}+ x_{v, 2}+\ldots +x_{v, M} = 1 $ holds, we have that for $ M $ strategies and $ N $ vertices the EGN leads to a system with $ N(M-1) $ ordinary differential equations. Furthermore, in this article we analyze the EGN equation for two-strategy games ($ M = 2 $). Therefore, for convenience, we drop the second index $ s $ of $ x_{v, s} $, introducing the variable $ y_{v} = x_{v, 1} $, whereas $ x_{v, 2} = 1 - y_{v} $. Thus, in our case the EGN becomes a system of $ N $ ODEs:

Equation (2.2) can be rewritten in a more convenient way as follows: let $ b^{v, u}_{s, r} $ be the payoff of player $ v $ against $ u $ when they use strategies $ s $ and $ r $, respectively. Then, the payoff function for vertex $ v $ against $ u $ can be defined by means of the payoff matrix:

We denote by $ \sigma^r_{v, u} = (-1)^{r+1}(b_{v, u}^{1, r}-b_{v, u}^{2, r}) $ the payoff difference of player $ v $ when $ u $ uses strategy $ r $. The sign of parameters $ \sigma $ is associated with the game characteristics:

● if $ \sigma^1_{v, u} > 0 $ and $ \sigma^2_{v, u} > 0 $, then $ v $ is playing a coordination game against $ u $. A prototypical example of this kind of games is the Stag Hunt game.

● if $ \sigma^1_{v, u} < 0 $ and $ \sigma^2_{v, u} < 0 $, then $ v $ is playing an anti-coordination game against $ u $. A prototypical example of this kind of games is the Chicken game.

● if $ \sigma^1_{v, u} < 0 $ and $ \sigma^2_{v, u} > 0 $, or $ \sigma^1_{v, u} > 0 $ and $ \sigma^2_{v, u} < 0 $, then $ v $ is playing a dominant game against $ u $. A prototypical example of this kind of games for which $ \sigma^1_{v, u} < 0 $ and $ \sigma^2_{v, u} > 0 $ is the well-known Prisoner's dilemma game.

According to ^[19], $ B_{v, u} $ can be equivalently rewritten as a diagonal matrix, namely

and Eq (2.2) reads as

where $ {\bf y} = (y_{1}, \ldots, y_{N})^{\top} $, $ f_{v}({\bf y}) = \sum_{u = 1}^{N} a_{v, u}f_{v, u}(y_{u}) $ and $ f_{v, u}(y_{u}) = y_{u}\text{Tr}\left({B_{v, u}}\right) - \sigma_{v, u}^{2} $, where $ \text{Tr}\left({B_{v, u}}\right) $ is the trace of matrix $ B_{v, u} $. Steady states of (2.5) are very important solutions because they influence significantly the asymptotic dynamics of the system. Moreover, they can be related to the Nash equilibria of the game described by the payoff matrix of Eq (2.4). Nash equilibria represent a cornerstone of game theory, since they correspond to strategies such that no player has any incentive to change his or her own strategy. The relationship between steady states and Nash equilibria will be clarified later in the paper.

A solution $ \bf{y^*} $ of the EGN is a steady state if, and only if, for all $ v $, $ y_v = 0 $, or $ y_v = 1 $, or $ f_v({\bf y^{*}}) = 0 $. But,

or equivalently

where $ \Sigma^{1} $ and $ \Sigma^{2} $ are matrices with $ \Sigma^{1}_{v, u} = \sigma_{v, u}^{1} $, $ \Sigma^{2}_{v, u} = \sigma_{v, u}^{2} $, $ A $ is the adjacency matrix, $ \bf 1 $ is the $ N $ dimensional vector with one in every entry, and $ \circ $ denotes the Hadamard product defined as $ P \circ Q = R $ where $ R = \{r_{i, j}\} : = \{p_{i, j}q_{i, j}\} $, provided that matrices $ P $ and $ Q $ have the same dimension.

Our goal is to study how the connectivity of the graph and the presence of self-loops impact the existence of an internal steady state. From ^[1] we know that if all players have the same payoff matrix and there are no self-loops, then the topology does not matter. We will start by looking at theoretical results on the existence of mixed equilibrium for more general cases than those studied in ^[1].

3.   Existence of the internal mixed equilibrium

If $ \bf{y^{*}} $ satisfies Eq (2.6), then it is a steady state for the ODE system (2.5). Whenever $ [(\Sigma^{1}+\Sigma^{2}) \circ A] $ is invertible, then we have a unique solution:

A steady state $ \bf{y^{*}} $ satisfying (2.6) is feasible if, and only if, $ y^{*}_{v} \in [0, 1], \; \forall v \in V $. A feasible steady state $ \bf{y^{*}} $ is pure if $ y_{v}^{*} \in \{0, 1\}^{N}, \; \forall v \in V $. A feasible steady state $ \bf{y^{*}} $ is said to be internal or mixed if, and only if, $ y^{*}_{v} \in (0, 1), \; \forall v \in V $. Finally, a feasible steady state is non pure if its components belong to both sets $ (0, 1) $ and $ \{0, 1\} $. We can relate steady states of EGN to Nash equilibria of the underlying game described by the payoff matrices (2.3). Indeed, in two-strategy games, if $ \bf{y^{*}} $ is a feasible internal steady state, then it is also a Nash equilibrium of the underlying static game ^[19].

However, it is not enough to guarantee the solvability of Eq (2.6) in order for the mixed steady states to exist, because we also need that the solutions of the linear equations (2.6) to belong to the interior of the hypercube $ {\Delta_{S}} = \{y \in \mathbb{R}^N: 0\leq y_i\leq 1 \mbox{, } \forall i \in V\} $. We start by giving necessary conditions on the values of the $ \sigma $s in order for the mixed steady states to be feasible.

Suppose that for every game, the payoff matrix that player $ v $ uses when it plays with his neighbors is equal for every opponent. In other words, $ \forall v \in V, B_{v, u} = B_{v} = \text{diag}(\sigma_{v, 1}, \sigma_{v, 2}), \; \forall u \neq v $. In contradistinction, the self-game of player $ v $ is represented by the matrix $B_{v, v}=B_{v}^{\circlearrowleft}=\operatorname{diag}\left(\sigma_{v, 1}^{\circlearrowleft}, \sigma_{v, 2}^{\circlearrowleft}\right)$. Now let us define $ \beta_v $ and $ \gamma_v $ as follows:

where $ T_{v} = \text{Tr}\left({B_{v}}\right) $ and $T_{v}^{\circlearrowleft}=\operatorname{Tr}\left(B_{v}^{\circlearrowleft}\right)$. Note that, if $ T_v = 0 $ for some $ v $, then either player $ v $ has a dominant strategy or it is indifferent to any strategy. In the case he has a dominant strategy, no internal equilibria can be obtained. In the case the player is indifferent, then he will always play the same strategy that he used at the beginning of the game; therefore, in order to look for an internal equilibrium, we could consider the network game without this player. We define $ d_{v} = \frac{\sigma_{v, 2}}{T_{v}} $ and $d_{v}^{\circlearrowleft}=\frac{\sigma_{v, 2}^{\circlearrowleft}}{T_{v}^{\circlearrowleft}}=\frac{\gamma_{v} \sigma_{v, 2}}{\beta_{v} T_{v}}=\frac{\gamma_{v}}{\beta_{v}} d_{v}$. The following theoretical result holds.

Proposition 3.1. Suppose that the adjacency matrix $ A $ is non-negative ($ A \in \mathbb{R}_{\geq 0}^{N \times N} $) and that each node has at least one neighbor. Moreover, suppose that $ T_{v} \neq 0 $. If $ \bf{y^{*}} $ is a mixed steady state, then for any $ v \in V $:

Proof. Let $ [A{\bf y}^{*}]_{v} $ and $ [A\boldsymbol{1}]_{v} $ be the $ v $-th component of the vector $ A {\bf y}^{*} $ and $ A\boldsymbol{1} $, respectively.

Since each node has at least one neighbor, then $ \text{deg}\left({v}\right) > 0, \; \forall v \in V $. Therefore,

Furthermore,

This implies that $ 0 < [A{\bf{y^{*}}}]_{v} < \text{deg}\left({v}\right) $, and hence

From Eq (2.6), we know that

$ \forall v \in V $. If $ a_{v, v} = 0 $ then

If $ a_{v, v} \neq 0 $, then dividing both sides of Eq (3.3) by $ \text{deg}\left({v}\right)T_v $, we have:

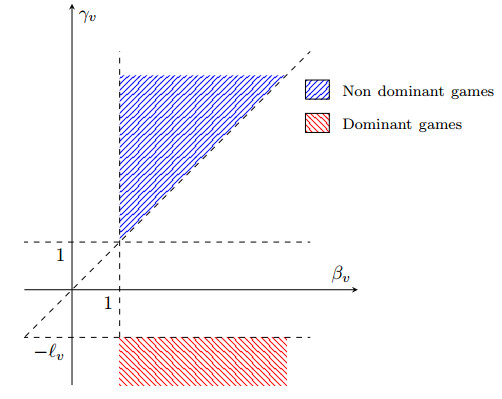
This result represents a necessary condition for having an internal steady state $ \bf{y^{*}} $. The condition depends on the game played, represented by the parameter $ d_{v} $, and on the self-loop, ruled by the parameters $ \delta_{v} $, $ \beta_{v} $ and $ \gamma_{v} $. If we know the components of $ \bf{y^{*}} $, no such condition is needed. However, the proposition allows us to prove the interesting corollary below. This result will give us a truly necessary condition for having an internal steady state in the cases where we have coordination and anti-coordination payoff matrices. It is also interesting to note that, if $ \delta_{v} = 0 $ (i.e., no self-loops), then we have that $ d_{v} \in (0, 1) $, recovering the results of ^[1] for the uniform payoff case. In this sense, the results in the previous theorem are an extension of the results presented in ^[1].

Corollary 3.1. Suppose that $ \bf{y^{*}} $ is a mixed steady state. Let $ \ell_{v} = \mathit{\text{deg}}\left({v}\right)-a_{v, v} $ be the $ v $-th element of the Laplacian matrix of the graph, i.e., $ L = \mathit{\text{diag}}(\mathit{\text{deg}}\left({v}\right)_{v \in V}) - A $. For each $ v $, then:

(a) $ $if $ \delta_v = 0 $, then $ B_{v} $ represents a coordination game if $ T_{v} > 0 $ or an anti-coordination game if $ T_{v} < 0 $;

(b) if $ \delta_v > 0 $ and $ 1 < \beta_{v} < \gamma_{v} $, then $ B_{v} $ represents a coordination game if $ T_{v} > 0 $ or an anti-coordination game if $ T_{v} < 0 $;

(c) if $ \delta_v > 0 $, $ \beta_{v} > 1 $ and $ \gamma_{v} < -\ell_{v} $, then the pure strategy $ y_{v}^{*} = 1 $ is dominant for the game represented by $ B_{v} $ if $ T_{v} > 0 $, or the pure strategy $ y_{v}^{*} = 0 $ is dominant for the game represented by $ B_{v} $ if $ T_{v} < 0 $.

Proof.

● Proof of (a)

If $ \delta_v = 0 $ then $ a_{v, v} = 0 $, by the previous proposition we have that $ d_v \in (0, 1) $, then if $ T_{v} > 0 $, then $ B_{v} $ represents a coordination game, while for $ T_{v} < 0 $ we have an anti-coordination game.

For the cases with $ \delta_v > 0 $, firstly, notice that

Moreover, since $ \delta_{v} > 0 \Rightarrow a_{v, v} = 1 $, then:

Secondly, if $ \beta_{v} > 1 $, then $ \delta_{v}(\beta_{v}-1) > 0 $. Furthermore:

and

yielding that

● Proof of (b)

If $ 1 < \beta_{v} < \gamma_{v} $, then $ 1+\delta_{v}(\gamma_{v}-1) > 0 $ and

Since $ \gamma_v > \beta_v $ then $ 1 + \delta_{v}(\gamma_{v}-1) > 1 + \delta_{v}(\beta_{v}-1) $, which implies $ d_v \in (0, 1) $ and the conclusion follows.

● Proof of (c)

$ \beta_{v} > 1 $ and $ \gamma_{v} < -\ell_{v} $, then $ \frac{1+\delta_{v}(\beta_{v}-1)}{1+\delta_{v}(\gamma_{v}-1)} < 0 $ and

It turns out that $ d_{v} $ is a negative number and hence $ \sigma_{v, 1} $ and $ \sigma_{v, 2} $ have different signs. In particular, if $ T_{v} > 0 $, then $ \sigma_{v, 2} < 0 $ and $ 0 < |\sigma_{v, 2}| < \sigma_{v, 1} $, while $ T_{v} < 0 $ implies that $ \sigma_{v, 1} < 0 $ and $ 0 < |\sigma_{v, 1}| < \sigma_{v, 2} $. In the former case, $ B_{v} $ represents a game with the pure strategy $ y = 1 $ dominant; instead for the latter case the pure strategy $ y = 0 $ is dominant.

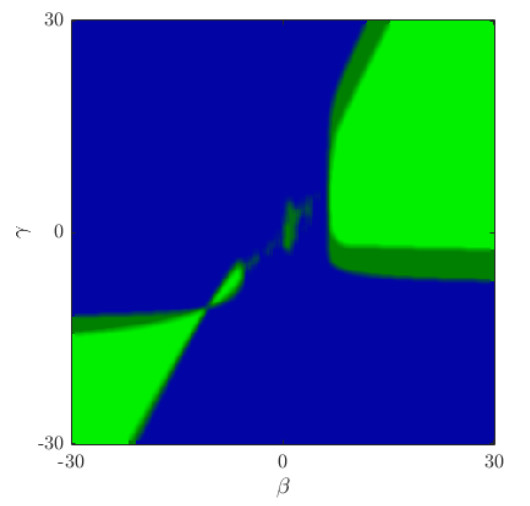
The results of Corollary 3.1 are depicted in Figure 1 for a generic player $ v $. We report the regions were an internal steady state is feasible. Blue and red colors indicates the areas where it is necessary a non-dominant game (bistable or coexistent) and a dominant game, respectively.

3.1.   Numerical results

Proposition 1 and Corollary 3.1 relate the existence of the internal steady state with the connectivity of each player $ v $, i.e., $ \delta_{v} $, the strength of its self-games, i.e., $ \beta_{v} $ and $ \gamma_{v} $, and the game itself. However, these results only provide necessary conditions for the existence of internal mixed steady states.

While sufficient conditions that work for particular graph structures will be proven in the next sections, here we show a numerical example using an Erdös-Rényi graph sample with $ N = 150 $ nodes and average degree $ 10 $. We assume that $ a_{v, v} = 1 $ for all $ v \in V $, i.e., each player has a self-loop. For this numerical example, we divide the nodes into six groups of $ 25 $ elements each. For each group, we choose the parameters $ \sigma_{v, 1} $ and $ \sigma_{v, 2} $ in the set $ \{(1, 1), (0.9, 1), (1, 0.9), (-1, -1), (-0.9, -1), (-1, -0.9)\} $. In this way, half of the nodes have a coordination game payoff matrix, while the other half play anti-coordination games. We also assume that $ \beta_{v} = \beta $ and $ \gamma_{v} = \gamma $ for all the players. Then, for each couple of values $ \beta $ and $ \gamma $ in the set $ [-30, 30] \times [-30, 30] $, we evaluated the solution $ {\bf y^{*}} $ of Eq (3.1). In Figure 2 we report in blue the couples $ (\beta, \gamma) $ for which Eq (3.1) has no solution, or if the solution cannot be classified as an internal steady state (i.e., $ y^{*}_{v} \not\in (0, 1) \; \forall v $). Instead, if the solution $ {\bf y^{*}} $ is internal, then the couple $ (\beta, \gamma $) is depicted in light green. Finally, in dark green we report the non internal steady states that anyway satisfy the condition of Proposition 1. We remark that light and dark green areas refer to the points $ (\beta, \gamma) $ which satisfy the condition of Proposition 1 for all the players.

4.   Feasibility of mixed steady states for complete graphs

In this section we report some theoretical results on the feasibility of mixed steady states for complete graphs. In order to study how connectivity plays a role on the existence of steady states, we start our study with the most connected graph: the complete one. Our result shows that the presence of many connections in the graph implies that the payoff matrices of the players should be very similar in order for the system to be able to have an internal steady state.

4.1.   Feasibility of mixed steady states with self-edges

Consider a complete undirected and unweighted graph of $ N $ nodes with self-edges. Then, the adjacency matrix $ A $ is equal to $ {\bf 1}_{N \times N} $. Moreover, we consider that the self-game strengths are given by $ \beta_{v} = \beta $ and $ \gamma_{v} = \gamma $ for all players. In this case, we get that $ (\Sigma^{1}+\Sigma^{2}) \circ A = \text{diag}(T_{v}) A_{\beta} $ and $ \Sigma^{2} \circ A = \text{diag}(\sigma_{v, 2}) A_{\gamma} $ where $ A_{\beta} = {\bf 1}_{N \times N} + (\beta-1) I_{N \times N} $ and $ A_{\gamma} = {\bf 1}_{N \times N} + (\gamma-1) I_{N \times N} $.

Lemma 4.1. Let $ N \in \mathbb{N}^+ $. If $ \beta \neq 1 $ and $ \beta \neq 1-N $, then $ A_{\beta} $ is invertible and its inverse is given by $ A_{\beta}^{-1} = [q_{v, u}] $ where

The proof of this lemma is a direct consequence of the remark that $ A_{\beta} $ is a circulant matrix.

To ease the discussion of the upcoming results, we introduce the average of a vector over a set of indices $ \Psi $, $ \langle {\bf x}\rangle_{\Psi} = \frac{1}{|\Psi|}\sum_{v \in \Psi}x_{v}, $ where $ |\Psi| $ is the cardinality of the set.

Theorem 4.2. Let $ A $, with $ N \geq 3 $ vertices, be the adjacency matrix of a complete graph with self-edges. If $ T_{v} \neq 0 $ and $ \beta_{v} = \beta \not\in \{1, 1-N\} $ for all $ v \in V $, then there is at most one non-pure steady-state $ {\bf y^*} $ for the system of ODEs in Eq (2.5) and $ \langle{\bf y^{*}}\rangle_{V} = \frac{\gamma+N-1}{\beta+N-1} \langle{\bf d}\rangle_{V} $. Moreover, $ {\bf y^*} $ is an internal steady-state if, and only if, for all $ v \in V $:

If $ \mathit{\text{sign}}\left({ \gamma+N-1}\right) = \mathit{\text{sign}}\left({\beta-1}\right) $, then:

If $ \mathit{\text{sign}}\left({ \gamma+N-1}\right)\neq\mathit{\text{sign}}\left({\beta-1}\right) $, then:

Remark 4.3. For the case $ N = 2 $, it is easy to check that $ {\bf y^*} $ is feasible if, and only if, $ 0 < d_{v} < 1 $ for $ v = 1, 2 $.

Proof. For $ \beta \not\in\{1, 1-N\} $ and $ \sigma_{v, 1}+ \sigma_{v, 2} \neq 0 $ we have that $ (\Sigma^{1}+\Sigma^{2}) \circ A $ is invertible. Then, Eq (3.1) becomes:

where $ D = \text{diag}(T_{v})^{-1}\text{diag}(\sigma_{v, 2}) = \text{diag}(d_{v}) $ is a diagonal matrix.

In this case, the components of the steady state in Eq (4.3) are defined as follows:

while the average of all the components of $ {\bf y^{*}} $ is:

Since each component $ y_{v}^{*} $ is in the set $ (0, 1) $, then:

If $ \text{sign}\left({ \gamma+N-1}\right) = \text{sign}\left({\beta-1}\right) $, then:

On the other hand, if $ \text{sign}\left({ \gamma+N-1}\right)\neq\text{sign}\left({\beta-1}\right) $, then:

Corollary 4.4. Under the assumptions of Theorem 4.2, if $ d_v = d $ for all $ v \in V $, then $ {\bf y^*} $ is internal to the simplex if, and only if,

The proof of the corollary is straightforward by plugging $ d_v = \langle{\bf d}\rangle_{V} $ in (4.1) or (4.2).

4.2.   Feasibility of mixed steady states with no self-edges

In the following theorems we discuss the feasibility of internal steady states for complete graphs with no self-edges. In this case Theorem 4.2 simplifies as follows.

Theorem 4.5. Let $ A $, with $ N \geq 3 $ vertices, be the adjacency matrix of a complete graph with no self-edges. If $ T_{v} \neq 0, \; \forall v \in V $, then there is at most one non-pure steady-state $ {\bf y^*} $ for the system of ODEs in Eq (2.5) and $ \langle{\bf y^{*}}\rangle_{V} = \langle{\bf d}\rangle_{V} $. Moreover, $ {\bf y^*} $ is an internal steady-state if, and only if,

Corollary 4.6. Under the assumptions of Theorem 4.2, if $ {\bf y^*} $ is an internal steady-state then:

Proof. From (4.4), we have that:

Since $ {\bf y^{*}} $ is an internal steady state and $ T_{v} \neq 0 $, then by Theorem (4.2), $ d_{v} \in (0, 1) $, since $ \beta_v = \gamma_v = 0 $. Therefore,

which is the statement of the corollary.

The Corollary 4.6 provides a necessary condition for the system (2.5) to have an internal steady state. If for any vertex $ v $, the distance of $ d_{v} $ to the average $ \langle{\bf d}\rangle_{V} $ is greater than or equal to $ \frac{1}{N-1} $, then the system can only have pure steady states. We can also see that if $ N $ is large, then we may only have internal steady states whose components $ d_v $s are very close, i.e., in a complete graph, the system can only have internal steady states if the payoff's ratio of every player $ d_v $, does not get more than $ \frac{1}{N-1} $ distant from the average of all payoff's ratios. For a large system, this will require similar payoffs for all players.

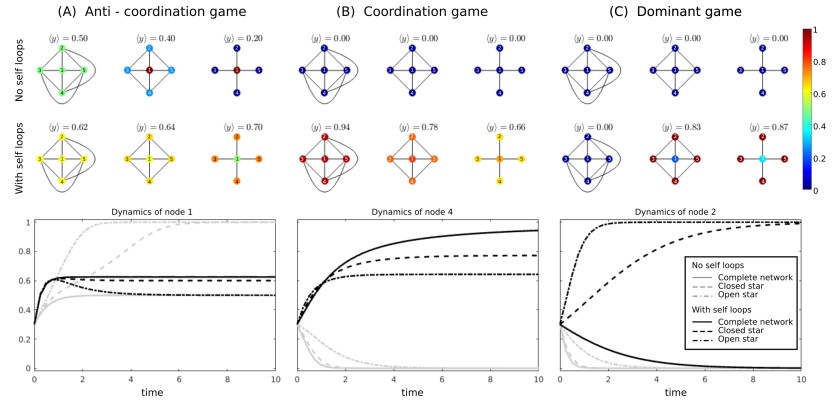
It is worthwhile to note that the results presented in Sections 3 and 4 highlight a strong dependence of the internal steady state on the connectivity of the network and on self-loops. The numerical experiments reported in Figure 3 show that the steady states reached by a population playing different game typologies without (first row) and with (second row) self-loops, may change significantly according to the network connectivity. The detail of the dynamics of a specific node is also reported (third row). In subplot $ (A) $, individuals play anti-coordination games, with $ \sigma_{v, 1} = \sigma_{v, 2} = -1 $ for all $ v $. For the case with self-loops, we set $ \beta_{v} = 4 $ and $ \gamma_{v} = 6 $ for all $ v $. In subplot $ (B) $, individuals play coordination games, with $ \sigma_{v, 1} = \sigma_{v, 2} = 1 $ for all $ v $. For the case with self-loops, we set $ \beta_{v} = -5 $ and $ \gamma_{v} = -6 $ for all $ v $. In subplot $ (C) $, individuals play coordination games, with $ \sigma_{v, 1} = -1 $ and $ \sigma_{v, 2} = 1.2 $ for all $ v $. For the case with self-loops, we set $ \beta_{v} = -2.5 $ and $ \gamma_{v} = -3.5 $ for all $ v $. Initial condition used for all experiments is $ x_{1}(0) = x_{2}(0) = x_{3}(0) = x_{4}(0) = x_{5}(0) = 0.3 $.

As a conclusive remark, while in ^[30] it has been shown that, generally, equilibrium agents are indifferent to small changes in games with two strategies, in our framework we show that modifications in the network structure, as well as the presence of self-loops, may produce significant changes in the dynamics of the system. This connects to Section 5, where the effect of link removal has been analyzed from both theoretical and numerical points of view.

5.   The effect of link removal

We now consider the following scenario: take a fully connected graph, choose one specific node and start deleting successively different links from this node. The general question under consideration is: what is the effect in the dynamics of such procedure? In general terms, such circle of ideas has attracted the attention of other researchers. For instance, in telecommunications and computer networks this corresponds to the so-called "bond percolation" process (see Section $ 16.1 $ of ^[33]). In Chapter $ 16 $ of ^[33], a comprehensive review of percolation and network resilience can be found. In contradistinction with such approach, we focus on one single node and analyze the resilience with respect to link removal in a deterministic fashion.

First, we study the effect of link removal from central player starting from a complete network. In particular, we report some theoretical results for the case of graphs with no self-edges $ (\beta_{v} = \gamma_{v} = 0, \forall v \in V) $. The case of networks including self-edges is then investigated by means of numerical simulations, showing that removing links can change dramatically the asymptotic behavior of the system, sometimes destroying the internal steady states.

5.1.   Theoretical results on games with no self-edges by removing links

Theorem 5.1. Let $ A $ be the adjacency matrix of a complete graph with $ N > 3 $ vertices and no self-edges. Assume that the connection between vertices $ v_0 $ and $ u_0 $ is removed and $ \Gamma = V \setminus \{v_{0}, u_{0}\} $. Moreover, assume that $ \sigma_{v, 1}+ \sigma_{v, 2} \neq 0 $ for all $ v $. If an internal steady state $ {\bf y^{*}} $ exists, then following conditions hold

Proof. Without loss of generality, let us assume $ v_0 = 1 $, $ u_0 = 2 $. Writing Eq (2.6) as a system of linear equations, we get

If $ d_{1} \neq d_{2} $ then the first two equations would be incompatible, therefore $ d_{1} = d_{2} $. In this case, the system has infinite solutions with $ y_1 $ and $ y_2 $ as free variables. Let $ z = y_1+y_2 $ and assume $ d_{1} = d_{2} $, then the system with $ N $ equations can be reduced to a system with $ N-1 $ equations

This system has only one solution given by:

If the solution is in the simplex, then for all $ v \in \Gamma $, it is true that $ 0 < z^{*} < 2 $ and $ 0 < y_{v}^{*} < 1 $. This implies that ⅰ) and ⅱ) must hold.

Suppose now that we start from an almost complete graph and iteratively remove additional links from the same vertex $ v_0 $. Let $ \Lambda = \{v_1, v_2, \dots, v_{M-1} \} $ be the set of vertices that have been disconnected from vertex $ v_0 $ and $ \Gamma = V \backslash \big(\Lambda \cup \{v_0\}\big) $ the set of vertex that is still connected to $ v_0 $.

Theorem 5.2. Let $ A $, with $ N > 3 $ vertices, be the adjacency matrix of a complete graph where $ K-1 $ vertices have been disconnected from vertex $ v_0 $. Let $ \Lambda $ be the set of disconnected vertices and $ \Gamma $ the remaining set of connected vertices. Moreover, let us assume that $ \sigma_{v, 1}+ \sigma_{v, 2} \neq 0 $ for all $ v \in V $. Then, there exists an internal steady state, if, and only if, all the following conditions hold:

i) $ (K-1) \langle{\bf d}\rangle_{\Lambda} -\frac{(N-1)(K-2)}{(N-2)}\langle{\bf d}\rangle_{\Gamma} < d_{v_0} < (K-1) \langle{\bf d}\rangle_{\Lambda} -\frac{(N-1)(K-2)}{(N-2)}\langle{\bf d}\rangle_{\Gamma} +\frac{K-2}{N-2}, $

ii) $ -1- \frac{N-K}{K-2}d_{v_0} + \frac{(N-2)(K-1)}{K-2}\langle{\bf d}\rangle_{\Lambda} < (N-2)d_{v} < - \frac{N-K}{K-2}d_{v_0} + \frac{(N-2)(K-1)}{K-2}\langle{\bf d}\rangle_{\Lambda}, \; \forall v \in \Lambda, $

iii) $ -1 +d_{v_0}+(N-1) \langle{\bf d}\rangle_{\Gamma} < (N-1)d_{v} < d_{v_0}+(N-1) \langle{\bf d}\rangle_{\Gamma}, \; \forall v \in \Gamma. $

Proof. Let us assume without loss of generality that $ \Lambda = \{2, 3, \cdots, K\} $. Then, $ A = (a_{v, u})_{N \times N} $ where

The matrix $ A $ is invertible for all $ N > 2 $ and its inverse is given by the block matrix

where

In the above formulas, $ I_{i} $ is the $ i $-dimensional identity matrix, and $ \boldsymbol{0}_{i \times j} $ and $ \boldsymbol{1}_{i \times j} $ are the $ i \times j $ matrices of all $ 0 $ and $ 1 $ entries, respectively.

By Eq (3.1), the steady state can be expressed as

The result thus follows from the fact the $ y_v^{*} \in (0, 1) $, for all $ v \in V $.

Remark 5.3 If $ d_{v} = d \in (0, 1) \, , \forall v \in V $, then we can show that inequalities i), ii) and iii) hold. Then, from Theorem 5.2, we have that the internal steady state exists. This is in agreement with the conclusions obtained by Theorem $ 1 $ in ^[1].

5.2.   Simulation results on games with self-edges by removing links

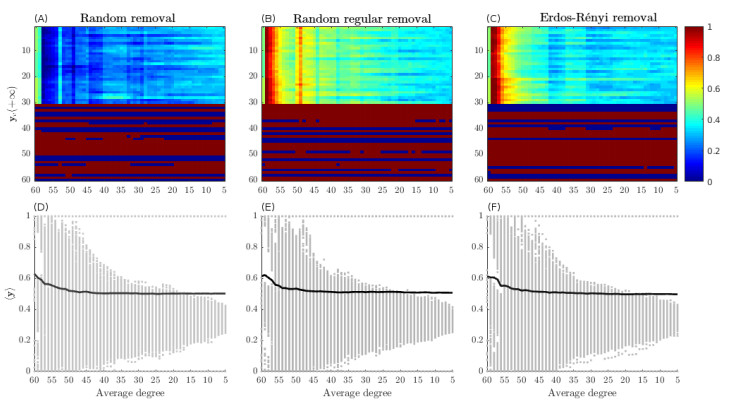
In the following, we report some numerical results on the effect of link removal in networks with self-edges. In order to study the link removal from networks including self-edges we develop a numerical experiment employing random graphs with $ 60 $ nodes. Starting from the complete graph, we use $ 3 $ different removal strategies to produce different graphs whose average degree is $ \overline{k} \in \{60, 59, 58, \ldots, 6, 5\} $, thus obtaining a sequence of $ 56 $ graphs with different degrees.

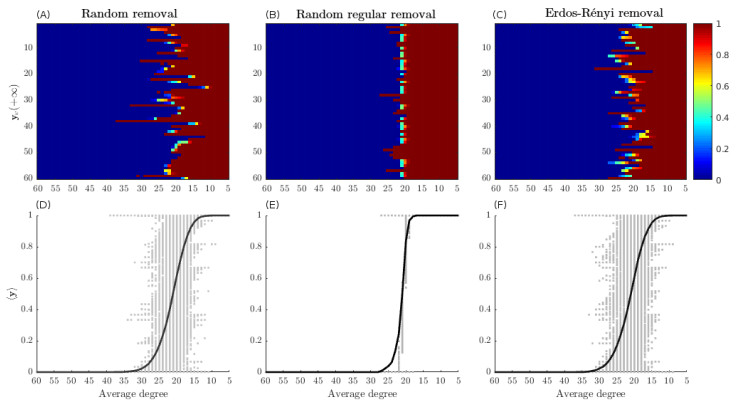
A comment concerning the different strategies for edge removal is in order. In the so-called random removal strategy, we start from a complete graph, and then we randomly remove $ 60 $ links, in order to obtain a new graph with an average degree of $ 59 $. In general, starting from a graph with average degree $ \overline{k} $, we remove $ 60 $ links in order to obtain a graph with average degree $ \overline{k}-1 $. The random regular removal strategy is similar to the random removal approach, but we remove exactly one link for each node, in order to obtain at each step a random regular graph (i.e., all nodes have the same degree). Finally, the Erdös-Rényi removal strategy consists of starting from an Erdös-Rényi graph sample with average degree $ \overline{k} $, then removing a certain amount of links in order to obtain an Erdös-Rényi graph sample with average degree $ \overline{k} $. An existing link remains with probability $ \frac{\overline{k}-1}{\overline{k}} $, otherwise, it is removed. In this way we are able to build Erdös-Rényi graph samples using a removal process. For each node we fix $ \beta_{v} = \gamma_{v} = -30 $. For this numerical example, we divide the nodes into six groups of $ 10 $ elements each. For each group, we choose the parameters $ \sigma_{v, 1} $ and $ \sigma_{v, 2} $ in the set $ \{(1, 1), (0.9, 1), (1, 0.9), (-1, -1), (-0.9, -1), (-1, -0.9)\} $. In this way, half on the nodes have a coordination game payoff matrix, while the other half play anti-coordination games. The three random removal strategies have been repeated $ 1000 $ times, thus obtaining $ 3 \cdot 56 \cdot 1000 = 168000 $ random graphs. For each of them, a random initial condition has been created (i.e., $ x_{v}(0) $ is a uniformly distributed random number in the set $ (0, 1) $). Thereafter, we let the solutions of the ODE (2.5) evolve towards a steady state. An example of the reached steady states is depicted in the subplots $ (A) $, $ (B) $ and $ (C) $ of Figure (4), where a colored point represents the value of the $ v $-th component of the steady state for a given graph whose average degree is reported in the abscissa. We notice that, for sparser graphs, the behavior of the bistable nodes (i.e., the first $ 30 $ nodes), becomes more regular, that is, it is easier for the whole population to reach the similar steady state of consensus as long as the neighbor's size decreases. For supporting this claim, in subplots $ (D) $, $ (E) $ and $ (F) $, we report with lines the average of the whole population steady states as a function of the average degree of the network for each link removal strategy. The lighter dots correspond to the steady states reached by members of the population over $ 1000 $ numerical experiments. The dots allow us to show that the variance of steady state decreases as the number of removed links increases. A similar numerical experiment has been performed for a population of players involved in a dominant game. More specifically, we assume that a prisoner's dilemma game, where strategies $ 1 $ and $ 2 $ stand for cooperation and defection, respectively, is simulated by means of the EGN Eq (2.5). For this numerical example, we divide the nodes into six groups of $ 10 $ elements each. For each group, we choose the parameters $ \sigma_{v, 1} $ and $ \sigma_{v, 2} $ in the set $ \{(-1, 1.1) $, $ (-1, 0.9) $, $ (-1.1, 1) $, $ (-1.1, 0.9) $, $ (-0.9, 1) $, $ (-0.9, 1.1)\} $. For each node we fix $ \beta_{v} = \gamma_{v} = -30 $. All the couples $ (\sigma_{v, 1}, \sigma_{v, 2}) $ represent games where strategy $ 2 $ is dominant, coherently with a prisoner's dilemma game. An example of the reached steady states is depicted in the subplots $ (A) $, $ (B) $ and $ (C) $ of Figure (5). The lines in subplots $ (D) $, $ (E) $ and $ (F) $ represent the average of the whole population steady states as a function of the average degree of the network for each link removal strategy. The lighter dots correspond to the steady states reached by members of the population over $ 1000 $ numerical experiments. Interestingly, this experiment shows that link removal policies, as well as the presence of self-loops, allow the system to converge toward strategy $ 1 $ for low connectivity, even though the original game is strategy $ 2 $ dominant. Moreover, this transition from a population of individuals all converging to strategy $ 2 $ to a population of individuals all converging to strategy $ 1 $ is sharper if the removal policy is random regular. This result may be useful for further studies investigating the interplay between cooperation and defection in a population of decision makers playing the prisoner's dilemma game. Indeed, Figure (5) shows that including the self-loop as well as removing links can drive individuals to reach some level of cooperation. As a final remark, we note that in ^[30] the authors conclude that changing the preference of one player usually will not lead a change in the system, which in fact depends on switching the number of strategies' players. We can see a similar effect for the link removal in Figure 5.

6.   Conclusions and future developments

In this paper, we study the relationship between network topology and self-loops in the Evolutionary Game Equation on Graphs. The mathematical form of this equation allows us to analyze separately the dynamics of any single individual, starting from his initial condition, which refers to his status in the beginning of the observation, to transient evolution of his strategy, until the asymptotic regime.

In this framework, we state some necessary results for the existence and feasibility of internal steady states. Necessary and sufficient conditions for the case of complete graphs have also been provided. In this scenario, we proved that we can only have a mixed steady state if all payoff matrices are almost similar in terms of the parameters $ d_v $ (i.e., these parameters must be sufficiently close to their average). In this respect, we also show that the larger the number of nodes of the network, the stronger the conditions for the mixed steady state to be feasible.

The investigation of the internal steady states conducted in this study is an attempt to solve a well-known problem related to games on networks, such as the cooperation in the prisoner's dilemma game from a different point of view. Specifically, the existence of mixed steady states is an alternative way of conceiving cooperation, moving from a discrete (a player cooperates or defects) to a continuous setup (a player can exhibit an intermediate level of cooperation). Then, we exploited the influence of varying the connectivity of the network by removing iteratively the edges of a single node. This link removal process has been studied starting from a complete network without and with self-loops. The former is developed through theoretical results, whereas the latter through numerical simulations. We showed that the effect of link removal may also favor the presence of mixed steady states, thus fostering the onset of a partial level of cooperation. The present research shows that self-loops and link removal have a deep impact on the steady states of each individual of a networked finite population, and consequently, on the whole dynamics. These two ingredients may be fruitfully used for control purposes: for instance, we showed that it is possible to control the dynamics of a population playing a dominant game like the prisoner's dilemma, driving individuals towards a more profitable strategy. Moreover, our approach shows that, although the individuals are involved in coordination and/or anti-coordination games, which naturally splits the population strategy, the presence of self-loops and the link removal may help to reduce the difference of these strategies, thus driving the population towards a consensus steady state.

A natural continuation of this research, which is presently under investigation by the authors, concerns the modification of the present model to account for the weak-selection limit, by preserving all the main peculiarities of the EGN equation. Similar investigations are under way concerning the effect of different network topologies, such as small world or scale-free networks, on the feasibility of the steady states of the EGN equation.

Acknowledgments

The research of Chiara Mocenni, Jean Carlo Moraes and Jorge P. Zubelli was supported by grant 313773/2013-0 of the Science without Borders Program of CNPq/Brazil. Jorge P. Zubelli was also supported by the CNPq under grant 307873 and by FAPERJ through the program Cientistas do Nosso Estado.

Conflict of interest

The authors do not have any conflict of interest.