Streamlining applications of integration by parts in teaching applied calculus

1.   Introduction

As is well known, in the practical application of neural networks (NNs), it is often necessary to use and design NN models with different dynamic characteristics for different application scenarios and purposes. Therefore, the study of the dynamic behavior of NNs has become an important issue that is widely concerned in both theoretical research and practical applications of NNs. Therefore, the dynamics of various types of NNs, especially numerous classical NNs such as recurrent NNs ^[1,2], bidirectional associative memory NNs ^[3], inertial NNs ^[4,5], Hopfield NNs ^[6], Cohen-Grossberg NNs ^[7], etc., have been widely studied. It should be mentioned here that due to the stronger approximation, faster convergence speed, larger storage capacity, and higher fault tolerance of high-order NNs compared to low-order NNs, the dynamics research of high-order NNs has received widespread attention ^{[8,9,10,11,12]}.

Meanwhile, owing to the fact that algebra-valued NNs, such as complex-valued ^[13,14], quaternion-valued ^{[15,16,17,18]}, Clifford-valued ^{[19,20,21,22,23]}, and octonion-valued NNs ^[24,25,26], are extensions of real-valued NNs and have more advantages than real-valued NNs in many application scenarios, research on the dynamics of algebra-valued NNs has gradually become a new hotspot in the field of NN research in recent years. It is worth mentioning here that the Clifford-valued high-order Hopfield fuzzy NN represents a sophisticated integration of Clifford algebra, high-order synaptic connections, and fuzzy logic, enabling it to achieve advanced applications in multidimensional data processing and complex system modeling. For example, it has applications in the fields of multidimensional signal processing, secure communication and image encryption, optimization and control systems, neuroscience, and cognitive modeling ^{[27,28,29,30]}.

On the one hand, from both theoretical and practical perspectives, NN models with time-varying connection weights and time-varying external inputs are more realistic than those with constant connection weights and constant external inputs. Meanwhile, time delay effects are inevitable. As a result, the rate of change in the state of a neuron depends not only on its current state but also on its historical state, and even more so, on the rate of change in its historical state. It is precisely for these reasons that researchers have proposed various neutral-type NN models with $D$ operators and conducted extensive research on their dynamics ^{[31,32,33,34]}. In addition, fuzzy logic and NNs complement each other: fuzzy systems provide interpretability and handle uncertainty, while NNs offer powerful learning from data. Their integration bridges the gap between data-driven machine learning and human-like reasoning, making systems more adaptable, transparent, and robust in real-world applications. Indeed, fuzzy NNs have been successfully applied in many fields such as signal processing, pattern recognition, associative memory, and image processing ^{[35,36,37,38,39]}.

On the other hand, as is well known, almost periodic oscillation is an important dynamic of NNs with time-varying connection weights and time-varying external inputs. In the past few decades, the almost periodic oscillations of various NNs have been studied by countless scholars ^{[23,31,33,34]}. We know that besides Bohr's concept of almost periodicity, there are also Stepanov almost periodicity, Weyl almost periodicity, Besicovitch almost periodicity, and so on ^[40]. It should be pointed out here that Besicovitch almost periodicity is the most complex almost periodicity among Bohr almost periodicity, Stepanov almost periodicity, and Weyl almost periodicity, and that Stepanov almost periodicity, Weyl almost periodicity, and Besicovitch almost periodicity are referred to as generalized almost periodicity. Meanwhile, it should be noted that the product of two generalized almost periodic functions in the same sense may not necessarily be a generalized almost periodic function in that sense. Because of this reason, the emergence of high-order terms in high-order NNs poses difficulties for studying the generalized almost periodic oscillations of high-order NNs. As a consequence, the results of generalized almost periodic oscillations for high-order NNs are still very rare. Thereupon, it is necessary to further study the generalized almost periodic oscillation problem of high-order NNs.

Inspired by the above observations, this paper considers a class of Clifford-valued high-order Hopfield fuzzy NNs with time-varying delays and $D$ operators as follows:

where $i \in\mathcal{J}: = \{1, 2, \cdots, n\}$, $x_i(t) \in\mathcal{A}$ indicates the state of the $i$th unit at time $t$; $\mathcal{A}$ is a real Clifford algebra; $b_{i}(t)\in\mathcal{A}$ represents the self feedback coefficient at time $t$; $\alpha_{ij}(t), \beta_{ij}(t), T_{ij}(t), S_{ij}(t)\in\mathcal{A}$ stand for the elements of the fuzzy feedback MIN template and fuzzy feed forward MAX template, respectively; $a_{i}(t), c_{ij}(t), u_{ij}(t)$ and $\theta_{ijk}(t), q_{ijk}(t), \nu_{ijk}(t) \in\mathcal{A}$ represent the first-order and second-order connection weights of the NN; $\gamma_{ij}(t)$ stands for the element of the feed forward template; $\bigwedge$ and $\bigvee$ denote the fuzzy AND and OR operations, respectively; $\mu_j(t)\in\mathcal{A}$ represents the input of the $j$th neuron; $I_{i}(t)\in\mathcal{A}$ corresponds to the external input to the $i$th unit; $f_j$ and $g_j: \mathcal{A}\to\mathcal{A}$ signify the nonlinear activation functions; and $\tau_i(t), \sigma_{ij}(t), \eta_{ij}(t), \delta_{ijk}(t)\in\mathbb{R^{+}}$ denote the transmission delays.

The initial value condition associated with (1.1) is given as

where $\varphi_{i}\in BC([-\varrho, 0], \mathcal{A}), \varrho = \max\limits_{i, j, k\in \mathcal{J}}\big\{\sup\limits_{t\in \mathbb{R}}\tau_i(t), \sup\limits_{t\in \mathbb{R}}\sigma_{ij}(t), \sup\limits_{t\in \mathbb{R}}\eta_{ij}(t), \sup\limits_{t\in \mathbb{R}}\delta_{ijk}(t)\big\}$.

The main purpose of this paper is to investigate the existence and stability of Besicovitch almost periodic solutions for system (1.1). The main contributions of this paper are as follows:

1. This paper is the first one to investigate the existence of Besicovitch almost periodic solutions for system (1.1), and the results of this paper still hold true and are new in the following special cases of system (1.1).

(ⅰ) System (1.1) is a real-valued, complex-valued, or quaternion-valued system.

(ⅱ) System (1.1) is a real-valued, complex-valued, or quaternion-valued system without $D$ operators, i.e. $a_i (t) = 0$.

(ⅲ) System (1.1) is a real-valued system without $D$ operators and fuzzy terms, i.e., $a_i (t) = \alpha_{ij}(t) = q_{ijk}(t) = \nu_{ijk}(t) = T_{ij}(t) = S_{ij}(t)\equiv 0$.

2. The research method proposed in the paper can be used to study the generalized almost periodic dynamics for other high-order NNs.

Remark 1.1. The method we propose can be summarized as follows: First, we use the fixed point theorem to prove the existence of solutions for system (1.1) that are bounded and continuous with respect to the Besicovitch seminorm on a closed subset of an appropriate Banach space. Then, we apply the definition and inequality techniques to prove that this solution is Besicovitch almost periodic.

The remaining part of the paper is arranged as follows: In the second section, we review some relevant concepts, introduce some symbols used in this article, cite a useful lemma, and state and prove the completeness of the space we will use. In the third section, we investigate the existence and stability of Besicovitch almost periodic solutions for system (1.1). In the fourth section, we provide an example to demonstrate the correctness of our results. Finally, in the fifth section, we provide a brief conclusion.

2.   Preliminaries

Let $\mathcal{A} = \Big\{\sum\limits_{A\in\Omega}x^{A}e_{A}\in\mathbb{R}\Big\}$ indicate a real Clifford algebra over $\mathbb{R}^m$ ^[41], where $\Omega = \{\emptyset, 1, 2, \cdots, A, \cdots, 12, \cdots, m\}$, $e_A = e_{h_1}e_{h_2}\cdots e_{h_v}$, $1\le h_1 < h_2 < \cdots < h_v\le m$, and in addition, $e_{\emptyset} = e_0 = 1$, and $e_h$, $h = 1, 2, \cdots, m$ are said to be Clifford generators and satisfy $e_p = 1, p = 0, 1, 2, \cdots, s, e_p^{2} = -1, p = s+1, s+2, \cdots, m$, where $s < m$, and $e_{p}e_{q}+e_{q}e_{p} = 0, p\neq q, p, q = 1, 2, \cdots, m.$ For every $x = \sum\limits_{A\in\Omega}x^{A}e_{A}\in\mathcal{A}$ and $y = (y_{1}, y_{2}, \cdots, y_{n})^{T}\in\mathcal{A}^{n}$, we define $|x|_{1} = \max\limits_{A\in\Omega}\{|x^{A}|\}$ and $|y|_{n} = \max\limits_{i\in\mathcal{J}}\{|y_{i}|_{1}\}$, respectively, and then the spaces $(\mathcal{A}, |\cdot|_1)$ and $(\mathcal{A}^n, |\cdot|)$ are Banach ones.

Since there is no order relation among Clifford numbers, as in ^[42], for $x = \sum\limits_{A\in\Omega}x^{A}e_{A}, y = \sum\limits_{A\in\Omega}y^{A}e_{A},$ we define $x\bigwedge y = \sum\limits_{A\in\Omega}(\min\{x^{A}, y^{A}\})e_{A}$ and $x\bigvee y = \sum\limits_{A\in\Omega}(\max\{x^{A}, y^{A}\})e_{A}.$ According to this regulation, for example, regarding the 6th and 7th terms on the right-hand side of Equation (1.1), we have

and

For $x = \sum\limits_{A\in\Omega}x^{A}e_{A}\in\mathcal{A}$, we indicate $x^c = x-x^{\emptyset}$.

For the sake of generality in the subsequent discussion of this section, let $(\mathbb{X}, \|\cdot\|)$ be a Banach space and $L_{loc}^{p}(\mathbb{R}, \mathbb{X})$ with $1\le p < +\infty$ be the space consisting of measurable and locally $p$-integrable functions from $\mathbb{R}$ into $\mathbb{X}$. In the next section, we will take $\mathbb{X} = \mathbb{R}$, $\mathbb{X} = \mathcal{A}$, or $\mathbb{X} = \mathcal{A}^n$.

Definition 2.1. ^[40] A bounded continuous function $\varphi: \mathbb{R} \rightarrow \mathbb{X}$ is said to be almost periodic, if for every $\varepsilon > 0$, there exists a number $\ell(\varepsilon) > 0$ such that for each $a\in \mathbb{R}$, there exists a point $\sigma \in [a, a+\ell]$ satisfying

The family of such functions will be signified by $AP(\mathbb{R}, \mathbb{X})$.

For $\varphi\in L_{loc}^{p}(\mathbb{R}, \mathbb{X})$, the Besicovitch seminorm is defined as the following:

Definition 2.2. ^[43] A function $\varphi\in L_{loc}^p(\mathbb{R}, \mathbb{X})$ is called $B^{p}$-continuous if $\lim\limits_{h\to0}\|\varphi(\cdot+h)-\varphi(\cdot)\|_{B^{p}} = 0$ and is called $B^{p}$-bounded if $\|\varphi\|_{B^{p}} < \infty.$

Henceforth, we will denote the set of all functions that are $B^{p}$-continuous and $B^{p}$-bounded by $BC B^p(\mathbb{R}, \mathbb{X}).$

Definition 2.3. ^[40] A function $\varphi\in L_{loc}^{p}(\mathbb{R}, \mathbb{X})$ is said to be Besicovitch almost periodic, if for every $\varepsilon > 0$, there exists a positive number $\ell > 0$ such that for each $a\in \mathbb{R}$, there exists a point $\sigma \in [a, a+\ell]$ satisfying

Denote by $B^{p}_{AP}(\mathbb{R}, \mathbb{X})$ the class of such functions and, for simplicity, call them $B^{p}$-almost periodic functions.

Lemma 2.1. ^[44] If $\alpha_{ij}, \beta_{ij}\in C(\mathbb{R}, \mathcal{A}), g_{j}\in C(\mathcal{A}, \mathcal{A}), i, j\in\mathcal{J},$ then one has

Let $L^{\infty}(\mathbb{R}, \mathbb{X})$ be the set of all essentially bounded measurable functions from $\mathbb{R}$ to $\mathbb{X}$, then $(L^{\infty}(\mathbb{R}, \mathbb{X}), \|\cdot\|_\infty)$ is a Banach space, where $\|\cdot\|_\infty: = ess\sup\limits_{t\in\mathbb{R}}\|\cdot\|$ denotes the essential supremum norm.

Denote

Then we have the following lemma which is crucial for the proof of our main result of this paper.

Lemma 2.2. The space $(\mathbb{Z}, \|\cdot\|_{\infty})$ is a Banach space.

Proof. Let $\{{\phi_{n}}\} \subset\mathbb{Z}$ be a Cauchy sequence, and then for every $\varepsilon > 0$, there is a positive integer $N_{1}$ such that for $n, m > N_{1},$

Since $\{\phi_n\}\subset\mathbb{Z}\subset L^{\infty}(\mathbb{R}, \mathbb{X})$ and $(L^{\infty}(\mathbb{R}, \mathbb{X}), \|\cdot\|_{\infty})$ is a Banach space, there exists $\phi\in L^\infty(\mathbb{R}, \mathcal{A}^n)$ such that $\phi_n\to \phi$ as $n\to\infty$ with respect to the norm $\|\cdot\|_\infty.$ To complete the proof, it suffices to prove that $\phi\in BCB^p(\mathbb{R}, \mathbb{X}).$ From $\lim\limits_{n\to\infty} \phi_n = \phi$ in regard to the essential supremum norm, it follows that there exists a positive integer $N_{2}$ such that for $n > N_{2}$,

Now, take $N_0 = \max\{N_1, N_2\}$, and then, due to the fact that $\phi_{N_0+1}\in BCB^p(\mathbb{R}, \mathbb{X})$, there exists a $\delta = \delta(\varepsilon) > 0$ such that for any $h\in \mathbb{R}$ with $|h| < \varepsilon$, it holds that

Consequently,

which implies $\phi\in BCB^p(\mathbb{R}, \mathbb{X}).$ The proof is completed. □

3.   Main results

In this section, for $x\in L^{\infty}(\mathbb{R}, \mathcal{A})$, we denote $|x|_{\infty} = \max\limits_{A\in\Omega}\{ess\sup\limits_{t\in\mathbb{R}}|x^{A}(t)|\}$ and for $z = (z_{1}, z_{2}, \cdots, z_{n})^{T} = (\sum\limits_{A}z_{1}^{A}e_A, \sum\limits_{A}z_{2}^{A}e_A, \cdots, \sum\limits_{A}z_{n}^{A}e_A)^{T}\in L^{\infty}(\mathbb{R}, \mathcal{A}^{n})$, we denote $\|z\|_{\infty} = \max\limits_{i\in\mathcal{J}}\{|z_i|_\infty\}$. Let $\mathbb{Z} = \{z|z\in L^{\infty}(\mathbb{R}, \mathcal{A}^n)\cap BCB^{p}(\mathbb{R}, \mathcal{A}^n)\},$ and then, according to Lemma 2.2, $(\mathbb{Z}, \|\cdot\|_{\infty})$ is a Banach space. For $x\in B^{p}_{AP}(\mathbb{R}, \mathcal{A})$ and $z\in B^{p}_{AP}(\mathbb{R}, \mathcal{A}^n)$, we will use $|x|_{B^p}$ and $\|z\|_{B^p}$ to represent the seminorms of $x$ and $z$, respectively.

In what follows, we will employ the following symbols:

where $g:\mathbb{R}\to\mathbb{Y}$ is a bounded function and $(\mathbb{Y}, \|\cdot\|_\mathbb{Y})$ is a normed space. Moreover, we will use the following assumptions:

$(A_1)$ For $i, j, k\in\mathcal{J}$, functions $b^\emptyset_i\in AP(\mathbb{R}, \mathbb{R}^+)$ with $\underline{b}_i^\emptyset > 0$, $a_{i}, b^c_i, \mu_{j}, c_{ij}, u_{ij}, \alpha_{ij}, \beta_{ij}, \theta_{ijk}, q_{ijk}, \\ \nu_{ijk}\in AP(\mathbb{R}, \mathcal{A}), \tau_{i}, \sigma_{ij}, \eta_{ij}, \delta_{ijk}\in AP(\mathbb{R}, \mathbb{R})\cap C^{1}(\mathbb{R}, \mathbb{R^{+}})$ with $\tau^\prime_{i}(t)\le\bar{\tau}_{i}^{\prime} < 1, \sigma^{\prime}_{ij}(t)\le\bar{\sigma}_{ij}^\prime < 1, \eta^{\prime}_{ij}(t)\le\bar{\eta}_{ij}^\prime < 1, \delta^{\prime}_{ijk}(t)\le\bar{\delta}_{ijk}^\prime < 1$, where $\bar{\tau}^\prime, \bar{\sigma}^{\prime}, \bar{\eta}^\prime, \bar{\delta}^{\prime}$ are constants, and $\gamma_{ij}, T_{ij}, S_{ij}, I_i\in L^{\infty}(\mathbb{R}, \mathcal{A}) \cap B_{AP}^{p}(\mathbb{R}, \mathcal{A}).$

$(A_2)$ For all $j\in\mathcal{J}$, functions $f_j, g_j\in C(\mathcal{A}, \mathcal{A})$ with $f_j(0) = 0, g_j(0) = 0$, and there exist positive constants $L_{j}^{f}, L_{j}^{g}, M_{j}^{g}$, and $M_{k}^{g}$ such that for any $u, v\in\mathcal{A}$,

$(A_3)$ For $i\in\mathcal{J}$, there exist positive constants $\vartheta_{i}$ such that

$(A_4)$ For the constants $\vartheta_{i}, i\in J$, mentioned in $(A_3)$, and $p, q > 1$ with $\frac{1}{p}+\frac{1}{q} = 1$, it holds that

For $i\in\mathcal{J}$, let $y_i(t) = \vartheta_{i}^{-1}x_i(t), Z_i(t) = y_i(t)-a_i(t)y_i(t-\tau_i(t))$, where $\vartheta_i > 0$ are constants, and then system (1.1) turns into

Multiplying both sides of (3.1) with $e^{\int_{t_0}^{t}b_i^{\emptyset}(u)du}$ and integrating over the interval $\left[t_0, t\right]$, then it holds that

where

It is easy to verify that if $y^{\ast}(t) = \left(y_1^{\ast}(t), y_2^{\ast}(t), \cdots, y_n^{\ast}(t)\right)$ solves system (3.1), then $x^{\ast}(t) = (x_1^{\ast}(t), x_2^{\ast}(t), \cdots, x_n^{\ast}(t)) = (\vartheta_{1}^{-1}y_1^{\ast}(t), \vartheta_{2}^{-1}y_2^{\ast}(t), \cdots, \vartheta_{n}^{-1}y_n^{\ast}(t))$ solves system (1.1).

Definition 3.1. A function $x = \left(x_1, x_2, \cdots, x_n\right):\mathbb{R}\rightarrow \mathcal{A}^n$ is called a solution of (1.1) provided that there exist positive numbers $\vartheta_i$ such that $y_i(t) = \vartheta_{i}^{-1}x_i(t), i\in \mathcal{J}$ fulfill (3.2).

Set

where

It is easy to see that $\hat{\varphi}$ is well defined under condition $(A_1)$. Choose a positive constant $r$ with $r > \|\hat{\varphi}\|_{\infty}$.

Then, we are now in a position to present and prove our existence result.

Theorem 3.1. Assume that $(A_{1})-(A_{4})$ hold. Then, system (1.1) admits a unique $B^p$-almost periodic solution in $\mathbb{Z}^*: = \{\varphi|\varphi\in\mathbb{Z}, \|\varphi-\hat{\varphi}\|_{\infty}\le \frac{\rho r}{1-\rho}\}$.

Proof. Letting $t_0\rightarrow \infty$, from (3.2), one gets

Define a mapping $T:\mathbb{Z}^*\rightarrow \mathbb{Z}^*$ by setting $(T\varphi)(t) = ((T\varphi)_{1}(t), (T\varphi)_{2}(t), \cdots, (T\varphi)_{n}(t))^{T}$ for $\varphi\in\mathbb{Z}$ and $t\in \mathbb{R}$, where $(T\varphi)_{i}(t) = a_{i}(t)\varphi_{i}(t-\tau_{i}(t))+\int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\emptyset}(u)du}(N^{\varphi})_{i}(s)ds, i\in\mathcal{J}.$

To begin with, we show that $T(\mathbb{Z}^*)\subset\mathbb{Z}^*.$

Note that, for any $\varphi\in\mathbb{Z}^*$, it holds that

and $\|N^\varphi\|_\infty < \infty.$

For every $\varphi\in\mathbb{Z}^*$, we infer that

In addition, by condition $(A_1)$ and the fact that $\varphi\in \mathbb{Z}$, we have that for every $\varepsilon > 0$, there exists a positive number $\delta = \delta(\varepsilon) (<\varepsilon)$ such that for any $h\in \mathbb{R}$ with $|h| < \delta$, it holds

Without loss of generality, in the sequel, we assume that $h > 0$, then we deduce that

which implies $T\varphi\in BCB^{p}(\mathbb{R}, \mathcal{A}^{n})$. Therefore, $T(\mathbb{Z}^*)\subset \mathbb{Z}^*$.

Next, we will prove that $T$ is a contraction mapping. In fact, for any $\varphi, \psi\in\mathbb{Z}^*, i\in\mathcal{J},$ we have

which combined with condition $(A_{3})$ means that $T$ is a contraction mapping. Thereupon, $T$ has a unique fixed point $\varphi^{*}\in\mathbb{Z}^*.$

Finally, we will examine that $\varphi^{*}$ is $B^p$-almost periodic.

Since $\varphi^{*}\in\mathbb{Z}^*\subset BCB^p(\mathbb{R}, \mathcal{A}^n)$, for any $\varepsilon > 0$, there exists a $\sigma > 0 (\sigma < \varepsilon)$ such that, for any $\hbar\in \mathbb{R}$ with $|\hbar| < \sigma$,

Based on this and $(A_1)$, there exists ${\flat}$ such that, for all $i\in\mathcal{J}$,

Then, we deduce that

Furthermore, based on inequalities (3.3)–(3.11), the Hölder inequality, and the Fubini theorem, we can deduce that

From the above estimates, it follows that

where $P$ is defined in condition $(A_4)$ and

Hence, by (3.12) and $(A_4)$, it holds that

which implies that $\varphi^{*}$ is $B^p$-almost periodic. The proof is finished. □

Remark 3.1. Although we can prove that $W = (L^\infty(\mathbb{R}, \mathcal{A})\cap B_{AP}^p(\mathbb{R}, \mathcal{A}), \|\cdot\|_\infty)$ is a Banach space, we still cannot directly use the fixed point theorem to determine the existence of almost periodic solutions for (1.1). Because there are higher-order terms in system (1.1), and $W$ is not an algebra, we cannot prove that operator $T$ is a self mapping.

It is easy to prove the following stability results using the same method as the proof of Theorem 4.1 in ^[33] or the proof of Theorem 15 in ^[31].

Theorem 3.2. Assume that $(A_{1})-(A_{4})$ hold. Then system (1.1) possesses a unique Besicovitch almost periodic solution, which is globally exponentially stable, i.e., if $\bar{x}$ is the Besecovitch almost periodic solution with initial value $\bar{\varphi}$ and $x(t)$ is an arbitrary solution of system (1.1) with initial value $\varphi$, then there exist positive numbers $\zeta > 0$ and $N > 0$ satisfying

in which $\|\varphi-\bar{\varphi}\|_{\varrho} = \max\limits_{i\in\mathcal{J}}\bigg\{\sup\limits_{t\in[- \varrho, 0]}|\varphi_{i}(t)-a_{i}(t)\varphi_{i}(t)-(\bar{\varphi}_{i}(t)-a_{i}(t)\bar{\varphi}_{i}(t))|_{1}\bigg\}$.

4.   Numerical examples

In this section, we provide an example to demonstrate the validity of the results obtained in this paper.

Example 4.1. In system (1.1), let $m = 3, n = 2$, and for $i, j, k = 1, 2$, take the coefficients are as follows:

Then, it is easy to see that conditions $(A_1)$ and $(A_2)$ are satisfied.

Moreover, take $\vartheta_{1} = \vartheta_{2} = 1, p = 3, q = \frac{3}{2}$, then through simple calculations, we obtain

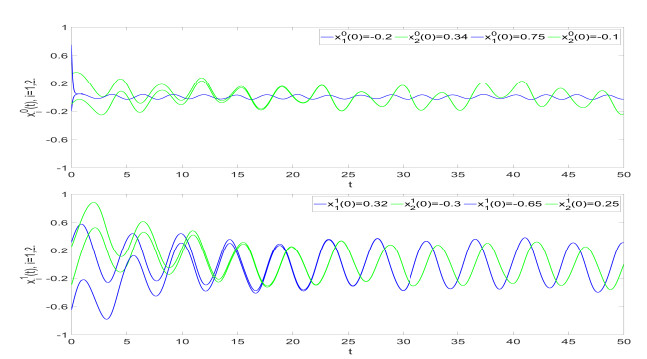
Hence, $(A_{3})$ and $(A_{4})$ are also satisfied. Consequently, in view of Theorem 3.2, we know that system (1.1) has a unique Besicovitch almost periodic solution that is globally exponentially stable (see Figures 1–4).

Remark 4.1. Even when the system considered in Example 4.1 degenerates into a real-valued system, there are no existing results to derive the results of Example 4.1.

5.   Conclusions

This article introduces a new method to establish the existence and global exponential stability of Besicovitch almost periodic solutions for Clifford-valued high-order Hopfield fuzzy NNs with $D$ operators. The methods and results of this article can be applied to study the generalized almost periodic and almost automorphic dynamics of high-order NNs.

Author contributions

Bing Li: Methodology, Conceptualization, Writing - review and editing; Yuan Ning: Writing - original draft, Visualization; Yongkun Li: Methodology, Conceptualization, Funding acquisition, Writing - review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China, grant number 12261098.

Conflict of interest

The authors declare no conflict of interest.