BV regularity of the adapted entropy solutions for conservation laws with infinitely many spatial discontinuities

1.   Introduction

Tapezoidal intuitionistic fuzzy number (TIFN), as a special intuitionistic fuzzy set on a real number, has the best capability to model ill-known quantities ^[1,2]. TIFNs are useful to deal with uncertain knowledge and data in management decision and financial engineering problems. Intuitionistic fuzzy number, as the extension of fuzzy number, has more flexibility in many real-time uncertain application fields such as multi-criteria decision ^[3,4,5,6], portfolio selection ^[7,8], and agammaegation ^[9]. Recently, the possibility measure theory of TIFN plays an important role in many application fields like mulit-criteria decision and portfolio selection problem. For example, Chakraborty ^[10] utilized possibility, necessity and credibility measure to solve intuitionistic fuzzy optimization problem. Garai ^[11] applied possibility-necessity-credibility measures of generalized trapezoidal intuitionistic fuzzy number (GTIFN) to multi-product manufacturing system.

As is well known, based on possibility theory the possibilistic mean and variance of fuzzy numbers were presented by Carlsson and Full´er ^[12] and had been widely applied in solving fuzzy portfolio decision problems ^{[13,14,15,16,17,18,19,20]}. Recently, inspired by the above-mentioned fuzzy possibilistic mean theory Wan ^[21] proposed a definition of possibilistic mean and variance of intuitionistic fuzzy number (IFN). And Wan ^[22,23,24] utilized the possibilistic mean and variance to intuitionistic fuzzy group decision-making and matrix game problems with incomplete information. Later, Chen ^[25] also discussed the mean-variance-skewness portfolio selection problems based on intuitionistic fuzzy optimization under the assumption that the returns of assets are intuitionistic fuzzy numbers. Although the possibilistic mean and variance of intuitionistic fuzzy numbers will have a lot of application prospects, there is few study on the relationship between the possibilistic mean, variance and covariance of two generalized trapezoidal intuitionistic fuzzy numbers, and it is not clear whether subsethood entails smaller variance for generalized trapezoidal intuitionistic fuzzy number.

Moreover, we notice that the existing definitions of possibilistic mean and variance by Wan ^[21] have some flaws. In his definitions the denominators of the fraction of possibilistic mean and variance are improper because the level $\lambda$ value and $\gamma$ value are taken in [0, 1] for granted. However, the level $\lambda$ value and $\gamma$ level value of generalized trapezoidal intuitionistic fuzzy number $\tilde A$ indeed lie in the limited interval [0, ${u_a}$] and [${v_a} ,$ 1], respectively. To overcome the flaw of Wan's definition ^[21], in this paper we will correct it and introduce the new definitions of lower and upper possibilistic mean, variance of generalized trapezoidal intuitionistic fuzzy numbers based on possibility distributions. We also give some properties of possibilistic mean, covariance and variance, such as that the possibilistic variance of linear combinations of generalized trapezoidal intuitionistic fuzzy numbers can easily be computed like in probability theory and that subsethood does entail smaller variance. Moreover, in this paper we show that the possibilistic mean of generalized trapezoidal intuitionistic fuzzy number remains additive in the sense of addition of GTIFNs. In particular, we easily deduce $Var(\tilde A) = Cov(\tilde A, \tilde A) = Cov(\tilde A, - \tilde A) ,$ which is not consistent with the properties of covariance in crisp probability theory. The contribution of this work is as follows. We show that the presented possibilistic variance and covariance of generalized trapezoidal intuitionistic fuzzy numbers reserve many important properties of variance and covariance in traditional probability theory, which is different from the known investigation results. We also investigate the important relationship between two kinds of possibilistic variance $\operatorname{var} (\tilde A)$ and ${\rm{var}}'(\tilde A)$ for generalized trapezoidal intuitionistic fuzzy numbers.

2.   Preliminaries

Let us first introduce some basic concepts of trapezoidal intuitionistic fuzzy numbers, which will be employed in the following sections.

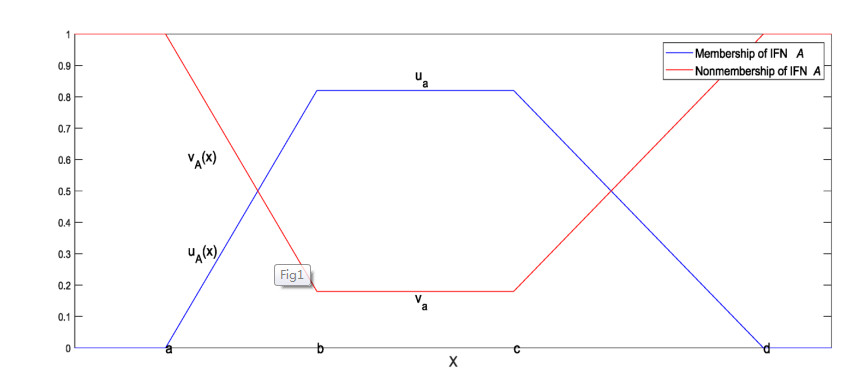
Definition 1 ^[11,21]. A generalized trapezoidal intuitionistic fuzzy number (GTIFN) $\tilde A = ((a, b, c, d);{u_a}, {v_a})$ is a special kind of intuitionistic fuzzy set on the real number set R, whose membership function and nonmembership function are defined as following forms, respectively (see Figure 1).

where ${u_a}, {v_a}$ are the greatest membership and the least nonmembership degree, respectively. And ${u_a}, {v_a} \in [0, 1],$ $0 \leqslant {u_a} + {v_a} \leqslant 1,$ ${\pi _{\tilde A}}(x) = 1 - {\mu _{\tilde A}}(x) - {\nu _{\tilde A}}(x)$ is called the hesitation degree of $x \in \tilde A .$

Remark 1 ^[22,24]. If $b = c ,$ then the generalized trapezoidal intuitionistic fuzzy number $\tilde A = ((a, b, c, d);{u_a}, {v_a})$ is reduced to a generalized triangular intuitionistic fuzzy number $\tilde A = ((a, b, d);{u_a}, {v_a}) .$

Definition 2. Let ${\tilde A_i} = (({a_i}, {b_i}, {c_i}, {d_i}), {u_{_i}}, {v_{_i}}) ,$ $i = 1, 2,$ be two generalized trapezoidal intuitionistic fuzzy numbers, the addition and scale multiplication of GTIFNs ^{[2,11,21,24,26]} are defined as follows.

(1) ${\tilde A_1} + {\tilde A_2} = (({a_1} + {a_2}, {b_1} + {b_2}, {c_1} + {c_2}, {d_1} + {d_2});\mathop {}\limits_{} {u_{a1}} \wedge {u_{a2}}, {v_{a1}} \vee {v_{a2}}).$

(2) $x{\tilde A_i} = ((x{a_i}, x{b_i}, x{c_i}, x{d_i}); {u_i}, {v_i}) ,$ $\forall x \geqslant 0 .$ $x{\tilde A_i} = ((x{d_i}, x{c_i}, x{b_i}, x{a_i}); {u_i}, {v_i}) ,$ $\forall x < 0 .$

Definition 3 ^[22,24]. Let $\tilde A = ((a,b,c,d);{u_{{a_{}}}},{v_{{a_{}}}})$ be a generalized trapezoidal intuitionistic fuzzy number, the $\lambda$-level cut set and $\gamma$ -cut set of membership and nonmembership of GTIFN $\tilde A$ are, respectively, defined as

where $\lambda \in [0, {u_a}],$ $\gamma \in [{v_a}, 1] ,$ and $0 \leqslant \lambda + \gamma \leqslant 1 .$

Theorem 1 ^[11,21]. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ , ${\tilde A_2} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ be two generalized trapezoidal intuitionistic fuzzy numbers, for any positive real number $\lambda \in (0,{u_a}],$ $\gamma \in [{v_a},1]$ , we can easily get

(1) ${({\tilde A_1} + {\tilde A_2})^{[\lambda]}} = {\tilde A_1}^{[\lambda]} + {\tilde A_2}^{[\lambda]} = [{a_1}^- (\lambda) + {a_2}^ - (\lambda), {a_1}^ + (\lambda) + {a_2}^ + (\lambda)] ,$ $\mathop {}\limits_{} \forall \lambda \in (0, {u_a}];$

(2) ${({\tilde A_1} + {\tilde A_2})^{[\gamma]}} = {\tilde A_1}^{[\gamma]} + {\tilde A_2}^{[\gamma]} = [{a_1}^- (\gamma) + {a_2}^ - (\gamma), {a_1}^ + (\gamma) + {a_2}^ + (\gamma)] ,$ $\forall \gamma \in [{v_a}, 1] ;$

(3) ${(x\tilde A)^{[\lambda]}} = x{\tilde A^{[\lambda]}} = [x{a^- }(\lambda), x{a^ + }(\lambda)], \forall x \geqslant 0;$ ${(x\tilde A)^{[\lambda]}} = x{\tilde A^{[\lambda]}} = [x{a^ + }(\lambda), x{a^ - }(\lambda)], \forall x < 0;$

(4) ${(x\tilde A)^{[\gamma]}} = x{\tilde A^{[\gamma]}} = [x{a^- }(\gamma), x{a^ + }(\gamma)], \forall x \geqslant 0;$ ${(x\tilde A)^{[\gamma]}} = x{\tilde A^{[\gamma]}} = [x{a^ + }(\gamma), x{a^ - }(\gamma)], \forall x < 0.$

The proof is straightforward from Definition 3 and Zadeh's fuzzy extension principle.

Definition 4 ^[21]. Let $\tilde A = ((a,b,c,d);{u_{{a_{}}}},{v_{{a_{}}}})$ be a generalized trapezoidal intuitionistic fuzzy number, the lower and upper possibilistic mean value of the membership function of GTIFN $\tilde A$ are, respectively, defined as

The possibilistic mean of membership of GTIFN $\tilde A$ can also be defined as

Definition 5. $\tilde A = ((a,b,c,d);{u_a},{v_a})$ be a generalized trapezoidal intuitionistic fuzzy number, the lower and upper possibilistic mean value of the nonmembership function of GTIFN $\tilde A$ are, respectively, defined as

The possibilistic mean of nonmembership of GTIFN $\tilde A$ can also be defined as

Definition 6. Let $\tilde A = ((a, b, c, d);{u_a}, {v_a})$ be a generalized trapezoidal intuitionistic fuzzy number, the possibilistic mean value of GTIFN $\tilde A$ is defined as $M(\tilde A) = \tfrac{1}{2}[{M_\mu }(\tilde A) + {M_\nu }(\tilde A)] .$

Definition 7. Let $\tilde A = ((a, b, c, d);{u_a}, {v_a})$ be a GTIFN with $\lambda, \gamma$ cut set ${\tilde A^{[\lambda]}} = [{a^- }(\lambda), {a^ + }(\lambda)] ,$ ${\tilde A^{[\gamma]}} = [{a^- }(\gamma), {a^ + }(\gamma)]$ of membership and nonmembership of $\tilde A ,$ the possibilistic variance of membership and nonmembership of GTIFN $\tilde A$ are respectively defined as ^[21,22],

where $M = c - b + (a - d){v_a} ,$ $N = d - c + b - a .$

Hence, the variance of GTIFN $\tilde A$ can be defined by $\operatorname{var} (\tilde A) = \tfrac{1}{2}[{\operatorname{var} _\mu }(\tilde A) + {\operatorname{var} _v}(\tilde A)] .$

Definition 8. Let ${\tilde A_1} = (({a_1}, {b_1}, {c_1}, {d_1}); {u_a}, {v_a})$ be a GTIFN with $\lambda, \gamma$ cut set ${\tilde A_1}^{[\lambda]} = [a_1^- (\lambda), a_1^ + (\lambda)] ,$ ${\tilde A_1}^{[\gamma]} = [a_1^- (\gamma), a_1^ + (\gamma)]$ and GTIFN ${\tilde A_2} = (({a_2}, {b_2}, {c_2}, {d_2}); {u_{{a_{}}}}, {v_{{a_{}}}})$ with $\lambda, \gamma$ cut set ${\tilde A_2}^{[\lambda]} = [a_2^- (\lambda), a_2^ + (\lambda)] ,$ ${\tilde A_2}^{[\gamma]} = [a_2^- (\gamma), a_2^ + (\gamma)]$ of membership and nonmembership, the possibilistic covariance of membership and nonmembership of GTIFNs ${\tilde A_1}, {\tilde A_2}$ are respectively defined as ^[17,19],

The covariance of GTIFNs ${\tilde A_1}, {\tilde A_2}$ can be also defined by $\operatorname{cov} ({\tilde A_1}, {\tilde A_2}) = \tfrac{1}{2}[{\operatorname{cov} _\mu }({\tilde A_1}, {\tilde A_2}) + {\operatorname{cov} _v}({\tilde A_1}, {\tilde A_2})] .$

Definition 9. $\tilde A = ((a,b,c,d);{u_a},{v_a})$ be a GTIFN with $\lambda$ cut set ${\tilde A^{[\lambda ]}} = [{a^ - }(\lambda ),{a^ + }(\lambda )]$ of membership and $\gamma$ cut set ${\tilde A^{[\gamma ]}} = [{a^ - }(\gamma ),{a^ + }(\gamma )]$ of nonmembership, the new possibilistic variance of membership and nonmembership of GTIFN $\tilde A$ are respectively defined as

The new possibilistic variance of GTIFN $\tilde A$ can also be computed by ${\rm{var}}'(\tilde A) = \tfrac{1}{2}[{{\rm{var}}'_\mu }(\tilde A) + {{\rm{var}}'_v}(\tilde A)] ;$ where ${a^ - }(\lambda), {a^ + }(\lambda)$ is the lower bound and upper bound of $\lambda$ level interval value of membership of GTIFN $\tilde A ,$ ${{\rm{var}}'_\mu }(\tilde A)$ expresses the weighted deviation squares between the membership mean and lower bound, upper bound of $\lambda$ level interval of membership of $\tilde A ;$ and ${a^ - }(\gamma), {a^ + }(\gamma)$ is the lower bound and upper bound of $\lambda$ level interval of nonmembership of GTIFN $\tilde A ,$ ${{\rm{var}}'_\nu }(\tilde A)$ expresses the weighted deviation squares between the nonmembership mean and lower bound, upper bound of $\lambda$ level interval of nonmembership of $\tilde A .$ However, the existing ${\operatorname{var} _\mu }(\tilde A)$ only indicates the weighted deviation squares between lower bound and upper bound of $\lambda$ level interval of membership of $\tilde A ;$ ${\operatorname{var} _v}(\tilde A)$ only indicates the weighted deviation squares between lower bound and upper bound of $\lambda$ level interval of nonmembership of $\tilde A .$ Moreover, the above-mentioned definition 9 of possibilistic variance coincides with the definition of crisp variance, so it is more meaningful and rathional than the existing possibilistic variance of GTIFN $\tilde A .$

Definition 10. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_a},{v_a})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [a_1^ - (\lambda ),a_1^ + (\lambda )]$ , ${\tilde A_1}^{[\gamma ]} = [a_1^ - (\gamma ),a_1^ + (\gamma )]$ and TIFN ${\tilde A_2} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_{}}}},{v_{{a_{}}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [a_2^ - (\lambda ),a_2^ + (\lambda )]$ , ${\tilde A_2}^{[\gamma ]} = [a_2^ - (\gamma ),a_2^ + (\gamma )]$ of membership and nonmembership, the new possibilistic covariance of membership and nonmembership of TIFNs ${\tilde A_1},{\tilde A_2}$ are respectively defined as

The new covariance of GTIFNs ${\tilde A_1}, {\tilde A_2}$ can be computed by ${\rm{cov}}'({\tilde A_1}, {\tilde A_2}) = \tfrac{1}{2}[{{\rm{cov}}'_\mu }({\tilde A_1}, {\tilde A_2}) + {{\rm{cov}}'_v}({\tilde A_1}, {\tilde A_2})] .$

Theorem 2. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$cut set ${\tilde A_1}^{[\lambda ]} = [a_1^ - (\lambda ),a_1^ + (\lambda )]$, ${\tilde A_1}^{[\gamma ]} = [a_1^ - (\gamma ),a_1^ + (\gamma )]$ and GTIFN${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [a_2^ - (\lambda ),a_2^ + (\lambda )]$, ${\tilde A_2}^{[\gamma ]} = [a_2^ - (\gamma ),a_2^ + (\gamma )]$, and ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},\mathop {}\limits_{} {v_{{a_1}}} = {v_{{a_2}}} = {v_a}$, and for any $x,{x_1},{x_2} \in R$, then we have

(1) $M({\tilde A_1} + {\tilde A_2}) = M({\tilde A_1}) + M({\tilde A_2}) ;$

(2) $M(x{\tilde A_1}) = xM({\tilde A_1}) ,$ $\forall x \in R ;$

(3) $M({x_1}{\tilde A_1} + {x_2}{\tilde A_2}) = {x_1}M({\tilde A_1}) + {x_2}M({\tilde A_2}) ,$ $\forall {x_1}, {x_2} \in R .$

Proof. (1) It follows from Definitions 4, 5 and Theorem 1 that

Therefore, we have

(2) By Definitions 4, 5 and Theorem 1, for any $x \ge 0$ we easily get

For any $x < 0 ,$ we also get

So we have

(3) From (1), (2) we easily conclude that, for any ${x_1}, {x_2} \in R ,$

Hence, $M({x_1}{\tilde A_1} + {x_2}{\tilde A_2}) =$ $\frac{{{M_\mu }({x_1}{{\tilde A}_1} + {x_2}{{\tilde A}_2}) + {M_v}({x_1}{{\tilde A}_1} + {x_2}{{\tilde A}_2})}}{2} = {x_1}M({\tilde A_1}) + {x_2}M({\tilde A_2}) .$

3.   Some important notes on possibilistic variances of GTIFN

Theorem 3.1. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [a_1^ - (\lambda ),a_1^ + (\lambda )]$ , ${\tilde A_1}^{[\gamma ]} = [a_1^ - (\gamma ),a_1^ + (\gamma )]$ and GTIFN ${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [a_2^ - (\lambda ),a_2^ + (\lambda )]$ , ${\tilde A_2}^{[\gamma ]} = [a_2^ - (\gamma ),a_2^ + (\gamma )]$ and ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},{v_{{a_1}}} = {v_{{a_2}}} = {v_a}$ , and let constant $\theta \in R$ . Then we have

(1) $\operatorname{cov} ({\tilde A_1}, {\tilde A_2}) = \operatorname{cov} ({\tilde A_2}, {\tilde A_1}) ;$

(2) $\operatorname{var} ({\tilde A_1}) = \operatorname{cov} ({\tilde A_1}, {\tilde A_1}) = \operatorname{cov} ({\tilde A_1}, - {\tilde A_1}) ;$

(3) $\operatorname{var} ({\tilde A_1} + \theta) = \operatorname{var} ({\tilde A_1}) .$

Proof. (1), (2) can be directly verified by Definition 8 of $\operatorname{cov} ({\tilde A_1}, {\tilde A_2})$ and Definition 7 of $\operatorname{var} ({\tilde A_1}) .$

(3) For any $\theta \in R$, by Zadeh's fuzzy extension principle we can know that $({\tilde A_1} + \theta )(x) = {\tilde A_1}(x - \theta )$, and

So, ${\operatorname{var} _\mu }({\tilde A_1} + \theta) = \tfrac{1}{2}\int_0^{{u_a}} {[({a_1}^- } (\lambda) + \theta) - ({a_1}^ + (\lambda) + \theta){]^2}\lambda d\lambda = \tfrac{1}{2}\int_0^{{u_a}} {[{a_1}^- } (\lambda) - {a_1}^ + (\lambda){]^2}\lambda d\lambda = {\operatorname{var} _\mu }({\tilde A_1}) ;$

${\operatorname{var} _v}({\tilde A_1} + \theta) = \tfrac{1}{2}\int_{{v_a}}^1 {[({a_1}^- } (\gamma) + \theta) - ({a_1}^ + (\lambda) + \theta){]^2}\gamma d\gamma = \tfrac{1}{2}\int_{{v_a}}^1 {[{a_1}^- } (\gamma) - {a_1}^ + (\lambda){]^2}\gamma d\gamma = {\operatorname{var} _v}({\tilde A_1}) .$

Hence, we have $\operatorname{var} ({\tilde A_1} + \theta) = \frac{{{{\operatorname{var} }_\mu }({{\tilde A}_1} + \theta) + {{\operatorname{var} }_v}({{\tilde A}_1} + \theta)}}{2} = \frac{{{{\operatorname{var} }_\mu }({{\tilde A}_1}) + {{\operatorname{var} }_v}({{\tilde A}_1})}}{2} = \operatorname{var} ({\tilde A_1}) .$

Theorem 3.2. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [{a_1}^ - (\lambda ),{a_1}^ + (\lambda )]$, ${\tilde A_1}^{[\gamma ]} = [{a_1}^ - (\gamma ),{a_1}^ + (\gamma )]$ and GTIFN ${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [{a_2}^ - (\lambda ),{a_2}^ + (\lambda )]$, ${\tilde A_2}^{[\gamma ]} = [{a_2}^ - (\gamma ),{a_2}^ + (\gamma )]$, and ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},{v_{{a_1}}} = {v_{{a_2}}} = {v_a}$, and for any constant $\theta \in R$, we also obtain

(1) ${\rm{cov}}'({\tilde A_1}, {\tilde A_2}) = {\rm{cov}}'({\tilde A_2}, {\tilde A_1}) ;$

(2) ${\rm{var}}'({\tilde A_1}) = {\rm{cov}}'({\tilde A_1}, {\tilde A_1}) ;$

(3) ${\rm{var}}'({\tilde A_1} + \theta) = {\rm{var}}'({\tilde A_1}) .$

Proof. (1), (2) can be directly proved by Definition 10 of ${\rm{cov}}'({\tilde A_1}, {\tilde A_2})$ and Definition 9 of ${\rm{var}}'({\tilde A_1}) .$

(3) Since $({\tilde A_1} + \theta )(x) = {\tilde A_1}(x - \theta )$, we know that

So, we get ${\rm{var}}'({\tilde A_1} + \theta) = {\rm{var}}'({\tilde A_1}).$

Theorem 3.1-3.2 show that possibilistic covariances have symmetry, the covariance between GTIFN itself reduces to the possibilistic variance of GTIFN. And if a GTIFN shifts a constant, the possibilistic variance is not altered.

Theorem 3.3. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [{a_1}^ - (\lambda ),{a_1}^ + (\lambda )]$ , ${\tilde A_1}^{[\gamma ]} = [{a_1}^ - (\gamma ),{a_1}^ + (\gamma )]$ and GTIFN ${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [{a_2}^ - (\lambda ),{a_2}^ + (\lambda )]$ , ${\tilde A_2}^{[\gamma ]} = [{a_2}^ - (\gamma ),{a_2}^ + (\gamma )]$ , and ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},{v_{{a_1}}} = {v_{{a_2}}} = {v_a}$ , for any ${x_1},{x_2} \in R$ , then

Proof. We only verify that the above formula holds in the case (1) if ${x_1} < 0 ,$ ${x_2} > 0.$

By employing Theorem 1 we can easily know that

So, by Definitions 7, 8 we easily get

and

So, we get $\operatorname{var} ({x_1}{\tilde A_1} + {x_2}{\tilde A_2}) = \frac{{{{\operatorname{var} }_\mu }({x_1}{{\tilde A}_1} + {x_2}{{\tilde A}_2}) + {{\operatorname{var} }_\nu }({x_1}{{\tilde A}_1} + {x_2}{{\tilde A}_2})}}{2}$

Similar reasoning holds for the other cases (2) ${x_1} > 0 ,$ ${x_2} > 0 ,$ (3) ${x_1} > 0 ,$ ${x_2} < 0$ and (4) ${x_1} \leqslant 0 ,$ ${x_2} \leqslant 0 .$

It follows that $\operatorname{var} ({x_1}{\tilde A_1} + {x_2}{\tilde A_2}) = {x_1}^2\operatorname{var} ({\tilde A_1}) + {x_2}^2\operatorname{var} ({\tilde A_2}) + 2\left| {{x_1}{x_2}} \right|\operatorname{cov} ({\tilde A_1}, {\tilde A_2})$ for any ${x_1}, {x_2} \in R .$

Theorem 3.3 show that the possibilistic variance of linear combinations of generalized trapezoidal intuitionistic fuzzy numbers can be computed like in probability theory, which reserves the same property of crisp variance.

Theorem 3.4. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [{a_1}^ - (\lambda ),{a_1}^ + (\lambda )]$ , ${\tilde A_1}^{[\gamma ]} = [{a_1}^ - (\gamma ),{a_1}^ + (\gamma )]$ and GTIFN ${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [{a_2}^ - (\lambda ),{a_2}^ + (\lambda )]$ , ${\tilde A_2}^{[\gamma ]} = [{a_2}^ - (\gamma ),{a_2}^ + (\gamma )]$ , and ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},{v_{{a_1}}} = {v_{{a_2}}} = {v_a}$ , for any $x,{x_1},{x_2} \in R$ , then

where $\varphi (x)$ is a signal function of $x \in R .$

Proof. We only need to prove it in the case (1) when ${x_1} > 0 ,$ ${x_2} < 0.$

By using Theorem 1 we easily have

With Definitions 9, 10 and Theorem 2 we get

By Definitions 9, 10 and Theorem 2 we also get

Hence, we verify that

Similar reasoning holds for the other cases (2) ${x_1} > 0$ , ${x_2} > 0;$ (3) ${x_1} < 0$ , ${x_2} > 0$ and (4) ${x_1} \leqslant 0 ,$ ${x_2} \leqslant 0,$ which ends the proof.

Theorem 3.4. shows that the new possibilistic variance of linear combinations of generalized trapezoidal intuitionistic fuzzy numbers can also be computed like in probability theory, which reserves the similar property of crisp variance in traditional probability space.

Theorem 3.5. Let ${\tilde A_1} = (({a_1},{b_1},{c_1},{d_1});{u_{{a_1}}},{v_{{a_1}}})$ be a GTIFN with $\lambda ,\gamma$ cut set ${\tilde A_1}^{[\lambda ]} = [{a_1}^ - (\lambda ),{a_1}^ + (\lambda )]$ , ${\tilde A_1}^{[\gamma [} = [{a_1}^ - (\gamma ),{a_1}^ + (\gamma )]$ and GTIFN ${\tilde A_2}_{} = (({a_2},{b_2},{c_2},{d_2});{u_{{a_2}}},{v_{{a_2}}})$ with $\lambda ,\gamma$ cut set ${\tilde A_2}^{[\lambda ]} = [{a_2}^ - (\lambda ),{a_2}^ + (\lambda )]$ , ${\tilde A_2}^{[\gamma [} = [{a_2}^ - (\gamma ),{a_2}^ + (\gamma )]$ , ${\mu _{{a_1}}} = {\mu _{{a_2}}} = {\mu _a},\mathop {}\limits_{} {v_{{a_1}}} = {v_{{a_2}}} = {v_a}$ , and ${\tilde A_1} \subset {\tilde A_2}$ . Then we have

(1) $\operatorname{var} ({\tilde A_1}) \leqslant \operatorname{var} ({\tilde A_2}) ,$ (2) ${\rm{var}}'({\tilde A_1}) \leqslant {\rm{var}}'({\tilde A_2}) .$

Proof.

(1) From ${\tilde A_1} \subset {\tilde A_2}$ it follows that $a_2^ - (\lambda) \leqslant a_1^ - (\lambda) \leqslant a_1^ + (\lambda) \leqslant a_2^ + (\lambda)$ and $a_2^ - (\gamma) \leqslant a_1^ - (\gamma) \leqslant a_1^ + (\gamma) \leqslant a_2^ + (\gamma) .$

For all $\lambda \in (0, {u_a}) ,$ $\gamma \in ({v_a}, 1) .$ That is to say, $M_\mu ^ - ({\tilde A_2}) \leqslant M_\mu ^ - ({\tilde A_1}) \leqslant M_\mu ^ + ({\tilde A_1}) \leqslant M_\mu ^ + ({\tilde A_2}) .$

Hence, ${\operatorname{var} _\mu }({\tilde A_1}) = \tfrac{1}{2}\int_0^{{u_a}} {[a_1^ + } (\lambda) - a_1^ - (\lambda){]^2}\lambda d\lambda \leqslant \tfrac{1}{2}\int_0^{{u_a}} {[a_2^ + } (\lambda) - a_2^ - (\lambda){]^2}\lambda d\lambda = {\operatorname{var} _\mu }({\tilde A_2}) ,$

${\operatorname{var} _v}({\tilde A_1}) = \tfrac{1}{2}\int_{{v_a}}^1 {[a_1^ + } (\gamma) - a_1^ - (\gamma){]^2}\gamma d\gamma \leqslant \tfrac{1}{2}\int_{{v_a}}^1 {[a_2^ + } (\gamma) - a_2^ - (\gamma){]^2}\gamma d\gamma = {\operatorname{var} _v}({\tilde A_2}) .$

So, we have

(2) From Definition 9, we know that

By Definition 4 and Tchebycheff inequalities we infer that

Similarly we can verify that ${{\rm{var}}'_\nu }({\tilde A_2}) - {{\rm{var}}'_\nu }({\tilde A_1}) \geqslant 0 .$

So, we have ${\rm{var}}'({\tilde A_2}) = \frac{{va{{r'}_\mu }({{\tilde A}_2}) + va{{r'}_\nu }({{\tilde A}_2})}}{2} \geqslant \frac{{va{{r'}_\mu }({{\tilde A}_1}) + va{{r'}_\nu }({{\tilde A}_1})}}{2} = {\rm{var}}'({\tilde A_1}).$

The above Theorem 3.5 in fact indicates that the subsethood of generalized trapezoidal intuitionistic fuzzy number does entail smaller variance.

Theorem 3.6. Let $\tilde A = ((a, b, c, d);{u_a}, {v_a})$ be a generalized trapezoidal intuitionistic fuzzy number with $\lambda, \gamma$ cut set ${\tilde A^{[\lambda]}} = [{a^- }(\lambda), {a^ + }(\lambda)] ,$ ${\tilde A^{[\gamma]}} = [{a^- }(\gamma), {a^ + }(\gamma)]$ of the corresponding membership and nonmembership of $\tilde A ,$ respectively, and $0 \leqslant {u_a} + {v_a} \leqslant 1 ,$ then we obtain $\operatorname{var} (\tilde A) \leqslant {\rm{var}}'(\tilde A) .$

Proof. From Definitions 7, 9, 4 we easily know that

From the Jensen inequality and $\int_0^{{u_a}} {\frac{{2\lambda }}{{u_a^2}}} d\lambda = 1,$ we get

That is,

$\frac{4}{{u_a^4}}[\int_0^{{u_a}} {\lambda (} {a^ - }(\lambda) + {a^ + }(\lambda))d\lambda {]^2} \leqslant$ $\frac{2}{{u_a^2}}\int_0^{{u_a}} {\lambda (} {a^ - }(\lambda) + {a^ + }(\lambda){)^2}d\lambda .$

i.e., $\tfrac{1}{{u_a^2}}[\int_0^{{u_a}} {\lambda (} {a^ - }(\lambda) + {a^ + }(\lambda))d\lambda {]^2} \leqslant \tfrac{1}{2}$ $\int_0^{{u_a}} {\lambda (} {a^ - }(\lambda) + {a^ + }(\lambda){)^2}d\lambda .$

So, ${\operatorname{var} _\mu }(\tilde A) - {{\rm{var}}'_\mu }(\tilde A)$

Similarly, by Definitions 7, 9, 5 we can prove

From the Jensen inequality and $\int_{{v_a}}^1 {\frac{{2\gamma }}{{1 - v_a^2}}} d\gamma = 1 ,$ we get

That is, $\frac{4}{{{{(1 - v_a^2)}^2}}}[\int_{{v_a}}^1 {\gamma (} {a^ - }(\gamma) + {a^ + }(\gamma))d\gamma {]^2} \leqslant$ $\frac{2}{{(1 - v_a^2)}}\int_{{v_a}}^1 {\gamma (} {a^ - }(\gamma) + {a^ + }(\gamma){)^2}d\gamma .$

i.e., $\frac{1}{{(1 - v_a^2)}}[\int_{{v_a}}^1 {\gamma (} {a^ - }(\gamma) + {a^ + }(\gamma))d\gamma {]^2} \leqslant$ $\frac{1}{2}\int_{{v_a}}^1 {\gamma (} {a^ - }(\gamma) + {a^ + }(\gamma){)^2}d\gamma .$

So, ${\operatorname{var} _\nu }(\tilde A) - {{\rm{var}}'_\nu }(\tilde A)$

Therefore, we get $\operatorname{var} (\tilde A) = \frac{{{{\operatorname{var} }_\mu }(\tilde A) + {{\operatorname{var} }_\nu }(\tilde A)}}{2} \leqslant \frac{{va{{r'}_\mu }(\tilde A) + va{{r'}_\nu }(\tilde A)}}{2} = {{\rm{var}}'_{}}(\tilde A) .$

The above Theorem 3.6 indicates that the new presented possibilistic variance ${\rm{var}}'(\tilde A)$ of generalized trapezoidal intuitionistic fuzzy number is greater than the existing variance $\operatorname{var} (\tilde A)$ because it considers all the weighted deviation squares between the lower bound, upper bound of level cut interval of membership of $\tilde A$ and possibilistic mean.

Remark 2. If $\tilde A = ((a, b, c, d);{u_{{a_{}}}}, {v_{{a_{}}}})$ is a symmetric generalized trapezoidal intuitionistic fuzzy number, ${u_a}, {v_a}$ are two constants satisfying $0 \leqslant {u_a} + {v_a} \leqslant 1 ,$ then we have $\operatorname{var} (\tilde A) = {{\rm{var}}'_{}}(\tilde A) .$

Proof. Since $\tilde A = ((a, b, c, d);{u_{{a_{}}}}, {v_{{a_{}}}})$ is a symmetric TIFN, we know $a + d = b + c$ and $d - c = b - a .$

For any $\lambda \in [0, {u_a}] ,$ $\gamma \in [{v_a}, 1] ,$ the $\lambda$-level cut set and $\gamma$ -cut set of TIFN $\tilde A$ can be expressed as follows.

where $s(\lambda) = b - a - (b - a)\lambda /{u_a} ,$ $q(\gamma) = [(a- b){v_a} + \gamma (b -a)]/(1 - {v_a}) .$

According to Definitions 4, 5 of possibilistic mean of TIFN $\tilde A ,$ one easily get

Hence,

And ${{\rm{var}}'_\mu }(\tilde A) = \int_0^{{u_a}} {[{{({M_\mu }(\tilde A) - {a^ - }(\lambda ))}^2} + {{({M_\mu }(\tilde A) - {a^ + }(\lambda ))}^2}]\lambda d\lambda }$

Thus, $\operatorname{var} (\tilde A) = \frac{{{{\operatorname{var} }_\mu }(\tilde A) + {{\operatorname{var} }_\nu }(\tilde A)}}{2} = \frac{{va{{r'}_\mu }(\tilde A) + va{{r'}_\nu }(\tilde A)}}{2} = {{\rm{var}}'_{}}(\tilde A).$

4.   Discussion on application advantage of possibilistic mean and variance of GTIFN

Recently, some arithmetic operations of generalized trapezoidal intuitionistic fuzzy numbers have been utilized in analyzing fuzzy system reliability ^[26,27]. Also, many multi-attribute decision making and programming methods based on generalized trapezoidal intuitionistic fuzzy number have been studied in ^[28,29,30]. Although GTIFNs have been applied in dealing with uncertain problem, there is few study on the possibilistic mean and variance of GTIFN. In this section we will discuss some advantages of the proposed possibilistic mean and variance of GTIFN below.

4.1.   A new ranking method for GTIFN considering the risk attitude of decision-maker

In fact, for any GTIFN $\tilde A = ((a, b, c, d);{u_{{a_{}}}}, {v_{{a_{}}}}) ,$ the possibilistic mean $M(\tilde A)$ may be respectively viewed as the central value of GTIFN $\tilde A ,$ and the possibilistic variance $Var(\tilde A)$ may be regarded as the global spreads of GTIFN $\tilde A .$ Thus, from the membership function point of view, the larger the possibilistic mean, the greater the GTIFN; the smaller the possibilistic variance, the greater the GTIFN.

Hence, we can define the rank index of generalized trapezoidal intuitionistic fuzzy number as

where $\rho$ represents the risk attitude of decision-maker(DM). If $0 \leqslant \rho < 0.5,$ it shows that DM is risk-like; If $\rho = 0.5,$ it shows that DM is risk-neutral; If $0.5 < \rho \leqslant 1,$ it shows that DM is risk-averse.

The new ranking method of GTIFNs $\{ {\tilde A_i}\}$ can be obtained according to the ascending order of rank index as following:

(1) If $Rank({\tilde A_i}) < Rank({\tilde A_j})$ then ${\tilde A_i} < {\tilde A_j} ;$

(2) If $Rank({\tilde A_i}) = Rank({\tilde A_j})$ then ${\tilde A_i} = {\tilde A_j} ;$

(3) If $Rank({\tilde A_i}) > Rank({\tilde A_j})$ then ${\tilde A_i} > {\tilde A_j} .$

4.2.   Intuitionistic fuzzy portfolio model based on the new possibilistic mean and variance of GTIFNS

In this part, we discuss the portfolio decision problem with generalized trapezoidal intuitionistic fuzzy number returns. Let us consider a fuzzy portfolio selection problem. Suppose investor has initial wealth 1 and may buy $m$ assets in the capital investment. The investor intends to allocate his/her wealth among the $m$ risky assets for making accounting investment plan. $X = ({x_1}, {x_2}, \cdots, {x_m})$ is the investor portfolio vector representing the capital allocation vector among $m$ securities, ${x_i}$ is the investment capital proportion of risky asset $i ;$ ${l_i} ,$ ${u_i}$ are the lower bound and upper bound of the capital invested in risky asset $i(1 \leqslant i \leqslant m) ,$ respectively. Suppose the future return rates of the alternative m assets are easily assessed by GTIFN ${\tilde A_i} = (({a_i}, {b_i}, {c_i}, {d_i}); {u_{{a_{_i}}}}, {v_{{a_{_i}}}}) ,$ $\forall i = 1, 2, \cdots, m.$ In order to construct the intuitionistic fuzzy portfolio decision model, we first introduce two important concepts which will be used in the proposed inutitionistic fuzzy portfolio decision model.

By using the previous Theorem 2 and Definition 6 we can compute the expected mean of fuzzy return of portfolio $X = ({x_1}, {x_2}, \cdots, {x_m})$ as $E(X) = \sum\nolimits_{j = 1}^m {{x_i}} M({\tilde A_i}) .$ By using the above-mentioned Theorem 3.4 and Definition 9 we can evaluate the possibilistic variance of intuitionistic fuzzy return of portfolio $X = ({x_1}, {x_2}, \cdots, {x_m})$ as

Assume that the whole investment process is self-financing, that is, the investor does not invest the additional capital during the portfolio selection. Inspired by the classic Markovitz portfolio theory, we establish the following intuitionistic fuzzy portfolio model by maximizing the expected mean of portfolio return and minimizing the possibilistic variance risk of portfolio as below.

where $\kappa$ is the selected parameters by investor reflecting the risk attitude of investor. It means the upper bound of risk tolerance of the portfolio movement.

By applying Lingo or Matlab Optimization Toolbox we can easily solve the above programming models. Finally, we can obtain the optimal portfolio strategy ${X^*} = (x_1^*, x_2^*, \cdots, x_m^*) ,$ which is the optimal solver corresponding to the maximum objective function value, $x_i^*$ is the optimal investment wealth proportion in risky asset $i$ $(1 \leqslant i \leqslant m)$ under the risk constraints.

5.   Conclusions

In this article, we introduce some notes of possibilistic variance of generalized trapezoidal intuitionistic fuzzy number and then discuss some important properties about possibilistic mean and variance of GTIFN based on possibility theory. The presented possibilistic mean and variance of GTIFN can be used to measure the expected return and risk of portfolio with GTIFN return. In the future, we will investigate the intuitionistic fuzzy portfolio decision-making and selection problem by maximizing possibilistic mean and minimizing possibilistic variance of portfolio.

Acknowledgments

We thank the Editor and the anonymous referees for their good suggestions and comments. This paper is supported by the Guangdong Basic and Applied Basic Research Foundation under Grant No. 2018A030313996.

Conflict of interest

The authors declare no conflict of interest in this paper.