| %C | %Si | %Mn | %P | %S | %Ni | %Cr | %Fe |
| 0.140 | 0.180 | 0.700 | 0.070 | 0.010 | 0.010 | 0.010 | Balance |
In this paper, we investigate the abstract integro-differential time-fractional wave equation with a small positive parameter ε. The Lp−Lq estimates for the resolvent operator family are obtained using the Laplace transform, the Mittag-Leffler operator family, and the C0−semigroup. These estimates serve as the foundation for some fixed point theorems that demonstrate the local-in-time existence of the solution in weighted function space. We first demonstrate that, for acceptable indices p∈[1,+∞) and s∈(1,+∞), the mild solution of the approximation problem converges to the solution of the associated limit problem in Lp((0,T),Ls(Rn)) as ε→0+. The resolvent operator family and a set of kernel k(t) assumptions form the foundation of the proof's primary methodology for evaluating norms. Moreover, we consider the asymptotic behavior of solutions as α→2−.
Citation: Yongqiang Zhao, Yanbin Tang. Approximation of solutions to integro-differential time fractional wave equations in Lp−space[J]. Networks and Heterogeneous Media, 2023, 18(3): 1024-1058. doi: 10.3934/nhm.2023045
| [1] | Andrea Tosin . Multiphase modeling and qualitative analysis of the growth of tumor cords. Networks and Heterogeneous Media, 2008, 3(1): 43-83. doi: 10.3934/nhm.2008.3.43 |
| [2] | Avner Friedman . PDE problems arising in mathematical biology. Networks and Heterogeneous Media, 2012, 7(4): 691-703. doi: 10.3934/nhm.2012.7.691 |
| [3] | Kota Kumazaki, Toyohiko Aiki, Adrian Muntean . Local existence of a solution to a free boundary problem describing migration into rubber with a breaking effect. Networks and Heterogeneous Media, 2023, 18(1): 80-108. doi: 10.3934/nhm.2023004 |
| [4] | Urszula Ledzewicz, Heinz Schättler, Shuo Wang . On the role of tumor heterogeneity for optimal cancer chemotherapy. Networks and Heterogeneous Media, 2019, 14(1): 131-147. doi: 10.3934/nhm.2019007 |
| [5] | Naoki Sato, Toyohiko Aiki, Yusuke Murase, Ken Shirakawa . A one dimensional free boundary problem for adsorption phenomena. Networks and Heterogeneous Media, 2014, 9(4): 655-668. doi: 10.3934/nhm.2014.9.655 |
| [6] | Antonio Fasano, Mario Primicerio, Andrea Tesi . A mathematical model for spaghetti cooking with free boundaries. Networks and Heterogeneous Media, 2011, 6(1): 37-60. doi: 10.3934/nhm.2011.6.37 |
| [7] | Achilles Beros, Monique Chyba, Oleksandr Markovichenko . Controlled cellular automata. Networks and Heterogeneous Media, 2019, 14(1): 1-22. doi: 10.3934/nhm.2019001 |
| [8] | Pierre Degond, Sophie Hecht, Nicolas Vauchelet . Incompressible limit of a continuum model of tissue growth for two cell populations. Networks and Heterogeneous Media, 2020, 15(1): 57-85. doi: 10.3934/nhm.2020003 |
| [9] | Marco Scianna, Luca Munaron . Multiscale model of tumor-derived capillary-like network formation. Networks and Heterogeneous Media, 2011, 6(4): 597-624. doi: 10.3934/nhm.2011.6.597 |
| [10] | Bing Feng, Congyin Fan . American call option pricing under the KoBoL model with Poisson jumps. Networks and Heterogeneous Media, 2025, 20(1): 143-164. doi: 10.3934/nhm.2025009 |
In this paper, we investigate the abstract integro-differential time-fractional wave equation with a small positive parameter ε. The Lp−Lq estimates for the resolvent operator family are obtained using the Laplace transform, the Mittag-Leffler operator family, and the C0−semigroup. These estimates serve as the foundation for some fixed point theorems that demonstrate the local-in-time existence of the solution in weighted function space. We first demonstrate that, for acceptable indices p∈[1,+∞) and s∈(1,+∞), the mild solution of the approximation problem converges to the solution of the associated limit problem in Lp((0,T),Ls(Rn)) as ε→0+. The resolvent operator family and a set of kernel k(t) assumptions form the foundation of the proof's primary methodology for evaluating norms. Moreover, we consider the asymptotic behavior of solutions as α→2−.
Steel is one of the metals types used in machine construction such as gears, shafts and sprocket [1]. Low to high strength steel can be easily formed into a desired product depend on the needs, properties and characters. Generally, steel has a variety of alloying elements such as Sulphur (S), Carbon (C), Silicon (Si), Phosphorus (P), Manganese (Mn) and another element. The most dominant element influencing the steel core is the carbon [2,3]. The amount of carbon content will have an impact on the mechanical properties of steel namely hardness, ductility and formability. Adding carbon content to steel able to increase the hardness and tensile strength, but make it brittle and reduce its tenacity [2].
Surface hardening process is one of the finishing stages to improve the product quality of steel. Several researchers reported that surface hardening make steel become hard on the surface and toughness in the core, for example in case of gears component: the surface must be hardened due to this component work in contact with one another component. The gear will wear out quickly if the surface hardness is low [1,4].
Sprocket is one of the most important driving gears from motor vehicle parts, the two-wheeled sprocket as a successor of transmission power which generated by the vehicle's engine. It is directly related to the chain in connected to the rear gear that functions to move the wheels. Therefore, the sprocket has to fulfill a requirement hardness on the edge of its teeth to prevent the sprocket from worn out due to friction caused by the chain [5,6].
Previous researcher conducted a study on the analysis of the effect carburizing media on the wear and hardness of a Supra X 125 motorcycle sprocket. In that case, they used 35% BaCO3 as activator with a temperature of 900 ℃ and holding time for 2 h. The hardness value before carburizing process of Supra X 125 motorcycle sprocket was 179.67 HV, whereas after the carburizing process achieved by the carburizing media of the “sirep” charcoal achieved in 629 HV [7].
Alias et al. stated that the increasing of hardness number is effective with surface hardening using carburizing method. Carburizing process is one phenomenon of the addition carbon into steel surface. The carbon will diffuse due to the activator and high temperature in the isolated pack. The active carbon content of each charcoal type is different depend on the source and process [8].
The research on surface hardening in SS400 steel was investigated by Sujita et al. using snail shell powder as an activator with teak (Tectona grandis) charcoal as a carburizing media. In that study, they did not report a hardness testing [9]. Therefore, this study examined the different things from previous studies namely surface hardening on SS400 steel with mahoni wood charcoal (MWC) as carburizing media and BaCO3 as an activator. Research information about surface hardening on SS400 steel is still enough considered limited, while SS400 steel is very applicable in the automotive industrial world for example sprocket and gear products. The variation of surface hardening was in volume fraction ratio of (MWC:BaCO3) and carburizing temperature. After carburizing, all samples were tested by using hardness and microstructural imaging.
Mahoni wood charcoal (MWC) was taken from a charcoal factory in Karang Duren village, Balung sub-district, Jember, East Java, Indonesia. The carbon content of MWC was calculated by using Equation 1 as according to previous research [10]. BaCO3 as activator was purchased from CV. Aneka Kimia, Jember, Indonesia. The SS400 steel was used as a steel material for surface hardened which has a carbon content for 0.140%. The detail chemical composition of SS400 steel can be seen in Table 1.
| %C | %Si | %Mn | %P | %S | %Ni | %Cr | %Fe |
| 0.140 | 0.180 | 0.700 | 0.070 | 0.010 | 0.010 | 0.010 | Balance |
DownLoad:
CSV
The MWC was crushed and sieved with a size of 60 mesh. The results of the 60 mesh sieve were sieved again in 80 mesh sieve. The results of charcoal powder that did not pass the 80 mesh sieve were used for the pack carburizing process. The chemical composition of the specimens of SS400 low carbon steel was shown in Table 1. The specimen and pack carburizing dimension were 3 cm × 3 cm × 0.6 cm and 15.9 cm × 10 cm × 9.5 cm, respectively. The BaCO3 activator was mixed with MWC in variations of 20, 30 and 40 wt%. The specimen was replicated for three pieces for each variation.
Before carburizing process, all specimens were weighted. Then, it was placed in a closed container pack steel which the content a mixed material of MWC and BaCO3 powder. The carburizing process was carried out at a temperature variation for 850 ℃ and 900 ℃ with a holding time 1 h. After that, it was quenched (rapid cooling) by distilled water for 8 s. All specimens were weighted to determine the mass changes after carburizing process. Then, it was prepared for hardness test and metallography observation.
The chemical composition of MWC was calculated using Equation 1 as reported by previous research [10]. Before determine the carbon content, there were several steps to obtain the fixed carbon from MWC namely: moisture, ash content and volatile matter calculation. After three steps above, we got fixed carbon. To determine the moisture, ash content and volatile matter, the extraction process accorded to [10,11]. The calculation of fixed carbon as Eq 1 below:
| Fixed carbon(%)=100%−[(moisture,%)+(ash,%)+(volatil matter,%)] | (1) |
Rockwell type C (HRC) with a 150 kg load was used to determine the hardness number of all specimens tested. All specimens were formed according to ASTM E18-15 standard [12]. The test was conducted with transversely direction on the surface. There were five times point of data test on the specimen surface. The results of hardness test were converted in Vickers Hardness Number (VHN). The Illustration of hardness test was presented in Figure 1.
Optical microscope BX451M was used to characterize the metallographic with magnification reaching 1000×. The specimens tested were raw materials (SS400 steel) and carburized materials. The carburized specimens were cut in the middle and then it was prepared for etching process. Before etching process, all specimens were sanded by using sandpaper until shiny (grid 80–2000). After that, metal polish autosol and velvet fabric material were applied for final etching. The etching process was conducted using comparison mixing between HNO3 (Nitridic acid) and ethanol for 2%: 98%. Finally, all specimens ready to be observed by optical microscope. As be noted, this observation aims to determine the total case depth of MWC in SS400 steel after carburizing.
The carbon percentage diffusion (CPD) into SS400 steel was calculated using a simple weighing method as the change in mass before and after the carburizing process. The CPD can be calculated using Eq 2:
| Carbon Percentage Diffusion(%)=wt−W0Wo×100% | (2) |
where, Wt and W0 were the specimen weight after and before carburizing process, respectively.
The chemical composition of MWC is presented in Table 2. The chemical composition test includes carbon, water, ash and vapor content. This test aims to determine the purity carbon after the carbonization process.
| No. | Water (%) | Ash (%) | Vapor (%) | Carbon (%) |
| 1. | 2 | 3 | 13 | 82 |
DownLoad:
CSV
It can be seen in Table 2 that the carbon content of MWC is 82%. This result was higher than previous report about charcoal wood from acacia (Acacia mangium) for 79% [13] and teak wood for 80.18% [14]. According to previous researcher, the high carbon content describes the level of purity of the charcoal produced. This case may be influenced by low levels of volatile matter and ash content. The place of the wood grows greatly influences the chemical composition of the wood, especially its carbon component [13].
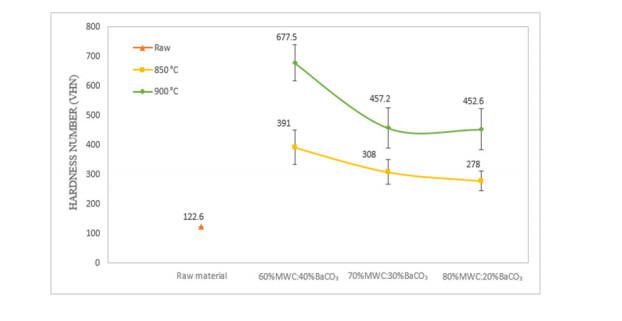
Figure 2 shows the hardness number of all samples tested by the Rockwell method. All samples tested were raw material, 60%MWC:40%BaCO3, 70%MWC:30%BaCO3, and 80%MWC:20%BaCO3 with different heating temperature for 850 ℃ and 900 ℃, respectively. The test was repeated three times for each variation. Each variation was carried out on five times point to determine the accurately hardness value.
It can be seen at the figure; the hardness value of raw material is lower than other materials tested for 122.6 HV. This value increase after carburizing process. The highest hardness value was obtained sample 60%MWC:40%BaCO3 with heating temperature 900 ℃ for 677.5 HV (increased 452% from raw material). High heating temperature makes the parent atomic (Fe) has the energy to vibrate, the vibration between the parent atomic affected in stretching (gaps between the parent atoms). The gap between the parent atoms is used by the C atomic to diffuse. The diffusion occurs in this case is interstitial due to the radius of the C atomic is less than 15% of the radius of the parent atomic (Fe) [15]. The heating temperature of 900 ℃ makes the raw material reach the austenite temperature in the Fe3C phase diagram. During the change phase to the austenite temperature, the raw material changes the its crystal structure from Body Center Cubic (BCC) to Face Centered Cubic (FCC) [16,17,18]. This change probably due to the metal has crossed the A3 line in the phase diagram Fe3C. Changing in crystal structure (BCC to FCC) make the carbon solubility in steel increased from 0.02% to 2.14% [16]. This phenomenon proves that the variations in the temperature of 900 ℃ have a higher hardness value than variations in 850 ℃.
The catalyst acts as a supplier of CO2 which able to bind C atomic directly to charcoal. The sample with variation of 60%MWC:40%BaCO3 produced more CO2 than another variation. According to previous report, the catalyst works as a CO2 carrier in binding the C atomic in the mahogany wood charcoal (MWC) to become CO. The C atomic transported by CO then bounded by Fe in steel. The Fe + CO bond produces [C] Fe + CO2 which [C] is denoted as a dissolved carbon to the Fe in this case steel [19].
Meanwhile, 80%MWC:20%BaCO3 at 900 ℃ has an average hardness for 452.5 HV. This value is lower than 60%MWC:40%BaCO3 at 900 ℃ sample. This is due to the differences in the volume fraction of MWC makes the low diffusion process. However, this sample is still in the austenite temperature. The diffusion process of C atoms continues until the C atoms in the environment have been used up, other than that the cooling method is influential on the pack carburizing method.
The cooling method used in this study was quenching. After the carburizing process was carried out at temperatures 850 ℃ and 900 ℃ with a holding for 1 h, the steel was removed and cooled quickly with water as a cooling medium. This case makes FCC crystal structure change to BCC structure quickly, but in rapid cooling is not enough time for carbon to diffuse out of the austenite in solid solution. Austenite has higher carbon content than ferrite due to the diffusion process should remove carbon from the solution. However, carbon is trapped because there is no more diffusion due to cold temperatures. This phenomenon affected in BCC structure become Body Centered Tetragonal (BCT) structure or martensite phase which indicated hard properties in steel material [16].
Microstructure observations were carried out to determine the changes in microstructure due to the influence of temperature and volume fraction of MWC before and after carburizing process (Figure 3). Figure 3a displays the microstructure of raw material (before carburizing process). It can be seen that raw material has ferrite and pearlite phase. The ferrite phase is shown in bright colors while the pearlite is shown in a dark color. The number of ferrite phases looks more than the pearlite phase. It synchronized with the hardness number result that raw material has low hardness for 122.6 HV. The ferrite phase makes a ductile property in a steel [20]. This is similar with the previous report which indicated ferrite phenomenon [9].
Figure 3b displays the specimen after carburizing process with 80%MWC:20%BaCO3 at 850 ℃. It shows the ferrite, pearlite and martensite structure. The martensite structure is formed on the surface while in the steel core material is formed pearlite-ferrite structure which is more dominated by ferrite phase. The martensite structure is formed due to the diffusion of C atom during pack carburizing process which is followed by the quenching process with the water as cooling media. This variation has the lowest total case depth diffusion for 0.20 mm compared to other variations. This phenomenon due to the carburizing process at 850 ℃ which affirmed by the carbon diffusion takes place on the body centered cubic (BCC) crystal structure. In this body, the carbon solubility value is 0.02%. The BaCO3 catalyst serves to produce CO2 which effected in C binding from MWC. This process produces CO which diffuses in the steel [19]. In contrast with Figure 3c (60%MWC:40%BaCO3 at 850 ℃), this specimen has total case depth diffusion for 0.32 mm even though the structure is similar with Figure 3b. The 40% catalyst helps to accelerate the rate of carbon diffusion due to the abundant supply of CO2.
Figure 3d shows the specimen microstructure in composition 80%MWC:20%BaCO3 at 900 ℃. The structure in this composition is ferrite, pearlite and martensite (lath martensite). The total case depth diffusion is 0.40 mm. This is due to the carburizing process carried out at 900 ℃ which occurs the structural changes from BCC to FCC with carbon solubility increases from 0.02% to 2.14%. This case effected in increasing the number of C atoms diffusion [21,22]. The different case was showed by Figure 3e (60%MWC:40%BaCO3 at 900 ℃). The structure has similar with Figure 3d. But the different is in total case depth diffusion. The total case depth diffusion in this specimen is 0.55 mm. This result was higher than all specimen tested. It is due to the role of temperature and activator during carburizing process which resulting in CO2 supply during carburizing [21].
Table 3 presents the percentage of carbon diffusion (CPD) from MWC into SS400 steel after carburizing treatment. The highest CPD was in specimen with composition 60%MWC:40%BaCO3 at 900 ℃ for 0.98%. This phenomenon was probably indicated by the addition of MWC which diffuses from the pack environment to the steel surface. The similar phenomenon was reported in previous report [23].
| Specimen | W0 (g) | Wt (g) | ΔW (g) | Percentage of diffusion (%) |
| 60%MWC:40%BaCO3 at 850 ℃ | 37.24630 | 37.55024 | 0.30394 | 0.81 |
| 70%MWC:30%BaCO3 at 850 ℃ | 36.27071 | 36.42082 | 0.15011 | 0.41 |
| 80%MWC:20%BaCO3 at 850 ℃ | 38.04883 | 38.05864 | 0.00981 | 0.02 |
| 60%MWC:40%BaCO3 at 900 ℃ | 40.03520 | 40.42880 | 0.39360 | 0.98 |
| 70%MWC:30%BaCO3 at 900 ℃ | 39.22458 | 39.57023 | 0.34565 | 0.88 |
| 80%MWC:20%BaCO3 at 900 ℃ | 38.04883 | 38.36106 | 0.31223 | 0.82 |
DownLoad:
CSV
Meanwhile, the specimen with composition 80%MWC:20%BaCO3 at 850 ℃ has the lowest CPD. From Table 3, it presents a little weight addition from 38.04883 to 38.05864 (CPD 0.02%). This phenomenon due to the slow process of carbon diffusion from the pack environment to the steel surface. The higher of the temperature and activator content then the deeper of carbon diffusion rate in steel.
The following conclusion could be derived from this study:
1. Pack carburizing process with temperature and volume faction variation influences SS400 steel hardness value, where the highest hardness value in composition 60%MWC:40%BaCO3 with temperature 900 ℃ for 677.4 HV, while the lowest hardness value in composition 80%MWC:20%BaCO3 at 850 ℃ for 278 HV. The higher temperature resulting in faster carbon diffusion.
2. Microstructure observation after carburizing process displays more dominant martensite phase but ferrite and pearlite phases are still present. Martensite phase in composition 60%MWC:40%BaCO3 sample is formed more due to the deeper carbon diffusion. The hardness value is recommended to improve the quality product and probably as potential material for sprocket parts application.
3. The mass changes occur in the pack carburizing process. The variation of 60%MWC:40%BaCO3 experienced as the highest mass increase of 0.39360 g. Meanwhile, the variation of 80%MWC:20%BaCO3 become the lowest variation of carbon additions which was 0.00981 g.
We thanks to University of Jember for its funding and supporting this research in the year of 2020.
We declare no conflict of interest.
| [1] | J. Prüss, Evolutionary Integral Equations and Applications, Basel: Birkhäuser Verlag, 87 (1993). https://doi.org/10.1007/978-3-0348-0499-8 |
| [2] | A. Lunardi, Analytic Semigroups and Optimal Regularity in Parabolic Problems, Basel: Birkhäuser, 16 (1995). |
| [3] | E. Bazhlekova, Fractional Evolution Equations in Banach Spaces, Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, 2001. |
| [4] |
X. Yang, Y. Tang, Decay estimates of nonlocal diffusion equations in some particle systems, J. Math. Phys., 60 (2019), 043302. https://doi.org/10.1063/1.5085894 doi: 10.1063/1.5085894
|
| [5] |
C. Gu, Y. Tang, Chaotic characterization of one dimensional stochastic fractional heat equation, Chaos Solitons Fractals, 145 (2021), 110780. https://doi.org/10.1016/j.chaos.2021.110780 doi: 10.1016/j.chaos.2021.110780
|
| [6] |
C. Gu, Y. Tang, Global solution to the Cauchy problem of fractional drift diffusion system with power-law nonlinearity, Netw. Heterog. Media, 18 (2023), 109–139. https://doi.org/10.3934/nhm.2023005 doi: 10.3934/nhm.2023005
|
| [7] |
J. P. C. Dos Santos, S. M. Guzzo, M. N. Rabelo, Asymptotically almost periodic solutions for abstract partial neutral integro-differential equation, Adv. Differ. Equ., 2010 (2010), 1–26. https://doi.org/10.1155/2010/310951 doi: 10.1155/2010/310951
|
| [8] |
J. P. C. Dos Santos, H. Henrˊiquez, Existence of s−asymptotically ω−periodic solutions to abstract integro-differential equations, Appl. Math. Comput., 256 (2015), 109–118. https://doi.org/10.1016/j.amc.2015.01.005 doi: 10.1016/j.amc.2015.01.005
|
| [9] |
R. C. Grimmer, A. J. Prichard, Analytic resolvent operators for integral equations in Banach space, J. Differ. Equ., 50 (1983), 234–259. https://doi.org/10.1016/0022-0396(83)90076-1 doi: 10.1016/0022-0396(83)90076-1
|
| [10] |
C. C. Kuo, S. Y. Shaw, C−cosine functions and the abstract Cauchy problem, Ⅰ, J. Math. Anal. Appl., 210 (1997), 632–646. https://doi.org/10.1006/jmaa.1997.5420 doi: 10.1006/jmaa.1997.5420
|
| [11] |
C. C. Kuo, S. Y. Shaw, C−cosine functions and the abstract Cauchy problem, Ⅱ, J. Math. Anal. Appl., 210 (1997), 647–666. https://doi.org/10.1006/jmaa.1997.5421 doi: 10.1006/jmaa.1997.5421
|
| [12] |
A. Lorenzi, F. Messina, Approximation of solutions to linear integro-differential parabolic equations in Lp−spaces, J. Math. Anal. Appl., 333 (2007), 642–656. https://doi.org/10.1016/j.jmaa.2006.11.042 doi: 10.1016/j.jmaa.2006.11.042
|
| [13] |
A. Lorenzi, F. Messina, Approximation of solutions to non-linear integro-differential parabolic equations in Lp−spaces, Differ. Integral Equ., 20 (2007), 693–720. https://doi.org/10.57262/die/1356039433 doi: 10.57262/die/1356039433
|
| [14] |
R. N. Wang, D. H. Chen, T. J. Xiao, Abstract fractional Cauchy problems with almost sectorial operators, J. Differ. Equ., 252 (2012), 202–235. https://doi.org/10.1016/j.jde.2011.08.048 doi: 10.1016/j.jde.2011.08.048
|
| [15] |
A. El-Sayed, M. Herzallah, Continuation and maximal regularity of an arbitrary (fractional) order evolutionary integro-differential equation, Appl. Anal., 84 (2005), 1151–1164. https://doi.org/10.1080/0036810412331310941 doi: 10.1080/0036810412331310941
|
| [16] |
R. Ponce, Hölder continuous solutions for fractional differential equations and maximal regularity, J. Differ. Equ., 255 (2013), 3284–3304. https://doi.org/10.1016/j.jde.2013.07.035 doi: 10.1016/j.jde.2013.07.035
|
| [17] | M. Conti, V. Pata, M. Squassina, Singular limit of differential systems with memory, Indiana Univ. Math. J., 55 (2006), 169–215. http://www.jstor.org/stable/24902350 |
| [18] | R. Agarwal, J. P. C. Dos Santos, C. Uevas, Analytic resolvent operator and existence results for fractional integro-differential equations, J. Abstr. Differ. Equ. Appl., 2 (2012), 26–47. |
| [19] | J. P. C Dos Santos, H. Henrˊiquez, E. Henˊaandez, Existence results for neutral integro-differential equations with unbounded delay, J. Integral Equ. Appl., 23 (2011), 289–330. http://www.jstor.org/stable/26163698 |
| [20] |
N. Tatar, Mittag-Leffler stability for a fractional Euler-Bernoulli problem, Chaos Solitons Fractals, 149 (2021), 1110777. https://doi.org/10.1016/j.chaos.2021.111077 doi: 10.1016/j.chaos.2021.111077
|
| [21] |
N. Tatar, Mittag-Leffler stability for a fractional viscoelastic telegraph problem, Math. Methods Appl. Sci., 44 (2021), 14184–14205. https://doi.org/10.1002/mma.7689 doi: 10.1002/mma.7689
|
| [22] |
P. Bedi, A. Kumar, T. Abdeljawad, A. Khan, J. Gomez-Aguilar, Mild solutions of coupled hybrid fractional order system with caputo-hadamard derivatives, Fractals, 29 (2021), 2150158. https://doi.org/10.1142/S0218348X21501589 doi: 10.1142/S0218348X21501589
|
| [23] |
H. Khan, T. Abdeljawad, J. Gomez-Aguilar, H. Tajadodi, A. Khan, Fractional order Volterra integro-differential equation with Mittag-Leffler kernel. Fractals, 29 (2021), 2150154. https://doi.org/10.1142/S0218348X2150153X doi: 10.1142/S0218348X2150153X
|
| [24] |
O. Martnez-Fuentes, F. Melndez-Vzquez, G. Fernndez-Anaya, J.F. Gómez-Aguilar, Analysis of fractional-order nonlinear dynamic systems with general analytic kernels: Lyapunov stability and inequalities, Mathematics, 9 (2021), 2084. https://doi.org/10.3390/math9172084 doi: 10.3390/math9172084
|
| [25] |
J. Asma, G. Rahman, M. Javed, Stability analysis for fractional order implicit ψ−Hilfer differential equations, Math. Methods Appl. Sci., 45 (2022), 2701–2712. https://doi.org/10.1002/mma.7948 doi: 10.1002/mma.7948
|
| [26] |
R. Dhayal, J. F. Gómez-Aguilar, J. Jimenez, Stability analysis of Atangana-Baleanu fractional stochastic differential systems with impulses, Int. J. Syst. Sci., 53 (2022), 3481–3495. https://doi.org/10.1080/00207721.2022.2090638 doi: 10.1080/00207721.2022.2090638
|
| [27] |
A. Gónzacutealez-Calderóna, L. X. Vivas-Cruzb, M. A. Taneco-Hernandezc, J. F. Gómezmez-Aguilar, Assessment of the performance of the hyperbolic-NILT method to solve fractional differential equations, Math. Comput. Simul., 206 (2023), 375–390. https://doi.org/10.1016/j.matcom.2022.11.022 doi: 10.1016/j.matcom.2022.11.022
|
| [28] |
A. Al-Omari, H. Al-Saadi, Existence of the classical and strong solutions for fractional semilinear initial value problems, Bound. Value Probl., 157 (2018), 1–13. https://doi.org/10.1186/s13661-018-1054-3 doi: 10.1186/s13661-018-1054-3
|
| [29] |
M. Benchohra, S. Litimein, J. J. Nieto, Semilinear fractional differential equations with infinite delay and non-instantaneous impulses, J. Fixed Point Theory Appl., 21 (2019), 1–16. https://doi.org/10.1007/s11784-019-0660-8 doi: 10.1007/s11784-019-0660-8
|
| [30] |
R. Chaudhary, M. Muslim, D. N. Pandey, Approximation of solutions to fractional stochastic integro-differential equations of order α∈(1,2], Stochastics, 92 (2020), 397–417. https://doi.org/10.1080/17442508.2019.1625904 doi: 10.1080/17442508.2019.1625904
|
| [31] | J. V. da C. Sousa, D. F. Gomes, E. C. de Oliveira, A new class of mild and strong solutions of integro-differential equation of arbitrary order in Banach space, arXiv, 2018. https://doi.org/10.48550/arXiv.1812.11197 |
| [32] |
M. Li, Q. Zheng, On spectral inclusions and approximations of α−times resolvent families, Semigroup Forum, 69 (2004), 356–368. https://doi.org/10.1007/s00233-004-0128-y doi: 10.1007/s00233-004-0128-y
|
| [33] |
K. Li, J. Peng, Fractional resolvents and fractional evolution equations, Appl. Math. Lett., 25 (2012), 808–812. https://doi.org/10.1016/j.aml.2011.10.023 doi: 10.1016/j.aml.2011.10.023
|
| [34] |
B. Li, H. Gou, Weak solutions nonlinear fractional integrodifferential equations in nonreflexive Banach spaces, Bound. Value Probl., 209 (2016), 1–13. https://doi.org/10.1186/s13661-016-0716-2 doi: 10.1186/s13661-016-0716-2
|
| [35] |
Z. D. Mei, J. G. Peng, J. H. Gao, General fractional differential equations of order α∈(1,2) and type β∈[0,1] in Banach spaces, Semigroup Forum, 94 (2017), 712–737. https://doi.org/10.1007/s00233-017-9859-4 doi: 10.1007/s00233-017-9859-4
|
| [36] |
S. A. Qasem, R. W. Ibrahim, Z. Siri, On mild and strong solutions of fractional differential equations with delay, AIP Conf. Proc., 1682 (2015), 020049. https://doi.org/10.1063/1.4932458 doi: 10.1063/1.4932458
|
| [37] |
H. Henrquez, J. Mesquita, J. Pozo, Existence of solutions of the abstract Cauchy problem of fractional order, J. Funct. Anal., 281 (2021), 109028. https://doi.org/10.1016/j.jfa.2021.109028 doi: 10.1016/j.jfa.2021.109028
|
| [38] |
I. Kim, K. H. Kim, S. Lim, An Lq(Lp)−theory for the time fractional evolution equations with variable coefficients, Adv. Math., 306 (2017), 123–176. https://doi.org/10.1016/j.aim.2016.08.046 doi: 10.1016/j.aim.2016.08.046
|
| [39] | P. Quittner, P. Souplet, Superlinear Parabolic Problems: Blow-up, Global Existence and Steady States, Basel: Birkhäuser Verlag, 2007. https://doi.org/10.1007/978-3-7643-8442-5 |
| [40] |
T. Kato, Blow-up of solutions of some nonlinear hyperbolic equations, Commun. Pure Appl. Math., 33 (1980), 501–505. https://doi.org/10.1002/cpa.3160330403 doi: 10.1002/cpa.3160330403
|
| [41] |
M. D'Abbicco, M. R. Ebert, T. H. Picon, The critical exponent(s) for the semilinear fractional diffusive equation, J. Fourier Anal. Appl., 25 (2019), 696–731. https://doi.org/10.1007/s00041-018-9627-1 doi: 10.1007/s00041-018-9627-1
|
| [42] |
B. T. Yordanov, Q. S. Zhang, Finite time blow-up for critical wave equations in high dimensions, J. Funct. Anal., 231 (2006), 361–374. https://doi.org/10.1016/j.jfa.2005.03.012 doi: 10.1016/j.jfa.2005.03.012
|
| [43] |
B. de Andrade, G. Siracusa, A. Viana, A nonlinear fractional diffusion equation: well-posedness, comparison results and blow-up, J. Math. Anal. Appl., 505 (2022), 125524. https://doi.org/10.1016/j.jmaa.2021.125524 doi: 10.1016/j.jmaa.2021.125524
|
| [44] |
P. M. de Carvalho-Neto, G. Planas, Mild solutions to the time fractional Navier-Stokes equations in Rn, J. Differ. Equ., 259 (2015), 2948-2980. https://doi.org/10.1016/j.jde.2015.04.008 doi: 10.1016/j.jde.2015.04.008
|
| [45] |
V. Keyantuo, M. Warma, On the interior approximate controllability for fractional wave equations, Discrete Contin. Dyn. Syst. Ser. A, 36 (2016), 3719–3739. https://doi.org/10.3934/dcds.2016.36.3719 doi: 10.3934/dcds.2016.36.3719
|
| [46] |
E. Alvarez, C. G. Gal, V. Keyantuo, M. Warma, Well-posedness results for a class of semi-linear super-diffusive equations, Nonlinear Anal., 181 (2019), 24–61. https://doi.org/10.1016/j.na.2018.10.016 doi: 10.1016/j.na.2018.10.016
|
| [47] |
J. P. C. Dos Santos, Fractional resolvent operator with α∈(0,1) and applications, Frac. Differ. Calc., 9 (2019), 187–208. https://doi.org/10.7153/fdc-2019-09-13 doi: 10.7153/fdc-2019-09-13
|
| [48] |
Y. Li, H. Sun, Z. Feng, Fractional abstract Cauchy problem with order α∈(1,2), Dyn. Partial Differ. Equ., 13 (2016), 155–177. https://dx.doi.org/10.4310/DPDE.2016.v13.n2.a4 doi: 10.4310/DPDE.2016.v13.n2.a4
|
| [49] |
Y. Li, Regularity of mild Solutions for fractional abstract Cauchy problem with order α∈(1,2), Z. Angew. Math. Phys., 66 (2015), 3283–3298. https://doi.org/10.1007/s00033-015-0577-z doi: 10.1007/s00033-015-0577-z
|
| [50] |
Q. Zhang, Y. Li, Global well-posedness and blow-up solution of the Cauchy problem for a time-fractional superdiffusion equation, J. Evol. Equ., 19 (2019), 271–303. https://doi.org/10.1007/s00028-018-0475-x doi: 10.1007/s00028-018-0475-x
|
| [51] | S. I. Piskarev, Evolution Equations in Banach Spaces. Theory of Cosine Operator Functions, Internet Notes, (2004), 122. |
| [52] | K. Boukerrioua, D. Diabi, B. Kilani, Some new Gronwall-bihari type inequalities and its application in the analysis for solutions to fractional differential equations, Int. J. Comput. Methods, 5 (2020), 60–68. |
| [53] |
I. Bihari, A generalisation of a lemma of Bellman and its application to uniqueness problems of differential equations, Acta Math. Hung., 7 (1956), 81–94. https://doi.org/10.1007/bf02022967 doi: 10.1007/bf02022967
|
| [54] |
V. V. Vasilev, S. I. Piskarev, Differential equations in Banach spaces Ⅱ. Theory of cosine operator functions, J. Math. Sci., 122 (2004), 3055–3174. https://doi.org/10.1023/B:JOTH.0000029697.92324.47 doi: 10.1023/B:JOTH.0000029697.92324.47
|
| [55] | A. Carpinteri, F. Mainardi, Fractional calculus, some basic problems in continuumand statistical mechanics, in Fractals and Fractional Calculus in Continuum Mechanics (eds. A. Carpinteri, F. Mainardi), Vienna: Springer-Verlag, 378 (1997), 291–348. https://doi.org/10.1007/978-3-7091-2664-6-7 |
| [56] | F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity, London: Imperial College Press, 2010. |
| [57] |
W. R. Schnrider, W. Wyss, Fractional diffusionand and wave equations, J. Math. Phys., 30 (1989), 134–144. https://doi.org/10.1063/1.528578 doi: 10.1063/1.528578
|
| 1. | Balaji Devarajan, Rajeshkumar LakshmiNarasimhan, Bhuvaneswari Venkateswaran, Sanjay Mavinkere Rangappa, Suchart Siengchin, Additive manufacturing of jute fiber reinforced polymer composites: A concise review of material forms and methods, 2022, 43, 0272-8397, 6735, 10.1002/pc.26789 | |
| 2. | Chung-Chun Wu, Effective Case Depth and Wear Resistance of Pack Carburized SCM 420 Steel Processed Using Different Concentrations of Natural Shell Waste Powders and Carburizing Duration, 2022, 12, 2073-4352, 296, 10.3390/cryst12020296 | |
| 3. | Chung-Chun Wu, Adel Shaaban, Mechanical Properties of Pack Carburized SCM 420 Steel Processed Using Natural Shell Powders and Extended Carburization Time, 2021, 11, 2073-4352, 1136, 10.3390/cryst11091136 | |
| 4. | Arif CANBULDU, Oğuz ERDEM, Katı Ortam Sementasyonunun Parametreleri ve Uygulama Alanları, 2023, 1308-5514, 10.29137/umagd.1401035 | |
| 5. | Clifford Ehi-Okoebor, Enesi Y. Salawu, Sunday A. Afolalu, Oluseyi O. Ajayi, Joseph F. Kayode, Sunday L. Lawal, 2023, Importance of hybrid organic carburizers on the Mechanical properties of mild steel: A Review, 979-8-3503-2478-5, 1, 10.1109/SEB-SDG57117.2023.10124621 | |
| 6. | Chung-Chun Wu, Study on microstructure and wear characteristics of carburized steel at different carburizing times using catalyst strombus turturella shell waste powders, 2023, 1267, 1755-1307, 012019, 10.1088/1755-1315/1267/1/012019 | |
| 7. | Ramzul Irham Riza, Ubaidillah Nur Fais, Nurmuntaha Agung Nugraha, Abdul Malik, 2024, 2838, 0094-243X, 060019, 10.1063/5.0185784 |
Yongqiang Zhao, Yanbin Tang. Approximation of solutions to integro-differential time fractional wave equations in Lp−space[J]. Networks and Heterogeneous Media, 2023, 18(3): 1024-1058. doi: 10.3934/nhm.2023045
| %C | %Si | %Mn | %P | %S | %Ni | %Cr | %Fe |
| 0.140 | 0.180 | 0.700 | 0.070 | 0.010 | 0.010 | 0.010 | Balance |
DownLoad:
CSV
| No. | Water (%) | Ash (%) | Vapor (%) | Carbon (%) |
| 1. | 2 | 3 | 13 | 82 |
DownLoad:
CSV
| Specimen | W0 (g) | Wt (g) | ΔW (g) | Percentage of diffusion (%) |
| 60%MWC:40%BaCO3 at 850 ℃ | 37.24630 | 37.55024 | 0.30394 | 0.81 |
| 70%MWC:30%BaCO3 at 850 ℃ | 36.27071 | 36.42082 | 0.15011 | 0.41 |
| 80%MWC:20%BaCO3 at 850 ℃ | 38.04883 | 38.05864 | 0.00981 | 0.02 |
| 60%MWC:40%BaCO3 at 900 ℃ | 40.03520 | 40.42880 | 0.39360 | 0.98 |
| 70%MWC:30%BaCO3 at 900 ℃ | 39.22458 | 39.57023 | 0.34565 | 0.88 |
| 80%MWC:20%BaCO3 at 900 ℃ | 38.04883 | 38.36106 | 0.31223 | 0.82 |
DownLoad:
CSV
| %C | %Si | %Mn | %P | %S | %Ni | %Cr | %Fe |
| 0.140 | 0.180 | 0.700 | 0.070 | 0.010 | 0.010 | 0.010 | Balance |
| No. | Water (%) | Ash (%) | Vapor (%) | Carbon (%) |
| 1. | 2 | 3 | 13 | 82 |
| Specimen | W0 (g) | Wt (g) | ΔW (g) | Percentage of diffusion (%) |
| 60%MWC:40%BaCO3 at 850 ℃ | 37.24630 | 37.55024 | 0.30394 | 0.81 |
| 70%MWC:30%BaCO3 at 850 ℃ | 36.27071 | 36.42082 | 0.15011 | 0.41 |
| 80%MWC:20%BaCO3 at 850 ℃ | 38.04883 | 38.05864 | 0.00981 | 0.02 |
| 60%MWC:40%BaCO3 at 900 ℃ | 40.03520 | 40.42880 | 0.39360 | 0.98 |
| 70%MWC:30%BaCO3 at 900 ℃ | 39.22458 | 39.57023 | 0.34565 | 0.88 |
| 80%MWC:20%BaCO3 at 900 ℃ | 38.04883 | 38.36106 | 0.31223 | 0.82 |
