Figure 1.
Even vertex magic total labelings of $ W_{3, 2} $ and $ W_{3, 3} $.
We study the Vlasov-Poisson-Fokker-Planck (VPFP) system with uncertainty and multiple scales. Here the uncertainty, modeled by multi-dimensional random variables, enters the system through the initial data, while the multiple scales lead the system to its high-field or parabolic regimes. We obtain a sharp decay rate of the solution to the global Maxwellian, which reveals that the VPFP system is decreasingly sensitive to the initial perturbation as the Knudsen number goes to zero. The sharp regularity estimates in terms of the Knudsen number lead to the stability of the generalized Polynomial Chaos stochastic Galerkin (gPC-SG) method. Based on the smoothness of the solution in the random space and the stability of the numerical method, we conclude the gPC-SG method has spectral accuracy uniform in the Knudsen number.
Citation: Yuhua Zhu. A local sensitivity and regularity analysis for the Vlasov-Poisson-Fokker-Planck system with multi-dimensional uncertainty and the spectral convergence of the stochastic Galerkin method[J]. Networks and Heterogeneous Media, 2019, 14(4): 677-707. doi: 10.3934/nhm.2019027
| [1] | Shahbaz Ali, Muhammad Khalid Mahmmod, Raúl M. Falcón . A paradigmatic approach to investigate restricted hyper totient graphs. AIMS Mathematics, 2021, 6(4): 3761-3771. doi: 10.3934/math.2021223 |
| [2] | Syed Ahtsham Ul Haq Bokhary, Zill-e-Shams, Abdul Ghaffar, Kottakkaran Sooppy Nisar . On the metric basis in wheels with consecutive missing spokes. AIMS Mathematics, 2020, 5(6): 6221-6232. doi: 10.3934/math.2020400 |
| [3] | Jing Su, Qiyue Zhang, Bing Yao . The connection between the magical coloring of trees. AIMS Mathematics, 2024, 9(10): 27896-27907. doi: 10.3934/math.20241354 |
| [4] | Gohar Ali, Martin Bača, Marcela Lascsáková, Andrea Semaničová-Feňovčíková, Ahmad ALoqaily, Nabil Mlaiki . Modular total vertex irregularity strength of graphs. AIMS Mathematics, 2023, 8(4): 7662-7671. doi: 10.3934/math.2023384 |
| [5] | Saeed Kosari, Yongsheng Rao, Zehui Shao, Jafar Amjadi, Rana Khoeilar . Complexity of signed total $k$-Roman domination problem in graphs. AIMS Mathematics, 2021, 6(1): 952-961. doi: 10.3934/math.2021057 |
| [6] | Kotte Amaranadha Reddy, S Sharief Basha . New classes of reverse super edge magic graphs. AIMS Mathematics, 2022, 7(3): 3590-3602. doi: 10.3934/math.2022198 |
| [7] | T. Deepa, Raúl M. Falcón, M. Venkatachalam . On the r-dynamic coloring of the direct product of a path with either a complete graph or a wheel graph. AIMS Mathematics, 2021, 6(2): 1470-1496. doi: 10.3934/math.2021090 |
| [8] | Linyu Li, Jun Yue, Xia Zhang . Double total domination number of Cartesian product of paths. AIMS Mathematics, 2023, 8(4): 9506-9519. doi: 10.3934/math.2023479 |
| [9] | Muhammad Amir Asif, Rashad Ismail, Ayesha Razaq, Esmail Hassan Abdullatif Al-Sabri, Muhammad Haris Mateen, Shahbaz Ali . An application on edge irregular reflexive labeling for $ m^t $-graph of cycle graph. AIMS Mathematics, 2025, 10(1): 1300-1321. doi: 10.3934/math.2025060 |
| [10] | Baolin Ma, Chao Yang . Distinguishing colorings of graphs and their subgraphs. AIMS Mathematics, 2023, 8(11): 26561-26573. doi: 10.3934/math.20231357 |
We study the Vlasov-Poisson-Fokker-Planck (VPFP) system with uncertainty and multiple scales. Here the uncertainty, modeled by multi-dimensional random variables, enters the system through the initial data, while the multiple scales lead the system to its high-field or parabolic regimes. We obtain a sharp decay rate of the solution to the global Maxwellian, which reveals that the VPFP system is decreasingly sensitive to the initial perturbation as the Knudsen number goes to zero. The sharp regularity estimates in terms of the Knudsen number lead to the stability of the generalized Polynomial Chaos stochastic Galerkin (gPC-SG) method. Based on the smoothness of the solution in the random space and the stability of the numerical method, we conclude the gPC-SG method has spectral accuracy uniform in the Knudsen number.
A graph labeling is an assignment of integers to the vertices or edges, or both, subject to certain conditions. Gallian [3] has written a dynamic survey of graph labeling. MacDougall et al. [5] introduced the notion of a vertex magic total labeling of graphs. Let $ G $ be a graph of order $ n $ and size $ m $. A vertex magic total labeling of $ G $ is defined as a one-to-one function
| $ f: V(G) \cup E(G) \rightarrow \{1, 2, \cdots, n+m\} $ |
with the property that for each vertex $ u $ of $ G $,
| $ f(u)+\sum\limits_{\substack{v\in N(u)}}f(uv) = k $ |
for some constant $ k $ where $ N(u) $ is the neighborhood of $ u $. The constant $ k $ is called the magic constant for $ f $. The vertex-magic total labelings of wheels and related graphs were studied in [6], and later in [11]. The properties of the general graphs such as cycles, paths, complete graphs, wheels, bipartite graphs and trees, which satisfy the vertex magic total labelings, were studied in [10]. MacDougall et al. [4] introduced the concept of a super vertex magic total labeling. They defined a vertex magic total labeling to be super if
| $ f[V(G)] = \{1, 2, \cdots, n\}. $ |
In 2017, Nagaraj et al. [7] introduced the concept of an even vertex magic total labeling. They called a vertex magic total labeling as even if
| $ f[V(G)] = \{2, 4, \cdots, 2n\}. $ |
A graph $ G $ is called an even vertex magic if there exists an even vertex magic total labeling of $ G $. We note that if $ G $ is an even vertex magic, then $ n \leq m $. The following results, which appeared in [7], are useful to us.
Theorem 1.1. [7] Let $ G $ be a nontrivial graph of order $ n $ and size $ m $. If $ G $ is an even vertex magic, then magic constant $ k $ is given by the following:
| $ {k = \frac{m^2+2mn+m}{n}}. $ |
A wheel $ W_n $, $ n \geq 3 $, is a graph of order $ n+1 $ that contains a cycle $ C_n $, for which every vertex in the cycle $ C_n $ is connected to one other vertex known as the hub. The edges of the wheel which are incident to the hub are called spokes. The vertices and edges of the cycle $ C_n $ in $ W_n $ are called rim vertices and rim edges, respectively. It was shown in [7] that a wheel $ W_n $ has no even vertex magic total labeling, as we state next.
Theorem 1.2. [7] A wheel $ W_n $ is not even vertex magic.
In this paper, the labeling problem is related to the work in [1]. In addition to the aforementioned vertex labeling by even numbers $ 2, 4, \cdots, 2n $, they studied vertex labelings by using three consecutive numbers $ 0, 1, 2 $ with some specific properties. These labelings were referred to as a weak Roman dominating function and a perfect Roman dominating function.
From the studies in [8,9,12], there exist graphs with the same order and size that are even vertex magics. Moreover, the wheel related graphs, namely fans, cycles and suns, having the even vertex magic total labelings were established in [7]. However, since these graphs have the same order and size, it is interesting and challenging to study wheel related graphs when the size is greater than the order, which have an even vertex magic total labeling.
The $ t $-fold wheel $ W_{n, t} $, $ n \geq 3 $, $ t \geq 1 $, is a wheel related graph derived from a wheel $ W_n $ by duplicating the $ t $ hubs, each adjacent to all rim vertices, and not adjacent to each other. It is observed that the $ t $-fold wheel $ W_{n, t} $ has a size $ nt+n $ that exceeds its order $ n+t $. The goal of this paper is to study conditions for an even vertex magic $ W_{n, t} $ in terms of $ n $ and $ t $. Furthermore, we also determine an even vertex magic total labeling of some $ t $-fold wheel $ W_{n, t} $.
Since the $ 1 $-fold wheel $ W_{n, 1} $ is isomorphic to the wheel $ W_n $ and by Theorem 1.1, $ W_n $ is not an even vertex magic. In this section, we consider the $ t $-fold wheel $ W_{n, t} $, where $ n $ and $ t $ are integers with $ n\geq 3 $ and $ t\geq2 $.
In order to present the conditions for an even vertex magic $ W_{n, t} $, we initially explore the magic constant of the $ t $-fold wheel $ W_{n, t} $ of order $ n+t $ and size $ nt+n $ by employing Theorem 1.1.
Proposition 2.1. Let $ n $ and $ t $ be integers with $ n\geq 3 $ and $ t\geq2 $. If the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic, then the magic constant is defined as follows:
| $ k = 2nt+3n+\frac{n^2t^2+2n^2t+n}{n+t}. $ |
We are able to show the bound of an integer $ t $ for the $ t $-fold wheel having an even vertex magic total labeling as follows.
Proposition 2.2. Let $ n $ and $ t $ be integers with $ n\geq 3 $ and $ t\geq2 $. If the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic, then $ 2 \leq t \leq n $.
Proof. Suppose that the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic with magic constant $ k $. By Proposition 2.1, we obtain the following:
| $ k = 2nt+3n+\frac{n^2t^2+2n^2t+n}{n+t}. $ |
On the contrary, assume that $ t > n $. Let $ t = n+r $, for some $ r \geq 1 $. Then,
| $ n^2t^2+2n^2t+n = n^4+2n^3r+n^2r^2+2n^3+2n^2r+n $ |
and
| $ n+t = n+(n+r) = 2n+r. $ |
Let
| $ P(n) = n^4+2n^3r+n^2r^2+2n^3+2n^2r+n. $ |
By using the remainder theorem, the remainder when $ P(n) $ is divided by $ 2n+r $ is as follows:
| $ P(-\frac{r}{2}) = \frac{r^4+4r^3-8r}{16}. $ |
If
| $ P(-\frac{r}{2}) = 0, $ |
then $ r = -2 $, which is a contradiction. Thus,
| $ P(-\frac{r}{2}) \neq 0. $ |
Specifically, $ n^2t^2+2n^2t+n $ is not divisible by $ n+t $. Thus, $ k $ is not an integer, which is a contradiction. Therefore, $ 2 \leq t \leq n $.
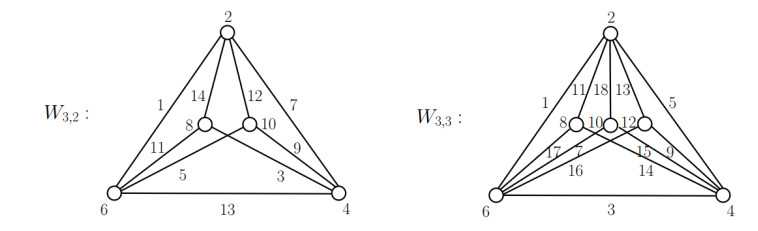
According to Proposition 2.2, the $ t $-fold wheel $ W_{3, t} $ is not an even vertex magic, where $ t \geq 4 $. Figure 1 shows the even vertex magics $ W_{3, 2} $ and $ W_{3, 3} $ with magic constants $ k = 36 $ and $ k = 50 $, respectively, where their vertices and edges are labeled by the even vertex magic total labelings. We present an even vertex magic total labeling of the $ t $-fold wheel $ W_{n, t} $ by considering only the integer $ n $ as the following results.
Proposition 2.3. For every integer $ n\geq 3 $, if the $ n $-fold wheel $ W_{n, n} $ is an even vertex magic, then $ n $ is odd.
Proof. Let $ n $ be an integer with $ n\geq 3 $. Suppose that the $ n $-fold wheel $ W_{n, n} $ is an even vertex magic with a magic constant $ k $. On the contrary, assume that $ n $ is even. There exists an integer $ q $ such that $ n = 2q $. By Proposition 2.1,
| $ k = 2n^2+3n+\frac{n^3+2n^2+1}{2}. $ |
Since
| $ n^3+2n^2+1 = 8q^3+8q^2+1 $ |
is odd, $ n^3+2n^2+1 $ is not divisible by $ 2 $. Thus, $ k $ is not an integer, which is a contradiction. Therefore, $ n $ is odd.
As we have seen in Figure 1, the $ 3 $-fold wheel $ W_{3, 3} $ is an even vertex magic, as indicated by Proposition 2.3. By an argument similar to the one used in the proof of Proposition 2.3, we obtain the condition for an even vertex magic $ W_{n, n-2} $, as we now show.
Proposition 2.4. For every integer $ n\geq 4 $, if the $ (n-2) $-fold wheel $ W_{n, n-2} $ is an even vertex magic, then $ n $ is even.
The even vertex magic total labeling of the $ 2 $-fold wheel $ W_{4, 2} $ with a magic constant $ k = 50 $ is shown in Figure 2.
In order to deduce an even vertex magic total labeling of the $ t $-fold wheel for achieving the main result, we need some additional notation for the $ t $-fold wheel $ W_{n, t} $. For every pair of integers $ n\geq 3 $ and $ t\geq2 $, let
| $ V(W_{n, t}) = \{u_1, u_2, \ldots, u_n, v_1, v_2, \ldots, v_t\} $ |
and
| $ E(W_{n, t}) = \{u_iu_{i+1} | 1 \leq i \leq n-1\}\cup\{u_nu_1\}\cup\{u_iv_j | 1 \leq i \leq n, 1 \leq j \leq t\}. $ |
Suppose the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic. Then, for any even vertex magic total labeling $ f $ of $ W_{n, t} $, let
| $ S_{rv} = \sum\limits_{i = 1}^{n}f(u_i), \ \ \ S_{re} = \sum\limits_{i = 1}^{n-1}f(u_iu_{i+1})+f(u_nu_1) $ |
and
| $ S_{h} = \sum\limits_{j = 1}^{t}f(v_j), \ \ \ S_{s} = \sum\limits_{j = 1}^{t} \sum\limits_{i = 1}^{n}f(u_iv_j). $ |
Next, we present the following lemma to show the necessary condition for an even vertex magic $ W_{n, t} $ with the following magic constant:
| $ k = 2nt+3n+\frac{n^2t^2+2n^2t+n}{n+t}. $ |
Note that
| $ S_{rv}+2S_{re}-S_{h} = (n-t)k. $ |
Lemma 2.5. Let $ n $ and $ t $ be integers where $ n\geq 3 $ and $ t\geq2 $. If the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic, then
| $ S_{rv}+2S_{re}-S_{h} = \\ (t^2+4t+3)n^2+(-2t^3-6t^2-3t+1)n+\frac{(t^3+2t^2-1)(2nt)}{n+t}. $ |
With the aid of Lemma 2.5 and Proposition 2.2, the necessary condition for an even vertex magic total labeling of the $ t $-fold wheel $ W_{n, t} $ can also be given in terms of $ n $ and $ t $.
Proposition 2.6. Let $ n $ and $ t $ be integers where $ n\geq 3 $ and $ t\geq2 $. If the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic, then
| $ (-t^2-2t+1)n^2+(2t^3+6t^2+7t+1)n-(t^2+t)-\frac{(t^3+2t^2-1)(2nt)}{n+t} \geq 0. $ |
Proof. Suppose that the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic. By Lemma 2.5,
| $ S_{rv}+2S_{re}-S_{h} = (t^2+4t+3)n^2+(-2t^3-6t^2-3t+1)n+\frac{(t^3+2t^2-1)(2nt)}{n+t}. $ |
Next, we consider the maximum of $ (S_{rv}+2S_{re}-S_{h}) $.
By Proposition 2.2, $ 2\leq t \leq n $, and then $ 2n+2t < nt+n+t+1 $. The maximum of
|
$ (Srv+2Sre−Sh)=∑2t+2≤i≤2n+2tiis eveni+2nt+2n+t∑i=nt+n+t+1i−∑2≤i≤2tiis eveni=(∑2≤i≤2n+2tiis eveni−∑2≤i≤2tiis eveni)+2(nt+2n+t∑i=1i−nt+n+t∑i=1i)−∑2≤i≤2tiis eveni=((2n+2t)(2n+2t+2)4−(2t)(2t+2)4)+2((nt+2n+t)(nt+2n+t+1)2−(nt+n+t)(nt+n+t+1)2)−(2t)(2t+2)4=2n2t+4n2+4nt−t2+2n−t. $
|
Since $ S_{rv}+2S_{re}-S_{h} $ does not exceed the maximum of $ (S_{rv}+2S_{re}-S_{h}) $, the maximum of
| $ (S_{rv}+2S_{re}-S_{h}) - (S_{rv}+2S_{re}-S_{h}) \geq 0. $ |
Therefore,
| $ (-t^2-2t+1)n^2+(2t^3+6t^2+7t+1)n-(t^2+t)-\frac{(t^3+2t^2-1)(2nt)}{n+t} \geq 0. $ |
Now, we investigate the sufficient condition for a labeling $ f $ that can be an even vertex magic total labeling of $ W_{n, n} $ when $ n $ is odd.
Theorem 2.7. Let $ n $ be an odd integer where $ n \geq 3 $. For every $ n $-fold wheel $ W_{n, n} $, let
| $ f: V(W_{n, n}) \cup E(W_{n, n}) \rightarrow \{1, 2, \ldots, n^2+3n\} $ |
be defined by the following:
|
$ f(ui) = 2i, if 1≤i≤n,f(vj) = 2n+2j, if 1≤j≤n,f(uiui+1) = 2n+1−2i, if 1≤i≤n−1,f(unu1) = 1, f(un+1−jvj) = n2+3n+1−2j, if 1≤j≤n,f[EH]−f[{un+1−jvj|1≤j≤n}] = {2n+1,2n+3,…,n2+n−1} ∪{4n+2,4n+4,…,n2+3n}, if EH={uivj|1≤i,j≤n}. $
|
If
| $ \sum\limits_{j = 1}^{n-1}f(u_1v_j) = \frac{n^3+4n^2-5}{2}, $ |
then $ f $ can be an even vertex magic total labeling of $ W_{n, n} $.
Proof. Assume that
| $ \sum\limits_{j = 1}^{n-1}f(u_1v_j) = \frac{n^3+4n^2-5}{2}. $ |
We have that
|
$ Ss−n∑j=1f(un+1−jvj)=∑2n+1≤i≤n2+n−1iis oddi+∑4n+2≤i≤n2+3niis eveni=(∑1≤i≤n2+n−1iis oddi−∑1≤i≤2n−1iis oddi)+(∑2≤i≤n2+3niis eveni−∑2≤i≤4niis eveni)=((n2+n)24−(2n)24)+((n2+3n)(n2+3n+2)4−4n(4n+2)4)=n4+4n3−4n2−n2, $
|
and then,
| $ \left(S_{s}-\sum\limits_{j = 1}^{n}f(u_{n+1-j}v_j)\right)-\sum\limits_{j = 1}^{n-1}f(u_1v_j) = \frac{n^4+3n^3-8n^2-n+5}{2}\, . $ |
Next, we consider the sum of the label of each vertex and the labels of all edges incident to this vertex. By the assumption, for $ 1 \leq j\leq n $,
|
$ f(vj)+n∑i=1f(uivj)=f(vj)+f(un+1−jvj)+∑1≤i≤ni≠n+1−jf(uivj)=f(vj)+f(un+1−jvj)+Ss−n∑j=1f(un+1−jvj)n=(2n+2j)+(n2+3n+1−2j)+n3+4n2−4n−12=n3+6n2+6n+12, $
|
|
$ f(u1)+f(u1u2)+f(unu1)+n∑j=1f(u1vj)=f(u1)+f(u1u2)+f(unu1)+f(u1vn)+n−1∑j=1f(u1vj)=2+(2n+1−2)+1+(n2+n−1+2)+n3+4n2−52=n3+6n2+6n+12. $
|
For $ 2 \leq i\leq n, $
|
$ f(ui)+f(uiui+1)+f(ui−1ui)+n∑j=1f(uivj)=f(ui)+f(uiui+1)+f(ui−1ui)+f(uivn+1−i)+∑1≤j≤nj≠n+1−if(uivj)=f(ui)+f(uiui+1)+f(ui−1ui)+f(uivn+1−i)+(Ss−n∑j=1f(un+1−jvj))−n−1∑j=1f(u1vj)n−1=2i+(2n+1−2i)+(2n+1−2i+2)+(n2+n−1+2i)+n3+4n2−4n−52=n3+6n2+6n+12. $
|
Therefore, $ f $ can be an even vertex magic total labeling of $ W_{n, n} $ with a magic constant
| $ k = \frac{n^3+6n^2+6n+1}{2}. $ |
Now, we investigate the sufficient condition for a labeling $ f $ that can be an even vertex magic total labeling of $ W_{n, n-2} $ when $ n $ is even.
Theorem 2.8. Let $ n $ be an even integer with $ n \geq 4 $. For every $ (n-2) $-fold wheel $ W_{n, n-2} $, let
| $ f: V(W_{n, n-2}) \cup E(W_{n, n-2}) \rightarrow \{1, 2, \ldots, n^2+n-2\} $ |
be defined by the following:
|
$ f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n−2,f[EC]={a1,a2,⋯,an},if EC={uiui+1,unu1|1≤i≤n−1},f[EH]={1,2,⋯,n2+n−2}−{2,4,⋯,2n+4,a1,a2,⋯,an},if EH={uivj|1≤i≤n,1≤j≤n−2}. $
|
If
| $ S_{s} = \frac{n^4+n^3-15n^2+20n-4}{2}, $ |
then $ f $ can be an even vertex magic total labeling of $ W_{n, n-2} $.
Proof. Assume that
| $ S_{s} = \frac{n^4+n^3-15n^2+20n-4}{2}. $ |
It suffices to show that for each vertex $ u $ of $ W_{n, n-2} $,
| $ f(u)+\sum\limits_{\substack{v\in N(u)}}f(uv) = k, $ |
where
| $ k = \frac{n^3+3n^2-3n}{2}. $ |
To do this, we consider the relevant sums, as follows.
Since the sum of the labels of all rim edges is equal to the sum of the labels of all vertices and the labels of all edges subtracted by the sum of the labels of all vertices and the labels of all spokes, it follows that
|
$ Sre=n2+n−2∑i=1i−∑2≤i≤4n−4iis eveni−Ss=(n2+n−2)(n2+n−1)2−(4n−4)(4n−2)4−n4+n3−15n2+20n−42=n3+5n2−11n+22. $
|
Since the sum of the labels of all hubs is equal to the sum of even integers from $ 2n+2 $ to $ 4n-4 $,
|
$ Sh+Ss=∑2n+2≤i≤4n−4iis eveni+Ss=(∑2≤i≤4n−4iis eveni−∑2≤i≤2niis eveni)+Ss=(4n−4)(4n−2)4−(2n)(2n+2)4+n4+n3−15n2+20n−42=n4+n3−9n2+6n2. $
|
Since the sum of the labels of all rim vertices is equal to the sum of even integers from $ 2 $ to $ 2n $,
|
$ Srv+2Sre+Ss=∑2≤i≤2niis eveni+2Sre+Ss=(2n)(2n+2)4+2(n3+5n2−11n+22)+n4+n3−15n2+20n−42=n4+3n3−3n22. $
|
Next, we consider the sum of the label of each vertex and the labels of all edges incident to this vertex. We have the sum of the label of each hub and the labels of all edges incident to this hub as follows.
For $ 1 \leq j\leq n-2 $,
| $ f(v_j)+\sum\limits_{i = 1}^{n}f(u_iv_j) = \frac{S_{h}+S_{s}}{n-2} = \frac{n^3+3n^2-3n}{2}. $ |
We obtain the sum of the label of each rim vertex and the labels of all edges incident to this rim vertex as follows.
For $ 2 \leq i\leq n-1, $
| $ f(u_i)+f(u_iu_{i+1})+f(u_{i-1}u_i)+\sum\limits_{j = 1}^{n-2}f(u_iv_j) = \frac{ S_{rv}+2S_{re}+S_{s}}{n} = \frac{n^3+3n^2-3n}{2}. $ |
Similarly,
| $ f(u_n)+f(u_nu_1)+f(u_{n-1}u_n)+\sum\limits_{j = 1}^{n-2}f(u_nv_j) = \frac{n^3+3n^2-3n}{2} $ |
and
| $ f(u_1)+f(u_1u_2)+f(u_nu_1)+\sum\limits_{j = 1}^{n-2}f(u_1v_j) = \frac{n^3+3n^2-3n}{2}. $ |
Therefore, $ f $ can be an even vertex magic total labeling of $ W_{n, n-2} $ with the following magic constant:
| $ k = \frac{n^3+3n^2-3n}{2}. $ |
In this section, we establish a characterization of an even vertex magic $ W_{n, t} $ for an integer $ 3\leq n \leq 9 $. First, we present an $ n $-fold wheel $ W_{n, n} $ which has an even vertex magic total labeling for every odd integer $ 3\leq n \leq 9 $ as follows.
Theorem 3.1. For every odd integer $ 3\leq n \leq 9 $, the $ n $-fold wheel $ W_{n, n} $ is an even vertex magic.
Proof. Let $ n $ be an odd integer where $ 3\leq n \leq 9 $. We define
| $ f: V(W_{n, n}) \cup E(W_{n, n}) \rightarrow \{1, 2, \cdots, n^2+3n\}, $ |
as the sufficient condition of Theorem 2.7, by
|
$ f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n,f(uiui+1)=2n+1−2i,if 1≤i≤n−1,f(unu1)=1, $
|
and for $ 1 \leq i, j \leq n $, $ f(u_iv_j) $ are shown in Tables 1–4,
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ |
| $ u_1 $ | 11 | 18 | 13 |
| $ u_2 $ | 14 | 15 | 9 |
| $ u_3 $ | 17 | 7 | 16 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ |
| $ u_1 $ | 15 | 21 | 36 | 38 | 31 |
| $ u_2 $ | 13 | 30 | 29 | 33 | 28 |
| $ u_3 $ | 40 | 24 | 35 | 19 | 17 |
| $ u_4 $ | 34 | 37 | 11 | 23 | 32 |
| $ u_5 $ | 39 | 27 | 26 | 22 | 25 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ |
| $ u_1 $ | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| $ u_2 $ | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| $ u_3 $ | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| $ u_4 $ | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| $ u_5 $ | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| $ u_6 $ | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| $ u_7 $ | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ | $ v_8 $ | $ v_9 $ |
| $ u_1 $ | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| $ u_2 $ | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| $ u_3 $ | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| $ u_4 $ | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| $ u_5 $ | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| $ u_6 $ | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| $ u_7 $ | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| $ u_8 $ | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| $ u_9 $ | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
DownLoad:
CSV
For every odd integer $ 3 \leq n\leq 9 $, the labeling $ f $, as defined above, is an even vertex magic total labeling of the $ n $-fold wheel $ W_{n, n} $ with magic constants $ k = 50, 153, 340 $ and $ 635 $, respectively. Therefore, $ W_{n, n} $ is an even vertex magic.
As a consequence of an even vertex magic $ W_{3, 2} $, Proposition 2.2 and Theorem 3.1, in any $ t $-fold wheel $ W_{3, t} $, we are able to show that both $ W_{3, t} $ and $ W_{3, t} $ are only even vertex magics.
Theorem 3.2. For every integer $ t \geq 2 $, the $ t $-fold wheel $ W_{3, t} $ is an even vertex magic if and only if $ t = 2, 3 $.
The following result gives the necessary and sufficient condition for the $ t $-fold wheel $ W_{n, t} $ to be an even vertex magic for every odd integer $ 5\leq n \leq 9 $.
Theorem 3.3. For every odd integer $ 5\leq n \leq 9 $ and an integer $ t \geq 2 $, the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic if and only if $ t = n $.
Proof. Let $ n $ be an odd integer where $ 5\leq n \leq 9 $ and $ t $ is an integer where $ t \geq 2 $. Assume that the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic. By Proposition 2.2, $ 2\leq t \leq n $.
Case 1. $ n = 5, 7. $ If $ 2\leq t \leq n-1 $, then $ n^2t^2+2n^2t+n $ is not divisible by $ n+t $, and hence $ k $ is not an integer, which is a contradiction. Therefore, $ t = n $.
Case 2. $ n = 9. $ If either $ t = 2 $ or $ 4\leq t \leq n-1 $, then $ n^2t^2+2n^2t+n $ is not divisible by $ n+t $, and hence $ k $ is not an integer, which is a contradiction. If $ t = 3 $, then,
| $ 2nt^3-n^2t^2-2n^2t+6nt^2+7nt+n^2-t^2+n-t-\frac{2nt^4+4nt^3-2nt}{n+t} = -174 < 0, $ |
which is a contradiction with Proposition 2.6. Therefore, $ t = n $.
Conversely, assume $ t = n $. By Theorem 3.1, $ W_{n, t} $ is an even vertex magic.
We show an even vertex magic total labeling of $ W_{n, n-2} $ for every even integer $ 4\leq n \leq 8 $ as follows.
Theorem 3.4. For every even integer $ 4 \leq n \leq 8 $, the $ (n-2) $-fold wheel $ W_{n, n-2} $ is an even vertex magic.
Proof. Let $ n $ be an even integer with $ 4 \leq n \leq 8 $. We define
| $ f: V(W_{n, n-2}) \cup E(W_{n, n-2}) \rightarrow \{1, 2, \ldots, n^2+n-2\} $ |
as the sufficient condition of Theorem 2.8, by
|
$ f(ui)=2i,if 1≤i≤n,f(vj)=2n+2j,if 1≤j≤n−2, $
|
for $ 1 \leq i\leq n-1 $, $ f(u_iu_{i+1}) $ and $ f(u_nu_1) $ are shown in Tables 5–7.
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_1) $ |
| 18 | 9 | 11 | 13 |
DownLoad:
CSV
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_1) $ |
| 40 | 39 | 38 | 13 | 17 | 19 |
DownLoad:
CSV
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_7) $ | $ f(u_7u_8) $ | $ f(u_8u_1) $ |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
DownLoad:
CSV
And for $ 1 \leq i\leq n $ and $ 1 \leq j\leq n-2 $, $ f(u_iv_j) $ are shown in Tables 8–10.
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ |
| $ u_1 $ | 16 | 1 |
| $ u_2 $ | 14 | 5 |
| $ u_3 $ | 7 | 17 |
| $ u_4 $ | 3 | 15 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ |
| $ u_1 $ | 36 | 24 | 3 | 29 |
| $ u_2 $ | 11 | 25 | 33 | 1 |
| $ u_3 $ | 26 | 9 | 5 | 30 |
| $ u_4 $ | 22 | 23 | 34 | 15 |
| $ u_5 $ | 37 | 21 | 28 | 27 |
| $ u_6 $ | 7 | 35 | 32 | 31 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ |
| $ u_1 $ | 69 | 3 | 40 | 56 | 39 | 50 |
| $ u_2 $ | 1 | 67 | 5 | 59 | 31 | 35 |
| $ u_3 $ | 21 | 17 | 65 | 7 | 44 | 46 |
| $ u_4 $ | 42 | 38 | 23 | 33 | 9 | 57 |
| $ u_5 $ | 61 | 27 | 37 | 34 | 30 | 15 |
| $ u_6 $ | 41 | 53 | 49 | 32 | 47 | 25 |
| $ u_7 $ | 29 | 60 | 54 | 52 | 63 | 36 |
| $ u_8 $ | 58 | 55 | 45 | 43 | 51 | 48 |
DownLoad:
CSV
For every even integer $ 4 \leq n \leq 8 $, the labeling $ f $, as defined above, is an even vertex magic total labeling of the $ (n-2) $-fold wheel $ W_{n, n-2} $ with magic constants $ k = 50, 153 $ and $ 340 $, respectively. Therefore, $ W_{n, n-2} $ is an even vertex magic.
There is a similar methodology of the proof of Theorem 3.4, which is also used in the study of graph operations (see [2]). Next, we determine a characterization of the $ t $-fold wheel $ W_{n, t} $ to be an even vertex magic for every even integer $ 4 \leq n \leq 8 $. In order to we need to present the following lemma involving a $ 3 $-fold wheel $ W_{8, 3} $.
Lemma 3.5. The $ 3 $-fold wheel $ W_{8, 3} $ is not an even vertex magic.
Proof. On the contrary, assume that the $ 3 $-fold wheel $ W_{8, 3} $ is an even vertex magic with a magic constant $ k $. Since $ W_{8, 3} $ has an order $ 11 $ and a size $ 32 $ and by Proposition 2.1, $ k = 160 $. We have that
| $ S_{rv} = 132, \ \ 2S_{re} = 1, 628-2S_{s} $ |
and
| $ S_{rv}+2S_{re}+S_{s} = 8k = 1, 280. $ |
Thus, $ S_{s} = 480 $. However, $ S_{h}+S_{s} = 3k = 480 $. This is a contradiction because $ S_{h} > 0 $. Therefore, $ W_{8, 3} $ is not an even vertex magic.
We are able to show that the necessary and sufficient condition for the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic for every even integer $ 4\leq n \leq 8 $.
Theorem 3.6. For every even integer $ 4\leq n \leq 8 $ and integer $ t \geq 2 $, the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic if and only if $ t = n-2 $.
Proof. Let $ n $ be an even integer where $ 4\leq n \leq 8 $ and $ t $ is an integer where $ t \geq 2 $. Assume that the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic. By Proposition 2.2, $ 2\leq t \leq n $.
Case 1. $ n = 4, 6. $ If either $ 2\leq t \leq n-3 $ or $ n-1\leq t \leq n $, then $ n^2t^2+2n^2t+n $ is not divisible by $ n+t $, and hence $ k $ is not an integer, which is a contradiction. Therefore, $ t = n-2 $.
Case 2. $ n = 8. $ If either $ 4\leq t \leq n-3 $ or $ n-1\leq t \leq n $, then $ n^2t^2+2n^2t+n $ is not divisible by $ n+t $, and hence $ k $ is not an integer, which is a contradiction. If $ t = 3 $, then, by Lemma 3.5, $ W_{n, t} $ is not an even vertex magic, which is a contradiction. If $ t = 2 $, then,
| $ 2nt^3-n^2t^2-2n^2t+6nt^2+7nt+n^2-t^2+n-t-\frac{2nt^4+4nt^3-2nt}{n+t} = -62 < 0, $ |
which is a contradiction with Proposition 2.6. Therefore, $ t = n-2 $.
Conversely, assume $ t = n-2 $. By Theorem 3.4, $ W_{n, t} $ is an even vertex magic.
In this paper, we have not only established the bound of an integer $ t $ for the even vertex magic total labeling of the $ t $-fold wheel, but have also presented the necessary condition for such labeling in terms of $ n $ and $ t $. Furthermore, we have conducted an investigation into the sufficient conditions for labelings that can serve as even vertex magic total labelings for $ W_{n, n} $ when $ n $ is odd, and $ W_{n, n-2} $ when $ n $ is even.
Our research has led us to the following significant conclusions:
● For every integer $ t \geq 2 $, the $ t $-fold wheel $ W_{3, t} $ is an even vertex magic total labeling if and only if $ t = 2, 3 $.
● For every odd integer $ 5 \leq n \leq 9 $ and an integer $ t \geq 2 $, the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic total labeling if and only if $ t = n $.
● For every even integer $ 4 \leq n \leq 8 $ and an integer $ t \geq 2 $, the $ t $-fold wheel $ W_{n, t} $ is an even vertex magic total labeling if and only if $ t = n-2 $.
In essence, our work has discussed the characterizations of $ t $-fold wheel $ W_{n, t} $ to possess an even vertex magic total labeling for an integer $ 3 \leq n \leq 9 $. It would be interesting to apply the results of this paper to further study under what conditions for $ W_{n, t} $ will be an even vertex magic, especially for a larger $ n $.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare that they have no conflicts of interest.
| [1] |
Low and high field scaling limits for the Vlasov- and Wigner-Poisson-Fokker-Planck systems. Transport Theory and Statistical Physics (2001) 30: 121-153. 
|
| [2] |
Galerkin finite element approximations of stochastic elliptic partial differential equations. SIAM Journal on Numerical Analysis (2004) 42: 800-825.
|
| [3] |
F. Bouchut, F. Golse and M. Pulvirenti, Kinetic Equations and Asymptotic Theory, Series in Applied Mathematics (Paris), 4. Gauthier-Villars, Éditions Scientifiques et Médicales Elsevier, Paris, 2000. |
| [4] | Stochastic probems in physics and astronomy. Reviews of Modern Physics (1943) 15: 1-89. |
| [5] |
Convergence rates of best $N$-term galerkin approximations for a class of elliptic sPDEs. Foundations of Computational Mathematics (2010) 10: 615-646.
|
| [6] |
Analytic regularity and polynomial approximation of parametric and stochastic elliptic PDE's. Analysis and Applications (2011) 9: 11-47.
|
| [7] |
A kinetic flocking model with diffusion. Communications in Mathematical Physics (2010) 300: 95-145.
|
| [8] |
Multidimensional high-field limit of the electrostatic Vlasov-Poisson-Fokker-Planck system. Journal of Differential Equations (2005) 213: 418-442.
|
| [9] |
A stochastic Galerkin method for the Boltzmann equation with uncertainty. Journal of Computational Physics (2016) 315: 150-168.
|
| [10] |
Uncertainty quantification for kinetic equations. Uncertainty Quantification for Kinetic and Hyperbolic Equations, SEMA SIMAI Springer Ser., Springer, Cham (2017) 14: 193-229.
|
| [11] |
On the Vlasov-Poisson-Fokker-Planck equation near Maxwellian. Discrete & Continuous Dynamical Systems-Series B (2013) 18: 681-691.
|
| [12] | Asymptotic preserving (AP) schemes for multiscale kinetic and hyperbolic equations: A review. Riv. Math. Univ. Parma (N.S.) (2012) 2: 177-216. |
| [13] |
S. Jin, J.-G. Liu and Z. Ma, Uniform spectral convergence of the stochastic Galerkin method for the linear transport equations with random inputs in diffusive regime and a micro-macro decomposition based asymptotic-preserving method, Research in the Mathematical Sciences, 4 (2017), 25 pp. |
| [14] |
Asymptotic-preserving methods for hyperbolic and transport equations with random inputs and diffusive scalings. Journal of Computational Physics (2015) 289: 35-52.
|
| [15] |
Hypocoercivity and uniform regularity for the Vlasov-Poisson-Fokker-Planck system with uncertainty and multiple scales. SIAM Journal on Mathematical Analysis (2018) 50: 1790-1816.
|
| [16] |
Uniform regularity for linear kinetic equations with random input based on hypocoercivity. SIAM/ASA J. Uncertainty Quantification (2017) 5: 1193-1219.
|
| [17] |
Hypocoercivity based sensitivity analysis and spectral convergence of the stochastic Galerkin approximation to collisional kinetic equations with multiple scales and random inputs. SIAM Multiscale Modeling and Simulation (2018) 16: 1085-1114.
|
| [18] |
High-field limit for the Vlasov-Poisson-Fokker-Planck system. Archive for Rational Mechanics and Analysis (2001) 158: 29-59.
|
| [19] |
Uniform regularity in the random space and spectral accuracy of the stochastic galerkin method for a kinetic-fluid two-phase flow model with random initial inputs in the light particle regime. Mathematical Modelling and Numerical Analysis (2018) 52: 1651-1678.
|
| [20] |
Asymptotic behaviour for the Vlasov-Poisson-Fokker-Planck system. Nonlinear Analysis: Theory, Methods & Applications (1997) 30: 5217-5228.
|
| [21] |
E. M. Stein, Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, No. 30 Princeton University Press, Princeton, N.J., 1970. |
| [22] |
Y. H. Zhu, Sensitivity analysis and uniform regularity for the Boltzmann equation with uncertainty and its stochastic Galerkin approximation, Preprint. |
Yuhua Zhu. A local sensitivity and regularity analysis for the Vlasov-Poisson-Fokker-Planck system with multi-dimensional uncertainty and the spectral convergence of the stochastic Galerkin method[J]. Networks and Heterogeneous Media, 2019, 14(4): 677-707. doi: 10.3934/nhm.2019027
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ |
| $ u_1 $ | 11 | 18 | 13 |
| $ u_2 $ | 14 | 15 | 9 |
| $ u_3 $ | 17 | 7 | 16 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ |
| $ u_1 $ | 15 | 21 | 36 | 38 | 31 |
| $ u_2 $ | 13 | 30 | 29 | 33 | 28 |
| $ u_3 $ | 40 | 24 | 35 | 19 | 17 |
| $ u_4 $ | 34 | 37 | 11 | 23 | 32 |
| $ u_5 $ | 39 | 27 | 26 | 22 | 25 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ |
| $ u_1 $ | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| $ u_2 $ | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| $ u_3 $ | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| $ u_4 $ | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| $ u_5 $ | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| $ u_6 $ | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| $ u_7 $ | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ | $ v_8 $ | $ v_9 $ |
| $ u_1 $ | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| $ u_2 $ | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| $ u_3 $ | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| $ u_4 $ | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| $ u_5 $ | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| $ u_6 $ | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| $ u_7 $ | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| $ u_8 $ | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| $ u_9 $ | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
DownLoad:
CSV
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_1) $ |
| 18 | 9 | 11 | 13 |
DownLoad:
CSV
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_1) $ |
| 40 | 39 | 38 | 13 | 17 | 19 |
DownLoad:
CSV
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_7) $ | $ f(u_7u_8) $ | $ f(u_8u_1) $ |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ |
| $ u_1 $ | 16 | 1 |
| $ u_2 $ | 14 | 5 |
| $ u_3 $ | 7 | 17 |
| $ u_4 $ | 3 | 15 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ |
| $ u_1 $ | 36 | 24 | 3 | 29 |
| $ u_2 $ | 11 | 25 | 33 | 1 |
| $ u_3 $ | 26 | 9 | 5 | 30 |
| $ u_4 $ | 22 | 23 | 34 | 15 |
| $ u_5 $ | 37 | 21 | 28 | 27 |
| $ u_6 $ | 7 | 35 | 32 | 31 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ |
| $ u_1 $ | 69 | 3 | 40 | 56 | 39 | 50 |
| $ u_2 $ | 1 | 67 | 5 | 59 | 31 | 35 |
| $ u_3 $ | 21 | 17 | 65 | 7 | 44 | 46 |
| $ u_4 $ | 42 | 38 | 23 | 33 | 9 | 57 |
| $ u_5 $ | 61 | 27 | 37 | 34 | 30 | 15 |
| $ u_6 $ | 41 | 53 | 49 | 32 | 47 | 25 |
| $ u_7 $ | 29 | 60 | 54 | 52 | 63 | 36 |
| $ u_8 $ | 58 | 55 | 45 | 43 | 51 | 48 |
DownLoad:
CSV
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ |
| $ u_1 $ | 11 | 18 | 13 |
| $ u_2 $ | 14 | 15 | 9 |
| $ u_3 $ | 17 | 7 | 16 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ |
| $ u_1 $ | 15 | 21 | 36 | 38 | 31 |
| $ u_2 $ | 13 | 30 | 29 | 33 | 28 |
| $ u_3 $ | 40 | 24 | 35 | 19 | 17 |
| $ u_4 $ | 34 | 37 | 11 | 23 | 32 |
| $ u_5 $ | 39 | 27 | 26 | 22 | 25 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ |
| $ u_1 $ | 15 | 51 | 64 | 40 | 29 | 68 | 57 |
| $ u_2 $ | 66 | 43 | 17 | 38 | 19 | 59 | 70 |
| $ u_3 $ | 25 | 45 | 56 | 48 | 61 | 32 | 47 |
| $ u_4 $ | 52 | 31 | 33 | 63 | 54 | 53 | 30 |
| $ u_5 $ | 42 | 35 | 65 | 34 | 60 | 36 | 46 |
| $ u_6 $ | 55 | 67 | 23 | 58 | 49 | 27 | 41 |
| $ u_7 $ | 69 | 50 | 62 | 37 | 44 | 39 | 21 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ | $ v_7 $ | $ v_8 $ | $ v_9 $ |
| $ u_1 $ | 73 | 33 | 102 | 69 | 19 | 79 | 63 | 86 | 91 |
| $ u_2 $ | 43 | 56 | 35 | 62 | 49 | 89 | 85 | 93 | 87 |
| $ u_3 $ | 75 | 61 | 48 | 53 | 104 | 92 | 95 | 23 | 50 |
| $ u_4 $ | 80 | 58 | 72 | 25 | 108 | 97 | 77 | 47 | 39 |
| $ u_5 $ | 51 | 96 | 59 | 81 | 99 | 37 | 55 | 57 | 70 |
| $ u_6 $ | 60 | 100 | 44 | 101 | 67 | 40 | 41 | 90 | 64 |
| $ u_7 $ | 38 | 83 | 103 | 82 | 74 | 78 | 29 | 76 | 46 |
| $ u_8 $ | 88 | 105 | 94 | 65 | 42 | 66 | 52 | 31 | 68 |
| $ u_9 $ | 107 | 21 | 54 | 71 | 45 | 27 | 106 | 98 | 84 |
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_1) $ |
| 18 | 9 | 11 | 13 |
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_1) $ |
| 40 | 39 | 38 | 13 | 17 | 19 |
| $ f(u_1u_2) $ | $ f(u_2u_3) $ | $ f(u_3u_4) $ | $ f(u_4u_5) $ | $ f(u_5u_6) $ | $ f(u_6u_7) $ | $ f(u_7u_8) $ | $ f(u_8u_1) $ |
| 70 | 68 | 66 | 64 | 62 | 19 | 13 | 11 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ |
| $ u_1 $ | 16 | 1 |
| $ u_2 $ | 14 | 5 |
| $ u_3 $ | 7 | 17 |
| $ u_4 $ | 3 | 15 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ |
| $ u_1 $ | 36 | 24 | 3 | 29 |
| $ u_2 $ | 11 | 25 | 33 | 1 |
| $ u_3 $ | 26 | 9 | 5 | 30 |
| $ u_4 $ | 22 | 23 | 34 | 15 |
| $ u_5 $ | 37 | 21 | 28 | 27 |
| $ u_6 $ | 7 | 35 | 32 | 31 |
| $ f(u_iv_j) $ | $ v_1 $ | $ v_2 $ | $ v_3 $ | $ v_4 $ | $ v_5 $ | $ v_6 $ |
| $ u_1 $ | 69 | 3 | 40 | 56 | 39 | 50 |
| $ u_2 $ | 1 | 67 | 5 | 59 | 31 | 35 |
| $ u_3 $ | 21 | 17 | 65 | 7 | 44 | 46 |
| $ u_4 $ | 42 | 38 | 23 | 33 | 9 | 57 |
| $ u_5 $ | 61 | 27 | 37 | 34 | 30 | 15 |
| $ u_6 $ | 41 | 53 | 49 | 32 | 47 | 25 |
| $ u_7 $ | 29 | 60 | 54 | 52 | 63 | 36 |
| $ u_8 $ | 58 | 55 | 45 | 43 | 51 | 48 |
