1. Introduction
The role of synapse elimination, observed in humans [1,2,3] and in animals [4,5,6,7,8,9,10], has been generally perceived as the removal, or "pruning", of redundant or weak synapses for the improvement of neural circuit performance. Although structural circuit modification has been suggested in general terms as means for long term memory [11], the specific function and mechanization of synapse elimination have remained essentially unclear. Reports that focal blockade of neurotransmission is more effective in synapse elimination than a whole junction blockade [11], and that synapse elimination precedes axon dismantling [12], have been challenged by claims that synapse elimination is a consequence of whole axon removal [13]. Dynamic firing effects of neural interaction under synapse elimination have been experimentally observed, noting that "active synaptic sites can destabilize inactive synapses in their vicinity" [11], although such effects may involve synapse silencing and reactivation [14] rather than synapse elimination. While early studies have associated synapse elimination with early development [12,15] and childhood [16], others have extended it to puberty [17], and, depending on brain regions, to age 12 for frontal and parietal lobes, to age 16 for the temporal lobe, and to age 20 for the occipital lobe [18]. Yet, grey matter [19] and cognition [20] studies, and persistent evidence of molecular processes involved in synaptic elimination throughout life [21], have suggested its relevance all the way to senescence.
Here, we study the mechanism and the implications of synapse elimination on neural circuit formation, modification and function in a model-based context. Noting that, albeit certain age-related differences in the time constants associated with membrane and synapse plasticity, the firing rate model produces essentially the same dynamic modes [22], we suggest that the model corresponding to maturity and aging represents a viable platform for analyzing the effects of synapse elimination throughout life. We further suggest that synapse weakening and eventual elimination is a consequence of asynchrony in the firing of interacting neurons and circuits. We proceed to show that while whole axon elimination removes asynchronous firing altogether, synapse elimination facilitates interference-free asynchrony between individual neurons and between neural circuit firing, maintaining internal circuit synchrony. This allows for cortical segregation into neurons and circuits having different characteristic firing rate modes corresponding to different cortical functions.
2. Developmental Maps and Global attractors of Neuronal Firing Rate
Both the mathematical analysis and the simulation of synapse elimination effects will require some specification of the models involved in order to demonstrate the functional implications. For a single isolated neuron, the firing rate model, evolving from the integrate-and-fire [23] and the conductance-based membrane current[24] paradigms, through cortical averaging [25], neuronal decoding [26] and spiking rate [27] models, is captured, in essence, by the discrete iteration map [28,22].
|
$
\upsilon (k) = \alpha \,\upsilon (k - 1) + \beta f\left( {\omega (k)\upsilon (k - 1) + u} \right)
$
|
(1)
|
where $\upsilon (k)$ is the firing rate, $\alpha = \exp (-1/{\tau _m})$ and $\beta = 1-\alpha $, with ${\tau _m}$the membrane time constant, $\omega (k)$is the self-feedback synaptic weight, $u$ is the external membrane activation and
|
$
f(x) = \left\{ xifx≥00ifx<0
\right.
$
|
(2)
|
is the conductance-based rectification kernel [29,30,31].
The Bienenstock-Cooper-Munro plasticity rule [32], enhanced by stabilizing modifications [33,34], is a widely recognized, biologically plausible, mathematical representation of the Hebbian learning paradigm [35], taking the discrete form
|
$
\omega (k) = \varepsilon \omega (k - 1) + \gamma \left( {\upsilon (k - 1) - \theta (k - 1)} \right){\upsilon ^2}(k - 1)
$
|
(3)
|
where
|
$
\theta (k) = \delta \sum\limits_{i = 0}^N {\exp ( - i/{\tau _\theta }){\upsilon ^2}(k - i)}
$
|
(4)
|
with $\varepsilon = \exp (-1/{\tau _\omega }), \, \, \gamma = 1-\, \varepsilon $ and $\delta = 1/{\tau _\theta }$, where ${\tau _\omega }$ and ${\tau _\theta }$ are the synaptic and the threshold time constants, respectively.
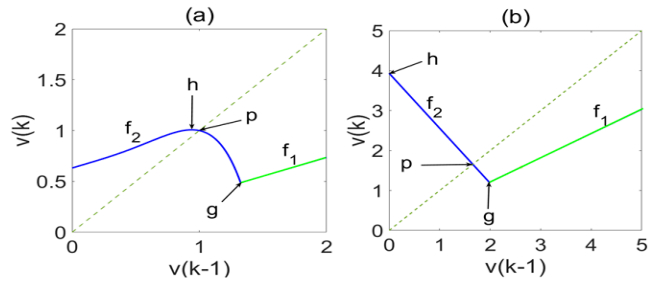
Different ranges of the time constants, ${\tau _m}$, ${\tau _\omega }$ and ${\tau _\theta }$, hypothesized to correspond to different developmental stages (smaller values corresponding to early development), have been shown to produce somewhat different maps of firing rate, possessing, however, essentially similar global attractors [22]. In critical period, immediately following birth and extending into early childhood, the plasticity time constants ${\tau _\omega }$ and ${\tau _\theta }$ are assumed to have near-zero values, while the membrane time constant, ${\tau _m}$ is assume to be higher, producing, by Eq. 1, the map depicted in Figure 1a. The inhibition onset and termination thresholds are h and g, respectively, where the slopes of the map change sign. The dynamic behavior induced by the map depends on the slope at the point p, where the map intersects the diagonal $\upsilon (k) = \upsilon (k-1)$.
For our present purposes, we continue with the case corresponding to synaptic maturity and rigidity (Figure 1b), so as to stress the relevance of circuit segregation beyond early development. For this case, $\omega (k)$ converges to a fixed value $\omega $ [34], yielding the model [22]
|
$
\upsilon (k) = \left\{ f1(υ(k−1))=λ1υ(k−1)forβωυ(k−1)+βu≤0f2(υ(k−1))=λ2υ(k−1)+βuforβωυ(k−1)+βu>0
\right.
$
|
(5)
|
where
|
$
{\lambda _1} = \alpha
$
|
(6)
|
and
|
$
{\lambda _2} = \alpha + \beta \omega
$
|
(7)
|
and the inhibition onset and offset points become
and
|
$
g = \frac{{\beta u}}{{{\lambda _1} - {\lambda _2}}}
$
|
(9)
|
while the fixed point representing the intersection of f2 with the diagonal $\upsilon (k) = \upsilon (k-1)$ is
|
$
p = \frac{{\beta u}}{{1 - {\lambda _2}}}
$
|
(10)
|
The parameters
|
$
{c_1} = 2\,{\lambda _1}{\lambda _2} + 1 + \sqrt {1 + 4\lambda _1^2}
$
|
(11)
|
and
|
$
{c_2} = {\lambda _1}{\lambda _2} + 1
$
|
(12)
|
define transition points from one global attractor type of the map to another [28].
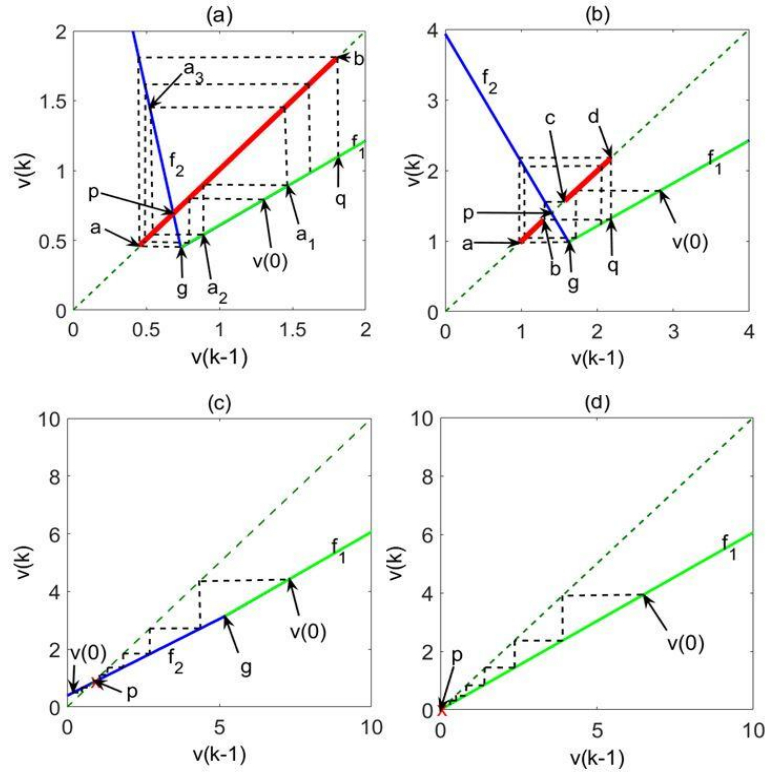
Scalar global attractors are graphically described by cobweb diagrams [36,37,38,39], which are initiated at some value, $\upsilon (0)$, on the map, then connected horizontally to the diagonal $\upsilon (k) = \upsilon (k-1)$, then connected vertically to the map, and so on. The cobweb diagrams depicted by the corresponding subplots of Figure 2 represent different global attractor types, which satisfy the following characteristic conditions:
(a) Chaotic attractor. For $u > 0$, ${\lambda _2} < -1$,
${c_1} \le 0$, and ${c_2} < 0$, yielding ${p_\upsilon } \le {q_\upsilon }$ (where $q$ is the point obtained from the bend point $g$ by a 4-step cobweb sequence, and where ${p_\upsilon }$ and ${q_\upsilon }$ are the vertical coordinates of the corresponding points on the map in Figure 2a), the attractor is represented in Figure 2a by the interval $ab$ on the diagonal $\upsilon (k) = \upsilon (k-1)$, with a and b created by a cobweb sequence initiating at the bend point g, which defines the boundaries of the attractor, as shown in the figure. An orbit of period three ${a_1} \to {a_2} \to {a_3} \to {a_1}$, rendering Li-Yorke chaos [40], is defined by ${a_1} = {f^3}({a_1})$, ${a_1} \ne f ({a_1})$, where f is the map Eq. 5, and ${f^3}(x) = f (f (f (x)))$. Starting with ${a_1} > g$, we obtain ${a_2} = {\lambda _1}{a_1}$, ${a_3} = \lambda _1^2{a_1}$,
${a_1} = {\lambda _2}\lambda _1^2{a_1} + \beta u$, yielding ${a_1} = \beta u/(1-{\lambda _2}\lambda _1^2)$.
(b) Largely-oscillatory attractor. For $u > 0$, ${\lambda _2} < -1$,
${c_1} > 0$, and ${c_2} < 0$, yielding ${q_\upsilon } < {p_\upsilon }$, the attractor, represented in Figure 2b by the two intervals ab and cd, separated by the repelling interval bc, is largely oscillatory. Within the attractor domain, defined by a cobweb initiating at the bend-point g, trajectories alternate between the two intervals ab and cd. As implied by the cobweb diagram, depending on the circuit parameters, this alternation may, but need not necessarily, repeat precisely the same points, which may then represent oscillatory or cyclically multiplexed dynamics (the two intervals ab and cd then reduce into two or four points, respectively [22,28]).
(c) Fixed-point (constant) attractor. For $u > 0$ and $-1 < {\lambda _2} \le 1$, we have a fixed-point attractor at p. For $-1 < {\lambda _2} \le 0$, the fixed point will be approached by alternate convergence (increasing $\upsilon (k)$ step followed by decreasing $\upsilon (k + 1)$ step and vice versa). For $0 < {\lambda _2} \le {\lambda _1}$, convergence will be monotone, bimodal (according to f1 far from p and according to f2 near p, as illustrated by Figure 2c for $0 < {\lambda _2} \le {\lambda _1}$, and unimodal (according to f2) for ${\lambda _1} < {\lambda _2} \le 1$.
(d) Silent attractor. For $\omega = 0$, the attractor is at the origin, as depicted in Figure 2d.
Specifically, the cobweb diagrams depicted in Figure 2 correspond to the following parameter values:
(a) $u = 10$, ${\tau _m} = 2$, ${\tau _\omega } = {\rm{10000}}$, ${\tau _\theta } = \, 0.1$, yielding
$\, {\lambda _1} = {\rm{0}}{\rm{.6055}}, \, {\lambda _2} = {\rm{-4}}{\rm{.7336}}, \, {c_1} = {\rm{-3}}{\rm{.1701}}, \, {c_2} = {\rm{-1}}{\rm{.8711, }}\omega = {\rm{-13}}{\rm{.5720}}$
(b) $u = 10, \, {\tau _m} = 2, \, {\tau _\omega } = {\rm{10000}}, \, {\tau _\theta } = \, 1$, yielding
$\, {\lambda _1} = {\rm{0}}{\rm{.6055}}, \, {\lambda _2} = {\rm{-1}}{\rm{.8160}}, \, {c_1} = {\rm{0}}{\rm{.3692}}, \, {c_2} = {\rm{-0}}{\rm{.1015, }}\, \omega = {\rm{-6}}{\rm{.1569}}$
(c) $u = 1, \, {\tau _m} = 2, \, {\tau _\omega } = {\rm{5}}, \, {\tau _\theta } = \, 1$, yielding ${\lambda _1} = {\rm{0}}{\rm{.6065}}, \, {\lambda _2} = {\rm{0}}{\rm{.5308, }}\, \omega {\rm{ =-0}}{\rm{.1925}}$
(d) $u =-1, \, {\tau _m} = 2, \, {\tau _\omega } = {\rm{5}}, \, {\tau _\theta } = \, 1$, yielding ${\lambda _1} = {\rm{0}}{\rm{.6065}}, \, {\lambda _2} = {\rm{0}}{\rm{.6065, }}\omega = 0$
For each of the cases, the steady-state value of the synaptic weight, $\omega $, was calculated by driving Eqs. 3 and 4, with $\omega (0) = 0$ and $\upsilon (0) = 1$, to convergence (practically, this was achieved for $N = 100$), and the corresponding values of ${\lambda _1}, \, {\lambda _2}, \, {c_1}$ and ${c_2}$ were calculated by Eqs. 6, 7, 11 and 12 respectively. As can be verified, the conditions stated above for the attractor types (a) chaotic, (b) largely-oscillatory, (c) fixed-point and (d) silent, are satisfied, respectively, by the parameter values obtained.
3. Neural Circuit Segregation by Synapse Elimination
For a circuit of n neurons, firing rate and plasticity would be governed by the equations
|
$
{\upsilon _i}(k) = {\alpha _i}\,{\upsilon _i}(k - 1) + {\beta _i}f\left( {{{\bf{\omega }}_i}^T(k){\bf{\upsilon }}(k - 1) + {u_i}} \right)
$
|
(13)
|
|
$
{{\bf{\omega }}_i}(k) = {\varepsilon _i}{{\bf{\omega }}_i}(k - 1) + {\gamma _i}\left[ {{\upsilon _i}(k - 1) - {\theta _i}(k - 1)} \right]\,{{\bf{\upsilon }}^2}(k - 1)
$
|
(14)
|
|
$
{\theta _i}(k) = {\delta _i}\sum\limits_{i = 0}^N {\exp ( - i/{\tau _{{\theta _i}}}){\upsilon _i}^2(k - i)}
$
|
(15)
|
where $i = 1, 2, ..., n$, ${\bf{\upsilon }}(k)$ is the vector of neuronal firing rates, ${{\bf{\omega }}_i}(k)$ is the vector of input synaptic weights (including self-feedback) corresponding to the i th neuron and ${{\bf{\upsilon }}^2}$ is the vector whose components are the squares of the components of ${\bf{\upsilon }}$. We have used N = 100, yielding convergence of ${\omega _{i, j}}, \, \, i, j = 1, \, 2, \ldots, n$, to constant values.
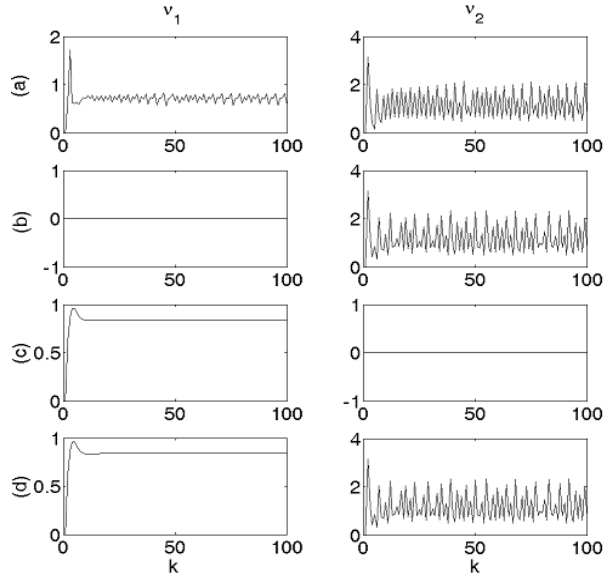
Consider first two neurons, one having the parameters of case (c) of the previous section, hence, a fixed-point global attractor of firing rate, and the other having the parameters of case (b) of the previous section, hence, a largely oscillatory global attractor of firing rate. Figure 3a shows the firing rate sequences of the two neurons, fully connected into a circuit. Eliminating the axon of the first neuron (Figure 3b) reveals the characteristic firing mode of the second neuron alone. Eliminating the axon of the second neuron (Figure 3c) reveals the characteristic firing mode of the first neuron alone. It can be clearly seen by comparison that full connectivity, resulting in the firing sequences displayed by Figure 3a, causes mutual interference between the two neurons. Inter-neuron asynchrony is assumed to imply, by the Hebbian paradigm, weakening of the corresponding synapses [35].
Eventual elimination of the receiving synapses of both neurons, represented by zero values of the corresponding synaptic weights, allows each of the neurons to display its own characteristic firing-rate mode without interference, as depicted in Figure 3d.
Next consider a fully connected circuit of n identical neurons receiving identical activation. The neurons will fire in synchrony. However, for n > 1, the neuronal firing mode will not be the same as that of an individual isolated neuron with the same property. This can be seen by noting that, for each of the synchronous circuit neurons, Eq. 13 will yield the firing rate model
|
$
\upsilon (k) = \alpha \,\upsilon (k - 1) + \beta f\left( {n\omega (k)\upsilon (k - 1) + u} \right)
$
|
(16)
|
which is different from Eq. 1. As $N \to \infty $, Eqs. 14 and 15 will take $\omega (k)$ to its constant limit value ${\omega _f}$ [34], yielding
|
$
\upsilon (k) = \alpha \,\upsilon (k - 1) + \beta f\left( {n\omega \upsilon (k - 1) + u} \right)
$
|
(17)
|
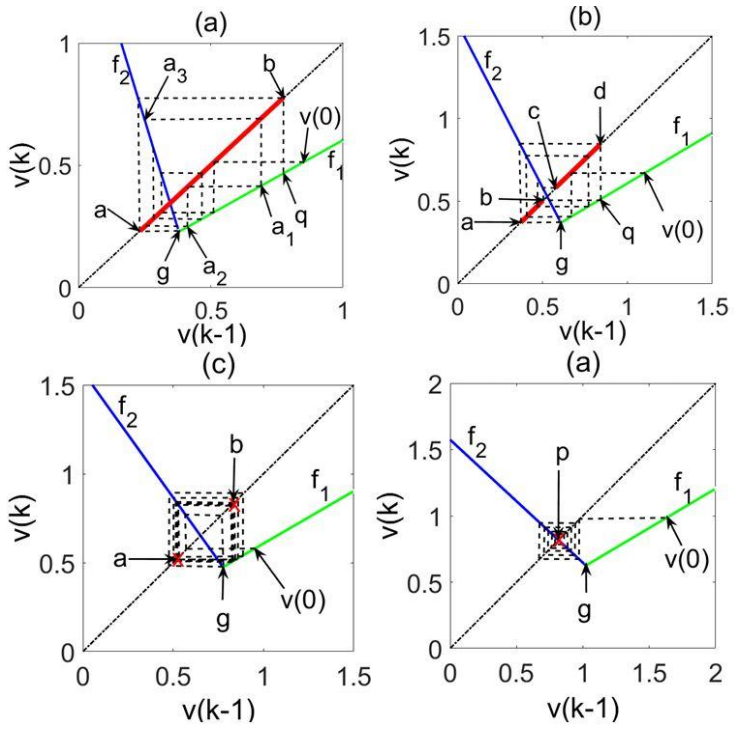
which is the firing rate model of an isolated individual neuron with feedback synaptic weight $n\omega $. This synchrony equivalence principle allows us to extend our results obtained for the neuronal firing rate modes and for asynchronous neuron segregation to synchronous circuits. Clearly, Eq. 17 will produce a different mode of firing rate dynamics for every circuit size n. This is illustrated by Figure 4, where the four subfigures depict attractors of fully connected circuits having identical neurons, but different circuit sizes. It can be seen that different circuit sizes result in different firing rate modes. Specifically, the circuits represented in Figure 4 obey the model of Eqs.13–15, with $N = 100$ (taking $\omega (k)$ to its constant limit $\omega $). For circuits of fully connected identical neurons, having the parameter values $u = 4$, ${\tau _m} = 2$, ${\tau _\omega } = 300$, ${\tau _\theta } = 0.1$ and circuit size values 10, 5, 2 and 1, we obtain the modal parameter and condition values specified below:
(a) $n = 10$, yielding $\omega \, {\rm{ = }}-{\rm{0}}{\rm{.7870}}, {\lambda _1} = {\rm{0}}{\rm{.6065}}, \, {\lambda _2} =-{\rm{2}}{\rm{.4901}}$, $\, {c_1} =-{\rm{0}}{\rm{.4485, }}{{\rm{c}}_2} =-{\rm{0}}{\rm{.5103}}$
(b) $n = 5$, yielding $\omega {\rm{ =-1}}{\rm{.3128}}, {\lambda _1} = {\rm{0}}{\rm{.6065}}, \, {\lambda _2} = {\rm{-1}}{\rm{.9762}}$, ${c_1} = {\rm{0}}{\rm{.1748, }}{{\rm{c}}_2} =-{\rm{0}}{\rm{.1987}}$
(c) $n = 2$, yielding $\omega \, {\rm{ = }}-{\rm{2}}{\rm{.5628}}, \, {\lambda _1} = {\rm{ 0}}{\rm{.6065}}, \, {\lambda _2} =-{\rm{1}}{\rm{.4103}}$, ${c_1} = {\rm{0}}{\rm{.8614, }}{{\rm{c}}_2} = {\rm{0}}{\rm{.1446}}$
(d) $n = 1$, yielding $\omega \, {\rm{ = }}-{\rm{3}}{\rm{.8993}}, {\lambda _1} = {\rm{0}}{\rm{.6065}}, \, {\lambda _2} =-{\rm{0}}{\rm{.9277}}$, ${c_1} = {\rm{1}}{\rm{.4467, }}{{\rm{c}}_2} = {\rm{ 0}}{\rm{.4373}}$
An examination of the conditions for the global attractor types specified in Section 2 shows that the above cases represent (a) chaotic, (b) largely-oscillatory, (c) oscillatory and (d) fixed-point global attractors, as ratified by Figure 4. As, except for the circuit size (i.e., the number of neurons) the neuronal parameters $u, \, {\tau _m}, \, {\tau _\omega }, \, {\tau _\theta }$ are identical for all neurons, the increasing number of neurons in cases (a–d) above may be viewed as representing synchronous circuit segregation into smaller synchronous sub-circuits.
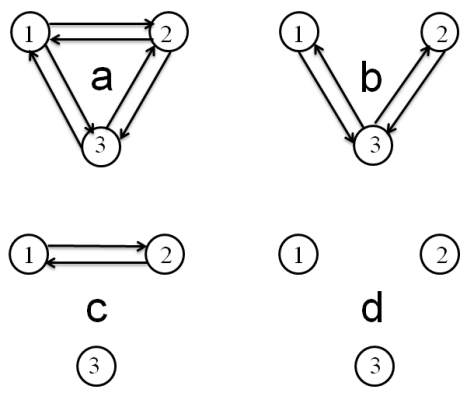
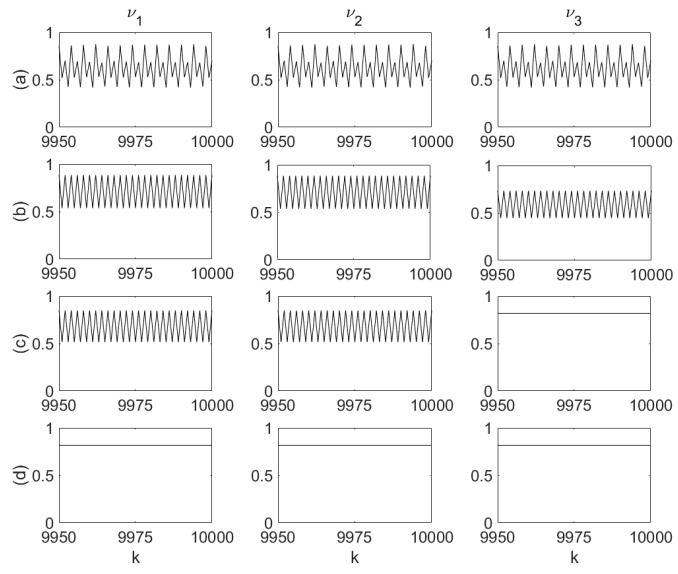
Finally, in order to illustrate the effects of synchronous circuit segregation into synchronous sub-circuits, consider a circuit of three identical neurons with the parameters (identical to those employed in Figure 4) $u = 4, {\tau _m} = 2, \, {\tau _\omega } = 300, \, {\tau _\theta } = 0.1$, starting with full connectivity and undergoing modification and segregation by synapse elimination (manifested by setting the corresponding synaptic weight at zero). The changes in circuit connectivity are illustrated in Figure 5, while the resulting changes in the neuronal firing modes, simulated by Eqs. 13–15, are displayed in Figure 6.
It can be seen in Figure 6 that the fully connected circuit (a) fires synchronously in a largely oscillatory multiplexed mode, whereas the transition to partial connectivity in the modified circuit (b) produces a change of the neuronal firing rate modes, which, while being similarly oscillatory, are unequal in amplitude. The circuit segregation into a two-neuron circuit and one individual neuron (c) results in synchronous oscillation and constant (fixed point) firing modes, respectively, while the segregation into three isolated neurons (d) results in each producing a constant firing rate. The firing modes are in agreement with those predicted by Figure 4 (the transition from a fully connected two-neuron circuit in case 4 (c) to a fully connected three-neuron circuit in case 5 (a) has resulted in the mode changing from oscillatory to largely oscillatory, multiplexing two oscillatory modes).
4. Conclusion
We have shown that, given internal neuronal property, the circuit connectivity structure defines the circuit firing mode as well. It is therefore justified to view circuit connectivity not only as means for information representation, but also as a manifestation of the function to be performed. The permanence of synapse elimination, as opposed to synapse silencing, makes it particularly relevant to long-term memory and to life-long functional proficiency. Synapse elimination results in circuit modification. It can segregate a synchronous circuit into smaller synchronous sub-circuits, isolated against mutual asynchronous interference. Conversely, the weakening of synapses, eventually resulting in their elimination, may be caused by asynchronous interference between neurons and synapses, as suggested by the Hebbian paradigm. Circuits of identical neurons, but different sizes, fire in different firing rate modes. While we have focused on the firing rate and plasticity dynamics corresponding to maturity, the essential persistence of the map and the corresponding global attractor code of firing rate through different developmental stages suggest the life-long relevance of synapse elimination to circuit formation, modification and function.
Acknowledgements
This study was supported by the Technion's Roy Matas/Winnipeg Chair in Biomedical Engineering.
Conflict of Interest
The author (Y. Baram) declares the existence of no conflicting interest.









 DownLoad:
DownLoad: