Abbreviations
| BHI | Brain Heart Infusion; |
| CLSM | confocal laser scanning microscopy; |
| DNA | deoxyribonucleic acid; |
| CFU | colony forming units; |
| DLS | dynamic light scattering; |
| FDA | Food and Drug Administration; |
| GRAS | Generally Recognized as Safe; |
| PDI | polydispersity index; |
| UV | ultraviolet; |
| PBS | phosphate-buffered saline; |
| SEM | scanning electron microscopy |
1. Introduction
Oral biofilms, which make up dental plaque, are major contributors to dental caries and periodontitis [1,2,3]. Current oral hygiene treatments are based on antimicrobial strategies, namely the killing of all of the microorganisms that are present in the oral cavity. These strategies, however, are often ineffective, illustrated by the frequency of oral infections and related diseases [4,5,6,7]. There is also much controversy on how broad-spectrum treatments affect the commensal microflora and the subsequent negative effects on human health [8,9]. There is an emerging body of research in alternative approaches to antimicrobials, for example, inhibitors that interrupt cell-cell signaling and/or virulence traits (e.g. biofilm formation, acid release, etc.) [10,11,12,13,14]. Such inhibitors may be attractive as they have potential for being more selective against pathogenic bacteria while leaving the commensal flora unperturbed. A major drawback to these approaches, however, is their lack of efficacy when used in acute, topical exposures (e.g. daily oral hygiene regimens), especially in comparison to their antimicrobial counterparts.
In order to enhance bioavailability and maximize efficacy of these agents in a complex and dynamic environment such as the oral cavity, it is necessary to maintain a constant reservoir of the agents in situ. This motivated us to design and synthesize a polymer-based nanocapsule system that is capable of being loaded with inhibitory agents, adheres to the surface of the teeth, and sustainably releases the agents for a prolonged period of time. To do just that, there have been several nanocapsule/particle-based strategies employed by other research groups, including bacterial-and biofilm-targeted liposomes [15,16,17], hydroxyapatite-targeted micelles [18,19,20], pH-responsive and/or -targeted synthetic polymer-based nanoparticles [21,22], and even inorganic nanoparticles for their antimicrobial and anti-adhesive effects [23,24]. However, these approaches often utilize complex syntheses with harsh organic solvents, which potentially limits their clinical applications. Therefore, we sought to design a natural product-based material with a simple formulation procedure.
Zein, an amphiphilic protein isolated from the endosperm of corn, is an attractive choice in this application for multiple reasons: (1) it has been designated as GRAS (generally recognized as safe) by the FDA [25], (2) it has been used in the food industry for decades [26], and (3) it has been extensively studied as a delivery vehicle capable of encapsulating and releasing a variety of effective agents [27]. Zein is noteworthy because of the simplicity of the procedure to form self-assembled micro/nanocapsules, and its versatility in encapsulating not only compounds of various structural types including hydrophilic molecules like heparin and nucleic acids [28,29], but also hydrophobic molecules such as omega-3 fatty acids and cholecalciferol (vitamin D3) [30,31]. A particularly notable characteristic of zein vehicles is their unique ability to form films at solid surface interfaces [29,32,33]. The resultant film could serve as a potential reservoir for sustained delivery of anti-biofilm agents.
In the present study, we encapsulated an inhibitor of Streptococcus mutans biofilm formation, S-phenyl-L-cysteine sulfoxide [10], into zein nanocapsules. The inhibitor-loaded nanocapsules were then used to cast a film and subsequent S. mutans biofilm formation was studied. This research demonstrates proof-of-concept that biofilm inhibitor-loaded zein nanocapsules can reduce S. mutans biofilm growth, and lays early groundwork for optimization of new approaches for oral biofilm treatment.
2. Materials and Methods
2.1. Preparation of zein nanocapsules
A stock solution of zein (Sigma) was prepared by dissolving 20 mg/ml zein in 70% (v/v) ethanol in dH2O and passing it through a 0.2 µm pore size filter. To form self-assembling nanocapsules, the zein stock solution was diluted 1:10 in dH2O and vortexed immediately. For nanocapsule suspensions under 2 mg/ml, an appropriate amount of 70% ethanol was added as a vehicle control. For all studies using S-phenyl-L-cysteine sulfoxide, this compound was added to dH2O at the appropriate concentration prior to precipitating the nanocapsules. S-Phenyl-L-cysteine sulfoxide was synthesized as described previously [10,34].
2.2. Analysis of nanocapsule morphology and size
Nanocapsules were imaged using a Hitachi S4800 cold-cathode field-emission secondary scanning electron microscope (FE-SEM). The samples were coated with a thin gold/palladium compound to reduce charging effects. During imaging, the secondary electron detector was used and the tool was operated at 2 kV acceleration voltage at a working distance of about 5.2 mm. Nanocapsule size and dispersity were analyzed using a Zetasizer Nano ZS (4 mW He-Ne laser, 633 nm incident beam, Malvern Instruments Ltd.).
2.3. Nanocapsule film preparation
In order to prepare films comprised of zein nanocapsules, 200 µl of unloaded nanocapsule suspensions, unencapsulated S-phenyl-L-cysteine sulfoxide, or S-phenyl-L-cysteine sulfoxide-loaded nanocapsule suspensions were aliquoted onto 96-well plates. For fluorescence-based microscopic analysis of biofilm development, glass-bottom 96-well plates (Thermo Fisher Scientific, Rochester, NY) were used. For biofilm quantification, 4 mm glass beads (Fisher Scientific) were placed, one per well, in a non-treated polystyrene 96-well plate (Nest Biotechnology Co., Ltd). Plates were placed in a 37 °C incubator until complete solvent evaporation (~36 h), leaving behind a film (or residue of unencapsulated S-phenyl-L-cysteine sulfoxide) and then sealed and stored at 4 °C until further use.
2.4. Bacterial culture
Streptococcus mutans UA159 was propagated on Brain Heart Infusion (BHI, Sigma-Aldrich) agar plates incubated at 37 °C, 5% CO2. Colonies were selected and used to inoculate a 5 ml culture in BHI broth, and incubated overnight (18 h) at 37 °C, 5% CO2. Overnight cultures were then diluted 1:100 in 50% BHI broth (v/v in dH2O) with 2% w/v sucrose (Sigma) to induce biofilm formation, and distributed in 200 µl aliquots on 96-well plates with dried nanocapsule films. Before seeding bacteria, 96-well plates were gently washed with 200 µl sterile PBS.
2.5. Confocal Laser Scanning Microscopy (CLSM) for analysis of biofilm development
After 24 h, planktonic bacteria were removed from glass-bottom 96-well plates and washed twice with 200 µl dH2O. Biofilms were stained with 50 µl LIVE/DEAD® BacLight™ (5 µM SYTO9/30 µM propidium iodide, Thermo Fisher Scientific) for 30 min, then washed twice again with dH2O. CLSM was performed with a Leica TCS SP5 II microscope using a 63x oil-immersion lens with 476 nm excitation and both 510-540 nm (SYTO9) and 620-650 nm (propidium iodide) emission detection. Three-dimensional image rendering was performed using Imaris software (Bitplane, Zurich, Switzerland).
2.6. Biofilm quantification
Because of non-specific staining of the nanocapsule film, relative quantification by fluorescence intensity was unreliable. Therefore, biofilms were grown on glass beads so they could be removed and the biofilm could be harvested. Biofilms were grown for a total of 48 h, with the media and planktonic cells removed at 24 h and replaced with fresh media. After 48 h, beads were removed from the plates, washed in 200 µl PBS to remove loosely adhered cells, and then placed in 1 ml PBS in a microcentrifuge tube. Microcentrifuge tubes were vortexed vigorously for 2 min. Bacterial suspensions were subjected to 10-fold dilutions in PBS, plated in triplicate on BHI agar, and incubated at 37 °C, 5% CO2. After 24 h, colony forming units (CFUs) were enumerated.
3. Results
3.1. Zein nanocapsule characterization
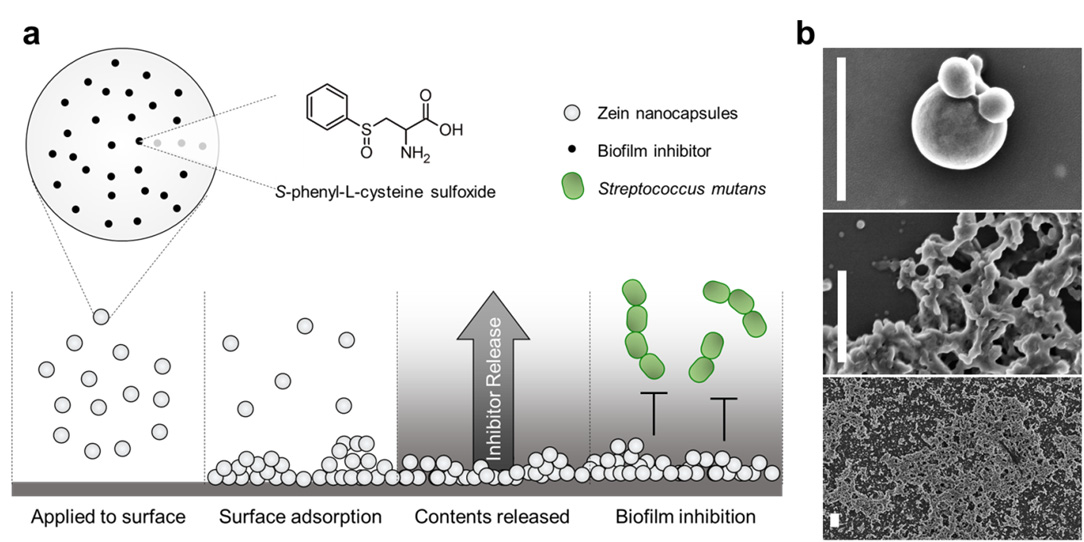
The goal of this research was to explore the potential of packaging biofilm inhibitors into zein-based nanocapsules, which could subsequently be applied as an aqueous suspension to coat surfaces and inhibit downstream bacterial biofilm formation (Figure 1a). When examined by scanning electron microscopy (SEM), nanocapsules appeared to form smooth spherical structures (Figure 1b, top panel). They also appeared to coalesce when in contact with neighboring nanocapsules, forming heterogeneous film-like structures (Figure 1b, middle and bottom panels).
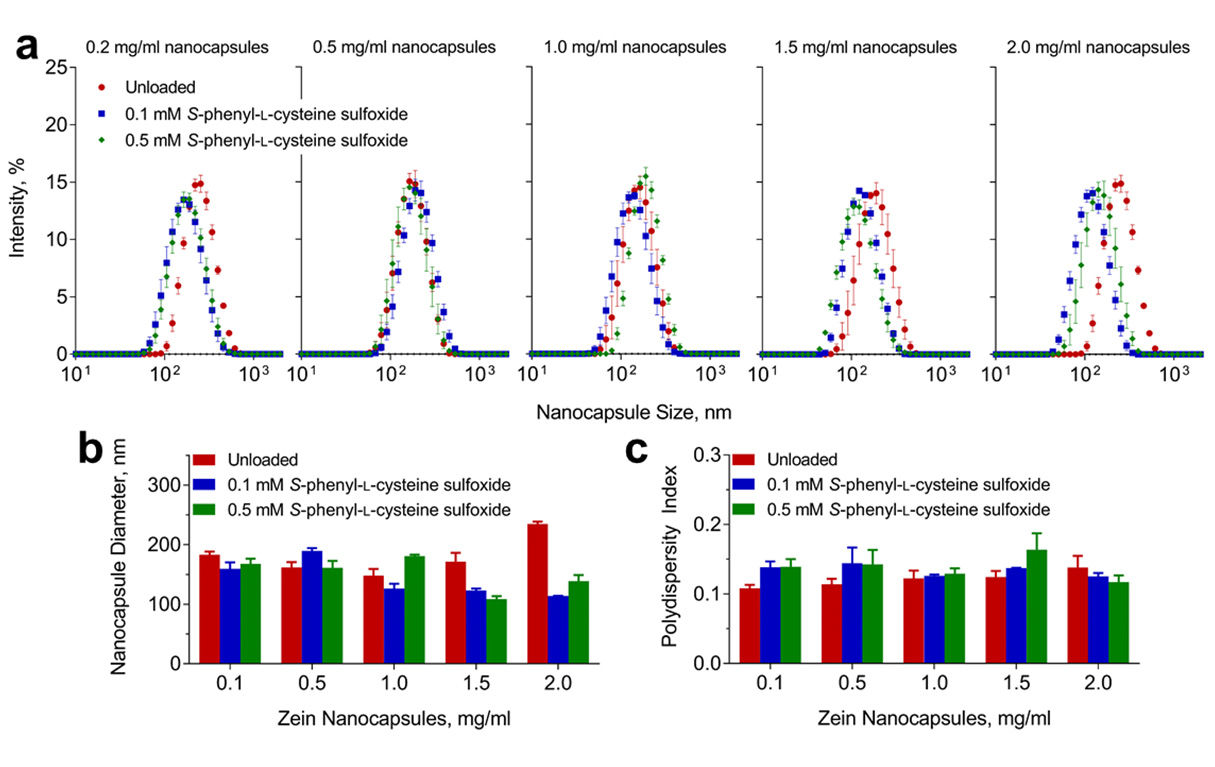
Our group has previously shown that a novel biofilm inhibitor, S-phenyl-L-cysteine sulfoxide, curtails biofilm formation at high micromolar-to-low millimolar concentrations [10,34]. Therefore, we first sought to determine if we could form stable nanocapsules with relevant concentrations of the inhibitor present. Zein in 70% ethanol was diluted 1:10 into deionized water containing S-phenyl-L-cysteine sulfoxide at predetermined concentrations. Nanocapsule suspensions were then analyzed using dynamic light scattering (DLS) to determine particle size and size uniformity (Figure 2a). At all concentrations tested, nanocapsules formed monodisperse suspensions (size PDI~0.1-0.15; Figure 2c) ranging in size from an average of 108.6±8.1 nm in diameter (1.5 mg/ml zein, 0.5 mM inhibitor) to 234.6±6.6 nm in diameter (2 mg/ml zein, no inhibitor), with the median for all samples being 161.3 nm in diameter (Figure 2b). At lower concentrations of zein (≤1.0 mg/ml), the inhibitor did not appear to have an effect on nanocapsule size. However, at higher zein concentrations (1.5 mg/ml, 2.0 mg/ml), the inhibitor appeared to affect nanocapsule formation, as smaller diameters were observed.
3.2. Inhibition of S. mutans biofilm development with inhibitor-loaded nanocapsules
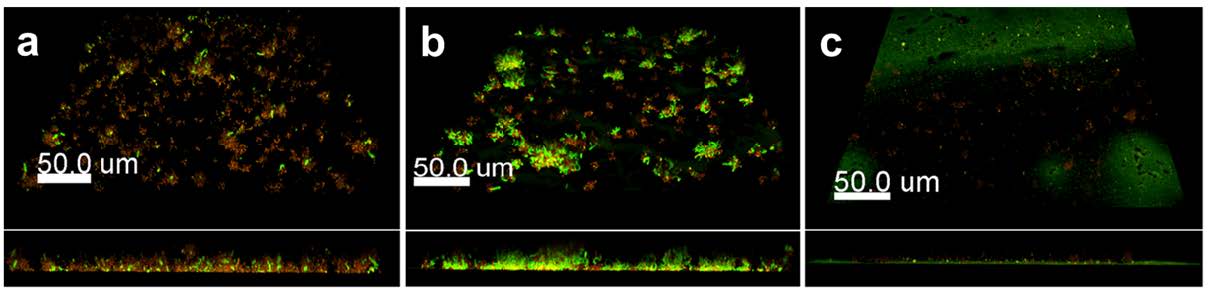
To study the effect of these nanocapsules on S. mutans biofilm formation, S-phenyl-L-cysteine sulfoxide-loaded nanocapsule suspensions were applied to glass-bottom 96-well plates and evaporated overnight to cast a film. Glass substrates are commonly used for their ease of optical analysis in studying S. mutans biofilm formation [35,36,37] and were used in our previous screening effort to identify biofilm inhibitors [10]. Previous studies in our lab have demonstrated that films of zein nanocapsules loaded with coumarin-6, a model fluorescent compound of similar size and hydrophobicity as S-phenyl-L-cysteine sulfoxide, sustainably release the payload for~10 h (data not shown). Dried nanocapsule-based films were washed with sterile PBS and incubated with S. mutans in the presence of sucrose to initiate biofilm formation. After 24 h, planktonic suspensions were removed, and the resultant biofilms were washed with PBS and then stained with SYTO9/propidium iodide for live/dead vi ability analysis. In comparison to the untreated surface (Figure 3a) and unloaded nanocapsule-treated surface (Figure 3b), demonstrably fewer microcolonies formed on the surface of the inhibitor-loaded nanocapsule-treated surface (Figure 3c). The reduction in biofilm initiation is made more evident by the X-Z cross sections of the 3-dimensional stacks obtained from CLSM, where there is very little evidence of 3-dimensional growth of S. mutans on the loaded nanocapsule-treated surfaces.
We observed non-specific labeling of the hydrophobic zein films with the lipophilic SYTO-9 dye (live cell marker used to permeate intact membranes). However, fluorescence from SYTO-9 stained zein is much dimmer in comparison to DNA-bound SYTO-9 in live cells. Additionally, the increased appearance of dead cells in the untreated surface samples can be attributed to extracellular DNA (eDNA), which is used to facilitate biofilm formation in several organisms [38,39], and whose presence in S. mutans biofilms is well-documented [40].
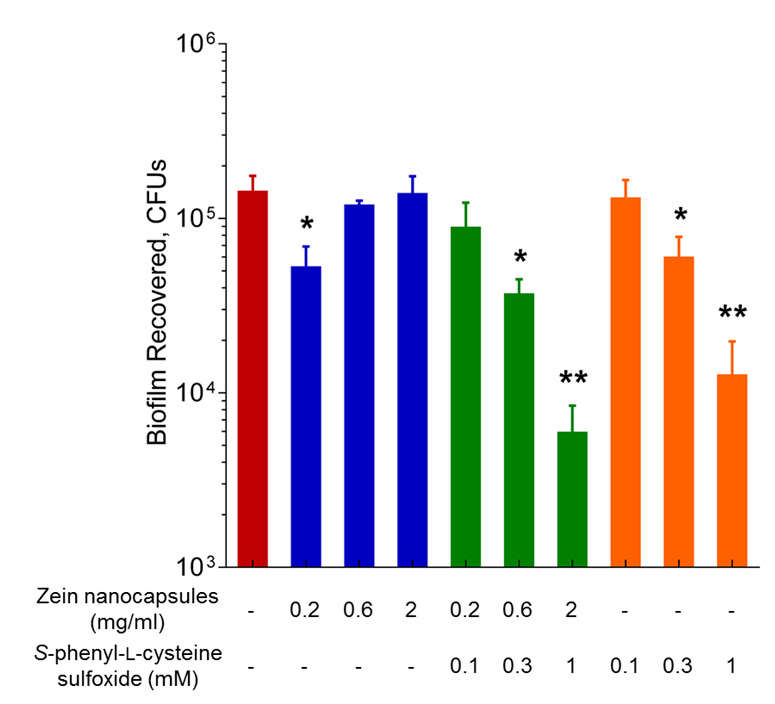
Because of these challenges in fluorescence-based analysis, quantification was performed by serial-dilution of biofilm harvested from the surface, and colony counts on agar media. In these experiments, glass beads were placed in each well of a 96-well plate before applying and drying the nanocapsule suspensions. As a nanocapsule-free control, S-phenyl-L-cysteine sulfoxide solution (without zein nanocapsules) was pipetted into wells, then dried to leave behind a residue which contained the inhibitor. All microplate wells were washed with sterile PBS, incubated with S. mutans in sucrose-based media and incubated for 48 h in total, with media replenishment at 24 h. After the incubation period, beads were removed and washed, and then adhered cells were harvested, diluted, and spotted on agar plates. The results indicated that S-phenyl-L-cysteine sulfoxide-loaded nanocapsules inhibit S. mutans biofilm in a dose-dependent manner, and that there was a more than one log reduction in cells (from the biofilm) recovered at the highest concentration of loaded nanocapsule used (2 mg/ml), in comparison to the untreated surface, (Figure 4). Additionally, the residue of S-phenyl-L-cysteine sulfoxide also appeared to inhibit biofilm formation in a dose-dependent fashion, with an approximate one log reduction at the highest concentration used (1 mM). Although the S-phenyl-L-cysteine sulfoxide-loaded nanocapsules appeared to inhibit biofilm to a greater extent than S-phenyl-L-cysteine sulfoxide residues at all relevant concentrations, these values were not shown to be statistically significant (by Student’s t-test). The nanocapsule film/residue drying and casting process is not representative of a reasonable “real world” application. Thus a more complete understanding of zein nanocapsule surface adsorption is necessary for determining feasibility of a topical treatment regimen and/or for designing strategies for enhanced surface adsorption.
4. Discussion
In the oral health field, nanoscale and microscale formulations for deterring pathogenic buildup have merited considerable interest [41,42,43,44]. In this study, we explored the use of zein nanocapsules for delivering bacterial biofilm inhibitors, as opposed to traditional antimicrobials, and explored several implementations to lay the foundation for future performance optimization.
Recent approaches for identifying small molecule S. mutans biofilm inhibitors have successfully uncovered multiple compounds, including (but not limited to) carolacton [13], walkmycin C [14], several 2-aminoimadazole and 2-aminobenzimidazole compounds [11], and several organosulfur compounds including S-phenyl-L-cysteine sulfoxide [10]. However, these results were based on microplate-based experimental procedures where the compound of interest was present throughout the duration of S. mutans biofilm growth (typically 1-2 days). This is not representative of what can be achieved in the oral cavity, where only short exposure times (on the order of minutes) can be achieved. This highlights the need for a drug delivery platform that can serve as a reservoir for sustained delivery of biofilm inhibitors in the oral cavity.
Zein has been used in several studies to encapsulate antibacterial compounds as a means of microbial control for a variety of applications [32,45,46,47], including oral disinfection [48,49]. Zein-based films loaded with essentials oils from cinnamon and mustard, which are established antimicrobials, have been shown to exhibit antimicrobial properties toward Salmonella enterica serovar Typhimurium [50]. In addition, zein films comprised of thymol, an active antimicrobial component of thyme essential oil, exhibit antimicrobial effects toward a variety of microbial pathogens including Bacillus cereus, Candida lusitaniae, and multiple Pseudomonas spp. [46]. However, none of these studies have explored the use of non-antimicrobial biofilm inhibitors and/or the formation of biofilm on the zein film.
Beyond delivery of antimicrobials, zein has been shown to be an interesting candidate for many other drug and nutraceutical delivery applications. Zein nanoparticles have been observed to exhibit liver targeting behavior, prolonged blood residence after intravenous injection in mice, and sustained release of the chemotherapeutic agent 5-fluorouracil in vitro, making it an interesting candidate for drug delivery in liver disease and/or cancer [51]. Zein nanoparticles coated with carboxymethyl chitosan were demonstrated to improve UV photostability of vitamin D3 when encapsulated, while also exhibiting controlled release properties in both PBS and a simulated gastrointestinal tract in vitro [31]. In vitro controlled release properties of several more bioactive compounds from zein-based films or nanoparticles have been explored, including the cardiac glycoside gitoxin [52], the anticoagulating agent heparin [29], vitamin B2 (riboflavin) [53], and omega-3 fatty acid [30].
Due to the simplicity of the procedure for forming compound-loaded nanocapsules using mild reagents, its commercial availability and GRAS-status, we postulated that zein would be an excellent candidate material for a drug delivery system for non-antimicrobial biofilm inhibitors in this topical application. Therefore, we casted films comprised of S-phenyl-L-cysteine sulfoxide-loaded zein nanocapsules and demonstrated that S. mutans biofilm formation could be inhibited in a concentration-dependent manner (Figure 4). Although a cast residue of unencapsulated S-phenyl-L-cysteine sulfoxide also inhibited S. mutans biofilm formation in a concentration-dependent manner, this is not likely representative of a feasible oral hygiene intervention. Future studies will investigate how long biofilm inhibition can be observed when inhibitor-loaded nanocapsules are applied.
5. Conclusion
In conclusion, as more studies identify oral biofilm inhibitors that do not target microbial viability, there will be an increased desire for a suitable platform for sustained inhibitor delivery. Zein-based nanocapsules offer interesting possibilities for this application. A biofilm inhibitor-loaded nanocapsule system provides significant potential for the targeting of bacterial pathogens while allowing commensal organisms to enjoy unaffected growth. This would provide a significant advantage over current broad spectrum antimicrobials that affect both pathogenic and commensal organisms indiscriminately. This work provides a basis for leveraging the unique properties of zein in this application.
Acknowledgements
We wish to thank Karsten Beckmann (SUNY Polytechnic Institute) for help with SEM.
Conflicts of Interest
All authors declare no conflicts of interest in this paper.








 DownLoad:
DownLoad: