We propose a sharp-interface model which describes
rate-independent hysteresis in phase-transforming solids (such as shape memory alloys) by resolving explicitly domain patterns and their dissipative evolution.
We show that the governing Gibbs' energy functional is the $\Gamma$-limit of a family of regularized Gibbs' energies obtained through a phase-field approximation.
This leads to the convergence of the solution of the quasistatic evolution problem associated with the regularized energy to the one corresponding to the sharp interface model.
Based on this convergence result, we propose
a numerical scheme which allows us to simulate mechanical experiments for both spatially
homogeneous and heterogeneous samples. We use the latter to assess the role that impurities and defects may have in determining the response exhibited by real samples. In particular, our numerical results indicate that small heterogeneities are essential in order to obtain spatially localized nucleation of a new martensitic variant from a pre-existing one in stress-controlled experiments.
1.
Introduction
Research on human helping behavior focuses on a series of core questions: Why and when do people help? Who does help? How can we reduce apathy and increase helping behavior? How do we improve the chance of successful help-seeking? [1]. These issues are critical to building a harmonious society of mutual assistance.
Social exchange theory [2,3] proposes that human social behavior results from an exchange process to maximize benefits and minimize costs. This theory suggests that the reasons for helping behaviors include external rewards, internal rewards, and social norms. Among them, internal rewards include alleviating a sense of guilt, happiness from a good mood, and bringing a sense of achievement, etc. Two fundamental concepts related to internal rewards are self-awareness and politeness. These two factors are closely related to the sense of guilt, achievement, and happiness on both sides of the helping behavior. However, existing research rarely touches on the connection of self-awareness and politeness to human help-seeking and help-giving behaviors, especially from the perspective of psychological game theory.
The conceptualization of self-awareness is complicated [4,5,6,7], and includes both intrapersonal and interpersonal perspectives [4,5,6,7]. Some researchers use the distinction between private and public aspects to describe its intra- and interpersonal aspects [8,9,10]. In these studies, the private aspect involves paying attention to one's inner thoughts and feelings, and the public aspect is the general perception of the self as a social object that influences others [11]. According to Carden et al., "Self-awareness consists of a range of components, which can be developed through focus, evaluation, and feedback, and provides an individual with an awareness of their internal state (emotions, cognitions, physiological responses), that drives their behaviors (beliefs, values, and motivations) and an awareness of how this impacts and influences others" [4]. The self-awareness related to help-seeking and help-giving behavior, applying the self-awareness definition given by Carden et al., includes a range of interpersonal components and intrapersonal components to develop connections between self and helpers or help seekers, it is developed through focus, evaluation, and feedback, and provides an individual with an intrapersonal aspect of self-awareness that drives their behaviors and the interpersonal aspect of self-awareness [4,6]. The interpersonal aspect of self-awareness leads people to pay attention to publicly displayed aspects of the self [12,13]. People pay attention to how others perceive them based on their behavior, etc. [14], and they are more likely to change their minds and behaviors when others are present [15,16,17]. Based on the above discussion, we identified self-awareness as one of the factors influencing helping behavior in this study. That is, helpers with a high level of self-awareness are strongly aware of other people's behavior and reflect on their own behavior when they are asked for help, so they change their behavior. Conversely, helpers with a low level of self-awareness generally are unaware of their own and others' behavior, so they don't change their behavior. In the same way, the above discussion also applies to help seekers [18]. Going a step further, when helpers with a high level of self-awareness are asked for help, they will concern about the help seekers' perceptions. Self-awareness promotes the belief that one has a relatively great personal responsibility for others and tends to increase helpfulness [19,20,21,22,23]. For help seekers, self-awareness is an essential reason for the embarrassment [24]. When help seekers with a high level of self-awareness cannot give back, they will feel belittled because they receive help. Therefore, people with a high level of self-awareness are often reluctant to seek help [25,26,27].
Politeness refers to people applying good manners or etiquette [28]. An understanding of politeness requires an understanding of its psychosocial underpinnings. At the same time, understanding the corresponding psychosocial phenomena can also be improved by studying the role of politeness in these psychosocial processes [29,30]. Politeness theory proposes that politeness can both indicate and create social distance [29,31,32]. Politeness is relevant to several research areas in social psychology, including person perception and impression management [29]. When people hold prosocial and impression management motivation, they attach importance to two results: helping others and improving their own image [33]. The desire to maintain a good image can stimulate helping behavior [34]. If the level of politeness of helpers is high, they would care more about their image and feel sympathy for help seekers when asked for help, so they would tend to help [35]. For help seekers, if they care about making trouble for others too much, it's hard to seek help [36]. If help-seeking is low yield and high cost to helpers, help seekers would also have negative emotions such as debt and apology [37]. They are afraid they will not be able to repay and are ungrateful. This politeness, as human nature, will affect people's help-seeking behavior.
Game theory refers to a theoretical framework for envisioning social situations between competing players, which implies optimal decisions for independent and competing players in an environment [38]. As a model of interactive situations between players, the game theory focuses on games where one player's payoff depends on another player's strategy [39]. Games identify players' identities, preferences, and available strategies and focus on the impact of those strategies on outcomes [40]. We establish a psychological game theory model to analyze people's help-seeking and help-giving behavior. According to the Bayesian Nash Equilibrium in this study, given the help seeker and helper characteristics, that is, the probability distribution of self-awareness and politeness, each person will choose the strategy that maximizes his/her expected utility.
This study aims to link two related social psychology concepts, self-awareness and politeness, with human helping behavior and demonstrate using a game-theory-based Bayesian Nash equilibrium approach. This study is thus expected to make the following potential contributions: First, this study would illustrate the influence of self-awareness and politeness on help-seeking and help-giving when people are in trouble. Second, this study would be able to clarify the relationship between politeness, self-awareness, and the willingness of the help seekers as well as the helpers. Third, this study will compare the results obtained by the method of Bayesian Nash equilibrium based on a psychological game in this study with the results obtained by the method of psychological experiments in previous studies, to verify the conclusion of social psychology about the influence of self-awareness and politeness on helping behavior, through the mathematical method of psychological game theory.
2.
Models
In this study, we firstly established a game theory model, which was proposed by Harsanyi [41] and adopted by many researchers, such as Myatt and Wallace; Huang and Zhu [42,43].
The characters on the stage are player A as a help-seeker and player B as a helper. Player A can be people with the low ability signed as $ L $ or high ability signed as $ H $. Player B can also be people with low ability or high ability. Low ability and high ability are basic settings in this study. Therefore, the utility function of each player is:
$ {U}_{1} $ is the utility of the actual cost paid. $ {U}_{1} $ is related to the basic cost c and the ability cost of that player, thus, $ {U}_{1} = -a\mathrm{c}; $ from player A's point of view, if player B does not help him, he/she has to work on it by himself; that is $ {U}_{A1} = -{a}_{A}\mathrm{c} $; If Player B helps, he/she can do it without effort; that is $ {U}_{A1} = 0 $; from player B's point of view, if he/she helps player A, he/she has to make his/her own efforts, that is $ {U}_{B1} = -{a}_{B}c $; If he/she does not help, he/she does not have to make an effort; that is $ {U}_{B1} = 0 $. The player with high ability costs less; on the contrary, the player with low ability costs more.
$ {U}_{2} $ is the utility of self-awareness, which is related to the degree of self-awareness; represented by $ \alpha $, and the speculation about how others think of himself, represented by $ E\left(a\right) $. Thus, $ {U}_{2} = -\alpha \left[E\left(a\right)-{a}_{}\right] $. $ {E}_{B}\left({a}_{A-Seek}\right) $ means player B speculates on player A's ability when player A seeks help; $ {E}_{B}\left({a}_{A-Not \ seek}\right) $ means player B speculates on player A's ability when player A does not seek help; $ {E}_{A}\left({a}_{B-Help}\right) $ means player A speculates on player B's ability when player B helps; $ {E}_{A}\left({a}_{B-Not \ help}\right) $ means player A speculates on player B's ability when player B does not help. $ {U}_{3} $ is the effect of politeness, and the degree of politeness β (0 < β < 1) is related to the basic cost and his actual ability, thus, $ {U}_{3} = -\beta ca $.
Player A's utility in seeking help is:
Player A's utility when he/she does not seek help is:
Player B's utility when he/she helps is:
Player B's utility when he/she does not help is:
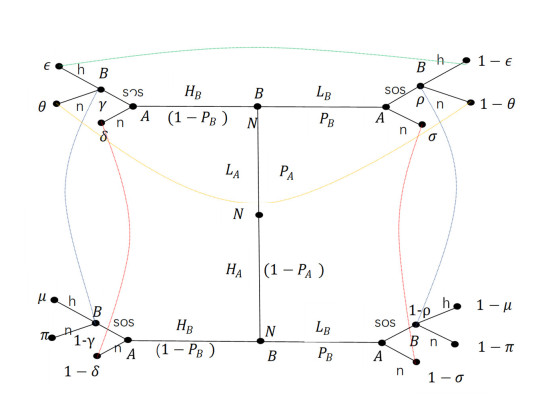
When the difference between the ability predicted by others and his actual ability is positive, it is $ {\alpha }_{1} $; and when it is negative, it becomes $ {\alpha }_{2} $. The relationship between $ {\alpha }_{1} $ and $ {\alpha }_{2} $ is $ {0 < \alpha }_{1} < {\alpha }_{2} $. The game tree is as follows:
The probability of $ {L}_{A} $ with high ability is $ {P}_{A} $; The probability of $ {H}_{A} $ with low ability is ($ 1-{P}_{A} $); $ {L}_{A} $ 's probability of seeking help is $ q $; its probability of not seeking help $ 1-q $; The probability of $ {H}_{A} $ 's help-seeking is $ q' $; Its probability of not seeking help is $ 1-q' $. Let the probability of $ {L}_{A} $ be $ {P}_{A} $, the probability of $ {H}_{A} $ be ($ 1-{P}_{A} $). Let the probability of $ {L}_{B} $ be $ {P}_{B} $, the probability of $ {H}_{B} $ be ($ 1-{P}_{B} $). The probability of $ {L}_{B} $ giving help is $ r' $, its probability of not helping is $ 1-r' $. The probability of $ {H}_{B} $ giving help is $ r $, its probability of not helping is $ 1-r $. Thus, the belief of players A and B at each point is:
Therefore, if player A seeks help, player B is in two situations: help or not help. Take the utility of player A when player B helps as $ {U}_{AseekO} $, and the utility of player A when player B does not help A as $ {U}_{AseekX} $. Thus,
Player A's utility is:
In the case of $ {H}_{A} $ with high ability:
Therefore, $ {\alpha }_{A} $ of both parties is $ {\alpha }_{A1} $. Player A's utility in seeking help is:
Player A's utility when he/she does not seek help is:
In the case of $ {L}_{A} $ with low ability:
Therefore, $ {\alpha }_{A} $ of both parties are $ {\alpha }_{A2} $. When player A seeks help, the utility is:
Player A's utility when he/she does not seek help is:
In the case of $ {H}_{B} $ with high ability:
Therefore, $ {\alpha }_{B} $ of both parties are $ {\alpha }_{B1} $. At this time, the utility of player B when he/she helps is:
The utility of player B when he/she does not help is:
In the case of $ {L}_{B} $ :
Therefore, $ {\alpha }_{B} $ of both parties are $ {\alpha }_{B1} $. At this time, the utility of player B when he/she helps is:
The utility of player B when he/she does not help is:
3.
Equilibrium analysis
Equilibrium analysis examines what happens when the system reaches equilibrium and the conditions required to achieve equilibrium [44]. Equilibrium analysis is critical in game theory because game equilibrium refers to the realization of the maximum utility of each party in the game, that is, to achieve the satisfaction of each party with the game result so that the actual utility and degree of satisfaction obtained by each party are different. In game equilibrium, such a relatively static state is in which all players do not want to change their strategies [45].
Bayesian Nash Equilibrium refers to a set of strategies: given the probability distribution of a player's own characteristics and the characteristics of other players, each player chooses a strategy to maximize his expected payoff; that is, no one has the incentive to choose other strategies [46]. This study uses a Bayesian Nash equilibrium to analyze the game between the helper and the help seeker.
Therefore, the player's decision-making goal is to maximize his/her expected utility given his/her own type and the relationship between the other player's types and strategic choices. Bayesian Nash Equilibrium is a type-dependent strategic combination [47].
We now start to analyze the equilibrium. When players A and B decide on their strategy, they would select the strategy with larger utility, thus this study should compare the difference in the utility of players' different selections.
Furthermore, player B with high ability can expect player A's ability as $ {a}_{A} = \gamma {L}_{A}+(1-\gamma ){H}_{A} $.The ability of player B with low ability can expect player A's ability as $ {a}_{A} = \rho {L}_{A}+(1-\rho ){H}_{A} $. We thus substitute them into the utility function. In addition, Player A with either the high ability or low ability would decide to seek help or not; player B with either the high ability or low ability would decide to help or not. When player A is helped by player B with high ability, $ r = 1 $; when player B with high ability does not help, $ r = 0 $; when player B with low ability helps, $ r' = 1 $; when player B with low ability does not help, $ r' = 0; $ when player A with low ability seeks for help, $ q = 1 $; when player A with low ability does not seek for help, $ q = 0 $; when player A with high ability seeks for help, $ q' = 1 $, when player A with high ability does not seek for help, $ q' = 0. $ In summary, there are situations including $ r = 1, r = 0, r' = 1, r' = 0, q = 1, q = 0, q' = 1, q' = 0 $. As a result, there are 16 combinations. According to calculating, there are nine equilibriums. The following section will discuss these equilibriums. For example, the first equilibrium is stated as follows: $ {H}_{B} $ help; $ {L}_{B} $ not help; $ {L}_{A} $ seek; $ {H}_{A} $ not seek.
1) $ r = 1, r' = 0, q = 1, q' = 1 $
In the case of $ {H}_{B}: $
In order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
In order to meet the condition $ {U}_{B-\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{p}}-{U}_{B-\mathrm{n}\mathrm{o}\mathrm{t} \ \mathrm{h}\mathrm{e}\mathrm{l}\mathrm{p}} < 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
Next, let $ {H}_{B} $ = $ {H}_{A}, {L}_{B} $ = $ {L}_{A}, {P}_{B} $ = $ {P}_{A}, {\alpha }_{B1} = {\alpha }_{A1} $ = $ {\alpha }_{1}, {\alpha }_{B2} = {\alpha }_{A2} $ = $ {\alpha }_{2}, {\beta }_{A} = {\beta }_{B} $. In this case, set the difference between $ {\alpha }_{1} $ and $ {\alpha }_{2} $ to ξ. Thus, $ {\alpha }_{2}-{\alpha }_{1} = \xi $. Because player B must meet the conditions of $ {H}_{B} $ and $ {L}_{B} $, we thus find the union set of $ {H}_{B} $ and $ {L}_{B} $. To put the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $. At this point:
In the case of $ {H}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-\mathrm{S}\mathrm{e}\mathrm{e}\mathrm{k}}-{U}_{A-\mathrm{N}\mathrm{o}\mathrm{t} \ \mathrm{s}\mathrm{e}\mathrm{e}\mathrm{k}} > 0 $, there must be:
Because there are $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, The relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} > 0 $, there must be:
Because there are $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0, $ the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Because player B must meet the conditions of $ {H}_{A} $ and $ {L}_{A} $, we thus find the union set of $ {H}_{A} $ and $ {L}_{A} $. Owing to $ \xi > 0 $, $ -\frac{{cL}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}}-\xi $ must be less than $ -\frac{{cH}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}} $. Therefore:
Players A and B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} $ or case $ {2}_{B} $. Thus, the result that satisfies the conditions of players A and B is 0 < ξ < C. The figure is as follows:
2) $ r = 1, r' = 0, q = 1, q' = 0 $
In the case of $ {H}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-help}-{U}_{B-not \ help} > 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-help}-{U}_{B-not \ help} < 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
To put the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $.
At this point:
In the case of $ {H}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-seek}-{U}_{A-not \ seek} < 0 $, there must be:
The relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-seek}-{U}_{A-not \ seek} > 0 $, there must be:
The relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
To put the two figures above together, we must distinguish occasions between $ \frac{{cL}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}}-\xi > \frac{{cH}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}} $ as case $ {1}_{A} $ and $ \frac{{cL}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}}-\xi < \frac{{cH}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}} $ as case $ {2}_{A} $. At this point:
Player A must satisfy all of the conditions of the game equilibrium case $ {1}_{A} $. Player B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} $. To satisfy both case $ {1}_{A} $ and case $ {1}_{B} $, there must be $ 0 < \xi < \mathrm{c}\left(1-{P}_{B}\right) $. The figure is as follows:
3) $ r = 1, r' = 0, q = 0, q' = 0 $
In the case of $ {H}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} < 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
To put the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $. At this point:
In the case of $ {H}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} < 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} < 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Owing to:
$ {\alpha }_{2}-{\alpha }_{1} = \xi $, $ \frac{{cL}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}}-\xi > \frac{{cH}_{B}\left(1-{P}_{B}\right)}{{(L}_{A}-{H}_{A})} $ as case $ {1}_{A}, \frac{{cL}_{A}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}}-\xi < \frac{{cH}_{B}\left(1-{P}_{B}\right)}{{L}_{A}-{H}_{A}} $ as case $ {2}_{A} $ are as follows:
Player A must satisfy all of the conditions of the game equilibrium case $ {1}_{A} $ and player B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} $ and case $ {2}_{B} $. Because case $ {2}_{B} $ is an empty set, the union set of case $ {2}_{B} $ and case $ {1}_{A} $ is also an empty set. To satisfy both case $ {1}_{B} $ and case $ {1}_{A} $, there must be $ 0 < \xi < \mathrm{c}\left(1-{P}_{B}\right). $ To satisfy both case $ {1}_{B} $ and case $ {2}_{A} $, there must be $ \mathrm{c}\left(1-{P}_{B}\right) < \xi < \mathrm{c}. $ Both of them are shown in the following figure:
4) $ r = 0, r' = 0, q = 1, q' = 1 $
In the case of $ {H}_{B}: $
Therefore, in order to meet the condition $ {U}_{A-Help}-{U}_{A-Not \ help} < 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 \ \mathrm{a}\mathrm{n}\mathrm{d} \ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} < 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 \ \mathrm{a}\mathrm{n}\mathrm{d} \ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
Owing to $ \xi > 0 $, $ -\frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi $ must be less than $ -\frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $. Therefore, the union set is:
In the case of $ {H}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} > 0 $, there must be: $ ({P}_{A}-\delta ) < 0. $ When $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A}: $
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} > 0 $, there must be: $ ({P}_{A}-\delta ) < 0 $. When $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
The condition of player B and player A is $ 0 < \xi $. As shown in the following figure:
5) $ r = 0, r' = 0, q = 0, q' = 0 $
In the case of $ {H}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-Seek}-{U}_{B-Not \ Seek} < 0 $, there must be: $ ({\beta }_{B} < -{\alpha }_{B1}\frac{\left({L}_{B}-{H}_{B}\right)[\varepsilon -(1-{P}_{B}\left)\right]}{c{[\gamma L}_{A}+(1-\gamma ){H}_{A}]}+\frac{{H}_{B}}{{[\gamma L}_{A}+(1-\gamma ){H}_{A}]} $, when $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} < 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
Since $ \xi > 0 $, $ -\frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi $ is always smaller than $ -\frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $. Thus, the union set is:
In the case of $ {H}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} < 0 $, there must be: $ (\mathrm{\gamma }-{P}_{A}) > 0 $, when $ \left(\gamma -\delta \right) > 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} < 0 $, there must be: $ (\mathrm{\gamma }-{P}_{A}) > 0 $, when $ \left(\gamma -\delta \right) > 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Player B's all conditions and player A's all conditions must be met. Thus, the result is $ 0 < \xi $. The figure is shown as follows:
6) $ r = 1, r' = 1, q = 0, q' = 0 $
In the case of $ {H}_{B}: $
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
To combine the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $. At this time,
In the case of $ {H}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{k}}-{U}_{A-not \ seek} < 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{k}}-{U}_{A-not \ seek} < 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Owing to $ {\alpha }_{2}-{\alpha }_{1} = \xi $, there is $ \frac{{cL}_{A}}{{L}_{A}-{H}_{A}}-\xi > \frac{{cH}_{A}}{{L}_{A}-{H}_{A}} $ as case $ {1}_{A}, \frac{{cL}_{A}}{{L}_{A}-{H}_{A}}-\xi < \frac{{cH}_{A}}{{L}_{A}-{H}_{A}} $ as case $ {2}_{A} $. At this time,
Player A must satisfy all of the conditions of the game equilibrium case $ {1}_{A} \ \mathrm{a}\mathrm{n}\mathrm{d} \ {2}_{A} $. Player B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} \ \mathrm{a}\mathrm{n}\mathrm{d} \ {2}_{B} $. Thus, the result of the union set of case $ {1}_{B} $ and case $ {1}_{A} $ is 0 < ξ < c. It is shown in the following figure:
Since the results of the union set of case $ {1}_{B} $ and case $ {2}_{A} $ are $ \xi < \mathrm{c} $, $ \xi > \mathrm{c} $, ξ does not exist. Since the results of the union set of case $ {2}_{B} $ and case $ {1}_{A} $ are $ \xi > \mathrm{c}, \xi < \mathrm{c}, $ $ \xi $ does not exist. The result of the union set of case $ {2}_{B} $ and case $ {2}_{A} $ is $ \xi > \mathrm{c} $. The figure is shown as follows:
7) $ r = 1, r' = 1, q = 1, q' = 1 $
In the case of $ {H}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-help}-{U}_{B-not \ help} > 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-help}-{U}_{B-not \ help} > 0 $, there must be:
When $ \left(\varepsilon -\theta \right) > 0 $ and $ \left(\varepsilon -\theta \right) < 0 $, the relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
To put the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $. At this point:
In the case of $ {H}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-seek}-{U}_{A-not \ seek} > 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-seek}-{U}_{A-not \ seek} > 0 $, there must be:
When $ \left(\gamma -\delta \right) > 0 $ and $ \left(\gamma -\delta \right) < 0 $, the relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Since $ \xi > 0 $, $ -\frac{{cL}_{A}}{{L}_{A}-{H}_{A}}-\xi $ is always smaller than $ -\frac{{cH}_{A}}{{L}_{A}-{H}_{A}} $. Thus, the union set is:
Player B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} $ or case $ {2}_{B} $, so does player A. Thus, the result that satisfies the conditions of players A and B is $ 0 < \xi < \mathrm{c} $. The figure is:
To satisfy case $ {2}_{B} $ and player A's conditions, the result is $ 1 > \xi > \mathrm{c} $. The figure is as follows:
8) $ r = 1, r' = 1, q = 1, q' = 0 $
In the case of $ {H}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B1} $ is shown in the following figure:
In the case of $ {L}_{B} $ :
Therefore, in order to meet the condition $ {U}_{B-Help}-{U}_{B-Not \ help} > 0 $, there must be:
The relationship between $ {\beta }_{B} $ and $ {\alpha }_{B2} $ is shown in the following figure:
To combine the two figures above together, we must distinguish occasions between $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi > \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {1}_{B} $ and $ \frac{{cL}_{B}}{{L}_{B}-{H}_{B}}-\xi < \frac{{cH}_{B}}{{L}_{B}-{H}_{B}} $ as case $ {2}_{B} $. At this point,
In the case of $ {H}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} < 0 $, there must be:
The relationship between $ {\beta }_{A} $ and $ {\alpha }_{A1} $ is shown in the following figure:
In the case of $ {L}_{A} $ :
Therefore, in order to meet the condition $ {U}_{A-Seek}-{U}_{A-Not \ seek} > 0 $, there must be:
The relationship between $ {\beta }_{A} $ and $ {\alpha }_{A2} $ is shown in the following figure:
Since $ {\alpha }_{2}-{\alpha }_{1} = \xi $, there are: $ \frac{{cL}_{A}}{{L}_{A}-{H}_{A}}-\xi > \frac{{cH}_{A}}{{L}_{A}-{H}_{A}} $ as case $ {1}_{A} $ and $ \frac{{cL}_{A}}{{L}_{A}-{H}_{A}}-\xi < \frac{{cH}_{A}}{{L}_{A}-{H}_{A}} $ as case $ {2}_{A} $. At this point,
Player B must satisfy all of the conditions of the game equilibrium case $ {1}_{B} $ or case $ {2}_{B} $, player A must satisfy all of the conditions of the game equilibrium case $ {1}_{A} $ or case $ {2}_{A} $. Because case $ {2}_{A} $ is an empty set, the union set of case $ {1}_{B} $ and case $ {2}_{B} $ is also an empty set. Thus, the result that satisfies both case $ {1}_{B} $ and case $ {1}_{A} $ is $ 0 < \xi < \mathrm{c}. $ The figure is as follows:
Since the result of the union set of case $ {2}_{B} $ and case $ {1}_{A} $ is $ \xi > \mathrm{c} $, $ \xi < \mathrm{c} $, ξ does not exist.
The above section discusses the eight equilibriums. The next section will discuss why the following eight situations are not equilibrium:
9) $ r = 0, r' = 0, q = 1, q' = 0 $
In the case of $ {L}_{A} $ :
Owing to $ {U}_{A-Seek}-{U}_{A-Not \ seek} > 0 $ must be satisfied, $ {U}_{A-Seek}-{U}_{A-Not \ seek} $ must be less than 0. It contradicts $ q = 1 $.
10) $ r = 0, r' = 0, q = 0, q' = 1 $
In the case of $ {L}_{A} $ :
Owing to $ -{\alpha }_{A2}(-1)\left({L}_{A}-{H}_{A}\right) $ is always positive, $ {U}_{A-Seek}-{U}_{A-Not \ seek} $ must be greater than 0. It contradicts $ q = 0 $.
11) $ r = 1, r' = 0, q = 0, q' = 1 $
In the case of $ {L}_{A} $ :
Owing to $ -{\alpha }_{A2}(-1)\left({L}_{A}-{H}_{A}\right) $ and $ \left(1-{P}_{B}\right)c\{{L}_{A}-{\beta }_{A}\left[{P}_{B}{L}_{B}+\left(1-{P}_{B}\right){H}_{B}\right]\} $ are always positive, $ {U}_{A-Seek}-{U}_{A-Not \ seek} $ must be greater than 0. It contradicts $ q = 0 $.
12) $ r = 0, r' = 1, q = 1, q' = 0 $
In the case of $ {L}_{B} $ :
Owing to $ {\alpha }_{B2}{(L}_{B}-{H}_{B})\left(-1\right) $ and $ c\left({\beta }_{B}{L}_{A}-{L}_{B}\right) $ are always negative, $ {U}_{B-Help}-{U}_{B-Not \ help} $ must be less than 0. It contradicts $ r' = 1 $.
13) $ r = 1, r' = 1, q = 0, q' = 1 $
In the case of $ {L}_{A} $ :
Owing to $ -{\alpha }_{A2}(-1)\left({L}_{A}-{H}_{A}\right) $ and $ c\{{L}_{A}-{\beta }_{A}\left[{P}_{B}{L}_{B}+\left(1-{P}_{B}\right){H}_{B}\right]\} $ are always positive, $ {U}_{A-\mathrm{S}\mathrm{e}\mathrm{e}\mathrm{k}}-{U}_{A-\mathrm{N}\mathrm{o}\mathrm{t} \ \mathrm{s}\mathrm{e}\mathrm{e}\mathrm{k}} $ must be greater than 0. It contradicts $ q = 0 $.
14) $ r = 0, r' = 1, q = 1, q' = 1 $
In the case of $ {L}_{B} $ :
Owing to $ {\alpha }_{B2}{(L}_{B}-{H}_{B})\left(-1\right) $ and $ c({\beta }_{B}{L}_{A}-{L}_{B}) $ are always negative, $ {U}_{B-Help}-{U}_{B-Not \ help} $ must be less than 0. It contradicts $ r' = 1 $.
15) $ r = 0, r' = 1, q = 0, q' = 0 $
In the case of $ {L}_{B} $ :
Owing to $ {\alpha }_{B2}{(L}_{B}-{H}_{B})\left(-1\right) $ and $ c({\beta }_{B}{L}_{A}-{L}_{B}) $ are always negative, $ {U}_{B-Help}-{U}_{B-Not \ help} $ must be less than 0. It contradicts $ r' = 1 $.
16) $ r = 0, r' = 1, q = 0, q' = 1 $
In the case of $ {L}_{B} $ :
Owing to $ {\alpha }_{B2}{(L}_{B}-{H}_{B})\left(-1\right) $ and $ c({\beta }_{B}{H}_{A}-{L}_{B}) $ are always negative, $ {U}_{B-Help}-{U}_{B-Not \ help} $ must be less than 0. It contradicts $ r' = 1 $.
4.
Discussion and implications
4.1. Discussion
Based on the above equilibrium analysis results, the difference in self-awareness ξ is greatest when it is larger than c, and it becomes equilibriums 6) and 7). It means when the degree of risk aversion of the player is the highest, the helper always helps, regardless of the help-seekers' ability. The reason is that risk aversion helpers care more about being looked down upon than being looked up to by others. Therefore, seeking help from someone with a high level of self-awareness increases the likelihood of getting help. This is consistent with the prior studies based on psychological experiments [19,21,22]. When ξ is slightly smaller, there are equilibriums 1)–3) and 6)–8). At this time, player B, with high ability, would help. Low ability does not necessarily help. In other words, when the difference in self-awareness is medium and slightly smaller, or the degree of risk aversion decreases, only people with high ability will help others. Although people with low ability want to help others, the price of helping others is too high, so they will not help others. Under this condition, self-awareness tends to increase helpfulness. This is consistent with the prior studies based on psychological experiments [19,22,23]. When ξ is the smallest, it is equilibriums 2), 4), 6), 7) and 9). When the difference in self-awareness is minimal, that is, when the degree of risk aversion is small, high-ability help seekers tend not to seek help from others. At this time, although the seeker does not care much about being looked down upon by others, once they seek help from others, the high-ability person will also reduce their utility due to reasons related to politeness, so the high-ability seeker is more inclined to not ask for help. This is consistent with previous literature based on psychological experiments [21].
Regarding the helper, by equilibriums 4) and 5), if the self-awareness α is large, but the politeness β is very small, neither player B with high ability nor low ability would help. In other words, even if the self-awareness is relatively high, but the degree of politeness is relatively low, both high and low ability people will not help. This is consistent with the previous literature based on psychological experiments [20]. We confirmed that when self-awareness and politeness are within a certain range, people help, as shown in equilibriums 1)–3). Suppose self-awareness α and politeness β are within a specific range; in other words, when self-awareness and politeness are within a specific range. In that case, people with high ability will help, and people with low ability will not help. In equilibriums 6)–8), when self-awareness and politeness are high, the helper will choose to help others regardless of their ability. Helpers with high levels of self-awareness tend to help, consistent with previous research based on psychological experiments [19]. Besides, Helpers with high levels of politeness tend to help, consistent with previous research based on psychological experiments [33,34,35].
Concerning the help-seeker, in equilibrium 7), If politeness $ \mathrm{\beta } $ is small when seeking help, either player A with low or high ability would seek help. It means when viewed from the perspective of the seeker, when the degree of politeness of the seeker is relatively low, no matter the seeker's ability, he/she will seek help from others.
In equilibriums 2) and 8), if self-awareness α and politeness β are within a specific range, which means the level of self-awareness and politeness are within a certain range, player A with high ability would not seek help. However, player A with low ability would seek help.
In equilibriums 3) and 6), when self-awareness α and politeness β are both large, either player B with the high ability or low ability would not seek help. It means when self-awareness and politeness are high, the help seeker will not ask for help, regardless of the ability of the seeker. On the one hand, help seekers with high levels of self-awareness tend not to seek help, consistent with previous research based on psychological experiments [25,26,27]. On the other hand, help seekers with high levels of politeness tend not to seek help, consistent with previous research [36,37].
In situations 12) and 14)–16) where there is no equilibrium, player B with high ability may help. While the psychological effect of self-awareness $ \mathrm{\alpha } $ and politeness $ \mathrm{\beta } $ affect human behavior, it is impossible to force others to do things beyond their abilities.
In situations 10), 11), 13), and 16), it is unlikely that a player with low abilities would not seek help, and a player with high abilities would seek help.
4.2. Theoretical contributions
To the best of our knowledge, this is the first application of Bayesian Nash equilibrium based on psychological game theory in studying human help-seeking and help-giving behavior. Through this study, we thus extend the generalizability of Bayesian Nash equilibrium based on psychological game theory to the study of human helping behavior.
Humans grow through mutual help, and society progresses accordingly. However, there are times when people are in deep trouble and are reluctant to ask for help; at other times, people are very hesitant to help others. By establishing a Bayesian Nash Equilibrium analysis, this study analyzes whether people would seek help or help others from two fundamental concepts related to internal rewards: self-awareness and politeness. We also demonstrate the extent to which self-awareness and politeness influence help-seeking and help-giving behaviors, which are regular and predictable. This study thus provides a theoretical understanding of the role of self-awareness and politeness in helping behavior.
For help-seeking behavior, we can understand why people do not seek help when they are clearly in trouble. Because people have the nature of politeness, it is difficult to ask for help if they are excessively polite and care about their image. Besides, people with an excessively high level of self-awareness often do not ask others for help because they are worried about exposing their flaws and incompetence in front of others [48].
From the perspective of helpers, we can also understand people tend to help others if they have a high level of self-awareness and politeness. However, it may not be their original intention. For one thing, helpers want to help others to create a positive personal impression and gain praise. For another, politeness, as a basic moral code, advocates the duty of helping others. It also motivates people to help those who are not life-threatening or in desperate need.
4.3. Practical implications
Many of our findings have practical implications for understanding and increasing helping behavior to build a harmonious and mutual aid society finally.
Based on this study, in the case of knowing the level of self-awareness and politeness of both parties, help seekers can judge whether the other party will help them, and thus decide whether to seek help. Helpers, on the other hand, can judge whether they help or not.
In terms of help-giving, after realizing that people with high levels of self-awareness tend to help, we can improve people's level of self-awareness to increase helping behavior. Specifically, we can encourage people to read, practice, reflect on themselves more, cultivate their independent awareness and thinking ability, and improve their self-awareness level. Besides, after realizing that people with high levels of politeness tend to help, we can promote the development of etiquette education and improve the level of etiquette cultivation ideologically, to improve the level of politeness. These measures can eventually increase the opportunity to give help. In brief, it is necessary to improve everyone's self-awareness and support and promote the moral code of being polite to others.
In terms of help-seeking, through this study, we found that individuals with a high level of self-awareness are often reluctant to seek help. So it is crucial to give the person being helped an opportunity to repay the favor. This has also been confirmed in other studies. People are more likely to commit to charities belonging to those who have given them favors [49]. This study suggests individuals with a high level of politeness tend to give up seeking help. Therefore, it is essential to eliminate the guilt of the seeker as much as possible and reduce the bad feeling.
There are many examples of helping behaviors in everyday life. For example, donation behavior is a typical helping behavior. For instance, in residential communities in China, when someone encounters difficulties such as sudden illness and needs to donate, there are often donation activities similar to love relays. These donation behaviors are influenced by two factors self-awareness and politeness in this study. In this context of donation behavior, people with a high level of self-awareness and politeness are more likely to donate to help those in need who are seriously ill but have no money for treatment. Patients who are short of money and unable to treat their illnesses may tend not to raise funds if their levels of self-awareness and politeness are too high, thus delaying treatment. In such a situation, on the one hand, we need to improve the level of self-awareness and politeness of as many people as possible in our society so that when someone needs help, as many people as possible will lend a helping hand. On the other hand, we can also build channels to provide opportunities for patients who seek help to thank donors so that patients who need help will not miss the opportunity to seek help for their own reasons.
5.
Conclusions
Although there are extensive studies on human helping behavior in existing literature, prior research emphasized methods of psychological experiments. Besides, studies on human help-seeking and help-giving behaviors rarely study the connection of self-awareness and politeness to human help-seeking and help-giving behaviors, especially from the perspective of psychological game theory. This paper thus links two related social psychology concepts, self-awareness and politeness, with human helping behavior and applies Bayesian Nash equilibrium analysis to compare with the results obtained from psychological experiments in previous studies. We found that a helper with a high level of self-awareness and politeness would help. In contrast, help seekers with a high level of self-awareness and politeness would tend not to seek help. The results obtained in this study through the mathematical method of psychological game theory validate the conclusion of the influence of self-awareness and politeness on helping behavior in social psychology studies based on the research method of psychological experiments.
Limitations and future directions: To simplify the model, the study has limitations. First, this study does not consider the repaying, in other words, whether the help will be repaid in the future. Second, this study only considered two psychological factors, politeness and self-awareness; other psychological factors could also influence human helping behavior.
Future studies can consider the act of repaying, and the game theory model can be set as a repeated game. In addition, other psychological factors can be considered in the game theory model to make the theoretical model richer and more realistic to understand human help-seeking and help-giving behavior better.
Acknowledgments
We sincerely thank the editors and the anonymous reviewers for their thoughtful reviews and constructive suggestions during the review process. This work was supported by Jiangxi Culture, Art and Science Planning Grant Numbers YG2021184. We also wish to thank Otsuka Toshimi Scholarship Foundation for its generous help.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:


























































