Figure 1.
(color online) The process of constructing the causality network between two variables $X$ and $Y$.
Citation: Daniel Roggen, Martin Wirz, Gerhard Tröster, Dirk Helbing. Recognition of crowd behavior from mobile sensors with pattern analysis and graph clustering methods[J]. Networks and Heterogeneous Media, 2011, 6(3): 521-544. doi: 10.3934/nhm.2011.6.521
| [1] | YongKyung Oh, JiIn Kwak, Sungil Kim . Time delay estimation of traffic congestion propagation due to accidents based on statistical causality. Electronic Research Archive, 2023, 31(2): 691-707. doi: 10.3934/era.2023034 |
| [2] | Ming Wei, Shaopeng Zhang, Bo Sun . Airport passenger flow, urban development and nearby airport capacity dynamic correlation: 2006-2019 time-series data analysis for Tianjin city, China. Electronic Research Archive, 2022, 30(12): 4447-4468. doi: 10.3934/era.2022226 |
| [3] | Yuxia Liu, Qi Zhang, Wei Xiao, Tianguang Chu . Characteristic period analysis of the Chinese stock market using successive one-sided HP filter. Electronic Research Archive, 2023, 31(10): 6120-6133. doi: 10.3934/era.2023311 |
| [4] | Jiping Xing, Xiaohong Jiang, Yu Yuan, Wei Liu . Incorporating mobile phone data-based travel mobility analysis of metro ridership in aboveground and underground layers. Electronic Research Archive, 2024, 32(7): 4472-4494. doi: 10.3934/era.2024202 |
| [5] | Moutian Liu, Lixia Duan . In-phase and anti-phase spikes synchronization within mixed Bursters of the pre-Bözinger complex. Electronic Research Archive, 2022, 30(3): 961-977. doi: 10.3934/era.2022050 |
| [6] | Zhihui Wang, Yanying Yang, Lixia Duan . Dynamic mechanism of epileptic seizures induced by excitatory pyramidal neuronal population. Electronic Research Archive, 2023, 31(8): 4427-4442. doi: 10.3934/era.2023226 |
| [7] | Li Li, Zhiguo Zhao . Inhibitory autapse with time delay induces mixed-mode oscillations related to unstable dynamical behaviors near subcritical Hopf bifurcation. Electronic Research Archive, 2022, 30(5): 1898-1917. doi: 10.3934/era.2022096 |
| [8] | Jianmin Hou, Quansheng Liu, Hongwei Yang, Lixin Wang, Yuanhong Bi . Stability and bifurcation analyses of p53 gene regulatory network with time delay. Electronic Research Archive, 2022, 30(3): 850-873. doi: 10.3934/era.2022045 |
| [9] | Jieqiong Yang, Panzhu Luo . Study on the spatial correlation network structure of agricultural carbon emission efficiency in China. Electronic Research Archive, 2023, 31(12): 7256-7283. doi: 10.3934/era.2023368 |
| [10] | Ariel Leslie, Jianzhong Su . Modeling and simulation of a network of neurons regarding Glucose Transporter Deficiency induced epileptic seizures. Electronic Research Archive, 2022, 30(5): 1813-1835. doi: 10.3934/era.2022092 |
The dollar is an international currency issued and endorsed by the Federal Reserve. As a stable currency, it is used for the most extensive payment and settlement. Gold is a precious metal, which contains commodity and monetary attributes. Accordingly, both have integrated vital risk aversion functions, whose has always been a concern to the financial media and the investors. So far, there have been multiple studies on the relationship between the gold price and the dollar index [1,2,3,4,5,6,7]. Most studies showed a significant negative correlation between them [8,9,10]; when the dollar depreciates, the nominal price of gold will rise. Therefore, gold behaves as a hedge against the dollar and provides exchange rate hedging for investors holding the dollar. On the contrary, observers have long noted a positive correlation of them, although this correlation will not last long [3,11,12,13,14]. Moreover, the relationship is not always stable [1,15]. When the financial markets run smoothly, gold and the dollar will show a trend of going up and falling on the other; and when there is a local political crisis or economic crisis in the world, the correlation will be positive.
The previous studies have obtained time-varying causal relationships between gold and the dollar based on the econometric framework [1,15], such as the error correction model, the standard bivariate $ GARCH $ models and the extension to the structural $ BEKK $ model. In addition, Lin et al. [16] utilized wavelet analysis to decompose the pair relations between oil-US dollar and gold-US dollar into short-term and long-term parts, they found that the pair relationship becomes weaker in the long run and the short-run correlations are much higher after the early $ 1990s $. Moreover, Mo et al. [3] investigated the long-term relationship by means of both fractional cointegration and $ DCC-MGARCH $ method and employed non-linear asymmetric causality to examine the effect of the $ 2007 $ global financial crisis on the short-term interdependence. However, both the causality's evolution rule and motif structure were ignored in these studies. It is still an open issue to discover the motifs and their relationships. The combined application of time-series analysis and complex network theory effectively describes the temporal evolution of relationships in complex systems [17,18,19]. Methods of complex networks have been proposed to analyze time series, such as visibility graph methods [20], recurrence network method [21], coarse-graining method [22], pseudo-periodic time series [23], quasi-isometric transformation [24], correlation matrix [25] and the state-transition network [26,27,28]. These methods can map the time series into the network. In this article, we apply the state-transition network method of easy-to-operate to convert the time series into a complex network. The method can reveal dynamic information as well as complicated behaviour in complex systems.
In recent years, causal analysis has attracted the attention of many researchers because it can reveal the internal laws between variables. For example, the Granger causality test has successfully revealed the non-linear causal relationship of separable variables [29,30]; transfer entropy can detect causality based on the information flowing between variables, by which the large sample size is required to estimate accurately [31]. Moreover, the cross-convergent mapping ($ CCM $) indicates that the time-series variables are causally linked if they are from the same dynamical system. Namely, they share a common attractor [32,33]. It can distinguish the causality from the correlation in inseparable systems, which complements the Granger causality test. The weakness for the $ CCM $ method is that it is sensitive to noise of which the influence inevitably exists in natural systems.
In order to decrease the impact of noise, Stavroglou et al. proposed the pattern causality algorithm ($ PC $) to investigate the symbolic dynamics based on the $ CCM $ [34,35]. The $ PC $ method can judge not only the causality intensity but also the causality type, by which the causality is divided into three types, i.e., positive, negative, and dark (a more complex causal relationship). The targeted partition allows the unique identification for both persistent causal structures and dominant influences that would otherwise be lost in the noise of disparate causalities(if we did not discern the three types of interactions). Moreover, this method reveals causality between variables from the perspective of non-linear dynamics.
In this article, a state-transition network was built to detect the evolutional or time-varying characteristics in the causality between gold price and the dollar index. Specifically, the idea is to extract all possible segments from the initial bivariate time-series of gold price and the dollar index by a sliding window. Then, for each segment, the non-linear causality is identified by the $ PC $ method, containing the causality type as well as causality intensity. The causality pattern is used to describe the state. We mapped all the states defined as nodes to a unique state chain. An edge is added between two states(nodes) if they appear successively. The resulting network is called a state-transition network whose topological structure can represent the dynamic characteristics of the causal relationship. Thus, the results of this paper provide a reference for studying the time-varying characteristics of causality between gold and the dollar. The structure of this article is as follows. In Section Ⅱ, we present (ⅰ) the data description of gold and the dollar analyzed in this study; (ⅱ) the steps of the method that combines $ PC $ and state-transition network; (ⅲ) definitions of concepts; Section Ⅲ shows (ⅰ) determination of an appropriate window size; (ⅱ) identification of important causality states; (ⅲ) identification of the transitions among nodes and among clusters, respectively; Section Ⅳ summarizes and discusses the results.
The daily closing prices of gold futures and the dollar index futures, respectively, were downloaded from the website, https://cn.investing.com/. They are issued by the Intercontinental Exchange of the United States, of which stock exchange codes are $ ZG $ and $ DX $, respectively. The data was selected from November $ 21 $, $ 1985 $ to June $ 22 $, $ 2022 $. The length of the bivariate series is $ 9248 $ after deleting a small number of missing data ($ 63 $ data points of gold and $ 83 $ data points of the dollar). Note that Saturdays and Sundays are excluded from the time series. Because the original data is unstable and there is a large difference between gold and the dollar, we performed the analysis based on the logarithmic return rate of daily closing prices.
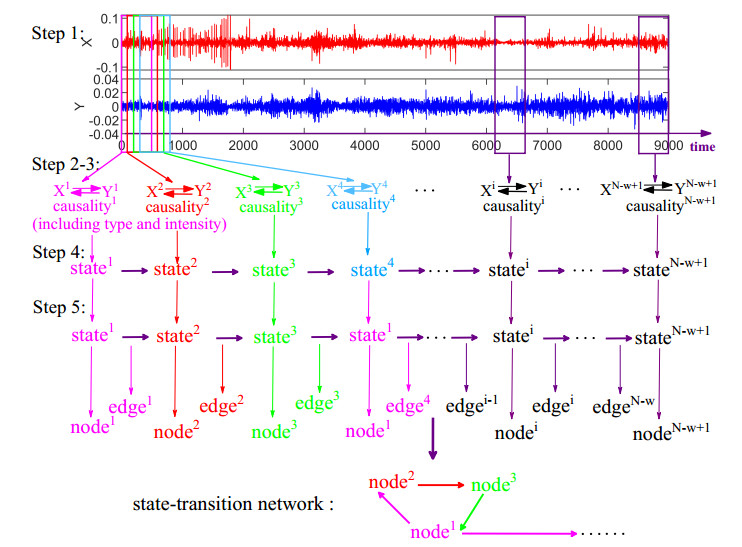
The specific process for building the state-transition network consists of the following five steps: (ⅰ) dividing the time series into segments of the equal length; (ⅱ) obtaining the reconstructed phase space for each fragment; (ⅲ) calculating the causality types as well as the causality intensities by the $ PC $ method; (ⅳ) transforming the causality types and the causality intensities into causality states; (ⅴ) constructing the state-transition network. The whole process is shown in Figure 1.
Step 1. Dividing the time series into segments of equal length.
For simplicity, let $ X $ and $ Y $ represent gold and the dollar, respectively. $ X $ and $ Y $ can be expressed as time series $ {X} = {X(1), \cdots, X(N)} $ and $ {Y} = {Y(1), \cdots, Y(N)} $, respectively, where $ N $ is the length of time series. Let the window size be $ w $ and the sliding step be $ 1 $. Accordingly, $ N-w+1 $ fragments are obtained for each time series. Then, the $ i_{th} $ fragment can be expressed as:
|
$ Xi={X(i),X(i+1),⋯,X(i+w−1)},1≤i≤N−w+1,Yi={Y(i),Y(i+1),⋯,Y(i+w−1)},1≤i≤N−w+1. $
|
(2.1) |
Step 2. Obtaining the reconstructed phase space for each fragment.
We reconstructed the phase space for each fragment defined by Eq (2.1) [36,37]. $ E $ and $ \tau $ represent the embedded dimension and delay time, respectively. A data point is an E-dimensional vector in the phase space [37]. The $ j_{th} $ point in the pase space of the $ i_{th} $ fragment can be expressed as
|
$ x(j)={Xi(j),Xi(j+τ),Xi(j+2τ),⋯,Xi(j+(E−1)τ))},1≤i≤N−w+1,1≤j≤w−(E−1)τ, $
|
(2.2) |
where $ E $ and $ \tau $ are the two parameters of which values are required to be determined. Their values will affect the accuracy of the results. If the values are too large, the system will lose much important information; and if the values are too small, the system will be easily disturbed by noise. A great deal of work have been done around this issue. In this article, the $ C-C $ method [38] is utilized to determine the values of $ E $ and $ \tau $, simultaneously. By this method, the optimal embedding dimensions were obtained for the two variables $ X $, $ Y $ are $ 2 $ and $ 3 $, respectively. The values of the dimensions are also limited by the application of $ PC $ method, i.e., the embedding dimension of each variable should be the same and the missing information of the system should be as little as possible. Therefore, the values of $ E $ and $ \tau $ were set to $ 3 $ and $ 1 $ in this article, respectively. According to Eq (2.2), $ i_{th} $ fragment of $ X $ can be expressed in the phase space by the matrix $ MX^{i} $:
|
$ Xi={X(i),X(i+1),⋯,X(i+w−1)}⇒MXi=(x(1)={Xi(1),Xi(1+τ),⋯,Xi(1+(E−1)τ)}x(2)={Xi(2),Xi(2+τ),⋯,Xi(2+(E−1)τ)}⋮x(w−(E−1)τ)={Xi(w−(E−1)τ),Xi(w−(E−2)τ),⋯,Xi(w)}), $
|
(2.3) |
Similarly, we can obtain the matrix $ MY^{i} $ by Eq (2.3).
Step 3. Calculating the causality patterns as well as the causality intensities.
$ PC $ is a method proposed by Stavroglou et al. to explore nonlinear causality between time series developed from $ CCM $ [34]. It can judge not only the the causality intensity but also the causality type. The $ PC $ method is described as below. The distance matrix $ DX^{i} $ is defined as:
|
$ DXi=(d(x(1),x(1))d(x(1),x(2))⋯d(x(1),x(w−(E−1)τ))d(x(2),x(1))d(x(2),x(2))⋯d(x(2),x(w−(E−1)τ))⋮⋮⋮⋮d(x(w−(E−1)τ),x(1))d(x(w−(E−1)τ),x(2))⋯d(x(w−(E−1)τ),x(w−(E−1)τ))), $
|
(2.4) |
where $ d(x(t), x(t+1)) $ is the Euclidean distance from $ x(t) $ to $ x(t+1) $ for a focused time $ t $. According to Eq (2.4), $ E+1 $ real nearest neighbors for $ x(t) $ represented by $ NN_{x(t)} $ were found in Eq (2.5). The reason why we chose $ E+1 $ nearest neighbor was that it requires at least $ E+1 $ point to form bounded simplicity in E-dimensional phase space. From these $ E+1 $ nearest neighbors, two pieces of information were recorded, i.e., their time indexes $ t_{x_{1}}, t_{x_{2}}, \cdots, t_{x_{E+1}} $, and their distance from a focused point $ x(t) $. Similarly, we can obtain $ y(t) $'s $ E+1 $ nearest neighbors and their time indices $ t_{y_{1}}, t_{y_{2}}, \cdots, t_{y_{E+1}} $. These time indices corresponding to the nearest neighbors to $ y(t) $ on $ MY^{i} $ are used to identify the points in $ MX^{i} $, i.e., $ x(t) $'s $ E+1 $ estimated nearest neighbors by $ y(t) $. Thus, the distances from $ x(t) $ to $ x(t) $'s $ E+1 $ real nearest neighbors and the distances from $ x(t) $ to $ x(t) $'s $ E+1 $ estimated nearest neighbors by $ y(t) $ are shown in Eq (2.6).
|
$ NNx(t)=min(E+1){d(x(t),x(1)),d(x(t),x(2)),⋯,d(x(t),x(t−(E−1)τ))}={NNx(t1),NNx(t2),⋯,NNx(tE+1)}⇒<tx1,tx2,⋯,txE+1>, $
|
(2.5) |
|
$ dj=d(x(t),x(txj)),1≤j≤E+1ˆdj=d(x(t),x(tyj)),1≤j≤E+1 $
|
(2.6) |
The real pattern of the $ MX^{i} $'s $ t_{th} $ point $ x(t) $ is:
|
$ Patternx(t)=signature(sigx(t)), $
|
(2.7) |
where
|
$ sigx(t)=E+1∑j=1Wjsj, $
|
|
$ Wj=edj∑E+1j=1edj,1≤j≤E+1, $
|
|
$ sj=(X(tj−τ)−X(tj)X(tj),X(tj−2τ)−X(tj−τ)X(tj−τ),⋯,X(tj−(E−1)τ)−X(tj−(E−2)τ)X(tj−(E−2)τ)),1≤j≤E+1, $
|
where the function $ signature $ stands for symbolization. In particular, when $ sig_{y(t)} $ is greater than $ 0 $, $ Pattern_{y(t)} $ stands for $ \nearrow $; when $ sig_{y(t)} $ is less than $ 0 $, $ Pattern_{y(t)} $ stands for $ \searrow $; when $ sig_{y(t)} $ is equal to $ 0 $, $ Pattern_{y(t)} $ stands for $ \rightarrow $. Furthermore, the estimated pattern of the $ MX^{i} $'s $ t_{th} $ point $ x(t) $ by $ MY^{i} $'s $ t_{th} $ point $ y(t) $ is:
|
$ ^Patternx(t)=signature(^sigx(t)), $
|
(2.8) |
where
|
$ ^sigx(t)=E+1∑j=1ˆWjsj, $
|
|
$ ˆWj=eˆdj∑E+1j=1eˆdj,1≤j≤E+1. $
|
Similarly, the real pattern and the estimated pattern of each point in $ MX^{i} $ and $ MY^{i} $ can also be obtained, $ i = 1, 2, ..., N-w+1 $. All the situations of $ PC $ pattern are shown for $ E = 3 $ in Figure 2. The left blue striped, right red striped, and purple boxes represent positive causalities, negative causalities and dark causalities, respectively. We recorded the point with the same pattern of $ Pattern_{x(t)} $ and $ \hat{Pattern}_{x(t)} $, i.e., the accurately estimated point. Each cell (the box in Figure 2) is filled with proportion of each pattern in the total accurately predicted points. Thus, the value of each cell is in the range from $ 0 $ to $ 1 $. The causality type of $ X $ on $ Y $ is the largest number's pattern in the $ i_{th} $ fragment denoted as $ p^{i}_{X\rightarrow Y} $; and the causality intensity is the proportion of the largest number's pattern in all patterns denoted as $ s^{i}_{X\rightarrow Y} $. By repeating this process, we can obtain both the causality type and the causality intensity from $ X $ to $ Y $ and from $ Y $ to $ X $ for all fragments.
Step 4. Transforming causality types and causality intensities into causality states.
The causality type and the causality intensity are transformed into a particular state, i.e., coarse-grained local features while retaining only some large-scale features. A four-letter string represents the state of each fragment. The first and third letters represent the causality type from $ X $ to $ Y $ and from $ Y $ to $ X $, respectively, and the second and fourth letters represent the causality intensity from $ X $ to $ Y $ and from $ Y $ to $ X $. For example, the first and second letters can be obtained by the following formula,
|
$ TypeiX→Y={P,piX→Y=PositiveN,piX→Y=Negative,1≤i≤N−w+1,D,piX→Y=Dark $
|
(2.9) |
|
$ IntensityiX→Y={a,0.8<siX→Y≤1b,0.6<siX→Y≤0.8c,0.4<siX→Y≤0.6,1≤i≤N−w+1.d,0.2<siX→Y≤0.4e,0≤siX→Y≤0.2 $
|
(2.10) |
Similarly, $ Type^{i}_{Y \rightarrow X} $ and $ Intensity^{i}_{Y \rightarrow X} $ can be obtained by Eqs (2.9) and (2.10). Therefore, the state of the $ i_{th} $ fragment is defined. If $ Type^{i}_{X \rightarrow Y} = N $, $ Intensity^{i}_{X \rightarrow Y} = b $, $ Type^{i}_{Y \rightarrow X} = P $, $ Intensity^{i}_{Y \rightarrow X} = d $, the state of $ i_{th} $ fragment is $ NbPd $. It means that the causality type from $ X $ to $ Y $ is negative, and the intensity is between $ 0.6 $ and $ 0.8 $; the causality type from $ Y $ to $ X $ is positive, and the intensity is between $ 0.2 $ and $ 0.4 $. According to this definition, the number of possible states is $ 225 $, and the combination rule is shown in Table 1.
| (the type of gold's influence on the dollar) | The second letter (the strength of gold's influence on the dollar) | The third letter (the type of dollar's influence on the gold) | The fourth letter (the strength of dollar's influence on the gold) |
| P | a, (0.8, 1] | P | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| N | a, (0.8, 1] | N | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| D | a, (0.8, 1] | D | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] |
DownLoad:
CSV
Step 5. Constructing the state-transition network.
We arranged states into a state chain according to the temporal order of appearance,
|
$ state1→state2→⋯→stateN−w+1, $
|
(2.11) |
in order to visualize the state chain, we mapped Eq (2.11) to a network by numbering each state, i.e., the first state $ PaPa $ as node $ 1 $, the second state $ PaPb $ as node $ 2 $, ..., the last state $ DeDe $ as node $ 225 $. Then, if two nodes appear adjacently, a directed edge is added between them. The network is called the directed and weighted state-transition network in which the direction is the order of the nodes appearing and the weight is the number of the edge between nodes.
1) Degree: incoming degree or outgoing degree is defined as the number of incoming or outgoing links for a focused node. Note that the incoming (or outgoing) degree for a focused state (node) is equal to the number of occurrences of this state, except the state which appears in the first or last position in the state chain.
2) Hub node: nodes with extremely large degrees in the network.
3) Edge: if two states appear adjacently ($ i $ before $ j $), a directed edge is added from $ i $ to $ j $. The directed linkage has a clear physical meaning as the occurrence of the transition from $ i $ to $ j $ in the state chain [27,28].
4) Edge weight: the edge weight indicates the strength of the relationship between the two connected nodes. Herein, the number of transfers between two nodes is defined as the weight of the edges between them. Note that this concept is very important, because we can obtained the transfer preferences between nodes based on this number. Moreover, according to the transition preferences from the focused state to other states, we can predict the subsequent state.
5) Shuffled data: the sequence is obtained by randomly disrupting the positions of the data in the original sequence.
6) Motif: if a node's degree for the original data is significantly larger than it in the shuffled data, the node is called a motif [39,40].
7) Node's position sequence: the sequence of positions where the focused state (node) appears in the state chain.
8) Hurst index ($ H $): a long-range correlation is common in actual data, which can be evaluated by estimating its Hurst index (scaling exponent). Different values of $ H $ indicate different evolution behaviors for the sequence. When $ 0 < H < 0.5 $, the sequence shows anti-persistent evolution behavior, i.e., the state of the next moment is the opposite state of the previous one with large possibility; when $ H = 0.5 $, the characteristic of the sequence is a random walk, i.e., the two successive states of the sequence have no correlation; when $ 0.5 < H < 1 $, a positive long-range correlation exists in the sequence, i.e., the next moment tends to maintain the same state as the previous one. The methods for estimating the Hurst index can be divided into the time-domain and frequency-domain methods. The time-domain methods include the variance-time method [41], the absolute values of the aggregated series method [41], the rescaled range analysis method ($ R/S $) [42,43] and the detrended fluctuation analysis method [44]; the frequency-domain methods include the periodic-diagram method [41], the whittle estimation method [45] and the wavelet analysis method [46].
9) Cluster: the cluster in the network is a sub-network for which the internal edges are denser and the external edges are sparse [47], i.e., nodes in the same cluster are more similar in specific attributes.
In general, the window size $ w $ impacts results [48]. If $ w $ is too large, the rules of causality evolution between gold and the dollar will be obscured; while if $ w $ is too small, it will be more vulnerable to noise, and both the complexity and research cost will be higher. In addition, $ w $ also affects the number of states, that is, the larger $ w $ is, the less the number will be. In order to ensure the stability as well as diversity of the number of states, a balanced value for $ w $ is required.
The effect of the size $ w $ is examined from $ 100 $ to $ 1000 $ (the interval is $ 100 $) in that we obtain $ 10 $ state-transition networks. The numbers of nodes $ N_n $ and the numbers of edges $ N_e $ in state-transition networks are shown in Figure 3(a). The results show that both $ N_n $ and $ N_e $ for the shuffled sequence are more than that of the original sequence. In addition, both $ N_n $ and $ N_e $ for the original sequence decrease sharply with the increase of $ w $ when $ w $ is less than $ 600 $. When $ w $ is around $ 600 $, both $ N_n $ and $ N_e $ tends to be stable. On the contrary, both $ N_n $ and $ N_e $ for the shuffled sequence do not tend to be stable as that of the original sequence when $ w $ is around $ 600 $, i.e., the network structures of the shuffled sequence are not stable. Moreover, when $ w $ is $ 600 $ or $ 900 $, $ r_n $ or $ r_e $ are the smallest (i.e., the radio is the most deviated from $ 1 $), respectively (see Figure 3(b)). Herein, $ r_n $ and $ r_e $ represent the ratio of number of nodes of the original sequence to it of the shuffled sequence and the ratio of number of edges of the original sequence to it of the shuffled sequence, respectively. Accordingly, the difference between the original network and the shuffled network is the largest. Since the larger the $ w $ is, the more the information is lost and the higher the complexity is. Therefore, we assume that the reasonable value for $ w $ is $ 600 $ (i.e., a segment of around $ 840 $ days). Without special statement, $ w $ is selected as $ 600 $ through this article.
Figure 4 shows the state-transition networks for the original data (a) and the shuffled data (b), respectively. There are $ 23 $ nodes and $ 86 $ edges in (a) that are much smaller than $ 225 $ nodes and 225 $ \times $ 225 = 50,625 edges for the all-to-all network. With regard to causality types, $ 10 $ nodes correspond to the states of negative causality from both directions (from gold to dollar and from dollar to gold), $ 4 $ nodes correspond to the states of dark causality from both directions, $ 9 $ nodes correspond to the state of negative causality from one direction and the state of dark causality from the other direction, and only one node $ 58 $ (i.e., State $ PdDc $) corresponds to the state of positive causality from one direction and state of dark causality from the other direction. With respect to the causality intensity, only it of negative causality can be strong, i.e., larger than $ 0.6 $, whereas it of dark causality or positive causality is relatively low.
The state-transition network is heterogenous in (a). Most nodes have small degrees, whereas several hubs have large degrees. For example, both the incoming degree and outgoing degree are equal to $ 8 $ for Node $ 113 $ (i.e., State $ NcNc $), and both the incoming degree and outgoing degree are $ 6 $ for Node $ 97 $ (i.e., State $ NbNb $). Both Nodes $ 113 $ and $ 97 $ correspond to the states of negative causality from both directions. The edge weights are extremely heterogenous because the total weights of the two hubs' self-connecting edges are large, which ratio to the sum of the edge weights for the whole network is $ 68\% $. The self-connecting edges represent that when the focused state (node) appears, the state of the next moment remains the focused one. The state-transition network for the shuffled time series is shown in (b). The network is less heterogenous for the shuffled data. There are $ 33 $ nodes and $ 227 $ edges in (b). Both the numbers of nodes and edges are relatively large and messy in this network, where only Node $ 193 $ (i.e., State $ DcDc $) appears more frequently. State $ DcDc $ corresponds to the dark causality from both directions, which exists between two independently random sequences. In a word, the hubs of state-transition networks for the original data (a) and the shuffled data (b) correspond to the states of negative causality and dark causality from both directions, respectively.
Figure 5 shows the comparison in the occurrence number of each state between the original data and the shuffled data. The numbers of occurrences for the two hubs (i.e., the incoming or outgoing degrees of Nodes $ 97 $ and $ 113 $) in the original data are apparently more than theirs in the shuffled data (a). Therefore, Nodes $ 113 $ and $ 97 $ are motifs. In addition, the number of occurrences for Node $ 193 $ in the shuffled data is visibly more than it in original data (a). Next, we examine whether the occurrence of the motifs are accidental or not. By the $ R/S $ method, we estimate the Hurst index for the time sequence composed of the positions where the nodes appear in turn in Figure 5(b)–(d). The Hurst indexes of Nodes $ 97 $ and $ 113 $ in the original data are larger than 0.5 ($ H_{97, O} = 0.58 $ and $ H_{113, O} = 0.69 $), respectively, and it of Node $ 193 $ in the shuffled data is close to 0.5 ($ H_{193, S} = 0.51 $). The results are entirely in line with intuitive expectations, i.e., the occurrences of Nodes $ 97 $ or $ 113 $ for the original data is long-range related, while the occurrence of Node $ 193 $ for the shuffled data is random.
The importance of a node is reflected not only in the occurrence number but also in the probability of it transferring to other nodes. If the transition probability from one focused node to another is relatively large, the node of the next moment can be predicted when the focused node appears. Furthermore, if several nodes often transfer to each other, these nodes form a cluster.
In this article, a fast heuristic algorithm [49] is utilized to find the clusters. There are $ 4 $ clusters (see Figure 6), each of which mainly contains the same causality types as well as causality intensities. For simplicity, we let "weak" represents the causality intensity "d" or "e", "medium" represents the intensity "c", and "strong" represents the intensity "a" or "b". The largest cluster (Cluster $ I $) is composed of $ 13 $ nodes that are mainly the states of weak dark causalities or the states of weak negative causalities. Although both the numbers of nodes and edges in Cluster $ I $ are the largest that are more than half of the whole network, the sum of its edge weights is meagre (see Figure 7(a)). In the second largest cluster (Cluster $ II $), four out of five nodes are the states of medium or strong negative causalities. Both the numbers of nodes and edges in Cluster $ II $ account for a small proportion, but the sum of its edge weights reaches $ 84\% $ of the whole network (see Figure 7(a)). In the third largest cluster (Cluster $ III $), all of the three nodes correspond to the states of strong negative causalities. In the smallest cluster (Cluster $ IV $), both of the two nodes are the states of strong negative causalities. In order to show the transition within each cluster more clearly, (b)–(e) show the structures of the four clusters, respectively. It is visible that most edges within each cluster are bi-directional, in other words, they can mutually transfer to each other within the cluster.
The connections across different clusters are different with the connections within each cluster. The edges across different clusters are much less than edges within the same cluster. The edges between clusters are very important, because they act as bridges in the transition across different clusters. Figure 7(b) shows the transition frequencies between clusters. Cluster $ II $ can transfer to the other three clusters, and the other three can also transfer to Cluster $ II $, whereas the other three can not transfer to each other. Therefore, Cluster $ II $ acts as a bridge in the transition among clusters. It means that even if there is a positive or dark causality (i.e., Cluster $ I $, Cluster $ III $ or Cluster $ IV $) between gold and the dollar, it is temporary and will soon transfer to Cluster $ II $. Thus, we suggest that the relationship between gold and the dollar is the negative causality of being relatively stable for a long time. In a word, we can more accurately predict the causality between gold and the dollar next moment by these transition preferences of intra-cluster and inter-clusters.
In this article, a method which combines the $ PC $ method [34,35] and the state-transition network was developed to identify the characteristics of the causality evolution between gold and the dollar. Based on the $ PC $ method, we can identify not only the causality intensity but also the causality type in the segments of the bivariate time series, including the types of positive causality, negative causality and the dark causality. Then, both the causality type and the causality intensity were transformed into a particular state in each segment, i.e., a four-letter string. Finally, the state-transition network was built to detect the characteristics in the causality evolution between them, where the node is the causality state and the edge is the transition between states.
Two nodes (States $ NbNb $ and $ NCNC $) were referred to motifs in the state-transition network. Surprisingly, both motifs corresponds to the strong or medium negative causality. The sum of the edge weights for these two motifs accounts for $ 68\% $ of the total edge weights for the whole network, in other words, the number of appearances for these two states also accounts for $ 68\% $ for the whole network. Thus, we suggest that the relationship between gold and the dollar is the negative causality of relatively stable for a long time, which corresponds to the previous research results [1,15].
Several nodes form a cluster because they often transfer to each other. The transition preferences between causality states are compared between intra-cluster and inter-cluster. With regard to the intra-cluster, the transitions of nodes are not only frequent but also bidirectional. The nodes within the cluster can transfer to each other, but it is rare to transfer from one cluster to another. It is the other reason why the relationship between gold and the dollar is negative causality of being relatively stable for a long time. With respect to the inter-cluster, although the transitions across different clusters are much less than transitions within clusters, they play a key role in the connections (transitions) between different clusters. We found that Cluster $ II $ was especially essential. It can transfer to the other three clusters, and the other three can also transfer to Cluster $ II $. However, the other three clusters can not transfer to each other. Therefore, Cluster $ II $ play a bridge role in the connections between clusters. It means that even if there is a positive or dark causality (i.e., Cluster $ I $, Cluster $ III $ or Cluster $ IV $) between gold and the dollar, it is temporary and will soon transfer to Cluster $ II $. In a word, these transition preferences of intra-cluster and inter-clusters provide helpful information to evaluate the current causality between gold and the dollar, and to predict the causality of the next moment.
Different clusters are different in both the causality type and causality intensity of the nodes (states). Cluster $ I $ is mainly composed of states of weak dark causality, $ II $ states of strong or medium negative causality, $ III $ states of strong negative causality, and $ IV $ states of weak negative causality. It means that not only the causality type of nodes but also the causality intensity within each cluster are roughly the same. From this perspective, we can also explain the long-term stability of the negative causality between gold and the dollar.
As mentioned in [48], the window size $ w $ impacts results. By comparing the properties of the network constructed under different $ w $, we found that the network structure tends to be stable when the $ w $ is around $ 600 $ (i.e., a segment of around $ 840 $ days). This discovery can provide a suitable time scale for future study.
The following suggestions may be of assistance to investors. Firstly, the number of appearances for two states accounts for $ 68\% $ for the whole network. This indicates a negative correlation between gold and the dollar. That is, gold prices rise as the dollar depreciates, when investors are more likely to make more profits by investing in gold. Conversely, gold prices fall as the dollar appreciates, accordingly, it is a good time for investors to be short gold. Secondly, the existence of many self-connected edges in the network indicates that the relationship between them is difficult to change in short-term. Thus, it is risky for long-term investment, but for adventurous investors it can yield high returns in a short-term. Thirdly, investors should also consider the transition preferences of intra-cluster and inter-cluster when making investment decisions to reduce investment risk. For example, if the current relationship between gold and the dollar belongs to Cluster $ II $, conservatives will likely believe the relationship will remain in Cluster $ II $ at the next moment (the self-connected edge weight is $ 7200 $), while adventurers will be more inclined to believe it will transfer to Cluster $ III $ (the transfer weight is $ 19 $). Finally, the length of $ 600 $ research window (i.e., a segment of around $ 840 $ days) is more conducive to the discovery of stable evolutionary rules that can assist investors in forming effective judgments.
Our research provides a new perspective to study the evolutional causality between two variables, i.e., gold and the dollar. In future, it is worth studying the evolutional causality between multiple variables, such as gold, the dollar, the price of crude oil, the financial crisis, and the political situation.
This work is supported by the National Natural Science Foundation of China under Grant No.11875042 and and the Natural Science Foundation of Shanghai under Grant No. 21ZR1443900.
The authors declare there is no conflicts of interest.
| [1] |
M. Bächlin, M. Plotnik, D. Roggen, I. Maidan, J. M. Hausdorff, N. Giladi and G. Tröster, Wearable assistant for parkinson's disease patients with the freezing of gait symptom, IEEE Transactions on Information Technology in Biomedicine, 14 (2010), 436-446. doi: 10.1109/TITB.2009.2036165
|
| [2] | K. Bao and S. Intille, "Activity Recognition from User-Annotated Acceleration Data," Proc 2nd Int Conf Pervasive Computing, (2004), 1-17. |
| [3] |
N. Bellomo and C. Dogbé, On the modelling crowd dynamics from scaling to hyperbolic macroscopic models, Mathematical Models and Methods in Applied Sciences, 18 (2008), 1317–-1345. doi: 10.1142/S0218202508003054
|
| [4] |
M. Benocci, C. Tacconi, E. Farella, L. Benini, L. Chiari and L. Vanzago, Accelerometer-based fall detection using optimized zigbee data streaming, Microelectronics Journal, 41 (2010), 703-710. doi: 10.1016/j.mejo.2010.06.014
|
| [5] |
C. Bettini, O. Brdiczka, K. Henricksen, J. Indulska, D. Nicklas, A. Ranganathan and D. Riboni, A survey of context modelling and reasoning techniques, Pervasive and Mobile Computing, 6 (2010), 161-180. doi: 10.1016/j.pmcj.2009.06.002
|
| [6] | I. Borg and P Groenen, "Modern Multidimensional Scaling: Theory and Applications," Springer Series in Statistics, Springer-Verlag, New York, 1997. |
| [7] | M. Buchanan, The science of subtle signals, Strategy+Business, 48 (2007), 68-77. |
| [8] | I. Cohen and M. Goldszmidt, Properties and benefits of calibrated classifiers, Proc. Knowledge Discovery in Databases, 2004, 125-136. |
| [9] |
V. Coscia and C. Canavesio, First-order macroscopic modelling of human crowd dynamics, Math. Mod. Meth. Appl. Sci., 18 (2008), 1217-1247. doi: 10.1142/S0218202508003017
|
| [10] |
N. Davies, D. P. Siewiorek and R. Sukthankar, Special issue: Activity-based computing, IEEE Pervasive Computing, 7 (2008), 20-21. doi: 10.1109/MPRV.2008.26
|
| [11] | R. O. Duda, P. E. Hart and D. G. Stork, "Pattern Classification," Second edition, Wiley-Interscience, New York, 2001. |
| [12] | P. Eades, A heuristic for graph drawing, Congressus Numerantium, 42 (1984), 149-160. |
| [13] |
N. Eagle, A. Pentland and D. Lazer, Inferring friendship network structure by using mobile phone data, Proc Natl Acad Sci U S A, 106 (2009), 15274-15278. doi: 10.1073/pnas.0900282106
|
| [14] | T. Fawcett, "ROC graphs: Notes and practical considerations for researchers," Tech. report, HP Laboratories, 2004. |
| [15] | D. Figo, P. Diniz, D. Ferreira and J. Cardoso, Preprocessing techniques for context recognition from accelerometer data, Pervasive and Mobile Computing, 14 (2010), 645-662. |
| [16] |
T. M. J Fruchterman and E. M. Reingold, Graph drawing by force-directed placement, Software - Practice and Experience, 21 (1991), 1129-1164. doi: 10.1002/spe.4380211102
|
| [17] |
M. González and A.-L. Barabási, Complex networks: From data to models, Nature Physics, 3 (2007), 224-225. doi: 10.1038/nphys581
|
| [18] |
D. Helbing, L. Buzna, A. Johansson and T. Werner, Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions, Transportation Science, 39 (2005), 1-24. doi: 10.1287/trsc.1040.0108
|
| [19] |
D. Helbing, I. Farkas and T. Vicsek, Simulating dynamical features of escape panic, Nature, 407 (2000), 487-–490. doi: 10.1038/35035023
|
| [20] | D. Helbing and A. Johansson, "Pedestrian, Crowd and Evacuation Dynamics," Meyers Encyclopedia of Complexity and Systems Science, Springer, Berlin, 2009. |
| [21] |
D. Helbing and P. Molnár, Social force model for pedestrian dynamics, Physical Review E, 51 (1995), 4282-4286. doi: 10.1103/PhysRevE.51.4282
|
| [22] |
S. Hoogendoorn and P. Bovy, Simulation of pedestrian flows by optimal control and differential games, Opt. Cont. Appl. Meth., 24 (2003), 153-172. doi: 10.1002/oca.727
|
| [23] |
A. Johansson, D. Helbing and H. Z. Al-Abideen, From crowd dynamics to crowd safety: A video-based analysis, Advances in Complex Systems, 11 (2008), 497-527. doi: 10.1142/S0219525908001854
|
| [24] |
A. Johansson, D. Helbing and P. S. Shukla, Specification of the social force pedestrian model by evolutionary adjustment to video tracking data, Advances in Complex Systems, 10 (2007), 271-288. doi: 10.1142/S0219525907001355
|
| [25] | S. Kallio, J. Kela, P. Korpipää and J. Mäntyjärvi, User independent gesture interaction for small handheld devices, International Journal of Pattern Recognition and Artificial Intelligence, 20 (2006), 505-524. |
| [26] |
A. Kesting, M. Treiber and D. Helbing, Connectivity statistics of store-and-forward intervehicle communication, IEEE Transactions on Intelligent Transportation Systems, 11 (2010), 172-181. doi: 10.1109/TITS.2009.2037924
|
| [27] |
J. Kleinberg, The convergence of social and technological networks, Communications of the ACM, 51 (2008), 66-72. doi: 10.1145/1400214.1400232
|
| [28] | M. H. Ko, G. West, S. Venkatesh and M. Kumar, "Online Context Recognition in Multisensor Systems Using Dynamic Time Warping," Proc. Conf. Intelligent Sensors, Sensor Networks and Information Processing Conference, (2005), 283-288. |
| [29] | N. D. Lane, E. Miluzzo, H. Lu, D. Peebles, T. Choudhury and A. T. Campbell, A survey of mobile phone sensing, IEEE Communications Magazine, 48 (2010), 140-150. |
| [30] |
D. Lazer, A. Pentland, L. Adamic, S. Aral, A.-L. Barabási, D. Brewer, N. Christakis, N. Contractor, J. Fowler, M. Gutmann, T. Jebara, G. King, M. Macy, D. Roy and M. Van Alstyne, Computational social science, Science, 323 (2009), 721-723. doi: 10.1126/science.1167742
|
| [31] |
S. Mann, Humanistic computing: "Wearcom" as a new framework and application for intelligent signal processing, Proceedings of the IEEE 86 (1998), 2123-2151. doi: 10.1109/5.726784
|
| [32] | S. McKeever, J. Ye, L. Coyle and S. Dobson, "Using Dempster-Shafer Theory of Evidence for Situation Inference," Proceedings of the 4th European conference on Smart sensing and context, Berlin, Heidelberg, EuroSSC'09, Springer-Verlag, (2009), 149-162. |
| [33] |
T. M. Mitchell, Mining our reality, Science, 326 (2009), 1644-1645. doi: 10.1126/science.1174459
|
| [34] |
M. Moussaïd, N. Perozo, S. Garnier, D. Helbing and G. Theraulaz, The walking behaviour of pedestrian social groups and its impact on crowd dynamics, PLoS One, 5 (2010), e10047. doi: 10.1371/journal.pone.0010047
|
| [35] | J.-K. Onnela, J. Saramäki, J. Hyvönen, G. Szabó, M. A. de Menezes, K. Kaski, A.-L. Barabási and J. Kertész, Analysis of a large-scale weighted network of one-to-one human communication, New Journal of Physics, 9 (2007). |
| [36] |
J. A. Paradiso, J. Gips, M. Laibowitz, S. Sadi, D. Merrill, R. Aylward, P. Maes and A. Pentland, Identifying and facilitating social interaction with a wearable wireless sensor network, Personal and Ubiquitous Computing, 4 (2010), 137-152. doi: 10.1007/s00779-009-0239-2
|
| [37] | A. Pentland, "Honest Signals: How They Shape Our World," Bradford Books, 2008. |
| [38] |
A. Pentland, T. Choudhury, N. Eagle and P. Singh, Human dynamics: Computation for organizations, Pattern Recognition Letters, 26 (2005), 503-511. doi: 10.1016/j.patrec.2004.08.012
|
| [39] |
H. Qian, Y. Mao, W. Xiang and Z. Wang, Recognition of human activities using SVM multi-class classifier, Pattern Recognition Letters, 31 (2010), 100-111. doi: 10.1016/j.patrec.2009.09.019
|
| [40] | C. Randell and H. Muller, "Context Awareness by Analysing Accelerometer Data," ISWC 2000: Proc. of the 4th Int'l Symposium on Wearable Computers, October 2000, 175-176. |
| [41] |
A. Ranganathan, J. Al-Muhtadi and R. H. Campbell, Reasoning about uncertain contexts in pervasive computing environments, Pervasive Computing, IEEE, 3 (2004), 62-70. doi: 10.1109/MPRV.2004.1316821
|
| [42] | S. Saxena, F. Brémond, M. Thonnat and R. Ma, "Crowd Behavior Recognition for Video Surveillance," Advanced Concepts for Intelligent Vision Systems (Berlin), Lecture Notes in Computer Science, 5259, Springer, (2008), 970-981. |
| [43] | S. E. Schaeffer, Graph clustering, Computer Science Review, 1 (2007), 27-64. |
| [44] | S. H. Shin, M. S. Lee, C. G. Park and H. S. Hong, "Pedestrian Dead Reckoning System with Phone Location Awareness Algorithm," Proc. Position Location and Navigation Symposium (PLANS), IEEE Press, 2010, 97-101. |
| [45] | T. Starner, J. Weaver and A. Pentland, Real-time American sign language recognition using desk and wearable computer based video, IEEE Transactions on Pattern Analysis and Machine Intelligence, 20 (1998), 1371-1375. |
| [46] |
T. Stiefmeier, D. Roggen, G. Ogris, P. Lukowicz and G. Tröster, Wearable activity tracking in car manufacturing, IEEE Pervasive Computing, 7 (2008), 42-50. doi: 10.1109/MPRV.2008.40
|
| [47] | J. A. Ward, P. Lukowicz, G. Tröster and T. Starner, Activity recognition of assembly tasks using body-worn microphones and accelerometers, IEEE Trans. Pattern Analysis and Machine Intelligence, 28 (2006), 1553-1567. |
| [48] | J. A. Ward, P. Lukowicz and H. Gellersen, Performance metrics for activity recognition, ACM Transactions on Information Systems and Technology, 2 (2011), 6:1-6:23. |
| [49] | M. Wirz, D. Roggen and G. Tröster, "Decentralized Detection of Group Formations from Wearable Acceleration Sensors," IEEE Int. Conf. on Computational Science and Engineering, IEEE Press, 2009, 952-959. |
| [50] | _____, "A Methodology Towards the Detection of Collective Behavior Patterns by Means of Body-Worn Sensors," UbiLarge workshop at the 8th Int. Conf. on Pervasive Computing, 2010. |
| [51] | _____, "User Acceptance Study of a Mobile System for Assistance During Emergency Situations at Large-Scale Events," 3rd International Conference on Human Centric Computing, 2010. |
| [52] | P. Zappi, C. Lombriser, E. Farella, D. Roggen, L. Benini and G. Tröster, "Activity Recognition from On-Body Sensors: Accuracy-Power Trade-Off by Dynamic Sensor Selection," 5th European Conf. on Wireless Sensor Networks (ed. R. Verdone), Springer, (2008), 17-33. |
| [53] |
B. Zhan, D. N. Monekosso, P. Remagnino, S. A. Velastin and L.-Q. Xu, Crowd analysis: A survey, Machine Vision and Applications, 19 (2008), 345-–357. doi: 10.1007/s00138-008-0132-4
|
| 1. | Ping Wang, Changgui Gu, Huijie Yang, Haiying Wang, Identify causality by multi-scale structural complexity, 2024, 633, 03784371, 129398, 10.1016/j.physa.2023.129398 |
Daniel Roggen, Martin Wirz, Gerhard Tröster, Dirk Helbing. Recognition of crowd behavior from mobile sensors with pattern analysis and graph clustering methods[J]. Networks and Heterogeneous Media, 2011, 6(3): 521-544. doi: 10.3934/nhm.2011.6.521
| (the type of gold's influence on the dollar) | The second letter (the strength of gold's influence on the dollar) | The third letter (the type of dollar's influence on the gold) | The fourth letter (the strength of dollar's influence on the gold) |
| P | a, (0.8, 1] | P | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| N | a, (0.8, 1] | N | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| D | a, (0.8, 1] | D | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] |
DownLoad:
CSV
| (the type of gold's influence on the dollar) | The second letter (the strength of gold's influence on the dollar) | The third letter (the type of dollar's influence on the gold) | The fourth letter (the strength of dollar's influence on the gold) |
| P | a, (0.8, 1] | P | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| N | a, (0.8, 1] | N | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] | ||
| D | a, (0.8, 1] | D | a, (0.8, 1] |
| b, (0.6, 0.8] | b, (0.6, 0.8] | ||
| c, (0.4, 0.6] | c, (0.8, 0.6] | ||
| d, (0.2, 0.4] | d, (0.8, 0.4] | ||
| e, [0, 0.2] | e, [0, 0.2] |
