A Hamiltonian perspective to the stabilization of systems of two conservation laws

1.   Introduction

Petroleum products and coal are the mains imported sources as primary energy requirements for the island of Mauritius in the Indian Ocean. Nearly 24% of the country's electricity was generated from renewable energies but only 5.1% electricity produced from photovoltaic (PV) plant. Solar PV systems transform solar energy into electric power. A main goal of the Mauritian government is to significantly increase from 13% to 60% the share of renewables in the energy mix. As regards key policy decisions, the government has outlined its intention to oversee and promote the PV technologies through the local electricity supplier or public utility company, the Central Electricity Board (CEB) and by the CEB Act. The latter has been amended for CEB to participate in PV projects and accommodating electrical PV output on its grids or micro grids as the country's national electricity grid has been modernized. A micro grid is a kind of electrical supplying network that can help to integrate large numbers of decentralized power systems into existing distribution grids acting in a grid-on or grid-off mode keeping voltage and frequency stability.

However, the solar energy intermittency can affect the PV power quality and cause grid instabilities especially when micro grids are concerned. The PV power variability is based on irradiance fluctuations time scales. Therefore, to study the balance of electrical grid or micro-grid power generated by PV systems, predicting models can help. Unlike time horizons predictions, many technics of irradiance forecasting have been proposed, long, medium and short term forecasting. For months variations known as long-term prediction ^[1], model such as weather research and forecasting ^[2] is well adapted. Meteorological ^[3] models based on satellite and ground observations better fit medium-term prediction such as intra-hour forecasts. For short-term time ^[4] scale from several minutes up to few hours, time series models using onsite measurements are adequate.

In this paper, a practical method of the Johansen vector error correction model (VECM) cointegration approach ^[5,6] is presented for a very short term prediction of 15-minutes to PV power output. The Johansen approach has been a popular tool in applied economics but when applied to renewable energies fields, most contributions were mainly in a multiple downstream direction. Either exploring the dynamic causal relationship between carbon dioxide (CO₂) emissions, renewable and non-renewable electricity consumption and economic growth ^[7,8] or determining ^[9,10] causality between main product and byproduct prices for PV cells or interaction between electricity generation sources and economic activity. Also sudden variability in PV power output to electrical grid can not only cause grid instability but can also affect power and frequency quality. Again solutions to grid instability due the renewable sources have been proposed ^[11,12], but still in a downstream direction. Therefore, the goal of this paper is to propose an upstream study of predicting PV power output before integration into power grids in order to reduce all execution time of any processes after injection on the grid.

This contribution is presenting experimental results that are based on previous studies ^[13,14] on the Johansen VECM cointegration model. Indeed, this is a new topic research work and actually the only known contribution in the field of application of Johansen cointegration technic to PV system. In a former study, rigorous statistical time series methods such as Augmented Dickey Fuller (ADF) and Engle & Granger (E & G) ^[5,6] had been used to determine relationship between variables in difference level and applied to a PV system in the North East of France. Then, a more robust statistical method, the Johansen vector error correction mechanism (VECM) had been proposed ^[15] to improve the ADF and E & G models. This method was based on measured time series data from a PV plant in Reunion Island in the Indian Ocean and endorsing the model for a very long horizon time.

The novelty of this study, is the long run equilibrium relationship of the Johansen model, that was initially determined in Reunion island is applied to a PV plant in the Island of Mauritius for a very short-term prediction from an hour to 15-minutes in a time scale. The experimental results are very promising and the proposed model seems to be a powerful tool for an upstream PV power output prediction before grid injection and in accordance with the grid connection requirements.

This paper is organized as follows. Section 2 is brief description of the ADF statistical method and Johansen principle. Section 3 specifies respectively, the two geographical zones and PV plant in the Island of Reunion and Mauritius. Section 4 deals with the experimental results and interpretations. An appropriate conclusion and future works are given in section 5.

2.   Procedure of statistical development

A time series ^[16,17] is a set of observations on the values that a variable takes at different times. Such data may be collected at regular time intervals, such as monthly, weekly, daily, hourly and data can also be collected over a short interval of time such as every 15 minutes as for this study. Time series data is assumed to be stationary if its mean and variance do not vary systematically over time. Regression analysis based on time series data implicitly assumes that the underlying time series are stationary and classical t tests, F tests, etc. are based on this assumption. Correlogram of time series which is an autocorrelation graph at various lags is a visual test of stationarity. However, at a strict level, stationarity can be tested by looking out if time series contains a unit root ^[18,19] appealing to ADF tests ^[20,21,22] when the error term is correlated. ADF test is fundamentally a statistical significance test where a hypothesis testing is involved with a null and alternate hypothesis and as a result a test statistic is computed and probability p-values are reported telling how likely data could have occurred under the null hypothesis.

The ADF tests can also be applied to determine whether a time series can be a trend stationary or difference stationary.

Regression of a time series variable on one or more-time series variables can often provide absurd results known as spurious regression. One way to guard against it is to find out if the time series are cointegrated. E & G ^[23] tests are first applied to find out the long-run or equilibrium relationship for cointegration between two-time series followed by the error correction mechanism (ECM) to reconcile the short-run behavior with its long-run behavior. If a set of variables are found to have one or more cointegrating vectors, then a suitable technique is the vector error correction mechanism (VECM) which adjusts to both short run changes in variables and deviations from equilibrium and that disequilibrium errors would tend to fluctuate around zero mean. The Johansen method ^[24] is a multivariate generalization of the ADF test to estimate all cointegrating vectors and to establish the number of cointegration equations between variables.

The Johansen's procedure builds cointegrated variables directly on maximum likelihood estimation. Johansen proposed two likelihood ratio tests namely trace and maximum eigenvalue. On one hand, the trace is a null hypothesis test of r cointegrating vectors against the alternative hypothesis of n cointegrating vectors. On the other hand, the maximum eigenvalue tests the null hypothesis of r cointegrating vectors against the alternative hypothesis of (r + 1) cointegrating vectors.

These methods and further statistic tests such as have been applied to our time series for variables such as PV power output, irradiance, PV module temperature.etc. We also tested the normal distribution of the differenced series, applying histogram and statistics. These resulting tests have proved ^[5,9] that the series are normally distributed for 5% significance level. The final determined cointegration relationship of Johansen model regarding data from Reunion Island ^[5,9] is then applied to the Island of Mauritius as indicated in the following sections.

3.   Tropical islands and PV systems

Compared to the northern hemisphere, the seasons are the other way round in the southern hemisphere. However, any notions of winter and summer are relative in the tropics. Instead of the classic four seasons, Reunion and Mauritius islands only have two seasons: a warm humid summer extending from November to April and a relatively cool dry winter from June to September. The month of October and May are commonly known as the transition months. Both island has about 350 days of sunshine and thus has excellent solar energy potential. The mean solar irradiance is nearly 1600 kWh/m²/year.

3.1.   Reunion Island

Reunion is an island in the Indian Ocean that is an overseas department and region of France mostly mountainous and the culmination peak is 3071 m. It is located approximately 950 km east of the island of Madagascar and 175 km southwest of the island of Mauritius. The latitude and longitude of the island is 21° 0' 41.321" S and 55° 16' 19.632" E. The climate in Reunion is very warm, with an annual average of 28 degrees and is characterized by a humid tropical climate, tempered by the oceanic influence of the trade winds blowing from east to west.

The PV system are tilted at Reunion Island latitude, for optimal energy extraction, the modules that make up the PV plant are polycrystalline type of 180 W peak each, equipped with solar, temperature and wind sensors. Irradiance dataset have been collected between year 2012 to 2016 every ten minutes and between 9:00 AM and 4:00 PM every day which is considered as PV irradiance duration and not the true solar duration.

3.2.   Island of Mauritius

Mauritius enjoys a mild tropical maritime climate throughout the year and is nearly a flat island, the most culmination point is 828 m. Mean summer temperature is 24.7 degrees Celsius and mean winter temperature is 20.4 degrees Celsius. The temperature difference between the seasons is only 4.3 degrees Celsius. The warmest months are December to February and the coolest months are July and August. The Island receives nearly 8 hours of bright sunshine daily on coastal regions during summer seasons and during winter months, the central plateau receives around 6 hours of bright sunshine whereas the coast receives above 7.5 hours of bright sunshine.

The data used in this study are measured from the PV system installed on the roof top of the University of Mauritius (UoM) that is located on the west coast of the island. All the PV strings have a north orientation and are tilted at the island latitude to receive a maximum insolation. The 20 kW PV plant is equipped with multiple sensors. Measurement of solar irradiance is done using a silicon irradiance sensor (Si sensors) especially for the monitoring of PV systems. This sensor has been chosen for its spectral response comparable to PV modules. Additionally, to the irradiance measurement of the Si sensor are temperature and wind speed measurements. The whole system is monitored to record all data sensors and PV power output every 15 minutes. The dataset spans over a one-year period from July 2019 to December 2022. The recorded data was filtered such that data between 4:30 PM and 7:30 AM of the following day and missing data was removed.

4.   Results and interpretations

An original Johansen cointegration equation was determined in a previous study ^[9] where data came from a building-mounted PV plant located on the west coast of the Reunion island and was designed for a grid connected system. The main aspect to be considered as common for modelling the PV output short term prediction in this paper, is this cointegration relationship. Indeed, the Johansen VECM model, that was determined from a specific yearly data of 2012, had been applied, to different time scale: for years 2013, 2014, 2016, then to months of year 2016 and days of a particular month of 2016, to corroborate the model for long term PV power output prediction.

This Johansen model is now applied to the PV system in Mauritius for the same corresponding time scale as in Reunion Island. The experimental results are very convincing and have showed that the proposed predicting method is suitable for the power output prediction at different time scale and meteorological sites. Therefore, on the basis of the application and the corresponding time scale required for short time PV power output prediction in Mauritius we have applied the Johansen model to a new predicting scheme for hourly one-day ahead PV output prediction and then 15 by 15 minutes predicting time approach.

As it is not relevant to present 8760 results hour by hour for every day of the year, instead we have randomly chose a month of a year N and then days of that month and applied the Johansen model for power output to hourly time scale between 9:00 AM and 4:00 PM. We then compared the results for the same period for year N+1 as if we were predicting the PV power output for that year. For this study, we have selected random days for two seasonal months, one month for the winter season and one month for the summer season.

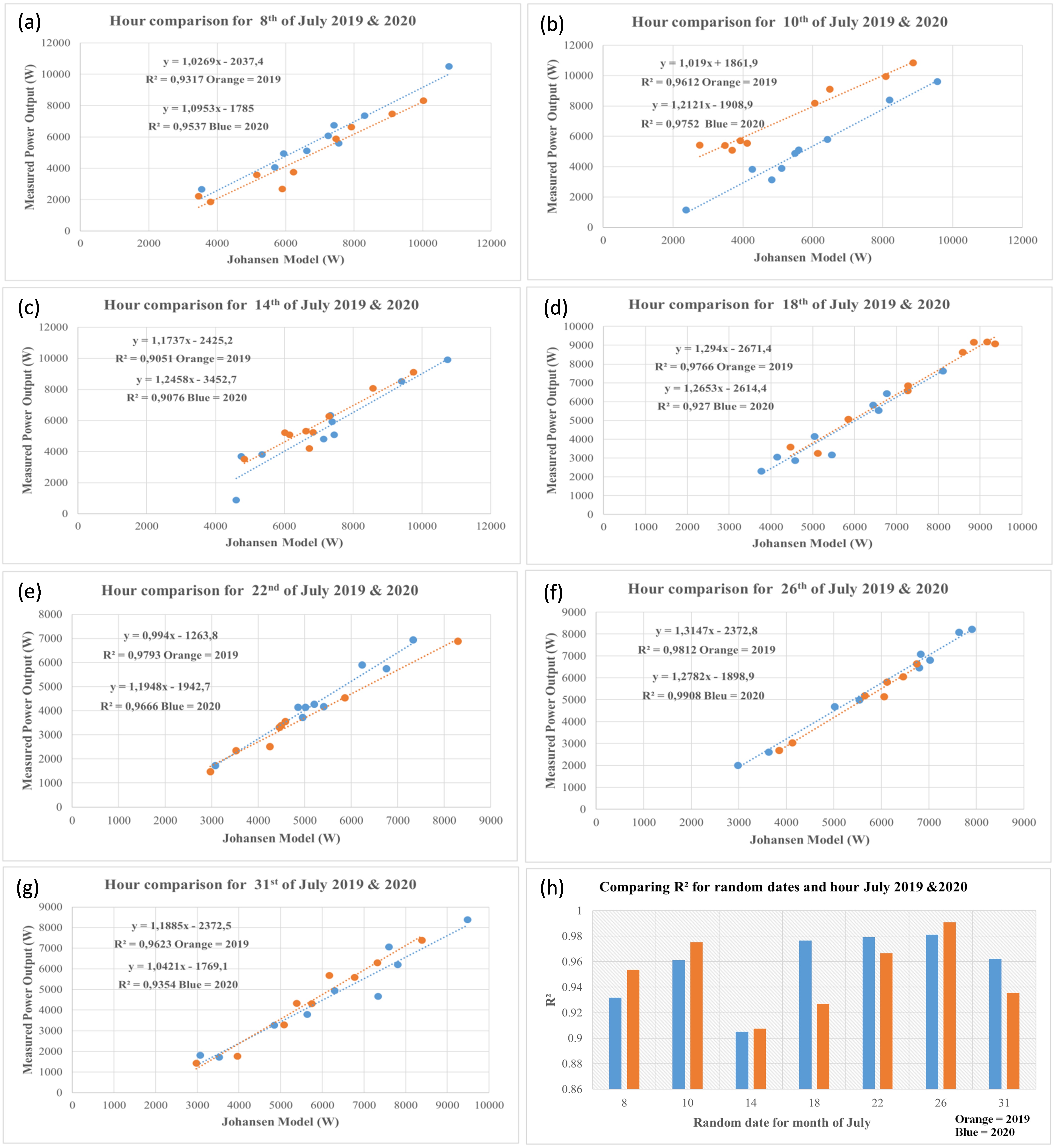
So, the random month for the winter season is the month of July for year N = 2019 and the random days of that month are 8^th, 10^th, 14^th, 18^th, 22^nd, 26^th and 31^st.

Figure 1a–h present the hourly measured PV power output against the Johansen model at different random days for the month of July. For each day, the orange linear regression represents year 2019 and the blue one is for year 2020 and respectively with their coefficient of determination R². As for interpretation, it can be observed that each measured power output is positively correlated with the Johansen model for each year as most of the R² value is greater than 91% as indicated on the histogram in Figure 1. While comparing the correlation results within the two consecutive years, it is clear that the prediction task is very pertinent for an hourly time scale.

Figure 1.  Hour comparison for the 8^th (a), 10^th (b), 14^th (c), 18^th (d), 22^nd (e), 26^th (f) and 31st (g) of July 2019 & 2020. Comparing measured power output to Johansen model every hour and bar chart of R² values (h).

DownLoad: Full-Size Img PowerPoint

Regarding to the 10th of July 2020 which was a lightly rainy day in intermittent with sunshine compared to year 2019. To enhance the model, it seemed appropriate to apply the Johansen model for a shorter time scale of that day for each year. Figure 2 shows the measured power output versus Johansen model for 15-minutes time interval every hour between 10:00 AM and 4:00 PM for both years. We can see that each correlation coefficient is comparable as indicated in Figure 3, but there are significant differences for year 2019 between noon and 1:00 PM and for year 2020 between 1:00 PM and 2:00 PM. This means that only for this very short period this predicting method would be wrong. However, we can argue that artificial intelligence should be able to learn from this training procedure and make the Johansen model a powerful predicting tool and if cloud cover information is considered, this can improve the predict accuracy.

Figure 2.  Comparing power each 15 mins between 10:00–16:00 for 2019 & 2020.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Comparing R² values at 15 mins for a random day of July 2019 & 2020.

DownLoad: Full-Size Img PowerPoint

We performed a second experimental test by applying the Johansen model to two other successive years for a random summer month. The random month is December, the successive years are 2021 & 2022, the random day is the 15th and the interval time is still 15-minutes. As daylight is earlier during summer season, the Johansen model is applied between 8:00 AM and 4:00 PM. The experimental results and linear regressions are indicated in Figure 4 and the R² values are compared in Figure 5. These results only confirm the performance of the Johansen model and further studies should allow to predict precise power output so as to reduce the impact of uncertainty of power PV generation for 15-minutes short term prediction.

Figure 4.  Comparing power each 15 mins between 8:00–16:00 for December 2021 & 2022.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Comparing R² values for a random day of December 2021 & 2022.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

The Island of Mauritius has excellent natural resources such as sunshine and it is undeniable that the power output from PV technologies to electrical grid or to micro-grid, should help to shift the island to more towards green and renewable energy. In this work, the Johansen model that was first designed from dataset in Reunion Island is applied to a PV plant in Mauritius, as they are close islands in the Indian Ocean. This statistical method that aims at creating a short-term predict model PV power generation has been proposed, in order to answer needs of electricity grid managers for multiple purposes. The novelty of the proposed model first uses hourly time scale for a random month and a random day, then 15 by 15-minutes predict of the PV power output. The experimental results show the Johansen model as a very efficient and convincing model. Indeed, results of the measured PV power output at an hourly or 15 minutes term horizon for random days of a random month for year N are compared to the same period for the supposed predicting year N + 1 or N + 2, the R² values are mostly greater than 93% indicating that Johansen model is positively and strongly correlated to onsite measurements. It was observed that for a particular period, for example, for the 15 minutes term horizon of the 15th December between 11:00 and 12:00, the R² value for year 2021 was 87% and that of year 2022 was 99%, meaning that sudden fluctuation in irradiance or other environmental factors must be considered to improve the model. Hence, to increase the predicting accuracy for this short term prediction, it is crucial to combine the Johansen model to a machine learning method that can learn from datasets. Future works will focus on the best artificial intelligence to fit to the model as sudden variability on PV power output due to sudden fluctuation in irradiance can have serious impact on grid stability.

Conflict of interest

The authors declare no conflict of interest in this paper