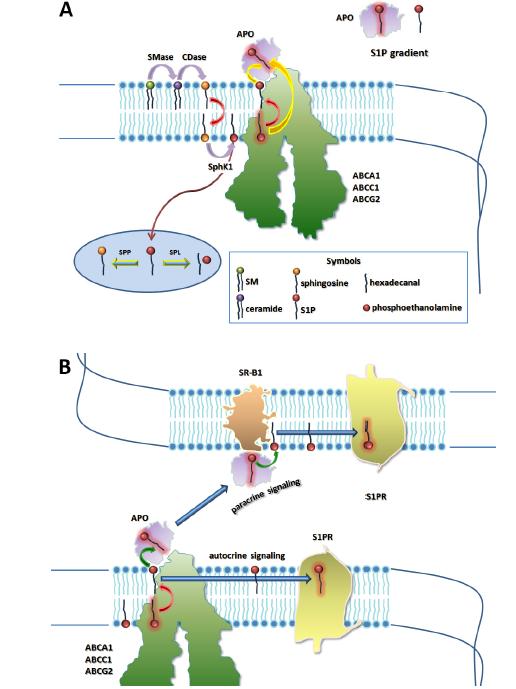
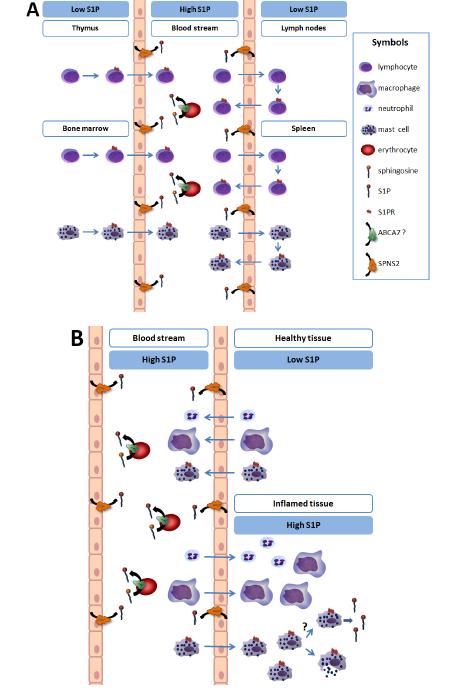
Sphingosine-1-phosphate transport and its role in immunology

1.   Introduction

Due to human interference and environmental noise, stochastic disturbances increase the complexity and unpredictability of system dynamics^[1]. Since the stochastic effects of the system are taken into account, the dynamics of industrial processes can be characterized more precisely. In recognition of this, stochastic nonlinear systems have drawn more attention and been thoroughly examined by numerous academics from a variety of disciplines, including mechanical systems, economics, and bioengineering^[2,3,4,5,6].

The majority of stability-related issues are managed by state feedback, which necessitates constant decision-making and state observation on the part of the controller. This operation has limits and is costly for real-world applications. In order to conserve resources, time-triggered control in conjunction with event-triggered control (ETC) is suggested as a transmission or communication technique. Time-triggered control, as a traditional control scheme, has a preset control transmission and control time, but it often leads to an inefficient use of communication width and computational resources, so an effective alternative, ETC, is proposed on this basis^[7,8,9]. Because ETC maintains the necessary closed-loop performance while updating control only when the state of the system at a given moment is above the threshold of the predetermined triggering mechanism, it further improves communication efficiency. A key concern in ETC design is ensuring a positive lower bound, which is the minimum time interval between consecutive events. Without this constraint, an infinite number of triggers could occur in a finite time, leading to undesirable Zeno behavior. In recent years, there has been a continuous increase in research related to ETC. For instance, ^[10] investigated the exponential stability of stochastic nonlinear systems using double-event-triggering mechanisms. In^[11], the design of event-triggered control schemes for nonlinear systems subject to external disturbances and dynamic uncertainties was investigated. Despite these advancements, the ETC still has limitations, and further resource optimization remains an important research direction.

Intermittent control (IC) was first proposed as a discontinuous control method and has attracted increasing attention^{[12,13,14,15,16,17]}. For example, ^[14] investigated the input-to-state stability of stochastic nonlinear systems under different event-triggering mechanisms—continuous, dynamic, and periodic—in combination with IC, providing valuable insights for further research. Unlike continuous control, fully controlling these systems in real-world applications is impractical, as it would impose a heavy communication burden on the controller and waste resources; therefore, the emergence of IC is of great significance. IC divides each control interval into 'working time' with operational control and 'rest time' without operational control. Additionally, IC limits the amount of transmitted information and extends the lifespan of the control equipment by allowing control signals to be applied only at predetermined time intervals. Periodically intermittent control (PIC) and aperiodically intermittent control (APIC) are two classifications of IC that depend on whether the control interval and control periods are fixed. However, the conditions might be conservative because PIC's control and free intervals must be fixed. The advantage of APIC is that it is no longer necessary to fix the length of the working time and rest time, which increases the randomness of the control intervals and therefore has a good application prospect. Therefore, with the advantages of APIC, many scholars have combined ETC with APIC to achieve better research results^{[18,19,20,21]}. Reference^[20] realized finite-time stabilization of nonlinear delayed systems under impulsive disturbance by designing time-triggered aperiodic intermittent control with event-triggered aperiodic intermittent control.

Quantization strategies as a control scheme not only ensure sufficient accuracy but also reduce the amount of transmitted information^{[22,23,24,25,26]}. Quantizers perform a discontinuous mapping from a continuous space to a finite set. However, due to the precision and range limitations of quantization, numerical discrepancies arise between the behavior of the ideal system and the calculated values.

The concept of stability studies the asymptotic behavior of states that tend to infinity with time. However, a state's properties in the finite time domain must be considered in practical engineering, so finite-time stability (FTS) has been widely studied as one of the concepts describing the state in the finite time domain^{[27,28,29,30,31,32,33,34]}. FTS due to the transient properties in the finite time sense can be divided into two categories of concepts: one is for a given initial value of the upper bound with a finite time interval, which is maintained within a finite time domain within another larger threshold value. The second concept states that the system's state reaches equilibrium in finite time. To avoid confusion, only the first concept is considered in this paper. However, finite-time stabilization alone is insufficient. A more practical approach is finite-time contraction stabilization (FTCS), which not only ensures boundedness but also requires that the system's state at the termination time must remain within a smaller bound compared with the initial upper limit. This makes FTCS particularly relevant for real-world applications. In^[35,36], FTS is investigated in a stochastic sense, where, unlike stochastic finite-time stability under probability^[37,38], such stability has states under expectation. Reference^[39] investigated the FTS of linear systems combined with state quantization.

However, little research has focused on nonlinear stochastic systems that integrate these three aspects, since stochastic state fluctuations are a primary cause of the system's instability and poor performance. Therefore, using ETC with APIC, and combining ETC with APIC and state quantization enables a more effective assessment of a system's performance through well-designed triggering mechanisms while conserving control resources.

On the basis of the motivation and inspiration of the abovementioned research, this paper presents the FTS and FTCS of stochastic nonlinear systems with two ETMs under APIC. The control system follows established ISS control laws and provides two settings for QbE and QaE, where paired quantizers are taken into consideration. By integrating ETC with quantization control, the approach aims to minimize the communication overhead. The Zeno phenomenon, in which the control is updated infinitely in finite time, is then avoided by designing a static ETM. In addition, aperiodically intermittent controllers are introduced to reduce the computational burden on controllers and mitigate reliance on continuous transmission. There are relatively few papers on stochastic nonlinear systems in ETC with IC to achieve FTS, so the theoretical results of our study are of interest. The results show that (1) under APIC, both ETMs significantly reduce the number of trigger events, and the control interval length can be adjusted according to the specific objectives of the ETMs; (2) both ETMs can achieve FTS and FTCS of stochastic nonlinear systems, and the relevant sufficient conditions are obtained. Therefore, the main innovation of this paper lies in the combination of intermittent state quantization and an event-triggered mechanism, which further reduces the computational costs and communication burdens. Compared with ^[14,26], this paper employs an aperiodically intermittent controller to further alleviate the controller's burden and achieve finite-time stability. In contrast to ^[20,39], this work extends the general nonlinear system to a stochastic nonlinear system setting and employs intermittent quantization control to achieve finite-time stability and Lyapunov stability.

The rest of the paper is structured as follows: Section 2 describes the model and provides background information, Section 3 presents the primary results, Section 4 provides numerical examples, and finally, Section 5 summarizes the key conclusions and outlines directions for future research.

Notations: In the whole paper, we have used $ \mathcal{N} $ to represent the set of natural numbers, $ \mathcal{R^+} = [0, +\infty) $ denotes the set of positive real numbers. $ V(x, t)\in \mathcal{C}^{2, 1} $ denotes the family of all non-negative functions in $ \mathcal{R}^d\times [0, +\infty) $ and is quadratically continuously differentiable with respect to $ x $ and once continuously differentiable with respect to $ t $. $ \mathbb{E}(\cdot) $ stands for the expectation operator. $ I_\mathcal{A}(x) $ represents the characteristic function. When $ x\in \mathcal{A} $, $ I_\mathcal{A}(x) = 1 $, and when $ x\notin \mathcal{A} $, $ I_\mathcal{A}(x) = 0 $. Define $ \mathcal{Z_+} $ as the set of positive integers and $ \mathbb{N} $ as the set of integers.

2.   Model description and preliminaries

Let $ (\Omega, \mathcal{F}, \mathrm{Pr\{\cdot\}}) $ be a complete probability space with a filtration $ \{\mathcal{F}_t\}_{t \geq 0} $ that meets the normal conditions. Study the following nonlinear stochastic system, which has a dynamical expression of the form

on $ t \geq 0 $ with the initial state $ x(t_0) = x_0 $, where $ x(t) \in \mathbb{R}^n $, $ f $, $ g \in \mathbb{R}^n \times \mathbb{R}_+ \rightarrow \mathbb{R}^n $ and satisfies $ f(0, t) = g(0, t) = 0 $, where $ u(t) \in \mathbb{R}^n $ is control input and $ \omega(t) $ is defined as an $ n $-dimensional Wiener process on the probability space satisfying the general conditions. Next, we define the intermittent control law as follows:

which is affected by state quantization and is event-triggered, where $ [t_m, t_{m+1}) $ represents the $ m+1 $th control period, $ [t_m, t_m+s_m) $ represents the $ m+1 $th working interval, and $ [t_m+s_m, t_{m+1}) $ represents the rest interval; $ t_{m, i} $ is the time at which the $ i $th event is activated in the $ m+1 $th work interval. This strategy has the advantage of allowing the controller to work for a while and then take a break to lessen the strain on communication. $ \alpha: \mathbb{R}^n \rightarrow \mathbb{R}^n $ stands for the controller function. Thus, with an intermittent control law $ u(t) $, the system's dynamic can be represented as follows:

where $ q:\mathbb{R}^n \rightarrow \Xi $, $ n \in \mathbb{Z_+} $ represents the logarithmic quantization function, $ \Xi $ is a discrete set of quantization values, and $ \{t_{m, i}\} $ indicates a time series consisting of the instant of event triggering. Next, we give a number of significant assumptions.

Assumption 2.1. ^[18] There are two constants $ \theta $, $ \omega $, satisfying $ 0 < \theta < \omega $ and for $ k = 1, 2, 3 \ldots $, such that the following holds true:

Remark 2.1. Here, $ \theta $ is the minimum work interval and $ \omega-\theta $ is the maximum rest interval, where the duration of the work interval will not be less than $ \theta $ and the duration of the rest interval will not be greater than $ \omega-\theta $. This prevents the controller from exerting control for long periods of time and ensures that the work interval alternates with the rest interval. The framework of the APIC strategy is shown in Figure 1.

Assumption 2.2. ^[22,39] The logarithmic quantizer $ q(\cdot) $ is defined as follows:

where $ q(v) $, $ v $ $ \in \mathbb{R} $, without taking the finite quantization level into account $ \Xi = \{\pm\xi:\xi_i = \rho^i\xi_0; i\in \mathbb{N}\}\cup\{0\}; $ $ 0 < \rho < 1; $ and $ \xi_0 > 0 $, where $ \delta = \frac{1-\rho}{1+\rho} \in (0, 1) $ is linked to the quantizer density $ \rho $ and is referred to as the sector bound. If $ q $ is a logarithmic quantization function and $ q(x) = \Gamma[q(\zeta_{x, 1}), q(\zeta_{x, 2}), \cdots, q(\zeta_{x, n})]^T $, where $ \zeta_x = \Gamma^{-1}x = [\zeta_{x, 1}, \zeta_{x, 2}, \cdots, \zeta_{x, n}]^T $, $ x\in \mathbb{R}^n $. The nature of the quantizer is as follows:

Assumption 2.3. The following equation holds true for every $ x $, $ \overline{x} \in \mathbb{R}^n $, $ t \in \mathbb{R_+} $, assuming there are positive constants $ L_1 $, $ L_2 $, and $ L_3: $

Assumption 2.4. Positive definite functions $ V(x, t)\in \mathcal{C}^{2, 1}(\mathbb{R}^n \times \mathbb{R_+}; \mathbb{R_+}) $ exist that are continuously differentiable in x twice and in t once. Positive variables $ c_1 $, $ c_2 $ also exist, so that for every $ x \in \mathbb{R}^n $, the equation that follows holds:

The operator $ \mathcal{L}V(x, t) $ is defined by

where $ \varphi(t) = \varphi_1 > 0 $ for $ t \in [t_m+s_m, t_{m+1}) $, $ \varphi(t) = \varphi_2 < 0 $ for $ t \in [t_m, t_m+s_m) $, and $ \mathrm{d}V(x, t) = \mathcal{L}V(x, t)\mathrm{d}t+V_x(x, t)\mathrm{d}\omega(t) $.

Assumption 2.5. ^[16] A positive definite function $ V(x, t)\in \mathcal{C}^{2, 1}(\mathbb{R}^n \times \mathbb{R_+}) $ and a positive constant $ L_4 $ exist, such that any $ x \in \mathbb{R}^n $ $ \frac{\partial V(x, t)}{\partial x} \leq L_4|x| $ holds.

Definition 2.1. For the given constants T, $ \varepsilon_1 $, and $ \varepsilon_2 $ with $ 0 < \varepsilon_1 < \varepsilon_2 $ and any trajectory $ x(t) $, if there is a control law such that $ \mathbb{E}|x_0| \leq \varepsilon_1 $ implies $ \mathbb{E}|x(t)| \leq \varepsilon_2 $, $ t \in [0, T] $, then the system (2.3) is called FTS with respect to $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2) $.

Definition 2.2. For the given constants T, $ \varepsilon_1 $, $ \varepsilon_2 $, $ \varrho $, and $ \tau $, where $ 0 < \varrho < \varepsilon_1 < \varepsilon_2 $ and $ \tau\in (0, T) $, the system (2.3) is FTCS with respect to $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2, \varrho, \tau) $. If there is a control law such that $ \mathbb{E}|x_0| \leq \varepsilon_1 $ implies $ \mathbb{E}|x(t)| \leq \varepsilon_2 $ for all $ t \in [0, T] $, for all $ t\in [T-\tau, T] $, there is $ \mathbb{E}|x(t)| \leq \varrho $.

Remark 2.2. (ⅰ) In Definition 2.1, all parameters $ \varepsilon_1 $, $ \varepsilon_2 $, and $ T $ are predesigned, and $ FTS $ indicates that the average value of the states from the initial data of the systems is within a predetermined initial bound and subsequently reaches another set bound after a finite amount of time. The $ FTS $ describes a kind of boundedness of the state of the system, whose state trajectory is depicted in Figure 2a.

(ⅱ) According to Definition 2.2, the trajectory of the system state reaches, within a small time interval $ [T-\tau, T] $ of the terminal time, another threshold $ \varrho $ that is smaller than the initial threshold, as shown in Figure 2b. Thus, we can see that the conditions for $ FTCS $ are much more restrictive than $ FTS $.

Lemma 2.1. ^[16] Consider stochastic nonlinear systems satisfying Assumptions 2.2, 2.4, and 2.5. When $ t \in [t_1, t_2) $, assuming the existence of some positive constants $ \hat{\beta_1} < 0 $, $ \check{\beta_1} > 0 $, and $ -\hat{\beta_1} > \check{\beta_1} > 0 $, for a positive definite function $ V(x(t), t) $, the following conditions are satisfied:

Then, we can derive

3.   Main result

To further investigate the connection between state quantization and ETMs under APIC, we designed the following two ETMs.

(Ⅰ). QbE: If the system's state is quantized before a trigger, the following ETM is available:

(Ⅱ). QaE: If the system's state is quantized after a trigger, the following ETM is available:

where $ t_0 = 0 $, $ \epsilon $, and $ \lambda $ are all constants, and (3.1) and (3.2) mean that the ETM will be suspended for a period of time $ \epsilon $ after execution; after that, it will continue to execute the current predesigned trigger mechanism until the next trigger threshold condition is met. Since the stopping time $ \epsilon $ is set in the ETM, the system (2.1) naturally avoids the Zeno behavior. Compared with traditional time-triggered, the event-triggered strategy used can further increase the time interval between events on this basis, due to the fact that the defined time sequence of event-triggered is determined by the current state of the system, thus reducing the network's communication burden. The description of ETM (3.1) and ETM (3.2) can be represented by the block diagrams in Figures 3 and 4. In addition, the utilization of APIC (2.2) can further save communication resources on this basis. Next, we give the following two error estimates $ e_1(t) = q(x(t_{m, i}))-x(t) $ and $ e_2(t) = x(t_{m, i})-x(t) $.

3.1.   State quantization before ETC

Lemma 3.1. Under Assumptions 2.1–2.3, $ \epsilon \geq 0 $, $ 0 \leq \delta \leq 1 $, and $ \epsilon < \sqrt{\frac{1}{12L_3^2(2\delta^2+1)}} $ exist, and for the system (2.1), the following holds:

where $ \kappa_1 = \frac{4(2\delta^2+1)(2\epsilon L_1^2+L_2^2)}{1-12\epsilon^2L_3^2(2\delta^2+1)} $, $ \kappa_2 = \frac{24\epsilon^2 L_3^2(2\delta^2+1)^2}{1-12\epsilon^2L_3^2(2\delta^2+1)}+4\delta^2+\lambda $.

Proof. For any fixed $ t $, define the set of time series $ \Lambda_i = \{\gamma_t = t_{m, i}\} $, $ \Lambda_{i, \epsilon} = \{\gamma_t = t_{m, i}, \; \mathrm{and} \; t \leq t_{m, i}+\epsilon\} $. We estimate the error $ e_1(t) $ in two separate cases.

Case 1: If $ t\in \Lambda_i \setminus \Lambda_{i, \epsilon} $, at this point, by ETM (3.1), we have $ |q(x(t_{m, i}))-x(t)|^2 \leq \lambda|x(t)|^2 $ a.s.(almost sure) on $ \Lambda_i \setminus \Lambda_{i, \epsilon} $, which implies

Case 2: If $ t \in \Lambda_{i, \epsilon} $, for the error $ e_1(t) $, we have

Next, we estimate $ e_2(t) $ conditional on ETM (3.1). Based on the system (2.3), we have

From H$ \mathrm{\ddot{o}} $lder's inequality and Assumption 2.3, we get

From Assumptions 2.2 and 2.3

Furthermore, from the $ It\hat{o} $ isometry and Assumption 2.3, we obtain

Then, substituting (3.7), (3.8), and (3.9) into (3.6) yields

Since $ \epsilon < \sqrt{\frac{1}{12L_3^2(2\delta^2+1)}} $, shifting the terms gives

Substituting the result of (3.10) into (3.5) gives

Thus, combining (3.4) and (3.11), we get

Therefore, when $ t \in [t_m, t_m+s_m) $, there are up to $ \lceil \frac{s_m}{\epsilon} \rceil $ communication times on $ [t_m, t_m+s_m) $, $ m \in \mathbb{N}^+ $. As a result, we can arrive at

let $ \kappa_1 = \frac{4(2\delta^2+1)(2\epsilon L_1^2+L_2^2)}{1-12\epsilon^2L_3^2(2\delta^2+1)} $, $ \kappa_2 = \frac{24\epsilon^2 L_3^2(2\delta^2+1)^2}{1-12\epsilon^2L_3^2(2\delta^2+1)}+4\delta^2+\lambda $, we conclude that

and the proof is completed. Next, we analyze the FTS and FTCS of the system (2.3) under APIC in terms of ETM (3.1) with state quantization.

Theorem 3.1. Under Assumptions 2.1–2.5 and Lemmas 2.1 and 3.1, there are $ \epsilon < \sqrt{\frac{1}{12L_3^2(2\delta^2+1)}} $ and some positive constants $ \lambda, \epsilon, \delta, \omega, \theta, \tilde{\mu}_1 $ that satisfy

and

where $ \mathcal{N}(0, t) $ delegates the number of the control period on $ (0, T] $ and $ T\neq t_n $, $ \check{\beta}_1 = \frac{L_3L_4\epsilon}{2c_1}\kappa_1 $, and $ \hat{\beta}_1 = \frac{L_3L_4}{2c_1}\kappa_2+\frac{L_3L_4}{2c_1}+\varphi_2 $, where $ \kappa_1 $ and $ \kappa_2 $ are the same as in Lemma 3.1. $ 0 < \tilde{\mu}_1 < \mu_1 $ and $ \mu_1 $ is the sole positive real root of equation $ \mu_1+\check{\beta}_1e^{\mu_1\Delta_1}+\hat{\beta}_1 = 0 $. The upper bound on the inter-event interval can be expressed as $ \underset{m, i\in \mathbb{N}}{sup}\{t_{m, i+1}-t_{m, i}\}\leq \Delta_1 $. We can then claim that the system (2.1) is capable of FTS $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2) $ under APIC with ETM (3.1).

Moreover, if for all $ t\in [T-\tau, T] $, there are

Then, we claim that system (2.1) is capable of FTCS $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2, \varrho, \tau) $ under APIC with ETM (3.1).

Proof. For $ 0 < |x_0|\leq \varepsilon_1 $, assume $ x(t) = x(t, 0, x_0) $ is a solution of the system (2.2) at $ (0, x_0) $, when $ t \in [t_m+s_m, t_{m+1}) $, from Assumption 2.4, we have

Integrating (3.15) over the interval $ [t_m+s_m, t) $ gives

When $ t \in [t_m, t_m+s_m) $, from Assumptions 2.4 and 2.5 and Condition (ⅱ) in Assumption 2.2, we obtain

Substituting the result of Lemma 3.1 into (3.17) yields

Substituting the result of Lemma 2.1, $ \check{\beta}_1 = \frac{L_3L_4\epsilon}{2c_1}\kappa_1 $, and $ \hat{\beta}_1 = \frac{L_3L_4}{2c_1}\kappa_2+\frac{L_3L_4}{2c_1}+\varphi_2 $ into Eq (3.18) yields

Further, let $ \dot{z}(t) = \check{\beta}_1z(t_{m, i})+\hat{\beta}_1z(t) $ and $ y(t) = z(t)e^{\tilde{\mu}_1(t-t_{m, i})} $ and assume that $ z(t) = \mathbb{E}V(x(t), t) $. Since $ z(t_{m, i}) > 0 $, we assert that $ \phi > 1 $ exists such that $ y(t) < \phi z(t_{m, i}) $. Otherwise, $ t > t_{m, i} $ exists such that $ y(t) > \phi z(t_{m, i}) $, and we define $ \hat{t} = \inf\{t > t_{m, i}\vert y(t) = \phi z(t_{m, i})\} $. Thus, we can derive $ y(\hat{t}) = \phi z(t_{m, i}) $, which means that $ \dot{y}(\hat{t})\geq 0 $. In this cases,

When $ t = \hat{t} $, the following equation holds:

Next, we define $ \vartheta(\mu_1) = \mu_1+\hat{\beta}_1+\check{\beta}_1e^{\mu_1\Delta_1} $. We then have $ \vartheta(\mu_1)' $ and, by $ \vartheta(0) < 0 $ and $ \vartheta(-\hat{\beta}_1) > 0 $, a unique positive root $ {\mu}_1 $ exists such that $ \mu_1+\hat{\beta}_1+\check{\beta}_1e^{\mu_1\Delta_1} = 0 $. Further, for $ 0 < \tilde{\mu}_1 < \mu_1 $, we have $ \tilde{\mu}_1+\hat{\beta}_1+\check{\beta}_1e^{\tilde{\mu}_1\Delta_1} < 0 $. In summary, we conclude that $ \dot{y}(\hat{t})\leq 0 $. This is contradictory to the above. Thus, $ y(t) < \phi z(t_{m, i}) $ holds. Therefore, when $ t \in [t_{m, i}, t_{m, i+1}) $ and when $ \phi\rightarrow 1 $, by the comparison principle, we have

When $ t\in[t_m, t_{m, 1}) $, Eq (3.20) becomes

If we let $ t = t_{m, 1} $, then we have

When $ t\in[t_{m, 1}, t_{m, 2}) $, we have

Substituting (3.21) into (3.22) yields

Suppose that the following equation still holds when $ t\in[t_{m, k}, t_{m, k+1}) $:

and when $ t = t_{m, k+1} $

When $ t\in[t_{m, k+1}, t_{m, k+2}) $, we have

Substituting (3.24) into (3.25) gives

The assumption still holds when $ t\in[t_{m, k+1}, t_{m, k+2}) $. Hence, for any $ t\in [t_{m, i}, t_{m, i+1}) $ and $ 0 \leq i \leq \lceil \frac{s_m}{\epsilon} \rceil $, we have $ \mathbb{E}V(x(t), t)\leq \mathbb{E}e^{-\tilde{\mu}_1(t-t_m)}V(x(t_m), t_m) $ holds true. Then for $ t\in [t_m, t_m+s_m) $, we still have $ \mathbb{E}V(x(t), t)\leq \mathbb{E}e^{-\tilde{\mu}_1(t-t_m)}V(x(t_m), t_m) $.

In summary, we have

for $ 0\leq t\leq T $, $ 0 < \varepsilon_1 < \varepsilon_2 $, and $ 0 < |x_0|\leq \varepsilon_1 $.

When $ t\in [t_0, t_0+s_0) $, we have

and

for $ t \in [t_0+s_0, t_1) $. Combining with (3.27) and (3.28), one has

and

When $ t\in [t_1, t_1+s_1) $, we have

and

For $ t \in [t_1+s_1, t_2) $, combining (3.27), (3.29), and (3.30), one has

and

When $ t\in [t_2, t_2+s_2) $, we have

and

For $ t \in [t_2+s_2, t_3) $, combining (3.27), (3.31), and (3.32), one has

and

In the same way, for $ t \in [t_n+s_n, t_{n+1}) $ and using Assumption 2.1, we have

From Condition (2.4) in Assumption 2.4 and (3.13), we can derive

which means that $ |x(t)|\leq \varepsilon_2 $, and thus $ \mathbb{E}|x(t)|\leq \varepsilon_2 $ holds on $ [0, T] $. As described, it can be concluded that the system (2.3) can achieve FTS on $ [0, T] $. The system (2.1) is FTS $ ($w, r, t$) $ $ (T, \varepsilon_1, \varepsilon_2) $ under APIC (2.2) with ETM (3.1).

When $ t\in [T-\tau, T] $, if Condition (3.14) in Theorem 3.1 is satisfied, from (3.33) we have

which shows that $ |x(t)|\leq \varrho $, and thus $ \mathbb{E}|x(t)|\leq \varrho $ hold on $ t\in [T-\tau, T] $. Then the system (2.1) can achieve FTCS $ ($w, r, t$) $ $ (T, \varepsilon_1, \varepsilon_2, \varrho, \tau) $ under APIC (2.2) with ETM (3.1).

The proof is complete.

3.2.   State quantization after ETC

Lemma 3.2. Under Assumptions 2.1–2.3 and Lemma 3.1, $ \epsilon \geq 0 $, $ 0 \leq \delta \leq 1 $, and $ \epsilon < \sqrt{\frac{1}{12L_3^2(2\delta^2+1)}} $ exists, and for the system (2.1), the following holds:

where $ \kappa_3 = \frac{2(2\epsilon L_1^2+L_2^2)}{1-12\epsilon^2L_3^2(2\delta^2+1)} $ and $ \kappa_4 = \frac{12\epsilon^2 L_3^2(2\delta^2+1)}{1-12\epsilon^2L_3^2(2\delta^2+1)}+\lambda $.

Proof. Similarly to Lemma 3.1, we discuss the same in two cases.

Case 1: If $ t\in \Lambda_i \setminus \Lambda_{i, \epsilon} $, at this point, by ETM (3.2), we have $ |(x(t_{m, i})-x(t)|^2 \leq \lambda|x(t)|^2 $ a.s. on $ \Lambda_i \setminus \Lambda_{i, \epsilon} $, which implies

Case 2: If $ t \in \Lambda_{i, \epsilon} $, using the results of (3.10) in Lemma 3.1, we have

Thus, combining (3.36) and (3.37), we get

The latter steps of the proof are similar to those in Lemma 3.1, so we omit this part of the proof process. In the end, we arrive at

The proof is complete.

Theorem 3.2. Under Assumptions 2.1–2.5 and Lemmas 2.1 and 3.2, we have $ \epsilon < \sqrt{\frac{1}{12L_3^2(2\delta^2+1)}} $ and some positive constants $ \lambda, \epsilon, \delta, \omega, \theta, \tilde{\mu}_2 $ that satisfy

and

where $ \mathcal{N}(0, t) $ delegates the number of the control period on $ (0, T] $ and $ T\neq t_k $, $ \check{\beta}_1 = \frac{L_3L_4\kappa_3\epsilon(2\delta^2+1)}{c_1} $, $ \hat{\beta}_2 = \varphi_2+\frac{L_3L_4}{2c_1}+\frac{2\delta^2L_3L_4}{c_1}+ \frac{L_3L_4(2\delta^2+1)\kappa_4}{c_1} $, $ \kappa_3 $, and $ \kappa_4 $ are the same as in the Lemma 3.2. Moreover, $ \kappa_3 = \frac{\kappa_1}{2\delta^2+1} $, $ 0 < \tilde{\mu}_2 < \mu_2 $, where $ \mu_2 $ is the sole positive real root of the equation $ \mu_2+\check{\beta}_1e^{\mu_2\Delta_2}+\hat{\beta}_2 = 0 $. The upper bound on the execution time between events can be expressed as $ \underset{m, i\in \mathbb{N}}{sup}\{t_{m, i+1}-t_{m, i}\}\leq \Delta_2 $. We then claim that the system (2.1) is capable of FTS $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2) $ under APIC with ETM (3.2).

Moreover, for all $ t\in [T-\tau, T] $, there are

Then, we claim that the system (2.1) is capable of FTCS $ (w.r.t) $ $ (T, \varepsilon_1, \varepsilon_2, \varrho, \tau) $ under APIC with ETM (3.2).

Proof. For $ 0 < |x_0|\leq \varepsilon_1 $, assume that $ x(t) = x(t, 0, x_0) $ is a solution of the system (2.2) at $ (0, x_0) $. When $ t \in [t_m+s_m, t_{m+1}) $, from Assumption 2.4, we have

Integrating the equation above over the interval $ [t_m+s_m, t) $ gives

When $ t \in [t_m, t_m+s_m) $, from Assumptions 2.2, 2.4, and 2.5 and Condition (ⅱ) in Assumption 2.3, we obtain

If we substitute the result of Lemma 3.2, the equation above becomes

Substituting the result of Lemma 2.1, $ \check{\beta}_1 = \frac{L_3L_4\kappa_3\epsilon(2\delta^2+1)}{c_1} $, and $ \hat{\beta}_2 = \varphi_2+\frac{L_3L_4}{2c_1}+\frac{2\delta^2L_3L_4}{c_1}+\frac{L_3L_4(2\delta^2+1)\kappa_4}{c_1} $ into Eq (3.42) yields

The latter steps are omitted because they closely resemble those in Theorem 3.1.

Remark 3.1. The proofs of Theorems 3.1 and 3.2 rely on the upper bound condition of the execution time between events. However, due to the arbitrariness of $ t_{m, i+1}-t_{m, i} $, determining the roots of the equation $ \mu_1+\hat{\beta}_1+\check{\beta}_1e^{\mu_1\Delta_1} = 0 $ is not straightforward. Nevertheless, it can be seen from the equation that if $ t_{m, i+1}-t_{m, i} $ is larger, then the roots of the equation $ \mu_1 $ can be appropriately small to satisfy $ 0 < \tilde{\mu}_1 < \mu_1 $. Therefore, we have the existence of $ 0 < \tilde{\mu}_1^{*} < \mu_1\leq{\mu}_1^{*} $ for an arbitrary $ t_{m, i+1}-t_{m, i} $, whose corresponding equation has the solution $ {\mu}_1^{*} $, such that $ \tilde{\mu}_1^{*}+\hat{\beta}_1+\check{\beta}_1e^{\tilde{\mu}_1^{*}\Delta_1} < 0 $ holds.

Remark 3.2. Theorem 3.1 is obtained from the trigger mechanism (3.1) on the basis of the error estimate (3.3), and Theorem 3.2 is obtained from the trigger mechanism (3.2) on the basis of the error estimate (3.35). Since (3.1) is based on quantization first and then event-triggered determination, the scheme is applicable to the overall quantization nature of the state trajectories, while (3.2) is based on event-triggered of the system's state and then realizing the quantization, which is more suitable for exploring the local quantization nature of the state trajectories under intermittent control. Therefore, according to (3.14) in Theorem 3.1, $ \varrho $ can be reduced with the change in $ \theta $ by increasing $ \theta $, which can better realize the 'contraction' in FTCS. By Eq (3.40) of Theorem 3.2, it can be seen that by decreasing $ \theta $ appropriately, $ \varrho $ can increase relatively with a change in $ \theta $, which makes it easier to achieve FTCS. See Section 4 for details.

4.   Numerical examples

This section illustrates our design approach using two examples of real process simulation and numerical simulation.

Example 1. Consider the following stochastic nonlinear system:

on $ t \geq 0 $, where

and

Consider the initial state $ x_0 = (0.4, 0, 3)^T $, where $ x(t) $ denotes the system's state vector and $ x_1(t) $, $ x_2(t) $ are the state components of $ x(t) $. Parameters $ a = 0.08 $, $ b = 0.03 $, $ c = 0.01 $, $ d = 0.99 $, and $ e = 0.03 $. We select the Lyapunov function $ V(x) = x_1^2+x_2^2+0.1x_1x_2 $. Then we define the aperiodically intermittent controller as follows:

Then, from Assumptions 2.2 and 2.5, we can obtain

Hence, according to Assumptions 2.3 and 2.5, we choose the appropriate parameters $ L_1 = 1.8 $, $ L_2 = 0.15 $, $ L_3 = 1.42 $, and $ L_4 = 2.1 $. Then, from Assumption 2.4, $ \varphi_1 $ and $ \varphi_2 $ can be set as $ 0.5 $ and $ -2.8 $. Next, we select the appropriate parameters on the basis of the results of Lemma 3.1 and Theorem 3.1: $ \delta = 0.01 $, $ \epsilon = 0.01 $, $ \lambda = 0.01 $, and $ \Delta_1 = 0.14 $. This makes it possible to calculate the roots of the equation $ \mu_1+\check{\beta}_1e^{\mu_1\Delta_1}+\hat{\beta}_1 = 0 $ in Theorem 3.1, selecting the appropriate $ \tilde{\mu}_1 $. Assume the maximum control interval $ \omega = 2.5 $ and the minimum working interval $ \theta = 1.9 $. From Definitions 2.1 and 2.2, let $ \varepsilon_1 = 0.51 $ and $ \varepsilon_2 = 0.55 $. Substituting into Eq (3.13) in Theorem 3.1 yields

Further, by Definition 2.2, let $ \varrho = 0.07 $ and $ \tau = 1 $, and use Formula (3.14) from Theorem 3.1

In summary, we can see that the system is not only FTS $ (w.r.t) $ $ (7.3, 0.51, 0.55) $ when $ t\in [0, 7.3] $ under the aperiodically intermittent ETM (3.1) with state quantization, but is also FTCS $ (w.r.t) $ $ (7.3, 0.51, 0.55, 0.07, 0.5) $ when $ t\in [6.8, 7.3] $ as shown in Figure 5. The state trajectory of the system, the ETM (3.1), the state quantization trajectory, and the intermittent controller are shown in Figures 6–9. As can be seen from Figures 5 and 6, the system $ (4.1) $ is not only FTCS but also has Lyapunov stability. Figure 6 shows the intermittent state quantization curve trajectory implemented on the basis of Figure 5. The ETM (3.1) is represented by Figure 7. The controller (4.2) is represented by Figure 8.

Similarly, we choose the maximum control interval $ \omega = 2.5 $, the minimum working interval $ \theta = 1.6 $, and the other parameters are the same as in Theorem 3.1, then we can find the solution to equation $ \mu_2+\check{\beta}_1e^{\mu_2\Delta_2}+\hat{\beta}_2 = 0 $ in Theorem 3.2, selecting the appropriate $ \tilde{\mu}_2 $. Further we set $ \varepsilon_1 = 0.51 $ and $ \varepsilon_2 = 0.55 $, replacing Eq (3.39) in Theorem 3.2 yields

Further by Definition 2.2, let $ \varrho = 0.09 $ and $ \tau = 1 $, use formula (3.40) from Theorem 3.2

Therefore, it can be obtained that the system (4.1) is FTS $ (w.r.t) $ $ (7.3, 0.51, 0.55) $ when $ t\in [0, 7.3] $ under aperiodically intermittent ETM (3.2) with state quantization and is FTCS $ (w.r.t) $ $ (7.3, 0.51, 0.55, 0.09, 0.5) $ when $ t\in [6.8, 7.3] $, as shown in Figure 10. Figures 11–14 represent the state quantization trajectory, the ETM (3.2), the intermittent controller, and the system state trajectory, respectively. Similarly, as shown in Figures 10 and 14, it can be seen that in Theorem 3.2, the system (4.1) is not only FTS but also has Lyapunov stability.

If we compare Figure 7 with Figure 12, it is clear that the number of ETM (3.1) communications is 118 and the number of ETM (3.2) communications is 100. Thus by decreasing $ \theta $, the number of communications is reduced to some extent. According to Remark 3.2, due to the different schemes of the two ETMs, the first scheme is chosen if all the states of the system are to be quantized in a finite time, and the second scheme is chosen if the states of the system are to be quantized in a certain part of the system in a finite time, as shown in Figures 6 and 11. Since we use intermittent state quantization, if the first scheme is chosen, $ \theta $ can be increased appropriately to achieve better quantization. If the second scheme is chosen, $ \theta $ can be decreased appropriately as a way to reduce the work burden of the controller and achieve a local quantization effect.

Furthermore, in Example 1, the number of communications under different control methods and trigger mechanisms is investigated, as shown in Table 1, and it can be clearly seen that there is a significant reduction in the number of communications under the effect of APIC and ETMs. In addition, by adjusting the suspension time $ \epsilon $ and the triggering parameter $ \lambda $, the number of communications can also be affected, as shown in Table 2.

Example 2. To further verify the validity of the proposed theory, we consider the following stochastic nonlinear system whose parameters contain:

and

Where $ t \geq 0 $, consider the initial state $ x_0 = (0.5, -0, 5)^T $ and $ x(t) $ is defined as the state vector and $ x_1(t) $, $ x_2(t) $ as the state components of $ x(t) $. We select the Lyapunov function $ V(x) = 0.1x_1^2+0.1x_2^2 $. Then we define the aperiodically intermittent controller as follows:

Similarly, according to Assumptions 2.3 and 2.5, we choose the appropriate parameters $ L_1 = 0.6 $, $ L_2 = 0.11 $, $ L_3 = 2.1 $, and $ L_4 = 0.21 $. Then, from Assumption 2.4, $ \varphi_1 $, $ \varphi_2 $ can be set as $ 0.5 $ and $ -3.4 $. We select the appropriate parameters according to the results of Lemma 3.1 and Theorem 3.1, $ \delta = 0.01 $, $ \epsilon = 0.01 $, $ \lambda = 0.01 $, and $ \Delta_1 = 0.45 $. Similar to Example 1, we can also calculate the roots of equation $ \mu_1+\check{\beta}_1e^{\mu_1\Delta_1}+\hat{\beta}_1 = 0 $ according to the above parameters. Assume the maximum control interval $ \omega = 2.5 $ and the minimum working interval $ \theta = 2 $. From Definitions 2.1 and 2.2, let $ \varepsilon_1 = 0.75 $ and $ \varepsilon_2 = 0.8 $, then substituting into Eq (3.13) in Theorem 3.1 yields

Furthermore, by Definition 2.2, let $ \varrho = 0.083 $ and $ \tau = 0.7 $, use formula (3.14) from Theorem 3.1

In summary, we can see that the system is not only FTS $ (w.r.t) $ $ (8.5, 0.75, 0.8) $ when $ t\in [0, 8.5] $ under the aperiodically intermittent ETM (3.1) with state quantization, but also FTCS $ (w.r.t) $ $ (8.5, 0.75, 0.8, 0.083, 0.7) $ when $ t\in [7.8, 8.5] $, as shown in Figure 15. The state trajectory of the system, the ETM (3.1), the state quantization trajectory, and the intermittent controller are shown in Figures 16–19. As can be seen from Figures 15 and 19, the system $ (4.1) $ is not only FTCS but also has Lyapunov stability. Figure 16 shows the intermittent state quantization curve trajectory implemented on the basis of Figure 15. The ETM (3.1) is represented by Figure 17. The controller (4.2) is represented by Figure 18.

Similarly, choose the maximum control interval $ \omega = 2.5 $ and the minimum working interval $ \theta = 1.8 $, and the other parameters are the same as in Theorem 3.1. Furthermore, we set $ \varepsilon_1 = 0.75 $ and $ \varepsilon_2 = 0.8 $, and then replacing Eq (3.39) in Theorem 3.2 yields

Furthermore, by Definition 2.2, let $ \varrho = 0.15 $ and $ \tau = 0.8 $, and use formula (3.40) from Theorem 3.2

Therefore, it can be seen that the system (4.1) is FTS $ (w.r.t) $ $ (7.8, 0.75, 0.8) $ when $ t\in [0, 7.8] $ under aperiodically intermittent ETM (3.2) with state quantization and is FTCS $ (w.r.t) $ $ (7.8, 0.75, 0.8, 0.15, 0.8) $ when $ t\in [7.0, 7.8] $ as shown in Figure 20. Figures 21–24 represent the state quantization trajectory, the ETM (3.2), the intermittent controller, and the system state trajectory, respectively. Similarly, as shown in Figures 10 and 14, it can be seen that in Theorem 3.2, the system (4.1) is not only FTS but also has Lyapunov stability. Comparing Figure 7 with Figure 12, it is clear that the number of ETM (3.1) communications is 33 and the number of ETM (3.2) communications is 50. If we set the controller to $ u(t) = 0 $, the system is unstable, as shown in Figure 25.

5.   Conclusions

This study uses ETC and APIC to investigate the FTS of stochastic nonlinear systems. First, the Zeno behavior is avoided by designing the hover time in ETM. After that, the state quantization strategy is introduced to implement the two triggering schemes, and quantization error estimation and sampling error estimation are used to further implement the FTS and the FTCS. The viability and efficacy of the theoretical results of state quantization and APIC are confirmed in two numerical examples, as are the feasibility and validity of the two ETMs that have been proposed. Finally, different triggering schemes can be selected by adjusting the size of the working interval to achieve different effects within a finite time, which further saves resources. However, since the logarithmic quantizer in Assumption 2.1 of this paper becomes more error-prone as the quantization level increases, exploring alternative quantization methods, such as dynamic quantization, could be a promising direction for future research. In addition, Assumptions 2.3 and 2.5 are more applicable to cases without time delay; therefore, these assumptions may no longer hold when studying a stochastic nonlinear time delay system. However, a similar approach is provided in ^[14]. Future research work on stochastic nonlinear systems containing delays with dynamic ETC is also needed.

Author contributions

Biwen Li: Supervision, writing–review and editing; Guangyu Wang: Writing–original draft. Both authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare that they have not used artificial intelligence (AI) tools in the creation of this paper.

Acknowledgments

The authors would like to thank the editors and referees for their very helpful comments and suggestions.

Conflicts of interest

The authors declare no conflicts of interest.

Appendix