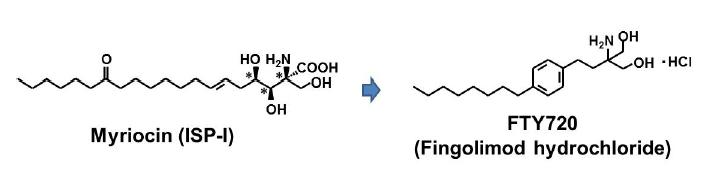
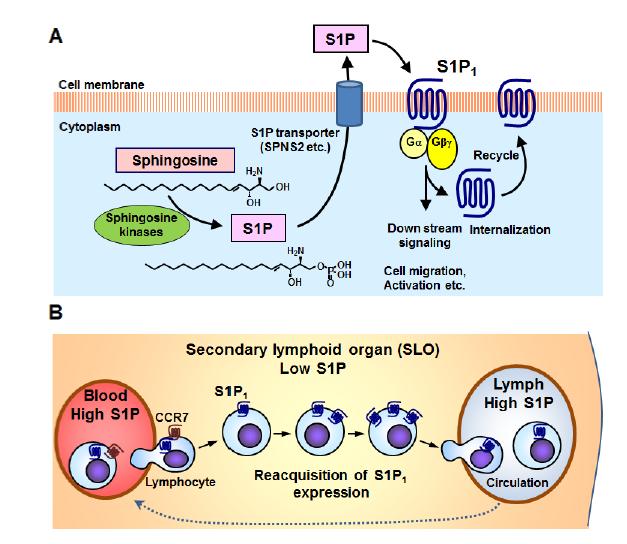
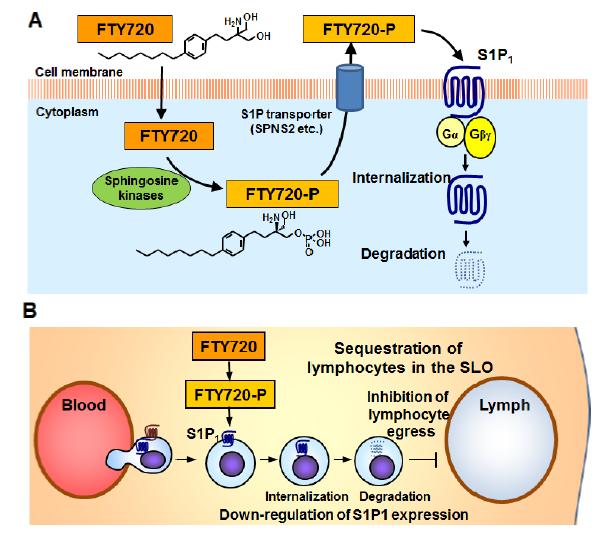
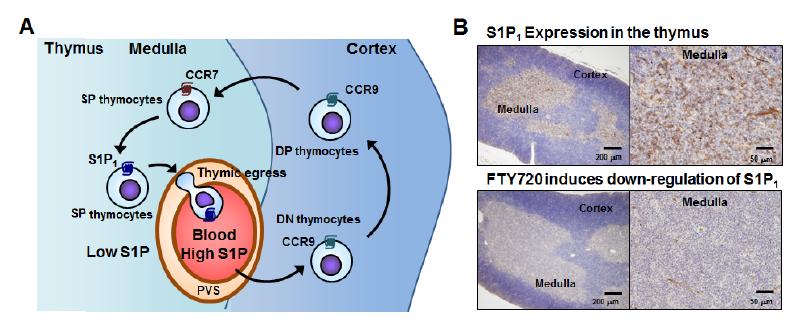
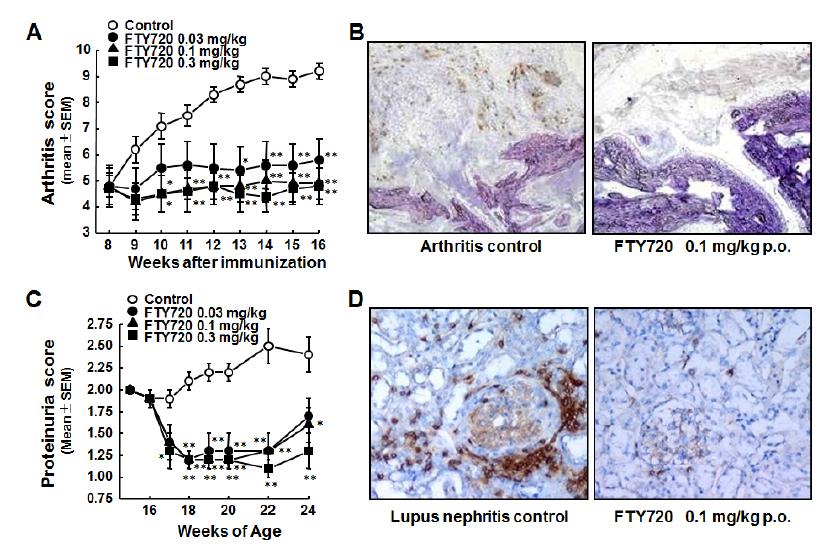
Sphingosine 1-phosphate (S1P), a multi-functional phospholipid mediator, is generated from sphingosine by sphingosine kinases and binds to five known G protein-coupled S1P receptors (S1P1, S1P2, S1P3, S1P4, and S1P5). It is widely accepted that S1P receptor 1 (S1P1) plays an essential role in lymphocyte egress from the secondary lymphoid organs (SLO) and thymus, because lymphocyte egress from these organs to periphery is at extremely low levels in mice lacking lymphocytic S1P1. Fingolimod hydrochloride (FTY720) is a first-in-class, orally active S1P1 functional antagonist which was discovered by chemical modification of a natural product, myriocin. Since FTY720 has a structure closely related to sphingosine, the phosphorylated FTY720 (FTY720-P) is converted by sphingosine kinases and binds 4 types of S1P receptors. FTY720-P strongly induces down-regulation of S1P1 by internalization and degradation of this receptor and acts as a functional antagonist at S1P1. Consequently, FTY720 inhibits S1P1-dependent lymphocyte egress from the SLO and thymus to reduce circulating lymphocytes including autoreactive Th17 cells, and is highly effective in experimental autoimmune encephalomyelitis (EAE), an animal model of multiple sclerosis (MS). In relapsing remitting MS patients, oral FTY720 shows a superior efficacy when compared to intramuscular interferon-β-1a. Based on these data, it is presumed that modulation of the S1P-S1P1 axis provides an effective therapy for autoimmune diseases including MS.
1.
Introduction
Estimating the flood hydrograph produced by a given storm is a primary goal in hydrologic modeling for water resource planning and management [1,2,3,4]. Hydrographs provide information on key parameters for flood assessment, such as the peak flow rate (Qp), the time at which it occurs (Tp), and the corresponding total runoff volume [5], and therefore constitute a useful concept in hydrology. Among the range of methods developed to estimate peak runoff rates from storms, the unit hydrograph (UH) model has evolved into one of the most powerful tools in applied hydrology [1,3,4]. The UH model is a discharge hydrograph resulting from one unit of excess rainfall generated uniformly over the basin area at a uniform rate during a specified duration [6]. Its concept and theory are simple and straightforward [3], but its practical application may be cumbersome if calibration data is unavailable, as different determination methods may lead to marked differences in the resulting key parameters governing the hydrological response of a given basin to storms [7,8,9,10].
The practical application of the unit hydrograph model in drylands faces two additional challenges. Dryland basins house some of the most poorly gauged rivers on Earth [11], therefore lacking the hydrological understanding required to calibrate UH parameters. In this regard, synthetic unit hydrograph models, defined as the UH derived from physical basin characteristics, are better suited to drylands than data-driven traditional approaches [1]. Furthermore, dryland rivers are among the most variable and unpredictable in the world [12]. This implies that a given set of UH parameters may not necessarily be suitable for the full range of flows that are expected to occur in the long term [13]; so, the reliability of results will depend on validation using as many flow conditions as possible to gauge.
Among the range of synthetic unit hydrograph models derived from basin characteristics, the traditional method of the Soil Conservation Service [now the Natural Resources Conservation Service (NRCS, USDA)] is one of the most popular in ungauged basins. The NRCS-UH is based on a dimensionless, curvilinear unit hydrograph derived from many natural hydrographs observed from basins varying widely in size and geographical location [6]. UH parameters are computed based on the basin time of concentration and are represented by equivalent triangular time and discharge relationships for a given percentage of volume on the rising side of the triangle. The shape of the UH determines the proportion of runoff contributing to discharge as well as the peak rate, given by a standard peak rate factor (PRF). Even so, the PRF was found to vary from steep to flat terrain [2,14], and simultaneous adjustments may also be required to ensure that the area under the UH equals unity [1]. In this regard, geomorphological models emerge as an alternative to determine the relationship between UH parameters and the physical properties of ungauged catchments. The geomorphological instantaneous unit hydrograph (GIUH), developed by Rodríguez Iturbe and Valdés [15], is widely used for both flood prediction and hydrograph analysis and is well-suited to treating the ungauged modeling problem over large areas [16]. The GIUH relies on water travel times along the stream network, described on the basis of Horton's ratio, so that the shape of the resulting unit hydrograph depicts the morphological basin properties governing surface runoff processes [1]. Qp and Tp are expressed as a function of flow velocity, which constitutes the only parameter to be calibrated. Although this has made GIUH a very promising method, the determination of flow velocity may represent a hydrodynamic problem to be solved in basins with no or limited data [17].
This paper examines and compares the potential applicability of NRCS-UH and GIUH to reconstruct flood hydrographs in the upper Napostá Grande, a dryland basin located in southwestern Buenos Aires (Argentina). In addition, two different estimates of the basin's time of concentration, the Kirpich equation and the watershed lag, were used along with varying retardance factors to inspect for variations in the resulting hydrographs. Building on historic stream flow and rainfall records, the present study aims to obtain a characteristic unit hydrograph allowing for flood assessment and prediction in this poorly gauged basin. It gives continuity to previous research efforts assessing different methods and parameters for unit hydrograph determination at the regional scale [18] and builds on prior assessments of the basin hydrological response to rainfall events by curve number fitting [19]. In addition to contributing to water resources planning and management within the study basin, results from this investigation provide a valuable framework for flood assessment within the remaining basin sections, as well as within ungauged, regional basins describing similar characteristics, highlighting the need for caution in the systematic use of standard parameters.
2.
Study area
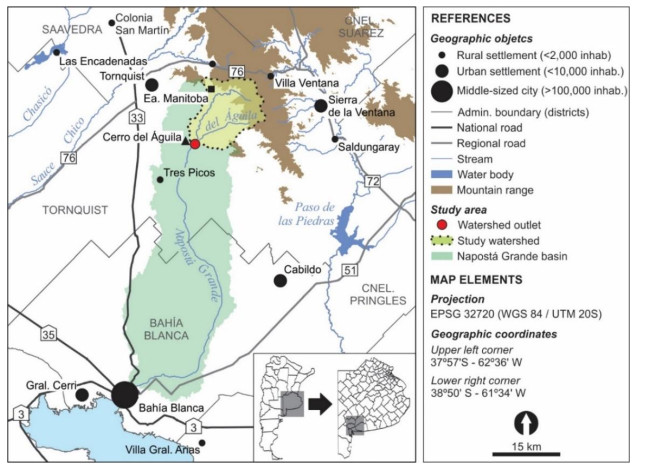
The Napostá Grande stream collects its waters on the southwestern slope of Ventania, a mountain system located in SW Buenos Aires province, Argentina (Figure 1). It flows down to the estuary of Bahía Blanca along 107 km and drains a basin area of 1260 km2. Main land uses are rainfed agriculture and livestock. Except for the city of Bahía Blanca, which is home to approximately 315, 000 people [20], population density is 3.5 inhabitants per km2 [21]. The climate is dry and subhumid. Mean annual temperature ranges from 14.7 ºC in the uplands to 15.6 ºC in the lowlands, while mean annual rainfall ranges from 730 to 605 mm, respectively (1981-2020). Interannual rainfall variability is marked [22], with up to a 1000 mm range between extreme dry and extreme wet years [23]. Rainfall variability is mainly due to the El Niño-Southern Oscillation phenomenon (ENSO) but also responds to other large-scale atmospheric and oceanic phenomena such as the Pacific Decadal Oscillation PDO [24,25]. Episodes of drier- and wetter-than-normal climate are common, with major implications for local water resources management.
The upper section of the Napostá Grande extends to the confluence of del Águila stream (Figure 1). It has a surface area of 182.4 km2 with a 31 km length reach. Main hydrologic soil cover complexes conform to two distinct units: (i) the headwaters, which exhibit quartzite rock outcrops and rather bare, shallow soils, and (ii) the lowlands, where the stream excavates its channel on loess sediments, mostly composed of fine sands, silts, and clayey silts, cemented by calcium carbonate [26]. The lowlands represent nearly 80% of the upper basin surface and exhibit clear dominance of croplands (85%) over wetlands, grasslands, and other land covers [19]. Mean daily flow (1935-1945) is 0.39 m3 s-1 and the flow regime is flashy and event-driven. Low flows are below 0.15 m3 s-1 and remain over long periods of time, while floods may reach more than 220 m3 s-1 in a few hours [27].
3.
Materials and methods
The analysis was built on a three-step procedure (Figure 2): (1) extracting input parameters, (2) determining parameters of the unit hydrograph, Tp, Qp, and Tb, and (3) validating the results. The methodology used to achieve each step is described below.
3.1. Extracting input parameters
3.1.1. Direct runoff hydrographs
A historic series of mean daily stream flow gauged at the station Cerro del Águila (1/9/1935-31/12/1945) was used as input data, along with concurrent series of daily rainfall depths for Ea. Manitoba (Figure 1). These series constitute the only reliable records available in the long term and encompass a good range of rainfall-runoff events. First, we separated the flow series into base flow (Qb) and direct runoff (Q) components (Figure 2). This was achieved using the local-minimum method with N = 0.83A0.2 [28]. In addition to providing the most conservative base flow estimates [29], this method yielded similar results to those obtained by previous studies on basin hydrogeology [27,30,31]. Second, we extracted direct runoff hydrographs produced by single rainfall events greater than 51 mm. For the upper Napostá Grande basin, the 51 mm threshold separates large rainfall events with 90% runoff probability, having been defined by López, Casado, Revollo Sarmiento, et al. [19] based on relative storm size analysis [32]. Corresponding rates of instantaneous peak flows were obtained from Carrica and Bonorino [30]. The selected hydrographs were transformed into dimensionless hydrographs by computing the ratio of time units to time to peak (T/Tp) and the ratio of discharge units to peak flow (Q/Qp). A simple analysis of variance (ANOVA) with unbalanced fixed factors was performed to detect significant differences between hydrographs.
3.1.2. Basin morphometry
Determining the unit hydrograph of a basin depends on an array of morphometric parameters (Table 1). To ensure readability, morphometric parameters were assembled into two groups accounting for (i) global basin characteristics and (ii) drainage composition. Global basin characteristics (geometry, average slope, and longest flow path length and slope) were extracted from terrain data using HEC-HMS GIS module (v4.11, U.S. Army Corps of Engineers). Input terrain data used a digital surface model with a resolution of 12.5 m corresponding to the ALOS PALSAR mission (NASA-JAXA, 2011) with radiometric terrain correction by the Alaska Satellite Facility. The drainage network was digitized from satellite map services in a geographic information system (GIS). Streams were classified using the Strahler method [33], and drainage composition parameters were computed in GIS using basic statistics from attribute tables.
3.2. Determining unit hydrograph parameters: Tp and Qp
The unit hydrograph (UH) is a well-known, commonly used empirical model allowing the determination of the relationship between excess rainfall and discharge rates [34]. UH can be constructed for any location on a regularly shaped watershed once the Tp and Qp values are defined [6]. Among the range of formal methods to determine Tp and Qp, this study evaluates and compares (i) the UH method of the Soil Conservation Service, now Natural Resources Conservation Service [6], and (ii) the geomorphologic instantaneous unit hydrograph method [15]. In addition, two different estimates of the basin time of concentration were compared, along with varying parameters, to compute the watershed lag (Figure 2).
3.2.1. NRCS unit hydrograph method
The NRCS-UH is a discharge hydrograph resulting from a unit depth of direct runoff generated by a unit depth of excess rainfall of a specified duration [6]. The method builds on geometric triangular relationships derived from the basin time of concentration (Tc) for a given surface area. Tp is computed as the basin lag from the center of mass of excess rainfall, as follows
where Tp is given in hours. Qp depends on the drainage area (A) and the direct runoff depth (Q) relative to Tp, and is given by the expression:
where Qp is in m3 s-1. The coefficient 0.278 is a conversion factor for the rate required to discharge 1 mm runoff from 1 km2 in 1 h, and K is a nondimensional factor of the hydrograph shape. For a triangular hydrograph having 37.5% of the total runoff volume on the rising limb, Tb is 2.67Tp, and K takes a value of 0.75. Substituting 0.278K into Eq. 2 gives 0.208. This is the default peak rate factor (PRF) used to compute peak discharge rates.
The basin time of concentration is the time from the end of excess rainfall to the point of inflection on the receding limb of the unit hydrograph [38]. Among the wide range of methods to compute the basin time of concentration, this study compares the Kirpich equation [39] and the watershed lag method [38]. These were selected as they build on few, global parameters, thus avoiding poor estimations of physical parameters frequently unknown in poorly gauged basins. The expressions provide Tc in hours. The Kirpich equation and the watershed lag method are described by Eqs. 3 and 4, respectively:
Both Kirpich and watershed lag estimates depend on the longest flow path length (LΩ) relative to the slope. The difference between the two is in the use of the stream slope (LS) or the basin slope (LB) for computation. Furthermore, the watershed lag method considers a retardance factor (S) that results from the basin curve number (CN); i.e., the runoff potential relative to the hydrologic soil cover complexes of the basin. Finding a CN value leading to acceptable differences between the model and reality may be particularly challenging within poorly gauged basins, as the runoff response of some basins was found to perform quite differently from the basic CN derived from tables [40,41]. Accordingly, the watershed lag method introduces a third parameter to inspect for an agreement of the resulting hydrograph. In this study, three CN values were tested, obtained by previous studies focusing on the upper Napostá Grande by means of different approximation methods (Table 2). By using two different estimates to calculate Tc, Kirpich and watershed lag equations, along with three different CN-derived values of S for the latter, we obtained four sets of UH parameters on which to test the performance of the NRCS-UH method.
3.2.2. Geomorphological instantaneous unit hydrograph (GIUH)
Rodríguez Iturbe and Valdés [15] introduced the GIUH as a unifying concept of the basin hydrologic response to surface runoff. The GIUH expresses the unit hydrograph as a function of the geomorphological basin properties, linking Horton's ratios along with scale and velocity parameters, and was found to be well-suited to treat the ungauged basin modeling problem over large areas [16]. Even though the GIUH is defined as a probability density function of runoff travel time along the stream channel network, Rodríguez Iturbe and Valdés [15] developed two relationships, tp (h) and qp (h-1), allowing for an accurate approximation of Tp and Qp. These are derived from expressions of the GIUH for a range of combinations of input parameters relative to flow velocity and are given by
where rb, ra, and rl are bifurcation, area, and length ratios, respectively. LΩ is the longest flow path length (km), and v is the flow velocity (m s-1).
Rodríguez Iturbe and Valdés [15] postulated that a triangular approximation is satisfactory as long as the UH parameters are correctly estimated. Indeed, the assumption of a certain form for the GIUH involves solving explicit relationships connecting the storm and the drainage network characteristics to produce the peak discharge and the time to peak [42]. The time to peak for a triangular GIUH takes the form
where D stands for excess rainfall duration (h). On the other hand, if one approximates the GIUH with a triangle, then
The functional dependence of tp and qp with flow velocity challenges the practical application of the GIUH in ungauged basins [17]. In this study, velocity was estimated based on the basin time of concentration. Assuming that Tc denotes some length over a certain velocity, v = LΩ / Tc. Using Eq. 3 and 4 with varying CN for Eq. 4 (Table 2), we obtained four Tc-derived velocity rates, allowing inspecting their influence on the resulting hydrograph. This provided four sets of UH parameters that are comparable to those obtained from the NRCS-UH method for equivalent Tc computations (Figure 2).
3.3. Validation of results
Each set of UH parameters obtained in Step 2 was used as a basis to construct the corresponding curvilinear unit hydrograph. Unit hydrographs derived from the NRCS-UH method used the standard dimensional unit hydrograph coordinates (DUH) provided by the NRCS [6]. Standard DUH coordinates have been developed for a shape factor K of 0.75 and therefore assume that 37.5% of the total runoff volume occurs on the rising limb of the UH. Even though GIUH-derived UH parameters were computed for a triangular hydrograph shape, they do not necessarily split the triangle into such proportions, and so the DUH coordinates may be different.
We determined whether standard DUH coordinates were suitable for a given GIUH-derived set of UH parameters solving for the shape factor K as follows:
where Tr is the recession time of the hydrograph, and the base time (Tb) is 2/qp. In cases where K was different from 0.75 (standard DUH), we computed the adjusted DUH ordinates using the NRCS gamma Eq. [6], which is given by
The shape factor m in Eq. 10 was found by solving Eq. 11 in order to obtain a peak rate factor (PRF) equal to that resulting from 0.278K, with K values corresponding to those obtained from Eq. 9.
The above yielded eight unit hydrographs on which to test their response to varying direct runoff depths. Direct runoff depths were obtained by separation of the hydrographs selected in Step 1. We first checked the volume under the curve to ensure a reasonable balance was attained relative to input runoff depths. The degree of agreement of the different unit hydrographs was then determined relative to errors in the computation of Qp and Tr values, using Tr as an alternative to Tp (which are in units of days for the available series). Two simple error statistics were used: (i) the mean error based on absolute differences (ME) and (ii) the mean relative error (MRE).
4.
Results
4.1. Direct runoff hydrographs
Inspection of historic stream flow records and concurrent rainfall gauges resulted in eight direct runoff hydrographs on which to validate UH approximations (Figure 3). Rainfall depths (P) relative to the median potential retention for the upper Napostá Grande basin (146 mm) separate the hydrographs into two classes of four events each. Class 1 assembles runoff events produced by large storms, i.e., the storms exceeding the initial abstraction under dry antecedent runoff conditions (P > 51 mm) with a runoff probability of 90%. Mean daily stream flow was between 4 and 8 m3 s-1, and peak flows ranged from 13 to 30 m3 s-1. The time to peak was within 1 and 2 days, and base times were between 3 and 5 days. Q/Qp values within Class 1 were not normal according to the normal probability plot but presented homoscedasticity (pLevene = 0.65). The analysis of variance (ANOVA) showed no significant differences between hydrographs (p = 0.93). On the other hand, Class 2 groups the runoff events responding to very large storms. These correspond to rainfall depths exceeding the initial abstraction under extreme dry antecedent runoff conditions (P > 59 mm), and the resulting runoff probability is 95%. Hydrographs in Class 2 reached peak flows between 10 and 220 m3 s-1 within 1 and 2 days, with base times between 3 and 7 days. Q/Qp values were not normal but were homoscedastic (pLevene = 0.89) and showed no significant differences (p = 0.12).
Irrespective of the storm at the origin of the hydrographs, the time to peak described by mean daily stream flow was within 1 day for 50% of cases (Figure 3). Even though hourly data were not available, concurrent instantaneous peak flow series were up to seven times the mean daily stream flow recorded on those days. In this regard, one may assume that the time to peak for the upper Napostá Grande basin is rather shorter than 24 h. In the case of the remaining hydrographs, it is assumed that a 2-day time to peak obeys to storms that initiated between the afternoon and nightfall, and so the rising limb was split into two consecutive days. For these events, the difference between instantaneous peak flows and mean daily flow was naturally smaller (1 to 2 times). Except for the event 8, where runoff ceases after 5 days, recession times were between 2 and 3 days for all hydrographs (Figure 5). Although locating the end of the direct runoff is less straightforward, this is close to the empirical relation to the basin area (2.3 days).
4.2. Basin morphometry
The upper Napostá Grande basin has a Strahler stream order of five. The compactness coefficient is close to unity (CC = 1.23) and therefore falls within the limits of variation for compact watersheds concentrating large volumes of runoff in short periods of time (Figure 4). Furthermore, the basin relief is high (973 m), and terrain gradients are steep (14% on average), which promotes the occurrence of floods with large relative magnitude. However, there is a marked topographic contrast between the headwaters and the transport zone, which may be delimited by the 450 m contour line. The elevation difference within the headwaters is 750 m, and terrain slope averages 48%. The drainage integrates a dense network of first- and second-order streams with a bifurcation ratio (rb) of 4 to 1. Even though lower-order streams are relatively short and activate only during wet periods, rb values denote a complex branching of collector streams. In opposition to the headwaters, the terrain gradient within the transport zone is smooth (ΔZ = 225 m and SB = 3%), and the drainage network integrates only three streams with a marked absence of tributaries. Considering that the transport zone constitutes the most representative basin unit in terms of surface (82% of the basin area), it is expected to have major implications for water response quantification.
4.3. Unit hydrograph parameters
Comparison between the eight sets of UH parameters revealed marked differences in the shape (timing and magnitude) of the resulting hydrograph (Figure 5). In this regard, it is worth noting that all sets of UH parameters were computed assuming 1 mm of excess rainfall in 1 h. Discrepancies respond first to the determination method (NRCS-UH and GIUH) and are therefore linked to the basin properties and relations assumed in each case. NRCS-UH parameters described hydrographs notably peaked and quicker than those derived from GIUH; Qp values for the NRCS-UH were more than twice those for GIUH, while Tp values were 40% shorter. NRCS-UH estimations depend on global basin characteristics that are assembled into time of concentration and area relationships (Eqs. 1 and 2). Within the study basin, flow length to slope relationships yielded Tc values between 3.9 h (TcKIR) and 11.1 h for the highest retardance factor (CN = 56). Given that the basin area is invariant, the smaller the basin time of concentration, the higher the peak discharge relative to the resulting time to peak. On the other hand, GIUH estimations depend primarily on the drainage complexity, given by bifurcation, length, and area relationships assembled into parameters tp (Eq. 5) and qp (Eq. 6). Even though the basin time of concentration is implicitly involved in GIUH estimations by parameter "velocity", the timing and the magnitude of the resulting hydrograph also depict the basin capacity and efficiency to evacuate water through the stream network. In this regard, lower peaks for larger times suggest a greater dominance of plain-related fluvial processes within this mountain basin.
Varying Tc and velocity estimations yielded important differences in UH parameters as well, irrespective of the main determination method used in the first place (Figure 5). Kirpich estimations provided higher peaks within the smaller times, reaching 14.5 m3 s-1 in 2.6 h (NRCS-UH) and 6.9 m3 s-1 in 4.6 h (GIUH). Qp and Tp values derived from the watershed lag method were comparatively lower and larger, respectively, in response to the factor S that results from the basin CN (Eq. 4). The smaller the basin CN, the higher the potential retention S, and so the larger the time of concentration. Accordingly, Tp values increased from 4.9 to 7.4 h (NRCS-UH) and from 7.9 to 11.6 h (GIUH), while Qp decreased along with increasing Tp from 7.8 to 5.2 m3 s-1 and from 3.8 to 2.5 m3 s-1, respectively.
4.4. Validation of results
Unit hydrographs obtained using different methods were inspected to determine their ability to reproduce the flood hydrographs observed within the study basin (Figure 6). Since the basin CN is one of the parameters to validate, hydrographs were reconstructed using direct runoff instead of excess rainfall. The area under the curve for NRCS-UH-derived hydrographs was 0.01% of the runoff depth for all cases, indicating a good fit of standard DUH coordinates to Qp and Tp estimates. GIUH-derived hydrographs, however, suggested that the proportion in which the runoff volume is distributed within the hydrograph was somehow different from the standard (37.5% of volume under the rising limb). Any change in such proportion causes the shape factor K to change, and so the coordinates of the DUH also change. Solving for parameter K (Eq. 9) yielded a value of 0.63 for the hydrographs using velocity rates derived from Kirpich Tc, and 0.58, 0.59, and 0.60 for those using velocities derived from the watershed lag method with CN values 56, 63, and 72, respectively. This resulted in lower-than-standard peak rate factors (0.161 < PRF < 0.176). Percentage runoff volumes were between 29.0% and 31.7%.
Lower peak rate factors for GIUH resulted in a better agreement of simulated hydrographs to observed peak flows and recession limbs (Figure 6). From these, hydrographs using velocities derived from watershed lag estimates were notably closer to reality than those derived from Kirpich estimates, in particular those using the higher retardance factors resulting from the lower CN values. Table 3 summarizes the errors in Qp and Tr estimations by simulation method and hydrograph class. The best results are found for GIUH hydrographs using velocity rates lagged by a basin CN of 56 (0.8 m s-1). ME and MRE in Qp estimates were higher for hydrographs in Class 1 than for Class 2. Major errors occurred for events 1 and 4, where peak flows were twice those observed for nearly equivalent runoff volumes among hydrographs of the same class (5.4 < Q < 6.9). This may respond to a dispersion of natural data, to different rainfall durations, to spatial variability in rainfall intensity, or to a combination of one or more phenomena. Large storms within the study basin have a 2-year return period for 2.6 mm h-1 mean intensity. Something similar occurred for event 5 in Class 2, for which Qp was underestimated by nearly 50%. This is due to low runoff depths (2 mm) relative to the peak (10 m3 s-1) and may be linked to low rainfall intensities, errors in readings, or both.
Errors in Tr estimations were comparatively lower for all methods (Table 3). GIUH hydrographs using 56-lag provided longer base times (Figure 6) and, therefore, the best agreement of recession times. Mean errors were lower than one day for both hydrographs classes, remaining below the smaller time step of data available. Relative errors were less than 20% except for Class 2, where the average MRE was affected by 40% underestimation for event 8 (5-day recession). Longer recession times obtained from simulation were 3.3 days.
5.
Discussion
Flood modeling within poorly gauged, dryland basins represents a major challenge for water resource planning and management. Synthetic unit hydrographs greatly contribute to solving the ungauged problem, as they rely on physical basin characteristics rather than on rainfall-runoff data [1]. However, literature assembles an array of determination methods building on traditional, conceptual, probabilistic, and geomorphological relationships, and a simple, general UH model has not yet been globally agreed [3]. The relationships, parameters, and coefficients involved in direct runoff hydrograph determinations may lead to a range of results that require validation to ensure their reliability relative to the hydrological response of the basin being modeled. In this regard, the lack of hydrological data relative to the marked variability of dryland rivers is an important issue.
For the upper Napostá Grande basin, Qp and Tp determined from the NRCS-UH method described hydrographs notably more pointed and sharp than those obtained from GIUH parameters, with Qp and Tp differences of up to 109% and −43%, respectively. In addition, the time factor of GIUH hydrographs suggested that the percentage of runoff volume on the rising limb was smaller than standard, leading to a greater proportion of receding volumes. Moreover, the difference between Kirpich- and watershed lag-derived estimates of the basin time of concentration was up to 7.2 h, which resulted in up to 1.4 m s-1 difference in velocity rates.
From the eight possible combinations between determination methods and Tc estimates, GIUH hydrographs using velocity rates derived from the highest retardance factors were better suited to reproduce observed flood hydrographs. This may be attributed to the physical parameters involved in the different formulae relative to the morphological and hydrological complexity of the study basin. NRCS-UH relies on the time of concentration [6] and therefore depends on the relationship between length and slope [38]. The marked topographic contrast between the headwaters and the transport zone, which clearly dominates in terms of surface area, probably leads to slope averages that do not necessarily represent the hydrological behavior of the study basin. As a result, peak discharges were overestimated and occurred within short periods of time. In this regard, Jena and Tiwari [8] recommended that, for middle-sized basins, it would be more suitable to derive UH for areas showing similar geomorphological characteristics and hypsometric curves. Even though the average slope is implicitly involved in GIUH hydrographs through velocity, it was found that geomorphological UH are most useful for complex terrain because they rely on drainage properties that result from such complexity [1,4]. However, the functional dependence of Qp and Tp on velocity challenges GIUH applications in ungauged basins [17]. Best agreements were found for velocity rates assuming CN-derived retardance factors. Yet, varying CN values yielded up to 32% and 50% differences in Tp and Qp estimations, with the lowest CN providing the most reliable results. Since the higher the CN, the smaller the retardance factor (or vice versa), the use of uncalibrated CN values along with standard parameters may affect the estimation of both key UH parameters with consequent implications for discharged volumes, as it was reported for a number of Andean basins [7,10,43].
Since there is no field and/or laboratory evidence to assume the existence of a linear relationship between the hydrological basin components, the above highlights the importance of assessing nonlinear relationships on the UH for each specific case study. In particular, UH methods assume that discharge is proportional to runoff volume at any time [6], which may not be fulfilled when considering integrated contributions from overland flow, interflow, bank storage, and groundwater flow with delayed restitution [26,27,30,31]. Within the upper Napostá Grande basin, this results in lower peak rates with notably longer recession times. Moreover, the topographic basin contrast, where gentle to flat slopes dominate over the steep terrain, coupled with lowland soils with high infiltration capacity, may explain the much lower CN values than those recommended by the literature [19,26]. These particularities lead to flatter hydrographs having smaller runoff volumes before the peak and consequent longer recession times, and were evidenced by peak rate factors close to those reported by Wilkening [44] for basins with moderate surface retention capacity.
Unit hydrographs are unique for each basin and reflect its invariant response to excess rainfall if the channel does not change over time and the storage in the basin is negligible. This fact highlights the need for caution in the systematic use of standard parameters as well as in the transfer of results between different basins and time periods if data for validation is unavailable. Validation of UH methods performed here used mean daily historic flow records. This is consistent with Kusumastuti and Jokowinarno [9] since, in general, smaller time steps may result in higher peak flow rates, whereas the time to peak remains invariant. Additionally, Oudin, Andréassian, Perrin, et al. [45] and Tegegne and Kim [46] indicated that hydrological predictions through gauging stations show similar behavior for physical and/or spatial similarity, verifying that the physiographic characteristics of the basin define its hydrological response. Even though the results from this investigation are acceptable and contribute to the hydrological understanding of this currently ungauged basin, it is worth highlighting the need for monitoring current hydrological conditions in order to guarantee the good quality of results relative to evolving changes in the basin properties and the regional climate.
6.
Conclusions
This paper examined the ability of different UH methods to reproduce flood hydrographs within a poorly gauged dryland basin. Results indicated great discrepancies between the determination methods NRCS-UH and GIUH. These were first linked to the basin parameters involved in computation but were also markedly influenced by the method used to estimate the time of concentration, Kirpich and watershed lag, along with varying CN values. NRCS-UH relies on global basin characteristics, which for the study basin are influenced by marked topographic contrast between the headwaters and the transport zone, yielding length-to-slope relationships that do not necessarily represent the basin hydrological behavior. Since the drainage composition and organization are a consequence of the basin morphology, GIUH models were best suited to reproduce flood hydrographs in the study basin. These findings reveal the importance of accurate analysis and calibration of typical hydraulic and hydrological relationships involved in the hydrological response of a given basin to storm events.
The best agreement was found for velocity rates lagged by CN = 56 and a peak rate factor of 0.161, with mean errors around 20% for both Tr and Qp estimations. A high retardance factor given by a low CN and a peak rate factor lower than standard (0.208) indicates GIUH's suitability for the incorporation of delayed flow contributions from bank storage and channel overflows. Methods and parameters implemented here have great potential for transferability to other regional basins of Buenos Aires province showing similar precipitation patterns and corresponding hydrological response. However, given the great discrepancies that may emerge between different determination methods and input parameters, it is highly recommended to verify the accuracy of the results whenever possible. This is under the knowledge that a given basin having similar physical and physiographic characteristics may exhibit comparable total runoff volumes for the same rainfall event, but not necessarily equivalent values of Tp, Qp, and Tb.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors sincerely thank Dr. Jorge C. Carrica for providing historic hydrological data for the upper Napostá Grande basin and for his valuable and permanent advice and consultation. This work was developed within the Research Group Project PGI 24/ZJ44 "Study of Water and Hydrological Balances in Basins by means of Computational Models with Adjustment to Historical Data Series", directed by Mg. Ing. N. C. López and financed by the Universidad Nacional del Sur, Argentina.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: