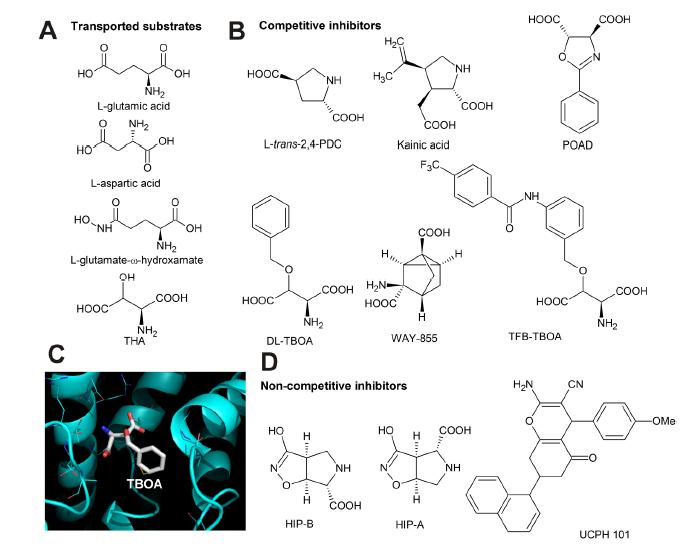
Glutamate transporters control the glutamate homeostasis in the central nervous system, and, thus, are not only crucial for physiological excitatory synaptic signaling, but also for the prevention of a large number of neurodegenerative diseases that are associated with excessive and prolonged presence of the neurotransmitter glutamate in the extracellular space. Until now, five subtypes of high-affinity glutamate transporters (excitatory amino acid transporters, EAATs 1–5) have been identified. These 5 high-affinity glutamate transporter subtypes belong to the solute carrier 1 (SLC1) family of transmembrane proteins: EAAT1/GLAST (SLC1A3), EAAT2/GLT1 (SLC1A2), EAAT3/EAAC1 (SLC1A1), EAAT4 (SLC1A6) and EAAT5 (SLC1A7). EAATs are secondary-active transporters, taking up glutamate into the cell against a substantial concentration gradient. The driving force for concentrative uptake is provided by the co-transport of Na+ ions and the counter-transport of one K+ in a step independent of the glutamate translocation step. Due to the electrogenicity of transport, the transmembrane potential can also act as driving force. Glutamate transporters are also able to run in reverse, resulting in glutamate release from cells. Due to these important physiological functions, glutamate transporter expression and, therefore, the transport rate, are tightly regulated. The EAAT protein family are structurally expected to be highly similar, however, these transporters show a functional diversity that ranges from high capacity glutamate uptake systems (EAATs 1–3) to receptor-like glutamate activated anion channels (EAATs 4–5). Here, we provide an update on most recent progress made on EAAT’s molecular transport mechanism, structure-function relationships, pharmacology, and will add recent insights into mechanism of rapid membrane trafficking of glutamate transporters.
1.
Introduction
In stochastic queueing-inventory(SQI) models, many authors assumed that the chosen item could not be delivered immediately at the initial period, because the customered item not only requires some random time to deliver it also cause the queue formation in front of the system. For example, in a mobile shop, the sales man do not sale the product directly without demonstrating the features of an item and this demonstration took some random time and cause the queue formation. Such situations allow us to develop the SQI system in the area of service facility. Initially, service facility was introduced by Melikov [31] and Sigman and Simchi-Levi [37]. Berman et al.[9] discussed the inventory management system(IMS) along with service channel assuming one item per service, deterministic customer and service rates, during the stock out period only queues can occur and determined the minimum total cost using optimal order quantity. Berman and Kim [10] determined the SQI problem with service facility in which arrival and service times follow Poisson and exponential distributions, including average inter-arrival time is larger than average service time. He et al. [18] analyzed the related model in the production inventory system(PIS) which is generated by a single machine for a batch of size one.
Berman and Sapna [11] analyzed inventory control problem(ICP) with service channel assuming one item per service, Poisson arrival, arbitrary service times, finite capacity and zero lead times. They determined the minimized total cost using the feasible order quantity under the specified cost structure. Schwarz et al. [36] examined the SQI system with the Poisson arrival, exponential service time and randomized ordering polices(ROP). Paul Manual et al.[30] considered the perishable SQI system with service facility(SF) and retrial customers under the assumption of Markovian arrival process(MAP), phase-type(PH) service distribution and life time, lead time are follows an exponential distribution.
Lopez-Herrero [29] concentrated on measuring the waiting time, reorder time and time of a pending demand for the finite retrial group. Artalejo et al. [7] considered the retrial QIS in which the any arriving customer who knows that the server is busy, immediately they join into the retrial group. They studied the waiting time of a retrial customers using Laplace-Stieltjes transform. Amirthakodi and Sivakumar [2] discussed the single server SQI system containing a finite queue. They assumed that the unsatisfied customer may join into the orbit in which the customer who can attempt the service directly if the server is free and studied the waiting time distribution for both queue and retrial queues. Yadavalli et al. [41] analyzed the multi server inventory system of a finite queues and discussed the expectation and variance of the waiting time on the impact of parameters. Recently, Jeganathan and Abdul Reiyas [24] investigated the IMS with parallel heterogeneous servers having vacations and they discussed the waiting time for both queues.
Threshold based service rates also play a sufficient role in the SQI to diminish the waiting time of customer in the queue. Harris [17] studied the queueing systems in which the they assumed that the service rates are stochastic and state-dependent. Lakshmanan et al. [27] discussed the SQI system under the threshold based priority service of N-policy. Gautam Choudhury et al. [13] and Tae-Sung Kim et al. [25] discussed the threshold based services in their queueing models. Elango [14] has discussed the perishable inventory system(PIS) with exponential service time and zero lead time. They assumed that the service parameter dependent on the number of customers in the waiting hall Kuo-Hsiung Wang and Keng-Yuan Tai [40] introduced the concept of additional servers, that is the number of service channel has been changed depending upon size of the queue. The related work has been generalized in [19]. Martin Reiser [35] analyzed the queue-dependent server in closed networks by applying mean value analysis and convolution method. In SQI system, Jeganathan et al. [22] studied three heterogeneous servers, including one with a flexible server. Subsequently, many authors proposed the multi-server and retrial models to reduce the congestion. A queue with retrial facility has been discussed in [15,16,23,26,39]. For more description on multi server retrial queues one may refer [5,8,12,32] whereas in SQI system with multi sever service facility has been considered by [3,41]. Similarly, the references [14,20,34,42] gave a brief idea about PIS.
There are some gaps in SQI literature, one can realize that, although a multi-server SQI system will reduce the waiting time of a customer for an unit item per service, in real life; there are many single server SQI system and we do not extend into multi-server models for example, in a juice shop, they provide the juice to the customer on first come first service (FCFS) basis because they had only single server and do not extend into multi-server model due to economic and space problems.
All the above mentioned models, the corresponding authors assumed that the system had a single/multi server and exponential service time which is homogeneous(uniform). In real life experience, SQI system need not have a homogeneous service rate for example, in a restaurant, one can observe that the time spent by the server varies from one customer to another customer and this may happens in supermarket, textiles shop etc. Nowadays, we are living in a congested emerging society, homogeneous service rate is not enough to satisfy the customer in concerning the queues because, by nature, we have three categories of customer: 1) Balking 2) Reneging and 3) Jockeying. In order to satisfy these types of customers, one should improve the service facility.
Stochastic queueing-inventory modeling has a widespread attention in the area of service facility along with infinite retrial group. With the emerging society, customers who do not have adequate time to wait in the queue. There are three categories of people on the basis of their behavior: 1) some of them get appointment previously to purchase the items, 2) half of the remaining people are ready to wait in the queue until they get a service and 3) another set of people will also prefer to wait in the queue, but they become impatient after some random time. As a business owner, one has to plan to attract the three categories of peoples by reducing the waiting time. One can experience this kind of situations in vegetable market, super market, mobile shop, textile show room, service center, jewel shop etc.
In this competitive economic world, customer satisfaction is a key factor to earn more profits; if they are not satisfied, then they will move to another firm. So the waiting time is one of the main determinants to satisfy the customer. Consider the real-life situation, during lunchtime, a customer wants to have lunch used to visit a restaurant. On seeing the queue, they will decide to wait in the queue. After some random time, they realize that the server is working without changing the service speed and the queue length is long, so they become impatient and immediately move to another one. This real-life situation motivates us to bring this mathematical model in order to carry out the waiting time issues and customer lost due to impatient.
In many situation, there is a necessity that the server should increase the service speed to reduce the waiting time of a customer, since a customer may become impatient due to the increase of waiting time and it causes the customer lost. It is generally perceived that the waiting time plays a significant role in the stochastic modeling of queueing-inventory system(SMQIS). A customer satisfaction not only depends on the fair items and cost but also on the waiting time. For example, consider a dam; if the level of water in the dam is high, the speed of releasing water becomes high due to heavy pressure and vice-versa.
The queue-dependent service rate will give the more advantages for both the inventory management and the customer. It mainly reduce the waiting time of a customer in the queue and the impatiences of a waiting customer. Also, the customer lost, balking, reneging are to be decreased. On the other hand, the management receives a more number of customer in the system, this leads a more sale and profit of the firm. We conclude that if the waiting time is less, then there will be increase in the arrival, for this purpose speed of the server should be increased according to the length of queue.
On seeking the solution to fill such a gap in the SQI system, very few papers are discussed in the single server SQI literature. In this context, Jeganathan [21] has filled the gap partially using the flexible server under the threshold based level $ L $ for the queue length. They defined only two non-homogeneous service rates before $ L $ and after $ L $. However, we can observe in real life, consider a footwear shop, for every customer the service time must be changed depending upon the customers waiting in the queue.
We extend this paper to the multi-threshold level; that is, the service rate is changed depend upon the number of customers in the queue. On utilizing this discussion, we present a model: single server queueing-inventory system(QIS) with queue-dependent service rates. In addition, any customer finds that the queue size is $ M $, they may enter into the orbit of infinite size under the Bernoulli trials, and they can compete only through the queue. Hence, we propose a new model as a single server perishable SQI system with queue-dependent service rates and an infinite orbit having $ (s, Q) $ ordering policy. In the rest of this paper, we present a description in section 2, methods of analysis in section 3, waiting time analysis in section 4, economic analysis in section 5 and conclusion in section 6.
2.
Descriptive analysis
2.1. Notations
2.2. Assumptions
This model explores a performance of single server service channel in the perishable QIS. This system consists a finite waiting hall(queue) whose capacity is denoted as $ M $, inventory of $ S $ items for sales and a single server. The server is always busy whenever the current inventory level and number of customers in the queue are positive. Otherwise the server become free. A customer approaches the QIS to purchase their inventory. Suppose any arriving customer finds that the server is busy, they must wait in the queue. The customer approaches QIS for the first time, say primary customer with an intensity $ \lambda_p $ and the primary customer arrival processes follows Poisson process.
This system provides the one more facility to attract their customer in order to avoid the customer lost, called the Orbit(virtual waiting place of infinite capacity). Whenever the arriving customer sees that the queue is fully occupied, they enter into an orbit with the probability $ p $ or leave the system with its complement $ 1-p $. The customer in an orbit, called orbital customer who finds that the queue size is less than $ M $, they immediately enter into the queue with an intensity $ \lambda_r $ under the classical retrial policy. Otherwise they repeatedly tries until get success. This process is known as retrial process. For retrial customer(a customer approaches QIS for the second time), the time interval between any two successive arrivals considered as exponential.
This system provides a well deserved service to their customer through a well experienced server. The server will change the speed of service according to the current queue size in order to reduce the customer waiting time. This service process follows an exponential process with an intensity $ \mu_w $ where $ 1 \leq w \leq M $. The customer receives their inventory only when the time of service completion. Since the service rate is dependent on the queue size, it considered as heterogeneous service rate(not homogeneous).
Further, this system also concentrates on two more things, called as (1) ordering policy and (2) perishable items. Here, the current inventory level of the system getting decreased by the two following process: (ⅰ) service process and (ⅱ) perishable process. Such processes allow us to make a reorder process. This takes place a reorder of $ Q( = S-s) $ items whenever the current inventory level falls into the fixed $ s $. This policy is known as $ (s, Q) $ ordering policy. The reorder process follows an exponential with an intensity $ \beta $.
Generally, not all the items are being perfect until they sold to the customer. The system also consists this natural defectiveness of an item which could be happened by manufacturing defect, warranty expires, damage on handling items, etc., with a classical perishable policy(any one of $ S $ items getting perished) with an intensity $ \gamma $ and this perishable process also follows an exponential process. Stability of the system are to be discussed by the Neuts MGA and the waiting time distribution of both customers are to be derived with Laplace-Stieltjes transform(LST).
Remark 2.1. 1) For the numerical calculations $ \mu_w $ can be defined as $ \mu_w = \mu w^{\alpha} $, where $ 0 \leq \alpha \leq 1 $.
2) If $ \alpha = 0 $, then the model deduced to homogeneous service rate model.
3) If $ \alpha \in (0, 1] $, then the model deduced to non-homogeneous service rate model.
2.3. Matrix building
Let $ P_1(t), P_2(t) $ and $ W(t) $ are the random variables and represent orbit size, present stock level(PSL), and queue size respectively. From the assumptions developed on the birth and death process of a SQIS in the descriptive analysis (subsection 2.2) forms a stochastic process $ \{P(t), t\geq 0\} = \{(P_1(t), P_2(t), W(t)), t\geq 0\} $ at time $ t $ and it is also said to be a continuous-time stochastic process(CTSP) with the state space $ D $ such that
Theorem 2.3.1. In a quasi birth and death process(QBD), the infinitesimal generator matrix, $ P $, with discrete state space $ D $, and the CTSP $ \{P(t), t\geq 0\} $, is defined by
where
and $ u = 0, 1, 2, \cdots, $
Proof: Using the assumptions of proposed model (subsection (2.2)), first consider $ P_{01} $ matrix which contains sub-matrix $ P_0 $ of dimension $ (M+1) $ along the diagonal whose entries are the transition rate of primary arrival enter into the orbit under the probability $ p $ as follows:
from Eq (2.7), the Eqs (2.2) and (2.3) are obtained.
Then the matrices below main diagonal, $ P_{u0} $, where $ u = 1, 2, \cdots, $ has the sub-matrix $ P_u $ of dimension $ (M+1) $ whose entries are the transition rate of retrial arrival enter into the waiting hall with classical retrial policy as follows:
by the Eq (2.8), the Eqs (2.4) and (2.5) are obtained. Then the diagonal matrices $ P_{uu} $ where $ u = 0, 1, 2, \cdots $ of dimension $ (M+1)(S+1) $ whose elements are of the transition rates as follows:
(1) $ \beta $ denotes the rate of reorder transition which follows the $ (s, Q) $ ordering policy,
(2) $ \lambda_p $ be the rate of primary arrival transition enter into the waiting hall,
(3) $ \gamma $ indicates the perishable transition rates which is dependent on the number of present inventory level,
(4) $ \mu $ represents the service rate of the arrivals but it is dependent on the size of the queue
(5) The diagonal element of the $ P_{uu} $ matrices are filled by the sum of all the entries in the corresponding rows of $ P_{uu}, P_{u0} $ and $ P_{01} $ with a negative sign in order to satisfy the sum of all entries in each row of a matrix $ P $ yield zero.
From (1)-(5), the Eq (2.6) is achieved. Hence all the sub-matrices obtained through the respective transitions give the infinitesimal generator matrix $ P $ as in Eq (2.1).
Remark 2.2. From the normalizing condition of the infinitesimal generator matrix $ P $, that is, $ {\bf \Phi} = \left(\Phi^{(0)}, \Phi^{(1)}, \ldots, \right) $ preserves
and one can obtain the solution of $ {\bf \Phi} $'s either using Direct truncation method or MGA. The partition of $ \Phi^{(u)} $ is defined as
3.
Methods of analysis
3.1. Direct truncation method (DTM)
This method is used to evaluate the stationary probability vector $ {\bf \Phi} $ of the CTSP, $ \{P(t), t\geq 0\} $, by truncating the orbit size as the finite instead of infinite size. Suppose $ K $ be the size of orbit in the truncation process, then the arrival a of customer to orbit upon the size $ K $ as considered as lost. However, choosing a sufficiently larger $ K $, one can reduce the customer lost. To get the smaller loss probability for this truncation system, we follow the below Theorem (3.1.1).
Theorem 3.1.1. Suppose $ K $ be the cut-off point for this DTM. Then the modified generator matrix $ \bar{P} $ and the steady state probability vector $ { \Phi^{(K)}} $, generates the truncation point $ K^* $, if
where $ \epsilon $ is an infinitesimal quantity.
Proof: The modified generator matrix for this DTM $ \bar P $ is obtained from the Eq (2.1) as follows:
Now, the corresponding steady state probability vector $ {\bf \Phi} $ can be partitioned into
These $ \Phi $'s can be determined by exploiting the significant structure of the coefficient matrices. We have several method to solve this system referring Stewart [38] such as Gauss-Seidel iterative process and agammaegate / dis-agammaegate iterative algorithm. But there is no proper algorithm to choose $ K $, one may proceed the iterative process by choosing $ K = 1 $ and increase gradually until there is no significant change happen in the elements of $ \bf \Phi $. At such stage, the corresponding $ K $ considered as a $ K^*, $ be the truncation point and it obviously satisfies the norm as in Eq (3.1).
3.2. Matrix geometric approximation (MGA)
3.2.1. Steady state behaviour
This is also a method to find the stationary probability vector $ \Phi $ of the SQIS, $ \{P(t), t\geq 0\} $ by assuming that whenever there exist almost $ N $ customer in the orbit, they follow the classical retrial policy to enter into the waiting hall. Suppose the orbit size exceeds $ N $, they follow the constant retrial policy to go to the waiting hall. This assumption is called MGA and $ N $ is said to be the truncation point of MGA process which is introduced by Neuts [33]. To find the steady state of the considered system $ \{P(t), t\geq 0\} $, we assume $ P_{U0} = P_{N0} $ and $ P_{UU} = P_{NN} $ for all $ U\geq N $ in Eq (2.1). The quasi birth and death process of this system have a repeating structure after a stage $ N $ which is sufficiently large, in particular, if the number of customer in the orbit exceeds $ N $, then the retrial rate of customer remains unchanged. Then the modified generator matrix for the MGA having the below structure:
Theorem 3.2.1. The steady-state probability vector $ \phi = \left(\phi^{(0)}, \phi^{(1)}, \ldots, \phi^{(S)}\right) $ corresponding to the generator $ { G_N} = P_{N0} + P_{NN} + P_{01}, N\geq 1 $ is given by
where
Then $ {\phi^{(Q)}} $ is obtained by solving
and
Proof: The normalizing condition to the generator matrix $ G_N $ is defined by
Here,
where
The Eq (3.8a) yields the set of equations:
On solving the set of Eqs (3.9a) and (3.9b), we get an Eq (3.5) and using Eqs (3.5) and (3.9c), the equation (3.6) is obtained. The Eq (3.8b) produces an Eq (3.7). Hence, $ \phi^{(Q)} $, is obtained by solving (3.6) and (3.7).
Note: The partition of $ \phi^{(v)} $ is defined as
Theorem 3.2.2. The stability condition of the system at truncation point $ N $ is given by
where $ k_1 = \sum\limits_{v = 0}^{S}\phi^{(v, M)} $ and $ k_2 = \sum\limits_{v = 0}^{S}\sum\limits_{w = 1}^{M}\phi^{(v, w)}N $.
Proof: By Neuts [33] stability condition and the matrices $ P_{01} $ and $ P_{N0} $, we have
Now, exploiting the structure $ P_{01} $ and $ P_{N0} $,
By the partition of $ \phi^{(v)} $ and exploiting $ P_0 $ and $ P_N $,
Hence, the Eq (3.10) is obtained as desired.
Remark 3.1. (1) Using (3.10), we get, $ \dfrac{k_1 p\lambda_p}{k_2 \lambda_r} < 1. $
(2) If $ \dfrac{k_1}{k_2} = k(say) $, then $ \dfrac{\lambda_p}{\lambda_r} < \dfrac{1}{kp}. $
Remark 3.2. The most interesting factor in the stability condition is that it is independent of $ \mu $ and $ \beta $.
Remark 3.3. Using Theorems (3.2.1) and (3.2.2), the rate matrix $ P $ in Eq (2.1) has Markov process $ \{(P(t), t \geq 0\} $ with the state space $ D $ is regular. Hence the limiting probability distribution
exists and it is never dependent of initial state.
Theorem 3.2.3.. Due to the specific structure of $ P $ using the vector $ {\bf \Phi} $ and $ R $ can be determined by
where $ R $ is the minimal non-negative solution of the matrix quadratic equation.
Proof: The stationary probability distribution exists and is given by Eqs (2.13a) and (2.13b). We assume
by the stability of $ R $ which has the spectral radius(supremum of the absolute values of the eigen values) less than one.
Then, we get
Then $ R $ is a minimal non-negative solution of matrix quadratic Eq (3.11) and we assume $ R $ matrix is of the form
This $ R $ has only $ (S+1) $ non zero rows of dimension $ (S+1)(M+1) $.
Now, due to the specified structure of $ P_{01} $, the structure of block matrix $ R_{vv'} $ is of the form
which is a square matrix of dimension $ (M+1) $.
Now, exploiting the co-efficient matrices $ P_{N0}, P_{NN}, P_{01} $ with $ R^2 $ and $ R $ equating with 0, we obtain a system of equations as follows:
Case (1): If $ v = 0, 1, \cdots S $ and $ w = 0, $ we have three sub-cases such as given below:
(ⅰ) $ \; v' = 0, 1, \cdots, s, $
(ⅱ) $ v' = Q, Q+1, \cdots, S-1, $
(ⅲ) $ v' = S, $
Case (2): If $ v = 0, 1, \cdots, S $ and $ w = 1, 2, \cdots, M $, we have three sub-cases such as given below:
(ⅰ) $ v' = 0, 1, \cdots, s, $
(ⅱ) $ v' = Q, Q+1, \cdots, S-1, $
(ⅲ) $ v' = S, $
On solving the set of non-linear equations, the $ R $ matrix is obtained as in (3.12) and (3.13).
Remark 3.4. The matrix $ R $ can also be obtained using Logarithmic Reduction Algorithm(LRA) which is introduced by Latouche and Ramaswamy [28]:
Step (ⅰ): $ R_1 \leftarrow (-P_{NN})^{-1}P_{01}, R_2 \leftarrow (-P_{NN})^{-1}P_{N0}, R_3 = R_2 $ and $ R_4 = R_1 $
Step (ⅱ):
Continue Step (ⅰ) until $ \lVert {\bf e} - R_3{\bf e} \rVert_{\infty} < \epsilon. $
Step (ⅲ): $ R = -P_{01}(P_{NN}+P_{01}R_3)^{-1}. $
Theorem 3.2.4. From the rate matrix $ P $ the vector $ {\bf \Phi} $ can be determined by
where $ R $ is defined in Eq (3.11) in Theorem (3.2.3) and the vector $ \Phi^{(u)}, u\geq 0 $
where
$ X^{(0)} $ can be obtained by solving
Proof: The sub-vector $ { (\Phi^{(0)}, \Phi^{(1)}, \dots, \Phi^{(N-1)}) } $ and the block partitioned matrix of $ P $ satisfies the following relation
Using equations (3.18a) and (3.18b) recursively, we obtain $ { \Phi^{(0)}} = { \Phi^{(1)}}P_{10}(-P_{0}')^{-1}\; \; {\rm{with}}\; \; P_0'$ = $P_{00}, { \Phi^{(1)}} = { \Phi^{(2)}}P_{20}(-P_{1}')^{-1} \; \; {\rm{with}} \; \; P_1'$ = $(P_{11}+P_{10}(-P_{0}')^{-1}P_{01})$, ${ \Phi^{(2)}} = { \Phi^{(3)}}P_{30}(-P_{2}')^{-1} \; \; {\rm{with}} \; \; P_2'$ = $(P_{22}+P_{20}(-P_{1}')^{-1}P_{01}) $ and so on up to $ N $ times.
Hence, we conclude that,
where
To find the sub-vector $ ({\Phi^{(N)}, \Phi^{(N+1)}, \Phi^{(N+2)} \dots}) $, we apply block Gaussian elimination method. The sub-vector $ ({ \Phi^{(N)}, \Phi^{(N+1)}, \Phi^{(N+2)} \dots}) $ can be determined by
Assume,
From (3.20), we get
Applying the Eq (3.22) in (3.23) and (3.14) along with $ \sum\limits_{i = 0}^{\infty}{ X^{(i)}\bf e} $ = 1, the Eqs (3.17a) and (3.17b) are obtained. The unique solution of $ X^{(0)} $ is found by solving the Eqs (3.17a) and (3.17b), and substituting it in (3.22), we get
Again by (3.19) and (3.22),
Therefore, combining (3.24) and (3.25), the Eq (3.15) is obtained as desired. And $ \sigma $ is found by applying the vector $ {\bf \Phi} $ in the Eq (2.13b).
Corollary 3.2.1. The mean inventory level(MIL) of the SQIS in the steady state, using the vector $ {\bf \Phi} $ along with positive inventory is defined by
Corollary 3.2.2. Suppose there are $ (s+1) $ items in the PSL, due to either a service can be completed or an item may be perished, then the PSL dropped into the level $ s $, we start the reorder process. The mean reorder rate(MRR) of the SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.3. The PSL may be diminished by perishing items. The mean perishable rate(MPR) of the SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.4. In the waiting hall, there should be at least one customer has to wait for getting a service and the PSL need not be positive. The mean customer in the queue(MCQ) of the SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.5. In the orbit, there should be at least one customer has to wait for entering into the waiting hall. The mean customer in the orbit(MCO) of the SQIS in steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.6. Suppose the waiting hall is full, the new arrival has the choice to take the decision to become lost. The expected primary customer lost in the queue(EPL) of the SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.7. The possible chances of an orbital customer for trying to enter into the waiting hall, called overall rate of retrial(ORR). The ORR of SQIS in steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.8. The possible successful chances of an orbital customer to enter into the waiting hall, called successful rate of retrial(SRR). The SRR of SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.9. The possible chances of any customer to enter into the waiting hall, say expected customer enter into queue(ECEQ). The ECEQ of SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.10. The expectation of a customer enter into the orbit, say ECEO. The ECEO of SQIS in the steady state, using the vector $ {\bf \Phi} $ is defined by
Corollary 3.2.11. The fraction of successful rate of retrial(FSSR) is defined by the ratio of ORR and SRR and is given by
4.
Waiting time analysis
The time interval between an epoch of arrival of a customer enter into the waiting hall and the instant at which their time of service completion, called waiting time($ WT $). We discuss the $ WT $ of a customer in the queue as well as orbit individually using LST. By nature, we restrict the orbit size to finite for finding the waiting time of the orbital customer as follows:
We represent $ W_p $ and $ W_o $ are the continuous time random variables to denote the $ WT $ of a customer in queue and orbit.
4.1. $ WT $ of a customer in queue
To find a $ WT $ of a customer in the queue, the state space $ D_{1}^{} $ is redefined and is given by, $ D_{2} = \{(u, v, w) : u = 0, 1, \cdots, L; \quad v = 0, 1, \cdots, S; \quad w = 1, 2, \cdots, M\} $
Theorem 4.1.1. The probability of a customer does not wait into the queue is considered as
Proof: Since the sum of probability of zero and positive waiting time is 1, we have
Clearly, the probability of positive waiting time of customer in the queue can be determined as
The Eq (4.3) can be found using Theorem (3.2.4) and substitute in equation (4.2) we get the stated result as desired.
To enable $ WT $ distribution of $ W_p $, we shall define some complementary variables. Suppose that the QIS is at state $ (u, v, w) $, $ w > 0 $ at an arbitrary time $ t $,
1). $ W_p(u, v, w) $ be the time until chosen customer become satisfied.
2). LST of $ W_p(u, v, w) $ is $ W_p^*(u, v, w)(x) $ and we denote $ W_p $ by $ W_p^*(x) $.
3). $ W_p^*(x) = E[e^{xW_P}] $ LST of unconditional waiting time(UWT).
4). $ W_p^*(u, v, w)(x) = E[e^{xW_P(u, v, w)}] $ LST of conditional waiting time(CWT).
Theorem 4.1.2. The LST $\{ W_p^*(u, v, w)(x), (u, v, w)\in D_2^c $ where $ D_2^c = D_2\cup\{c\}\} $ satisfy the following system
$ Z_p(x) = (A-xI) $, the matrix $ A $ is obtained from $ P $ by removing the following state $ (u, v, 0), 0 \leq u \leq K, 1\leq v \leq S $ and $ \{c\} $ be the absorbing state and the absorption occurs if the primary customer is satisfied.
Proof: To obtain the CWT, we apply first step analysis as follows:
For $ 0 \leq u \leq L, v = 0, 1\leq w \leq M $
$ \rm{ where}\; \; \; a = (x+\bar\delta_{Mw}\lambda_p+\beta+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p) $
For $ 0\leq u \leq L, 1 \leq v \leq S, 1\leq w \leq M $
where $ b = (x+\bar\delta_{Mv}\lambda_p+H(s-v)\beta+v\gamma +\mu_w+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p). $
From the linear system of Eqs (4.5) and (4.6), we obtain a co-efficient matrix of the unknowns as a block tri-diagonal yields a stated result.
Theorem 4.1.3. The $ n^{th} $ moments of CWT is given by
and
Proof: On exploring the set of equations which are obtained in Theorem (4.1.2), we get a recursive algorithm to find a CWT and UWT.
Now, we differentiate the Eqs (4.5) and (4.6) for $ (n+1) $ times and computing at $ x = 0 $, we have, for, $ 0 \leq u \leq L, \; \; \; v = 0, \; \; \; 1\leq w \leq M, $
$ \rm{ where}\; \; \; a = (x+\bar\delta_{Mw}\lambda_p+\beta+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p). $
for $ 0\leq u \leq L, \; \; \; 1 \leq v \leq S, \; \; \; 1\leq w \leq M $
where $ b = (x+\bar\delta_{Mw}\lambda_p+H(s-v)\beta+v\gamma +\mu_w+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p). $
With reference to equations (4.9) and (4.10), one can examine the unknowns $ E[W_p^{n+1}(u, v, w)] $ in terms of moments having one order less. On setting $ n = 0 $, we attain the desired moments of particular order in an algorithmic way.
Theorem 4.1.4. The LST of UWT of a customer in the queue is given by
Proof: Using PASTA(Poisson arrival see time averages) property, one can obtain the LST of $ W_p $ as follows:
using the expression (4.12), we get the stated result. By referring Euler and Post-Widder algorithms in Abatt and Whitt [1] for the numerical inversion of (4.11), $ W_p $ is obtained.
Corollary 4.1.1. 1. The $ n^{th} $ moments of UWT, using Theorem (4.1.4), is given by
Proof: To evaluate the moments of $ W_p $, we differentiate Theorem (4.1.4), $ n $ times and evaluate at $ x = 0 $, we get the desired result which gives the $ n^{th} $ moments of UWT in terms of the CWT of same order.
Corollary 4.1.2. The expected waiting time of a customer in the queue is defined by
proof: Using equation (4.1.1) in Corollary (12), and substitute $ n = 1 $, we get the desired result as in (4.14).
4.2. $ WT $ of orbital customer
To find a $ WT $ of a customer in the orbit, the state space $ D_{1}^{} $ is redefined and is given by, $ D_{3} = \{(u, v, w) : u = 1, \cdots, L; \quad v = 0, 1, \cdots, S; \quad w = 0, 1, \cdots, M\} $
Theorem 4.2.1. The probability of an orbital customer does not wait into the orbit is given by
where $ b_1 = \sum\limits_{u = 1}^{L-1}\sum\limits_{v = 0}^{S}\Phi^{(u, v, M)} $
Proof: Since the sum of probability of zero and positive waiting time is 1, we have
Clearly, the probability of positive $ WT $ of orbital customer can be determined as
The Eq (4.17) can be found easily using Theorem (3.2.4) and substitute in Eq (4.16) we get the stated result as desired in (4.15).
To enable the distribution of $ W_o $, we shall define some complementary variables. Suppose that the QIS is at state $ (u, v, w), u > 0 $ at an arbitrary time $ t $,
1). $ W_o(u, v, w) $ be the time until chosen customer become satisfied.
2). LST of $ W_o(u, v, w) $ is $ (u, v, w)(x) $ and we denote $ W_o $ by $ W_o^*(x) $.
3). $ W_o^*(x) = E[e^{xW_o}] $ LST of UWT.
4). $ W_o^*(u, v, w)(x) = E[e^{xW_o(u, v, w)}] $ LST of CWT.
Theorem 4.2.2. The LST $\{ W_o^*(u, v, w)(x), (u, v, w)\in D_3^d $ where $ D_3^d = D_3\cup\{d\}\} $ satisfy the following system
$ Z_o(x) = (B-xI) $, the matrix $ B $ is derived from $ P $ by deleting the following state $ (0, v, w), \; \; 0 \leq v \leq S, \; \; 0\leq w \leq M $ and $ \{d\} $ be the absorbing state and the absorption appears if the orbital customer enters into the waiting hall.
Proof: To analyze the CWT, we apply first step analysis as follows:
for $ 1 \leq u \leq L, \; \; \; v = 0, \; \; \; 0\leq w \leq M $
$ \rm{ where}\; \; \; a = (x+\bar\delta_{Mw}\lambda_p+\beta+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p) $,
for $ 1\leq u \leq L, \; \; \; 0 \leq v \leq S, \; \; \; 0\leq w \leq M $
where, $ b = (x+\bar\delta_{Mv}\lambda_p+H(s-v)\beta+v\gamma +\mu_w+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p). $
From the equations (4.19) and (4.20) we attain a co-efficient matrix of the unknowns as a block tri-diagonal yields a stated result as in (4.18).
Theorem 4.2.3. The $ n^{th} $ moments of conditional waiting time is given by
and
Proof: Linear equations which are obtained in Theorem (4.2.2), we get a recursive algorithm to find a conditional and unconditional waiting times.
Now, we differentiate the equations (4.19) and (4.20) for $ (n+1) $ times and setting at $ x = 0 $, we have, For $ 1 \leq u \leq L, \; \; \; v = 0, \; \; \; 0\leq w \leq M $
$ \rm{ where}\; \; \; a = (x+\bar\delta_{Mw}\lambda_p+\beta+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p) $
For $ 1\leq u \leq L, 1 \leq v \leq S, 0\leq w \leq M $
where, $ b = (x+\bar\delta_{Mw}\lambda_p+H(s-v)\beta+v\gamma +\mu_w+u\lambda_r+\delta_{Mw}\bar\delta_{Lu}p\lambda_p) $
With reference to Eqs (4.23) and (4.24), one can determine the unknowns $ E[W_p^{n+1}(u, v, w)] $ in terms of moments of one order less. On setting $ n = 0 $, we obtain the desired moments of particular order in an algorithmic way.
Theorem 4.2.4. The LST of UWT of orbital customer is given by
Proof: Using PASTA property, one can obtain the LS transform of $ W_o $ as follows:
using the expressions (4.26), we get the stated result. By considering Euler and Post-Widder algorithms in Abatt and Whitt [1] for the numerical inversion of (4.25), we obtain $ W_o $.
Corollary 4.2.1. 1. The $ n^{th} $ moments of UWT, using Theorem (4.2.4), is given by
Proof: To evaluate the moments of $ W_o $, we differentiate Theorem (4.2.4), $ n $ times and evaluate at $ x = 0 $, we get the desired result which gives the $ n^{th} $ moments of UWT in terms of the CWT of the same order.
Corollary 4.2.2. The expected waiting time of a orbital customer is defined by
proof: Using Eq (4.27) in Corollary (4.2.1) and substitute $ n = 1 $, we get the desired result as in (4.28).
5.
Economical analysis
Here, we discuss the feasibility of a proposed model through the system characteristics and sufficient economical illustrations. The expected total cost(ETC) is given by
where
$ \; \; \; \; \; \; C_h $- holding cost per unit at time $ t $.
$ \; \; \; \; \; \; C_s $- set up cost per unit at time $ t $.
$ \; \; \; \; \; \; C_p $- perishable cost per unit at time $ t $.
$ \; \; \; \; \; \; C_{pl} $- primary customer cost per customer at time $ t $.
$ \; \; \; \; \; \; C_{wp} $- waiting cost of a customer in the queue at time $ t $.
$ \; \; \; \; \; \; C_{wo} $- waiting cost of a customer in the orbit at time $ t $.
To analyze numerically, we first fix the parameter as follows: $ S = 19, s = 8, \lambda_p = 0.4, \lambda_r = 0.002, \beta = 0.6, \alpha = 0.06, \gamma = 0.005, p = 0.3, M = 7 $ and $ \mu = 8 $ and the cost values are $ C_h = 0.01. C_s = 0.02, C_p = 0.01, C_{wp} = 0.5 $ and $ C_{wo} = 0.4 $. The truncated point for the matrix geometric method is $ N = 80 $.
Note: Under the behaviour of $ \alpha $, we can have a classification of the proposed model as follows:
1) If $ \alpha = 0 $, then the model become a single server SQI system with homogeneous service rates.
2) If $ 0 < \alpha < 1 $, then this is a single server SQI system non-homogeneous service rates.
3) If $ \alpha = 1 $, then it will be a single server SQI system with linear service rates.
Example 1:
In Table 1, we discuss the local convex point on the ETC varying $ S $ and $ s $. We observe that the minimum ETC exist in each row and column. Here, the minimum ETC in each row and column are differentiated by underlined numbers and bold numbers respectively. The intersection of underlined and bold numbers, called optimum point and indicated by $ (S^*, s^*) $ where $ S^* = 19 $ is the optimum PSL and $ s^* = 8 $ is the optimum reorder level and they gave a optimum total cost $ ETC^* = 4.711953 $.
Example 2: (Investigation on $ N $)
We investigate the truncation point in the MGA by Neuts-Rao algorithms varying parameters in Tables 2 and 3.
$ \bullet $ The value of $ N $ decreases as $ \alpha $ increases along with the increasing service rate $ \mu $.
$ \bullet $ Whenever $ \lambda_r $ increases $ N $ decreases relating to the increasing service rate.
$ \bullet $ Generally, if $ \mu $ increases, one can observe from the Table 1, the truncation point $ N $ decreases, this SQI system become stable quickly.
$ \bullet $ We can observe that, $ p $ is high, then $ N $ become significantly larger, that is they are directly proportional and highly sensitive.
$ \bullet $ If $ \beta $ increases, then $ N $ decreases. Suppose $ \alpha $ and $ \beta $ are small, then $ N $ is highly differ under $ \mu $.
$ \bullet $ In Tables 2 and 3, we assure that, $ \lambda_r $ is small, $ N $ will be very larger.
$ \bullet $ The appearance of truncation point become small, if we increase the $ \alpha, \lambda_r $ and $ \mu $ but $ p $ should be decreased.
Example 3: Investigation of fraction of successful rate of retrial(FSRR)
$ \bullet $ From Table 4, one can observe that, although there is an increase in each $ \lambda_p $ for each $ \mu $, FSRR decreases if each $ \alpha $, but the very notable point is FSRR increases if $ \alpha $ increases. Hence, $ \alpha $ become a decision factor to increase the FSRR.
$ \bullet $ Meanwhile, there is an increase in $ \lambda_r $, FSRR will increase for each $ \alpha $ and $ \mu $ because when we increase $ \mu $, MCQ will decrease and it cause the increase of FSRR.
$ \bullet $ It is interesting to observe that if $ \gamma $ increases, FSRR will increases for every $ \alpha, \lambda_p, \lambda_r $ and $ \mu $. However. the behaviour of $ \gamma $ never affect the increase of FSRR because $ \gamma $ and $ \mu $ diminished the PSL to $ s $, then replenishment should be placed immediately.
$ \bullet $ The parameters $ \lambda_p $ and $ \mu $ behave contrary to each other on the FSRR with respect to $ \alpha $.
$ \bullet $ If we increase both $ \lambda_p $ and $ \lambda_r $, then the FSRR decreases considerably.
$ \bullet $ On comparing $ \lambda_r $ and $ \mu $, we note that, both are behave likely to each other for each $ \alpha $ on FSRR.
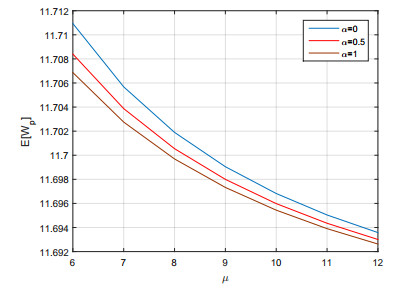
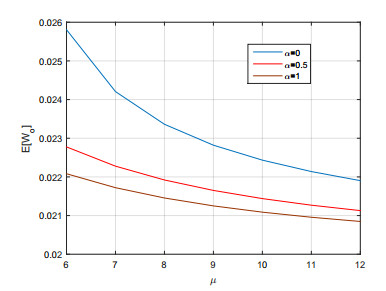
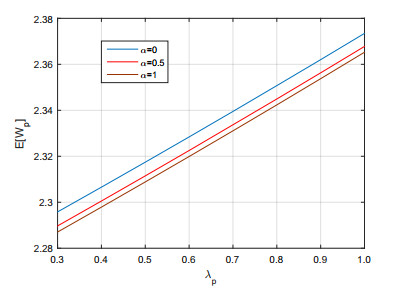
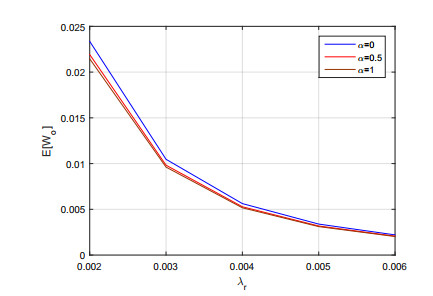
Example 4: The $ E[W_p] $ and $ E[W_o] $ had been discussed in Figure 1 and Figure 2 respectively.
$ \bullet $ Figure 1 shows that $ WT $ of a customer in the queue decreases as $ \mu $ increases. As we predicted that the case $ \alpha = 0 $(homogeneous service rate) has higher $ WT $ than the case $ \alpha = 0.5 $ and $ \alpha = 1 $. Then the aim of model can be achieved.
$ \bullet $ Figure 2 explains $ E[W_o] $ with the non-homogeneous service rates. We observe that $ E[W_o] $ decreases when we increase $ \mu $, that is figure 1 and 2 have shown that $ WT $ and service rates are inversely proportional to each other. In particular, $ \alpha = 0.5 $ gave the predicted result when we analyzing both $ \alpha = 0 $ and $ \alpha = 1 $.
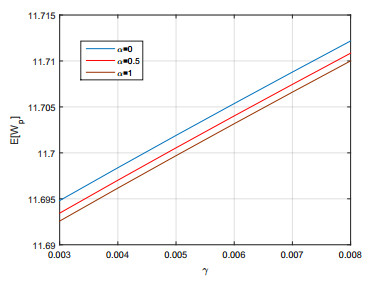
$ \bullet $ Figure 3 depicts that the expected $ WT $ of a queue is increases when the perishable rate $ \gamma $ increases. Clearly, $ \alpha = 0 $ gave the higher $ WT $ than the other cases $ \alpha = 0.5 $ and $ \alpha = 1 $.
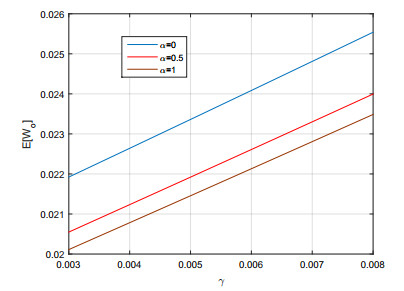
$ \bullet $ Figure 4 shows that the $ WT $ of orbital customer also increases if we increase $ \gamma $ and here also, $ \alpha = 0.5 $ gave the feasible result.
$ \bullet $ In Figure 5 depicted that $ E[W_p] $ increases when we increase $ \lambda_p $ for each $ \alpha $. When $ \alpha = 0 $, $ E[W_p] $ is higher the other $ \alpha $'s.
$ \bullet $ In Figure 6 depicted that $ E[W_o] $ decreases when we increase $ \lambda_r $ for each $ \alpha $. When the case $ \alpha = 0 $, $ E[W_o] $ is greater than the other two cases.
Example 5:
Table 5 shows that the domination of $ p $ and $ \lambda_p $ on the MCQ and MCO.
$ \bullet $ Whenever we increase $ \lambda_p $, we can observe the increased MCQ as well as MCO. However it is interesting to note that both MCQ and MCO decreases as $ \alpha $ increases.
$ \bullet $ The remarkable thing is, on increasing $ p $, it never affect the MCQ but the domination of $ p $ reflects in MCO towards increasing.
$ \bullet $ In Table 6, when $ \lambda_r $ increases, MCQ increases where as MCO decreases and both has been decreased as $ \alpha $ increases, this is because due to faster service, MCQ will decrease which cause the decreasing MCO.
$ \bullet $ Here, when we increase $ p $, both MCQ and MCO will increase.
$ \bullet $ On comparing Table 5 and Table 6, we can realize the significant of $ p $ with $ \lambda_p $ is that the MCQ is unchanged and $ \lambda_r $ has the considerable increment in MCQ.
Example 6: Investigation of $ \beta $ and $ \gamma $ on ETC with $ \mu $ and $ \alpha $} We investigate the influence of the parameters $ \beta, \gamma, \mu $ and $ \alpha $ on the ETC in Table 7.
$ \bullet $ As $ \mu $ increases, the corresponding ETC decreases, in particular, for every increasing $ \alpha $, there can be seen that the ETC decreases.
$ \bullet $ As we predicted earlier, the increase of $ \gamma $ provide the increasing ETC considerably for each $ \mu $ and $ \alpha $.
$ \bullet $ Although the $ \gamma $ sustains the ETC in an increasing manner, $ \beta $ dominates the ETC in a decreasing manner.
$ \bullet $ However, when we increase $ \beta, \gamma, \mu $ and $ \alpha $ at time $ t $, we get a minimized ETC, that is the optimum ETC is achieved.
$ \bullet $ In the case $ \alpha = 0 $, the ETC always larger when we comparing other $ \alpha $'s and Table 7 assures that the choice of $ \alpha $ plays the key role to provide the best optimum ETC.
$ \bullet $ Here, the impact of $ \gamma $ and $ \beta $ on ETC are contrary to each other where as $ \beta $ and $ \mu $ behave the same but $ \gamma $ and $ \mu $ are reacting against to each other.
6.
Conclusions and future work
The performance of a single server system in a perishable SQIS is investigated with the queue-dependent service rate. The stability condition and stationary probability vector of the proposed model is derived by the Neuts MGA. The waiting time of both primary and an orbital customer are constructed by the LST. The illustrated numerical examples explored the impact of queue-dependent service rate. With the system performance measures, the discussion made in the numerical section proved that queue-dependent service rate(non-homogeneous service rate) is much better than the homogeneous service rate. In all the examples, the case $ \alpha = 0 $ and $ \alpha \in (0, 1] $ are distinguished properly. Since the paper thoroughly analyzes the homogeneous and non-homogeneous service rates, it will give the generalized result for both cases(homogeneous and non-homogeneous service rates). Due to the increase of the service speed, number of customer serviced in the system is increased. This leads not only a more sale and profit to the management also this will reduce the impatient mindset of a customer. If a customer getting service quickly with the satisfaction, they will prefer the same system for the next purchase. Subsequently, the number of arriving customer to the system will increase day-by-day. Most of the inventory management purely dependent on the customer only. In this competitive society, every management wants to survive with a wealthy growth. For this growth, the concept made in this paper, will be much helpful to all the inventory management.
In future, this model can be extended into a multi server SQIS system involving additional service for a feedback customer of an infinite queue size.
Acknowledgments
The corresponding author thanks to Phuket Rajabhat University, Phuket Thailand-83000 for supporting this research. The authors would like to express their gratitude to the anonymous referees for precious remarks and suggestions that resulted in notable improvement and the excellence of this paper.
Conflicts of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.









 DownLoad:
DownLoad: