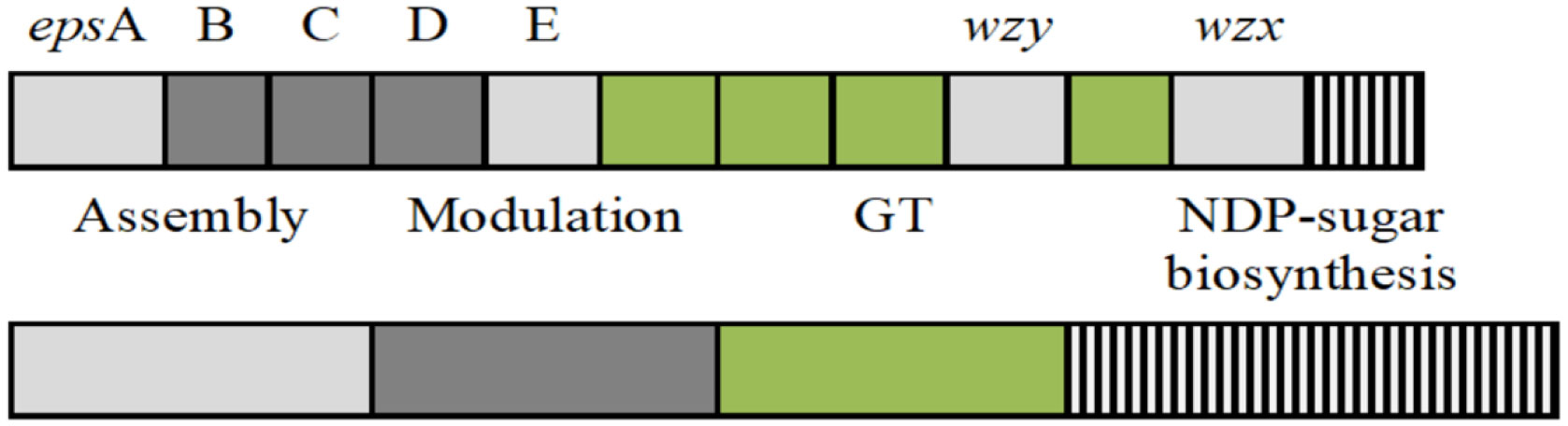
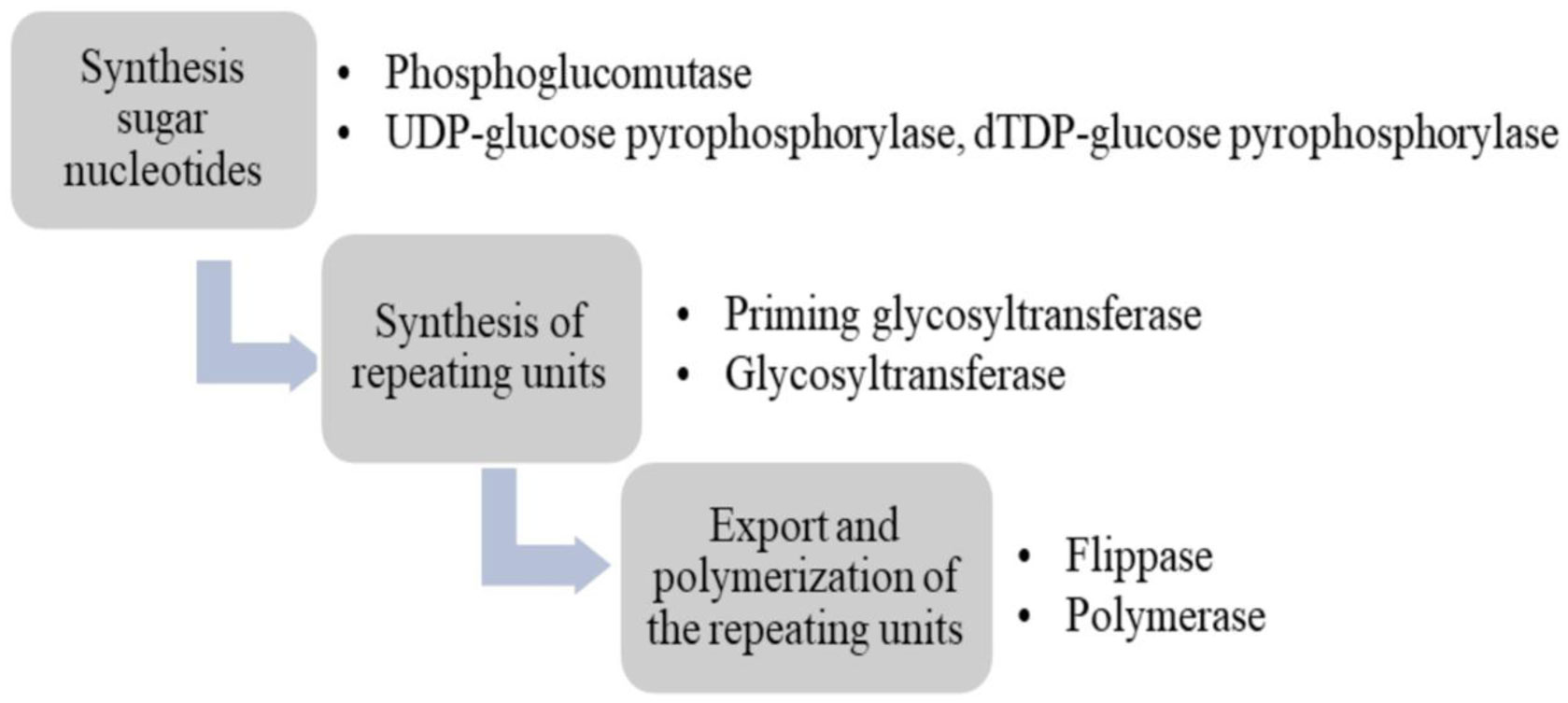
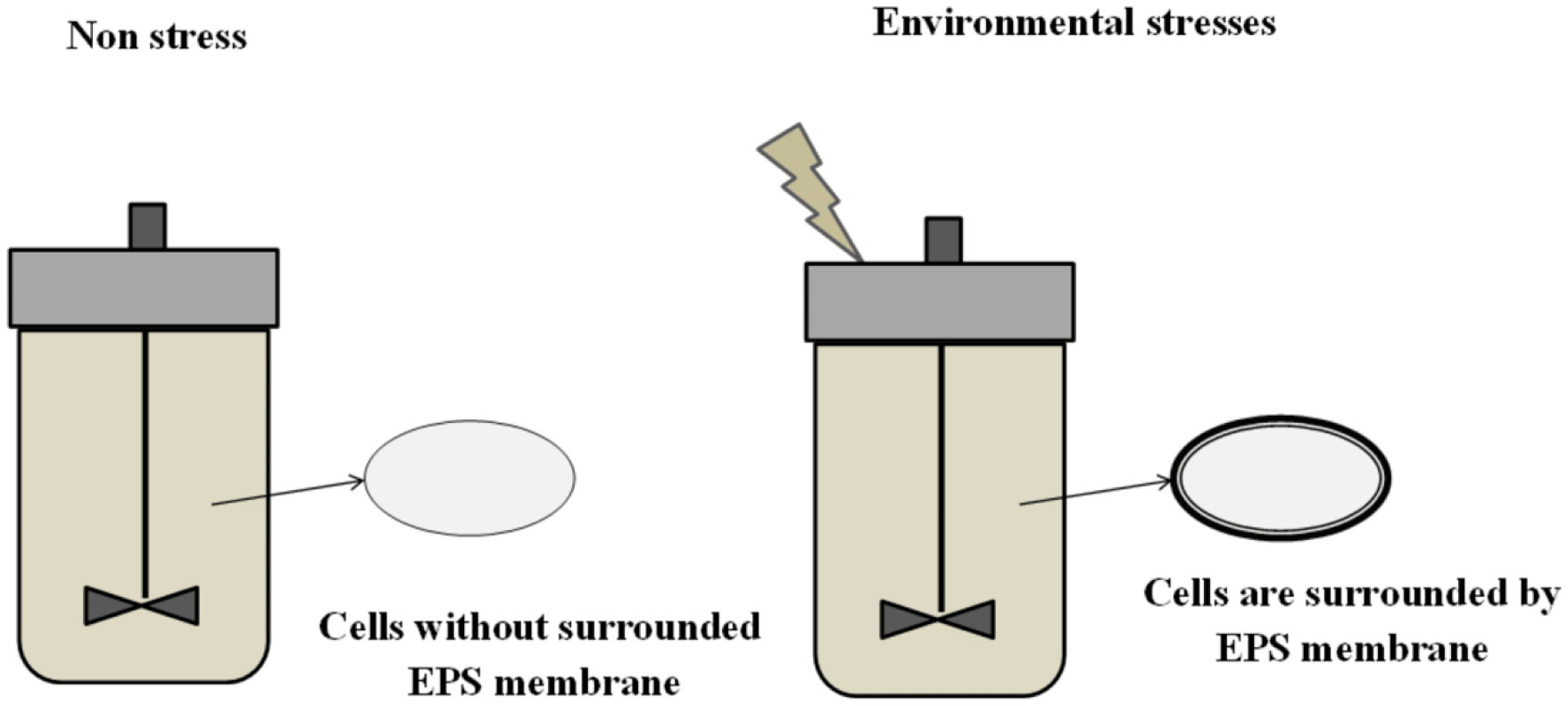
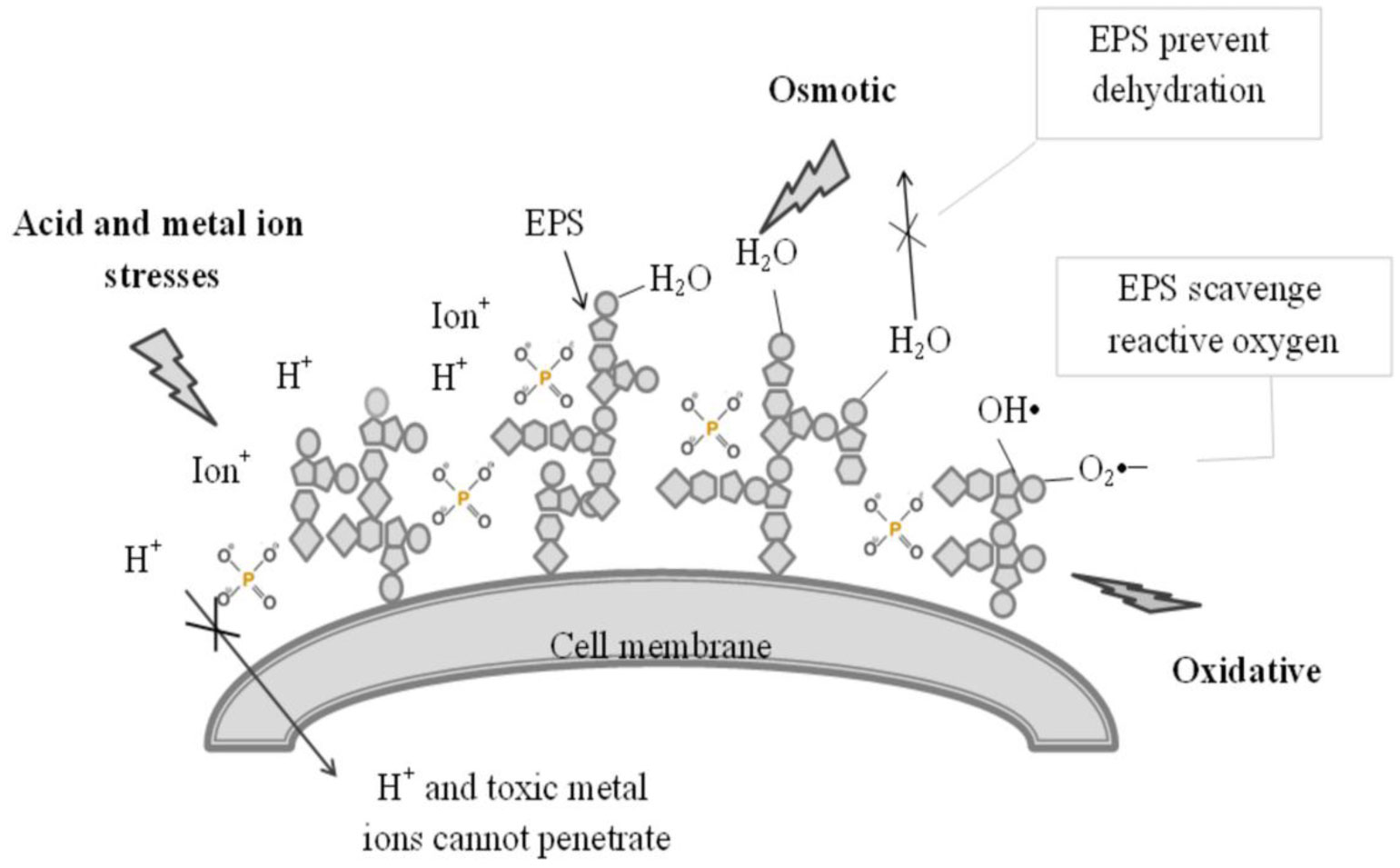
Exopolysaccharide production by lactic acid bacteria: the manipulation of environmental stresses for industrial applications

1.   Introduction and main results

In this paper, we are concerned with the existence of positive solutions for the following Kirchhoff equation in $\mathbb{R}^N$:

having prescribed mass

where $c > 0$ is prescribed, $N\geqslant4$, $\mu\in\mathbb{R}$, $a > 0$ and $b > 0$ are positive parameters, $2 < q < p\leqslant 2^*$, $2^*$ is the Sobolev critical exponent, $2^* = \frac{2N}{N-2}$ if $N\geqslant 3$, $2^* = +\infty$ if $N = 1, 2$.

Problem $(\mathcal{K})$ is analogous to the stationary case of the following equation:

where $\Omega\subset \mathbb{R}^N$ is a smooth domain, $u$ stands for the displacement, $f\in C(\Omega\times \mathbb{R}, \mathbb{R})$ is the external force, $a$ is the initial tension and $b$ is related to the intrinsic properties of the string. Such a hyperbolic equation is a general version of the following equations

proposed by Kirchhoff ^[1] as an extension of the classical D'Alembert's wave equation for transversal oscillations of a stretched string, particularly, taking into account the subsequent change in string length during the oscillations. In addition, nonlocal problems similar to $(\mathcal{K})$ also arise in biological systems that can be applied to describe the growth and movement of a specific species^[2]. In this situation, $u$ may describe a process that depends on the average of itself, for example, the population density.

After the pioneering work of ^[3], problem $(\mathcal{K})$ with fixed $\lambda$, or even with an additional external and fixed potential $V(x)$ has been extensively studied in the last ten years, see e.g., ^[2,4,5,6,7] and the references therein. Compared with Schrödinger type problem, the main difficulty for Kirchhoff type problem is how to obtain the compactness of the Palais-Smale sequence. Tang-Cheng ^[5] proposed a new approach to recover the compactness for the Palais-Smale sequences. Tang-Chen ^[6] proposed a new approach to recover the compactness for the minimizing sequences.

In this situation, it is well known that solutions of $(\mathcal{K})$ are the critical points of the associated energy functional

In the present paper, motivated by the fact that physicists are more interested in solutions satisfying the prescribed mass (1.1) which are called normalized solutions, we search for solutions of $(\mathcal{K})$ having a prescribed $L^2$-norm. This type of solutions can be obtained as a constrained critical point of the following functional

on the $L^2$-sphere

where the Hilbert space $H^1(\mathbb{R}^N)$ is defined as

with the inner product and norm given by

When $a = 1, b = \mu = 0$, problem $(\mathcal{K})$ is reduced to the classical Schrödinger equation with pure power nonlinearity:

where $N\geqslant1$, $p\in(2, 2^*)$. It is well known that the $L^2$-critical exponent

plays an important role in dealing with the Schrödinger equation. For the pure power nonlinearity $|u|^{p-2}u$ satisfying $L^2$-subcritical growth, i.e., $2 < p < \bar{p}$, then the energy functional associated to (1.3) is bounded from below. Cazenave-Lions ^[8] and Shibata ^[9] proved the existence of normalized solution via minimizing methods. We also refer the reader to the references ^[10,11]. While for $L^2$-supercritical and Sobolev subcritical case $\bar{p} < p < 2^*$, the energy functional associated to (1.3) cannot be minimized on the $L^2$-sphere $S(c)$. Jeanjean ^[12] proved for the first time the existence of a normalized solution in this case. When $a = 1, b = 0$ and $\mu\neq0$, problem $(\mathcal{K})$ is reduced to the Schrödinger equation with combined power nonlinearities:

where $N\geqslant1$, $\mu\in \mathbb{R}$, the nonlinearity satisfies the mixed growth, i.e., $2 < q\leqslant\bar{p}\leqslant p\leqslant 2^*$. Recently, a very complete analysis of the various cases that may occur for (1.4), depending on the values of $p$ and $q$, has been studied exhaustively in ^[13,14]. The paper ^[13] deals with the Sobolev subcritical case and ^[14] with Sobolev critical case.

It is well known that two exponents play a special role for existence and properties of the solutions for the Kirchhoff equation, in addition to the energy (Sobolev) critical exponent

we have the mass ($L^2$-) critical one

The mass and energy critical exponents define the thresholds for the existence of global minima and $H^1$-solution, respectively. It follows from

that $N\leqslant3$. For this reason possibly, there are many results on normalized solution of Kirchhoff problem in low dimensions $N\leqslant3$, we refer the readers to ^{[15,16,17,18,19]} and references therein. Howover, to the best of our knowledge, the Kirchhoff type problems with prescribed $L^2$-norm in high dimensions $N\geqslant4$ remains unsolved in the existing literature. This motivates us to study this kind of problem in the present paper for the case of $N = 4, 6, 8$. When $N \geqslant 4$, since $2^*\leqslant 4$, it is difficult to study the geometric structure of the energy functional. Also, it is not easy to prove the boundedness and convergence of the Palais-Smale sequence.

Particularly, in dimension $N = 4$, there is a special phenomenon for Kirchhoff problems that will never happen for the Schrödinger equation, i.e., the mass critical exponent $2+\frac{8}{N}$ is the same as the energy critical exponent $2^* = \frac{2N}{N-2}$. We call this special phenomenon the new doubly critical case, which is first considered to happen for the Kirchhoff equation in this paper. For other types of double critical exponents, we refer the readers to ^[20,21] and references therein. Moreover, it is worth mentioning that when $N\geqslant4$, if we consider the mass ($L^2$-) supercritical case, the problem will no longer have a variational structure owing to the fact that the mass critical exponent is larger than the energy critical exponent. Thus, there will be no mass supercritical and mixed cases.

Motivated by the works mentioned above, our contribution in this paper is to find appropriate transformation to get the following equivalent system of $(\mathcal{K})$ in different dimension spaces with respect to $(v, \beta)\in \mathbb{R}^{N} \times \mathbb{R}^{+}$:

where

$\theta = \frac{1}{3}\arccos\left(-\frac{3}{2}\sqrt{3d}a\right)\in\left(\frac{\pi}{6}, \frac{\pi}{3}\right)$, and

We take two steps to get the existence of solutions for system $\left(\mathcal{P}_{N}\right)$. First, we solve the equation

for the special given $\tilde{\beta}_N$. Then, when $v$ is known, coincidentally, $\tilde{\beta}_N$ can solve the algebra equation

Therefore, Some known difficulties can be overcome by establishing equivalent results, which is the key ingredient to prove the nonexistence, existence and multiplicity of normalized solutions for the Kirchhoff equation $(\mathcal{K})$.

Theorem 1.1. Let $N = 4, 6, 8.$ Then equation $(\mathcal{K})$ has at least one positive, radially symmetric normalized solution $u\in S(c)$ if and only if the system $\left(\mathcal{P}_{N}\right)$ has at least one solution $(v, \tilde{\beta}_N)\in S(\tilde{\beta}_N ^{-\frac{N}{4}}c)\times \mathbb{R}^+$ such that $u$ is positive and radially symmetric, where $\tilde{\beta}_N$ is defined by $(1.5)$.

To state our another main results, we introduce some frequently used constants. For $p\in(2, 2^*)$, we use the notation

and we denote by $C_{N, p}$ the best constant in the Gagliardo-Nirenberg inequality^[22]

In the special case $p = \bar{p}$, we denote by $\bar{C}_N(\beta) = \left(\frac{\bar{p}\beta}{2C_{N, \bar{p}}^{\bar{p}}}\right)^{\frac{N}{4}}$ the critical mass. For $2 < q\leqslant\bar{p} < p < 2^*$ and $\mu > 0$, we denote:

For $2 < q\leqslant\bar{p} < p < 2^*$ and $\mu < 0$, we denote:

For $2 < q < \bar{p} < p = 2^*$ and $\mu > 0$, we denote:

For $q = \bar{p} < p = 2^*$ and $\mu > 0$, we denote:

For $\bar{p} < q < p = 2^*$ and $\mu > 0$, we denote:

where the optimal Sobolev embedding constant $\mathcal{S}$^[23] is given by

where $\mathcal{D}^{1, 2}(\mathbb{R}^N)$ denotes the completion of $C_0^{\infty}(\mathbb{R}^N)$ with respect to the semi-norm $\|u\|_{\mathcal{D}^{1, 2}(\mathbb{R}^{N})}: = \|\nabla u\|_{L^2(\mathbb{R}^N)}$.

Applying Theorem 1.1, we can prove the following results. Firstly, in the Sobolev subcritical case $2 < q < p = \bar{p}$ or $2 < q\leqslant\bar{p} < p < 2^*$, we have:

Theorem 1.2. Suppose that $a, b > 0$ and $2 < q < p < 2^*$ hold. Let $\tilde{\beta}_N$ and $d$ be defined by $(1.5)$ and $(1.6)$, respectively. If one of the following conditions holds:

$(1) \; 2 < q < p = \bar{p}$, $0 < c < \bar{C}_N(\tilde{\beta}_N)$ and $\mu > 0$;

$(2) \; 2 < q\leqslant\bar{p} < p < 2^*$, $c > 0$ and $0 < \mu < \min\{\mu^*(\tilde{\beta}_N), \mu^{**}(\tilde{\beta_N})\}$;

$(3) \; 2 < q\leqslant \bar{p} < p < 2^*$, $c > 0$ and $-\mu_{*}(\tilde{\beta}_N) < \mu < 0$;

then we have the following conclusions:

$(i)$ for $N = 4$, equation $(\mathcal{K})$ has a positive, radially symmetric solution $u\in S(c)$ if $d\in(0, 1)$, and has no nontrivial solution if $d\in[1, +\infty)$;

$(ii)$ for $N = 6, 8$, equation $(\mathcal{K})$ has two positive, radially symmetric solutions $u_1$, $u_2\in S(c)$ if $d\in(0, d_N)$, has one positive, radially symmetric solution $u\in S(c)$ if $d = d_N$, and has no nontrivial solution if $d\in (d_N, +\infty)$, where $d_N = \frac{1}{4a}$ when $N = 6$ and $d_N = \frac{4}{27a^2}$ when $N = 8$.

Next, in the Sobolev critical case $2 < q < p = 2^*$, we have the following result:

Theorem 1.3. Suppose that $a, b, c > 0$ and $2 < q < p = 2^*$ hold. Let $\tilde{\beta}_N$ and $d$ be defined by $(1.5)$ and $(1.6)$, respectively. If one of the following conditions holds:

$(1) \; 2 < q < \bar{p} < p = 2^*$ and $0 < \mu < \min\{\check{\mu}(\tilde{\beta}_N), \hat{\mu}(\tilde{\beta}_N)\}$;

$(2) \; \bar{p} = q < p = 2^*$ and $0 < \mu < \bar{\mu}(\tilde{\beta}_N)$;

$(3) \; \bar{p} < q < p = 2^*$ and $0 < \mu < \mu_{**}(\tilde{\beta}_N)$;

then we have the following conclusions:

$(i)$ for $N = 4$, equation $(\mathcal{K})$ has a positive, radially symmetric solution $u\in S(c)$ if $d\in(0, 1)$, and has no nontrivial solution if $d\in[1, +\infty)$;

$(ii)$ for $N = 6, 8$, equation $(\mathcal{K})$ has two positive, radially symmetric solutions $u_1$, $u_2\in S(c)$ if $d\in(0, d_N)$, has one positive, radially symmetric solution $u\in S(c)$ if $d = d_N$, and has no nontrivial solution if $d\in (d_N, +\infty)$, where $d_N = \frac{1}{4a}$ when $N = 6$ and $d_N = \frac{4}{27a^2}$ when $N = 8$.

Remark 1.1. Theorem 1.3 covers the doubly critical case that the mass critical exponent is the same as the energy critical exponent i.e., in dimension $N = 4$,

Remark 1.2. As far as we know, Theorems 1.2 and 1.3 seem to be the first results on the existence and multiplicity of normalized solutions for equation $(\mathcal{K})$ in high dimensions $N = 4, 6, 8$. We also remark that it is interesting to know whether $(\mathcal{K})$ has a normalized solution for $a^{\frac{N-4}{2}}b$ small in more general dimensions $N\geqslant 4$. However, we can not solve this question now. So far, we just know that $(\mathcal{K})$ has at least a positive normalized solution for $a^{\frac{N-4}{2}}b$ small, and has no nontrivial solution for $a^{\frac{N-4}{2}}b$ large in the special dimensions $N = 4, 6, 8$. Moreover, it is reasonable to regard $a$ and $b$ as parameters in $(\mathcal{K})$ since, as already noted before, $a$ is the initial tension and $b$ is related to the intrinsic properties of the string.

Finally, in the doubly Sobolev critical case $q = p = 2^*$, based on the Pohožaev identity, we have the following nonexistence result, which is not related to the equivalent results but interesting in itself.

Theorem 1.4. Suppose that $p = q = 2^*$ and $N = 4$ holds, then equation $(\mathcal{K})$ has no positive solutions $u\in S(c)$ for any $\mu > 0$.

This paper is organized as follows: In Section 2, we present some preliminaries. In Section 3, we show some results of $\left(\mathcal{P}_{N}\right)$. In Section 4, we give the proofs of Theorems 1.1–1.4.

2.   preliminaries

In this section, we introduce some preliminaries that will be used to prove Theorems 1.2–1.4.

Lemma 2.1. Let $\mu > 0$, $N \leqslant 4$ and $u\in S(c)$ be a solution of $(\mathcal{K})$. If $u\geqslant0$ and $u\not\equiv0$, then $\lambda > 0$.

Proof. Arguing indirectly, suppose that $\lambda\leqslant 0$. It follows from $u\geqslant 0$ that

Thus $-\Delta u\geqslant 0$. Moreover, from standard regularity results we have that $u\in C^2(\mathbb{R}^N)$. By the Liouville's result [24,Lemma A.2], we obtain that $u\equiv0$. This contradicts with $u\not\equiv0$. Thus $\lambda > 0$.

Lemma 2.2. Let $a, b > 0$, $p, q\in(2, 2^*]$ and $\mu, \lambda\in\mathbb{R}$. If $u\in H^1(\mathbb{R}^N)$ is a weak solution of the Kirchhoff equation $(\mathcal{K})$, then the following Pohožaev identity holds:

Proof. Let $M = \|\nabla u\|_{L^2(\mathbb{R}^N)}^2$, then $u\in H^1(\mathbb{R}^N)$ is a weak solution of the following problem

Then the elliptic regularity theory implies that $u\in C^2(\mathbb{R}^N)$. Combining

with

we conclude that (2.1) holds.

Lemma 2.3. For $m, n\in \mathbb{R}$ and $(\frac{n}{2})^2+(\frac{m}{3})^3 < 0$, then the following cubic

has three distinct real roots, which can be written in the form

where $r = \sqrt{-(\frac{m}{3})^3}$ and $\theta = \frac{1}{3}\arccos(-\frac{n}{2r}).$

Proof. This lemma is a special case of Cardano's formulas, and for the convenience of the reader, we give a simple proof. Set

it follows from the Binomial Theorem that $x = y+z$ always satisfies (2.2). From (2.4), we can obtain that $y^3$ and $z^3$ are the two roots of the quadratic

Furthermore, by $(\frac{n}{2})^2+(\frac{m}{3})^3 < 0$, without loss of generality, we may assume that

and

where $r = \sqrt{-(\frac{m}{3})^3}$ and $\theta = \frac{1}{3}\arccos(-\frac{n}{2r})\in (0, \frac{\pi}{3}).$ It follows that

and

Note that $x = y+z$, we then conclude that (2.2) has three distinct real roots, which can be expressed as in (2.3).

3.   Existence of solutions of $\left(\mathcal{P}_{N}\right)$

We devote to solve system $\left(\mathcal{P}_{N}\right)$ in this section. We will prove the following results which will be used to conclude Theorems 1.2 and 1.3.

Firstly, in the Sobolev subcritical case $2 < q < p = \bar{p}$ or $2 < q\leqslant\bar{p} < p < 2^*$, we have:

Proposition 3.1. Suppose that $a > 0$ and $2 < q < p < 2^*$ hold. Let $\tilde{\beta}_N$ and $d$ be defined by $(1.5)$ and $(1.6)$, respectively. If one of the following conditions holds:

$(1) \; 2 < q < p = \bar{p}$, $0 < c < \bar{C}_N(\tilde{\beta}_N)$ and $\mu > 0$;

$(2) \; 2 < q\le\bar{p} < p < 2^*$, $c > 0$ and $0 < \mu < \min\{\mu^*(\tilde{\beta}_N), \mu^{**}(\tilde{\beta}_N)\}$;

$(3) \; 2 < q\le \bar{p} < p < 2^*$, $c > 0$ and $-\mu_{*}(\tilde{\beta}_N) < \mu < 0$;

then we can obtain the following results:

$(i)$ for $N = 4$, system $\left(\mathcal{P}_{N}\right)$ has a positive, radially symmetric solution $(v, \frac{a}{1-d})$ if $d\in(0, 1)$, and has no nontrivial solution if $d\in[1, +\infty)$;

$(ii)$ for $N = 6, 8$, system $\left(\mathcal{P}_{N}\right)$ has two positive, radially symmetric solutions $(v, \tilde{\beta}_{N}^{1})$ and $(v, \tilde{\beta}_{N}^{2})$ if $d\in(0, d_N)$, has one positive, radially symmetric solution $(v, \frac{1}{2d})$ if $d = d_N$, and has no nontrivial solution if $d\in (d_N, +\infty)$, where $d_N = \frac{1}{4a}$ when $N = 6$ and $d_N = \frac{4}{27a^2}$ when $N = 8$.

Next, in the Sobolev critical case $2 < q < p = 2^*$, we have the following result.

Proposition 3.2. Suppose that $c > 0$ and $2 < q < p = 2^*$ hold. Let $\tilde{\beta}_N$ and $d$ be defined by $(1.5)$ and $(1.6)$, respectively. If one of the following conditions holds:

$(1) \; 2 < q < \bar{p} < p = 2^*$ and $0 < \mu < \min\{\check{\mu}(\tilde{\beta}_N), \hat{\mu}(\tilde{\beta}_N)\}$;

$(2) \; \bar{p} = q < p = 2^*$ and $0 < \mu < \bar{\mu}(\tilde{\beta}_N)$;

$(3) \; \bar{p} < q < p = 2^*$ and $0 < \mu < \mu_{**}(\tilde{\beta}_N)$;

then we have the following results:

$(i)$ for $N = 4$, system $\left(\mathcal{P}_{N}\right)$ has a positive, radially symmetric solution $(v, \frac{a}{1-d})$ if $d\in(0, 1)$, and has no nontrivial solution if $d\in[1, +\infty)$.

$(ii)$ for $N = 6, 8$, system $\left(\mathcal{P}_{N}\right)$ has two positive, radially symmetric solutions $(v, \tilde{\beta}_{N}^{1})$ and $(v, \tilde{\beta}_{N}^{2})$ if $d\in(0, d_N)$, has one positive, radially symmetric solution $(v, \frac{1}{2d})$ if $d = d_N$, and has no nontrivial solution if $d\in (d_N, +\infty)$, where $d_N = \frac{1}{4a}$ when $N = 6$ and $d_N = \frac{4}{27a^2}$ when $N = 8$.

In order to obtain conclusions of Proposition 3.1 and 2, we first recall some results about existence of normalized solutions for the equation (1.7).

Theorem 3.1. ^[13] Suppose that $c, \tilde{\beta}_N > 0$, $N\geqslant 4$ and $2 < q < p < 2^*$ hold. If one of the following conditions holds:

$(1) \; 2 < q < p = \bar{p}$, $0 < c < \bar{C}_N(\tilde{\beta}_N)$ and $\mu > 0$;

$(2) \; 2 < q\leqslant\bar{p} < p < 2^*$, $c > 0$ and $0 < \mu < \min\{\mu^*(\tilde{\beta}_N), \mu^{**}(\tilde{\beta}_N)\}$;

$(3) \; 2 < q\leqslant \bar{p} < p < 2^*$, $c > 0$ and $-\mu_{*}(\tilde{\beta}_N) < \mu < 0$;

then Eq $(1.7)$ has at least one positive, radially symmetric solution.

Theorem 3.2. [14,Theorem 1.1] Suppose that $c, \tilde{\beta}_N > 0$, $N\geqslant 4$ and $2 < q < p = 2^*$ hold. If one of the following conditions holds:

$(1) \; 2 < q < \bar{p} < p = 2^*$ and $0 < \mu < \min\{\check{\mu}(\tilde{\beta}_N), \hat{\mu}(\tilde{\beta}_N)\}$;

$(2) \; \bar{p} = q < p = 2^*$ and $0 < \mu < \bar{\mu}(\tilde{\beta}_N)$;

$(3) \; \bar{p} < q < p = 2^*$ and $0 < \mu < \mu_{**}(\tilde{\beta}_N)$;

then Eq $(1.7)$ has at least one positive, radially symmetric solution.

Remark 3.1.

$(i)$ Theorem 3.1 can be obtained from ^[13] with some minor modifications. Specifically, (i), (ii) and (iii) of Theorem 3.1 can be derived from Theorems 1.1, 1.3 and 1.6, 1.9 of ^[13], respectively.

$(ii)$ In dimension $N = 4$, the right hand side of the condition (1.6) in ^[14] is positive infinity. In dimension $N\geqslant 5$, instead, the value is finit. For more detail, we refer to the formula (6.1) in ^[14].

Proof of Proposition 3.1. By Theorem 3.1, equation (1.7) has at least one positive, radially symmetric solution $v$ when the assumptions in any case are satisfied. We define the function $f_v(\beta)$ as

Case 1: $N = 4$. In this case, by (1.6), (3.1), we have

It follows that if $d\in(0, 1)$, then

defined as in (1.5), is a solution of $f_v(\beta) = 0$, and $(v, \tilde{\beta}_4)$ is a solution of $\left(\mathcal{P}_{N}\right)$. If $d\in[1, +\infty)$, $\left(\mathcal{P}_{N}\right)$ has no nontrivial solution. This implies that Proposition 3.1 (i) holds.

Case 2: $N = 6$. In this case, by (1.6), (3.1), we have

Then it is easy to know that $\lim\limits_{\beta\to+\infty}f_v(\beta) = -\infty$ for any $a, b > 0$ and $f_v(\beta) < 0$ for any $\beta\in(0, a]$. If $d\in(0, \frac{1}{4a})$, then there exist

and

such that $(v, \tilde{\beta}_{6, 1})$, $(v, \tilde{\beta}_{6, 2})$ solve $\left(\mathcal{P}_{N}\right)$. If $d = \frac{1}{4a}$, then $(v, \frac{1}{2d})$ solves $\left(\mathcal{P}_{N}\right)$. If $d\in(\frac{1}{4d}, +\infty)$, then $\left(\mathcal{P}_{N}\right)$ has no nontrivial solution. Thus, we can obtain that Proposition 3.1 (ii) holds.

Case 3: $N = 8$. In this case, by (1.6), (3.1), we have

Then it is easy to know that $\lim\limits_{\beta\to+\infty}f_v(\beta) = -\infty$ for any $a, b > 0$ and $f_v(\beta) < 0$ for any $\beta\in(0, a]$. For each $v\neq0$, we have

It is easy to see that $f_{v}(\beta)$ has a unique maximum point $\beta_{v} = \frac{1}{\sqrt{3d}} > 0,$ and

If $d\in(0, \frac{4}{27a^2})$, it follows from Lemma 2.3 that the equation $f_v(\beta) = 0$ has three distinct real solutions

where

It is easy to see that one of which is negative and two of which are positive. Due to $\beta > 0$, we next wish to exclude the negative solution. Note that (3.2) and $d\in(0, \frac{4}{27a^2}),$ it follows that

and then

This leads to $\tilde{\beta}_{8, 0}, \tilde{\beta}_{8, 2} > 0 \text{ and } \tilde{\beta}_{8, 1} < 0.$ Moreover, it is easy to see that $\tilde{\beta}_{8, 0} > \tilde{\beta}_{8, 2}$. Therefore, we conclude that if $d\in(0, \frac{4}{27a^2})$, then there exist

and

such that $(v, \tilde{\beta}_{8, 0})$, $(v, \tilde{\beta}_{8, 2})$ solve $\left(\mathcal{P}_{N}\right)$. If $d = \frac{4}{27a^2}$, the equation $f_v(\beta) = 0$ has a unique positive real solution

then $(v, \tilde{\beta}_{8})$ solves $\left(\mathcal{P}_{N}\right)$. If $d\in(\frac{4}{27a^2}, +\infty)$, then $\left(\mathcal{P}_{N}\right)$ has no nontrivial solution. Thus, we can obtain that Proposition 3.1 (iii) hold.

Proof of Proposition 3.2. Similar to the proof of Proposition 3.1, and applying Theorem 3.2, we can prove Proposition 3.2.

4.   Proof of the main results

Proof of Theorem 1.1. Firstly, it is clear that $u$ and $v$ have the same sign and radial symmetry. We next prove the equivalence.

Necessary condition. Suppose the equation $(\mathcal{K})$ has a normalized solution $u\in S(c)$, we then have

Let $\beta = a+b\|\nabla u\|_{L^2(\mathbb{R}^N)}^2$ and $v(x) = u(\beta^{\frac{1}{2}}x) = u(y)$, we conclude that

Let $\tilde{\beta}_N$ be defined by (1.5), i.e.,

where $d = b\|\nabla v\|_{L^2(\mathbb{R}^N)}^{2}$, by a similar argument as used in the proof of Proposition 3.1, we obtain that $\beta = \tilde{\beta}_N > 0$ can solve (4.1) in dimensions $N = 4, 6, 8$. Furthermore, let $\phi(x) = \varphi(\beta^{\frac{1}{2}}x) = \varphi(y)$, we have

Moreover, $\int_{ \mathbb{R}^N}|v|^2\mathrm{d}x = \tilde{\beta}_N^{-\frac{N}{2}}\int_{ \mathbb{R}^N}|u(y)|^2\mathrm{d}y = \tilde{\beta}_N^{-\frac{N}{2}}c^2,$ which implies that $(v, \tilde{\beta}_N)\in S(\tilde{\beta}_N^{-\frac{N}{4}}c)\times \mathbb{R}^+$ is a solution of $\left(\mathcal{P}_{N}\right)$.

Sufficient condition. Suppose the system $\left(\mathcal{P}_{N}\right)$ has a solution $(v, \tilde{\beta}_N)\in S(\tilde{\beta}_N ^{-\frac{N}{4}}c)\times \mathbb{R}^+$. At least in a weak sense, we then have, in dimensions $N = 4, 6, 8,$

and

Let $u(x) = v(\tilde{\beta}_N^{-\frac{1}{2}}x) = v(y)$ and $\varphi(x) = \phi(\tilde{\beta}_N^{-\frac{1}{2}}x) = \phi(y)$ we can obtain that

and

which implies that $u\in S(c)$ is a solution of $(\mathcal{K})$.

Proof of Theorem 1.2. The conclusions follow directly from Theorem 1.1 and Proposition 3.1.

Proof of Theorem 1.3. The conclusions follow directly from Theorem 1.1 and Proposition 3.2.

Proof of Theorem 1.4. Suppose that $u\in S(c)$ is a positive solution of $(\mathcal{K})$ with $p = q = 2^*$, then

It follows from Lemma 2.2 and $u\in S(c)$ that

Since $p = q = 2^*$, we have $\gamma_p = \gamma_q = 1$, it follows that $\lambda c^2 = 0$. However, by Lemma 2.1, we have $\lambda > 0$, which is a contradiction. Hence, equation $(\mathcal{K})$ has no positive solutions $u\in S(c)$ for any $\mu > 0$.

Acknowledgments

This work is supported by National Natural Science Foundation of China (No. 12071486).

Conflict of interest

The authors declare there is no conflicts of interest.