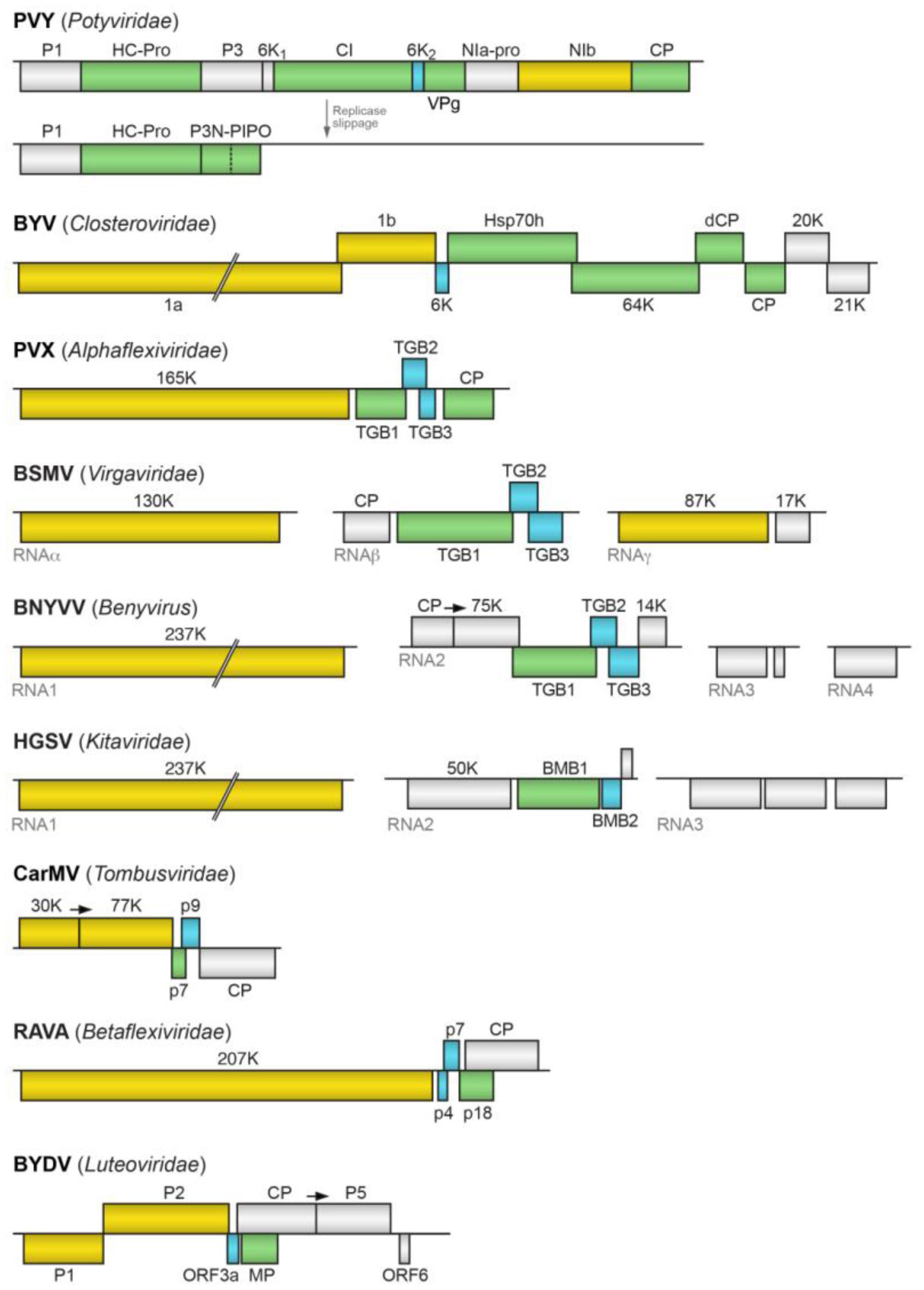
Most plant viruses code for movement proteins (MPs) targeting plasmodesmata to enable cell-to-cell and systemic spread in infected plants. Small membrane-embedded MPs have been first identified in two viral transport gene modules, triple gene block (TGB) coding for an RNA-binding helicase TGB1 and two small hydrophobic proteins TGB2 and TGB3 and double gene block (DGB) encoding two small polypeptides representing an RNA-binding protein and a membrane protein. These findings indicated that movement gene modules composed of two or more cistrons may encode the nucleic acid-binding protein and at least one membrane-bound movement protein. The same rule was revealed for small DNA-containing plant viruses, namely, viruses belonging to genus Mastrevirus (family Geminiviridae) and the family Nanoviridae. In multi-component transport modules the nucleic acid-binding MP can be viral capsid protein(s), as in RNA-containing viruses of the families Closteroviridae and Potyviridae. However, membrane proteins are always found among MPs of these multicomponent viral transport systems. Moreover, it was found that small membrane MPs encoded by many viruses can be involved in coupling viral replication and cell-to-cell movement. Currently, the studies of evolutionary origin and functioning of small membrane MPs is regarded as an important pre-requisite for understanding of the evolution of the existing plant virus transport systems. This paper represents the first comprehensive review which describes the whole diversity of small membrane MPs and presents the current views on their role in plant virus movement.
1.
Introduction
In 1922, the mathematician Banach [1] proved the well-known fixed-point theorem named the Banach contraction principle in the settings of complete metric spaces. He proved that every contraction mapping on a complete metric space has a unique fixed-point. Thereafter, various generalizations and fixed-point results have been proved by many authors and some are recently appeared in [2,3,4].
In 2007, Huang and Zhang [5] introduced the concept of cone metric spaces by replacing real numbers with a cone in a normed space. They also defined the convergence and Cauchyness concepts of sequences in terms of the interior points of the given cone. Moreover, they proved some important fixed-point theorems and extended the well-known Banach contraction principle to the settings of cone metric spaces where the respective cones are normal and solid. Such a line allows for investigating lots of studies and results in fixed-point theory without assuming the normality property of the underlying cone. The results of Huang and Zhang were generalized by Rezapour and Hamlbarani [6] by eliminating the normality assumption of the underlying cone. There are actually lots of generalizations of metric spaces in which the distance function takes values in ordered cones.
Unfortunately, when cones are assumed to be normal and solid, these generalizations become impractical due to the equivalent of the topology induced by a metric and the topology induced by a cone metric. In fact; the equivalent characterizations have been shown by many authors, see for instance [7,8,9,10,11,12,13,14] and references cited therein. We also mention that Azam and Mehmood [15] introduced the notion of tvs-valued cone metric space to present the same notions in more general settings.
In 2006, Bhaskar and Lakshmikantham [16] studied the existence and uniqueness of coupled fixed-point theorems for maps with mixed monotonic properties in metric spaces with a partial order. The obtained results were investigated using the assumption of weak contraction type.
In 2009, Lakshmikantham and Ćirić [17] introduced more notations of mixed g-monotone maps and proved coupled coincidence and coupled common fixed-point theorems for such types of contractive maps in the case of partially ordered complete metric spaces. These presented results are a generalization of the results given in [16].
In 2011, Janković et al. [18] showed that all fixed-point results in cone metric spaces wherein the underlying cone is normal and solid are proper copies of classical results in metric spaces. Therefore, any generalizations of fixed-point from metric space to cone metric space are repeated.
In 2012, Sönmez [19,20] defined a partial cone metric space and studied its topological properties. In the same paper, fixed-point results for some contractive types of operators are proved in the generalized complete partial cone metric spaces.
In 2012, Samet et al. [21] initially considered the notion of α-admissible mappings in metric spaces and they gave some examples to elucidate and support the concept. Furthermore, they presented some relevant fixed-point results for such a class of mappings in this space. Subsequently, a number of authors have exploited the concept of α-admissible contraction types of mappings to study the existence of fixed-points in many generalized spaces.
In 2013, Malhotra et al. [22], Jiang and Li [23] extended the results of [19] and [20] to θ-complete partial cone metric spaces without using the normality condition of the ordered cones. In all the results listed before, the given Banach space is considered to be with a solid cone.
In 2017, Basile et al. [24] defined the notion of semi-interior point as a partial treatment of the non-solidness problem of cones and hence solved many equilibrium and computer problems in this setting.
In 2018, Aleksi´ et al. [25] gave a survey on some properties and results of (non)-normal and (non)-solid cones. On the other hand, they showed that any solid cone in a topological vector space can be replaced by a solid and normal cone in a normed space. Consequently, most of the problems in (TVS) cone metric spaces can be reduced to their standard metric counterparts.
In 2019, Mehmood et al. [26] defined a new concept of convergence by means of semi-interior points of the positive cone in the settings of E-metric spaces. The authors proved some generalizations of fixed point theorem of contraction, Kannan and Chatterjea types of mappings in the context of E-metric spaces where the underlying positive cone of a real normed space E is non-solid and possibly non-normal.
After that, Huang et al. [27] explored some topological properties and fixed point results in cone metric spaces over Banach algebras. Also, Huang [28] gave some fixed points theorems with some applications in E-metric spaces using the concept of semi-interior points.
In 2020, 2021 and 2022 Sahar Mohamed Ali Abou Bakr [29,30,31,32] studied various types of cone metric spaces and made some generalizations in the case of b-cone metric spaces, cone metric spaces, θ-cone metric spaces and b-cone metric spaces and applied these generalizations to some fixed-point and coupled fixed-point theorems.
In 2022 Sahar Mohamed Ali Abou Bakr [33] considered non-normal and non-solid cones and proved more generalized fixed-point theorems in the case of generalized b-cone metric spaces over Banach algebras.
Motivated by the preceding studies, most of our efforts in this research are directed to study the topological structure of partially satisfactory cone metric spaces when cones in normed spaces fail to have interior points but have semi-interior points and the cones possibly non-normal. As a sequel, in the settings of partial satisfactory cone metric spaces, we generalize many concepts of α-admissible types of mappings and define improved wider categories of these generalized functions of α-admissibility types. Since the class of α-admissible mappings are a special case of these improvements, we find results valid to a wider range of contraction classes of mappings. Further, we investigate a new aspect of fixed-point theory where the real contraction constant of the fundamental contraction inequality is replaced by a suitable control sequence of positive real numbers backed by a certain condition to make the generalized inequality more general. Besides that, we will stick to looking for coincidence points, coupled coincidence points, coupled fixed-point and fixed-points of the contraction mapping in a small set of points rather than the whole domain of the mapping. In fact; we precisely combine all of the above trends in our obtained main results.
2.
Basic definitions and mathematical preliminaries
For the sake of simplicity in notation, here and in what follows, let E be a real Banach space, θ be the zero vector in E, C be a cone in E, IntC denotes the set of all interior points of C, U:={x∈E:‖x‖≤1} denotes the closed unit ball of E and the set U+:=U∩C denotes the positive part of the unit ball of E defined by C.
Whenever misunderstandings might occur, we write UE to confirm that UE is the closed unit ball in the space E and we denote by UE+, the positive part of UE.
Any cone C⊂E defines the following partial ordered relations:
and
The following basic definitions and facts are mostly presented in [5,6,7,8,9,10,12,13,14,15,19,20,22,23,24,29,30,31,32,33,34].
Definition 2.1. A cone C of a real Banach space E is solid if and only if IntC≠∅ and it is normal if and only if there exists a real number M>0 such that ‖x‖≤M‖y‖ for every x,y∈E with θ⪯x⪯y. The smallest positive constant M for which the above inequality holds is called the normal constant of C.
Lemma 2.2. Let C be a solid cone of the normed space (E,‖.‖) and {un}n∈N be a sequence in E. Then, un‖.‖→θ implies that for each c∈IntC, there exists a positive integer n0 such that un≪c for all n≥n0.
Definition 2.3. A partial cone metric on a non-empty set X is a mapping p:X×X→C such that for all x,y,z∈X, the following conditions are satisfied:
(PCM1):θ⪯p(x,x)⪯p(x,y);
(PCM2):Ifp(x,x)=p(x,y)=p(y,y), then x=y;
(PCM3):p(x,y)=p(y,x);
(PCM4):p(x,y)⪯p(x,z)+p(z,y)−p(z,z).
The quadruple (X,E,C,p) in this case is said to be partial cone metric space.
Theorem 2.4. Any partial cone metric space (X,E,C,p) is a topological space. If C is a normal cone, then (X,E,C,p) is T0−space.
Definition 2.5. Let (X,E,C,p) be a partial cone metric space over a solid cone C and {xn}n∈N be a sequence in X. Then, we have the following:
(1) {xn}n∈N converges to x∈X if and only if for each c≫θ, there exists a positive integer n0 such that p(xn,x)≪p(x,x)+c for all n≥n0. This type of convergence denoted by xnτp→x.
(2) {xn}n∈N strongly converges to x∈X, if limn→∞p(xn,x)=limn→∞p(xn,xn)=p(x,x), the limit is taken with respect to the norm ‖.‖ on E. This type of convergence denoted by xns−τp→x.
(3) {xn}n∈N is a θ-Cauchy if and only if for each c≫θ, there exists a positive integer n0 such that p(xn,xm)≪c for all n,m≥n0.
(4) The partial cone metric space (X,E,C,p) is a θ-complete, if each θ-Cauchy sequence {xn}n∈N of X converges to some point x∈X with p(x,x)=θ.
(5) {xn}n∈N is Cauchy, if there exists u∈C such that limn→∞p(xn,xm)=u.
(6) The partial cone metric space (X,E,C,p) is complete if and only if every Cauchy sequence {xn}n∈N of X strongly converges to some point x∈X with p(x,x)=u.
Remark 2.6. Every complete partial cone metric space (X,E,C,p) is θ-complete, but the converse is not generally true. In fact; example (3) in [32] is an example of θ-complete partial cone metric space with a Cauchy sequence which is not strongly convergent to any element in X. Consequently, it represents an example of θ-complete partial cone metric space which is not complete.
Now, we recall a class of cones in an ordered normed spaces (E,‖.‖) defined by means of points in C, cones with semi-interior points, that are weaker than the one of interior points of C. The concept of semi-interior point of cone C and some of its characteristics can be found in [24,28].
Definition 2.7. The vector x0∈C is called semi-interior point of C if there exists a positive real number ρ>0 such that x0−ρU+⊆C.
The set of semi-interior points of C is generally denoted by C⊖. The partial ordered relation ⋘ can be defined for x,y∈E as follows:
In particular; we have
Remark 2.8. (1) We have the following relations:
(a) C⊖+C⊖⊂C⊖.
(b) C⊖+C⊂C⊖.
(c) αC⊖⊂C⊖ for any real number α>0.
(2) Any interior point of a cone C is a semi-interior point of C with respect to the norm ‖.‖ on E, while the converse is not true. Some examples of non-solid cones in normed and Banach spaces having some semi-interior points can be found in [24].
By the help of example (2.5) in [24], we rebuild an illustrative example to support definition (2.7) in the following way:
Example 2.9. Let Xn:=(R2,‖.‖n) be the Banach space R2 ordered by the point-wise ordering and equipped with the norm ‖.‖n defined by the following formula:
Figure 1 sketches the closed unit ball of Xn whose vertices are the points (1,0), (0,1), (−n,n), (−1,0), (0,−1) and (n,−n).
Let β={βn}n∈N be any sequence of positive numbers, βn>0 for all n∈N. Denote by E:=(⨁n∈NXn)ℓ∞(β), the linear space of all sequences defined by:
Endow the space E:=(⨁n∈NXn)ℓ∞(β) with the following norm:
Assume that the space E is ordered by the cone
Choose in particular the weighted sequence β={1n}n∈N and let x={(n,n)}n∈N. Since ‖x‖ℓ∞({1n}n∈N)=supn∈N{2n⋅ 1n}=2<∞, we see that x∈C is not an interior point of C.
Now, take any y={(yn1,yn2)}n∈N∈UE+. Then, we have
Clearly, x−y={(n−yn1,n−yn2)}n∈N. It is easy to check that
Similarly, we have n−yn2≥0foralln∈N. Thus, we find a real number ρ=1>0 such that x−y∈Cforall y∈UE+. Therefore, x={(n,n)}n∈N∈C⊖.
Depending on Huaping Huang results [28] in 2019, the following results are based on the assumption that the cone C has a semi-interior points.
Definition 2.10. A sequence {xn}n∈N in C is called s-sequence, if for each c∈C⊖, there exists n0∈N such that xn⋘c for all n≥n0.
Lemma 2.11. Let {xn}n∈N be a sequence in E and xn→θ as n→∞. Then, {xn}n∈N is s−sequence.
Proposition 2.12. Let x,y,z∈E. Then, x⋘z if one of the following holds:
Proposition 2.13. If θ⪯u⋘c holds for any c∈C⊖, then u=θ.
Proposition 2.14. Let (X,E,C,p) be a partial cone metric space. Then, some topology τp is generated on X and defined by:
The base of this topology is given by βp={Bp(x,c):(x,c)∈X×C⊖}, where the set Bp(x,c):={y∈X:p(x,y)⋘c+p(x,x)} is the neighborhood of x with radius c.
In the following, redefined versions of the convergent and Cauchy sequences in our space are given by exchanging roles of ⋘ and ≪. Therefore, the new definitions are controlled by C⊖ instead of IntC.
Definition 2.15. Let (X,E,C,p) be a partial cone metric space, x∈X and {xn}n∈N be a sequence in X. Then,
(1) {xn}n∈N is convergent to x, we denote this by xnτp→x, whenever for every c∈E with c⋙θ, there is n0∈N such that p(xn,x)⋘p(x,x)+c for all n≥n0.
(2) {xn}n∈N is strongly convergent to x, we denote this by xns−τp→x, if limn→∞p(xn,x)=limn→∞p(xn,xn)=p(x,x).
(3) {xn}n∈N is a θ-Cauchy whenever for every c∈E with c⋙θ, there is n0∈N such that p(xn,xm)⋘c for all n,m≥n0. That is; a sequence {xn}n∈N is a θ-Cauchy if and only if ‖p(xn,xm)‖→θ asn,m→∞.
(4) The partial cone metric space (X,E,C,p) is said to be θ-complete, if each θ-Cauchy sequence {xn}n∈N of X converges to x in X such that p(x,x)=θ.
(5) {xn}n∈N is Cauchy, if there is u∈C such that limn,m→∞p(xn,xm)=u.
(6) The partial cone metric space (X,E,C,p) is complete, if each Cauchy sequence {xn}n∈N in X is strongly convergent to x∈X such that p(x,x)=u.
Remark 2.16. (1) A sequence {xn}n∈N is a θ-Cauchy if and only if {p(xm,xn)}m,n∈N is s-sequence in E.
(2) For s−sequence which is not convergent, one can see example (2) in [23].
(3) Each strongly convergent sequence of a partial cone metric space (X,E,C,p) is convergent with respect to τp. However, the converse of this fact need not hold. In particular; the converse is true if C is a normal cone. In fact; example (3) in [23] showed the existence of some sequences of a partial cone metric space which are convergent, but not strongly convergent if the cone C is non-normal.
Now, we are going to highlight two new classes of cones in normed spaces, namely; semi-solid cones and satisfactory cones. These classes will play a key role in our results and enable moving the roles from interior points to semi-interior points of cones.
Definition 2.17. A cone C in the normed space E is called semi-solid if and only if it has a non-empty set of semi-interior points, C⊖≠∅, and it is called a satisfactory cone if and only if cone C satisfies any one of the following:
(1) C is normal and solid,
(2) C is not-normal and solid,
(3) C is normal and semi-solid,
(4) C is not-normal and semi-solid.
A partial cone metric space (X,E,C,p) is said to be a partial satisfactory cone metric space if and only if the cone C is satisfactory.
With this notion, the above-mentioned conclusions are still working with non-normal semi-solid cones and hence generally for partial (satisfactory) cone metric spaces. Particularly, the following remark is a direct consequence of Lemma (2.11) and part (3) of Definition (2.15).
Remark 2.18. Let (X,E,C,p) be a partial (satisfactory) cone metric space. Then,
(1) A complete partial (satisfactory) cone metric space is a subcategory of a θ-complete partial (satisfactory) cone metric space. In particular; if C is a normal cone of the normed space (E,‖.‖), then every θ−Cauchy sequence in (X,E,C,p) is a Cauchy sequence and every complete partial (satisfactory) cone metric space is θ−complete.
(2) If {yn}n∈N is s-sequence in E satisfying p(xn,xm)⪯yn for all m,n∈N withm>n, then {xn}n∈N is a θ-Cauchy sequence in X.
(3) If {xn}n∈N is a sequence in X, {αn}n∈N is a sequence in E that converges to θ and satisfying p(xn,xm)⪯αnforallm,n∈Nwithm>n, then {xn}n∈N is a θ-Cauchy sequence.
(4) The limit of a convergent sequence in a partial (satisfactory) cone metric space may not be unique. In fact; the partial (satisfactory) cone metric space (X,E,C,p) need not be T1−space. Actually, Example (3.1) in [35] and Examples (3), (11) in [32] showed that the limit of convergent sequence in (X,E,C,p) is not necessarily unique.
(5) The partial (satisfactory) cone metric p is not always continuous mapping, in the sense of xnτp→x and ynτp→y imply that p(xn,yn)‖.‖→p(x,y). In other words; the fact that p(xn,yn)‖.‖→p(x,y) if xnτp→x and ynτp→y, is not guaranteed. See example (11) in [32].
Now, we are going to display the concept of α-admissible mappings defined by Samet [21] and review the essential definition of generalized α-admissible mappings given by Zhu [36].
Definition 2.19. Let X be a non-empty set, α:X×X→[0,∞) be a mapping and S,T:X→X be two self-mappings. Then,
(1) T is said to be an α-admissible, if for every x,y∈X,
(2) S and T are called generalized α-admissible, if for every x,y∈X,
Before starting the core results, we need to recall some standard terminology from fixed-point theory.
Definition 2.20. [37] Let X be a non-empty set and T,S:X→X be mappings such that TX⊆SX. If v=Tu=Su for some u∈X, then u is a coincidence point of T and S, and v is a point of coincidence of T and S. Furthermore, if Tv=Sv=v, then v is a common fixed-point of T and S. Finally, if TSw=STw, whenever Tw=Sw for some w∈X, then T and S are said to be weakly compatible. That is; if they commute at their coincidence points.
For simplicity, we use the notation Λ to denote the set of coincidence points of T and S.
Proposition 2.21. [37] Let T and S be coincidentally commuting self-mappings on a set X. If T and S have a unique point of coincidence w=Tx=Sx, then w is the unique common fixed-point of T and S.
We need to consider the followings which will be effectively used in the proof of our next main results.
Definition 2.22. [16] Let (X,⩽) be an ordered set and T:X×X→X. Then, T is said to have the mixed monotone property in X, if for any x,y∈X,
Definition 2.23. [16] An element (x,y)∈X×X is said to be a coupled fixed-point of the mapping T:X×X→X, if T(x,y)=x and T(y,x)=y.
Definition 2.24. [17] Let T:X×X→X and S:X→X be two mappings. An element (x,y)∈X×X is called a coupled coincidence point of the mappings T and S, if T(x,y)=SxandT(y,x)=Sy, and (Sx,Sy) is called coupled point of coincidence.
Definition 2.25. [17] Let (X,⩽) be a partially ordered set, T:X×X→X and S:X→X be two mappings. Then, T is said to have the mixed S-monotone property, if T is monotone S-non-decreasing in its first argument and is monotone S-non-increasing in its second argument. That is; for any x,y∈X
The following definitions are part of the main topics in our work.
Remark 2.26. Suppose that (X,⩽) is a partially ordered set and let (X,E,C,p) be a partial (satisfactory) cone metric space. Then, a partial ordered relation ⩽ on X can be induced on X×X in the following way: for every (x,y)and(u,v)∈X×X,
The element (x,y) is said to be comparable to (u,v), if either (x,y)≲(u,v), or (x,y)≳(u,v) and the sequence {(xn,yn)}n∈N⊂X×X is non-decreasing with respect to ≲, if (xn,yn)≲(xn+1,yn+1)foralln.
Definition 2.27. Let (X,E,C,p) be a θ−complete partial (satisfactory) cone metric space ordered with the relation ⩽. Then, (X,E,C,p,⩽) is said to be regular, if X has the following properties:
(1) If for every non-decreasing sequence {xn} in X such that xnτp→x, then xn⩽xfor alln.
(2) If for every non-increasing sequence {yn} in X such that ynτp→y, then yn⩾yfor alln.
Definition 2.28. [38] Let T:X×X→X and α:X2×X2→[0,∞) be given mappings. Then, T is said to be an α-admissible mapping, if for all (x,y),(u,v)∈X×X, the following is satisfied
Definition 2.29. [39] Let T:X×X→X,S:X→X and α:X2×X2→[0,∞) be mappings. Then, T and S are said to be α−admissible, if
for all x,y,u,v∈X.
3.
Main results: Generalized classes of admissible mappings
Let T:X→X be a given self-mapping. The set of all fixed-points of the mapping T is denoted by Fix(T)={x∈X:Tx=x}.
Lemma 3.1. Every contraction mapping on a metric space (X,d) is an α-admissible mapping for some mapping α:X×X→[0,∞). However, not every α-admissible mapping is a contraction mapping.
Proof. Let T be a contraction mapping on a metric space (X,d). Then, there exists a constant k∈(0,1) such that d(Tx,Ty)≤kd(x,y) for every x,y∈X. Consider the mapping α:X×X→[0,∞) be defined by
Then, T is an α-admissible mapping. More exactly, we need here to think over two situations as follows:
Case(1): For any x≠y in X, we have 1k1d(x,y)≤1d(Tx,Ty). This implies α(x,y)≤kα(Tx,Ty). Since 0<k<1, then we have α(x,y)<α(Tx,Ty). It is fairly simple to see that α(Tx,Ty)≥1 whenever α(x,y)≥1.
Case(2): Otherwise, we know that x=yimpliesd(x,y)=0. Imposing that T is a contraction mapping on X, it yields d(Tx,Ty)=0 and so Tx=Ty. Eventually, the conclusion that α(Tx,Ty)=α(x,y)=1 is valid for x=y. In both cases, the contraction mapping T is an α−admissible mapping, but not conversely in general.
We demonstrate that the converse of Lemma (3.1) is not true as in the following example.
Example 3.2. Let X be the metric space ([0,∞),d) with the absolute value metric function d(x,y)=|x−y| for all x,y∈[0,∞). Let T:X→X andα:X×X→[0,∞) be defined by
Then, T is an α-admissible mapping, but it is not contraction because T has two fixed-points on the given complete metric space, Fix(T)={0,1}.
Remark 3.3. By virtue of Lemma (3.1) and Example (3.2), we can understand that the class of α−admissible mappings is effectively more generalized than the class of contraction mappings.
In the sequel, we will continue to modify the concept of α-admissible operators by generalizing a new function class of such mappings in more general conditions.
We state Definition (3.4) in the line of Definition (2.19) as follows:
Definition 3.4. Let (X,E,C,p) be a partial (satisfactory) cone metric space and C be a cone of a normed space (E,‖.‖). In a non-empty set X, define T:X→X and α:X×X→C. Assume that crunsthroughC−{θ}. Then,
(1) T is said to be α−c−admissible mapping if and only if
(2) (X,E,C,p) is α−c−regular, if for any sequence {xn}n∈N in X such that α(xn,xn+1)⪰c for all n∈N and xnτp→x∗∈X, we have α(xn,x∗)⪰c for sufficiently large n.
Inspired by Definition (3.4), we went further, defining a new class of α−admissible mappings which is different from and stronger than the one introduced in Definition (3.4). The refinement version of these mappings will be crucial in our main results.
Definition 3.5. Let (X,E,C,p) be a partial (satisfactory) cone metric space and C be a cone of a normed space (E,‖.‖). In a non-empty set X, define T:X→X and α:X×X→C. Assume that {cn}n∈N be a non-zero sequence in C. Then,
(1) T is said to be α−sequentially admissible mapping if and only if
(2) (X,E,C,p) is said to be α−sequentially regular, if for any sequence {xn}n∈N in X such that α(xn,xn+1)⪰cn+1 for all n∈N and xnτp→x∗∈X, we have α(xn,x∗)⪰cn+1 for sufficiently large n.
Remark 3.6. (1) Note that the class of all α−admissible operators described in Definition (2.19), is included in two classes of all α−c−admissible and α−sequentially admissible operators. Indeed; in Definition (3.4), let (E,‖.‖):=(R,|.|), where the normed space E is endowed with the usual ordering of real numbers ≤ and ordered by the cone C:=[0,∞). Further, if c=1, then T is an α-admissible mapping. Similarly, in Definition (3.5), let (E,‖.‖),Cand⪯ be the same ones as those stipulated above. Moreover, let {cn}n∈N be the constant sequence cn=1 for all n∈N. Thus, T is an α-admissible mapping.
(2) The class of all α−c−admissible operators is included in the class of all α−sequentially admissible operators. In fact; suppose that T is α−c−admissible operator. In Definition (3.5), we can take {cn}n∈N equals the constant sequence cn=c for all n∈N. Thus, T is α−sequentially admissible operator. It is obvious that the last category is the widest.
(3) If T is α−sequentially admissible and {cn}n∈N is an increasing sequence starting with the element cn0≠θ, then T is α−cn−admissible mapping for every n≥n0. This is true in particular for arithmetic sequences with base c∗ belonging to C, where c1=c1,c2=c1+c∗,…,cn=c1+(n−1)c∗,n∈N.
(4) If T is α−sequentially admissible mapping and {cn}n∈N is a decreasing sequence bounded below by θ≠c∗∈C, then for every θ≠c∈C, there is n(c)∈N such that c∗⪯cn(c)≺c∗+c. Now, the inequality α(x,y)⪰c∗+c implies α(x,y)⪰cn(c), and the later one suggests that α(Tx,Ty)⪰cn(c)+1. Using the lower bound c∗, it follows that α(Tx,Ty)⪰c∗.
Taking inspiration from Definition (2.19), we shall establish our newly corresponding generalizations in the following way:
Definition 3.7. Let (X,E,C,p) be a partial (satisfactory) cone metric space and C be a cone of a normed space (E,‖.‖). In a non-empty set X, define T,S:X→X and α:X×X→C. Assume that crunsthroughC−{θ} and {cn}n∈N be a non-zero sequence in C. Then,
(1) The mapping T is called αS−c−admissible, if
(2) T is called αS−sequentially admissible if and only if
Remark 3.8. Every α−c−admissible is αI−c−admissible, where I denotes the identity mapping on X. Similarly, every α−sequentially admissible mapping is αI−sequentially admissible.
To ensure clarity, we will deal particularly with partial satisfactory cone metric spaces in which the cone C is semi-solid and need not be normal. The results in the case of ordering solid cones will be the same as those concerning the case of semi-solid cones. It is important to mention that our results are valid in all cases of the satisfactory cone C.
We begin with the following main generalized theorem.
Theorem 3.9. Suppose that (X,E,C,p) is a θ-complete partial satisfactory cone metric space. Let α:X×X→C be a symmetric mapping and T,S:X→X be two self-mappings. Presume that {cn}n∈N is a non-zero sequence in C. Also, assume that the following assumptions are fulfilled:
(1) TX⊆SX and SX is a closed subset of X;
(2) T is αS−sequentially admissible mapping;
(3) There exists x0∈X such that α(Sx0,Tx0)⪰c1;
(4) (X,E,C,p) is αS−sequentially regular;
(5) There is a sequence of positive real numbers {kn}n∈N such that limn→∞kn<1 and satisfying the following condition:
Then, T and S have coincidence points. Moreover, if T and S are weakly compatible such that for all x,y∈Λ we have α(Sx,Sy)⪰c1, then T and S have a unique common fixed-point in X.
Proof. From assumption (3), there exists x0∈X such that
Since TX⊆SX, we get an element x1∈X such that Sx1=Tx0. Again, we set Sx2=Tx1. In a similar manner, we define two sequences {xn}n∈N and {yn}n∈N as follows: yn+1=Sxn+1=Txnfor alln∈N.
First, if we can find some N∈N such that yN=yN+1, then we have
Thus, xN is a coincidence point of T and S and the conclusion is checked. Without any loss of generality, we consider that yn≠yn+1 for all n∈N.
Since α(Sx0,Tx0)=α(Sx0,Sx1), inequality (3.1) gives the following:
Since T is αS−sequentially admissible, inequality (3.2) implies α(Tx0,Tx1)⪰c1. Consequently, we have α(Sx1,Sx2)⪰c2 and so α(Tx1,Tx2)⪰c2. By repetition of the above procedure, we get α(Sxn,Sxn+1)⪰cn+1 which implies α(Txn,Txn+1)⪰cn+1. Equivalently; we get
This in turns implies the following:
Taking advantage of the given generalized contractive condition (5), we arrive at
Using a similar way of the above process up to n times, we obtain
Consider the sequence
with an:=∏nj=1kj, we have limn→∞anan−1=limn→∞kn<1. Hence, the sequence s1 should converge to zero sequence, limn→∞an=0, and we have
For any n,p∈N, we have
Consider the sequence
with bn:=∏n+p−1i=n+1ki, we have limn→∞bnbn−1=limn→∞kn+p−1<1. Hence, using the usual form of the Ratio test of series, the sequence of partial sums of s2 should converge to some number (say) k such that
Thus, one can see that {∑lm=1[∏n+1+mj=n+1kj]}l∈N is convergent to some number (say) K such that
In conclusion, we proved the following:
Since {anKp(y0,y1)}n∈N is convergent to zero, limn→∞anKp(y0,y1)‖.‖→θ, it is s−sequence. Now, let c∈E with c⋙θ, then there exists n0∈N such that
Hence, for any n,p∈N, we have
This concluded that for any n,p∈N and any c⋙θ, there exists n0∈N such that
Owing to the above arguments, we find that {yn}n∈N is a θ-Cauchy sequence in (X,E,C,p).
Regarding the θ-completeness of the space, there exists an element (say) y′∈X such that ynτp→y′ and p(y′,y′)=θ. Since {yn}n∈N⊆SX and SX is closed set in X, it leads that y′∈SX. Then, there exists z∈X such that y′=Sz.
Now, we wish to show that Tz=Sz. Employing (PCM4), we have
Since α(yn,yn+1)⪰cn+1 for all n∈N and ynτp→y′, by making use of condition (4), we obtain α(yn,y′)=α(Sxn,Sz)⪰cn+1 for sufficiently large n.
Accordingly, we find p(Tz,Sz)⪯kn+1p(y′,yn)+p(yn+1,y′). Since ynτp→y′, then for c∈E with c⋙θ and for allm∈N, choose n3∈N such that
Hence, for all c⋙θ and for allm∈N, it follows that p(Tz,Sz)⋘cm. Taking the limit as m→∞, we get p(Tz,Sz)=θ and so Tz=Sz.
Therefore, T and S have a coincidence point in X. As a last step, we claim that T and S possess a unique point of coincidence. In order to obtain the claim, consider that Tw=Sw be another point of coincidence of T and S. So, we assume that Tw=Sw≠Tz=Sz. By the hypothesis α(Sw,Sz)⪰c1, we have p(Tw,Tz)⪯k1p(Sw,Sz)=k1p(Tw,Tz). As 0<k1<1, we get p(Tw,Tz)=θ and so Tw=Tz. This contradicts the assumption that Tw=Sw≠Tz=Sz. Thus, the point of coincidence is uniquely determined. Bearing the assertion that the mappings T and S are weakly compatible in mind, we deduce that Sv=STz=TSz=Tv. Regarding to the uniqueness of the point of coincidence of T and S, we get Tv=Sv=v.
As a consequence, v is the unique common fixed-point of T and S and so the proof is done.
Once again, we can here replace the condition C⊖≠∅ with the other states of the satisfactory cone C, if we wish.
Remark 3.10. As a special case, if we replace the mapping S with I, the identity mapping on X, in the statement of Theorem (3.9), we conclude that any mapping with these prescribed conditions has fixed-points in X.
Now our purpose is to determine sufficient conditions to acquire the uniqueness of the fixed-point of the mapping T stipulated in Theorem (3.9) with S=I.
Proposition 3.11. Assume that all the hypothesis of Theorem (3.9) are verified with S=I. Furthermore, suppose that the following properties are hold:
Let c∗∈C such that c∗⪰ci0 for some ci0∈C−{θ} and i0∈N. Let the set {α(x,y):x,y∈Fix(T)} be bounded below by c∗. Under these conditions, we obtain that the fixed-point of T is uniquely determined.
Proof. Since T satisfies the hypothesis of Theorem (3.9), then the fixed-point of T exists. We show that the set Fix(T) is in fact reduced to a single point. For this, if possible, let x,y∈Fix(T). Then, α(x,y)⪰c∗ and so α(x,y)⪰ci0. Making use of condition (2) in Theorem (3.9), we guarantee that α(Tx,Ty)=α(x,y)⪰ci0+1. Continuing in this way, we derive that α(x,y)⪰cnfor alln≥i0. We can now apply assumption (4), which leads to p(Tx,Ty)⪯knp(x,y)for alln≥i0. That is; p(x,y)⪯knp(x,y)for alln≥i0. On taking the limit as n→∞ of the sequence {(kn−1)p(x,y)}n≥i0 gives us −p(x,y)∈C. Thus, we have p(x,y)∈−C, but p(x,y)∈C and so p(x,y)∈C∩−C={θ}. Then, p(x,y)=θ implies x=y. Therefore, the set Fix(T) should be singleton.
As a usual relationship between more and less general theorem, we have the following one:
Corollary 3.12. Suppose that (X,E,C,p) is a θ-complete partial satisfactory cone metric space. Let α:X×X→C be a symmetric mapping and T:X→X be a self-mapping. Presume that {cn}n∈N is a non-zero sequence in C. Also, assume that the following assumptions are fulfilled:
(1) There exists N∈N such that TN is α−sequentially admissible;
(2) There exists x0∈X such that α(x0,TNx0)⪰c1;
(3) (X,E,C,p) is α−sequentially regular;
(4) There is a sequence of positive real numbers {kn}n∈N such that limn→∞kn<1 and satisfying the following condition:
Then, the mapping T has fixed-points in X.
Theorem 3.13. Suppose that (X,E,C,p) is a θ-complete partial satisfactory cone metric space. Let α:X×X→C be a symmetric mapping and T:X→X be a bijective self-mapping. Presume that {cn}n∈N is a non-zero sequence in C. Also, assume that the following assumptions are fulfilled:
(1) T−1 is α−sequentially admissible mapping;
(2) There exists x0∈X such that α(x0,T−1x0)⪰c1;
(3) (X,E,C,p) is α−sequentially regular;
(4) There is a sequence of positive real numbers {kn}n∈N such that limn→∞(kn)−1<1 and satisfying the following condition:
Then, the mapping T has fixed-points in X.
Proof. Since T is bijective, then it is an invertible mapping, say T−1:X⟶X is the inverse mapping of T. Let x0∈X be a chosen point and define the sequence x1=T−1x0, x2=T−1x1=(T−1)2x0, …, xn=T−1xn−1=(T−1)nx0for alln∈N. Since α(x0,T−1x0)⪰c1, we conclude that
Inductively, we get α(xn,xn+1)⪰cn+1for alln∈N.
We can employ condition (4) as follows: p(xn−1,xn)=p(Txn,Txn+1)⪰knp(xn,xn+1)for alln∈N. This is equivalent to p(xn,xn+1)⪯(kn)−1p(xn−1,xn)for alln∈N. Set ηn=(kn)−1 for all n∈N, we infer that
For n,p∈N, consider
The next step is easily obtained by following the related lines from the proof of Theorem (3.9). Hence, we assure that {xn}n∈N={(T−1)nx0}n∈N is a θ-Cauchy sequence. For the sake of θ-completeness of the space, there exists x∈X such that xnτp→x with p(x,x)=θ. Now, we show that x is a fixed-point of T. Since T is onto, there exists u∈X such that x=Tu. Since we have xnτp→x and α(xn,xn+1)⪰cn+1 for alln∈N, then it follows that α(xn,x)⪰cn+1 for sufficiently large n.
Thereafter, by using assumption (1), we get α(xn+1,u)⪰cn+2. Suppose now that condition (4) takes place, we conclude that
Hence, p(xn+1,u)⪯ηn+1p(xn,x). Since xnτp→x, then for any c⋙θ, there exists n0∈N such that
For all n≥n0 and for any c⋙θ, consider that
In conclusion, we arrive at
Which leads us to u=x=Tu. Since T is injective mapping, then Tx=Tu=x. Therefore, x∈X is a fixed-point of T and Fix(T)≠∅.
Now, let us introduce our newly major concepts.
Definition 3.14. Let (X,E,C,p) be a partial satisfactory cone metric space. In a non-empty set X, define T:X×X→X, S:X→X and β:X2×X2→C. Let {cn}n∈N be a non-zero sequence in C. Then,
(1) T is called βS−sequentially admissible mapping if and only if
foralln∈Nandforallx,y,u,v∈X.
(2) (X,E,C,p) is said to be βS-sequentially regular, if {xn} and {yn} are two sequences in X such that
foralln∈N and Sxnτp→x∗,Synτp→y∗, then
Theorem 3.15. Let (X,⩽) be a partially ordered set induced with partial satisfactory cone metric p such that (X,E,C,p) is a θ-complete partial satisfactory cone metric space. Let T:X×X→X and S:X→X be such that T has S-mixed monotone property. Presume that β:X2×X2→C is a symmetric mapping. Also, assume that the following assertions are fulfilled:
(1) T is βS−sequentially admissible mapping;
(2) There exist x0,y0∈Xsuch that
(3) T(X×X)⊆SXandSXis closed subset ofX;
(4) (X,E,C,p)isβS−sequentially regular and (X,E,C,p,⩽) is regular;
(5) There is a sequence of positive real numbers {kn}n∈N such that limn→∞kn<1 and satisfying the following condition:
with(Sx,Sy)≲(Su,Sv)andβ((Sx,Sy),(Su,Sv))⪰cn,n∈N. Under these conditions, if there exist x0,y0∈X such that Sx0⩽T(x0,y0) and Sy0⩾T(y0,x0), then T and S have coupled coincidence points.
Proof. By starting from arbitrary points x0,y0∈X such that Sx0⩽T(x0,y0) and Sy0⩾T(y0,x0). Since T(X×X)⊆SX and x0,y0∈X, there exist x1,y1∈X such that Sx1=T(x0,y0) and Sy1=T(y0,x0). Let x2,y2∈X be such that Sx2=T(x1,y1) and Sy2=T(y1,x1).
Inductively, we construct the sequences {xn}n∈N and {yn}n∈N in X by
for alln∈N∪{0}. By Mathematical Induction, we verify that Sxn⩽Sxn+1 and Syn⩾Syn+1 for all n∈N∪{0}. Given that Sx0⩽T(x0,y0) and Sy0⩾T(y0,x0). Thus, the statement is true for n=0. Suppose that the claim is true for some fixed n=k. That is; Sxk⩽Sxk+1 and Syk⩾Syk+1. By S-mixed monotone property of T, we obtain Sxk+1⩽Sxk+2andSyk+1⩾Syk+2. Thus, the statement is true for n=k+1. The later lines guarantee that
Without loss of generality, we assume that (xn+1,yn+1)≠(xn,yn)for alln∈N∪{0}. From assumption (2), we have
Due to the fact that T is βS-sequentially admissible, it follows that
By continuing this procedure, we have β((Sxn,Syn),(Sxn+1,Syn+1))⪰cn+1 for all n∈N. Similarly, we obtain that β((Syn,Sxn),(Syn+1,Sxn+1))⪰cn+1 for alln∈N. Now, we can apply condition (5) as follows:
On adding the previous two inequalities, one has
Repeating the above process, we deduce
For any n,p∈N, we infer
By a similar manner, we obtain
Therefore, we arrive at
Since limn→∞kn<1, using the usual form of the Ratio test of series, one can easily see that {∑mi=n[∏ni=1ki][p(Sx0,Sx1)+p(Sy0,Sy1)]}m∈N is convergent to the limit ∑∞i=n[∏ni=1ki][p(Sx0,Sx1)+p(Sy0,Sy1)] and its n's term {∏ni=1ki}n∈N tends to zero. Therefore, for given ε>0, there exists n1∈N such that
For all n≥n1, we consider
Thus, ∑n+p−1i=n[∏ij=1kj][p(Sx0,Sx1)+p(Sy0,Sy1)]‖.‖→θ. It follows that, for any c∈E with c⋙θ, there exists n2∈N such that
Owing to the above arguments, we deduce that the sequences {Sxn}n∈N and {Syn}n∈N are θ-Cauchy in the θ-complete partial satisfactory cone metric space (X,E,C,p). Then, there exist x,y∈X such that Sxnτp→x and Synτp→y with p(x,x)=θ and p(y,y)=θ. Since {Sxn}n∈N⊆SX and SX is closed, it leads that x∈SX. So, there must be some x′∈X such that Sx′=x. Similarly, Sy′=y for some y′∈X.
Now, since {Sxn} is a non-decreasing sequence that converges to Sx′, we get Sxn⩽Sx′for alln.
Similarly, we have Sy′⩽Synfor alln. That is; (Sxn,Syn)≲(Sx′,Sy′)for alln. Since (X,E,C,p,⩽) is βS−regular, we obtain
Since then for with and for all , choose such that and
For all we have
Proceeding limit as , we get and so In such a similar way, one can easily get Therefore, we reach that is a coupled coincidence point of and is a coupled point of coincidence of
Remark 3.16. If we replace the mapping by , the identity mapping on in the statements of Theorem (3.15), we have a new type of mappings for which we proved the existence of the coupled fixed-point of the mapping .
4.
Applications of fixed-point theory to ordinary differential equations
In this section, we apply Theorem (3.9) with to study the existence of a unique solution for the following two-point boundary value problem of the second-order differential equation:
where is a continuous function.
Theorem 4.1. Presume that the following hypotheses hold:
For all is a non-decreasing function;
If for all then we have
There exists a continuous function such that
for all with
There exists such that
There exists a symmetric function with the following properties:
There exists such that for all we have
For all and for any
If in such that for all and , we have for sufficiently large
Then, the mentioned second-order differential equation (4.1) has a unique solution in
Proof. Clearly, the problem (4.1) is equivalent to the integral equation
where is the Green function defined by
It is clear that the existence of a solution of (4.1) is equivalent to the existence of the integral equation (4.2).
Let be the Banach space of all real continuous functions on the closed unit interval and which is a solid (semi-solid) cone.
Define by
where Then, easily one can verify that is a complete partial satisfactory cone metric space.
We endow with the partial order given by
Let be defined by
Obviously, the fixed-point of is a solution of (4.1) or, equivalently; a solution of the problem (4.2).
We will check that the mapping satisfies all the conditions of Theorem (3.9) with .
First, we show that is non-decreasing with regards to Since is non-decreasing with respect to its second variable, then for any with and for any we have
since for any Thus, we have
Define by
where and If then or Observe that If implies then by condition , we get and thus Therefore, is sequentially admissible mapping with
Since there exists such that
for all then
From condition it is easy to verify that is sequentially regular.
Now, let such that Then, we have
Therefore,
for any and for certain
Hence, we find a constant sequence of positive real numbers for any such that and satisfying
for any with Therefore, all the conditions of Theorem (3.9) hold with and thus has a unique fixed-point in Thus, there is a unique solution of problem (4.1).
5.
Applications of coupled fixed-point to integral equations
In this section, we study the existence of solutions for the following system of integral equations:
where and
Theorem 5.1. Assume that the following conditions hold:
and for all
for some positive real number
There exists a symmetric function with the following properties:
For all implies
There exist such that
For all with and the following Lipschitzian-type conditions hold:
If and are two sequences in such that
and , then
With these conditions, the system of integral equations (5.1) has at least one solution in
Proof. Let be the Banach space of all real continuous functions on and which is a solid (semi-solid) cone. Define by
where Then, is a complete partial satisfactory cone metric space. Suppose that is endowed with the natural partial ordered relation, that is;
The set is partially ordered under the following ordered relation:
For any are the upper and lower bounds of and , respectively. Therefore, for every there is that comparable to and
Define by
for all
First, we show that has the mixed monotone property. If then for all we have
Thus, Similarly, whenever
Let be defined by
If then
By condition , we get and thus Therefore, is -sequentially admissible mapping with
From condition it follows that there exist with such that and Thus, condition in Theorem (3.15) is satisfied with
The property is sequentially regular follows trivially from the corresponding condition of the mapping
Next, suppose that is a monotone non-decreasing sequence in that converges to a point Then, for any the sequence of real numbers
converges to Thus, for all we have and thus for all Similarly, if is a limit of a monotone non-increasing sequence in then and thus for all Therefore, is regular.
For all with and it follows that
for any . Therefore, we can find a constant sequence of positive real numbers for all such that and satisfying
for all and Which is just the contractive condition in Theorem (3.15). All the hypotheses of Theorem (3.15) with are satisfied. Therefore, has a coupled fixed-points in .
6.
Conclusions
The study of this article along with our defined distance structure represents a new research direction that included updated versions of some abstract results and some methods in fixed-point lectures. Many of the previously known results found in fixed-point theory consider direct generalizations and special occurrences of the results of this article. In the present paper, there are multiple appearances of various types of generalized admissible mappings and mappings have mixed monotone property associated with several interesting conditions. In this regard, we discussed the problem of finding coincidence points, coupled coincidence points, coupled fixed-point and fixed-points of such mappings. For showing efficiency of the obtained main results we gave some applications. In one approach, we introduced a novel fixed-point technique to ordinary differential equations in partial satisfactory cone metric spaces, and in another approach we studied the existence of solutions in a system including non-linear integral equations.
Acknowledgments
The authors are grateful to the reviewers and the editorial board for their valuable suggestions and remarks which helped to improve the quality of current manuscript.
Conflict of interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: