Alcohol consumption and HIV disease prognosis among virally unsuppressed in Rural KwaZulu Natal, South Africa

1.   Introduction

In mathematics, computer science and economics, as well as in other disciplines like geophysics, solving an optimization problem consists of finding the best of all possible solutions in a given model space ^[1]. This target can be realized by minimizing (or maximizing) some type of objective function that includes, in many practical cases, the difference between observed and predicted quantities. For instance, in geophysics, a typical optimization problem is finding an Earth-model consisting of seismic-velocity spatial distribution that minimizes the differences between observed and predicted seismic travel times ^[2].

Optimization techniques can be divided into approaches that allow exploring locally the model space, and approaches that allow a global or quasi-global search of the solution. In the first case, we generally incur in the problem of convergence towards local minima (or local maxima) of the cost function. In fact, the final solution will depend strongly on the initial model and on the exploration path in the parameters space. In general, when we apply local optimization techniques, we search for a solution in a limited portion of the model space, converging towards solutions that could not correspond with the best one for our specific problem. In order to face this problem, Global optimization techniques are addressed to find the global minimum (or the global maximum) of the objective function over the given set. Unfortunately, finding the global minimum (or maximum) of a function commonly represents a difficult task. Analytical methods are frequently not applicable and the use of numerical solution strategies often is not sufficient ^[3]. Typical techniques based on global or quasi-global search in the model space ^[4], include stochastic methods like Direct Monte-Carlo sampling approaches. Other methods are based on heuristic approaches to explore the model space in a more or less intelligent way. These include, for instance, Ant Colony optimization (ACO), Simulated annealing, Evolutionary algorithms (e.g., genetic algorithms and evolution strategies), and so forth. Despite the many advantages, these types of global optimization methods are generally difficult to put in practice in many situations, especially in three dimensions, due to the very expensive computational process when dealing with large parameter spaces.

In order to face the intrinsic problems of both local and global optimization methods, in this paper, we propose to reformulate the optimization problems in terms of Reinforcement Learning (RL). Our approach aims to teach an "artificial agent" to search for the global minimum of the cost function in the model space using the advantages offered by a large suite of Reinforcement Learning algorithms. These are aimed at mapping situations to actions through the maximization of a "numerical reward signal" ^{[5,6,7,8,9,10,11,12,13]}. In every particular state, an artificial agent learns progressively by continuous interaction with its environment. This can be a true physical environment, as it happens, for instance, in case we desire to teach an agent to move through a real physical space. More in general, the environment can consist of a virtual space with which one or more artificial agents interact. The effects of every agent's action will be returned by the modified environment in terms of a reward (or a punishment) and a new state. The reward depends on the "quality" of the agent's actions. High rewards correspond with positive impact of the actions on the agent's target, and vice versa. For instance, if the objective of the artificial agent is to find the exit from a maze in the shortest possible time (or through the shortest path), the agent will receive a positive reward every time it moves properly to reach the exit.

The final objective of such a learning strategy is to maximize the total reward accumulated during all iterations (cumulative reward), and not just the immediate reward. In the example of the maze, it means that the agent's objective is to find a global strategy to escape from the maze, rather than just selecting a single local step forward that could lead him into a dead end. This is a crucial point, because the goal of Reinforcement Learning methods is optimizing the agent's actions for a long-term horizon. Such an intrinsic forward-looking approach of RL algorithms can be used with profit to find global solution(s) in many optimization/inversion problems in geophysics (as well as in other fields). In fact, it is easy to grasp the analogies and possible points of connection between geophysical inversion problems and Reinforcement Learning. In the first case, the goal is to find an Earth model that corresponds to a minimum value of a certain cost function. In the second case, the goal is to find an optimal policy through which an agent can maximize its total reward. These are both examples of optimization problems.

In the next methodological section, we will see how the geophysical inverse problem can be reformulated in terms of Reinforcement Learning strategy. For that purpose, we will use a combination of Q-Learning, Temporal Difference and Epsilon-Greedy algorithms. We will see that these methods fit the purpose of optimizing the exploration of the parameter-space in inversion problems. Finally, we will test our approach using synthetic geo-electric data, plus a seismic data set available in the public domain.

2.   Theoretical framework

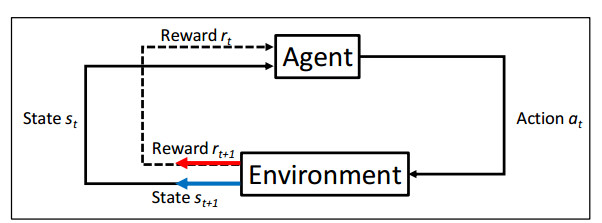
Reinforcement Learning includes a suite of algorithms and techniques through which an "artificial agent" learns an optimal "behavior" by interacting with a dynamic "environment" and by maximizing a "reward metric" for the task, without being explicitly programmed for that task and without human intervention. The artificial agent selects those actions that allow increasing the cumulative reward, r ∈ R, achievable from a given state, s ∈ S (Figure 1).

A "discount factor", γ, is applied to the long term rewards with the scope of giving progressively lower weights to rewards received far in the future. The agent's goal is to learn, by trials and errors, a "policy" for maximizing such cumulative long-term reward. The policy is often denoted by the symbol π. It consists of a function of the current environment state, s, belonging to the set S of all possible states, and returns an action, a, belonging to the set A of all possible actions.

There are many different Reinforcement Learning techniques. Among the various methods, the Q-Learning method ^[14] is a suitable approach for solving optimization/inverse problems. The name derives from the Q-function that provides a measure of the Quality (in terms of effectiveness for a given task) of an action that the agent takes starting from a certain state. It is defined as follows:

The Bellman equation below provides an operative definition of the maximum cumulative reward. This is given by the reward r that the agent received for entering the current state s and action a, plus the maximum future reward for the next state s', taking all the possible actions ${a}^{'}$ from that state:

In formula (3), the symbol γ indicates the "discount factor". It is introduced for balancing the contribution of future rewards with respect to the immediate reward. The value of Q(s, a) can be found recursively: the algorithm starts by using random values (or any guess value) for the Q-function. Then, when the agent proceeds exploring its environment, the initial Q values progressively converge towards the optimal ones, based on the positive and/or negative feedback that the agent receives from its environment. The "Temporal Difference" (briefly TD) method (formula 4 below) provides a practical way for updating the Q values, as follows:

We can see that the new value of Q for state ${s}_{t}$ and action ${a}_{t}$, is obtained by adding to the previous Q value a new term (in the square parenthesis) called temporal difference. This, in turn, is multiplied by a factor α that represents the learning rate and is commonly determined empirically by the user. The temporal difference consists of the immediate reward, ${r}_{t}$, plus the difference between the maximum Q value for all the actions that the agent can take from the state s_t+1, minus the old value of Q. The $\underset{a}{\mathrm{max}}Q\left({s}_{t+1}, a\right)$ term is multiplied by the above mentioned discount factor, γ.

Now, we must explain how we define the Q values in the frame of our integrated Inversion-Reinforcement Learning (called, briefly, RL-Inv) approach. In other words, we must clarify how we assign a reward to the artificial agent (the optimization algorithm) while it explores the model space. In our method, we set the Q-function inversely proportional to the cost function (that, in turn, depends on the difference between observed and predicted responses) after a certain number N of iterations. The user determines such N value empirically. Indeed, we assume that a good convergence path towards a final low misfit represents a reasonable long-term reward for our Reinforcement Learning agent. In that case, low misfit (as well as low values of the cost function) correspond to high rewards and high Q values.

For instance, let us suppose that we apply a Least Square optimization algorithm to solve our inverse problem; that algorithm coincides with our agent. In that case, we can define the cost function Φ(m) as follows:

In formula (5), m represents the vector of model parameters, or model vector; d_obs represents the data vector (observations); g(m) is the forward operator by which we calculate the predicted response in the model vector m; the symbol T indicates "transpose"; W_d is he data covariance matrix for taking data uncertainties into account; R is a smoothing operator applied to the model vector m as a regularization term; η is a factor regulating the weight of the smoothing term in the cost function.

In our procedure, we calculate Φ(m) at each iteration and store its value at every iteration. In such a way, we can calculate and store the correspondent Q value as follows:

Next, let us clarify how the Q-Learning formulas contribute to the inversion. In the frame of the Q-Learning approach, we need to estimate a cumulative reward by taking into account both the immediate as well as the long-term reward. In our approach, the immediate reward is given by the inverse of the cost function after just one or two iterations, as in formula (6). Instead, the long-term reward is given by the inverse of the cost function estimated after a "significant number" of iterations (such number depends on the inverse problem and is decided by the user, case by case). In such a way, we intend to set a policy that minimizes the cost function through a balanced combination of both short-term and-long term views. This concept will be further expanded in the next two sections.

The Bellman equation (3) and the Temporal Difference iterative method (4) allow us estimating and progressively updating the values of the Q-function during the optimization (inversion) process. These values depend on the starting models and on the exploration paths in the model-space. The goal of our approach is to find an optimal policy for our optimization agent. Such a policy will coincide with the "optimal" exploration/exploitation path in the model space aimed at maximizing the Q-function. Hence, a crucial point is how the model space (that represents the environment of our Reinforcement Learning approach) is explored.

2.1.   Q-Learning, model space exploration and inversion

In the frame of geophysical inversion (as well as in other optimization problems), the environment of the Reinforcement Learning problem is represented by the space of model parameters, or model space (Figure 2). As we said earlier, the agent corresponds with the optimization algorithm through which we try to minimize the cost function. At each iteration, the algorithm performs an action: it explores the environment in order to update the current geophysical model with the goal to reduce the misfit between observed and predicted responses. In our approach, we perform such an exploration using the Epsilon-Greedy algorithm. This provides an effective strategy for facing the well-known "Exploration vs. Exploitation" question. Let us explain the basics of this strategy and the reason why we included it in our approach.

Exploration allows an agent improving its current state at each action, leading to a long-term benefit. In the frame of geophysical inversion, this corresponds to retrieve a distribution of model parameters that allows lowering the cost function (or the misfit) and, consequently, improving the Earth model. On the other hand, exploitation means to choose the greedy action to get the most short-term reward by exploiting the agent's current action-value. For instance, in case of Gradient-based optimization methods, this action corresponds to taking repeated steps in the opposite direction of the gradient of the cost function. The crucial point is that by being greedy with respect to immediate action-reward estimates, may not actually lead towards the maximum long-term reward, causing a sub-optimal behaviour. In other words, trying to minimize the cost function at each step could not represent the optimal inversion policy.

2.2.   Epsilon-Greedy approach

Epsilon-Greedy is an effective approach aimed at balancing exploration and exploitation by choosing randomly between these two possibilities. The term "epsilon" refers to the probability of choosing to explore that is commonly lower than the probability to exploit. In other words, the optimization/inversion algorithm exploits most of the time with a small chance of exploring. It means that it updates the model parameters respecting the condition of reducing the cost function at each iteration (exploitation). However, it explores the model parameters (with lower probability: epsilon < < 1) in different directions too, even if that choice could imply a temporary increase of the cost function. Figure 3 shows a scheme of such approach and its pseudo-code.

At the same time, by applying the Bellman equation and the Temporal Difference method, we aim to a long-term reward that is minimizing the cost function after a significant number N of iterations (and not just the cost function at each individual iteration). This strategy allows us sampling large portions of the model space that otherwise would be excluded by a traditional greedy optimization strategy. Finally, we will get the optimal inversion policy. This uses the best exploitation/exploration strategy, produces the lowest final value of the cost function and the best inverted model.

The block diagram of figure 4 summarizes the entire procedure, showing the sequence of steps through which we update the model parameters by maximizing the Q-function through a combination of Epsilon-Greedy exploration strategy and Bellman/Temporal Difference equations.

With reference to figure 4, in order to clarify better how and where the Q-Learning formulas contribute to the inversion process, we schematize the entire workflow through the following key steps:

1) Create m starting models (process initialization). 2) Choose n (number of iterations). 3) Run n iterations for each model. 4) Update each model after n iterations. 5) Calculate the inverse of cost function (eq.6) after 1 or 2 iterations (short-term reward for each model). 6) Calculate the inverse of cost function (eq.6) after n iterations (long-term reward for each model). 7) Calculate (or update) the cumulative reward (Q values) using the Bellman and TD formulas (eqq.3 and 4). 8) Store Q values and update the Q-Table. 9) Chose epsilon (for the epsilon-Greedy method), as shown in figure 3. 10) Select model with the highest total reward with probability = 1-epsilon (exploitation). 11) Alternatively, select random model with probability = epsilon (exploration). 12) Use the selected model, perturb it and create other m initial models. 13) Iterate from step 3. 14) Exit from the loop when the cost function and the cumulative reward Q is stationary. 15) Finally, select the model with the highest Q-value (lowest cost function).

3.   Examples

In this section, we discuss two tests where we apply the RL-Inv method to two types of data set. In the first case, we use synthetic data obtained through a simulated resistivity survey. In the second case, we use refraction seismic data available in the public domain. For each test, we compare the final models obtained through a "standard" inversion/optimization approach and the RL-Inv methodology.

3.1.   Synthetic test on geo-electric data

In this test, we simulated the acquisition of DC (Direct Current) geo-electric data along a line 550 m long, with electrodes deployed with a regular spacing of 10 m. The upper panel of figure 5 shows the "true" resistivity scenario in which we simulated the resistivity survey. The model consists of two stacked resistive layers embedded in a conductive uniform background. The lower panel of the same figure shows the data (apparent resistivity section) of the simulated DC response. After adding 5% of Gaussian noise to the simulated response, our goal was to invert the synthetic data in order to retrieve the correct resistivity model. We started from a half-space initial guess, assuming no a priori information.

Despite its apparent simplicity, the resistivity model shown in figure 5 is not easy to retrieve by data inversion without using any prior information. Many equivalent geophysical models can honour the data equally well if we do not use any constraint. The inversion algorithm that we used in this case is a "standard" Damped Least Square optimization algorithm that minimises iteratively the cost function, like the one expressed by eq. (5). The regularization operator consists of a smoothing functional that allows finding smoothed model solutions. The effect will be that the two resistive layers cannot be adequately distinguished and, after the inversion process, they appear "mixed" into a unique layer. This is clearly shown in figure 6.

Next, we performed again the inversion of the same synthetic data, but this time through our Reinforcement Learning approach (RL-Inv), in order to verify if it was possible to find an inverse solution more consistent with the original resistivity model. Figure 7 shows the inverted resistivity model (upper panel). In this case, the RL-Inv solution shows the two resistive layers properly separated. Furthermore, they were retrieved with almost correct resistivity values, although the resistivity of the upper layer is slightly overestimated.

Figure 8 shows the cross plot of predicted vs. observed apparent resistivity for both inversion results. This type of graph is useful because it provides a synoptic view of the misfit between observed and predicted geo-electrical responses. In case of perfect fit, the points should be on a 45-degree tilted line (green line in the figure). The scattering of the points above the ideal best-fit line is a measure of the misfit and of the noise in the data. Both cross plots show some level of scattering and of resistivity overestimation; however, the misfit of the second inversion result (from RL-Inv) is less than the one obtained through the traditional Damped Least Square approach. Furthermore, the second scattering cross-plot shows two clusters of scattered points that are related with the two separate resistivity layers.

In summary, the RL-Inv approach produced results that are more consistent with the original resistivity scenario used for the simulation.

3.2.   Test with public seismic data

In this second example, we applied the RL-Inv method to a classical refraction seismic data set with heterogeneous overburden and some high-velocity bedrock. This data set is included in the examples provided in the public-domain repository prepared for testing the open source "pyGIMLi software library" ^[15]. Figure 9 shows the data set in terms of travel times vs. offsets. The complex trends of the travel-time curves vs. offset suggest significant variability in the velocity field. We can observe frequent variations in the slope of the curves that indicate lateral as well as vertical velocity changes. Such complexity in the data space corresponds to a similar complexity in the model space. In scenarios like this, our RL-Inv approach can be useful to find a global solution for the refraction tomography problem, limiting the risk to fall in local minima of the cost function during the inversion process. We followed the scheme of Figure 3 by exploring the model space through the Epsilon-Greedy approach. First, we created an initial Q-Table based on the cost function values (here expressed in terms of Chi² values) for a set of different starting models (Table 1). Next, the optimization agent started exploring the model-space (in this case, the unknown model parameter is P-Velocity, V_p) through the Epsilon-Greedy approach.

Figure 10 shows an example of "Model selection histogram" obtained through exploration of the model space with the Epsilon-Greedy method. The bars of each histogram are proportional to the probability to select one model among many possible starting models. In this example, we have considered just 20 possible candidate models, for illustrative purposes. For each model, we calculated the cumulative reward using the Bellman formulas, as explained earlier in the methodological section. We can see that for low values of the epsilon parameter, the method selects almost exclusively the model(s) with high cumulative reward (some examples are indicated by the arrows in the figure 10). This corresponds to adopt a greedy strategy, with prevalence of exploitation of the model(s) with high reward. On the other side, by choosing high values of epsilon, model selection tends to be random, allowing exploring the model space through directions that would otherwise have been ignored. In other words, an appropriate setting of the epsilon parameter allows a balanced policy between exploration and exploitation in the model space during the inversion process. In this specific test, we performed many tests by setting the epsilon parameter in the range between 0.0 and 1.0. There is not any absolute rule to find the optimal value of epsilon. However, a good strategy is to make epsilon variable: as trials increase, epsilon should decrease. Indeed, as trials increase, we have less need of exploration and more convenience of exploitation, in order to get the maximum benefit from our policy.

During the inversion process, the Q-Table was progressively updated. As explained earlier, the rule for updating the Q-Table is given by the Bellman equation and the iterative Temporal-difference method. In summary, the agent (the minimization algorithm) explores the model space and selects the optimal path that corresponds with the direction in the space of parameters with the highest cumulative reward. At the same time, it does not neglect to explore alternative directions in the model space, although with lower probability. After many iterations, the agent learns to move in the model space following the most convenient policy. This corresponds with the one that allows finding the global minimum of the cost function. Our inversion test seems to confirm the effectiveness of such strategy, as in the previous test. Figure 11 shows some examples of velocity models obtained by travel-time tomography, with the correspondent ray tracing. Each individual model corresponds to a certain point of the cost function in the model space. For each path explored in the model space, we have a correspondent suite of values of the cost function. Finally, the best model (left panel of Figure 12) is the one retrieved through the RL-Inv approach. It shows the V_p parameter distribution that corresponds to the highest cumulative reward. For comparison, the right panel of the same figure shows the V_p model obtained without the support of the RL approach, using a "standard" optimization approach. Compared with the RL-Inv solution, the "standard" solution tends to overestimate the bedrock velocity and is not able to highlight properly the heterogeneities in the overburden.

4.   Conclusions

We introduced a new optimization/inversion approach fully integrated with Q-Learning, Temporal Difference and Epsilon-Greedy methods. These allow expanding the exploration of the model-space, minimizing the misfit and limiting the problem of falling in local inversion minima. The advantages of our approach are clearly highlighted through the comparative test results on multidisciplinary data (electrical and seismic). Finally, we remark that we expect the greatest benefits from our method in those applications where an extended exploration of the model-space is difficult or prohibitive, due to the size of the data-model space and the complexity of the inversion problem. For instance, interesting cases include full-wave seismic inversion and simultaneous joint inversion of multi-physics data.

Conflict of interest

The author declares no conflict of interest.

Web links

pyGIMLi examples data repository: https://github.com/gimli-org/example-data/blob/master/traveltime/koenigsee.sgt.