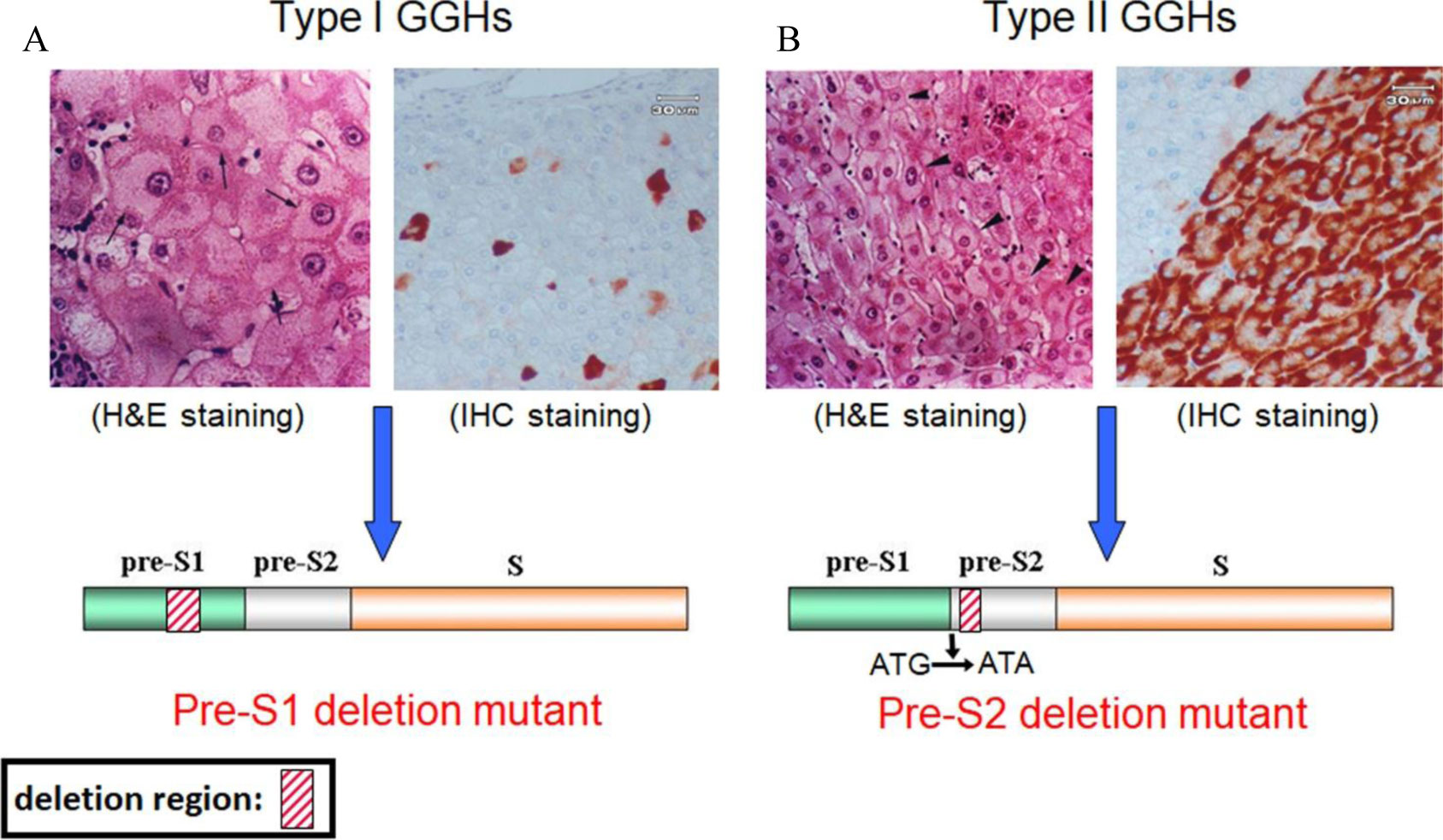
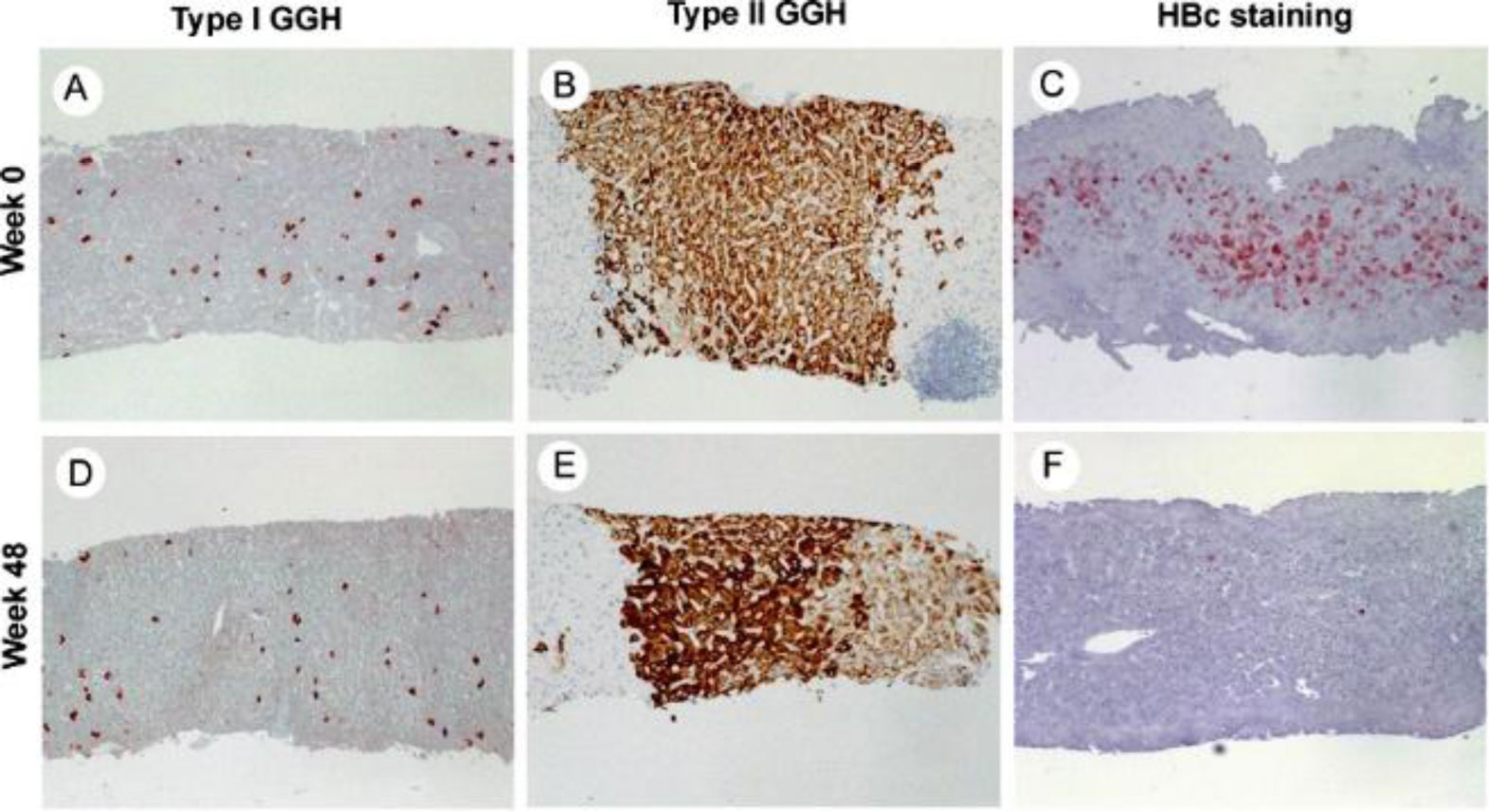
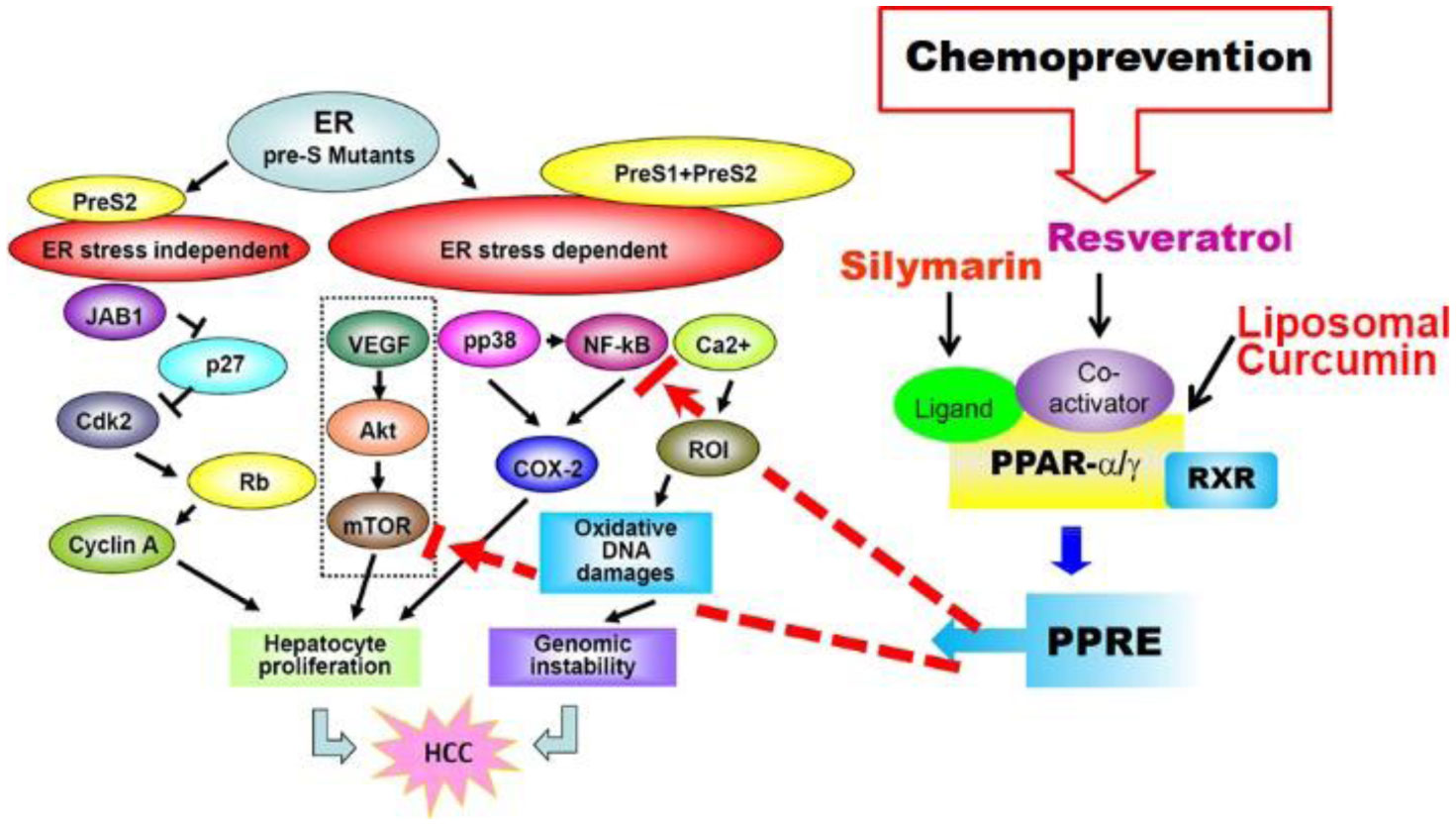
Ground glass hepatocyte (GGH) represents a histologic hallmark of chronic hepatitis B virus (HBV) infection and is characterized by the accumulation of pre-S mutant surface antigens in the endoplasmic reticulum (ER). In the past decade, GGHs have been recognized as pre-neoplastic lesions of hepatocellular carcinoma (HCC). The accumulation of pre-S mutant protein in ER may induce a misfolded protein response or ER stress signals with activation of VEGF/Akt/mTOR and COX-2/NF-κB signals, leading to oxidative DNA damage, aneuploidy, and genomic instability. Molecular studies revealed clonal HBV DNA integration in type II GGHs which continue to express and secrete surface antigens, representing the sustained surface antigens in the serum after NA antiviral treatment. The persistence of GGHs in the liver after anti-viral therapy not only constitute the challenge to eliminate HBV infection but also carry the high risk to develop HCC. DNA chip and ELISA kit are designing to detect the pre-S mutants in serum. Novel or second generation anti-HBV drugs are under phase II development and include the combination of anti-virals, immunomodulators, agents for host DNA damage, and siRNA to target at the transcription of HBsAg gene in cccDNA or integrated HBV DNA. In the past years, we explored the possibility to provide drugs or natural agents targeting at ER stress signals in GGHs to prevent HCC development. In a transgenic mice model of pre-S mutant and HBx, a combination of silymarin and resveratrol targeting at mTOR and NF-κB signals could reduce a 80% of HCC development. In a pilot clinical trial, liposomal curcumin (Meriva®) combined with anti-virals and immumodulators P1101 have been designed and attempted to eliminate the serum surface antigen and hence the recurrence of HCC after surgical resection. Therefore, the detection of pre-S mutants in serum or GGHs in the liver should provide rational target design for therapy or prevention of HCC in these high risk patients of chronic HBV infection.
1.
Introduction
In meteorology, wind speed is a fundamental atmospheric quantity caused by the movement of air from high to low pressure, usually due to temperature variations. Alongside wind speed, wind direction plays a pivotal role in the analysis and prediction of weather patterns and the global climate. Wind speed and direction significantly affect factors such as evaporation rates, sea surface turbulence, and the formation of oceanic waves and storms. Moreover, these factors have substantial impacts on water quality, water levels, and various fields, including weather forecasting, climatology, renewable energy, environmental monitoring, aviation, and agriculture. Therefore, a comprehensive understanding of wind speed is important for managing potential impacts. Additionally, using wind speed data for analysis can help researchers and experts understand and address issues related to wind speed across various areas. For wind speed data, a normal distribution may not be appropriate, even though the normal distribution is one of the most widely used statistical distributions. If the data exhibits skewness, it is advisable to consider alternative distributions. Many new distributions have been developed using certain transformations from the normal distribution. One such distribution is the Birnbaum-Saunders distribution. Importantly, Mohammadi, Alavi, and McGowan [1] investigated the application of the two-parameter Birnbaum-Saunders distribution for analyzing wind speed and wind energy density at ten different stations in Canada. Their results demonstrated that the Birnbaum-Saunders distribution was especially effective at all the chosen locations. The Birnbaum-Saunders distribution was introduced by Birnbaum and Saunders [2] for the purpose of modeling the fatigue life of metals subjected to periodic stress. As a result, this distribution is sometimes referred to as the fatigue life distribution. The Birnbaum-Saunders distribution has been applied in various contexts, such as engineering, testing, medical sciences, and environmental studies. It is well known that the Birnbaum-Saunders distribution is a positive skewed one. However, some data to be analyzed may have both positive and zero values. Therefore, if zero observations follow a binomial distribution combined with the Birnbaum-Saunders distribution, the resulting distribution is the zero-inflated Birnbaum-Saunders (ZIBS) distribution, which is a new and interesting distribution. This ZIBS distribution was inspired by Aitchison [3], and several researchers have studied the combination of zero observations with other distributions to form new distributions, such as the zero-inflated lognormal distribution [4], the zero-inflated gamma distribution [5], and the zero-inflated two-parameter exponential distribution [6].
The coefficient of variation (CV) of wind speed is important for several reasons. Since the CV measures the dispersion of data relative to the mean, it is expressed as the ratio of the standard deviation to the mean. The CV assesses the variability of a dataset, regardless of the unit of measurement. Additionally, using the CV to evaluate wind speed is beneficial in various contexts. For instance, calculating the CV helps in understanding how much wind speed fluctuates compared to its average. If the CV is high, it indicates that the wind speed is highly variable, making it more difficult to predict wind conditions. In the context of wind energy, the CV can help assess the reliability of energy sources. If wind speed variability is high, it may result in inconsistent energy production, which could affect the stability of energy output from wind farms. Additionally, the coefficient of variation has been used in many fields, including life insurance, science, economics, and medicine. Importantly, many researchers have constructed confidence intervals (CIs) for the coefficient of variation, which have been applied to various distributions. For example, Vangel [7] constructed the CIs for a normal distribution coefficient of variation. Buntao and Niwitpong [8] introduced the CIs for the coefficient of variation of zero-inflated lognormal and lognormal distributions. D'Cunha and Rao [9] proposed the Bayes estimator and created CIs for the coefficient of variation of the lognormal distribution. Sangnawakij and Niwitpong [10] developed CIs for coefficients of variation in two-parameter exponential distributions. Janthasuwan, Niwitpong, and Niwitpong [11] established CIs for the coefficients of variation in the zero-inflated Birnbaum-Saunders distribution.
In the analysis and comparison of wind variability across multiple weather stations or wind directions, without needing to account for the differences in average wind speed at each station or direction, it is necessary to use the common CV. The common CV provides a single indicator representing the overall variability of wind speed, which is crucial when planning wind energy projects, designing wind turbines, or calculating the power production of wind farms that require knowledge of wind stability across different areas. Additionally, the common CV is useful in meteorological and climatological research, as it allows for the analysis of wind variability across multiple regions simultaneously. It can also assist in examining the relationship between wind variability and long-term climate changes or recurring events, such as storms or shifts in wind patterns. Therefore, the common coefficient of variation is a crucial aspect when making inferences for more than one population. This holds particularly true when collecting independent samples from various situations. Consequently, numerous researchers have investigated methods for computing the common coefficient of variation in several populations from variety distributions. For instance, Tian [12] made inferences about the coefficient of variation of a common population within a normal distribution. Then, Forkman [13] studied methods for constructing CIs and statistical tests based on McKay's approximation for the common coefficient of variation in several populations with normal distributions. Sangnawakij and Niwitpong [14] proposed the method of variance of estimate recovery to construct CIs for the common coefficient of variation for several gamma distributions. Next, Singh et al. [15] used several inverse Gaussian populations to estimate the common coefficient of variation, test the homogeneity of the coefficient of variation, and test for a specified value of the common coefficient of variation. After that, Yosboonruang, Niwitpong, and Niwitpong [16] presented methods to construct CIs for the common coefficient of variation of zero-inflated lognormal distributions, employing the method of variance estimate recovery, equal-tailed Bayesian intervals, and the fiducial generalized confidence interval. Finally, Puggard, Niwitpong, and Niwitpong [17] introduced Bayesian credible intervals, highest posterior density intervals, the method of variance estimate recovery, generalized confidence intervals, and large-sample methods to construct confidence intervals for the common coefficient of variation in several Birnbaum-Saunders distributions. Previous research has shown that no studies have investigated the estimation of the common coefficient of variation in the context of several ZIBS distributions. Therefore, the primary objective of this article is to determine the CIs for the common coefficient of variation of several ZIBS distributions. The article presents five distinct methods: the generalized confidence interval, the method of variance estimates recovery, the large sample approximation, the bootstrap confidence interval, and the fiducial generalized confidence interval.
2.
Materials and methods
Let $ {Y}_{ij}, i = \mathrm{1, 2}, \dots, k $ and $ j = \mathrm{1, 2}, \dots, {m}_{i} $ be a random sample drawn from the ZIBS distributions. The density function of $ {Y}_{ij} $ is given by
where $ {\vartheta }_{i}, {\alpha }_{i} $, and $ {\beta }_{i} $ are the proportion of zero, shape, and scale parameters, respectively. $ \mathrm{{\rm I}} $ is an indicator function, with $ {\mathrm{{\rm I}}}_{0}\left[{y}_{ij}\right] = \left\{1;yij=0,0;otherwise,
\right. $ and $ {\mathrm{{\rm I}}}_{\left(0, \infty \right)}\left[{y}_{ij}\right] = \left\{
0;yij=0,1;yij>0
\right. $. This distribution is a combination of Birnbaum-Saunders and binomial distributions. Suppose that $ {m}_{i} = {m}_{i\left(1\right)}+{m}_{i\left(0\right)} $ is the sample size, where $ {m}_{i\left(1\right)} $ and $ {m}_{i\left(0\right)} $ are the numbers of positive and zero values, respectively. For the expected value and variance of $ {Y}_{ij} $, we have applied the concepts from Aitchison
[3], which can be expressed as follows:
and
respectively. Hence, the coefficient of variation of $ {Y}_{ij} $ is defined as
The asymptotic distribution of $ {\widehat{\vartheta }}_{i} $ is calculated by using the delta method, which is given by $ \sqrt{{m}_{i}}\left({\widehat{\vartheta }}_{i}-{\vartheta }_{i}\right)\sim N\left(0, {\vartheta }_{i}(1-{\vartheta }_{i})\right) $, where $ {\widehat{\vartheta }}_{i} = {m}_{i\left(0\right)}/{m}_{i} $. According to Ng, Kundu, and Balakrishnan [18], the asymptotic joint distribution of $ {\widehat{\alpha }}_{i} $ and $ {\widehat{\beta }}_{i} $ is obtained as
where $ {\widehat{\alpha }}_{i} = {\left\{2\left[{\left({\stackrel{-}{y}}_{i}{\sum }_{j = 1}^{{m}_{i\left(1\right)}}\frac{{y}_{ij}^{-1}}{{m}_{i\left(1\right)}}\right)}^{\frac{1}{2}}-1\right]\right\}}^{\frac{1}{2}} $, $ {\widehat{\beta }}_{i} = {\left\{{\stackrel{-}{y}}_{i}{\left({\sum }_{j = 1}^{{m}_{i\left(1\right)}}\frac{{y}_{ij}^{-1}}{{m}_{i\left(1\right)}}\right)}^{-1}\right\}}^{\frac{1}{2}} $, and $ {\stackrel{-}{y}}_{i} = {\sum }_{j = 1}^{{m}_{i\left(1\right)}}\frac{{y}_{ij}}{{m}_{i\left(1\right)}} $. The estimator of $ {\theta }_{i} $ is given by
According to Janthasuwan, Niwitpong, and Niwitpong [11], the asymptotic variance of $ {\widehat{\theta }}_{i} $, derived using the Taylor series in the delta method, is given by
where $ {\varPsi }_{i} = {\left(2+{\alpha }_{i}^{2}\right)}^{2}\left(1-{\vartheta }_{i}\right)\left[{\alpha }_{i}^{2}\left(4+5{\alpha }_{i}^{2}\right)+{\vartheta }_{i}{\left(2+{\alpha }_{i}^{2}\right)}^{2}\right] $. According to Graybill and Deal [19], the common CV of several ZIBS distributions can be written as
where $ \widehat{V}\left({\widehat{\theta }}_{i}\right) $ denotes the estimator of $ V\left({\widehat{\theta }}_{i}\right) $, which is defined in Eq (2) with $ {\alpha }_{i} $ and $ {\vartheta }_{i} $ replaced by $ {\widehat{\alpha }}_{i} $ and $ {\widehat{\vartheta }}_{i} $, respectively. This can be expressed as follows:
where $ {\widehat{\varPsi }}_{i} = {\left(2+{\widehat{\alpha }}_{i}^{2}\right)}^{2}\left(1-{\widehat{\vartheta }}_{i}\right)\left[{\widehat{\alpha }}_{i}^{2}\left(4+5{\widehat{\alpha }}_{i}^{2}\right)+{\widehat{\vartheta }}_{i}{\left(2+{\widehat{\alpha }}_{i}^{2}\right)}^{2}\right] $.
The following subsection provides detailed explanations of the methods employed for constructing confidence intervals.
2.1. Generalized confidence interval
Weerahandi [20] recommended the generalized confidence interval (GCI) method for constructing confidence intervals, which is based on the concept of a generalized pivotal quantity (GPQ). To construct the confidence interval for $ \theta $ using the GCI, we get the generalized pivotal quantities for the parameters $ {\beta }_{i} $, $ {\alpha }_{i} $, and $ {\vartheta }_{i} $. Sun [21] introduced the GPQ for the scale parameter $ {\beta }_{i} $, which can be derived as
where $ {\varLambda }_{i} $ follows the t-distribution with $ {m}_{i\left(1\right)}-1 $ degrees of freedom. $ {\beta }_{i1} $ and $ {\beta }_{i2} $ are the two solutions of the following quadratic equation:
where $ {\varOmega }_{1} = \left({m}_{i\left(1\right)}-1\right){A}_{i}^{2}-\frac{1}{{m}_{i\left(1\right)}}{B}_{i}{\varLambda }_{i}^{2} $, $ {\varOmega }_{2} = \left({m}_{i\left(1\right)}-1\right){A}_{i}{C}_{i}-\left(1-{A}_{i}{C}_{i}\right){\varLambda }_{i}^{2} $, $ {A}_{i} = \frac{1}{{m}_{i\left(1\right)}}{\sum }_{j = 1}^{{m}_{i\left(1\right)}}\frac{1}{\sqrt{{Y}_{ij}}} $, $ {B}_{i} = {{\sum }_{j = 1}^{{m}_{i\left(1\right)}}\left(\frac{1}{\sqrt{{Y}_{ij}}}-{A}_{i}\right)}^{2} $, $ {C}_{i} = \frac{1}{{m}_{i\left(1\right)}}{\sum }_{j = 1}^{{m}_{i\left(1\right)}}\sqrt{{Y}_{ij}} $, and $ {D}_{i} = {\sum }_{j = 1}^{{m}_{i\left(1\right)}}{\left(\sqrt{{Y}_{ij}}-{C}_{i}\right)}^{2} $. Next, considering the GPQ for the shape parameter $ {\alpha }_{i} $ as proposed by Wang [22], the GPQ for $ {\alpha }_{i} $ is derived as
where $ {E}_{i1} = {\sum }_{j = 1}^{{m}_{i\left(1\right)}}{Y}_{ij} $, $ {E}_{i2} = {\sum }_{j = 1}^{{m}_{i\left(1\right)}}\frac{1}{{Y}_{ij}} $, and $ {{\rm K}}_{i} $ follows the chi-squared distribution with $ {m}_{i\left(1\right)} $ degrees of freedom. Subsequently, the GPQ for the proportion of zero $ {\vartheta }_{i} $ was recommended by Wu and Hsieh [23], who proposed using the GPQ based on the variance stabilized transformation to construct confidence intervals. Therefore, the GPQ for $ {\vartheta }_{i} $ is defined as
where $ {W}_{i} = 2\sqrt{{m}_{i}}\left(\mathrm{arcsin}\sqrt{{\widehat{\vartheta }}_{i}}-\mathrm{arcsin}\sqrt{{\vartheta }_{i}}\right)\sim N\left(\mathrm{0, 1}\right) $. Now, we can calculate the GPQs for $ {\theta }_{i} $ and the variance of $ {\widehat{\theta }}_{i} $ using Eqs (5) and (6), resulting in
and
where $ {G}_{{\varPsi }_{i}} = {\left(2+{G}_{{\alpha }_{i}}^{2}\right)}^{2}\left(1-{G}_{{\vartheta }_{i}}\right)\left[{G}_{{\alpha }_{i}}^{2}\left(4+5{G}_{{\alpha }_{i}}^{2}\right)+{G}_{{\vartheta }_{i}}{\left(2+{G}_{{\alpha }_{i}}^{2}\right)}^{2}\right] $. Therefore, the GPQ for $ {\theta }_{i} $ is the weighted average of the GPQ $ {G}_{{\theta }_{i}} $ based on $ k $ individual samples, given by
Then, the $ \left(1-\rho \right)100\% $ CI for the common CV of several ZIBS distributions employing the GCI method is given by
where $ {G}_{\theta }\left(\rho /2\right) $ and $ {G}_{\theta }\left(1-\rho /2\right) $ denote the $ 100\left(\rho /2\right)\mathrm{t}\mathrm{h} $ and $ 100\left(1-\rho /2\right)\mathrm{t}\mathrm{h} $ percentiles of $ {G}_{\theta } $, respectively.
Algorithm 1 is used to construct the GCI for the common coefficient of variation of several ZIBS distributions.
Algorithm 1.
For $ g = 1 $ to $ n $, where $ n $ is the number of generalized computations:
1) Compute $ {A}_{i}, {B}_{i}, {C}_{i}, {D}_{i}, {E}_{i1} $, and $ {E}_{i2} $.
2) At the $ p $ step:
a) Generate $ {\varLambda }_{i}\sim t\left({m}_{i\left(1\right)}-1\right) $, and then compute $ {G}_{{\beta }_{i}}\left({y}_{ij}; {\varLambda }_{i}\right) $ from Eq (4);
b) If $ {G}_{{\beta }_{i}}\left({y}_{ij}; {\varLambda }_{i}\right) < 0, $ regenerate $ {\varLambda }_{i}\sim t\left({m}_{i\left(1\right)}-1\right) $;
c) Generate $ {{\rm K}}_{i}\sim{\chi }_{{m}_{i\left(1\right)}}^{2} $, and then compute $ {G}_{{\alpha }_{i}}\left({y}_{ij}; {K}_{i}, {\varLambda }_{i}\right) $ from Eq (5);
d) Compute $ {G}_{{\vartheta }_{i}} $, $ {G}_{{\theta }_{i}} $, and $ {G}_{V\left({\widehat{\theta }}_{i}\right)} $ from Eqs (6)–(8), respectively;
e) Compute $ {G}_{\theta } $ from Eq (9).
End $ g $ loop.
3) Repeat step 2, a total of G times;
4) Compute $ {L}_{GCI} $ and $ {U}_{GCI} $ from Eq (10).
2.2. Method of variance estimates recovery
The method of variance estimates recovery (MOVER) estimates a closed-form confidence interval. Let $ {\widehat{\omega }}_{i} $ be an unbiased estimator of $ {\omega }_{i} $. Furthermore, let $ \left[{l}_{i}, {u}_{i}\right] $ represent the $ \left(1-\rho \right)100\% $ confidence interval for $ {\omega }_{i}, i = \mathrm{1, 2}, ..., k $. Assume that $ {\sum }_{i = 1}^{k}{c}_{i}{\omega }_{i} $ is a linear combination of the parameters $ {\omega }_{i} $, where $ {c}_{i} $ are constants. According to Zou, Huang, and Zhang [24], the lower and upper limits of the confidence interval for $ {\sum }_{i = 1}^{k}{c}_{i}{\omega }_{i} $ are defined by
and
Considering Eq (7), the $ \left(1-\rho \right)100\% $ CI for $ {\theta }_{i} $ based on the GPQs has become
where $ {G}_{{\theta }_{i}}\left(\rho /2\right) $ and $ {G}_{{\theta }_{i}}\left(1-\rho /2\right) $ represent the $ 100\left(\rho /2\right)\mathrm{t}\mathrm{h} $ and $ 100\left(1-\rho /2\right)\mathrm{t}\mathrm{h} $ percentiles of $ {G}_{{\theta }_{i}} $, respectively. Hence, the $ \left(1-\rho \right)100\% $ CI for the common CV of several ZIBS distributions employing the MOVER method is given by
and
where $ {c}_{i}^{\#} = \frac{{\eta }_{i}}{{\sum }_{j = 1}^{k}{\eta }_{j}} $ and $ {\eta }_{i} = \frac{1}{\widehat{V}\left({\widehat{\theta }}_{i}\right)} $.
Algorithm 2 is used to construct the MOVER for the common coefficient of variation of several ZIBS distributions.
Algorithm 2.
1) Compute $ {\widehat{\alpha }}_{i} $ and $ {\widehat{\vartheta }}_{i} $;
2) Compute $ {\widehat{\theta }}_{i} $ and $ \widehat{V}\left({\widehat{\theta }}_{i}\right) $;
3) Compute $ {l}_{i} $ and $ {u}_{i} $ from Eq (11);
4) Compute $ {L}_{MOVER} $ from Eq (12);
5) Compute $ {U}_{MOVER} $ from Eq (13).
2.3. Large sample approximation
Recall that the estimator of $ {\theta }_{i} $ from Eq (1) is
and the estimated variance of $ {\hat \theta _i} $ is
where $ {\widehat{\varPsi }}_{i} = {\left(2+{\widehat{\alpha }}_{i}^{2}\right)}^{2}\left(1-{\widehat{\vartheta }}_{i}\right)\left[{\widehat{\alpha }}_{i}^{2}\left(4+5{\widehat{\alpha }}_{i}^{2}\right)+{\widehat{\vartheta }}_{i}{\left(2+{\widehat{\alpha }}_{i}^{2}\right)}^{2}\right] $. The large sample (LS) estimate of the CV for the ZIBS distribution is a pooled estimate, as described in Eq (3). Accordingly, the $ \left(1-\rho \right)100\% $ CI for the common CV of several ZIBS distributions employing the LS method is as follows:
where $ {\eta }_{i} = \frac{1}{\widehat{V}\left({\widehat{\theta }}_{i}\right)} $.
Algorithm 3 is used to construct the LS for the common coefficient of variation of several ZIBS distributions.
Algorithm 3.
1) Compute $ {\widehat{\alpha }}_{i} $ and $ {\widehat{\vartheta }}_{i} $;
2) Compute $ {\widehat{\theta }}_{i} $ and $ \widehat{V}\left({\widehat{\theta }}_{i}\right) $;
3) Compute $ {L}_{LS} $ and $ {U}_{LS} $ from Eq (14).
2.4. Bootstrap confidence interval
Efron [25] introduced the bootstrap method, which involves repeated resampling of existing data. According to Lemonte, Simas, and Cribari-Neto [26], the constant-bias-correcting parametric bootstrap is the most efficient method for reducing bias. As a result, we used it to estimate the confidence interval for $ \theta $. Assuming that there are $ D $ bootstrap samples available, the $ {\widehat{\alpha }}_{i} $ series for those samples can be computed, which is shown as $ {\widehat{\alpha }}_{i1}^{\#}, {\widehat{\alpha }}_{i2}^{\#}, ..., {\widehat{\alpha }}_{iD}^{\#} $. Here, $ {\widehat{\alpha }}_{ir}^{\#} $ is a sequence of the bootstrap maximum likelihood estimation (MLE) of $ {\alpha }_{ir} $ for $ i = \mathrm{1, 2}, ..., k $ and $ r = \mathrm{1, 2}, ..., D $. The MLE of $ {\alpha }_{ir} $ can be calculated using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton nonlinear optimization algorithm. The bias of the estimator $ {\alpha }_{i} $ is defined as
and then the bootstrap expectation $ E\left({\widehat{\alpha }}_{i}\right) $ could be approximated using the mean $ {\widehat{\alpha }}_{i}^{/} = \frac{1}{D}{\sum }_{r = 1}^{D}{\widehat{\alpha }}_{ir}^{\#} $. As a result, the bootstrap bias estimate for $ D $ replications of $ {\widehat{\alpha }}_{i} $ is derived as $ \widehat{D}\left({\widehat{\alpha }}_{i}, {\alpha }_{i}\right) = {\widehat{\alpha }}_{i}^{/}-{\widehat{\alpha }}_{i} $. According to Mackinnon and Smith [27], the corrected estimate for $ {\widehat{\alpha }}_{i}^{\#} $ is obtained by applying the bootstrap bias estimate, which is
Let $ {\widehat{\vartheta }}_{i}^{\#} $ be observed values of $ {\widehat{\vartheta }}_{i} $ based on bootstrap samples. In accordance with Brown, Cai, and DasGupta [28], the bootstrap estimator of $ {\vartheta }_{i} $ is given by
By using Eqs (15) and (16), the bootstrap estimators of $ {\theta _i} $ and the variance of $ {\widehat{\theta }}_{i} $ can be written as
and
where $ {\widehat{\varPsi }}_{i}^{*} = {\left(2+{\left({\widehat{\alpha }}_{i}^{*}\right)}^{2}\right)}^{2}\left(1-{\widehat{\vartheta }}_{i}^{*}\right)\left[{\left({\widehat{\alpha }}_{i}^{*}\right)}^{2}\left(4+5{\left({\widehat{\alpha }}_{i}^{*}\right)}^{2}\right)+{\widehat{\vartheta }}_{i}^{*}{\left(2+{\left({\widehat{\alpha }}_{i}^{*}\right)}^{2}\right)}^{2}\right] $. Now, the common $ \theta $ based on $ k $ individual sample is obtained by
Consequently, the $ \left(1-\rho \right)100\% $ CI for the common CV of several ZIBS distributions employing the bootstrap confidence interval (BCI) method is provided by
where $ {\widehat{\theta }}^{*}\left(\rho /2\right) $ and $ {\widehat{\theta }}^{*}\left(1-\rho /2\right) $ denote the $ 100\left(\rho /2\right)\mathrm{t}\mathrm{h} $ and $ 100\left(1-\rho /2\right)\mathrm{t}\mathrm{h} $ percentiles of $ {\widehat{\theta }}^{*} $, respectively.
Algorithm 4 is used to construct the BCI for the common coefficient of variation of several ZIBS distributions.
Algorithm 4.
For $ b = 1 $ to $ n $ :
1) At the $ q $ step:
Fa) Generate $ {y}_{ij}^{*} $, with replacement from $ {y}_{ij} $ where $ i = \mathrm{1, 2}, ..., k $ and $ j = \mathrm{1, 2}, ..., {m}_{i} $;
b) Compute $ {\widehat{\alpha }}_{i}^{/} $ and $ \widehat{D}\left({\widehat{\alpha }}_{i}, {\alpha }_{i}\right) $;
c) Compute $ {\widehat{\alpha }}_{i}^{*} $ from Eq (15);
d) Generate $ {\widehat{\vartheta }}_{i}^{*} $ from Eq (16);
e) Compute $ {\widehat{\theta }}_{i}^{*} $ from Eq (17);
f) Compute $ {\widehat{V}}^{*}\left({\widehat{\theta }}_{i}\right) $ from Eq (18);
g) Compute $ {\widehat{\theta }}^{*} $ from Eq (19).
End $ b $ loop.
2) Repeat step 1, a total of B times;
3) Compute $ {L}_{BCI} $ and $ {U}_{BCI} $ from Eq (20).
2.5. Fiducial generalized confidence interval
Hannig [29] and Hannig [30] introduced the concept of the generalized fiducial distribution by assuming a functional relationship $ {R}_{j} = {Q}_{j}\left(\delta, \boldsymbol{U}\right) $ for $ j = \mathrm{1, 2}, ..., m $, where $ \boldsymbol{Q} = \left({Q}_{1}, ..., {Q}_{m}\right) $ are the structural equations. Then, assume that $ \boldsymbol{U} = \left({U}_{1}, ..., {U}_{m}\right) $ are independent and identically distributed samples from a uniform distribution $ U\left(\mathrm{0, 1}\right) $ and that the parameter $ \delta \in \mathrm{\Xi }\subseteq {R}^{p} $ is $ p $ -dimensional. Consequently, the generalized fiducial distribution is absolutely continuous with a density
where $ L\left(\boldsymbol{r}, \boldsymbol{\delta }\right) $ represents the joint likelihood function of the observed data and
where $ \frac{d}{dr}{\boldsymbol{Q}}^{-1}\left(r, \delta \right) $ and $ \frac{d}{d\delta }{\boldsymbol{Q}}^{-1}\left(r, \delta \right) $ are $ m\times p $ and $ m\times m $ Jacobian matrices, respectively. In addition, Hannig [29] deduced that if the sample $ r $ was independently and identically distributed from an absolutely continuous distribution with cumulative distribution function $ {F}_{\delta }\left(r\right) $, then $ {\boldsymbol{Q}}^{-1} = \left({F}_{\delta }\left({R}_{1}\right), ..., {F}_{\delta }\left({R}_{m}\right)\right) $. Let $ {Z}_{ij}, i = \mathrm{1, 2}, ..., k, j = \mathrm{1, 2}, ..., {m}_{i\left(1\right)} $, be a random sample drawn from the Birnbaum-Saunders distribution. The likelihood function can be written as
Therefore, from Eq (20), the generalized fiducial distribution of $ \left({\alpha }_{i}, {\beta }_{i}\right) $ is
where
as obtained by Li and Xu [31]. Let $ {\alpha }_{i}^{\#} $ and $ {\beta }_{i}^{\#} $ be the generalized fiducial samples for $ {\alpha }_{i} $ and $ {\beta }_{i} $, respectively. According to Li and Xu [31], the adaptive rejection Metropolis sampling (ARMS) method was used to obtain the fiducial estimates of $ {\alpha }_{i} $ and $ {\beta }_{i} $ from the generalized fiducial distribution. Thus, the calculation of $ {\alpha }_{i}^{\#} $ and $ {\beta }_{i}^{\#} $ can be implemented using the function arms in the package dlm of R software. Additionally, Hannig [29] recommended methods for estimating the fiducial generalized pivotal quantities for binomial proportion $ {\vartheta }_{i} $, with simulation results indicating that the best option is the mixture distribution of two beta distributions with weight ½, which is
Currently, the approximate fiducial generalized pivotal quantities for $ {\theta }_{i} $ and the variance of $ {\widehat{\theta }}_{i} $ can be computed by
and
where $ {\varPsi }_{i}^{\#} = {\left(2+{\left({\alpha }_{i}^{\#}\right)}^{2}\right)}^{2}\left(1-{\vartheta }_{i}^{\#}\right)\left[{\left({\alpha }_{i}^{\#}\right)}^{2}\left(4+5{\left({\alpha }_{i}^{\#}\right)}^{2}\right)+{\vartheta }_{i}^{\#}{\left(2+{\left({\alpha }_{i}^{\#}\right)}^{2}\right)}^{2}\right] $. As a result, the common $ \theta $ based on $ k $ individual samples is calculated as
The $ \left(1-\rho \right)100\% $ confidence interval for the common CV of several ZIBS distributions employing the fiducial generalized confidence interval (FGCI) method is obtained by
where $ {\theta }^{\#}\left(\rho /2\right) $ and $ {\theta }^{\#}\left(1-\rho /2\right) $ denote the $ 100\left(\rho /2\right)\mathrm{t}\mathrm{h} $ and $ 100\left(1-\rho /2\right)\mathrm{t}\mathrm{h} $ percentiles of $ {\theta }^{\#} $, respectively.
The algorithm 5 is used to construct the FGCI for the common coefficient of variation of several ZIBS distributions.
Algorithm 5.
For $ g = 1 $ to $ n $ :
1) Generate $ G $ samples of $ {\alpha }_{i} $ and $ {\beta }_{i} $ by using the arms function in the dlm package of R software;
2) Burn-in $ F $ samples (the number of remaining samples is $ G-F $);
3) Thin the samples by applying sampling lag $ L > 1 $, and the final number of samples is $ {G}^{\text{'}} = \left(G-F\right)/L $. Because the generated samples are not independent, we must reduce the autocorrelation by thinning them;
4) Generate $ {\vartheta }_{i}^{\#} $ from Eq (22);
5) Compute $ {\theta }_{i}^{\#} $ and $ {V}^{\#}\left({\widehat{\theta }}_{i}\right) $ from Eqs (23) and (24), respectively;
6) Compute $ {\theta }^{\#} $ from Eq (25);
End $ g $ loop.
7) Repeat steps 1–6, a total of $ G $ times;
8) Compute $ {L}_{FGCI} $ and $ {U}_{FGCI} $ from Eq (26).
3.
Simulation results and discussion
To evaluate the performance of the proposed methods, Monte Carlo simulations in R software were conducted under various scenarios using different sample sizes, proportions of zeros, and shape parameters, as shown in Table 1. The scale parameter was consistently fixed at 1.0 in all scenarios. In generating a simulation, we set the total number of replications to 1000 replicates, 3000 replications for the GCI and FGCI, and 500 replications for the BCI. The performance comparison was based on a coverage probability (CP) greater than or equal to the nominal confidence level of 0.95, as well as the narrowest average width (AW). Algorithm 6 shows the computational steps to estimate the coverage probability and average width performances of all the methods.
The simulation results for k = 3 are shown in Table 2 and Figure 1. The coverage probabilities of the confidence intervals for the GCI method are greater than the nominal confidence level of 0.95 in almost all scenarios, while the coverage probabilities for the MOVER method are close to the specified coverage probability value when proportions of zeros equal 0.13. For the BCI method, they are close to the target, especially when the sample size is large. For the LS and FGCI methods, they provide coverage probability values lower than 0.95 in all scenarios. In terms of average width, the LS and MOVER methods have narrower confidence intervals than other methods in most scenarios. However, the coverage probabilities of both confidence intervals are less than 0.95 in almost all scenarios, so they do not meet the requirements. Among the remaining methods, the GCI method has the shortest average width in all scenarios studied, while the BCI method has the widest.
The simulation results for k = 5 are shown in Table 3 and Figure 2. The coverage probabilities of the LS and BCI methods are close to the nominal confidence level of 0.95 in almost all scenarios. In contrast, the MOVER and FGCI methods have values below the specified target. For the GCI method, the coverage probability meets the target when the proportions of zeros are unequal. In terms of the average width, the confidence interval of the MOVER method is the narrowest. However, this method has a coverage probability lower than 0.95 in all scenarios, thus failing to meet the criteria. The LS and BCI methods have the widest confidence intervals compared to the other methods.
The simulation results for k = 10 are shown in Table 4 and Figure 3. In almost all scenarios, the LS and BCI methods have coverage probabilities greater than or close to 0.95, except when the proportions of zeros equal 0.510. Both methods have wider average widths compared to the other methods. The GCI method has coverage probabilities close to 0.95 when the sample size is large and the shape parameters are equal to 2.0. For the MOVER method, even though it has the narrowest average width, it has coverage probabilities lower than 0.95 in all scenarios.
Figures 1–3 exhibit similar patterns, showing consistent trends. As the sample size increases, all the proposed methods tend to decrease. Similarly, as the shape parameter increases, all the proposed methods also tend to decrease. Conversely, when the proportion of zeros increases, all the proposed methods tend to increase. These observations are all based on the average width.
Algorithm 6.
For a given $ \left({m}_{1}, {m}_{2}, ..., {m}_{k}\right) $, $ \left({\alpha }_{1}, {\alpha }_{2}, ..., {\alpha }_{k}\right) $, $ \left({\vartheta }_{1}, {\vartheta }_{2}, ..., {\vartheta }_{k}\right) $, and $ {\beta }_{1} = {\beta }_{2} = ... = {\beta }_{k} = 1 $,
for $ r = 1 $ to $ M $
1) Generate sample from the ZIBS distribution;
2) Compute the unbiased estimates $ {\widehat{\alpha }}_{i} $ and $ {\widehat{\vartheta }}_{i} $;
3) Compute the 95% confidence intervals for $ \theta $ based on the GCI, MOVER, LS, BCI, and FGCI via Algorithms 1–5, respectively;
4) If $ \left[{L}_{r}\le \theta \le {U}_{r}\right] $, set $ {D}_{r} = 1 $; else set $ {D}_{r} = 0 $;
End $ r $ loop.
5) The coverage probability and average width for each method are obtained by $ CP = \frac{1}{M}{\sum }_{r = 1}^{M}{D}_{r} $ and $ AW = \frac{{U}_{r}-{L}_{r}}{M} $, where $ {U}_{r} $ and $ {L}_{r} $ are the upper and lower confidence limits, respectively.
4.
An empirical application
In this study, we leverage wind speed data from all directions to construct CIs for the common coefficient of variation of several ZIBS distributions. The data were collected from January 1 to 7, 2024, from three weather stations: Chanthaburi Weather Observing Station in Chanthaburi Province, Chumphon Weather Observing Station in Chumphon Province, and Songkhla Weather Observing Station in Songkhla Province. The selection of these three stations is due to their proximity to the Gulf of Thailand, which makes them directly influenced by sea breezes and tropical storms. This results in high wind speed fluctuations and also impacts the livelihoods, economy, and environment of the surrounding communities. All data were collected by the Thai Meteorological Department and are presented in Table 5 (Thai Meteorological Department Automatic Weather System, https://www.tmd.go.th/service/tmdData). To visualize the data distribution, we plotted histograms of wind speed data from all three stations, as shown in Figure 4. Table 6 provides statistical summaries for wind speed data at each station, revealing that the coefficients of variation of the wind speed data for the Chanthaburi Weather Observing Station, Chumphon Weather Observing Station, and Songkhla Weather Observing Station are 2.6799, 2.5111, and 2.7118, respectively. When considering the entire wind speed dataset, we observe a mixture of zero values (no wind) and positive values. For the positive values, we evaluate the suitability of the data distribution using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) calculated as $ AIC = 2ln\left(L\right)+2p $ and $ BIC = 2ln\left(L\right)+2pln\left(o\right) $, respectively, where p is the number of parameters estimated, o is the number of observations, and L is the likelihood function. From Table 7, it is evident that the Birnbaum-Saunders distribution exhibits the lowest AIC and BIC values compared to other distributions, indicating its best fit for positive wind speed data. Additionally, to confirm that the positive wind speed data follows the Birnbaum-Saunders distribution, we plotted the cumulative distribution function (CDF) derived from the positive wind speed data and the estimated CDF from the Birnbaum-Saunders distribution. As shown in Figure 5, both graphs are similar, indicating a good fit. Therefore, the wind speed data comprises both positive and zero values and follows the ZIBS distribution. This distribution was thus used to compute the CIs for the common coefficient of variation of the wind speed data. Table 8 presents the 95% confidence intervals for the common coefficient of variation of wind speed data from the three weather observing stations using the GCI, MOVER, LS, BCI, and FGCI methods. We compared wind speed data with parameters generated from simulation using a sample size of $ {m}_{i} $ = 1003, parameter $ {\alpha }_{i} $ = 2.53, and parameter $ {\vartheta }_{i} $ = 0.53, as shown in Table 2. The simulation results indicate that the GCI and BCI methods meet the criterion of coverage probability greater than or equal to the nominal confidence level of 0.95. When considering the average width, the GCI method provides the narrowest confidence interval. The results in Table 8 show that the confidence interval for the common coefficient of variation for the wind speed data using the GCI method is [2.5001, 2.7224], with a confidence interval width of 0.2224, which is the narrowest among all methods. This leads to the conclusion that the appropriate method for the wind speed data is consistent with the simulation results.
5.
General discussion
Based on the study results, it is evident that the GCI demonstrates good performance in almost all scenarios, as the coverage probability is greater than or close to the nominal confidence level of 0.95, which is consistent with the previous research by Ye, Ma, and Wang [32], Thangjai, Niwitpong, and Niwitpong [33], Janthasuwan, Niwitpong, and Niwitpong [11]. When k is large, both LS and BCI perform well. In most scenarios, MOVER and FGCI have coverage probabilities below acceptable levels, indicating that these methods may not be suitable for many situations, which aligns with the previous research by Puggard, Niwitpong, and Niwitpong [17]. Considering the average width, all proposed methods tend to decrease as the sample size and shape parameters increase, which improves their efficiency. Conversely, when the proportion of zeros increases, all proposed methods tend to decrease, leading to reduced efficiency. In our case, the simulation results showed that the MOVER method provided the narrowest confidence intervals for most scenarios and performed well with small sample sizes combined with a low proportion of zeros. However, the MOVER method yielded coverage probabilities lower than the specified confidence level in almost all scenarios. Similarly, the FGCI method achieves a coverage probability close to the specified confidence level in scenarios with a low proportion of zeros. This could be attributed to certain weaknesses that affect the fiducial generalized pivotal quantities for the proportion of zeros. Additionally, the issues with both the MOVER and FGCI methods likely arise from the upper and lower bounds for zero values used in constructing the confidence intervals and the combined effect with other parameters; this results in insufficient coverage probability. Finally, wind energy is a vital, renewable source of power, primarily generated by capturing wind speed. However, fluctuations in wind speed can introduce uncertainty. According to Lee, Fields, and Lundquist [34], understanding these variations is crucial for assessing wind resource potential.
6.
Conclusions
This article presents an estimation of the common coefficient of variation of several ZIBS distributions. The methods proposed include GCI, MOVER, LS, BCI, and FGCI. The performance of each method was evaluated through Monte Carlo simulations, comparing their coverage probabilities and average widths. The simulation results for k = 3 recommend the GCI method due to its acceptable coverage probability and narrow confidence intervals in almost all scenarios, while the BCI method is another option for situations with large sample sizes. For k = 5, we recommend the GCI method when $ {\vartheta }_{i} $ is unequal, the LS method when $ {\vartheta }_{i} $ is small and the sample size is large, and the BCI method when $ {\vartheta }_{i} $ is large. For k = 10, the BCI and GCI methods are recommended: the BCI method (for small to medium sample sizes) and the GCI method for large sample sizes. Additionally, in all sample cases (k = 3, 5, and 10), the MOVER method has the narrowest confidence intervals but a coverage probability below the acceptable level in most situations, and the FGCI method has a coverage probability below the acceptable level in almost all situations. Therefore, these two methods are not recommended. Finally, all the proposed methods were applied to wind speed data in Thailand and yielded results consistent with the simulation findings. In future research, we will explore new methods for constructing confidence intervals, potentially using Bayesian and highest posterior density (HPD) approaches to enhance their effectiveness. Additionally, we will use other real-world data to conduct a more comprehensive study.
Author contributions
Usanee Janthasuwan conducted the data analysis, drafted the initial manuscript, and contributed to the writing. Suparat Niwitpong developed the research framework, designed the experiment, and reviewed the manuscript. Sa-Aat Niwitpong provided analytical methodologies, validated the final version, and obtained funding.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to express their sincere gratitude to the editor and reviewers for their valuable comments and suggestions, which have significantly improved the quality of the manuscript. This research was funded by the King Mongkut's University of Technology North Bangkok, contract no: KMUTNB-68-KNOW-17.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: