Numerical and graphical simulation of the non-linear fractional dynamical system of bone mineralization

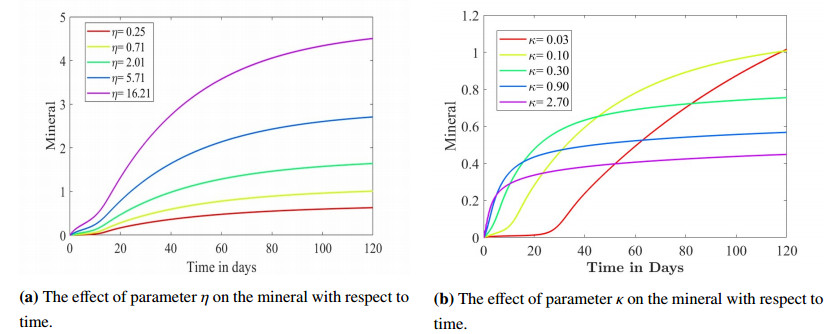
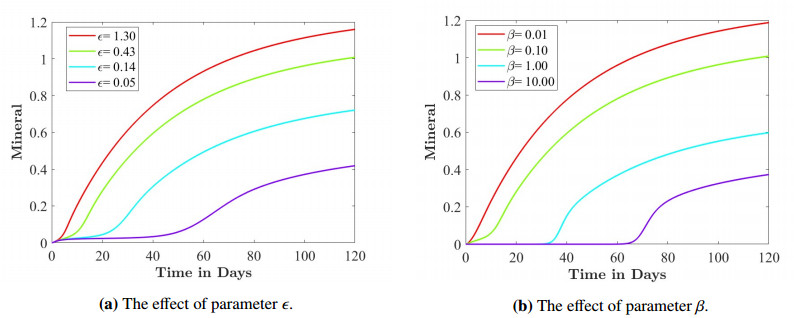
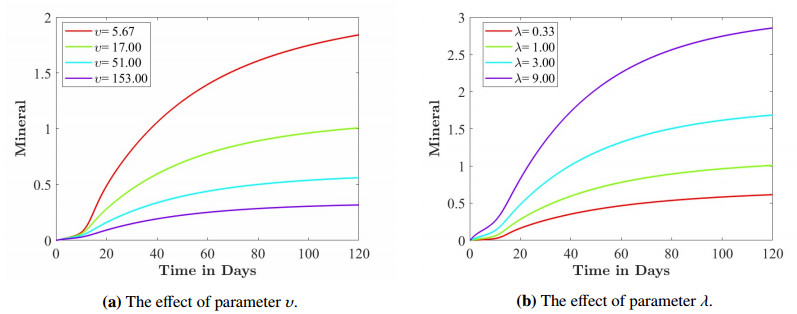
1.   Introduction

The risk of privacy leakage is often encountered in the exchange of medical data, especially between institutions. Because auxiliary algorithms used by institutions come from different manufacturers, some data analysis tools even need to be connected to the Internet. Commercial biometric estimators with face recognition algorithms (FRAs) may steal facial data to a third party during transmission. Biometric Privacy-Enhancing Techniques (PETs) have been invented, but none can cope with all situations. There are three classifications to hit the target. One is parts shelter. The characteristic is that the human can see the local content, and the information of the specific information is hidden. Additional computational overhead is required while the image is restored, e.g., pixelation and blurring. Another is in pixels recoding. Anyone can hardly recognize the content in the image unless they know the cipher. For this reason, a password is required whenever the image is used, e.g., chaos ^[1] or RCDP ^[2] method. And the most suitable for daily use is cloak perturbation. It can not only hide specific features but also be recognizable to humans, e.g., Fawkes ^[3] and federated privacy ^[4]. The first two categories are almost impeccable, but in most cases, face images still need some readability in daily research, e.g., medical institutions exchange toddler images to record the relationship between eye distance and height. In contrast, the desensitization of children's images deserves more attention than the research itself. However, if the face image is hidden roughly, it may bring inconvenience to doctors to identify patients.

PET methods are currently formulated for one or several types of FRAs. Hence, those excellent cases become helpless once the scenes are changed. These studies were not widely adopted because FRAs upgraded and developed rapidly, and the computing power and network update for face tasks were also fast. Further, the average annual compound growth rate of the face recognition market alone is 30.7% from 2010 to 2018, and the market scale will exceed 7 billion dollars by 2024 ^[5]. More importantly, everyone can get and collect FRAs easily. Since 2014, commercial FRAs have sprung up, and they have a perfect development to after-sales process, so their recognition accuracy is approaching 99.99% as shown in Table 1. After the COVID-19 outbreak, FRAs for deep occlusion have also emerged. They can identify covered faces (gauze mask), even the face covered over 50%. We can't conclude whether a camera applies an FRA, and manufacturer of the FRA.

The classification of PET can be roughly divided into 6 groups ^[28]: 1) Data applicable, 2) Mapping type, 3) Biometric attributes, 4) Ways to address biometric utility, 5) Guarantee of the possibility of reconstructing information, 6) Hidden biometric targets (humans and/or machines). As for the specific response measures, only three categories are widely used. Only Image means, representation means and inference means can produce effective algorithms.

Image means are used to process graphics or videos. Their target may be humans or machines. Confusion, confrontation and synthesis technology is used to change visual data to protect privacy ^[29,30]. Representation means are based on the method of transformation and elimination. It suppresses some target aspects of data by transforming the original template into another form. It can also delete the meta element with the largest amount of information about the target attribute in the template ^[31], and used only for a pre-defined purpose ^[28]. Inference means usually change the biometric template and the comparison/classification process used to drive the similarity/comparison score ^[32]. Unlike image means PET, this group's technology is specifically aimed at automatic machine learning models rather than humans. However, our research mainly focuses on an image processing method that allows human beings to know who's that in the picture while the machine cannot, so we need to combine both image and inference. It is more important to disable many machine recognition algorithms as much as possible, rather than a certain class.

All privacy protection networks based on neural networks are easily affected by the neural network itself. Therefore, even if the PET algorithm is extremely advanced, it cannot keep up with the frequently upgraded FRA. PET algorithms are usually targeted for research and development. Take Fawkes ^[3] for example, the training for ArcFace V1 has been outstanding, and the success probability (SP) can reach over 90%. However, this algorithm is failed to work with V2 soon after it was proposed. Even if we retrained the model, SP dropped below 50%. FlowSAN ^[33] as representative of semi-advertising networks will make the face look more and more strange with the high threshold. Thus, some face attributes are hidden. As shown in Figure 1. Later, some algorithms were compared. Few PETs can cope with multiple types of FRAs at the same time.

As shown in Table 2, almost every method is not competent for non-anticipatory situations. If the retrained model copes with the new FRA version, it may lead to data rewriting. It's necessary to study a sustainable PET without retraining. Algorithm convergence leads to complex and huge networks. Therefore, no ideal neural network can be fast and flexible for multiple FRAs. High intensity GAN often leads to output distortion to the eyes or failure to FRAs.

In short, the main point is to keep the generator adapting to the newly added discriminator (black box FRAs) continuously. It is more important to find a fast gradient descent method when the parameters are increasing.

The main contributions of this work can be summarized as follows:

1) The model can integrate many face recognition algorithms without caring about their structure and training sets.

2) The algorithm proposes an inverse back coupling mechanism to make the output play the opposite role to the input and automatically balance the target error.

3) Keeping the network stable with the help of the principle of social animal hunting.

4) Use the validator to score and maintain a stable visual effect.

2.   Related works

2.1.   Privacy and security technology

Privacy-Preserving and Security Mining Framework (PPSF) offers algorithms for data anonymity, privacy-preserving data mining, and privacy-preserving utility mining ^[41]. It comprises 13 data anonymity algorithms. However, these state-of-the-art algorithms mainly hide sensitive information ^[42], making the targets they try to read become incomprehensible, including humans.

Lin et al. proposed an ant colony optimization (ACO) method ^[43], which uses multiple objectives and transaction deletion to protect confidential and sensitive information. This method mainly deletes transactions to protect confidential and sensitive information, which belongs to representation means. That protected information will not apply to the data without dedicated tools, e.g., CT graphics.

Shan et al. ^[3] use the Generative Adversarial Networks to cheat the ArcFace algorithm at the image level. As a result, they can magically disable the specific FRA, to protect the textured face ID from being collected. The biggest disadvantage of this method is that it can only be used for a certain FRA. If FRA changed, the network needs to be retrained.

Wang et al. ^[44] introduced the nearest neighbor method to calculate the cosine similarity of feature vectors into edge computing, which can effectively improve the security of face data in the cloud. The fault tolerance of identity authentication systems is improved by the secret sharing of homomorphism technology of distributed computing.

The research of soft biometrics considers the use of feature templates to infer information about a person's gender, age, race, sexual orientation, and health status ^[32]. The server preserves a full amount of face feature templates ^[45]. In the business process, face privacy is safe, but if the server receives an intrusion, there is still a risk of privacy disclosure.

In brief, the existing privacy protection methods are described for a certain pattern of FRA, and most of them are for machine recognition.

2.2.   Information fusion

Damer et al. suggested the concept of algorithm fusion in 2013 ^[46]. The algorithm results from different sources are normalized, and then the scores are fused to improve compatibility. However, after our evaluation, the time to reach the deviation of multiple algorithms is unacceptable, especially in the black box state. Baseline weighting algorithms ^[47] were applied in the second year. Although the robustness has been improved, the experimental results show significant differences for different data sets.

Subsequently, Damer then focused on an asynchronous combination-based score-level weighted-sum fusion approach ^[48]. Its focus is on the trusted model, not the attack model. We believe that the attack model is the key to protect privacy. Face Morphing Attacks were invoked ^[49] by the minimum, maximum, and mean fusion rules, and at most 3 detectors of different protocols can be fused. The new method is totaling up to six fused detectors in different attacks.

Literature ^[50] gives us some enlightenments. Even if we integrate some algorithms, some repair methods can still judge the changed area in the image, resulting in the attack's failure. There must be a network structure with both automatic mechanism and manual intervention mechanism to prevent the generated attack image from being seen through.

3.   Methods

A face image should be blocked by some cloaks so that the corresponding FRA recognition can be prevented as shown in Figure 2. Considering the variety and self-renewal of FRA, the algorithm should be compatible. The overall goal is to make function f that exerts some perturbation on the input image x to satisfy the following properties:

It believes that the facial feature template corresponding to each algorithm is different. We define the characteristic set of each FRA as the two-dimensional representation of its feature template, and its mapping to image x is s. The original image feature c_x∈s and the output image feature c_y∉s.

If the feature set of x in FRA1 and FRA2 are s₁ and s₂ respectively, then the output image meets c_y∉(s₁∪s₂).

3.1.   Adversarial fusion network

The best way to inherit human visual recognizance is to add small perturbations to the image, therefore the main research objective is to utilize the cloak pixels to encrypt the image. The proposed Adversarial Fusion Network (AFN) is divided into two categories: build a generative adversarial network (GAN) and inverse back coupling validator. In order to improve the compatibility of the algorithm, the adversary nozzles are used to carry out black box attacks instead of the discriminator. True and false images at the nozzles can be docked to parallel FRAs and compared constantly until they are decided to be different results completely by FRAs. To keep the visibility of the output image, a validator scores the output image to determine the generation effect, as shown in Figure 3.

The output contains random factors related to the distribution of feature points corresponding to the target FRA. The greater the Euclidean distance between the output vector and the original vector, the weaker FRA's ability. If multiple FRAs are compatible, try to keep the output vector consistent with the original image when the current FRA fails. The original image can be restored by printing random factors and calculating with the protected image. According to this idea, we assume that the regression function f is the feature point mapping learned in an FRA. In the training stage, the same mask template distribution needs to be got from images of different scales, and the complete feature space should comply with Eq (1). Vector $\boldsymbol{\varphi }$ is the n_th feature distribution of different scales (s) in the original images. Equation (2) makes the network learn the hyperparameters. The relatively simple idea is the translation and scaling for the aim function in Eq (3).

Set I represent input eigenvector, ${\mathrm{\omega }}_{\mathrm{*}}$ is hyper parameter, * refers regional coordinate of the feature point, ${f}_{\mathrm{*}}$ is predicted value, which should have the smallest Euclidean distance from the real value ${t}_{\mathrm{*}}$, Eq (4) is the loss function for adversary nozzles, which distinguishes the difference between the generated image and the original image. The function optimization goal is defined as Eq (5).

Input images are samples of different scales and distinct faces which are mapped to a fixed size landmark template image, and the feature output is given by the same FRA. The feature points region output by the algorithm is pre-processed in 4 × 4 × 3 pixels or 4 × 4 × 1 pixels to reduce the amount of computation (the result of a grey scale image is sometimes not ideal, because some algorithms are sensitive to color channels). Normalizing a random facial mask model is expected to have 30 million super parameters, so it is necessary to establish a simple network. Each layer adopts batch normalization layer to speed up model training and prevent over fitting ^[51]. We use a filter of 4 × 4 pixels and the same convolution (stride is 2). After 2 consecutive convolutions with 16 filters, the image is compressed to 128 × 128 × 32 pixels through the pooling layer. Then there are several convolution layers again, by using 64 filters and some same convolution. After pooling, it becomes a 64 × 64 × 64 matrix. Subsequently, matrix data of 16 × 16 × 128 pixels are gained through 128 filters and maximum pooling twice respectively. After passing through two full connection layers, it is input into the Softmax layer for activation, as shown in Figure 4.

The concept of adversarial example transferability was first proposed by Szegedy et al. ^[52], in that the training models with different structures on different subsets set results in the target model have high confidence error classification. If the trained model is universal, Feature-representation-transfer ^[53] can be used as a node to fit different FRAs. Adversary nozzles establish a connection between the generator and FRAs, it aggregates the vectors with close feature distance into a subset that reduces the network parameters. The set φ is used to describe the characteristics of FRAs. The regrouped distribution f_{(x, y)} is continuously fed back to the generator and compares the distance of the same feature with the real image. e.g., the tip and wing of nose are mapped to vector τ for different FRAs as shown in Figure 5. Next, more new FRAs can be added, and old memories are stored in the set φ.

However, feeding data only through the nozzle will make the output image unattractive with high probability. If the generated image is approaching an unacceptable level, the nozzle should be closed in time. In the formula, the distribution parameter θ comes from the validator which makes the Euclidean distance between desired distribution t_* and measurement f_* as small as possible. The validator comprises six deconvolution layers and a human face tracking network. On the one hand, the deformation degree of the generated image is detected by the visual semi supervised window ^[54]. On the other hand, if the face cannot be detected, the training will be stopped by nozzles.

The generated template can be regarded as a reserved room. If it is filled with noise, the image is encrypted. Using the template to do XOR operation with the encrypted image can also restore the image.

3.2.   Group hunting in AFN

When carrying out multi-objective AFN tasks, training time is a thorny problem. Attacker, barrier, chaser, and driver are simulated in expectation, extreme value, data distribution, and minimum loss ^[55]. We use the division of labor of chimpanzees in hunting behavior to improve the cooperation ability of the network. Each hidden layer in AFN is treated as a chimpanzee. The characteristic distribution plane is considered as a tree.

In nature, there are two main differences between chimpanzee groups and other biological groups:

1) Individual diversity: in a group of chimpanzees, the abilities and intelligence of individuals are not similar, but they are all members of the hunting team, and there is no discrimination when performing tasks. In view of their different abilities, chimpanzees will be responsible for different hunting operations according to their special abilities. In the algorithm, different models with different curvature, slope, and interception points are used to give chimpanzees different behaviors, just like in natural hunting tasks.

2) Sexual motivation: besides the great advantages of group hunting, research shows that the hunting behavior of chimpanzees is also affected through the social benefits brought by obtaining meat. After obtaining meat, chimpanzees have a certain reputation. They can use the meat for corresponding returns, such as sex, being groomed by their companions, and so on. Unfortunately, chimpanzees will shuffle their duties after each round of hunting. The chaos stimulates them to obtain meat quickly. This unconditional behavior improves the exploitation and convergence speed in the final.

Attackers need more cognitive effort to predict the subsequent movement of prey, so after successful hunting, they will get a larger piece of meat. This aggressive behavior is positively correlated with initial position, empirical value, and time. In addition, chimpanzees can choose roles in each round of hunting according to their advantages ^[56].

Different FRAs are regarded as prey in AFN. The target FRA can appear simultaneously or separately, depending on the distance between the pursuer and the prey in the initial stage. Of course, every chimpanzee is constantly changing its position for driving and chasing its prey. The driver followed the FRA without trying to catch. And the barrier places itself on a tree to prevent FRA from escaping (Upgrading). The chaser chased the FRA and explored its route. Finally, the attacker predicts the FRA's downward escape route and grabs it at the shortest distance.

The driving model d in the exploration and exploitation phase represents the relative distance between the position of driver ${x}_{c}$ and the position of prey ${x}_{p}$. Where t (<500) stands for the iteration sequence number, a, m, and c are the coefficient vectors in [0, 2]. The smaller d, the better, but it cannot be 0. Its goal is to make prey move, the Eqs (6) and (7) are proposed.

According to experience, let the initial value x of f be 0.1 and the nonlinear descent space be [3.57, 4]. In which, ${\boldsymbol{r}}_{1}$ and ${\boldsymbol{r}}_{2}$ are the random vectors in the range of [0, 1]. Equations (8)–(10) respectively.

Finally, m is a logistic mapped vector that represents the effect of the chaotic stimulates (sexual motivation) of chimpanzees after hunting. Convergence rate is improved via the chaotic function in complex and high-dimensional problems. All particles behave similarly in both local and global searches, so individuals can be considered as a single population with a common search strategy.

Chimpanzees can be divided into several hunting groups. The roles of each group are the same, and the members of the group can be adjusted after several rounds of hunting. In Table 3, where t refers to the current iteration and T indicates the maximum number of iterations.

There are no known parameters of an FRA. In order to compare gaining FRA characteristics to chimpanzees hunting, it is assumed that any member can be a chaser to report the location x. These recommended role models are applied and the other members update their positions based on the recommended initial values to get the best formation. The relational model is expressed by the Eqs (11)–(13).

The hunting role of chimpanzees is represented by subscript R; n is the group number of the next change. When the prey weight c > 1, the hunting group hunts (encircle and intercept), otherwise, it will divide food or reassign roles. This parameter also contributes to the randomization of the optimization process and reduces the probability of local minimization. Note that the c vector follows the same random function mapping from the beginning to the end of the iteration.

3.3.   Ensemble training

Federated learning ^[39] and transfer learning ^[4] can also deal with multiple FRA attacks. However, their parameters are relatively large, and the gradient explosion or gradient disappearance often occurs. Too many training rounds will often lead to an unsatisfactory feeling for the human being. ChOA theory can realize rapid gradient descent, and the acceptance of the output image can be effectively optimized.

All the feature points can't be clustered separately ^[57], because there will always be some unknown data. Chimpanzees need to know the focus of each FRA. According to the assumption, if the key points of an image correspond to the positions of different prey, the way to reduce the network parameters is to drive the prey to a certain position and then attack. It can reduce the capture time (training speed) and make the focus on the prey closer to the attacker (gradient explosion).

Attackers attack the prey on the grassland named $\sigma$, the lowest gradient acceptable to the human. After AFN began, chimpanzees entered the stage of exploration. They search for prey (local extremum) separately and attack intensively. The vector a with a random value from -1 to 1, so that searchers focus on tracking prey far away from others. When inequality |a| > 1 the chimpanzees abandon the current route to find new prey, as shown in Figure 6.

As mentioned earlier, after several iterations of hunting activities, each chimpanzee adjusts its weight and position (satisfaction after eating), and then released or inherited its previous responsibilities. Therefore, the chaotic way helps to balance the division of labor among hunting groups. This chaotic behavior helps chimpanzees to further ease falling into local optimization and slow convergence speed in solving high-dimensional problems. Once the prey is captured, the nearest four groups of chimpanzees will regroup and start new exploitation.

Every one-dimensional vector can be regarded as a chimpanzee to indicate the candidate points in AFN. Further, the weights are the coefficients of social roles, in which the total length is equal to the vector's in $\boldsymbol{\varphi }$, in Equation 14, where h is the number of neurons in the hidden layer and n is the number of inputs ^[58]. As an example of this analogy, the ensemble training is shown in Figure 7. Mean square error (MSE) is used to measure the fitness of the chimpanzee, which calculates the difference between the expected value f and evaluation value $\widehat{f}$ of all training in Eq (15). Where n is the number of instances in the training dataset.

3.4.   Template application

The captured prey is mapped to a two-dimensional grassland. It not only affects the behavior of chimpanzees' social factor but also stores it in a room to generate templates. In other words, the main purpose of the attack is to determine the position of the prey on the σ plane, which continuously forms a template corresponding to the feature points collected by FRAs. And the template is transformed into printed patch ^[59] by texture visualization technology as shown in Figure 8..

Because the location of prey driven to the ground is random, each template file is different. They are combined with perturbation technology to encrypt face images. For the generator, in order to improve the quality of samples and the speed of convergence, all pooling layers and full connection layers are cancelled ^[60]. This method can reduce the difficulty of search σ. The only problem is that it will produce noise pollution.

By mapping Gaussian noise onto the template file and XOR with the original image, the features concerned by FRAs can be hidden. In order to make the generated image more realistic, we conduct Y-axis mapping on the images of less than 2KB in CelebA dataset, convert them into Gaussian noise and give them to AFN. The protected image is a set of pixels at specific regions generated by random noise. If template file XOR with the disturbed image again and the pure image can be restored. The template file can be saved again through image encryption technology ^[61] to increase its security.

4.   Results

4.1.   Datasets and experimental setup

This section compares the effects of several famous privacy protection methods, famous FRAs will also take part in the experiments. Distributed training conducted by the GPU of ARM mali-t860 MP4 and the development board of 16 core NPUs. CelebA, LFW, and Andy_Lau datasets are used to assess the performance.

Privacy protection methods include: Chaos ^[62] and cryptography ^[2], zero-watermark ^[63], Feature area twist ^[6], Fawkes ^[3], ADVHAT ^[64] in the image level. Parameters of paper ^[65] are used in the inference experiment.

FRAs include: Baidu ^[18], Azure face ^[66], Face++ ^[19], ArcFace ^[22] and open source face recognition algorithm based on Dlib ^[67]. They are renamed as ${M}_{B}$, ${M}_{Az}$, ${M}_{F}$, ${M}_{Ar}$, ${M}_{D}$ for convenience.

4.2.   Visual effect experiments

This experiment is aimed at implementing ArcFace algorithm. ADVHAT and Fawkes algorithms are not updated for other FRAs. Principal component analysis (PCA) ^[68] method is used to reduce dimensionality to accept a two-dimensional space of visual features. To keep the interpretation of the original data to the greatest extent, this paper uses the minimum loss theory to make the first principal component have the largest variance, and each subsequent principal component is orthogonal to the previous ones. An image covered by every protection shows that chaos and cryptography are strongest and zero-watermark almost impossible to protect privacy, the algorithms of changing the eigenvector with cloak all work well, as shown in Figure 9. Although from the mathematical, most algorithms have the basic elements of hiding privacy. However, the printed image can't be recognized except ADVHAT, Fawkes, and the mask template.

4.3.   Template mapping deviation experiments

We refer to ^[65] and use 70% of CelebA as a data training set and 30% as a test set. Performance evaluation is conducted with a test set. Images from LFW are used to assess the generalization capabilities of AFN. To have a consistent evaluation setup, face recognition, gender, and age are organized into the experiments Learning-based and Strict (LBS) evaluation protocol ^[69] is used to train, and the dataset is organized into 5 folds. The commercialized FRA will not abide by the rules. The only way to prove whether the privacy protection is effective is whether the attacked FRA outputs the correct face ID. We use err to analyze the average ratio of genuine pair comparison.

Privacy-gain identity-loss coefficient (PIC) is used to evaluate the performance of the model. Where $fi{c}^{{'}}$ and $eer{'}$ were computed from the attribute suppressed representations, whereas the errors fic and eer were calculated from the original (unmodified) face representations ^[37], shown in Eq (16) ^[37], the higher value of PIC the performance is better. The model maps the initial face representations into disentangled representations z, z_id, and z_att, where z represents the template information of a face, z_id shows identity information and z_att encodes information about biometric attributes.

The fraction of incorrectly classified images fic and equal error rates err are reported for the face id and attribute recognition. In table 4, the impact of the model on potential space is concentrated on z_id, and the information of z_att includes age and gender are not been affected. The experimental results show our model does not care about the specific attributes of the face, we only care about whether FRA can output face ID. Existing state-of-the-art e.g., PE-MIU ^[32], Unsupervised privacy-enhancement (PE-UP) ^[37], feature disentanglement (PE-FD) ^[65], prefer to hide some key attributes and preserve the recognizability of face.

This implies that the total privacy cost remains unchanged. It is important to apply an adaptive iterative privacy budget allotment to a fixed allotment ^[70]. In terms of latent space, the goal is to maneuver latent space to achieve a given image's transformations ^[71]. After mapping, the template coordinates of Arcface algorithm are output in the training network as shown in Figure 10, where x_s is the original image and x_t is the image template in AFN. It can be seen that the feature distribution of the processed image has changed. All the test samples are collected as shown in Table 5. We have added liveness (images of volunteers) experiments to deal with reality.

It can be seen from the experiment that the single FRA algorithm can change the image feature distribution and make the detector ineffective. The best experimental result is Andy_ Lau's data set has a change rate of over 40% in the Arcface V2 algorithm. M_D is not intelligent, so it is only recorded and not included in the experimental data.

4.4.   Cheat experiments

The comparison processes adopt the black box method, and the evaluation index uses the protection score ${s}_{p}$, which objectively evaluates the effect of algorithm output on the targeted FRA.${F}_{p}$ represents error samples on target FRA, ${T}_{p}$ means accuracy given by FRA authors. ${F}_{t}^{n}$ stands for the correct samples of the image after the protection algorithm in other FRA. $\beta$ is the perception coefficient, which is based on the subjective evaluation of the tester comparing all the experimental results' weight from 0.10 to 0.99, n is FRA's ID. Shown as Eq (17), 1500 samples were tested in Table 6.

The results indirectly proved that the method proposed in this paper has compatibility when dealing with multiple FRAs. Chaos method is more efficient without considering the visual effect.

4.5.   FRAs superposition experiments

There is a catastrophic forgetting (feature confusion) phenomenon. Obviously, the pixel coordinates have shifted, as shown in Figure 11. Intuitively, it should be substantial differences in landmarks specifications of these enumerated FRAs, which may be related to the initial chaotic function of the chimpanzee hunting group. Logistic chaotic mapping with values of [0.01, 0.4] is used. If Singer mapping was used, the effect is much better. If users do more chaotic mapping experiments, they can save a lot of time, because they often find that the vision is affected after many rounds of model training.

The output image results from the XOR operation between the noise and the original image through the mask template in Figure 12. Therefore, in order to restore the image, we only need to make the output image XOR with the mask template again. The mask template can be saved by image encryption. When the image needs to be decoded, restore the graphical mask template by decryption, to ensure the security of the mask template key.

The average error rate of cumulative FRAs ${\overline{F}}_{p}$ proves the generality of the algorithm studied in this paper. Even if the generated image is far from expected, it must be able to restore to the original state. Table 7 records the results of accumulating different FRAs, where Perception is the author's subjective opinion, and ${\overline{R}}_{\boldsymbol{p}}$ is the recognition accuracy after restoring. It can be demonstrated that the number of FRA is not directly proportional to the training time.

To investigate the performance of the algorithm switching between different versions of FRA from the same manufacturer, V1 and V2 of ${M}_{Ar}$ is chosen because these two versions are easy to download and have different interfaces. V1 training took 19,333 minutes to generate a template, but it is invalid when applied to V2. Then V2 is directly turned into prey without changing the network structure and protected image. The result can be successful and takes another 6010 minutes. In contrast, Fawkes takes 61,028 minutes to train on V1 and AdvHat takes 93,110 minutes (two gradient explosions).

5.   Discussion

The facial mask from AFN has great efficiency, but the solution to the template coordinate drift is only to change the chaotic function. The main reason is that we do not fully use the social behavior of chimpanzees. In other words, when the target features are captured, the weight of various roles in the network does not form an effective replacement. This causes that if the roles and tasks assigned at the beginning are not reasonable and the follow-up work is not tuned, we can only get good results from the random chaotic function. In the next work, we will focus on the optimization of task allocation and let the network adjust the weight of hunting members automatically.

6.   Conclusions

The model proposed in this paper can ensure that the target face recognition algorithm cannot recognize the protected Face ID. the model improves the existing algorithms that can only protect the privacy for specific face recognition algorithms, and can deal with multiple recognition algorithms at the same time. In addition, a negative feedback network is added to intervene in image distortion, so that it can ensure that human beings can recognize the protected Face ID. In order to speed up the speed, the optimization algorithm of chimpanzee group hunting is introduced. Experiments show that the model can change the feature distribution of the facial image by up to 42% without obvious visual changes. It can be connected in parallel at least five commercial face recognition algorithms. Using a chaotic function to initialize network parameters can reduce the difficulty of network design, but it will produce slight noise on the output image. This will reduce the possibility of a gradient explosion. Compared with other biological privacy protection methods based on small perturbation, our method can improve the training speed by 4.8 times.

Acknowledgments

This research was partially funded by the Strategic Priority Research Program of the Chinese Academy of Sciences, grant number XDB41020104 and Scientific Research Project of Beijing Educational Committee, grant number KM202110005024.

Conflict of interest

The authors declare no conflict of interest.