1. Introduction
Dynamics of prey-predator systems has been an important research theme in ecology. It is well known that prey-predator interaction is not only one of the basic interspecies relations for ecological and social systems, but also the basic block of more complicated food chains, food webs, and biochemical network structures [21]. In the biological world, there are many examples of precesses that involve significant delays that cannot be ignored [13]. Examples include the time between fertilization and birth in the case of sexual reproduction, the time between initiation of cellular division and effective division in the case of mitosis, and the time required for digestion in the case of consumption of nutrient and its conversion to viable biomass [1]. Time delay plays a vital role in population dynamics of prey-predator, which has been recognized to contribute critically to the stable or unstable outcomes of prey population due to predation [10]. Population systems are exposed to the impact of a large number of random unpredictable factors. Then, environmental noise component is another important factor that affects prey-predator dynamics and, it related to climate, geographical distribution, geological features, disaster, human intervention, and other environmental factors [14]. Thus, a realistic prey-predator model should include both time delays and environmental noise.
For example, it is reasonable to assume that the death of prey is instantaneous when attacked by their predator but its contribution to the growth of predator population must be delayed by some time delay [25]. Kuang [10] mentioned that animals must take time to digest their food before further activities and responses taking place. Samanta [26] argued that the effect of time delay due to the time required in going from the egg stage to the adult stage, gestation period etc, has to be taken into account. Three different ways of incorporating a constant time delay into the prey-predator models were presented by Martin and Ruan [18]. In the first case, a time delay appears in the prey specific growth term, which is based on the assumption that in the absence of predators prey satisfies the Hutchinson's equation x′(t)=x(t)(1−x(t−τ)), that is also called the delayed logistic equation [19]. In the second case, there is a delay in the predator response term of the predator equation, that is, y′(t)=y(t)(−d+p(x(t−τ))), which can be regarded as a gestation period or reaction time of predators. The third one is a time delay in the interaction term of the predator equation, that is, y′(t)=−dy(t)+y(t−τ)p(x(t−τ)), which assumes that the change rate of predators depends on the number of preys and of predators present at some previous time. In this work, we incorporate the second type of delay in the functional response term of the predator growth equation.
Since the nature is full of uncertainty and random phenomena, the natural growth of species often does not follow strictly deterministic laws but rather oscillate randomly about some average, so that the population density never attains a fixed value with the advancement of time rather exhibits continuous oscillation around some average values [14]. The basic mechanism and factors of population growth like resources and vital rates—birth, death, immigration and emigration, change non-deterministically due to continuous fluctuations in the environment (e.g. variation in intensity of sunlight, temperature, water level, etc.) [20]. It is necessary and important to consider the corresponding stochastic population model, i.e., the effects of environmental noise, which undeniably arise from either environmental variability or internal species. For example, in [3], the authors extended a classical epidemic model from a deterministic framework to a stochastic differential equation one through introducing random fluctuations. Among the various ways of constructing a stochastic model systems for a given deterministic system, Cai et al. [4] propose a stochastic version of the epidemic model with nonlinear incident rate. Mao et al. [16] revealed that given population systems are subject to environmental noise, it can suppress a potential population explosion. That is to say, different structures of environmental noise may have different effects on the population systems. In our work, we would include noise processes in both prey and predator.
As we mentioned earlier, a realistic prey-predator model should include both time delays and environmental noise. There is a considerate amount of work done by many scholars, for instance [17,2,22,11,23,27,6,12,28,24,5]. Of them, Mao et al. considered the effects of environmental noise on the delay Lotka-Volterra in [17]. Vasilova [27] studied a stochastic Gilpin-Ayala predator-prey model with time-dependent delay. He established sufficient conditions for the existence of a global positive solution of the considered system, and proved stochastically ultimate boundedness, the long-time behavior of trajectories and extinction of species. In [6], Han et al. investigated two-species Lotka-Volterra delayed stochastic predator-prey system, with and without pollution, respectively. They revealed that there exists a unique nonnegative solution in each system that is permanent in time average under certain conditions. The convergence of the distributions of the solutions of a stochastic two-predator one-prey model with time delay was considered by Liu, Bai and Jin et al. [12]. Wang et al. [28] investigated the dynamics of a stochastic FIV model with seasonality analytically and numerically and, established sufficient criteria for extinction and weak persistence of the disease in the mean.
Motivated by the works of [17,27,12], we propose to study a delayed Harrison-type predator-prey model with noise terms that is lack in literature. We aim to explore and address the following questions through our analytic and numerical results via comparisons to the corresponding ODE model:
1. What are the dynamical effects of time delay in the functional response term of the predator growth equation on the Harrison-type predator-prey model?
2. What are the joint effects of time delay and noise on the Harrison-type predator-prey model?
The remaining of this paper is organized as follows. In Section 2, we derive our model and provide a summary on the dynamics of the corresponding ODE model. And we analyze the stability of a positive equilibrium under the effect of time delay or noise or both of them, and provide sufficient conditions that guarantee the existence of Hopf bifurcation at a positive equilibrium. In Section 3, numerical simulations are given to verify the theoretic analysis. In Section 4, the paper provides a brief conclusion and remarks. All proofs of our theoretical results are presented in the last section.
2. Model derivations and the related dynamics
The general predator-prey model can be expressed by the model of nonlinear ordinary differential equations [7]:
|
{dNdt=u(N)−f(N)g(P),dPdt=αf(N)g(P)−v(P),
|
(1)
|
where N=N(t) and P=P(t) denote the prey and predator population at time t, respectively. The function u(N) represents the growth rate of the prey in the absence of predation and is given by the traditional logistic form u(N)=rN(1−NK). The product f(N)g(P) gives the rate at which prey is consumed, while αf(N)g(P) describes per capita production rate of the predator. When these functions are defined by
|
f(N)=cN,g(P)=PmP+1,c,m>0,
|
and the function v(P) is given by v(P)=dP where d>0 is the natural death rate of the predator population. Then, we make a change of variables and the according Harrison-type functional response predator-prey model is described by the following form:
|
{dNdt=N(1−N)−cNPmP+1,dPdt=P(−d+bNmP+1),
|
(2)
|
where b=αc stands for conversion rate from prey to predator. Model (2) and its many kinds of extended forms have been widely studied in ecological literature [8,31,29,30,9]. In [29], Wang and Cai presented a theoretical analysis of processes of pattern formation that involves organisms distribution and their interaction of spatially distributed population with cross-diffusion in a Harrison-type predator-prey model. Wang et al. [30] investigated the complex dynamics induced by Allee effect in the reaction-diffusion predator-prey model. Jin [9] studied the solution moment stability for a Harrison-type predator-prey model with parametric dichotomous noises.
In this paper, we will study the effects of fluctuating environment on the dynamical behaviors of the Harrison-type predation model (2) with time delay τ (>0) which is introduced into the functional response term of the predator growth equation, and incorporate white noise in each equations of the model. Moreover, we assume that fluctuations in the environment show themselves as fluctuations in the growth rate of prey N and in the death rate of predator P, then the corresponding stochastic delayed Harrison-type predator-prey model can be described as:
|
{dN(t)=N(t)(1−N(t)−cP(t)mP(t)+1)dt+σ1N(t)dB(t),dP(t)=P(t)(−d+bN(t−τ)mP(t−τ)+1)dt+σ2P(t)dB(t),
|
(3)
|
where σ1,σ2(>0) represent the noise intensity. B(t) is a standard one-dimensional independent Wiener process defined on a complete probability space (Ω,F,{Ft}t≥0, P) with filtration {Ft}t≥0 satisfying the usual conditions (i.e., it is right continuous and increasing while F0 contains all P-null sets). We denote by Rn+ the positive cone in Rn, that is Rn+={x∈Rn:xi>0for all1≤i≤n}, and denote by ˉRn+ the nonnegative cone in Rn, that is ˉRn+={x∈Rn:xi≥0for all1≤i≤n}. Let C([−τ,0];Rn+) denote the family of continuous functions from [−τ,0] to Rn+. If x∈Rn, its norm is denoted by |x|=(∑ni=1x2i)12 [17].
Since our proposed model (3) is the population model, we restrict the state space being the closed first quadrant in the (N,P) plane ˉR2+={(N,P):N≥0,P≥0}.
Theorem 2.1. The positive quadrant int(R2+) is invariant for model (3).
2.1. With only delay in the predator growth term
Before further studying the dynamics of our full model (3), we provide the following results regarding its corresponding ODE model (2) and the following delayed model
|
{dN(t)dt=N(t)(1−N(t))−cN(t)P(t)mP(t)+1,dP(t)dt=P(t)(−d+bN(t−τ)mP(t−τ)+1).
|
(4)
|
Model (3) has the trivial constant steady state E0=(0,0) and the boundary equilibrium E1=(1,0), and the other nonnegative constant steady states of (3) are the nonnegative constant steady states of the corresponding ODE model (2) in the absence of delay and noise. Let
|
Ni=b(m−c)±√4bcdm+b2(m−c)22bm,Pi=bNi−ddm,i=1,2,N1<N2,
|
where equilibrium point (N1,P1)=(b(m−c)−√4bcdm+b2(m−c)22bm,bN1−ddm) is always negative.
Theorem 2.2(Dynamics of the ODE model). The ODE model (2) always has two boundary equilibria: the extinction equilibrium E0=(0,0) which is always saddle; and the prey-only-equilibrium E1=(1,0) which is locally stable if d≥b holds while it is a saddle otherwise. As a summary, the conditions of the number of equilibria of the ODE model (2) are provided as follows:
1. If d≥b holds, then the ODE model (2) has no interior equilibrium with two boundary equilibria: E0=(0,0) being a saddle and E1=(1,0) being locally stable.
2. If d<b holds, then the ODE model (2) has a unique interior equilibrium E∗=(N∗,P∗) which is locally stable. Moreover, it is globally asymptotically stable in domain R2+.
The existence and stability conditions of the equilibrium of the ODE model (2) is listed in Table 1.
Table 1. The existence and stability of equilibria for model (2) where N∗=b(m−c)+√4bcdm+b2(m−c)22bm,P∗=bN∗−ddm.
| Equilibrium |
Existence Condition |
Stability Condition |
| (0,0) |
Always exists |
Always saddle |
| (1,0) |
Always exists |
Sink if d≥b;
Saddle if d<b |
| (N∗,P∗) |
d<b |
Always sink |
The proof of Theorem 2.2 is rather standard, and detailed investigations relating to the ODE model may be found in Ref. [29], hence is omitted.
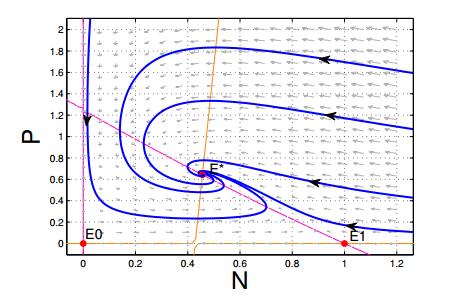
Remark 1. We would like to point out that Wang and Cai [29] provided similar results of the ODE model (2). For the ODE model (2), some preliminary results are presented, including dissipativeness, boundedness, permanence of the solutions, and the equilibria stability analysis of the model. Model (2) has two boundary equilibria E0=(0,0), E1=(1,0) and a unique positive equilibrium E∗=(N∗,P∗). From Theorem 2.2, for the equilibrium E1=(1,0), ecologically it means that if the natural death rate of predator d is more than the conversion rate from prey to predator b, then it leads to the extinction of predator population. For the equilibrium E∗=(N∗,P∗), ecologically it implies that if the natural death rate of predator d is less than the conversion rate from prey to predator b, then model (2) will be locally asymptotically stable around E∗. We also know that E∗=(N∗,P∗) of the ODE model (2) is globally asymptotically stable if it attracts all positive solutions of the model. That is, the boundedness of the solution together with the saddle nature of boundary equilibrium point E1=(1,0) and asymptotical stability of E∗=(N∗,P∗) leads to the conclusion that all the trajectories will approach E∗ with increasing time t. Hence E∗ is a global attractor and the model is globally asymptotically stable. When we take the parameters as c=0.9,b=0.7,d=0.3,m=0.1 for model (2), the positive equilibrium E∗=(0.46,0.64) exists which is spiral sink and shown in Fig. 1.
For model (3), when σ1=σ2=0, we study the DDE model (4) with initial conditions N(ϑ)=ψ1(ϑ)≥0,P(ϑ)=ψ2(ϑ)≥0 for all ϑ∈[−τ,0], where ψ1(ϑ),ψ2(ϑ)∈C([−τ,0],R2+).
Theorem 2.3. For the DDE model (4),
(i) The nonnegative solution (N(t),P(t)) of the model satisfies lim supt→∞N(t)≤1 and
|
lim supt→∞P(t)≤(b−d)exp(τ)dm
|
for τ>0 with d<b.
(ii) If the condition d≥b holds, then limt→∞(N(t),P(t))=(1,0) holds true.
Remark 2. In the case of τ=0, i.e., model (4) without time-delay, or model (2), the dissipation and boundedness of the solution are similar to the results in Theorem 2.3. That's to say, the solutions of the model with or without time-delay effect are always dissipative and uniformly bounded. Moreover, when the natural death rate of predator d is more than the conversion rate from prey to predator b, the boundary equilibrium E1=(1,0) of model (4) is stable.
Theorem 2.4. If the condition
|
b(m+exp(τ)−√(m+exp(τ))2−4mcexp(τ))2m<d<min{b,b(m+exp(τ)+√(m+exp(τ))2−4mcexp(τ))2m}
|
(5)
|
with 0<c≤(m+exp(τ))24mexp(τ) for τ>0 holds, then the DDE model (4) is permanent.
Remark 3. Biologically, Theorem 2.4 means that all the species of the DDE model (4) are survivor under 0<c≤(m+exp(τ))24mexp(τ) when the natural death rate of predator d is more than b(m+exp(τ)−√(m+exp(τ))2−4mcexp(τ))2m and less than min{b,b(m+exp(τ)+√(m+exp(τ))2−4mcexp(τ))2m}.
Let ˉN=N−N∗,ˉP=P−P∗ and dropping the bars for simplicity if notations, then the DDE model (4) can be transformed into the following:
|
{dN(t)dt=(N∗+N(t))(1−(N∗+N(t)))−c(N∗+N(t))(P∗+P(t))m(P∗+P(t))+1,dP(t)dt=(P∗+P(t))(−d+b(N∗+N(t−τ))m(P∗+P(t−τ))+1),
|
(6)
|
which can be rewritten as an abstract differential equation in the phase space C([−τ,0],R2+),
|
dU(t)dt=L(U(t))+G(U(t)),
|
(7)
|
where U(t)=(N(t),P(t))T,
|
L(U(t))=(q1N(t)+q2P(t)q3N(t−τ)+q4P(t−τ)),
|
(8)
|
and
|
G(U(t))=(−N2(t)−cN(t)P(t)(mP∗+1)2+cmN∗P2(t)(mP∗+1)2bN(t−τ)P(t)mP∗+1−bmN∗P(t)P(t−τ)+P∗N(t−τ)P(t−τ)(mP∗+1)2+bm2N∗P∗P2(t−τ)(mP∗+1)3),
|
(9)
|
here,
|
q1=−N∗,q2=−cN∗(mP∗+1)2,q3=bP∗mP∗+1,q4=−bmN∗P∗(mP∗+1)2.
|
(10)
|
Referring to [10], we can know that given initial data (N(ϑ),P(ϑ))∈C([−τ,0];R2+), model (4) will have a unique local or global solution dependent on the parameters qi,i=1,2,3,4.
The characteristic equation of the linearization model dU(t)dt=L(U(t)) is
|
λ2−q1λ+(q1q4−q2q3−q4λ)e−λτ=0,
|
(11)
|
where qi,i=1,2,3,4 are defined by (10). After a little algebraic calculation, then we get a unique positive root:
|
ω0=√−(q21−q24)+√(q21−q24)2+4(q1q4−q2q3)22,
|
(12)
|
and the corresponding critical value of delay τ=τk at which E∗=(N∗,P∗) loses stability is given by
|
τk=1ω0arcsin(−q4ω30+(q1q4−q2q3)q1ω0(q1q4−q2q3)2+q24ω20)+2kπω0,k=0,1,2,…
|
(13)
|
Hence, we have the following theorem.
Theorem 2.5. For the DDE model (4), if d<b holds, then there is a critical value τ0 which is the least positive value of τk given by (13), such that the positive equilibrium E∗=(N∗,P∗) is asymptotically stable when τ∈(0,τ0) and unstable when τ>τ0. Moreover, model (4) undergoes Hopf bifurcation around E∗=(N∗,P∗) at τ=τk (k=0,1,2,…), that is, a family of periodic solutions bifurcate from E∗ as τ passes through the critical value τk (k=0,1,2,…).
Remark 4. In the absence of delay τ=0, when the natural death rate of predator d is less than the conversion rate from prey to predator b, then the ODE model (2) remain locally asymptotically stable around E∗=(N∗,P∗). In the presence of delay τ≠0, when the conditions of Theorem 2.5 hold for the DDE model (4) implies that the interior equilibrium E∗ is conditionally stable. Based on the above analysis, we can see that if E∗=(N∗,P∗) of model (4) is stable for τ=0, then there is a positive constant τ0 which is the least positive value of τk given by (13), such that for τ>τ0, E∗ becomes unstable. It is worthy to mention here that the amplitudes of both prey and predator population increase with the increase of time delay (see our simulations below for details).
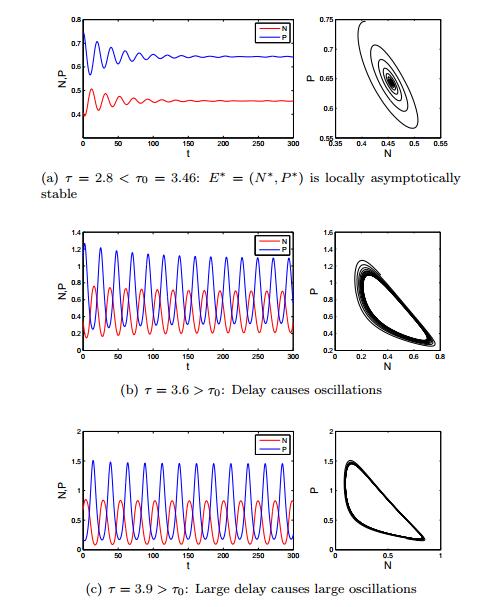
Fig. 2 shows the time-series plots of prey N and predator P and phase portraits of the DDE model (4) with different time delay τ, other parameters are taken as c=0.9,b=0.7,d=0.3,m=0.1 which are the same as in Fig. 1, and the initial value is set to (N(0),P(0))=(1.2,1.0). According to Theorem 2.5, there is a critical value τ0=3.46, Hopf bifurcation occurs and a bifurcation periodic solution exists at τ=τ0, which displays that both prey and predator population reach periodic oscillations around the equilibrium E∗=(0.47,0.64) in finite time. The equilibrium E∗ is asymptotically stable when τ=2.8<τ0 (see Fig. 2(a)), that is to say, the delay model (4) is conditionally stable at the unique positive equilibrium E∗. The equilibrium E∗ loses its stability and becomes unstable when τ>τ0 (see Figs. 2(b) and 2(c)). Comparing Figs. 2(a), 2(b) with 2(c), one can see that a stable limit cycle arises, which is caused by the Hopf bifurcation. It implies that time delay can induce instability and oscillations via Hopf bifurcation in the model. We also realize that a large enough time delay can increase the amplitude of the oscillating orbit of species.
2.2. With both delay and noise effect
In the following, we turn our focus on the dynamical behaviors of the SDDE model (3) with both time delay and noise effect. Denote Z(t)=(N(t),P(t)) and |Z(t)|=√N2(t)+P2(t).
Theorem 2.6. For any given initial value Z(ϑ)={(N(ϑ),P(ϑ)):−τ≤ϑ≤0}∈C([−τ,0];R2+), if |Z(t−τ)|<d−1b on t≥−τ, then there is a unique positive solution Z(t)=(N(t),P(t)) to the SDDE model (3) on t≥−τ and the solution will remain in R2+ with probability one.
Remark 5. Theorem 2.6 shows that the solution of the SDDE model (3) will remain in R2+. It can be said that model (3) can reserve the global stability of the positive equilibrium E∗=(N∗,P∗) of the ODE model (2).
The property of Theorem 2.6 makes us continue to discuss how the solution varies in R2+ in more detail. And we present that the definition of stochastic ultimate boundedness [14] is one of the important topics in population dynamics and defined as follows.
Definition 2.7. The solution of the SDDE model (3) is said to be stochastically ultimately bounded if for any ε∈(0,1), there is a positive constant χ=χ(ϵ), such that for any initial value Z(ϑ)={(N(ϑ),P(ϑ)):−τ≤ϑ≤0}∈C([−τ,0];R2+), the solution of model (3) has the property that
|
lim supt→∞P{|(N(t),P(t))|>χ}<ε.
|
(14)
|
Theorem 2.8. For any θ∈(0,1), if d≤θb2θb+mexp(−τ) for τ>0, there is a positive constant C=C(θ), which is independent of initial value Z(ϑ)={(N(ϑ),P(ϑ)):−τ≤ϑ≤0}∈C([−τ,0];R2+), such that the solution of the SDDE model (3) has the property that
|
lim supt→∞E|(N(t),P(t))|θ≤C.
|
(15)
|
Theorem 2.9. For any θ∈(0,1), if d≤θb2θb+mexp(−τ) for τ>0, the SDDE model (3) is stochastically ultimately bounded.
Remark 6. The above analyses show that under certain conditions, the original ODE model (2) and the associated SDDE model (3) behave similarly in the sense that both have positive solutions which will not explode to infinity in a finite time, and actually, will be ultimately bounded. That is to say, under certain conditions the noise will not spoil these nice properties.
The following result gives the almost surely asymptotic property of model (3).
Theorem 2.10. Assume the same conditions of Theorem 2.6 hold. For any given initial value Z(ϑ)={(N(ϑ),P(ϑ)):−τ≤ϑ≤0}∈C([−τ,0];R2+), the solution Z(t)=(N(t),P(t)) to the SDDE model (3) has the property that
|
lim supt→∞ln|Z(t)|t≤1+d+˘C22ˆσ2a.s.
|
where ˆσ=min{σ1c1,σ2c2},ˇC=max{b,c}.
3. Numerical simulations
In this section, numerical simulation results of the SDDE model (3) for different values of τ and σ1,σ2 will be mentioned in subsequent two cases, firstly for τ=0 and secondly for τ≠0 by increasing the magnitude of noise σ1,σ2 step by step. Other parameters are taken as
|
c=0.9,b=0.7,d=0.3,m=0.1
|
(16)
|
and the initial value is set to (N0,P0)=(1.2,1.0).
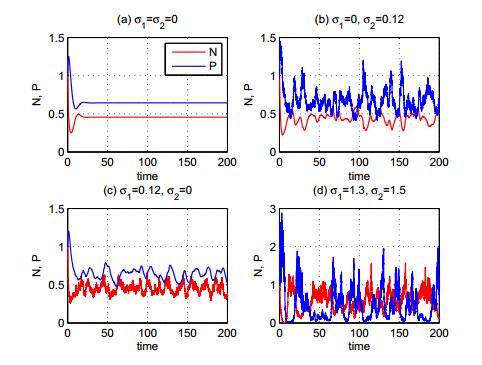
Fig. 3 shows the time-series plots of model (3) only with different noise intensities σ1,σ2 and τ=0, other parametric values as (16) which are the same as in Fig. 1. In Fig. 3(a), without noise, i.e., σ1=σ2=0, the interior equilibrium E∗=(0.46,0.64) of the ODE model (2) is asymptotically stable. Let σ1=0,σ2=0.12 in Fig. 3(b), we can see that the positive solution of model (3) is stochastic fluctuation. In Fig. 3(c), take σ1=0.12,σ2=0, the fluctuation of prey species N occurs, thus the predator species P will become instability. Choosing σ1=1.3 and σ2=1.5 in Fig. 3(d), it shows the stochastically fluctuating population distribution for both prey and predator species when the magnitude of environmental noises increase.
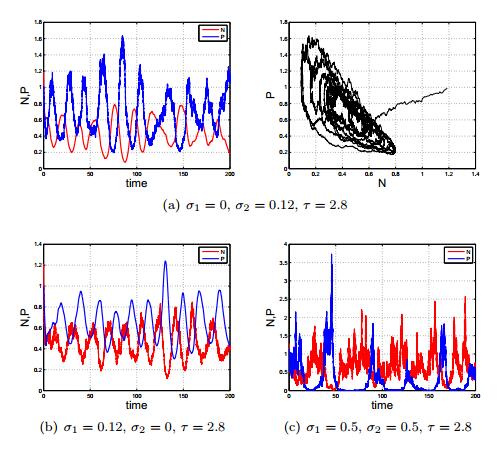
Fig. 4 shows the evolution of both the prey and predator species of the SDDE model (3) with different noise intensities σ1,σ2 and keeping τ=2.8<τ0=3.46. In Fig. 4(a), let σ1=0 and σ2=0.12, it indicates that the prey and predator species fluctuate around the steady state value (0.46,0.64) with small oscillation. In Fig. 4(b), take σ1=0.12 and σ2=0, one can see that the stochastic oscillation happens in both species with the weak fluctuation. In Fig. 4(c), increasing σ1,σ2 to σ1=σ2=0.5, it illustrates the prey and predator species fluctuation with strong fluctuation over time t and the amplitude of oscillation is amplified due to environmental noise increases.
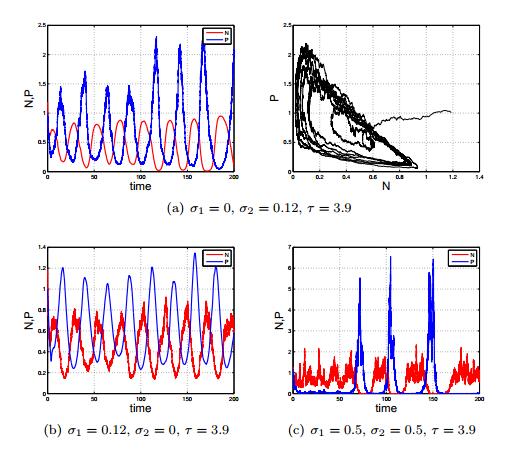
Fig. 5 shows the fluctuation in population densities of the prey and predator species of model (3) for different values of σ1,σ2 and τ=3.9>τ0 as mentioned in the caption. Fig. 5 illustrates the stochastic oscillation in population densities of both the species are relatively significant and they oscillate as if there is no external noises, see Figs. 5(a) and 5(b). Also, the amplitude of stochastic fluctuations increase appreciably for larger magnitudes of τ and σ2, see Figs. 5(c).
4. Conclusions and remarks
For the stochastic delayed Harrison-type predator-prey model (3), one of our interesting findings is that our proposed delayed predation model can exhibit Hopf bifurcation. And we prove that the positive equilibrium is asymptotically stable when the delay is less than a certain critical value and unstable when the delay is greater than the critical value. These findings have also been reported in the delayed Harrison-type predator-prey system with diffusive effects under Neumann boundary conditions in [31]. The work of [31] shows that the system has a Hopf bifurcation and, the authors analyze the direction of Hopf bifurcation and the stability of bifurcating periodic solution. In addition, we provide the conditions of dissipative, uniformly bounded, and permanent of our proposed delayed model.
We also provide additional results on the case when the Harrison-type predation model is added by both time delay and environmental noise under certain conditions. Our analysis and numerical simulations suggest that large delay could destabilize the model; and the combination of delay and noise could intensify the periodic instability of the SDDE model (3). Complicated analytical conditions for the above results depend upon certain parametric restrictions involving the parameters of model (3) and magnitudes of time delay and environmental noise. Our analytical results partially provide answers to the two questions proposed in the introduction: What are the dynamical effects of time delay in the functional response term of the predator growth equation on the Harrison-type predator-prey model? What are the joint effects of time delay and noise on the Harrison-type predator-prey model? More specifically, we have follows:
1. The effect of delay induces instability: Theorem 2.5 indicates that the large time delay can induce instability and oscillations via Hopf bifurcation whereas the corresponding model without delay is asymptotically stable at the interior equilibrium. Delay induced instability is shown in Figs. 2(b) and 2(c) and cause the populations to fluctuate. If the time delay τ is smaller than the critical value τ0, the positive equilibrium E∗=(N∗,P∗) of the DDE model (4) maintains its stability when E∗ is stable in the corresponding ODE model (2), see Fig. 2(a). If the time delay τ is larger than the critical value τ0, the time delay can induce a stable limit cycle generated through the Hopf bifurcation and the larger time delay can increase the amplitude of the oscillating orbits of two species.
2. The synergistic effects of delay and noise: We illustrate some relevant properties of the corresponding stochastic delayed predator-prey model (3) and reveal the effect of environmental noise on the model. The increase of the noise intensity has a drastic impact on the dynamical behavior of both species with or without the delay effect. Theorem 2.6 shows that under some conditions, the stochastically perturbed SDDE model (3) of the delay model (4) will remain to have a positive stable solution, and this theorem gives a result on the robustness of the positive stable solution. Under the conditions of Theorems 2.8 and 2.9, the property of the ultimate boundedness of the SDDE model (3) will not change no matter the environmental noise is large or small. That is to say, the property of this boundedness is very robust under the noise. In short, under certain conditions, the DDE model (4) and the associated SDDE model (3) behave similarly in the sense that both the prey and predator species have positive solutions which will not explode to infinity in a finite time and, in fact, will be ultimately bounded. That is, under certain conditions environmental noise will not spoil these nice properties. Moreover, Theorem 2.10 shows model (3) has almost surely asymptotic property. By fixing the values of c,b,d and m in model (3), we perform a large number of computer simulations with different values of the time-delay τ and the noise σ1,σ2. Without the time-delay τ=0, increasing the noise intensity can induce the fluctuation of the ODE model (2), see Fig. 3. With the time-delay, when τ<τ0, add the noise intensity to the DDE model (4), it shows that the positive constant steady state E∗=(N∗,P∗) of the model is unstable due the noise effects, see Fig. 4. When τ>τ0, both the time-delay and noise factors can produce instability and increase the amplitude of the periodic oscillating orbits of two species, see Fig. 5.
5. Proofs
Proof of Theorem 2.1.
Proof. For all t∈[0,t0] where t0∈(0,∞), we need to show that N(t)>0 and P(t)>0. Suppose that is not true. Then, there exists T∈(0,t0) such that for all t∈[0,T], N(t)>0 and P(t)>0, and either N(T)=0 or P(T)=0. For all t∈[0,T], we obtain
|
{N(t)=N(0)exp(∫t0(1−N(s)−cP(s)mP(s)+1)ds+∫t0σ1dB(s)),P(t)=P(0)exp(∫t0(bN(s−τ)mP(s−τ)+1−d)ds+∫t0σ2dB(s)).
|
(17)
|
As (N,P) is defined and continuous on [−τ,T] and B(t) is a standard Brownian motion, there is a C≥0 such that for all t∈[−τ,T],
|
{N(t)=N(0)exp(∫t0(1−N(s)−cP(s)mP(s)+1)ds+σ1B(t))≥N(0)exp(−CT),P(t)=P(0)exp(∫t0(bN(s−τ)mP(s−τ)+1−d)ds+σ2B(t))≥P(0)exp(−CT).
|
(18)
|
Taking the limit, as t→T, we get
|
N(T)≥N(0)exp(−CT)>0,P(T)≥P(0)exp(−CT)>0,
|
which contradicts the fact that either N(T)=0 or P(T)=0. So, for all t∈[0,t0], N(t)>0 and P(t)>0.
Proof of Theorem 2.3.
Proof. For our full model (3), when σ1=σ2=0, it is the following delayed model
|
{dN(t)dt=N(t)(1−N(t))−cN(t)P(t)mP(t)+1,dP(t)dt=P(t)(−d+bN(t−τ)mP(t−τ)+1),
|
(19)
|
with initial conditions N(ϑ)=ψ1(ϑ)≥0,P(ϑ)=ψ2(ϑ)≥0 for all ϑ∈[−τ,0], where ψ1(ϑ),ψ2(ϑ)∈C([−τ,0],R2+). From the first equation of (19), we can get dN(t)dt≤N(t)(1−N(t)). A standard comparison theorem shows that lim supt→∞N(t)≤1. As a result, for any ϵ>0, there exists a T>0, such that N(t)≤1+ϵ for t>T. Then from the second equation of (19), we define P on all interval [kτ,(k+1)τ] with k=0,1,2…, then one can see that P is bounded on [0,t0] if t0<∞.
From the predator equation of model (19), we get
hence, for t>τ,
which is equivalent, for t>τ, to
For any ε>1, there exists positive Tε, such that for t>Tε, N(t)<ε. According to the above inequality, we obtain, for t>Tε+τ,
|
dP(t)dt<P(t)(εb(mP(t)exp(−ετ)+1)−d),
|
which implies by the same arguments use for N that,
|
lim supt→∞P(t)≤(εb−d)exp(ετ)dm.
|
(20)
|
Conclusion of this Theorem holds by letting ε→1.
In addition, based on the above analysis, if d≥b, for t>Tε+τ, we have limt→∞P(t)=0.
Proof of Theorem 2.4.
Proof. From Theorem 2.3, there is a A=max{1,(b−d)exp(τ)dm}>0 independent of the initial condition such that
|
max{lim supt→∞N(t),lim supt→∞P(t)}≤A.
|
Then, we will show that there is a B>0, independent of the initial condition, such that
|
min{lim inft→∞N(t),lim inft→∞P(t)}≥B.
|
From model (4), for any ε>1 and for large enough t, we get P(t)<ε(b−d)exp(τ)dm. Then, we have
|
dN(t)dt>N(t)(1−N(t)−cε(b−d)exp(τ)dm).
|
Based on the standard comparison arguments, it follows that
|
lim inft→∞N(t)≥(1−cε(b−d)exp(τ)dm)
|
and letting ε→1, we have
|
lim inft→∞N(t)≥(1−c(b−d)exp(τ)dm).
|
(21)
|
Set C1=(1−c(b−d)exp(τ)dm), if c<dmexp(−τ)b−d holds, then C1>0. From (21) and Theorem 2.3, for any ε>1, there exists a positive constant Tε, such that for t>Tε, N(t)>C1ε and P(t)<ε(b−d)exp(τ)dm. Thus, for t>Tε+τ, we obtain
|
dP(t)dt>P(t)(bC1ε(mP(t−τ)+1)−d).
|
(22)
|
On the one hand, for t>Tε+τ, these inequalities lead to
|
dP(t)dt>P(t)(C1bdε(ε(b−d)exp(τ)+d)−d),
|
which involves, for t>Tε+τ,
|
P(t−τ)<P(t)exp(−(C1bdε(ε(b−d)exp(τ)+d)−d)τ).
|
(23)
|
On the other hand, from (22) and (23), for t>Tε+τ, we obtain
|
dP(t)dt>P(t)(bC1εmP(t)exp(−(C1bdε(ε(b−d)exp(τ)+d)−d)τ)+ε−d)
|
which yields
|
lim inft→∞P(t)≥bC1−εdεdmexp(−(d−C1bdε2(b−d)exp(τ)+εd)τ).
|
When ε→1, we have
|
lim inft→∞P(t)≥bC1−ddmexp(−(d−C1bd(b−d)exp(τ)+d)τ)=C2.
|
Let be B=min{C1,C2}>0. Therefore, model (4) is permanent.
Proof of Theorem 2.5.
Proof. In the absence of delay, i.e., τ=0, from Theorem 2.2, the positive equilibrium E∗=(N∗,P∗) of model (4) is locally asymptotically stable provided that d<b.
Assume that for some τ>0, iω (ω>0) is a root of Eq.(11), then
|
−ω2−iq1ω+(q1q4−q2q3−iq4ω)e−iωτ=0.
|
(24)
|
Separating the real and imaginary parts, we have
|
{ω2=(q1q4−q2q3)cosωτ−q4ωsinωτ,q1ω=−(q1q4−q2q3)sinωτ−q4ωcosωτ,
|
(25)
|
thus,
|
sinωτ=−q4ω3+(q1q4−q2q3)q1ω(q1q4−q2q3)2+q24ω2,cosωτ=−q2q3ω2(q1q4−q2q3)2+q24ω2,
|
(26)
|
which leads to the following equation
|
ω4+(q21−q24)ω2−(q1q4−q2q3)2=0.
|
(27)
|
Solving for ω2 in (27), we obtain
|
ω2=−(q21−q24)±√(q21−q24)2+4(q1q4−q2q3)22.
|
(28)
|
Thus, Eq. (27) has a unique positive root
|
ω0=√−(q21−q24)+√(q21−q24)2+4(q1q4−q2q3)22,
|
(29)
|
and substituting this value in (25), then the corresponding critical value of delay τ=τk at which E∗=(N∗,P∗) loses stability is given by
|
τk=1ω0arcsin(−q4ω30+(q1q4−q2q3)q1ω0(q1q4−q2q3)2+q24ω20)+2kπω0,k=0,1,2,…
|
(30)
|
Let λ(τ)=α(τ)+iω(τ) be the root of Eq.(11) such that α(τk)=0,ω(τk)=ω0. Substituting λ(τ) into Eq.(11) and differentiating both sides of it with respect to τ, we have
|
(dλ(τ)dτ)−1=(2λ−q1)eλτ−(q1q4−q2q3)τ−(1+λτ)q4λ(q1q4−q2q3+q4λ)=(2λ−q1)eλτλ(q1q4−q2q3+q4λ)−q4λ(q1q4−q2q3+q4λ)−τλ,
|
(31)
|
which, together with (25), (26) and (29), leads to
|
sign{Re(dλdτ)}τ=τk=sign{Re(dλdτ)−1}τ=τk=q21+2ω20ω20(q21+ω20)+q24(q1q4−q2q3)2+q24ω20>0.
|
(32)
|
This implies that all the roots cross the imaginary axis at iω from left to right as τ increases. Hence, the transversality condition is satisfied. Hopf bifurcation occurs at τ=τk given by (30), which are Hopf bifurcation values of model (4). This completes the proof.
Proof of Theorem 2.6.
Proof. From the biological meaning, we only consider the positive solution to the SDDE model (3). Taking the change of variables as N(t)=eu(t),P(t)=ev(t) and using Itˆo's formula, model (3) can be reformulated as follows:
|
{du(t)=(1−eu(t)−cev(t)mev(t)+1−σ212)dt+σ1dB(t),dv(t)=(−d+beu(t−τ)mev(t−τ)+1−σ212)dt+σ2dB(t),
|
(33)
|
the coefficient of (33) satisfy the local Lipschitz condition, then for any given initial values u(ϑ)=lnN(ϑ),v(ϑ)=lnP(ϑ),ϑ∈[−τ,0], there is a unique local solution u(t),v(t) on [−τ,te), where te is explosion time. Referring to [14,15], to show this solution is global, we need to show te=∞ a.s. Let l0>0 be sufficiently large for
|
1l0<min−τ≤t≤0|Z(t)|≤max−τ≤t≤0|Z(t)|<l0.
|
For each integer l≥l0, define the stopping time
|
tl=inf{t∈[0,te):N(t)∉(1l,l),P(t)∉(1l,l)},
|
where we set inf∅=∞ (∅ represents the empty set) in this paper. tl is increasing as l→∞. Let t∞=liml→∞tl, then t∞≤te a.s.
If we can show that t∞=∞ a.s., then te=∞ a.s. and Z(t)∈R2+ a.s. for all t≥0. To show this statement, we define a C2-function V:R2+→R+ by
|
V(Z)=(N−logN−1)+(P−logP−1),
|
(34)
|
which is a nonnegative function on N>0,P>0. Let l≥l0 and T>0 be arbitrary. For 0≤t≤tl∧T=min{tl,T}, we apply the Itˆo's formula and obtain
|
d[∫tt−τ(N(s)+P(s))ds+V(Z(t))]=[N−N(t−τ)+(N−1)(1−N−cPmP+1)+P−P(t−τ)+(P−1)(bN(t−τ)mP(t−τ)+1−d)+σ21+σ222]dt+σ1(N−1)dB(t)+σ2(P−1)dB(t)≤[54+cm+d−N(t−τ)−(N−32)2+(1−d)P−P(t−τ)+bN(t−τ)P+σ21+σ222]dt+σ1(N−1)dB(t)+σ2(P−1)dB(t)≤[54+cm+d−N(t−τ)−(N−32)2−P(t−τ)−(d−1−b|Z(t−τ)|)P+σ21+σ222]dt+σ1(N−1)dB(t)+σ2(P−1)dB(t)≤Cdt+σ1(N−1)dB(t)+σ2(P−1)dB(t),
|
(35)
|
where C is a positive number. Integrating both sides of the above inequality from 0 to tl∧T=min{tl,T} and then taking the expectations give rise to,
|
E[∫tl∧Ttl∧T−τ(N(s)+P(s))ds+V(N(tl∧T),P(tl∧T))]≤∫0−τ(N(s)+P(s))ds+V(N(0),P(0))+CT,
|
thus,
|
EV(N(tl∧T),P(tl∧T))≤∫0−τ(N(s)+P(s))ds+V(N(0),P(0))+CT.
|
(36)
|
Set Ωl={tl≤T} for l≥l1. For every μ∈Ωl, N(tl,μ) and P(tl,μ) equal either l or 1l, hence,
|
V(N(tl,μ),P(tl,μ))≥min{l−logl−1,1l+logl−1}.
|
(37)
|
It then follows from (36) that
|
∫0−τ(N(s)+P(s))ds+V(N(0),P(0))+CT≥E[1Ωl(μ)V(N(tl),P(tl))]≥P{tl≤T}min{l−logl−1,1l+logl−1},
|
(38)
|
where 1Ωl is the indicator function of Ωl. Letting l→∞ leads to liml→∞P{tl≤T}=0. Since T>0 is arbitrary, we get P{t∞<∞}=0, hence P{t∞=∞}=1 as required. This completes the proof.
Proof of Theorem 2.8.
Proof. Define a function by
|
V(N,P)=Nθ+Pθ,(N,P)∈R2+.
|
(39)
|
For any t>0, using Itˆo's formula it gives that
|
LV(N,P)=θNθ(1−N−cPmP+1)+σ212θ(θ−1)Nθ+θPθ(bN(t−τ)mP(t−τ)+1−d)+σ222θ(θ−1)Pθ,
|
(40)
|
as 0<θ<1, then,
|
LV(N,P)≤θNθ(1−N)−σ212θ(1−θ)Nθ+θPθbN(t−τ)mP(t−τ)+1−σ222θ(1−θ)Pθ≤θNθ−σ212θ(1−θ)Nθ+bθ(b−d)exp(τ)dm|Z(t−τ)|2−σ222θ(1−θ)Pθ=F(N,P)−V(N,P)−eτ|Z(t)|2+bθ(b−d)exp(τ)dm|Z(t−τ)|2
|
(41)
|
where F(N,P)=(θ+1)Nθ+Pθ−σ212θ(1−θ)Nθ−σ222θ(1−θ)Pθ+eτ|Z(t)|2≤C0 for (N,P)∈R2+. Thus,
|
LV(N,P)≤C0−V(N,P)−eτ|Z(t)|2+bθ(b−d)exp(τ)dm|Z(t−τ)|2.
|
Hence, we obtain
|
dV(N,P)=LV(N,P)dt+σ1θNθdB(t)+σ2θPθdB(t)≤(C0−V(N,P)−eτ|Z(t)|2+bθ(b−d)exp(τ)dm|Z(t−τ)|2)dt+σ1θNθdB(t)+σ2θPθdB(t).
|
(42)
|
Applying Itˆo's formula yields
|
d(etV(N,P))=etV(N,P)dt+etdV(N,P)≤et(C0−eτ|Z(t)|2+bθ(b−d)exp(τ)dm|Z(t−τ)|2)dt+etσ1θNθdB(t)+etσ2θPθdB(t).
|
(43)
|
If bθ(b−d)exp(τ)≥dm, then
|
etEV(N,P)≤V(N(0),P(0))+C0et−E∫t0es+τ|Z(s)|2ds+bθ(b−d)exp(τ)dmE∫t0es|Z(s−τ)|2ds=V(N(0),P(0))+C0et−E∫t0es+τ|Z(s)|2ds+bθ(b−d)dmE∫t−τ−τes+τ|Z(s)|2ds≤V(N(0),P(0))+C0et+bθ(b−d)dmE∫0−τes+τ|Z(s)|2ds,
|
which implies that
|
lim supt→∞EV(N(t),P(t))≤C0.
|
(44)
|
Since
|
|(N,P)|θ≤√2θmax{Nθ,Pθ}≤√2θV(N,P),
|
(45)
|
we get
|
lim supt→∞E|(N(t),P(t))|θ≤√2θlim supt→∞EV(N(t),P(t))≤√2θC0=C(θ).
|
(46)
|
The proof is complete.
Proof of Theorem 2.9.
Proof. The solutions of model (3) will remain in R2+ for all t≥0 with probability one from Theorem 2.6. From Theorem 2.8, there exists C>0 such that
|
lim supt→∞E|(N(t),P(t))|θ≤C.
|
(47)
|
Then, we choose a constant ϵ>0 sufficiently large such Cϵ<1. By Chebyshev inequality,
|
P{Nθ+Pθ>ϵ}≤1ϵE[Nθ+Pθ]≤Cϵ:=ε,
|
which implies that
|
1−ε≤P{Nθ+Pθ<ϵ}≤P{1ϵ≤N(t)+P(t)≤ϵ}.
|
Noting (N(t)+P(t))2≤2|(N(t),P(t))|2≤2(N(t)+P(t))2, we obtain
|
P{1√2ϵ≤N(t)+P(t)√2≤|(N(t),P(t))|≤N(t)+P(t)≤ϵ}≥1−ε.
|
(48)
|
According to the Definition 2.7, the SDDE model (3) is stochastically ultimately bounded.
Proof of Theorem 2.10.
Proof. Define a function by V(Z)=N+P, using Itˆo's formula it gives that
|
lnV(Z(t))=lnV(Z(0))+∫t0(NV(Z(s))(1−N−cPmP+1)−σ21N22V2(Z(s)))ds+∫t0(PV(Z(s))(bN(s−τ)mP(s−τ)+1)−d)−σ22P22V2(Z(s)))ds+M1(t)+M2(t),
|
(49)
|
where Mi(t) is a martingale defined by Mi(t)=∫t0σiZiV(Z(s))dB(s),i=1,2. The quadratic variation of this martingale is
|
⟨Mi(t),Mi(t)⟩=∫t0σ2iZ2iV(Z(s))ds,i=1,2.
|
Let ε∈(0,1) and for arbitrary positive constant θ, by the exponential martingale inequality [14], for each k≥1,
|
P{sup0≤t≤k(Mi(t)−ε2⟨Mi(t),Mi(t)⟩)>θlnkε}≤k−θ.
|
Since the series Σ∞k=1k−θ converges, applying the Borel-Cantelli lemma, there is Ω0⊂Ω with P(Ω0)=1 such that for ρ∈Ω0 there exists an integer k0=k0(ρ) and choosing θ=2, we have
|
Mi(t)≤ε2⟨Mi(t),Mi(t)⟩+2εlnk
|
for all 0≤t≤k and k≥k0(ρ). Substituting this inequality into (49) we obtain
|
lnV(Z(t))≤lnV(Z(0))+∫t0(NV(Z(s))(1−N−cPmP+1)−(1−ε)σ21N22V2(Z(s)))ds+∫t0(PV(Z(s))(bN(s−τ)mP(s−τ)+1)−d)−(1−ε)σ22P22V2(Z(s)))ds+4εlnk
|
(50)
|
for all 0≤t≤k,k≥k0(ρ) and ρ∈Ω0. By computing the following,
|
NV(Z(s))(1−N−cPmP+1)≤1+cP,PV(Z(s))(bN(s−τ)mP(s−τ)+1)−d)≤bN(s−τ)+d,σ21N22V2(Z(s))≥σ21c21N2,σ22P22V2(Z(s))≥σ22c22P2
|
(51)
|
where c1,c2∈(0,1) are positive constants. Substituting (51) into (50) has
|
lnV(Z(t))≤∫t0(1+cP(s)+bN(s−τ)+d−(1−ε)σ21c21N2−(1−ε)σ22c22P2)ds+lnV(Z(0))+4εlnk≤∫t0(1+cP(s)+bN(s−τ)+d−(1−ε)ˆσ2|Z|22)ds+lnV(Z(0))+4εlnk
|
(52)
|
for all 0≤t≤k,k≥k0(ρ) and ρ∈Ω0. From (52), we get
|
lnV(Z(t))+(1−2ε)ˆσ24∫t0|Z(s)|2ds≤lnV(Z(0))+4εlnk+∫t0(1+cP(s)+bN(s−τ)+d−ˆσ2|Z|22)ds≤C1+∫t0(1+cP(s)+bN(s)+d−ˆσ2|Z|22)ds+4εlnk,
|
where C1=lnV(Z(0))+b∫0−τN(s)ds. Due to
|
1+d+cP(t)+bN(t)−ˆσ2|Z|22≤1+d+ˇC|Z|−ˆσ2|Z|22≤1+d+ˇC22ˆσ2=C2,
|
thus, if ρ∈Ω0,
|
lnV(Z(t))+(1−2ε)ˆσ24∫t0|Z(s)|2ds≤ˇC+4εlnk+C2t
|
for all 0≤t≤k,k≥k0(ρ). Hence, for all ρ∈Ω0, if k−1≤t≤k,k≥k0(ρ), it gives that
|
1t(lnV(Z(t))+(1−2ε)ˆσ24∫t0|Z(s)|2ds)≤1k−1(ˇC+4εlnk)+C2,
|
which implies
|
lim supt→∞1t(lnV(Z(t))+(1−2ε)ˆσ24∫t0|Z(s)|2ds)≤C2.
|
(53)
|
Letting ε→0, from (52), we have
|
lim supt→∞1t(lnV(Z(t))+ˆσ24∫t0|Z(s)|2ds)≤C2a.s.
|
(54)
|
and using V(Z)≥|Z|√2, we obtain
|
lim supt→∞1t(ln|Z(t)|+ˆσ24∫t0|Z(s)|2ds)≤C2a.s.
|
The desired assertion is derived.
Acknowledgments
This research is partially supported by the National Natural Science Foundation of China (Grant Nos. 11601226, 11426132, 71501094), the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20140927, BK20150961), and the research funds from Nanjing Tech University and Jiangsu Government Scholarship for Overseas Studies. The work is also partially supported by NSF-DMS (1313312&1716802); NSF-IOS/DMS (1558127), and The James S. McDonnell Foundation 21st Century Science Initiative in Studying Complex Systems Scholar Award (UHC Scholar Award 220020472). This project has been partially supported by grants from the National Science Foundation (DMS-1263374 and DMS-1261211), and the Offices of the President and the Provost of Arizona State University.









 DownLoad:
DownLoad: