1.
Introduction
Differential equation models, such as infectious disease models [1,2,3,4,5,6,7] and neurodynamic models [8,9], are common tools for describing natural and social phenomena changes. They are powerful tools for understanding, explaining, and predicting the behavior of complex systems in the real world. The defensive behavior of a population plays a crucial role in its survival and reproduction of the whole population. It is necessary to further study the intrinsic nature of predation systems with defensive behavior (Holling-IV functional response function). The Holling-type IV predation model has been a popular topic in biomathematics and the research mainly includes bifurcation, equilibria and patterns. Some scholars performed bifurcation analysis in a Holling-type IV predation model and showed that the system undergoes a Codimension-2 Bogdanov-Takens (B-T) bifurcation [10], B-T singularity of Codimension-4 and also multiple other nonhyperbolic and degenerate equilibria, bistability, tristability or even tetrastability [11], as well as the Hopf bifurcation by choosing the level of fear as a bifurcation parameter [12], the Hopf bifurcation of coexisting steady-state for both the delayed and non-delayed systems [13] or supercritical Hopf bifurcation independently of the growth rate of the prey [14]. While other researchers obtained the sufficient conditions for the existence of a periodic solution [15], discussed the existence, uniqueness, non-negativity, and boundedness of the solutions [16], or carried out the existence of equilibrium points and stability analysis for correlation model [17], or considered predation model with combined continuous white noise and discontinuous Lvy noise, and proved the global positive solutions' existence and uniqueness [18]. Some scholars derived the Turing instability condition for the spatial predation system [19].
Harmful algal blooms (HABs) are ecological anomalies caused by the explosive proliferation or high aggregation of many plankton in seawater under certain environmental conditions. With the rapid development of modern industrial and agricultural production and the increase in population in coastal areas, a lot of industrial and agricultural wastewater and domestic sewage are discharged into the ocean, resulting in an increasing degree of eutrophication in offshore and harbor areas [20]. At the same time, the increase in the degree of coastal development and the expansion of mariculture has brought about the pollution of the marine ecological environment and mariculture itself [21]. On the other hand, the development of the maritime industry has led to the introduction of exotic and HABs species; global warming has also led to the frequent occurrence of HABs [22]. The events of HABs cause significant economic losses and threaten human health [23].
The paper gives the systematic-dynamical analysis of equilibria in section two. In section three, we analyze conditions for several bifurcations (such as transcritical, saddle-node, Hopf and Bogdanov-Takens bifurcation). Finally, we have some discussions in section four. Some interesting results are obtained, which help us better learn the dynamics in the real world.
To better explain the causes of HABs, we next briefly consider the formation mechanism of HABs from the differential equations perspective. We first consider the following equation
where x is the concentration of nutrient at time s, y is the density of plankton at time s, r is the conversion rate of inorganic nutrients into biomass, k is the carrying capacity of the nutrient, m>0 is the mortality of plankton (natural death, predation, etc.), μ is the maximum plankton rate, xa+bx+x2 is the Holling-IV functional response, a is the half-saturation constant of nutrient concentration growth, b is the denominator of the functional response [24] and c is the effect changes in the nutrient ratio of seawater. Changes in the nutrient ratio of seawater directly change the composition and structure of marine planktonic ecosystems [25]. For example, a low nitrogen-to-phosphorus concentration ratio is conducive to Cyanobacteria blooms [26]. When the nutrient proportion of silicate in seawater is high, the growth of plankton can be promoted. Diffusion and convection dominate the transfer of HABs from one area to another. HABs, in many parts of the world, are due to the influence of ocean currents, such as G. breve off the coast of West Florida and Diphysis sp off the coast of Sweden [27,28]. In addition, the results of population dynamics, especially the nonlinear population dynamics, show that the complex dynamics of the food chain and food web structure can occur in plankton systems. HABs are likely to be a reflection of such complex dynamics. We researched the system with the diffusion network as follows:
The description of the network Laplacian matrix L={Lij} can be found in [29].
2.
Systematic-dynamical analysis existence of equilibria
Theorem 1∗. All solutions {(x0,y0)|x0>0,y0>0} of (1.2) with positive initial values are uniformly bounded.
Proof. For convenience, we define a function Ψ by
Differentiating Ψ with respect to t, together with (1.2), one has
where Φ=k4r(r+c+m)2. Via the theory of differential equations and inequalities, we obtain
It is easy to know that the righthand limit of the above equation is Φm as t→∞, from which Ψ(t) is bounded. It can be further deduced that the solution of the system is bounded in R2+.
The system (1.2) has a trivial equilibrium, an axial equilibrium and, at most, two internal equilibrium, recorded as E0=(0,0),E1=(k(1+cr),0),E∗1=(x∗1,y∗1),E∗2=(x∗2,y∗2), respectively. The trivial equilibrium E0 always exists. The actual value of the function of nutrients should be positive, so the axial equilibrium E1 exists when cr>−1, x∗1 and x∗2 are determined by
Note that Δ=(bm−μ)2−4m2a. If Δ>0 and r(1−x∗ik)+c>0, then internal equilibria E∗1 and E∗2 exist with
and
If Δ<0, then there is no internal equilibrium; especially if Δ=0, then there is one internal equilibrium E∗.
Theorem 2∗.
(a) if a=(μ−mb)24m2, the system (1.2) has one internal equilibrium E∗ given by E∗(x∗,y∗)=(√a,(2a+b√a)[r(1−√ak)+c]).
(b) if a>(μ−mb)24m2, the system (1.2) has no interior equilibrium point.
(c) if a<(μ−mb)24m2 and r(1−x∗ik)+c>0, the system (1.2) has two internal equilibrium.
We now analyze the equilibrium points' stability by using the stability theory, and the Jacobian matrix JiE (i=1,...,n) of the system (1.2) is
Theorem 3∗.
If c+r<0, the trivial equilibrium point E0 is globally asymptotically stable; E0 is saddle point when c+r>0.
Proof. The Jacobian matrix JiE0 (i=1,...,n) of the system (1.2) is
Clearly, the eigenvalue of the matrix JiE0 is λi1=c+r and λi2=−m. If λi1<0, E0 is stable and E0 is saddle point when λi1>0.
Theorem 4∗.
If λi2<0, the axial equilibrium point E1 is locally asymptotically stable; E1 is a saddle point when λi2>0, where λi2=krμ(c+r)bkr(c+r)+k2(c+r)2+ar2−m.
Proof. The Jacobian matrix JiE1 (i=1,...,n) of the system (1.2) is
The eigenvalues of the matrix JiE1 are λi1=−(c+r)<0 and λi2=krμ(c+r)bkr(c+r)+k2(c+r)2+ar2−m. It follows that for λi2<0, E1 is stable, and for λi2>0, E1 is a saddle point.
Now, let's think about the stability of the internal equilibrium and assume that equilibrium points E∗1,E∗2 exist.
Theorem 5∗.
(a) If tr(JiE∗1)<0, then the internal equilibrium point E∗1 is locally asymptotically stable and E∗1 is unstable when tr(JiE∗1)>0;
(b) E∗2 is a saddle point in its existence interval.
Proof. The Jacobian matrix JiE∗1 (i=1,...,n) of the system (1.2) is
from which one has tr(JiE∗1)=kyim2(b+2xi)−rx2iμ2kμ2xi and det(JiE∗1)=yim2(μ−m(b+2xi))μ2xi. The characteristic equation is
So, λ1+λ2=tr(JiE∗1), λ1λ2=det(JiE∗1) and
since a<(μ−mb)24m2, (mb−μ)2−4m2a>0, one has
If tr(JiE∗1)<0, then eigenvalues λ1 and λ2 are negative and E∗1 is locally asymptotically stable; if tr(JiE∗1)>0, then eigenvalues λ1 and λ2 are positive and E∗1 is unstable. It's easy to calculate that det(JiE∗2)<0, then in the existence range of E∗2, it is always a saddle point.
To sum it up theoretically, the stability of the system solution is conditional and the conditions for stability are different between different equilibrium states. There is a phenomenon of overlapping between different equilibrium states. The stability of the equilibrium state E0 is straightforward. However, for E1, although there is a possibility of stability in theory, it is impossible in practice.
3.
Bifurcation of the System
The linear part of (1.2) is
where a11=r(1−2xk)+(x2−a)y(a+bx+x2)2+c, a12=−xa+bx+x2, a21=μy(a−x2)(a+bx+x2)2 and a22=μxa+bx+x2−m. We expressed the general solution as in [30]
where ∑njLijϕkj=Λiϕki. Plug (3.2) into (3.1) and the Jacobian matrix Bi (i=1,...,n) reads
where Λk (0=Λ1>Λ2>⋯>Λn) denotes the eigenvalues of the matrix L.
3.1. Transcritical bifurcation
Theorem 6∗.
For system (1.2), when a=−k(c+r)(r(bm−μ)+km(c+r))mr2≐aTc and d2=0, the system (1.2) has a transcritical bifurcation.
Proof. When a≐aTc and d2=0, the Jacobian matrix JiE1 (i=1,...,n) of the system (1.2) is
Clearly, det(JiE1)=0 and JiE1 has an eigenvalue λ=0. Let its corresponding eigenvector be piT and the eigenvector (λ=0) of the transpose matrix JTiE1 is qiT, then
Furthermore,
It follows that
Therefore, the transcritical bifurcation condition is satisfied.
3.2. Saddle-node bifurcation
In section two, we researched the interior equilibrium point's existence when Δ>0. The system (1.2) has two distinct internal equilibria when Δ=0, i.e. a=(μ−mb)24m2≐a∗ and two equilibrium points merged into one, which is called a degenerate equilibrium, denoted by E∗.
Theorem 7∗. When a=a∗ and d2=0, the system (1.2) exists a saddle-node bifurcation.
Proof. When a=a∗ and d2=0, the Jacobian matrix JiE∗ (i=1,...,n) of the system (1.2) is
Clearly, det(JiE∗)=0 and JiE∗ has an eigenvalue λ=0. Let its corresponding eigenvector be pis and the eigenvector (λ=0) of the transpose matrix JTiE∗ is qis, then
Furthermore,
It follows that
Therefore, the saddle-node bifurcation condition is satisfied.
3.3. Hopf bifurcation
Theorem 8∗. For the system (1.2), we assume that the parameters satisfy the existence condition of equilibrium point E∗1. Let
be such that tr(JE∗1)|c=c∗=0, then the stability of E∗1 changes and the system (1.2) exists a Hopf bifurcation.
Proof. When c=c∗, the Jacobian matrix JiE∗1 (i=1,...,n) of the system (1.2) is
and it is easy to verify that
We then compute the first Lyapunov coefficient [31]. Let c=c∗, where the coordinates of the internal equilibrium point are (x, y). Change variables
the Taylor expansion is performed and the system becomes
where p10+q01=0,p10q01−p01q10>0, and
p01=−μm, p20=ky∗1m3(ab+3ax∗1−x∗31)μ3x∗31−r, p11=m2(x∗21−a)μ2x∗21, p30=y∗1m4((x∗21−a)2−a(b+2x∗1)2)μ4x∗41, p21=m3(ab+3ax∗1−x∗31)μ3x∗31, p10=p12=p02=p03=0,
q10=m2y∗1(a−x∗21)μx∗21, q20=m3y∗1(x∗21−3ax∗1−ab)μ2x∗31, q21=m3(x∗31−3ax∗1−ab)μ2x∗31, q11=m2(a−x∗21)μx∗21, q30=m4y∗1(a(b+2x∗1)2−(a−x∗21)2))μ3x∗41, q01=q02=q12=q03=0.
The expression of the first Lyapunov coefficient is
if lc1<0 (resp.>0), the limit cycle is stable(resp. unstable).
3.4. Bogdanov-Takens bifurcation
Now, we will discuss the Bogdanov-Takens bifurcation of (1.2). Let d2=0 (meaning Plankton at each node do not spread out due to human intervention), then the Jacobian matrix about E∗ is
then tr(JiE∗)=r+c−r(μ−mb)km+d1Λk, det(JiE∗)=0. If tr(JiE∗)=0, i.e. c=r(μ−mb)km−r−d1Λk≐c∗, then JiE∗ has two zero characteristic roots. Now we will use the method given by Xiao and Ruan in [32] to verify that E∗ is a cusp of codimensional two and that there exists B-T bifurcation in the neighborhood of the equilibrium point E∗.
We select (a,c) as the bifurcation parameters to study the bifurcation of the system (1.2). (a,c) changes in a small neighborhood near (a∗,c∗), where (a∗,c∗) is the B-T bifurcation point. We consider the following system
where (εa,εc) are small parameters. Through the following transformation
the system (3.3) becomes
where
Pj(Xi1,Yi1) (j=1,2) is a smooth function and Pj(Xi1,Yi1)=O(∣Xi1,Yi1∣3).
Then, in the small neighborhood of (0,0), we make the following C∞ transformation
and system (3.4) becomes
where
P3(Xi2,Yi2) is a smooth function and P3(Xi2,Yi2)=O(∣Xi2,Yi2∣3). Introducing a new time variable τ that satisfies ds=(1−p02Xi2), and τ is still recorded as s, then system (3.5) becomes
Note that
The system (3.6) becomes
where P4(Xi3,Yi3) is a smooth function and P4(Xi3,Yi3)=O(∣Xi3,Yi3∣3). Note that the sign of p20−2p02p10+p00p202 is difficult to determine. We consider the following two scenarios.
Case I: If p20−2p02p10+p00p202>0, then we make the following variable transformation
and τ is still recorded as s, then system (3.7) becomes
where
P5(Xi4,Yi4) is a smooth function and P5(Xi4,Yi4)=O(∣Xi4,Yi4∣3). Note that
The system (4.1) becomes
where r00=q00−q2104, r01=q01−q10q112, r11=q11, P6(X5,Y5) is a smooth function and P6(Xi5,Yi5)=O(∣Xi5,Yi5∣3). If p11−p01p02≠0, then r11=q11=p11−p01p02√p20−2p02p10+p00p202≠0 and, hence, we make another variable transformation as follows:
from which we are able to get the universal fold of the system (1.2)
where ξ00=r00r411,ξ01=r01r11, P7(Xi6,Yi6) is a smooth function and P7(Xi6,Yi6)=O(∣Xi6,Yi6∣3).
(i) Saddle-node bifurcation curve SN={(εa,εc):ξ00(εa,εc)=0,ξ01(εa,εc)≠0};
(ii) Hopf bifurcation curve H={(εa,εc):ξ00(εa,εc)<0,ξ01(εa,εc)=√−ξ00(εa,εc)};
(iii) Homoclinic orbit bifurcation curve HL={(εa,εc):ξ00(εa,εc)<0,ξ01(εa,εc)=57√−ξ00(εa,εc)}.
Case II: If p20−2p02p10+p00p202<0, then we make the following variable transformation:
and τ is still recorded as s, then system (3.7) becomes
where
P5(Xi4,Yi4) is a smooth function and P5(Xi4,Yi4)=O(∣Xi4,Yi4∣3). Note that
The system (10') becomes
where r00=q00−q2104, r01=q01−q10q112, r11=q11, P6(Xi5,Yi5) is a smooth function and P6(Xi5,Yi5)=O(∣Xi5,Yi5∣3).
If p11−p01p02≠0, then r11=q11=p11−p01p02√−(p20−2p02p10+p00p202)≠0, and we make another variable transformation as follows:
from which one can get the universal fold of the system (1.2)
where ξ00=−r00r411,ξ01=−r01r11, P7(Xi6,Yi6) is smooth function and P7(Xi6,Yi6)=O(∣Xi6,Yi6∣3).
(i) Saddle-node bifurcation curve SN={(εa,εc):ξ00(εa,εc)=0,ξ01(εa,εc)≠0};
(ii) Hopf bifurcation curve H={(εa,εc):ξ00(εa,εc)<0,ξ01(εa,εc)=−√−ξ00(εa,εc)};
(iii) Homoclinic orbit bifurcation curve HL={(εa,εc):ξ00(εa,εc)<0,ξ01(εa,εc)=−57√−ξ00(εa,εc)}.
4.
Numerical simulation
To further discuss the stability of the solution of the model equation, considering the actual situation of HABs occurrence and the critical influence of human behavior on the food chain model, taking a and c as control variables, the stability of the equilibrium state of the model equation was studied by using the bifurcation theory. We consider the following system (4.1)
To get the model dynamics in the neighborhood of the Transcritical, Saddle-node, Hopf, Bogdanov-Takens bifurcations, we give a series of simulations to illustrate the emergence of complex patterns that arise for the system (4.1). We choose some parameter values for which (4.1) attains these bifurcations (see Figures 1a, 2a, 4a, 7a). To observe the peculiarities of patterns that arise in the neighborhood of these bifurcations, we choose two sets of parameter values (see Figures 1b, 2b) and four sets of network connection probability values (see Figures 5 and 8).
4.1. Transcritical bifurcation
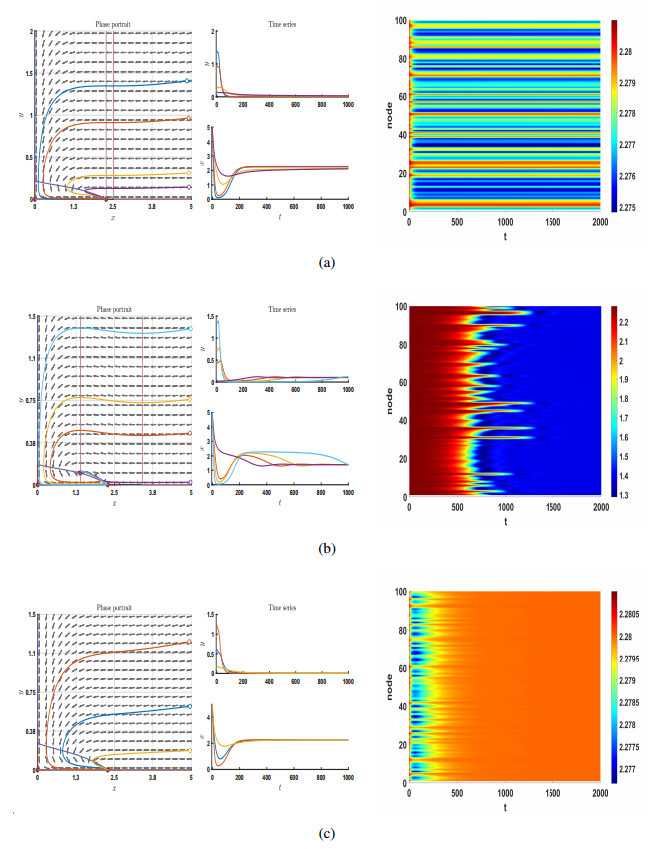
When transcritical bifurcation occurs, it can be seen from the comparison that the equilibrium point's stability has changed in Figure 1 (left). In general, the distribution of plankton is uneven and will vary due to regional differences, as shown in Figure 1a (right). When a<aTc, the equilibrium point E1 of (1.2) is in a stable state in Figure 1b (left), and the nodes of the network decrease first and then increase successively in Figure 1b (right). When a>aTc, the equilibrium point E1 of (1.2) becomes unstable in Figure 1c (left), and the nodes of the network tend to another stable equilibrium point in different ways in Figure 1c (right).
Regarding biological mechanism, the physical meaning is the idealized initial level for the equilibrium point E1; that is, the population density of plankton is zero. The half-saturation constant a can be used as the critical concentration to maintain the practical form of nutrients in the water for the average growth of algal cells. It can also be used to compare the ability of different phytoplankton to absorb nutrients. When light intensity, water temperature and other conditions were suitable but nutrient content was low (a<aTc), phytoplankton with a smaller a value were likelier to become the dominant species. The growth of phytoplankton with a higher a value was limited due to the need for more nutrients. However, when nutrients are too abundant (a>aTc), the community structure of phytoplankton will change significantly, which may lead to the rapid reproduction of some harmful phytoplankton; that is, transcritical bifurcation occurs (transition from one equilibrium point to another equilibrium point). It's also how organisms choose profitable ways to adapt to their environment.
4.2. Saddle-node bifurcation
For the equilibrium point E∗, the cell density of plankton is not zero; E∗>0 is necessary for HABs to occur. As can be seen from Figure 2 (left), c=−1.95<0 means de-eutrophication of effluent wastewater when the parameter crosses the critical value a∗ (other parameters were fixed) and the equilibrium points number goes from zero to one. Then, it splits into two, and their stability changes accordingly. With a=a∗, there is one stable positive equilibrium in Figure 2a (left). Due to the network's action, each node region's stable point is different. That is, turing instability occurs in Figure 2a (right). As a<a∗, there is one stable positive equilibrium point and one unstable positive equilibrium point in Figure 2b (left). Due to the effect of the network, almost all nodes simultaneously tend to be stable in an exponential decay way in Figure 2b (right). With a>a∗, the positive equilibrium point disappears in Figure 2c (left). In this case, plankton tends to be extinct in this environment, resulting in too abundant nutrients. However, nutrients will not grow indefinitely. Still, it will reach a stable state, and under the action of the network, this stabilization is synchronous in Figure 2c (right). Similarly, the simulation showed that the network connection probability still could not affect the pattern.
4.3. Hopf bifurcation
In the following, a is selected as Hopf bifurcation parameters. Using the MATCONT toolbox for analysis, it is observed that the system has a Branch point (labelled as BP), Limit point (fold) bifurcation (labelled as LP) and two Hopf bifurcations (labelled as H), as shown in Figure 3. Obtained in the MATLAB command window,
First Lyapunov coefficient =−1.289975×10−2,
First Lyapunov coefficient =−6.228478×10−2.
First Lyapunov coefficient =−1.289975×10−4<0, so the Hopf bifurcation is supercritical. When the bifurcation value a=5.5015, the stability of the system changes abruptly, a limit cycle "pops out" around it and the system oscillates violently and continuously, as in Figure 4a. It can be seen from Figure 4 that if HABs break out at this time, the explosive growth of HABs must be related to the Hopf bifurcation behavior of the system. The periodic outbreak period at each node is different in the Nutrient-Plankton network due to the different environments in each region. However, the system at each node is periodic in Figure 4b for the whole network. With the increase of the network connection probability(p=0.01,0.05), it is evident that the outbreak period of each node gradually tends to be consistent in Figure 5.
Due to the limitation of environmental factors and physiological characteristics of algae, algae growth shows periodicity. When the surrounding environment is suitable, a specific population density of algae simultaneously begins to multiply and consume nutrients from the surrounding environment. The first HABs occur when the thickness of algae is above a particular value. When algae concentrations first peak (when the effects of HABs are most severe), they reach their limits. Due to nutrient restriction (Figure 4, nutrient concentrations decreased to low values during the same period), algal densities declined sharply until they reached deficient levels. Nutrient concentrations gradually recover due to the dramatic decrease in algae density, the degradation of algae metabolism and dead algae and the diffusion effect of ocean currents. Under these conditions, algae enters a period of rapid growth, forming the second HABs (the appearance of the second peak).
4.4. Bogdanov-Takens bifurcation
In this section, (a,c) are selected as Bogdanov-Takens bifurcation parameters. Using the MATCONT toolbox for analysis, we can get that (1.2) has a Bogdanov-Takens bifurcation point (labelled as BT) and a Cusp bifurcation point (labelled as CP), as shown in Figure 6. Obtained in the MATLAB command window,
According to the previous analysis on the existence of the internal equilibrium point (Theorem 2), we know that when Δ=0, the two positive equilibrium points of (1.2) merge into one equilibrium point. The only positive equilibrium point E∗ is a cusp of codimension two, and the system state is shown in Figure 7. The positive equilibrium point E∗ is unstable in Figure 7a. Moreover, when the connection probability is small, as can be seen from the figure Figure 7b, the orbits near the equilibrium point far away from the equilibrium point are almost out of sync, which means eutrophication of effluent wastewater at each node in the network almost does not affect each other. However, with the increase of the connection probability (p=0.035,0.04), this lack of mutual influence has almost disappeared in Figure 8.
Ultimately, we conclude the relationship between harmful algal blooms and bifurcation. First, marine eutrophication is the essential condition leading to the outbreak of HABs; when the nutrient concentration is low, there will be no HABs (nutrient concentration is below the threshold). Second, the explosion of HABs also depends on the point of algae concentration. On one hand, the location of bifurcation changes with the change of parameters. If the bifurcation location reaches the threshold of HABs occurrence, it may trigger HABs. On the other hand, it is often determined that the equilibrium point of the system loses stability and bifurcations occur (such as transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, B-T bifurcation), which causes a significant change in the concentration of algae. Once the threshold of the concentration of algae required for the occurrence of HABs is reached at some time, it will lead to an outbreak of HABs. Therefore, using the nonlinear dynamics theory to discuss the stability and bifurcation behavior of the model near the equilibrium point helps us study the HABs generation mechanism and explore the HABs outbreak's internal mechanism and the dependence on dynamic parameters and environmental factors. The study of the stability and bifurcation behavior of the plankton ecosystem plays an essential role in the prediction and early warning of HABs.
5.
Conclusions
The paper deals with equilibria (local and global), Saddle-node, Transcritical, Hopf-Andronov and B-T bifurcation of the Nutrient-Plankton system on networks. In the numerical simulations, by controlling the change of parameters and observing the transformation process of the pattern, we observed several types of dynamics and the evolution process of the population of each node, which will bring great reference value to scientific research. When the system produces transcritical or saddle-node bifurcation, the change of parameters a and c will lead to changes in the number of equilibrium points or stability of (1.2), and the corresponding pattern will also change greatly. Moreover, in the simulation process, it was found that the change in network connection probability will not affect the changing trend of the pattern. The pattern does not change much before, after or on the critical value of the transcritical bifurcation (saddle-node bifurcation). The simulation results also show that when Hopf or B-T bifurcation was generated in (1.2), the network connection probability greatly influenced the pattern.
Regarding biological mechanism, the half-saturation constant a and de-eutrophication of effluent wastewater c<0 directly affect the occurrence of HABs. When transcritical bifurcation (saddle-node bifurcation, B-T bifurcation) occurs, the system tends to be stable. The nutrient was relatively deficient and a limiting environmental factor at this time. Therefore, the growth rate of plankton is slow, the mortality rate and environmental loss rate are more significant than the growth rate and the concentration of plankton decreases or even tends to extinction. When Hopf bifurcation occurs, the nutrient is relatively sufficient so that the plankton multiply rapidly and the concentration increases quickly, thus causing periodic HABs outbreaks. Due to the influence of diffusion, convection etc. and under the network's action, the stabilization or the periodic outbreak of HABs will reach synchronization.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by National Natural Science Foundation of China (12002297, 12272135, 12202146), Basic research Project of Universities in Henan Province (21zx009), Program for Science & Technology Innovation Talents in Universities of Henan Province (22HASTIT018), The Scientific Research Innovation Team of Xuchang University (2022CXTD002), Outstanding Young Backbone Teacher of Xuchang University (2022) and Key scientific research projects of Henan Institutions of Higher learning in 2024 (24B110017).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:










