Mathematical modelling of the interactive dynamics of wild and Microsporidia MB-infected mosquitoes

1.   Introduction

Reaction-diffusion systems have attracted a considerable amount of attention in recent years. They arise naturally in various biological, chemical and physical models to describe the spatio-temporal concentration change of one or more species which involve both local reaction and diffusion simultaneously. The reaction-diffusion system consists of a set of partial differential equations (PDEs) to represent the behaviour of each species individually. Recently, the interest in the study of reaction-diffusion systems has been extended to fractional reaction-diffusion systems ^[1,2,3,4,5] which from one side exhibit self-organization phenomena and from the other side introduce a new parameter to these systems, which is a fractional derivative index. It gives a greater degree of freedom for diversity of self-organization phenomena and it can exhibit new types of solutions that are not possible to find in classical reaction-diffusion equations with integer derivatives ^[6,7,8]. From numerical point of view, several methods have been developed, including, for example, finite element schemes ^[9], finite volume ^[] and finite difference methods ^[11,12] and spectral ones ^[13,14].

In this paper, we consider a system of two coupled nonlinear time-fractional reaction-diffusion equations (TF-RDEs)

where $\partial_t^\alpha$ is the Riemann-Liouville fractional derivative operator ^{[15,16,17,18,19,20]}

$u(t, x)$ and $v(x, t)$ being the field variables with $t$ and $x$ independent variables, $k_1 > 0$ and $k_2 > 0$ the diffusion coefficients, and $f = f(t, x, u, v)$ and $g = g(t, x, u, v)$ the nonlinear interaction terms. This kind of fractional problem has been numerically studied in a lot of papers, see, for example ^{[21,22,23,24]}.

The main aim of this paper is to solve the system of reaction-diffusion equations (1.1) by applying the procedure recently proposed that combines the Lie symmetry analysis with the numerical methods to get exact and numerical solutions. This procedure was applied to a wide class of FDES: time-fractional advection–diffusion–reaction equations ^[25,26], space-fractional advection–diffusion–reaction equations with linear ^[27] and nonlinear sources terms ^[28], time-fractional and space-fractional advection-diffusion-reaction equations with linear and nonlinear sources terms ^[29], two dimensional time-fractional reaction-diffusion equations ^[30].

As well known, classical Lie symmetries allow to reduce the partial differential equations to ordinary differential equations, for this reason, recently the Lie symmetries theory has been extended to the FDES ^{[31,32,33,34]}. By using this extension of Lie symmetries approach to FPDEs, we find the Lie symmetries admitted by the model (1.1), then Lie transformations that map the coupled nonlinear FT-PDEs to a system of nonlinear fractional ordinary differential equations (FODEs). We find solutions of a system of two nonlinear time-fractional reaction-diffusion equations by solving the reduced FODEs such that the solutions of the reduced equations lead to obtain solutions of the original equations. The original model is written in terms of the Riemann-Liouville fractional derivative in order to determine the Lie symmetries by applying the MAPLE package, that automates the method of finding symmetries for FDEs as proposed in ^{[31,32,33,34]}. After the reduction of the model to a fractional ordinary differential equation, we introduce the Caputo derivative, and rewrite the FODE in terms of this derivative so that we are able to compute the numerical solutions. Classical finite difference methods are proposed with the aim of showing the simplicity of application of the procedure and to obtain, at the same time, highly accurate solutions and a low computational cost.

The plan of the paper is the follows: In Section $2$, the Lie symmetries theory for FDEs is presented; in Section $3$, we describe the reduction of the original model to FODEs and report some examples of mathematical models obtained by suitable choices of involved parameters and functions; the Section $4$ is devoted to describe the numerical method used to obtain solutions of the reduced FODEs and, then, of the assigned original model. Finally, we end with the concluding remarks.

2.   Lie symmetries theory for FDEs

In general, for a $2\times2$ system of (integer order) partial differential equations

where $t, x$ are the independent variables, $u$ and $v$ are the dependent variables, and $u_{(r_1)}$, $v_{(r_2)}$ are all partial derivatives of the $u$ and $v$ with respect to $t$ and $x$ up to the maximum order $r_1$ and $r_2$ (integer order) respectively, we recall that the invertible transformations of the variables $t, x, u, v$

depending on a continuous parameter $a$, are said to be one-parameter $(a)$ Lie point symmetry transformations of the Eq (2.1) if the Eq (2.1) has the same form in the new variables $T, X, U, V$.

The set $G$ of all such transformations forms a continuous group, also known as the group admitted by the Eq (2.1).

According to the Lie theory, by expanding (2.3) in Taylor's series around $a = 0$, we get the infinitesimal transformations

where their infinitesimals $\xi_1$, $\xi_2$, $\eta_1$ and $\eta_2$ are given by

The corresponding operator

is known in the literature as the infinitesimal operator or generator of the group $G$.

The point transformations leaving a differential equation (2.1) invariant are found by means of the straightforward Lie's algorithm, requiring that the $k$-order prolongation of the operator (2.6) acting on (2.1) is zero along the solutions, i.e.:

where $k$ is the maximum order of derivations.

The invariance condition (2.7) provides an overdetermined set of linear differential equations (determining equations) for the infinitesimals whose integration gives the generators of Lie point symmetries admitted by the Eq (2.1).

Recently, in a series of papers of Buckwar, Luchko, Gazizov et al. ^{[31,32,33,34,35]}, Lie symmetry methods have been extended to to FDEs. By extending transformations (2.5) to the operator of Riemann-Liouville fractional differentiation on derivatives of $u$ with respect to $t$, $D_{ t} ^\alpha u_j$, and $v$ with respect to $t$, $D_{ t} ^\alpha v$, we have

where $\zeta_{\alpha}^1$ and $\zeta_{\alpha} ^2$ the infinitesimals of fractional derivatives, are given by prolongation formula i.e. ^[32,36],

where $D_t$ denotes the total derivative. Moreover, in order to conserve the structure of the fractional derivative operator, the following invariance condition is also required

Finally, the coefficients of the determining equation depend on all derivatives of variable $u$, $v$, $D_t^{\alpha} u$ and $D_t^{\alpha} v$.

For the determination of the Lie point symmetries of (1.1), the authors apply an algorithm that has been implemented in the MAPLE package FracSym ^[37,38]; this algorithm uses some routines of the MAPLE symmetry packages DESOLVII ^[37] and ASP ^[38]; the routines in FracSym automate the method of finding symmetries for FDEs as proposed in ^{[31,32,33,34]}; these are the first routines to automate the search of symmetries for FDEs in MAPLE. A limit of the algorithm FracSym is that only the fractional derivatives of Riemann-Liouville type are considered. Moreover, it is important to note that the generator of the dependent variables $u$ and $v$ are assumed linear in $u$ and $v$ respectively, as usually done in the literature ^{[33,34,35,36,37,38,39,40]}.

3.   Lie symmetries and reduction to FODEs

The extend Lie symmetries method leads to get the following infinitesimals for Eq (1.1)

where the function $\chi_1 = \chi_1(t, x)$ and $\chi_2 = \chi_2(t, x)$ satisfy the constraints

that link the arbitrary functions $\chi_1 = \chi_1(t, x)$ and $\chi_2 = \chi_2(t, x)$ to the nonlinear reaction terms $f = f(t, x, u, v)$ and $g = g(t, x, u, v)$, where $a_i$, $i = 0, \ldots, 3$, are the arbitrary parameters.

In the following, the stretching symmetry (i.e. $a_3$) is neglected; then the constraints (3.2) reduce to

and the infinitesimals read

We obtain the transformation

where we choose $a_0 = 1$. By integrating the constraints (3.3) with respect to $x$, and using the properties of the Riemann-Liouville fractional derivatives, the following forms of $f$ and $g$ are determined

where $\phi_1 = \phi_1(T, U, V)$ and $\phi_2 = \phi_2(T, U, V)$ are arbitrary functions of their arguments.

When the transformation (3.5) and the previous forms of $f$ and $g$ are inserted into the system (1.1), it is reduced into the following system of fractional nonlinear ordinary differential equations

The choice of the arbitrary functions $\phi_1$ and $\phi_2$ characterize the solutions of the Eqs (3.8) and (3.9) that, with a suitable choice of $\chi_1$ and $\chi_2$, specialize the source terms $f$ and $g$ and, then, the classes of solutions given by (3.5).

In order to perform some example of solutions of the system under study, we decide to choose $\phi_1$ and $\phi_2$ as nonlinear functions of two field variables $U$ and $V$

that lead to get a reaction-diffusion model describes the interaction between two filed variables. The functions $\phi_1$ and $\phi_2$ characterize the source terms (3.6) and (3.7) of mathematical models that can be used in order to describe several natural phenomena where the fractional order temporal variation of the field variables involves both the reaction and diffusion processes, simultaneously. They have been applied in several contexts such as chemical reactions ^[41], genes behaviour ^[42], populations evolution ^[43], biological pattern formation ^[44], epidemics ^[45] and computer virus spreading ^[46]. Moreover, they are strictly valid to describe spatially distributed chemical and biochemical system, and can also be applied with considerable success to model non-molecular ensembles of interacting and diffusing objects ^[47]. The functions $h_1 = h_1(T)$ and $h_2 = h_2(T)$ are arbitrary ones of the time variable.

By these assumptions, the FODEs (3.8) and (3.9) read

The system (3.12)–(3.13) reduces to the following FODE

if we impose that

Under non-vanishing initial condition

and by the Laplace transform, it demonstrates that the FODE (3.14) admits the following exact solution (see ^[18] for more details)

where $E_{\alpha, \alpha}(t) = { \sum\limits_{k = 0}^{\infty}\frac{t^k}{\Gamma(\alpha(k+1))}}$ is the Mittag-Leffler function. Substituting in (3.12), we get the following FODE

By solving the (3.17), we find the solution $U(T)$ that leads to compute the solution $V(T)$ by the (3.16) and, then, by the inverse transformations (3.5), the solutions of the proposed system of FPDEs (1.1) with source terms (3.6) and (3.7) characterized by (3.10) and (3.11). In general, Eq (3.17) could be not analytically resolvable, except for suitable choices of parameters and arbitrary functions, then numerical methods are proposed in order to compute the approximation of the exact solutions, as shown in the following Sections.

3.1.   Examples of mathematical models

Starting from Eq (3.17) and setting $c_1 = k_1 a_1^2$ and $b_0 = 0$, we get the following FODE

Suitable choices of the functions $h_1(T)$ and $h_2(T)$, involved in (3.18), are proposed with the aim to perform examples of mathematical models of interest in many fields of the applied sciences.

Example 1: By following choice of the functions $h_1(T)$ and $h_2(T)$

with $h_0$ and $\lambda$ arbitrary constants, the Eq (3.18) reads

Computed $U(T)$, the solution $V(T)$, given in (3.16), reads

Finally, (3.10) and (3.11) assume the following form

Found $U(T)$ and $V(T)$, by inverse transformations (3.5), we get the solutions $u(t, x)$ and $v(t, x)$ of target model (1.1) with source terms obtained by inserting $\phi_1$ and $\phi_2$ in (3.6) and (3.7).

Remark 1: For $\alpha = 1$, we are able to solve the FODE (3.19) that assumes the following form

whose exact solution, when $U(0) = 0$, is

and substituting in (3.16), we obtain

By inverse transformation (2.3), assumed $\chi_1(x, t) = \chi_2(x, t) = 0$, we get the solutions

of the system of PDEs with the source terms

The exact solution of the model with $\alpha = 1$ is considered in the following numerical examples as a reference for testing the qualitative behavior of the numerical solution of the model (3.19) for values of the $\alpha$ parameter increasing towards $1$.

Example 2: By following choice of the functions $h_1(T)$ and $h_2(T)$

with $h_0$ and $\lambda$ arbitrary constants, the Eq (3.18) reads

Computed the solution $U(T)$, the solution $V(T)$, given in (3.16), reads

and (3.10) and (3.11) assume the following form

Found $U(T)$ and $V(T)$, by inverse transformations (3.5), we get the solutions $u(t, x)$ and $v(t, x)$ of target model (1.1) with source terms obtained by inserting $\phi_1$ and $\phi_2$ in (3.6) and (3.7).

Remark 2: For $\alpha = 1$, the FODE (3.22) reduces to

whose the exact solution, when $U(0) = b_1$, is

Substituting in (3.16), it has

and, by the inverse transformation, we obtain the solutions

of the system of PDEs with the following source terms

The exact solution of the model with $\alpha = 1$ is considered in the following numerical examples as a reference for testing the qualitative behavior of the numerical solution of the model (3.22) for values of the $\alpha$ parameter increasing towards $1$.

4.   Numerical method and numerical solutions

In this Section, we find the numerical solution of the system of FPDEs (1.1) computed by solving the following FODE

obtained in the previous Section by the suitable choice of the parameters. Computed the numerical solution $U(T)$, we obtain the solution $V(T)$ by (3.16) and, then the solutions $u(t, x)$ and $v(t, x)$ of the target model (1.1) by the inverse transformations (3.5).

We introduce the $\alpha$-order Caputo fractional derivative of the solution $U(T)$

and its connection with the $\alpha$-order Riemann-Liouville fractional derivative

with $U(0)$ initial condition. We remark that the Caputo definition of the fractional derivative allows to define a FIVP whose the initial conditions are given in terms of the field variable and its integer order derivatives in agreement with the clear physical meaning of most of the processes arising in the real world. In terms of the Caputo derivative, the following fractional initial value problem (FIVP) is obtained

where

In order to numerically solve the FIVP (4.1), the classical implicit trapezoidal method (PI$_2$ Im) is used. We built a computational uniform mesh of grid points denoted by $T^n$, with $T^n = T^0 + n \Delta T$ and integration step sizes $\Delta T$ and $N$ positive integer. We denote by $U^n$ the numerical approximation provided by the numerical method of the exact solution $U(T^n)$ at the mesh points $T^n$, for $n = 0, \cdots, N$. The numerical method reads

where the coefficient values $\beta_k$, for $k = 0, \cdots, n+1$, are computed as follows

The convergence order of the scheme is $O((\Delta T)^{min(1+\alpha, 2)})$. Note that, the convergence order of the trapezoidal method usually is $1 + \alpha$ when $0 < \alpha < 1$, and only when $\alpha > 1$ or when the solution is sufficiently smooth we obtain the reached order two ^[48]. In general, the numerical method (4.2) leads to obtain a nonlinear equation for whose resolution a root-finding solver is needed. The classical Newton method is proposed.

In the follows, we report some test problems with the aim to validate the proposed approach. Note that the proposed mathematical models represent a wide class of mathematical ones that can be used in order to describe several natural phenomena arising in many field of the applied sciences. Different simulation parameters, initial conditions and fractional $\alpha$ parameter values are considered as the input features of the proposed models. The exact solutions, reported in Remarks $1$ and $2$, are considered as references for testing qualitative behavior of the numerical solutions of the models (3.19) and (3.22) for values of the $\alpha$ parameter increasing towards $1$. All numerical simulations are performed on Intel Core i7 by using Matlab 2020 software.

Example 1: In this example, we recall the FIVP (3.19), obtained in the previous Section, and we rewrite it in term of the Caputo fractional derivative choosing $U^0 = 0$

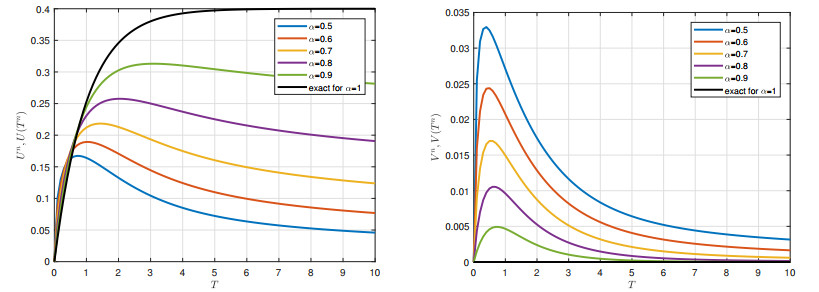
We set the parameters values as follows: $c_0 = 5$, $h_0 = 1$ and $\lambda = -1$ and choose a computational domain $[0, T_{max}]$ with $T_{max} = 10$ and $N = 100$ grid points. In Figure 1, we report the numerical results obtained for different values of the $\alpha$ parameter: in the left frame, the numerical solution $U^n$ obtained by solving the FIVP (4.3) by using the PI$_2$ Im numerical method; in the right frame, the numerical solution $V^n$ (3.20) obtained by applying the (3.16). The black lines represent the exact solution $U(T)$ given by (3.21) of the model with $\alpha = 1$ and the exact solution $V(T)$ computed by the (3.16). They are reported in order to test the qualitative behavior of the numerical solutions as the $\alpha$ parameter increases towards $1$. The solutions reveal a similar behaviour: Both starts from the value $0$, both increase at the beginning of the integration process and, after, decreases as the time evolves. Note that, as the value of $\alpha$ increases, the solution $U(T)$ increases unlike the solution $V(T)$ decreases.

In Figure 2, we report the numerical solutions $u_j^n$ and $v_j^n$, approximations of the exact solutions obtained by the inverse transformations (3.5),

solutions of the model (1.1) with source terms

computed by setting $k_1 = k_2 = 0.5$, for $\alpha = 0.5$, with $c_1 = k_1 a_1^2$ and $c_2 = k_2 a_2^2$ with $a_1 = a_2 = -1$, on a computational domain $[0, T_{max}]\times[0, X_{max}]$ with $T_{max} = 10$, $X_{max} = 1$ and $N = J = 100$ grid points.

Example 2: In this example, we recall the FIVP (3.22), obtained in the previous Section, and we rewrite it in term of the Caputo fractional derivative choosing $U^0 = b_1 = -h_0$

We choose the initial condition $U^0 = 1$ and set the parameters values as follows: $c_0 = 0.5$ and $\lambda = -1$ and consider a computational domain $[0, T_{max}]$ with $T_{max} = 10$ and $N = 100$ grid points. In Figure 3, we report the numerical results obtained for different values of $\alpha$ parameter: in the left frame, the numerical solution $U^n$ obtained by solving the FIVP (4.4) by using the PI$_2$ Im numerical method; in the right frame, the numerical solution $V^n$ (3.23) obtained by the (3.16). The black lines represent the exact solution $U(T)$ given by (3.24) of the model with $\alpha = 1$ and the exact solution $V(T)$ computed by the (3.16). They are reported in order to test the qualitative behavior of the numerical solutions as the $\alpha$ parameter increases towards $1$. The solutions reveal a different behaviour: both starts from the value $1$ but, the solution $U(T)$ immediately decreases as the time evolves, unlike the solution $V(T)$ increases at the beginning of the integration process and, after, decreases. As the value of $\alpha$ increases, the solution $U(T)$ decreases unlike the solution $V(T)$ increases.

In Figure 4, we report the numerical solutions $u_j^n$ and $v_j^n$, approximations of the exact solutions obtained by the inverse transformations (3.5), $u(t, x) = U(t) e^{a_1 x}$ and $v(t, x) = V(t) e^{a_2 x}$, solutions of the model (1.1) with source terms

computed by setting $k_1 = k_2 = 0.5$, for $\alpha = 0.5$, with $c_1 = k_1 a_1^2$ and $c_2 = k_2 a_2^2$ with $a_1 = a_2 = -1$, on a computational domain $[0, T_{max}]\times[0, X_{max}]$ with $T_{max} = 10$, $X_{max} = 1$ and $N = J = 100$ grid points.

For the second test, we set the parameters values as before and $c_0 = 5$ in order to provide an example of how this parameter, that represent the rate of interaction between the two solutions, affects their behaviour as the time evolves. In Figure 5, we report the numerical results obtained for different values of $\alpha$ parameter: in the left frame, the numerical solution $U^n$ obtained by solving the FIVP (4.4) by using the PI$_2$ Im numerical method, in the right frame, the numerical solution $V^n$ (3.23) obtained by the (3.16). The black lines represent the exact solution $U(T)$ given by (3.24) of the model with $\alpha = 1$ and the exact solution $V(T)$ computed by the (3.16). The solutions reveal a very similar behaviour: both starts from the value $1$ and both immediately decrease as the time evolves. As the values of $\alpha$ increases, the solution $U(T)$ decreases. A slightly different behaviour appears for the solution $V(T)$ in the last part of the domain.

In Figure 6, we report the numerical solutions $u_j^n$ and $v_j^n$, approximations of the exact solutions obtained by the inverse transformations (3.5), solutions of the model (1.1) with source terms given by (4.5), computed by setting $k_1 = k_2 = 0.5$, for $\alpha = 0.5$, with $c_1 = k_1 a_1^2$ and $c_2 = k_2 a_2^2$ with $a_1 = a_2 = -1$, on a computational domain $[0, T_{max}]\times[0, X_{max}]$ with $T_{max} = 10$, $X_{max} = 1$ and $N = J = 100$ grid points.

5.   Concluding remarks

This paper deals with the solutions of coupled nonlinear time-fractional reaction–diffusion equations, where the fractional derivatives are defined in terms of the Riemann-Liouville ones. We apply the strategy that combines an analytical and numerical approach in order to solve the problem under study, used recently in ^{[25,26,27,28,29,30]}. By Lie symmetries, the assigned system of two FPDEs is reduced into a system of two nonlinear FODEs and, under suitable assumptions of the involved parameters and functions, it is reduced into a nonlinear FODE. By introducing the Caputo derivative, we are able to properly handle the obtained FIVP and, then, by the trapezoidal numerical method, to find the solutions. Finally, the inverse transformations deal to compute the solutions of the original model. We remark that the Caputo definition of the fractional derivative allows to define a FIVP whose the initial condition is given in terms of the field variable in agreement with most of the processes with a clear physical meaning. Numerical examples are performed in order to show how the proposed approach good works with nonlinear systems of FPDEs confirming the clear advantage, from numerical point of view, to use a combined strategy: we numerically solve only a FODE whose solution allows to compute the solution of the original model of FPDEs. We remark that the presented test problems, performed in order to confirm the efficiency of the proposed approach, represent a wide class of mathematical models that can be used in order to describe several natural phenomena arising in many field of the applied sciences.

Acknowledgements

A. J. acknowledges the financial support by G.N.C.S. of I.N.d.A.M.

M.P.S. acknowledges the financial support by G.N.F.M. of I.N.d.A.M.

Conflict of interest

The authors declare no conflict of interest.