Stability and Hopf bifurcation of an SIR epidemic model with density-dependent transmission and Allee effect

1.   Introduction

The study of the self-assembly properties of biological membranes has been the object of intensive research both from the experimental and theoretical point of view, as their structure-function relationship and their related dynamic processes represents a central topic at the crossroad of different research fields, including physics, biochemistry, chemical engineering, biotechnology, and nano-medicine [1]–[3]. Many fundamental functions of biological membranes (such as signaling, selective transport, cell adhesion communication and recognition) are connected to processes that take place in a wide range of relevant distances and time scales, and involve the collective behavior of numerous interacting macromolecules [4]–[6]. Moreover, the interaction of biomolecules and nanoparticles with biomembranes strongly influences its biodistribution at the target sites within the tissues and organisms [7]–[9]. Therefore, the investigation of the processes occurring on the cellular and model membranes, as well as their interaction with nanocarriers in the physiological (or pathological) situations, is crucial for the development of novel therapeutic potential strategies [10]–[14]. For those scopes, the structural and dynamic description of biomembranes requires the calculation of a large number of simultaneous factors and development of interdisciplinary approaches in order to support the conceptual understanding and to establish fruitful cross-disciplinary connections.

2.   Biomembranes: A central topic at the crossroad of different research fields

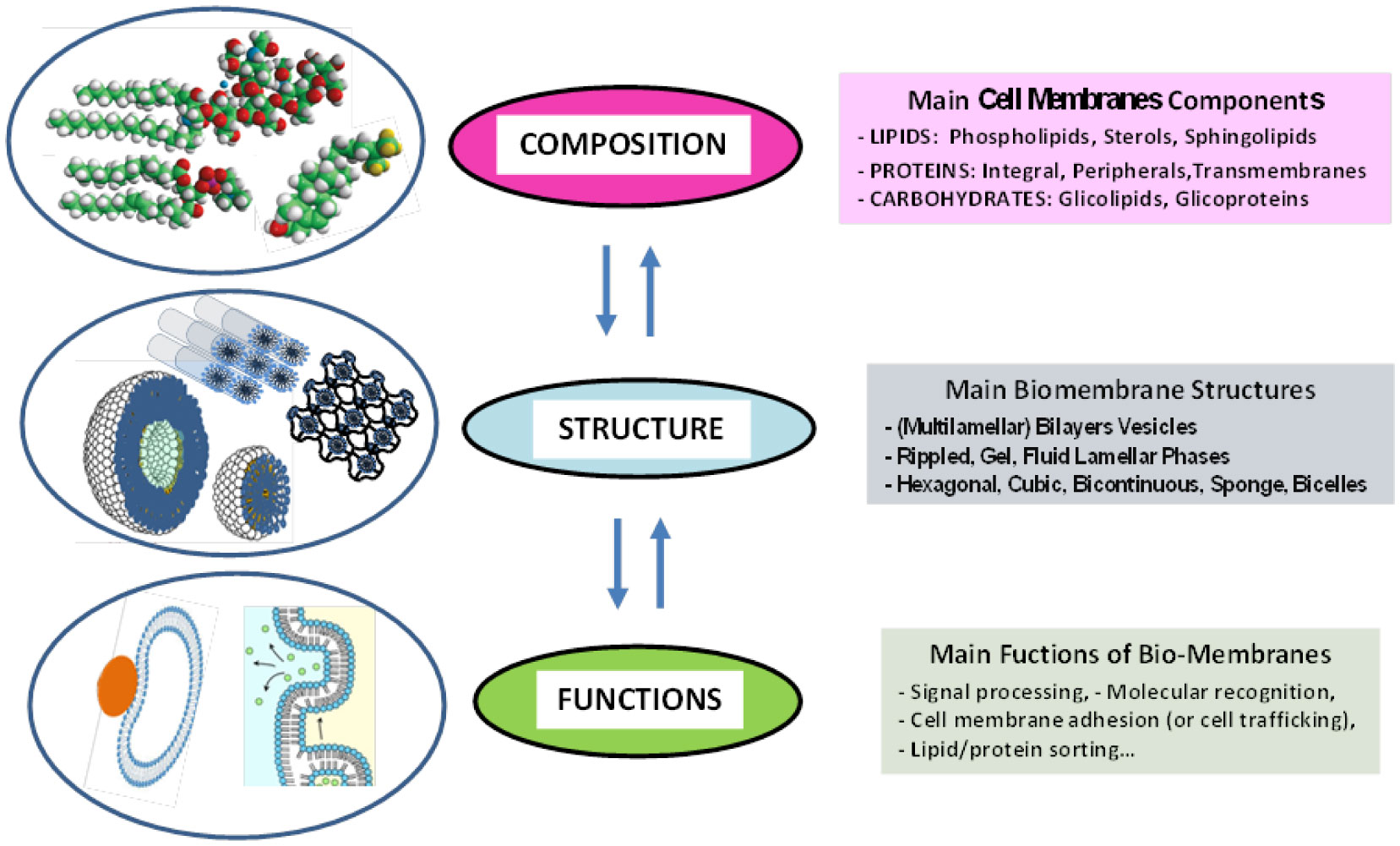
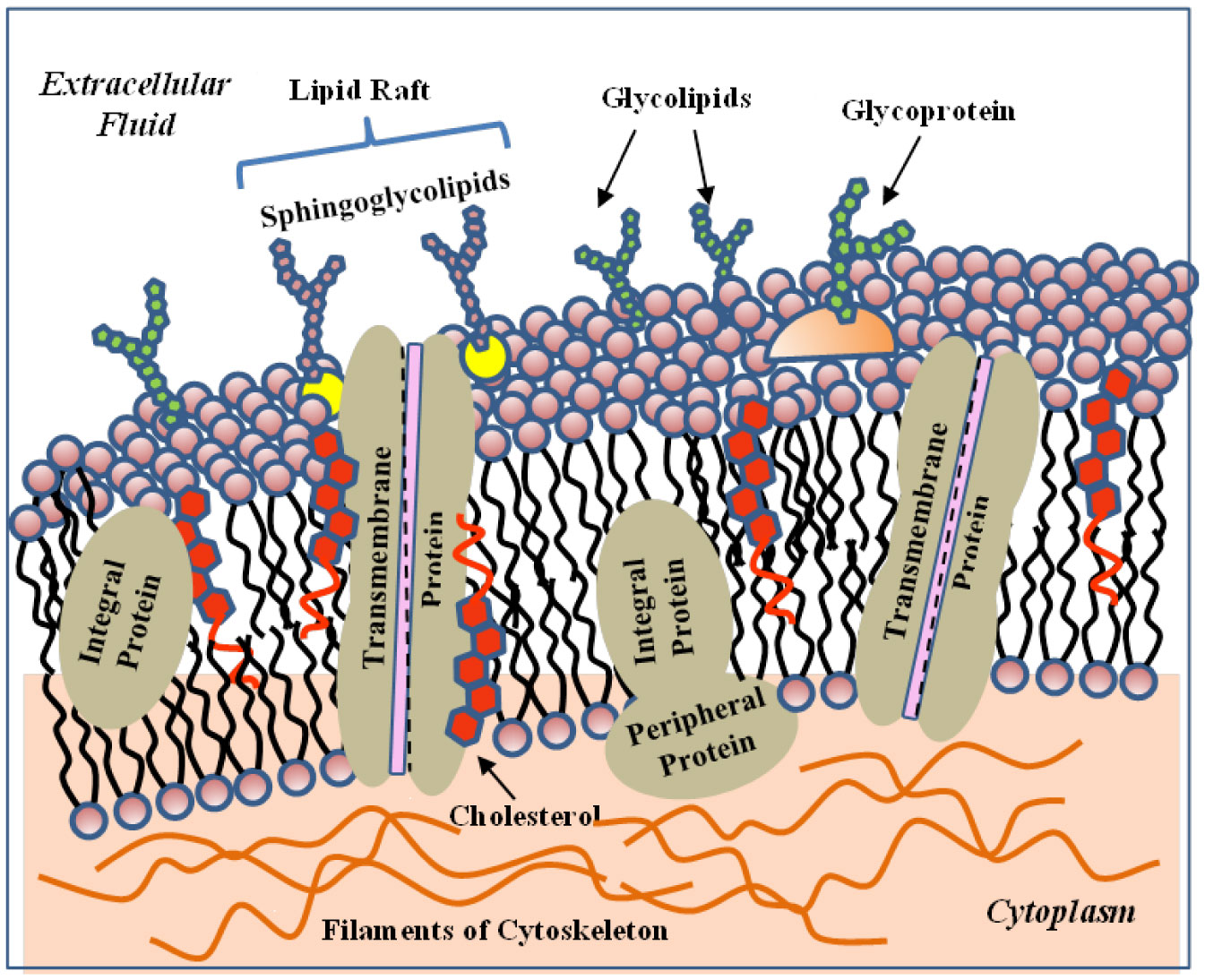
The cellular membranes of living organisms are permeable interfaces between the environment of the extracellular fluid and the internal cytoplasm. This protective barrier of the cell, which is mainly composed of lipids, proteins and carbohydrates, is involved in many important cellular functions such as sensing and signaling, transport of drug components, adhesion and recognition processes [15],[16]. According to the model proposed by Singer and Nicolson (fluid mosaic model) [17], the biological membranes in living systems look like a mosaic of (highly flexible) fluid lipids bilayer structures containing both integral protein (which are anchored within the lipid bilayers by means of hydrophobic interactions), and peripheral proteins (which are attached, by weak ionic bonds, to the polar headgroups of the biomembranes lipids or to the integral proteins). Finally, the transmembrane proteins that span the biomembrane bilayer are responsible for transporting ions or small molecules between the two sides the cell membrane (Figure 1). The (affinity-based) assembly of amphipathic lipids and proteins confers a highly dynamic character to the fluid membranes structures, thus allowing rotation (around their individual axes perpendicular to the membrane), translation (across and parallel to the membrane), and trans-bilayer (lipids flipping between opposite external planes) movements [2]. Moreover, plasma membrane of mammalian cells exhibit an asymmetry in (internal and external) membrane leaflets, whereby phosphatidylcholine and sphingomyelin are predominantly located in the outer monolayer, whereas amino-phospholipids are mainly located in the inner monolayer [3]. Finally, (long) carbohydrate macromolecules are attached to proteins on the outside leaflet of the plasma membrane. Proteins that are embedded in the plasma membranes favors the cell interaction with its bio-environment and facilitate the carrying out of nutrients and active compounds across the biomembrane. Moreover, they favor the cell anchoring in the transmission/translation of chemical signals from outside the cell (for intracellular tasks and processes) [16],[17]. Proteins also help in anchoring some fibers (cytoskeleton) to give the cell its shape, while some membrane-bound enzymes allow to perform certain reactions which are needed for some specific cellular activities.

The cytoskeleton is composed of a network of interlinking long protein filaments present in the cytoplasm of eukaryotic cells. Those filaments, that extends from the cell nucleus to the cell membrane, create a framework that maintains the shape of the cells and give them a mechanical resistance to deformation. The cytoskeleton underlies many aspects of cell physiology, including cell division, mitosis, and extracellular matrix patterning [18],[19]. The proteins of the cytoskeleton interact with membranes and regulates the cytoskeletal dynamic remodelling. The cytoskeletons contributes to the cell wall biosynthesis by regulating the transportation and deposition of the components of the cell walls. This control is achieved by the tethering of these structures to the plasma membrane. The cell wall, plasma membrane and cytoskeleton nexus (mediated by the bridging of a single or several proteins) form a scaffolding structure that may participate in signaling pathways. Cytoskeleton signals transmission across cellular membranes is far less understood [18],[19]. Recent work has demonstrated that the membrane alone (or through membrane-associated proteins) can stimulate dynamic changes to the cytoskeleton [18],[19]. Some mechanistic links between membranes and the cytoskeletal networks (composed of actin, microtubule, and septin) are able to integrate various signals received at the membrane, and facilitate distinct functions in response [19]. These studies highlight the membrane's central role in coordinating these cytoskeletal systems to carry out important cell physiology processes, such as endocytosis and cellular compartmentalization. The membrane–cytoskeleton interactions are central to understand how the cytoskeletal remodelling process is integrated throughout cells and tissues. Most of the intracellular and extracellular signaling cues, in fact, have to signal through a lipid bilayer before reaching the cytoskeleton, that receives, integrates, and transmits the signals across the plasma and intracellular membranes.

The presence of some specialized sub-domains of cell membranes called lipid rafts were proposed in order to explain the protein role in some specific cellular membrane processes [20]–[22]. Lipid rafts are (tightly packed) liquid-ordered phases composed of cholesterol and sphingolipids in the outer exoplasmic leaflet, that are connected to cholesterol and phospholipids (such as phosphatidylcholine, phosphatidylethanolamine, and phosphatidylserine) in the inner cytoplasmic leaflet of the lipid bilayer [22]–[24]. Moreover, a recent study evidenced that plasma membranes are asymmetric in lipid unsaturation, packing and protein shape, with the cytoplasmic leaflet being approximately twofold more unsaturated than the exoplasmic leaflet (which exhibit a more packed and less diffusive behavior than the inner leaflet) [25]. Because the different composition of the two monolayers of the plasma membrane the free energy of each monolayer will change differently when absorbing a cholesterol molecule. Therefore, to compensate for this inherent difference, cholesterol must distribute itself in such a way that both monolayers have the same chemical potential. Cholesterol is known to be strongly attracted to sphingomyelin because of its saturated tail. Although it is assumed to be most abundant (> 90%) in the outer mono-layer of the plasma membrane, a controversy of cholesterol distribution is still present, due to the inherent difficulty in its precise detection [26]. Recently, a study that make use of tuneable orthogonal cholesterol sensors evidenced a marked transbilayer asymmetry of plasma membrane cholesterol in various mammalian cells, with the concentration in the inner leaflet being about 12-fold lower than that in the outer leaflet [27]. The lipid rafts assemblies, that present a more ordered (fluid state) than the surrounding bilayer, are presumed to have a role in specific biological functions (such as in membrane protein sorting or the building of signal transduction complexes). When activated, they self-agammaegate to form versatile larger nanostructures that favor specific cellular membrane processes, and help the proteins to perform highly functional tasks (such as signaling, processing, and transport processes) [22]–[24]. Moreover, anomalies in raft composition are supposed to be associated with various diseases such as atherosclerosis, muscular dystrophy, neurodegenerative disorders, Alzheimer's disease [20]–[23]. Finally, it is worth mentioning that the raft hypothesis is a subject of controversy since the raft agammaegation process is poorly understood and little is known about the main factors that determine the (proteins and lipids) raft association and how those nanodomains realize specific membrane functions [21]–[24]. In this respect the clustering process involving lipid rafts represent an interesting interdisciplinary research topic in the fields of the biomembrane science, human physiology (and physiopathology), and nanomedicine.

Apart from the lipid rafts, the co-presence of lipids and proteins stimulate specific biophysical and biochemical interaction that control and regulate a large variety of other cell tasks. Most of the assembly ability depends on the specific lipid properties such as their composition, chemical structure and morphology (headgroup size, length/saturation of acyl chain tails) [5],[6]. Moreover, the lipid physical properties have a templating effect for the membrane thickness, curvature, and tension that play important roles in some crucial processes such as cell molecular recognition and signaling. For example, some lipids, that are tightly bound to cell-surface receptors (non-annular lipids) are able to bind to membrane proteins and may help membrane receptors acquire specific 3D functional nano-structures, while annular lipids, which are less tightly bound to the protein surface are exchangeable on a faster time scale with the surrounding (bulk membrane) lipids [29]. A special role is also played by the interactions of water molecules adsorbed on surfaces of lipids and proteins bio-molecules. Various investigations evidence the way in which biomolecular activity of water is involved in protein and biomembrane structures, stability and dynamics [30]–[33]. Critical investigation and analyses of the water properties in biological systems merging from the recent studies, evidence the important role of the interaction at the complex interface between the biomolecular systems (such as proteins or biomembranes) and water molecules, in realizing a functional network in which the biological systems may be considered as a complex structure stabilized by water [34]–[37]. In this case the hydrogen bonds and hydrophobic effect play a crucial role for the establishment of the protein structure and stability within the biomembrane environment [38],[39]. More specifically, the investigation of the properties of the structural water, confined at the hydration sites, and the functional water, which is located around the lipids headgroups (and modulated by the lipids hydrophobic hydrocarbon chains), represent a crucial step for the understanding of complex bio-processes in biomembranes at the level of tissues and cells [38]–[41]. For example, disaccharides (such as trehalose, maltose, or sucrose) have received considerable interest over the past decades for their preservation properties toward cells, or therapeutic proteins, as they can be added to biologically active solutions to overcome the limited stability of proteins (in pH, temperature, salt concentration, etc.) and to prevent the partial (or total) degradation of biological molecules caused by the dehydration or thermal stresses [42]–[47].

In basic research, the investigation concerning model and biological membranes are also important for the study involving their interaction with active components (such as food, drugs, enzymes and genetic material) and their drug delivery processes through the living cell membranes and other biological barriers [48],[49]. For this reason the biological membranes can be considered the most multifunctional and performant cellular structure, while its study represents a central topic at the crossroad of different disciplines including biochemistry, food industry, biotechnology and nano-medicine.

3.   Experimental approaches for the study of biomembranes

The structural properties of biomembranes in living systems, which encompasses rich variety of different nanostructures and morphologies, require the combination of different techniques in order to identify the basic properties of the involved association processes as well as the underling (collective) molecular phenomena involved in the resulting biological functions [50],[51]. One of the main research challenges in biomembranes science is to decipher the intimate relation between the structural configuration of its main components (i.e., lipids, proteins and carbohydrates) and the interactions (at the molecular level) within the micro-environment of the biological system under study. This allows to connect the self-assembly properties (that regulate the composition-structure relationship) to the underlying biological functions of the biomembranes. In order to characterize the structure and the interactions of drugs with (model) biomembrane, from both a quantitative and qualitative point of view, the combination of complementary, experimental methods are necessary.

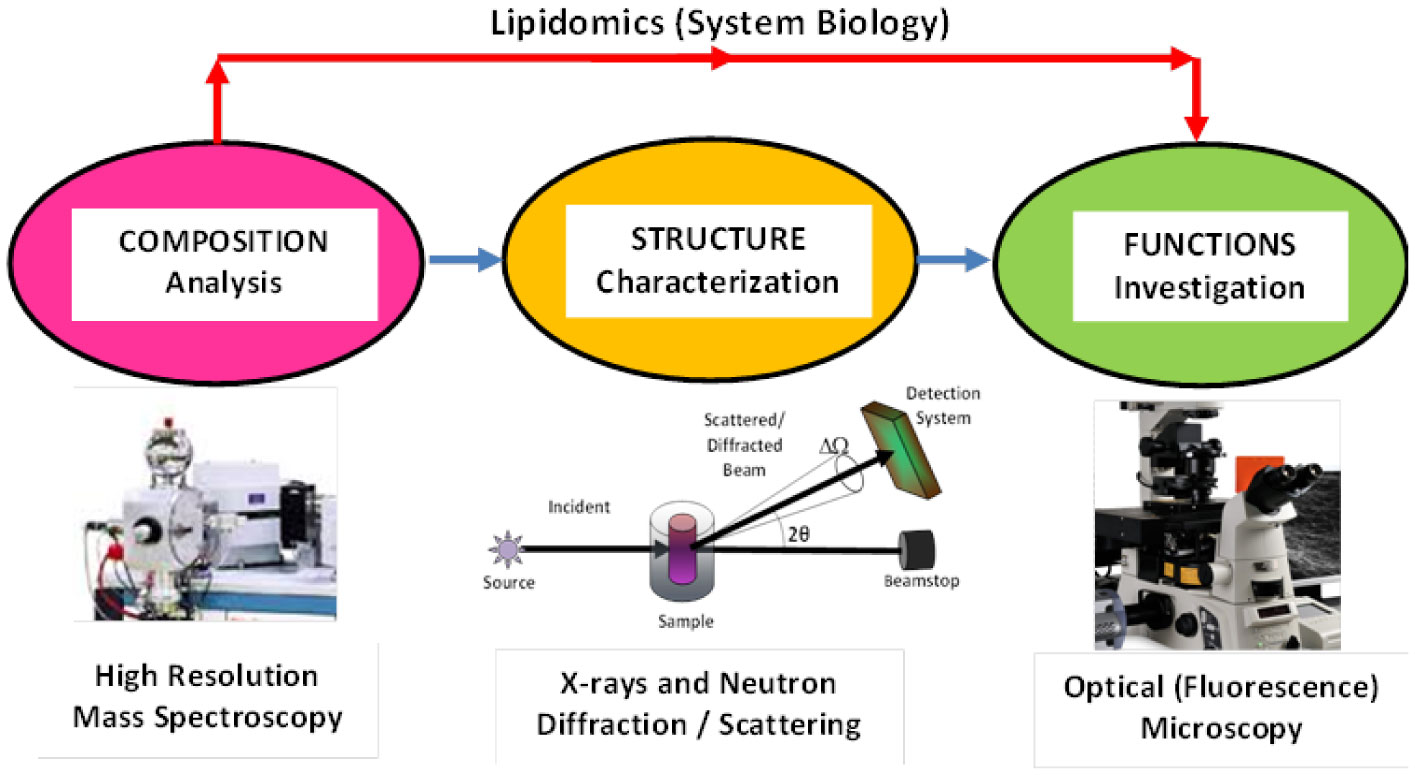
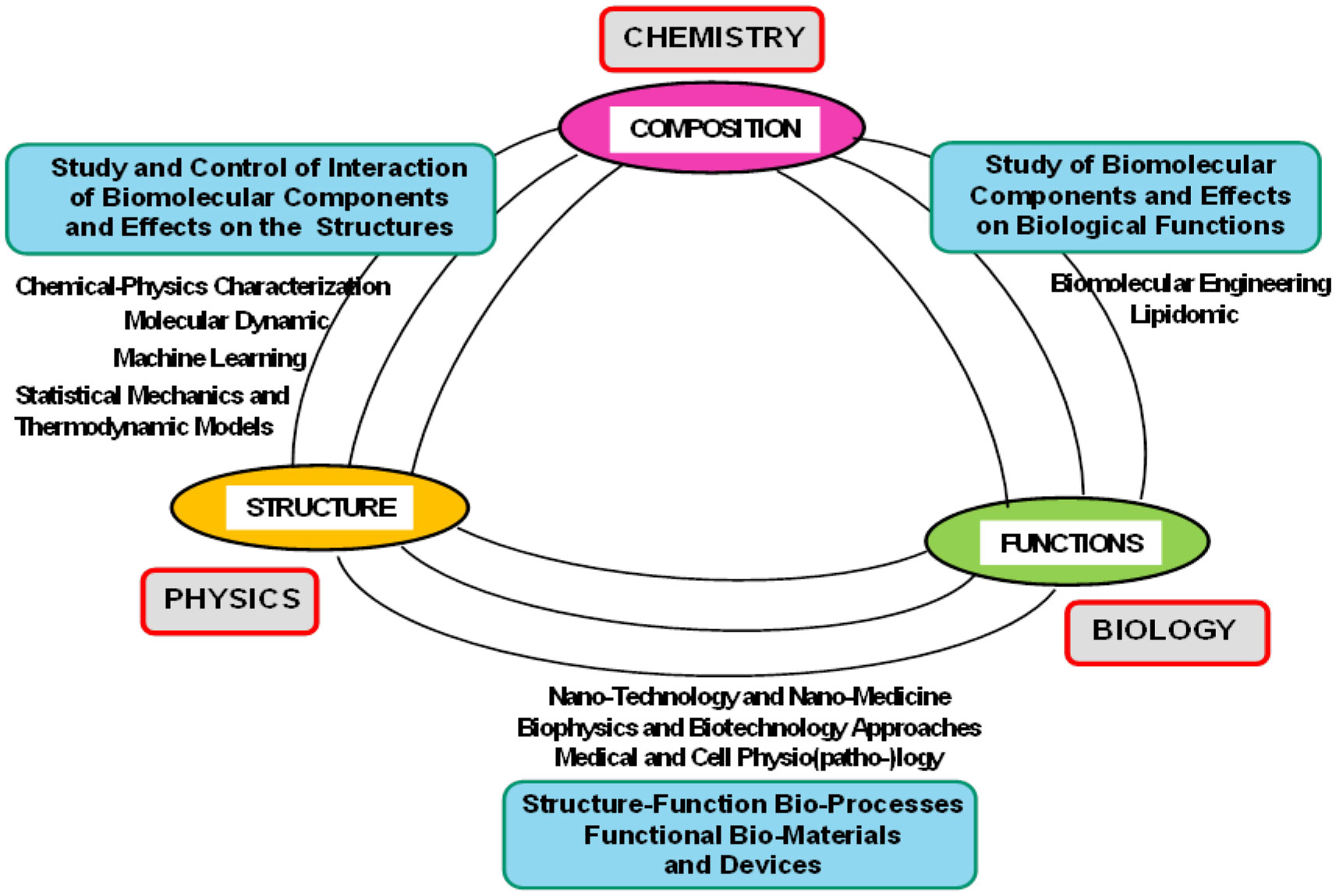
As reported in Figure 2, it possible to identify a relationship between the biomembranes composition, structure and functions, while their experimental characterization methods can be grouped into three main conceptual stages.

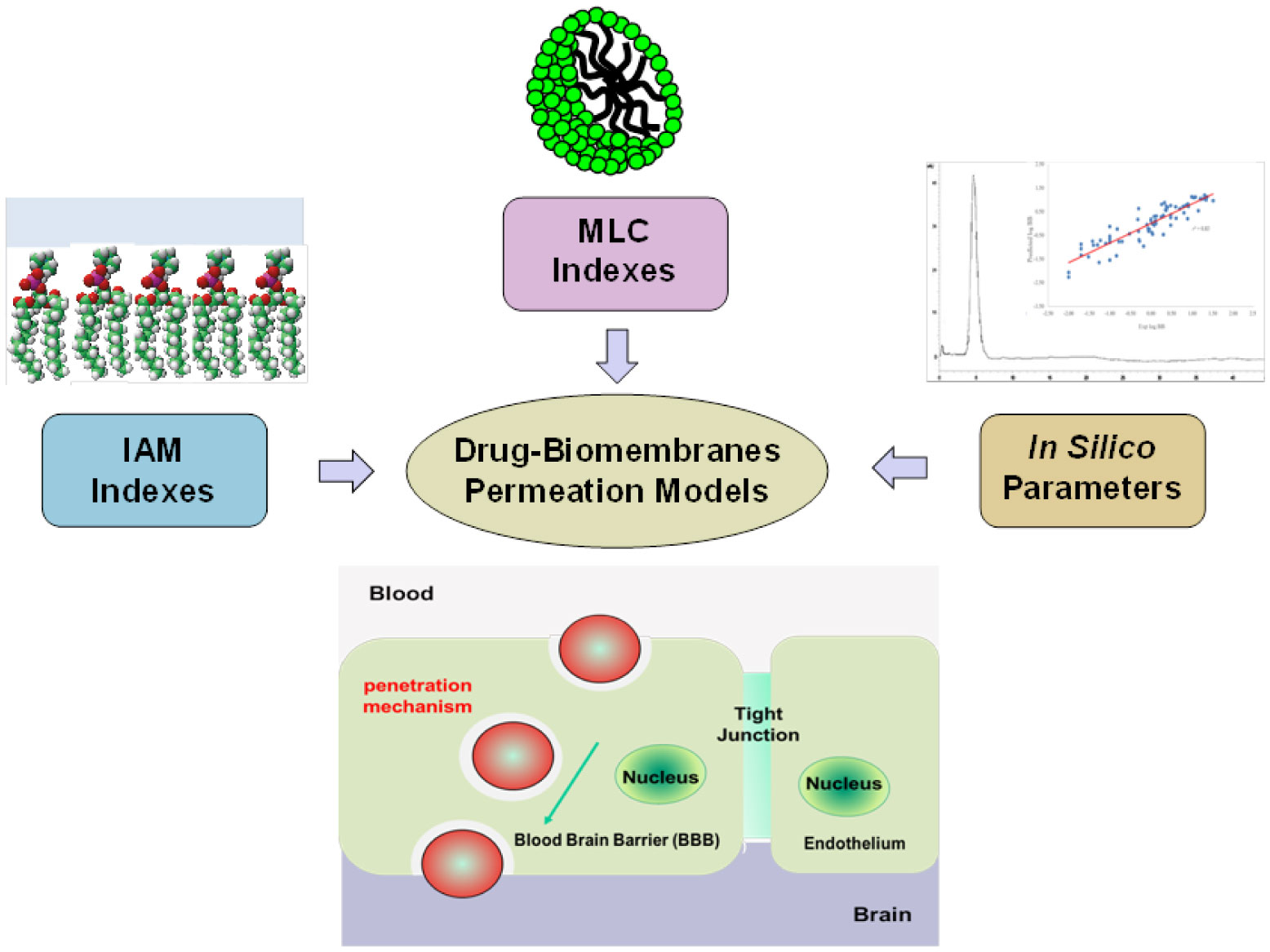
The first stage of the investigation consists in the analysis of the composition of the (model or real) biological membranes. One important (composition analysis) approach consist in the use of the high-resolution mass spectroscopy techniques [52]. Detailed information about the population distribution of the biomembrane components is also obtained by using the size-exclusion chromatography (SEC) [53]. This approach allows to separate (and quantify) the liposome populations distribution by exploiting the separation process (based on the elution velocity from a column equipped with a porous substrate) which depends on the compound hydrodynamic size. Among the chromatographic approaches, the immobilized artificial membrane (IAM) chromatography allows to efficiently discriminate the liposome/water partitioning as well as the permeation of cell membranes. [54],[55]. Moreover IAM chromatography give complementary information on drug-membrane interactions (binding) and passive diffusion (permeation) of drugs, thus allowing an estimate of the passive transport through a variety of biological barriers, and the pharmacokinetic/pharmacodynamic properties of the drugs [54],[55]. A further advance in this field is represented by bio-partitioning (BP) chromatography, a technique that combine the chromatographic method with biomembrane-mimetic structures (such as the phospholipid vesicles, polymer micelles, niosomes and microemulsions). This technique represents a (high-throughput) screening platform for the investigation of the drug-biomembrane permeability and interaction and their connection with the biological functions. Recently, bio-partitioning micellar liquid chromatography (MLC) and immobilized artificial membrane (IAM) (liquid) chromatography have been used for in silico and in vitro determination of phenols penetration across the Blood-Brain Barrier (BBB) [51]. The MLC is a reversed-phase liquid chromatographic (RPLC) technique based on the addition of surfactants (ionic or non-ionic) to aqueous mobile phases at concentrations higher than their critical micelle concentrations (CMC), under specific experimental conditions [56],[57]. As in classical micellar chromatography, the retention process of compounds in MLC depends on the types of interactions between modified reversed stationary phase and micelles present in the mobile phase, and is sensitively influenced by the hydrophobic, electronic and steric properties of the included compounds. This technique can be useful in describing the biological behavior of different kinds of organic compounds and can mimic many biological processes such as blood–brain barrier penetration, skin permeability, intestinal absorption and drug partitioning process in biological systems [56],[57]. Biomimetic partition chromatography systems have been successfully introduced also with the IAM chromatography method, that uses a stationary phase which consists of a monolayer of phosphatidylcholine (the major component of biological membranes) covalently immobilized on an inert silica support. IAM columns are thought to mimic very closely a membrane bilayer and are used in a high performance liquid chromatography (HPLC) system with a physiological buffer as eluent [56],[57]. Furthermore, chromatographic retention coefficients of the analytes on stationary phases can be assumed as direct measures of their lipophilicity, (i.e., their affinity for lipids) [58]. The lipophilicity of a substance is an important physico-chemical property affecting the permeability and the passive transport through biological membranes (barriers) of compounds. Drug molecules possessing a sensitive affinity for lipophilic biological membranes, in fact, can be easily adsorbed and distributed within the organisms with a sensitive effect on pharmacokinetic processes and on the interactions with bioreceptors. Reversed (stationary) phase high-performance liquid chromatography has attracted great interest for lipophilicity measurement, due to its advantages, including speed, reproducibility, insensitivity to impurities and degradation products, broad dynamic range, on-line detection, and reduced handling and sizes of samples [58].

The MLC and IAM chromatographic indexes, including the calculated topological and physicochemical parameters in silico, can be used for the development of blood–brain barrier passage-predictive statistical models [56],[57]. The BBB is one of the most complex and extensively studied biological membrane systems, whose main function is to preserve mammalian brain integrity against possible injurious substances. Apart from active transport mechanisms, whose occurrence is difficult to predict on a solely chemical structure basis, drugs can therefore cross the BBB by the passive transcellular route. One of the most used and reputed method of in vivo, ex vivo, and in vitro methods for measuring BBB partitioning of analytes is the determination of the quantity log BB=log(C_Brain/C_Blood), expresses as a function of the concentration of the analyte is the in the brain tissues (C_Brain) and in the in the blood (C_Blood). This method generally involves the use of animal models (that may cause potential source of ethical issues), or the employment of cultured cell. Those approaches, however, are time-consuming and do not provide any mechanistic information about the nature of the analyte passage. On the other hand, the in silico methods, although is unable to take into account all phenomena occurring in vivo, are much faster and simple to perform, as they are based on the calculation of physicochemical parameters and the screening of large libraries of compounds, thus allowing a more exhaustive investigation of the molecular mechanisms involved in membrane permeation. Moreover, in vitro methods based on the use of biomimetic stationary phases coupled with high performance liquid chromatography (HPLC) are much more reproducible and can be able to provide an in-depth understanding of the mechanisms involved in membrane barrier passage. Both IAM and MLC chromatographic indexes, combined with in silico calculated descriptors, have demonstrated effectiveness in the prediction of BBB drug penetration [59].

The main steps of the approach is given by the following stages (Figure 3):

- setup of (medium/high-throughput) methods for IAM and MLC indexes;

-validation of obtained parameters and development statistical models for the prediction of BBB llpenetration (log BB) by using the chromatographic indexes (and in silico calculated descriptors);

-elucidation of the molecular mechanism involved in BBB passive diffusion of drugs

-optional molecular docking studies, to investigate the possibility the occurrence of further interaction mechanisms (such as the active efflux, or other self-assembly mechanisms).

The molecular modeling performed is simple, easy-to-perform and can be configured to run automatically in case of batch analyses [57],[59]. Therefore, it can be of interest for pharmaceutical industries as a high-throughput BBB penetration screening methods.

The second stage in the study of the biomembranes consists in the structural characterization methods by means of in vitro experiments. In this respect, the X-rays and Neutron small angle scattering (SAXS and SANS) and diffraction methods are among the most employed experimental techniques for the investigation, in non-invasive way, of the structural properties of biomembranes in complex biological systems [60]–[63]. Those non-destructive methods efficiently evidence the formation of different biomembrane structures and morphologies thus highlighting the important role of the relevant molecular conformations in many different processes of life science [64]–[67]. Small-angle X-ray scattering (SAXS) furnish information on (lipid-based) biomembranes under different solution conditions providing information on lipid domains (and phases), size, spacing and thicknesses in the range of a few nanometres and up to some tens of nanometres. On the same experimental set-up of the SAXS techniques (that typically operate at scattering angle between 0.1–5°) it is possible to set a further detection system allowing wide angle X-ray scattering (WAXS) experiments (at the scattering angle typically > 5°), that provides complementary information on the nature of hydrocarbon chain packing and lamellar phases (at the Å scale) when crystalline-like ordered phases exist in the biomembrane system [62]. Diffraction is a structural investigation method for the study of ordered lipid bio-membrane systems with large repeat distances and allows to resolve the existence of a variety of crystalline domain structures (such as lipid monolayers, bilayers, or multilayers) in lipid mixtures model systems as well as their hierarchical level of organization. Crystalline structure of several biomembranes composed of lipid bilayers and monolayers (with saturated alkyl chains) vary little for different lipids composition, and present similar unit cell dimensions of about 5.0 × 8.0 Ų. [61],[62]. This characterization method is crucial for the investigation of biomembrane functions, thus furnishing useful information of their relevant role in important bio-processes such as phase separation, physiological and/or pathological crystallizations and protein sorting, just to name few [64]. For example, X-ray diffraction proved to be a very sensitive tool on detecting the periodical spacing and phase changes induced by antimicrobial peptides interacting with lipid membranes, such as the Alamethicin on dipalmitoyl–phosphatidyl–choline (DPPC) bilayers, as well as to predict the peptides doses necessary to trigger cell death through plasma membrane alterations [68]. Small angle neutron scattering (SANS) shares similar principles with SAXS. While SAXS patterns (that originates from electrons scattering) is only sensitive to the hydrophilic part of a lipid bilayer, the SANS technique (that depends on the scattering of neutrons) provides useful information on the hydrophobic tail part as they present a better “contrast” for that region. Therefore, SAXS and SANS can be used as complementary techniques for a fine structural description of the biological membranes [60]–[62]. Moreover neutron diffraction experiments on selectively deuterated lipids provide an important method of determining the mean conformation of a lipid molecule at different positions in the polar head group as well as in the hydrocarbon chains region [69],[70].

Nuclear magnetic resonance (NMR) is a non-invasive, non-destructive, and quantitative spectroscopy technique for the investigation of the drug-membrane interactions and provides detailed molecular level information on the structure and dynamics of (lipid) membranes (at a sub-Ångstrom resolution) [71]. As the nuclei of many atoms possess a magnetic moment (which gives rise to different energy levels and resonance frequencies in presence of an external magnetic field) many intermolecular interaction, including the drug binding to the lipid, may lead to variations in the local electronic environment surrounding the nucleus and thus cause a specific chemical shift in NMR spectrum with respect to a reference resonant frequency. More specifically multinuclear solid state NMR provides information on the nature of the membrane phase (lamellar, hexagonal, cubic, bicelle, micelle, etc.), its dynamics (fluid, gel, or liquid-ordered), and the molecular structure of embedded lipids when using the magic angle sample spinning (MAS) apparatus. Structural properties of lipid-based membranes are characterized by positional and orientational order. Moreover, the order parameters measured in solid-state NMR spectroscopy give complementary structural information on the distribution of the lipids with respect to the bilayer normal. Solid-state ²H NMR provides knowledge of segment orientations and their fluctuations at a site-resolved atomistic level. Solid state NMR has the advantage that the anisotropic magnetic or electric couplings (dipolar, quadrupolar, chemical shift) yield segmental order parameters as model-free experimental observables. The disadvantage is that the broad spectral width requires special high-power NMR technology, and rather large amounts of sample material are needed. Relaxation time measurements are also described to measure lipid motional processes from the picosecond to the second timescale [66]. Recently, a ¹H NMR Relaxometry technique provides information on the timescales of motional processes involved in the proton relaxation (on a time scale of microseconds) and allows the study of water dynamics in hydrated systems in the range of a few nanometers. The approach can provide valuable information to discriminate the different molecular mechanisms associated with water motion as a function of the hydration state, highlighting the variations of the relaxation rates connected with solvation processes, aqueous clusters and hydrogen bond network formation [72],[73]. Recently, an investigation integrate the results of ²H NMR with small-angle X-ray scattering (SAXS) studies and MD simulations to achieve new insights. In the case of scattering methods (SAXS and SANS), lipid membranes are investigated as multilamellar dispersions or aligned on planar substrates, enabling comparisons with solid-state NMR spectroscopy [74].

A recent experimental method enable simultaneous measurement of optical and thermal properties of macromolecular nano-structures, such as biological membranes, by combining the photothermal (PT) microscopy and spectroscopy with photoacoustic (PA) techniques, and the application of broadband light sources and interferometer techniques [75],[76]. Those techniques (that exploit the generation of heat due to the absorption of light) provide a broader complementary spectrum of information compared to standard spectroscopies based on to monochromators (such as the UV/VIS or IR) which require numerous separate measurements of physical quantities in different spectral ranges. A recent investigation evidenced the potential of photoacoustics experiments in the identification of the mechanisms underlying drug transport through tissue-mimicking systems and biomembranes, in a model transdermal delivery system consisting of dithranol and dodecanol-collodion (DDC) membrane samples [77]. The proposed approach may help to develop new strategies for the experimental investigation of the interactions processes in skin-mimicking membranes and may provide a better understanding of the principles of drug transport (and permeation) processes in biomembranes.

Many other complementary experimental techniques can be used, with the special scope to determine the affinity of active compounds for biomembranes inclusion, including several spectroscopy techniques such as dynamic light scattering (DLS), FT-infrared (IR), ultraviolet (UV), electron spin resonance (ESR), electron paramagnetic resonance (EPR), circular dichroism, [78],[79]. Furthermore, the use of complementary highly sensitive biophysical techniques, such as the differential scanning calorimetry (DSC) [80] and isothermal titration calorimetry (ITC) [81], allow the investigation of the thermodynamics of protein–lipid (and drug-lipid) interactions (and binding). Those experimental approaches together the solid state NMR technique, allow to obtain some complementary useful thermodynamic information on the investigated systems.

Finally, (cryo-) transmission electron microscopy (TEM) experiments provide detailed insights into biomembrane packing and phase behavior, protein conformations and folding, and drug inclusion processes [82],[83]. Cryo-TEM can provide high-resolution images for studying self-assembly, phase transition mechanisms, and dynamic phenomena in complex lipid-based biomembrane nanostructures. Moreover, advanced cryo-tomography can provide valuable 3D information on the structure and morphology of biomolecules, drug-loaded (and drug-free) liposomes, cubosomes, hexosomes and other biomembranes phases. As the cryo-imaging technique is not a quantitative methodology it should be a part of an integrated analysis with quantitative biophysical techniques. For this reason, cryo-TEM is very useful when combined with SAXS or SANS techniques, and self-diffusion NMR for detailed structural and morphological characterization of self-assembled nanostructures [82],[83].

Finally, the third stage is focused on the investigation of the main features of biological membrane functions. Biological membranes are involved, in fact, in many important cellular functions including signaling and sensing, (selective) transport of active compounds, cell adhesion and cell recognition. Moreover, a number of other functional processes (such as the metabolic processes, antigen-antibody recognition or DNA synthesis) take place within biomembranes systems present in the form of internal compartments inside the cytoplasmatic region, such as in lysosomes, mitochondria, chloroplasts. [15]–[17]. The experimental investigation of biomembranes functions within the complex environment of living cells is a complex task. Given the nanoscale dimensions and the dynamic nature of these membrane nanodomains and compartments, highly performing methods that allow the observation of lipid and protein structure and dynamics at high spatial and temporal resolution are needed. Unfortunately, no single experimental approach can combine high spatial resolution and fast image acquisition in one instrument. Among the various experimental approaches that allow the investigation of biomembrane functions, the optical far-field microscopy is a method of choice [84], since it facilitate the structural and dynamics investigation in an (almost) non-invasive way, by fluorescence labeling of the macromolecular components under observation. Until few years ago, the near-field scanning optical microscopy has been the only (optical) technique with resolution beyond the diffraction limit of light. The potential of far-field fluorescence microscopy is limited by the diffraction, to about 200 nm, for visible light (in spatial resolution) and limited by the image recording speed (in temporal resolution) [84]. High-resolution fluorescence microscopy technique is compatible with the live cell imaging. It provides excellent spectral contrast and, in combination with sensitive detectors, allows the detection of individual molecules. Recent progresses enhanced the optical microscopy resolution up to the molecular level range of the living cells (in a non-invasive way) by means of fluorescence correlation spectroscopy (FCS) [85]. This technique allows the observation of the interaction dynamics and molecular diffusion in the millisecond time scale resolution. In Figure 4 we report a conceptual map of the main experimental techniques for the study of biomembranes.

4.   Elaboration of models for biomembranes structure and interaction

As bio-membranes functions emerge at multi-scale hierarchical levels across a wide ranges of space and time domains, the bottom up approach of cell membranes (i.e., from molecules to cells) requires detailed information over the complete space-time range (from fast to slow and from small to large). More specifically, the combination (and intensity) of the involved soft interactions (such as electrostatic forces, H-bonds, steric hindrance and hydrophobic effects) determine the self-assembly morphology (ordered/disordered, ripple phase, liquid-crystal) and their pattern agammaegation (bilayer, multi-lamellar, hexagonal/cubic phases). Those structural properties regulate the formation of energetic barriers controlling the thermally activated (diffusional, rotational and vibrational) molecular dynamics of the building-block molecules forming the biomembranes domains. Even though a considerable progress has been made with the experimental investigations of biomembrane structure and dynamics, the investigation of relevant self-assembly mechanisms is still limited by the space-time resolution of the experimental methods. Moreover, as the natural cell membranes present a great complexity of structures, with a large variety of cross-connections and functionality, the study of simplified (artificial) model systems, greatly helps the scientists to understand the effects of membrane lipids in many processes (including drug transport and uptake into cells). The use of artificial nanostructured materials as simplified models for the study of cell membranes processes has given a strong input to the understanding of the complex interactions that a biomolecule can develop toward biological membranes. For this reason, the adoption of artificial membrane models allows the carrying out of particular studies in specific experimental conditions (such as temperature, or ionic strength). In these models some great part of the cell membrane properties are obviously lost, (such as the presence of functionalized membrane proteins, receptors, endocytosis, and other active processes) and may not reproduce exactly all the aspects of the biomembrane environment. Generally speaking, three main kinds of lipid membrane models have been identified: monolayers, vesicle-forming bilayers (liposomes), and supported bilayers [1],[8]. The well-defined, simplified, composition and material configuration of these models allow to better reproduce the complex phenomena and colloidal stability that are present in vivo during drug transport, pharmacokinetic distribution.

An important modeling method in biomembrane research is given by the quantitative structure-activity relationship (QSAR) approaches [86]. The QSAR methods allow the prediction of the biological activity and effect of chemical compounds based on mathematical and statistical models [86]. The QSAR approach relies on the basic principle of chemistry, that states that the biological activity of any compound (such as a macromolecule, drug or ligand) is intimately connected with the structural arrangement of atoms forming its molecular structure. In this respect, structurally related molecules, that can be defined in terms of a series of parameters (called molecular descriptors), possess similar biological activities. The QSAR studies therefore involve selection of active and inactive compounds with the measurement of their biological activity, description and calculation of molecular descriptors, selection of appropriate features followed by construction of the mathematical model and its evaluation. These approaches are a great alternative to cost and intensive experiments carried out in laboratories. QSAR finds applicability in a wide range of fields including toxicology, drug design and discovery, nanomedicine [86]. The QSAR approach in biomembrane research assume that the biological activity is viewed as a sum of the various interactions (and reactions) that compounds undergoes with the sites of action (receptors) during the transport processes through bio-membranes. These interactions are assumed to be strongly regulated by the chemical structure of the compound, while a specific change in its structure can result in a change in biological response and activity [87]. An Alternative to the QSAR models, the quantitative retention–activity relationship (QRAR) models represent other kind of modeling techniques, in which chromatographic retention parameters are used as descriptor (or predictor) parameters of a specific biological response of chemicals [86]. Different QRAR models based on retention factors obtained using BMC and IAM chromatographic systems have been utilized to compare different physicochemical and biological parameters, in order to extimate phenols penetration across BBB [88]. For this purpose, the Linear Solvation Energy Relationship (LSER) of Abraham model [89], was applied to characterize IAM and BMC systems. Finally, the use of combined and hybrid approaches proved fast and effective in the development of highly predictive BBB permeation models, thus shedding new light into the molecular mechanism involved in the BBB uptake of therapeutics.

Many investigation concerning the study of the structure-function relationship in biological membranes make use of the concepts of the thermodynamic and statistical physics approaches. On the theoretical side, there is a large variety of analytical and computational techniques, which have shown potential usefulness in study of the collective properties of model biomembranes. Besides the methods of classical and statistical thermodynamics, new approaches have been proposed, for instance: the theories of phase transitions, the approaches of out-of-equilibrium thermodynamics, the application of the continuum elasticity, and viscoelasticity theories to lipid membranes and so on. Among them, the mean-field approximation (MFA) and the Ornstein-Zernike (O. Z.) integral equation approach are widely employed in the field of nano-colloids, biomaterials and soft matter [90]–[92]. Those approaches has been employed to study the range and strength of a large variety of soft interactions usually encountered in biological and nanostructured systems, including amphiphiles [93]–[97], proteins [98], dendrimers [99],[100], hybrid and polymers-based nanostructures [101]–[103], and model biomembranes [104],[105].

Moreover, the progress of molecular dynamics (MD) simulations methods offers the opportunity to study of collective behavior of multicomponent systems for a wide range of biophysical processes, in great space-time resolution [106],[107]. They range from highly idealized coarse-grained pictures of lipids, proteins, and water, to complete simulations at an atomistic level [108]–[111]. Simulations are gaining broader and broader applications because they provide, with a steady increasing level of accuracy, information on both the structural details (geometry) and the collective property of the system, including system total energy, lipid order parameters, and bilayer elastic constants.

5.   System biology and the lipodomic approach

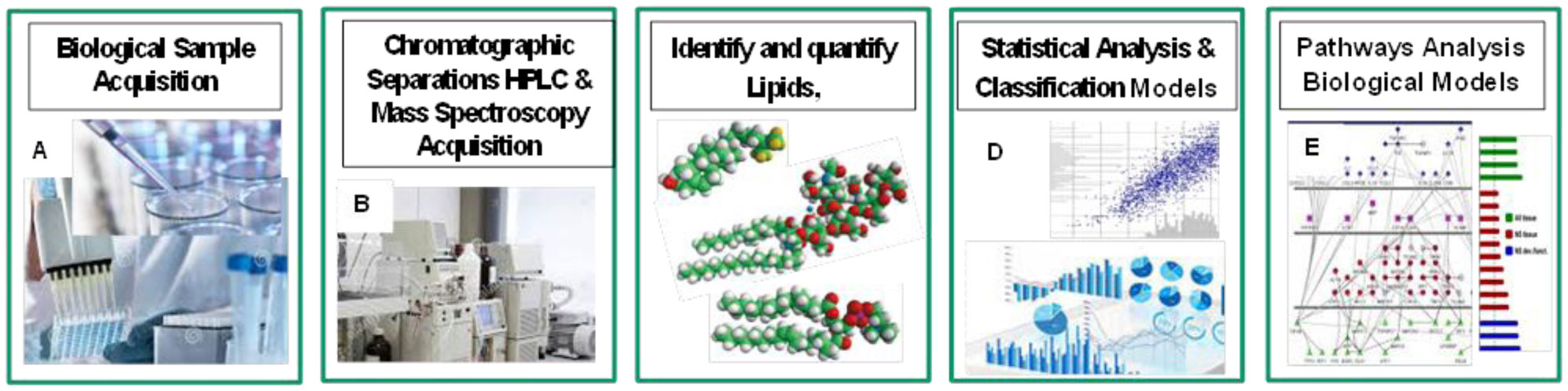
A modern interdisciplinary method in life science is given by the systems biology approach [112]. This method is based on the collection of data and information from many components in parallel, using the so called “-omics” technologies, (such as the metabolomics, proteomics and genomics approaches) [112]. This approach aims to investigate the complex interactions and functioning of the living cell at various levels, by inferring the complex pathways and intermediaries that govern every biological (physiological/pathological) process. As lipid bilayers membranes represent one of the main components of biological membranes, the lipodomics research field emerged as an important subfield of system biology method for the study of biological membranes systems at an interdisciplinary level [114]. A schematic representation of the lipidomic workflow is reported in Figure 5. More specifically, the lipidomics method investigate the pathways (and networks) of cellular lipids that attempt a large-scale mapping of the complete lipid profile within a variety of biological systems (such as a cell, tissue, or organism). Dynamics profiles of cellular lipids and the changes that occur after the perturbation of the cell system, are examined in order to identify biomarkers and elucidate the main changes in its physiological or pathological state.

As lipids play an important role in many metabolic diseases (such as diabetes, obesity, atherosclerosis and hypertension) the lipidomics approach is considered as a subset of the more general field of “metabolomics” which includes three other major classes of biological molecules (proteins/amino-acids, sugars and nucleic acids). Lipids bilayers biomembranes also regulate protein functions and gene transcription, and for this reasons they are also considered as a part of a dynamic “interactome” within the cell [113],[114]. Those rapidly expanding fields complement the huge progress made in proteomics and genomics, within the large family of systems biology. This novel conceptual organization of disciplines facilitates the framing of the study of biomembrane within a true interdisciplinary approach at the crossroad between chemistry, informatics, mathematics, biology and medicine.

6.   Strengthening the interdisciplinary and transdisciplinary aspect of biomembranes study

As previously described, biomembranes in living organisms, which have the prominent role of tissues and cells protection from foreign molecules, allow the exchange of information between extra- and intra-cellular environments due to its biochemical-active surface (that include amount of associated enzymes, ion channels, receptors and signaling molecules). Supramolecular structures of biomembranes also have a crucial role in cellular homeostasis, metabolism, growth, and even cellular death. Therefore, the study of the alterations in the structure/functions relationship of relevant biological membranes is crucial for the understanding of the pathological effects that are at the origin of many diseases. The specific dynamical processes observed in a biological membrane and in bio-nanostructured assemblies depend on a rich scenario of multicomponent inter-molecular interactions which allows the formation of supramolecular structures at different levels of complexity. The traditional bottom up approach for the study of bio-membranes involves the investigation of the structural and dynamic processes of relevant nanostructured assemblies over a wide range of distances and relevant time scales, starting from the analysis of molecular interactions (∼10 nm), to the assemblies of lipid-protein complexes (∼100 nm) up to the meso-scale (∼1 µm) and macro-scale (tissues and cells). The study of the molecular events occurring on cell membranes, as well as the multiplicity of interactions that involve bioactive compounds (in either physiological or pathological situations) requests then an interdisciplinary effort of many different field of science (Figure 4). A novel conceptual framework towards an interdisciplinary approach is therefore of paramount importance, to enlarge our knowledge of many diseases and to identify further potential therapeutic targets.

The difficulty to predict the structural behavior and functional responses of complex biomaterials is connected with the difficulty to fully describe (and model) the complex structural and dynamic processes involved in biological systems [115]–[117]. In this respect, none of the single experimental (or theoretical) method alone will be sufficient to fully describe the complex interplay between components, structure and function of biomembranes. Therefore, the possibility of using more experimental or theoretical methods (or a combination of them) represent a first step to integrate the main results coming from different investigations. For example, the interpretation of small angle X-ray measurements guided by molecular dynamics simulations of lipid bilayers has been recently investigated [118]. The direct comparison between the computer simulation results and experimental form factors drive the choice of the main interactions that, at the molecular level, can been directly inferred from the “best” simulated biomembrane structure [119],[120]. In this respect, the integration and use of different computational (or theoretical) methods with experimental techniques will provided valuable opportunities to extend the domain of applicability of each methods. Several example indicate the use molecular dynamic approach to identify the main inter-molecular interactions in complex biomembrane systems, by combining the information coming from different experimental techniques, including the combination of SAXS (and SANS) technique with neutron spin echo [119], atomic force microscopy (AFM) [120], or nuclear magnetic resonance (NMR) [121]. The combination of these techniques demonstrated a great potential to generate atomistic resolution dynamical models of biomembranes (and their interaction with biomolecules) in biologically relevant microenvironment. However, the main barrier that currently needs to be overcome seems to be the limited complexity of the interactions described in MD models [121].

The possible choice of the appropriate combination of experimental (and/or theoretical) approach(es) depend on the complexity of the processes under investigation and on the type (quantity and quality) of information available on those processes in the literature (or in public databases). This approach, whic have been applied especially in crucial biotechnology investigations, demands new ideas and an intense coordination effort between the expertise from different fields [122]–[125]. The combination of the knowledge coming from different disciplines allow to develop a conceptual framework that drive the exploration of complex processes and the related bio-physicochemical interactions at the biological interface (such as membrane surfaces, endosomal compartments, organelles and cytoplasm). However, the integration of the (sometimes heterogeneous) structural (and/or biological, chemical, clinical) data into a unified workflow is a challenging task. For this reason, the study of a multiplicity of simultaneous factors and biological functionality may be replaced with the systematic study of the effect of a few parameters at a time (such as surface charge density and/or nanoparticle size/topology). The choice of a simplified version of the system allow to identify the key factors for the design of novel nanostructured systems, and represents then the fundamental (initial) step to decipher the complexity involved in complex biological processes. Future efforts should be directed toward the creation of suitable links within the complex network that relates components, structure and functions of biological membranes (Figure 6). A network-based method built upon these indications will likely provide a better integration of multidisciplinary research work.

Conclusions

The study of the biological membranes represents a central topic at the crossroad of different disciplines including biochemistry, biotechnology, and nano-medicine. Their scientific investigation involves the study of the collective behavior of numerous interacting (macro-)molecules, while their complete structural description requires the simultaneous calculation (and simulation) of a large number of parameters. The future challenge must provide an efficient integration of the different experimental research approaches and theoretical models into a common background. To achieve this objective, together with the improvement of the resolution of experimental approaches, we need an improvement of the theoretical models and computational efforts, with the aim to integrate them into a multi-scale description of the complex bio-systems. This effort requires an integration of multi- and interdisciplinary approaches that combine results coming from a wide range of sub-disciplines.