Upper and lower bounds for the pull-in voltage and the pull-in distance for a generalized MEMS problem

1.   Introduction

This paper is a continuation of Cheng, Hung and Wang ^[1]. In this paper, we study some structures of bifurcation diagrams of positive solutions $u \in C^{2}(-L, L) \cap C[-L, L]$ for the one-dimensional prescribed mean curvature problem arising in electrostatic MEMS (Micro-Electro-Mechanical Systems)

where $\lambda > 0$ is a bifurcation parameter, and $p, L > 0$ are two evolution parameters. In particular, we study upper and lower bounds, monotonicity properties and asymptotic behaviors for the pull-in voltage and the pull-in distance. The singular nonlinearity in (1.1)

satisfies

Notice that the improper integral of $f$ over $[0, 1)$ satisfies

The one-dimensional prescribed mean curvature problem

and $n$-dimensional problem of it, with general nonlinearity $\tilde{f}(u)$ or with many different types nonlinearities, like $u^{p}$ ($p > 0$), $u^{p}+u^{q}$ ($0\leq p < q < \infty$), $(1+u)^{p}$ ($p > 0$), $\exp (u)$, $\exp (u)-1$, $\exp \left(\frac{au}{a+u}\right)$ ($a > 0$), $\exp \left(\frac{au}{ a+u}\right) -1$ ($a > 0$), $a^{u}$ ($a > 0$), $u-u^{3},$ and $(1-u)^{-p}$ ($p > 0$) have been investigated intensively since 1990, see, e.g., ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}.

A solution $u\in C^{2}(-L, L)\cap C[-L, L]$ of (1.3) with $u^{\prime }\in C([-L, L], [-\infty, \infty])$ is called classical if $\left \vert u^{\prime }(\pm L)\right \vert < \infty$, and it is called non-classical if $u^{\prime }(-L) = \infty$ or $u^{\prime }(L) = -\infty$, see ^[8]. Notice that it can be shown that (see ^[2,8]), for (1.3),

$\rm(i)$ Any non-trivial positive solution $u\in C^{2}(-L, L)\cap C[-L, L]$ is concave on $(-L, L)$ if $\tilde{f}(u) > 0$ for $u > 0$, since the equation in (1.3) can be written in the equivalent form

$\rm (ii)$ A positive solution $u\in C^{2}(-L, L)\cap C[-L, L]$ must be symmetric on $[-L, L]$. Thus $u^{\prime }(-L) = -u^{\prime }(+L)$.

In this paper for prescribed mean curvature problem (1.1), we simply consider classical positive solutions $u$. For any fixed $p, L > 0$, we define the bifurcation diagram $C_{p, L}$ of (1.1) by

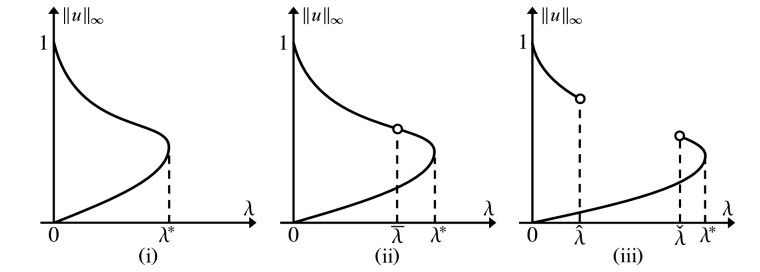
We say the bifurcation diagram $C_{p, L}$ is $\supset$-shaped (see e.g., Figure 1(i) depicted below) on the $(\lambda, \left \Vert u\right \Vert _{\infty })$-plane if there exists $\lambda ^{\ast } > 0$ such that $C_{p, L}$ consists of a continuous curve with exactly one turning point at some point $(\lambda ^{\ast }, \left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty })$ where the bifurcation diagram $C_{p, L}$ turns to the left.

Brubaker and Pelesko ^[3] studied existence and multiplicity of positive solutions of the $n$-dimensional prescribed mean curvature problem

where $\lambda > 0$ is a bifurcation parameter and $\Omega _{L}\subset \mathbb{R}^{n}$ ($n\geq 1$) is a smooth bounded domain depending on some parameter $L > 0$. Problem (1.5) with an inverse square type nonlinearity $f(u) = (1-u)^{-p},$ $p = 2$ is a derived variant of a canonical model used in the modeling of electrostatic Micro-Electro Mechanical Systems (MEMS) device obeying the electrostatic Coulomb law with the Coulomb force satisfying the inverse square law with respect to the distance of the two charged objects, which is a function of the deformation variable (cf. [16,p. 1324].) The modeling of electrostatic MEMS device consists of a thin dielectric elastic membrane with boundary supported at $0$ below a rigid plate located at $+1$. In (1.5), $u$ is the unknown profile of the deflecting MEMS membrane, $\lambda$ is the drop voltage between the ground plate and the deflecting membrane, and the term $\left \vert \nabla u\right \vert ^{2}$ is called a fringing field (cf. ^[3]). When a voltage $\lambda$ is applied, the membrane deflects towards the ceiling plate and a snap-through may occur when it exceeds a certain critical value $\lambda ^{\ast },$ referred to as the "pull-in voltage". (So if voltage $\lambda$ exceeds pull-in voltage $\lambda ^{\ast }$, an equilibrium defection is no longer attainable and the lower surface will touch up on the upper plate.) This creates a so-called "pull-in instability" which greatly affects the design and manufacture of MEMS devices. Also, in the actual design of a MEMS device, typically, one of the primary device design goals is to achieve the maximum possible stable steady-state deflection (that is, $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ ($< 1$), cf. Theorems 1.1–1.2 and Figures 1 and 2 below), referred to as the "pull-in distance", with a relatively small applied voltage. We refer to ^[3,17] for detailed discussions on MEMS devices modeling. Notice that the physically relevant dimensions are $n = 1$ and $n = 2$. In the case for $n = 1$, $\Omega _{L}$ is a rectangular strip with two opposite edges at $x = \pm L$ fixed ($2L$ is the length of the strip) and the remaining two edges free, the deflection $u = u(x, y)$ may be assumed a function of $x$ only. In the case for $n = 2$, $\Omega _{L}$ is a planar bounded domain with smooth boundary, and $L$ is the characteristic length (diameter) of the domain. In particular, $\Omega _{L}$ could be a circular disk of radius $L$.

With general $p > 0$, (1.1) is a generalized MEMS problem under the assumption that the Coulomb force satisfies the inverse $p$-th power law with respect to the distance of the two charged objects, where $p > 0$ characterizes the force strength. See ^[18].

Brubaker and Pelesko ^[4] and Pan and Xing ^[11] studied global bifurcation diagrams and exact multiplicity of positive (classical) solutions for the one dimensional problem of (1.5),

Brubaker and Pelesko [4,Theorem 1.1] and Pan and Xing [11,Theorem 1.1] independently proved that, for (1.6), which corresponds to the case $p = 2$ in (1.1) with $L > 0$, there exists a positive number $L^{\ast }\approx 0.34997$ such that, on the $(\lambda, \left \Vert u\right \Vert _{\infty })$-plane, the bifurcation diagram $C_{2, L}$ consists of a (continuous) $\supset$-shaped curve which emanates from the origin and has exactly one (left) turning point at some point $(\lambda ^{\ast }, \left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty })$ when $L\geq L^{\ast }$, and as $L$ transitions from greater than or equal to $L^{\ast }$ to less than $L^{\ast }$ the upper branch of the bifurcation diagram $C_{2, L}$ splits into two parts. See Figure 1 depicted below and see [4,Theorem 1.1] and [11,Theorem 1.1] for details. In addition, for (1.6), Brubaker and Pelesko [4,Theorem 1.1] proved that the pull-in voltage $\lambda ^{\ast } = \lambda ^{\ast }(L)$ satisfies

and Pan and Xing [11,Theorem 1.1,part (4)] proved that the pull-in voltage $\lambda ^{\ast }(L)$ is a strictly decreasing function of $L > 0.$ Brubaker and Pelesko [4,Figure 1.2(b)] also gave numerical simulation of the pull-in distance $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ for $0.1\leq L\leq 0.8,$ which show that $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ is a strictly increasing function of $L\in \lbrack 0.1, 0.8]$.

In following Theorems 1.1–1.2, Cheng, Hung and Wang [1,Theorems 2.1-2.3] extended and improved the results of Brubaker and Pelesko [4,Theorem 1.1] and Pan and Xing [11,Theorem 1.1] by generalizing the nonlinearity $f(u) = (1-u)^{-2}$ in (1.6) to $f(u) = (1-u)^{-p}$ with general $p\in (0, \infty)$. Theorems 1.1–1.2 show that $p$ is a bifurcation parameter to prescribed mean curvature problem (1.1). Note that this result remains hold for the standard MEMS problem

see [19,Section 2]. The standard MEMS problem (1.8) and $n$ -dimensional (generalized) problems of it have been studied by numerous authors, see e.g., ^[20,21,22]. For semilinear problem (1.8) with any $p > 0$ and $L > 0$, by applying (1.2) and Laetsch [23,Theorems 2.5,2.9 and 3.2], we obtain that, on the $(\lambda, \left \Vert u\right \Vert _{\infty })$ -plane, the bifurcation diagram of positive solutions consists of a (continuous) $\supset$-shaped curve which emanates from the origin, initially continues to the right, and making a left turn at some point $(\lambda ^{\ast }, \left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty })$ which is a bifurcation point with neutral stability, then continues to the left, and ends at $(0, 1)$, cf. Figure 1(i). For semilinear problem (1.8) with $p = 2$ and $L = 1,$ Ghoussoub and Guoand [22,Theorem 1.1,part 4] proved that the pull-in voltage $\lambda ^{\ast }\leq 9/8 = 1.125.$ For semilinear problem (1.8) with $p = 2$ and $L = 1,$ the value of the pull-in voltage was numerically determined as $\lambda ^{\ast }\approx 1.400016469/4\approx 0.350004$ in [21,Theorem 2.2] (see also [24,FIGURE 2(a)]), and the value of the pull-in distance was numerically determined as $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }\approx 0.38$ in [24,FIGURE 2(a)]. Cowan and Ghoussoub [20,Corollary 2.1,part 1] proved that, for Laplacian problem (1.8) with $p > 0$ and $L = 1,$ the pull-in distance

This implies that

Theorem 1.1 (See Figure 1). Consider classical positive solutions $u$ of (1.1) with $p\geq 1$. There exists $L^{\ast } = L^{\ast }(p) > 0$ such that the following assertions (i)–(iii) hold:

(i) $($See Figure 1(i).$)$ If $L > L^{\ast }$, then there exists $\lambda ^{\ast } > 0$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $0 < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $\lambda = \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

(ii) $($See Figure 1(ii).$)$ If $L = L^{\ast }$, then there exist $0 < \bar{\lambda}$ $( = \bar{\lambda}(p))$ $< \lambda ^{\ast }$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $0 < \lambda < \bar{\lambda}$ and $\bar{\lambda} < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $\lambda = \bar{\lambda}, \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

(iii) $($See Figure 1(iii).$)$ If $0 < L < L^{\ast }$, then there exist $0 < \hat{\lambda} < \check{\lambda} < \lambda ^{\ast }$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $0 < \lambda < \hat{\lambda}$ and $\check{\lambda} < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $\hat{\lambda}\leq \lambda \leq \check{\lambda}$ and $\lambda = \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

Theorem 1.2 (See Figure 2). Consider classical positive solutions $u$ of (1.1) with $0 < p < 1$. There exist $0 < L_{\ast }$ $( = L_{\ast }(p))$ $< L^{\ast }$ $( = L^{\ast }(p))$ such that the following assertions (i)–(iv) hold:

(i) $($See Figure 2(i)–(ii).$)$ If $L > L^{\ast },$ then there exist $0 < \lambda _{\ast } < \lambda ^{\ast }$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $\lambda _{\ast } < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $0 < \lambda \leq \lambda _{\ast }$ and $\lambda = \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

(ii) $($See Figure 2(iii).$)$ If $L = L^{\ast },$ then there exist $0 < \lambda _{\ast } < \bar{\lambda}$ $( = \bar{\lambda}(p))$ $< \lambda ^{\ast }$ satisfying $\lambda _{\ast } < 1-p < \bar{\lambda}$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $\lambda _{\ast } < \lambda < \bar{\lambda}$ and $\bar{\lambda} < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $0 < \lambda \leq \lambda _{\ast }$ and $\lambda = \bar{ \lambda}, \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

(iii) $($See Figure 2(iv).$)$ If $L_{\ast } < L < L^{\ast }$, then there exist $0 < \lambda _{\ast } < \hat{\lambda} < \check{\lambda} < \lambda ^{\ast }$ satisfying $\lambda _{\ast } < 1-p < \hat{\lambda}$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $\lambda _{\ast } < \lambda < \hat{\lambda}$ and $\check{\lambda} < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $0 < \lambda \leq \lambda _{\ast }$, $\hat{\lambda}\leq \lambda \leq \check{\lambda}$ and $\lambda = \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

(iv) $($See Figure 2(v).$)$ If $0 < L\leq L_{\ast }$, then there exist $0 < \check{\lambda} < \lambda ^{\ast }$ satisfying $1-p < \check{\lambda}$ such that (1.1) has exactly two positive solutions $u_{\lambda }$, $v_{\lambda }$ with $\left \Vert u_{\lambda }\right \Vert _{\infty } < \left \Vert v_{\lambda }\right \Vert _{\infty }$ for $\check{\lambda} < \lambda < \lambda ^{\ast }$, exactly one positive solution $u_{\lambda }$ for $0 < \lambda \leq \check{\lambda}$ and $\lambda = \lambda ^{\ast }$, and no positive solution for $\lambda > \lambda ^{\ast }$.

The paper is organized as follows. Section 2 contains statements of the main results (Theorems 2.1–2.3). Section 3 contains several lemmas needed to prove Theorem 2.3. Section 4 contains the proofs of the main results.

2.   Main results

The main results in this paper are next Theorems 2.1–2.3 for the generalized MEMS problem (1.1), in which we first study upper and lower bounds for the pull-in voltage $\lambda ^{\ast }$ and the pull-in distance $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$. We further study monotonicity properties and asymptotic behaviors of the pull-in voltage $\lambda ^{\ast }$ and the pull-in distance $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ with respect to positive parameters $p$ and $L$.

Theorem 2.1 (See Theorems 1.1–1.2 and Figures 1 and 2). Consider (1.1) with $p > 0$ and $L > 0$. Then the pull-in voltage $\lambda ^{\ast } = \lambda ^{\ast }(p, L)$ satisfies the following assertions (i)–(iii):

(i) For $p > 0$ and $L > 0$,

(ii) For any fixed $L > 0,$ $\lambda ^{\ast }(p, L)$ is a strictly decreasing function of $p > 0$, and

(iii) For any fixed $p > 0$, $\lambda ^{\ast }(p, L)$ is a strictly decreasing function of $L > 0$, $\lim_{L\rightarrow 0^{+}}\lambda ^{\ast }(p, L) = \infty,$ and $\lim_{L\rightarrow \infty }\lambda ^{\ast }(p, L) = 0$.

Remark 2.2. In (2.1) for (1.1) with $p > 0$, the upper bound $\min \left \{ L^{-1}, \tfrac{p^{p}}{4(p+1)^{p+1}}\pi ^{2}L^{-2}\right \}$ for $\lambda ^{\ast }(p, L)$ is reduced to $\min \left \{ L^{-1}, \tfrac{\pi ^{2}}{27} L^{-2}\right \}$ when $p = 2;$ that is, our result for the upper bound for $\lambda ^{\ast }(p, L)$ generalizes (1.7). In particular, when $p = 2$ and $L = 1$, then (2.1) is reduced to

This suggests that (2.1) give suitable upper and lower bounds for the pull-in voltage $\lambda ^{\ast }(p, L)$ with general $p, L > 0.$

Theorem 2.3 (See Theorems 1.1–1.2 and Figures 1–5). Consider (1.1) with $p > 0$ and $L > 0$. Then the pull-in distance $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } = \left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }(p, L)$ satisfies the following assertions (i)–(iv):

(i) For $p > 1$ and $L > 0$,

where

and $(p, \bar{U}(p))$ is the unique positive solution pair of the equation

and $\bar{U}(p)$ satisfies

see Figure 4.

(ii) For $p = 1$ and $L > 0$,

where

(iii) For $0 < p < 1$ and $L > 0$,

where

(iv) (a) For fixed $L > 0$,

In addition, for fixed $L\geq 3$,

and for fixed positive $L < 3,$

(b) For fixed $p > 0$,

Remark 2.4. In particular, when $p = 2$, then in (2.2) we have that $\bar{U} (p = 2) = 1/2$ and

Hence, for $L\geq 1/6$, the estimates give

and, for $0 < L < 1/6$, the estimates give

Our analytic result in (2.2) also agrees with some numerical simulations obtained by Brubaker and Pelesko [4,Figure 1.2(b)–(d)] for $p = 2$ and $0.1\leq L\leq 0.8$.

Remark 2.5. We conjecture that, for any fixed $L > 0,$ $\lim_{p\rightarrow 0^{+}}\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } = 1$; cf. (2.6)–(2.7) and (1.9). In addition, for any fixed $p > 0$ and $\lambda ^{\ast } = \lambda ^{\ast }(L),$ $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ is a strictly increasing function of $L > 0$. Note that, when $p = 2$, our numerical simulation shows that $\lim_{L\rightarrow \infty }\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } = \zeta \approx 0.388$ for some $\zeta$, cf. [4,Figure 1.2(b)] and (2.8). Further investigations are needed.

3.   Lemmas

To prove the upper and lower bounds for $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ in Theorem 2.3(i)–(iii) for (1.1) with $p > 0$, we need the following Lemmas 3.1–3.6. We first establish sufficient conditions on $r$ and $p$ such that $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } < r$ for all $L > 0$. To this purpose, we recall the time map formula $T_{p, \lambda }(r)$ for (1.1) as follows:

where

and $I$ is the domain of $T_{p, \lambda }(r)$. Notice that the domain $I$ of $T_{p, \lambda }(r)$ depends on the value $p$. We have that:

$\rm(I)$ If $p\geq 1$, $F:[0, 1)\rightarrow \lbrack 0, \infty)$ is strictly increasing, and hence $F^{-1}$ is well defined on $[0, \infty)$. Then for any $\lambda > 0$, the domain $I$ of $T_{p, \lambda }(r)$ is

$\rm(II)$ If $0 < p < 1$, $F:[0, 1]\rightarrow \lbrack 0, \frac{1}{1-p}]$ is strictly increasing, and hence $F^{-1}$ is only defined on $[0, \frac{1}{1-p}]$. Then for any $\lambda > 0$, the domain $I$ of $T_{p, \lambda }(r)$ is

See [1,p. 286].

Observe that positive solutions $u_{\lambda }$ for (1.1) correspond to

Thus, studying of the exact number of positive solutions of (1.1) for any fixed $\lambda > 0$ is equivalent to studying the shape of the time map $T_{p, \lambda }(r)$ on its domain $I$. Moreover, we observe that

where

See [1,(3.2)].

First, we have the next lemma which shows that $T_{p, \lambda }(r)$ for (1.1) has exactly one critical point, a local maximum, on its domain.

Lemma 3.1 ([1,Lemma 3.2]). Consider $T_{p, \lambda }(r)$ for (1.1). The followingassertions (i)–(iii) hold:

(i) For fixed $p\geq 1$, $T_{p, \lambda }(r)$ has exactly one criticalpoint, a local maximum, on $(0, F^{-1}(1/\lambda))$ for any $\lambda > 0$.

(ii) For fixed $p\in (0, 1)$, $T_{p, \lambda }(r)$ has exactly onecritical point, a local maximum, on $(0, F^{-1}(1/\lambda))$ for any $\lambda > 1-p$.

(iii) For fixed $p\in (0, 1)$, $T_{p, \lambda }(r)$ has exactly onecritical point, a local maximum, on $(0, 1)$ for any $0 < \lambda \leq 1-p$.

In the following Lemma 3.2 with $p > 1$, and Lemma 3.3 with $p = 1$, we prove that $T_{p, \lambda }^{\prime }(r) < 0$ for $\lambda \in (0, 1/F(r))$, where $r$ satisfies some conditions stated below. Thus $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } < r$ for $L > 0$ by applying Theorem 1.1.

Lemma 3.2. Suppose that $0 < r < 1\ $and $p > 1$. Then $T_{p, \lambda}^{\prime }(r) < 0$ for $\lambda \in (0, 1/F(r))$ if $\left(p, r\right)$satisfies $\Gamma (p, r) = (p+1)r+2(1-r)^{p}-2 = 0$.

Lemma 3.3. Suppose that $p = 1$. Then $T_{1, \lambda }^{\prime}(1-2e^{-2}) < 0$ for $\lambda \in (0, 1/F(1-2e^{-2}))$.

Proof of Lemma 3.2. For $p > 1$, we have that $f(u) = (1-u)^{-p}$ and $F(u) = \frac{1-(1-u)^{1-p}}{1-p}$. Hence, by (3.5), we compute that

where

For any fixed positive $r, s < 1$, $\tilde{\Phi}(\lambda)\equiv \Phi (\lambda, r, s)$ is a quadratic polynomial in $\lambda$. To prove this lemma, by (3.1)–(3.6), for $p > 1$, it suffice to prove that $\tilde{\Phi} (\lambda) < 0$ on $[0, 1/F(r)]$ which follows by proving that $\tilde{\Phi} (\lambda)$ is convex on $[0, 1/F(r)]$, $\tilde{\Phi}(0) < 0$ and $\tilde{\Phi} (1/F(r)) < 0$.

$\rm(I)$ First, we consider the leading coefficient of the quadratic polynomial $\tilde{\Phi}(\lambda)$. Let

We have that $a_{1}(1) = 0$ and

Hence, $a_{1}(s) > 0$ for $0 < r, s < 1$. So $\tilde{\Phi}(\lambda)$ is convex on $[0, 1/F(r)]$.

$\rm(II)$ Secondly, we let

We find that $a_{2}(1) = 0$, and

by the assumption. On the other hand, since

and

we find that

That is, for $s\in (0, 1)$, we find that $a_{2}^{\prime \prime }(s) < 0$ whenever $a_{2}^{\prime }(s) = 0$. Hence $a_{2}(s) > 0$ for $s\in (0, 1)$. This implies that $\tilde{\Phi}(0) < 0$.

$\rm(III)$ Thirdly, we obtain that

We have that $a_{3}(1) = 0$ and $a_{3}(0) = -r\left(p-1\right) (1-r)^{-p} < 0$ for $p > 1$ and $0 < r < 1$. Moreover, we compute that

Then we compute that $\phi _{1}(0) = 2(p-1) > 0$ and

We claim that $\phi _{1}(1) > 0$ if $\left(p, r\right)$ satisfies $\Gamma (p, r) = \left(p+1\right) r+2\left(1-r\right) ^{p}-2 = 0.$ We next give a proof of this claim. First, it is easy to see that

since $\left(p, r\right) = (2, 1/2)\in \hat{\Phi}$. Now, suppose $\left(p, r\right)$ satisfies $\left(p+1\right) r-1 = 0$. We find that

since $2\left(\frac{p}{p+1}\right) ^{p}-1 = 0$ when $p = 1$ and it is a strictly decreasing function of $p\geq 1.$ So, in addition to (3.9), for $p > 1$, $0 < r < 1$, we obtain that $\left(p+1\right) r-1 > 0$ if $\left(p+1\right) r+2\left(1-r\right) ^{p}-2\geq 0$; i.e.,

So, by (3.8) and (3.10), $\phi _{1}(1) > 0$ if $\left(p, r\right)$ satisfies $\left(p+1\right) r+2\left(1-r\right) ^{p}-2 = 0$.

We also compute that, if $p\geq \frac{3}{2}$,

So we find that $\phi _{1}^{\prime \prime }(s) < 0$ whenever $\phi _{1}^{\prime }(s) = 0$. This implies that $\phi _{1}(s) = \frac{(1-rs)^{p}}{r} a_{3}^{\prime }(s) > 0$ for $s\in (0, 1)$ (Observe $\phi _{1}(0) > 0$ and $\phi _{1}(1) > 0$). Therefore, $a_{3}(s) < 0$ for $s\in (0, 1)$, and hence

$\rm(IV)$ If $1 < p < \frac{3}{2}$, we claim that

We next give a proof of this claim. We compute that

Then

and

So, if $\left(p, r\right)$ satisfies

then

Next, we have that, for $1 < p < \frac{3}{2}$,

see Figure 6. (Note that we can provide an analytic proof for (3.14) but we omit it here since it is too tedious.) If $p\in (1, 3/2)$, then

by (3.11)–(3.14). So we find that $\phi _{1}^{\prime \prime }(s) < 0$ whenever $\phi _{1}^{\prime }(s) = 0$. This implies that $\phi _{1}(s) = \frac{(1-rs)^{p}}{r}a_{3}^{\prime }(s) > 0$ for $s\in (0, 1)$ (Observe $\phi _{1}(0) > 0$ and $\phi _{1}(1) > 0$). Therefore, $a_{3}(s) < 0$ for $s\in (0, 1)$, and hence

We conclude that, by above parts (I)–(IV), $\tilde{\Phi}(\lambda)$ is convex on $[0, 1/F(r)]$, $\tilde{\Phi}(0) < 0$ and $\tilde{\Phi}(1/F(r)) < 0$. So $\tilde{\Phi}(\lambda) < 0$ on $[0, 1/F(r)]$ for $p > 1$. By (3.4)–(3.7), $T_{p, \lambda }^{\prime }(r) < 0$ for $\lambda \in (0, 1/F(r))$ if $p > 1$, $r\in (0, 1)$, and $\left(p, r\right)$ satisfies $\Gamma (p, r) = (p+1)r+2(1-r)^{p}-2 = 0$.

The proof of Lemma 3.2 is complete.

Proof of Lemma 3.3. For $p = 1$, we have that $f(u) = \frac{1}{1-u}$ and $F(u) = -\ln (1-u)$, and (3.5) can be reduced to

where

Let $r_{0}\equiv 1-2e^{-2}$ ($\approx 0.729$), since $\ln (1-r_{0}s)-\ln (1-r_{0}) > 0$ for $s\in (0, 1)$, $\tilde{\Theta}(\lambda)\equiv \Theta (\lambda, r_{0}, s)$ is a convex quadratic polynomial in $\lambda$. In the following, we will prove that

and

Let

Then $\theta _{1}(0) = -2\ln (1-r_{0})-\frac{r_{0}}{1-r_{0}}\approx -0.0808 < 0$, $\theta _{1}(1) = 0$,

and

We compute that

This implies that $\theta _{1}^{\prime \prime }(s) > 0$ whenever $\theta _{1}^{\prime }(s) = 0$. Thus, $\theta _{1}(s) < 0$ for all $s\in (0, 1)$ and then $\tilde{\Theta}(0) < 0$ for $s\in (0, 1)$.

On the other hand, let

Then $\theta _{2}(0) = \frac{-r_{0}}{1-r_{0}}$ $(\approx -2.695) < 0$, $\theta _{2}(1) = 0$,

and

We compute that $\theta _{2}^{\prime }(1) = \frac{r_{0}}{\left(1-r_{0}\right) ^{2}}\left(2r_{0}-1\right)$ $(\approx 4.566) > 0$, and

Furthermore, let

Then $\theta _{3}(0) = 1 > 0$, $\theta _{3}(1) = \frac{6\left(1-r_{0}\right) }{ \ln (1-r_{0})}-1$ $(\approx -0.243) < 0$, and

This implies that $\theta _{3}^{\prime \prime }(s) > 0$ whenever $\theta _{3}^{\prime }(s) = 0$. Then there exists $s_{0}\in (0, 1)$ such that

By (3.17)–(3.19), we obtain that $\theta _{2}^{\prime \prime }(s) > 0$ (resp. $\theta _{2}^{\prime \prime }(s) = 0$, $\theta _{2}^{\prime \prime }(s) < 0$) whenever $\theta _{2}^{\prime }(s) = 0$ and $s\in (0, s_{0})$ (resp. $s = s_{0}$, $s\in (s_{0}, 1)$). We next show that $\theta _{2}(s) < 0$ for all $s\in (0, 1)$. Observe $\theta _{2}(0) < 0$, $\theta _{2}(1) = 0$ and $\theta _{2}^{\prime }(1) > 0$. Assume $\theta _{2}(s)\geq 0$ for some $s\in (0, 1)$, then there exist $0 < s_{1} < s_{2} < 1$ such that $\theta _{2}(s_{1})\geq 0$ is a local maximum of $\theta _{2}(s)$ and $\theta _{2}(s_{2}) < 0$ is a local minimum of $\theta _{2}(s)$. Thus $\theta _{2}^{\prime \prime }(s_{1})\leq 0$ and $\theta _{2}(s_{2})\geq 0$, which contradicts to (3.17)–(3.19). So $\theta _{2}(s) < 0$ for all $s\in (0, 1)$.

Finally, by the above analyses with $r_{0} = 1-2e^{-2}$, $\tilde{\Theta} (\lambda)$ is convex on $[0, 1/F(r_{0})]$, $\tilde{\Theta}(0) < 0$ and $\tilde{ \Theta}(1/F(r_{0})) < 0$. So $\tilde{\Theta}(\lambda) < 0$ on $[0, 1/F(r_{0})]$. By (3.4), (3.5), (3.15) and (3.16), $T_{1, \lambda }^{\prime }(r_{0}) < 0$ for $\lambda \in (0, 1/F(r_{0}))$.

The proof of Lemma 3.3 is complete.

In the following Lemma 3.4 with $p > 1$, Lemma 3.5 with $p = 1$, and Lemma 3.6 with $0 < p < 1$, we prove that $T_{p, \lambda }^{\prime }(r_{p}) > 0$ for $\lambda \in (0, 1/L]$, where $r_{p}$ is defined below. Thus $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } > r_{p}$ for $L > 0$ by applying Theorems 1.1–1.2.

Lemma 3.4. Consider $p > 1$. Then $T_{p, \lambda }^{\prime }(r_{p}) > 0$for $\lambda \in (0, 1/L]$, where

Lemma 3.5. Consider $p = 1$. Then $T_{1, \lambda }^{\prime }(r_{1}) > 0$for $\lambda \in (0, 1/L]$, where $r_{1}\equiv \min \left \{ 1-e^{-\frac{L}{3}}, \frac{1}{10}\right \}$.

Lemma 3.6. Consider $0 < p < 1$. Then $T_{p, \lambda }^{\prime }(r_{p}) > 0$for $\lambda \in (0, 1/L]$, where

Proof of Lemma 3.4. For $p > 1$, we have that $f(u) = (1-u)^{-p}$ and $F(u) = \frac{(1-u)^{1-p}-1}{p-1}$. Let $\lambda = \frac{q }{L}$ with $q\in (0, 1]$. Hence by (3.5), we compute that

Assume that $M > 1$ is a given number. Then, for $0 < r, s < 1$ satisfying $\frac{1 }{1-r}\leq M$, by applying Cauchy's Mean Value Theorem, it is easy to check that

Therefore,

where

Note that $0 < (1-r)^{1-p}-(1-rs)^{1-p} < (1-r)^{1-p}-1\leq M^{p-1}-1$. Let

We aim to find a number $M_{0} > 1$ such that $g_{M_{0}}(z) > 0$ for $0\leq z\leq M_{0}^{p-1}-1$. This implies that

with $\frac{1}{1-r}\leq M_{0}$. Since $g_{M}^{\prime }(0) = -3\left(p-1\right) L < 0$ and $g_{M}$ is convex on $(0, \infty)$, we only need to prove that $g_{M_{0}}^{\prime }(M_{0}^{p-1}-1)\leq 0$ and $g_{M_{0}}(M_{0}^{p-1}-1)\geq 0$ for some $M_{0} > 1$. We have that

and

Thus we choose $M_{0}\equiv \min \left \{ \left[1+\frac{1}{3}\left(p-1\right) L\right] ^{\frac{1}{p-1}}, 1+\frac{1}{9p}\right \}$. Then

So $g_{M_{0}}^{\prime }(M_{0}^{p-1}-1)\leq 0$ and $g_{M_{0}}(M_{0}^{p-1}-1) \geq 0$ by (3.24) and (3.25).

Finally, we choose

Then we obtain that $T_{p, \lambda }^{\prime }(r_{p}) > 0$ for $\lambda \in (0, 1/L]$ by (3.4), (3.5), and (3.20)–(3.25). Observe that $r_{p}\in (0, F^{-1}(\frac{1}{\lambda }))$ for $\lambda \in (0, 1/L]$.

The proof of Lemma 3.4 is complete.

Proof of Lemma 3.5. For $p = 1$, we have that $f(u) = (1-u)^{-1}$ and $F(u) = -\ln (1-u)$. Let $\lambda = \frac{q}{L}$ with $q\in (0, 1]$. Hence by (3.5), we compute that

Assume that $M > 1$ is a given number. Then, for $0 < r, s < 1$ satisfying $\frac{1 }{1-r}\leq M$, by applying Cauchy's Mean Value Theorem, it is easy to check that

Therefore,

where

Note that $0 < \ln (1-rs)-\ln (1-r) < \ln \frac{1}{1-r}\leq \ln M$. Let

We aim to find a number $M_{0} > 1$ such that $j_{M_{0}}(z) > 0$ for $0\leq z\leq \ln M_{0}$. This implies that

with $\frac{1}{1-r}\leq M_{0}$. Since $j_{M}^{\prime }(0) = -3L < 0$ and $j_{M}$ is convex on $(0, \infty)$, we only need to prove that $j_{M_{0}}^{\prime }(\ln M_{0})\leq 0$ and $j_{M_{0}}(\ln M_{0})\geq 0$ for some $M_{0} > 1$. We have that

and

Thus we choose $M_{0}\equiv \min \left \{ e^{\frac{L}{3}}, \frac{10}{9} \right \}$. Then

So $j_{M_{0}}^{\prime }(\ln M_{0})\leq 0$ and $j_{M_{0}}(\ln M_{0})\geq 0$ by (3.30) and (3.31).

Finally, we choose

Then we obtain that $T_{1, \lambda }^{\prime }(r_{1}) > 0$ for $\lambda \in (0, 1/L]$ by (3.4), (3.5), and (3.26)–(3.31). Observe that $r_{1}\in (0, F^{-1}(\frac{1}{\lambda }))$ for $\lambda \in (0, 1/L]$.

The proof of Lemma 3.5 is complete.

Proof of Lemma 3.6. For $0 < p < 1$, we have that $f(u) = (1-u)^{-p}$ and $F(u) = \frac{1-(1-u)^{1-p}}{1-p}$. Let $\lambda = \frac{q }{L}$ with $q\in (0, 1]$. Hence by (3.5), we compute that

Assume that $M > 1$ is a given number. Then, for $0 < r, s < 1$ satisfying $\frac{1 }{1-r}\leq M$, by applying Cauchy's Mean Value Theorem, it is easy to check that

Therefore,

where

Note that $0 < (1-rs)^{1-p}-(1-r)^{1-p} < 1-(1-r)^{1-p}\leq 1-M^{p-1}$. Let

We aim to find a number $M_{0} > 1$ such that $h_{M_{0}}(z) > 0$ for $0\leq z\leq 1-M_{0}^{p-1}$. This implies that

with $\frac{1}{1-r}\leq M_{0}$. Since $h_{M}^{\prime }(0) = -3\left(1-p\right) L < 0$ and $h_{M}$ is convex on $(0, \infty)$, we only need to prove that $h_{M_{0}}^{\prime }(1-M_{0}^{p-1})\leq 0$ and $h_{M_{0}}(1-M_{0}^{p-1})\geq 0$ for some $M_{0} > 1$. We have that

and

Thus we choose

Then

and

In (3.36) and (3.37), notice $p-1 < 0$ and hence $M_{0}^{p-1}\geq 1-\frac{1}{k}\left(1-p\right) L$.

Finally, we choose

Then we obtain that $T_{p, \lambda }^{\prime }(r_{p}) > 0$ for $\lambda \in (0, 1/L]$ by (3.4), (3.5), and (3.32)–(3.37). Observe that $r_{p}\in (0, F^{-1}(\frac{1}{\lambda }))$ for $\lambda \in (0, 1/L]$.

The proof of Lemma 3.6 is complete.

4.   Proofs of main results

Proof of Theorem 2.1.

$\rm(I)$ We prove Theorem 2.1(i). First, for $p > 0,$ the upper bound $\min \left \{ L^{-1}, \tfrac{p^{p}}{4(p+1)^{p+1}}\pi ^{2}L^{-2}\right \}$ for $\lambda ^{\ast }(p, L)$ in (2.1) can be obtained by slightly modifying the proof of the upper bound for $\lambda ^{\ast }$ for $p = 2$ in (1.7) in [4,Theorem 1.1]; we omit the proof. Also, it is easy to see that

since $\tfrac{p^{p}}{(p+1)^{p+1}}$ is a strictly decreasing function of $p > 0$ and $\lim_{p\rightarrow 0^{+}}\tfrac{p^{p}}{(p+1)^{p+1}} = 1$.

We then prove the lower bound for $\lambda ^{\ast }$ in (2.1) by modifying the proof of Wang and Ruan [25,Ineq. (2.10)] and by Pan and Xing [12,Theorem 3.1]. We first take the function

which satisfies $w(x) > 0$ on $(-L, L)$ and $w(\pm L) = 0$. We then compute that, for $x\in (-L, L),$

So for

$w(x)$ is a supersolution of (1.1) on $(-L, L)$ as (1.1) can be written in the equivalent form

see (1.4) with $\tilde{f}(u) = \frac{1}{(1-u)^{p}}$. Since $w_{0}(x)\equiv 0$ is a subsolution of (1.1) on $(-L, L)$ and $f(0) = 1 > w(x) > w_{0}(x) = 0$ on $(-L, L)$, by applying Pan and Xing [12,Theorem 3.1] obtained by the lower and upper solution method, there exists a (classical) solution $\tilde{w}(x)\in C^{2}[-L, L]$ of (1.1) satisfying $0 < \tilde{w}(x)\leq w(x)$ on $(-L, L)$. This proves that

$\rm(II)$ We prove Theorem 2.1(ii). Consider $L > 0$ be fixed. For any fixed $\lambda > 0$, $r\in I$ and $0 < u < r$, in $T_{p, \lambda }(r)$ in (3.1), the integrand $\frac{1+\lambda F(u)-\lambda F(r)}{\sqrt{1-\left[1+\lambda F(u)-\lambda F(r)\right] ^{2}}}$ is strictly decreasing in $p > 0$ since

is increasing in $p > 0$. So $T_{p, \lambda }(r)$ is a strictly decreasing function of $p > 0$. Hence $\lambda ^{\ast }(p, L)$ is a strictly decreasing function of $p > 0$. The rest of part (ii) follow from part (i) and by simple calculus with the fact that $\lim_{p\rightarrow 0^{+}}\tfrac{p^{p}}{ (p+1)^{p+1}} = 1$ and $\lim_{p\rightarrow \infty }\tfrac{p^{p}}{(p+1)^{p+1}} = 0$.

$\rm(III)$ We prove Theorem 2.1(iii). Consider fixed $p > 0$. Let

See [1,(1.9) and (1.11)]. By [1,Lemma 3.3(ii)], $h_{p}(\lambda)$ is a continuous, strictly decreasing function of $\lambda > 0$, $\lim_{\lambda \rightarrow 0^{+}}h_{p}(\lambda) = \infty$ and $\lim_{\lambda \rightarrow \infty }h_{p}(\lambda) = 0$. Thus we obtain that

see [1,Proofs of Theorems 2.1 and 2.2]. Moreover, we obtain that $\lambda ^{\ast }(p, L)$ is a strictly decreasing function of $L > 0$, $\lim_{L\rightarrow 0^{+}}\lambda ^{\ast }(p, L) = \infty$ and $\lim_{L\rightarrow \infty }\lambda ^{\ast }(p, L) = 0$.

The proof of Theorem 2.1 is complete.

Proof of Theorem 2.3.

In (3.3), positive solutions $u_{\lambda }$ for (1.1) correspond to

Thus, studying of the exact number of positive solutions of (1.1) for any fixed $\lambda > 0$ is equivalent to studying the shape of the time map $T_{p, \lambda }(r)$ on its domain $I$. Moreover, $T_{p, \lambda }(r)$ has exactly one critical point, a local maximum, on its domain $I$ by Lemma 3.1. Hence we have that:

$\rm(i)$ If there exists $r^{\ast } > 0$ such that $T_{p, \lambda }^{\prime }(r^{\ast }) < 0$ for $\lambda \in (0, 1/F(r^{\ast }))$, then $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } < r^{\ast }$ and hence $r^{\ast }$ is an upper bound of $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$.

$\rm(ii)$ If there exists $r_{\ast } > 0$ such that $T_{p, \lambda }^{\prime }(r_{\ast }) > 0$ for $\lambda \in (0, 1/L]$, then $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } > r_{\ast }$ and hence $r_{\ast }$ is a lower bound of $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$. Observe $\lambda ^{\ast }(p, L) < 1/L$ by Theorem 2.1(i).

We are now in a position to prove Theorem 2.3(i)–(iii).

$\rm(I)$ We prove the upper bounds for $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ in Theorem 2.3(i)–(iii).

(A) For $p > 1$ and $r = \bar{U}(p)$, by Lemma 3.2, we have that $T_{p, \lambda }^{\prime }(r) < 0$ for $\lambda \in (0, 1/F(r))$, and hence

for $L > 0$ by applying (3.3) and Lemma 3.1. See also Theorem 1.1. It is easy to check that $\bar{U}(p)$ is bounded above by $U(p)$ in (2.3) for $p > 1$, we omit the proof.

(B) For $p = 1$, similarly, we have that $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } < 1-2e^{-2}\approx 0.729$ for $L > 0$ by applying (3.3), Lemmas 3.1 and 3.3. See also Theorem 1.1.

(C) For $0 < p < 1,$ it is trivial that $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } < 1$ for $L > 0$.

By above (A)–(C), we obtain the upper bounds for $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ in Theorem 2.3(i)–(iii).

$\rm(II)$ We prove the lower bounds for $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ in Theorem 2.3(i)–(iii).

(A) For $p > 1$ and

by Lemma 3.4, we have that $T_{p, \lambda }^{\prime }(r_{p}) > 0$ for $\lambda \in (0, 1/L]$. Hence

for $L > 0$ by applying (3.3) and Lemma 3.1. See also Theorem 1.1.

(B) For $p = 1$ and

by Lemma 3.5, we have that $T_{1, \lambda }^{\prime }(r_{1}) > 0$ for $\lambda \in (0, 1/L]$. Hence

for $L > 0$ by applying (3.3) and Lemma 3.1. See also Theorem 1.1.

(C) For $0 < p < 1$ and

by Lemma 3.6, we have that $T_{p, \lambda }^{\prime }(r_{p}) > 0$ for $\lambda \in (0, 1/L]$. Hence

for $L > 0$ by applying (3.3) and Lemma 3.1. See also Theorem 1.2.

By above (A)–(C) in this part (II), we obtain the lower bounds for $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }$ in Theorem 2.3(i)–(iii).

$\rm(III)$ We prove Theorem 2.3(iv). Assertion (2.5) follows immediately by (2.2)–(2.3) and since

In addition, (2.6) and (2.7) follow easily by (2.4).

We then prove (2.8). For any fixed $L > 0$, by (4.1), we obtain that $h_{p}(\lambda ^{\ast }) = h_{p}(\lambda ^{\ast }(L)) = L$. Since $\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty }\in (0, F^{-1}(\frac{1 }{\lambda ^{\ast }})) = (0, F^{-1}(\frac{1}{\lambda ^{\ast }(L)}))$, we have that

Thus $\lim_{L\rightarrow 0^{+}}\left \Vert u_{\lambda ^{\ast }}\right \Vert _{\infty } = 0$. So (2.8) holds.

The proof of Theorem 2.3 is complete.

Acknowledgments

The authors thank the referees for constructive comments and recommendations which will help to improve the readability and quality of the paper. Most of the computation in this paper has been checked using the symbolic manipulator Mathematica 11.0. This work was partially supported by the Ministry of Science and Technology of the Republic of China under grant No. MOST 110-2115-M-167-001-MY2.

Conflict of interest

The authors declare there is no conflict of interest.