Strategy of boundary discretization in numerical simulation of laser propagation in skin tissue with vascular lesions

1.   Introduction

Port wine stain (PWS), one of the most frequent congenital vascular lesions in dermis, is mostly treated by laser therapy ^[1]. The numerical method has been widely used to investigate the laser treatment of PWS for an improved understanding of the mechanism of photonic-thermal response in biological tissues, quantification of thermal damage, and optimization of treatment protocols ^[2]. As the first step in simulation, the numerical method of laser propagation is very important.

The radiative transfer equation (RTE) is highly accurate for describing photon transportation in a turbid medium, but the diffuse radiance is difficult to evaluate ^[3]. Thus, various radiative transfer models, such as spherical harmonic, phase approximation, and diffusion approximation models, have been developed to deal with RTE efficiently ^[4]. Monte Carlo (MC) simulation, an effective, easy-to-parallel technique, can solve RTE with high accuracy, thus eliciting considerable attention in modeling light transportation in biological tissues. Wang et al. ^[5] developed the MC method in multi-layered tissues (MCML) and applied it to a succession of homogeneous layers.

PWS birthmarks are observed in a disorderly pattern with the development of histopathological survey ^[6]. A lack of recognition of blood vessel injury caused by laser propagation in a complex structure of PWS birthmarks leads to a low curative rate. Hence, the adaptability of complicated vessel structures has been proposed in MC simulation. MCML has been developed to adapt curved surface by employing Snell's law in circular or elliptical cross-section, which was referred to as geometrical Monte Carlo (GMC) ^[7]. In GMC, boundaries of adjacent objects (tissue structures) are defined geometrically, which is most accurate but limited in the burdensome mathematical descriptions of more complicated tissue structures. In terms of light transportation in arbitrarily complex 3D tissue morphology, Pfefer et al. ^[8] proposed the voxel-based Monte Carlo (VMC) algorithm, which is represented by a group of 3D stacked hexahedron voxels. However, major errors (80%-120%) of photon deposition occur in round or oblique tissue boundaries when a great inclination exists between the faces of hexahedron and the axis planes due to the fixed mesh connection in VMC ^[9,10]. According to the notable results in the work of Majaron et al. ^[11], the VMC introduces large artifacts to the results of energy deposition which do not converge towards zero with ever finer spatial discretization. This phenomenon confirms that the VMC method suffers from inherent disadvantages due to inaccurate treatment of light transportation at curved tissue interfaces.

In order to improve the ability of MC to accurately model curved boundaries, new algorithms have been described ^[12,13,14]. Compared with a voxel, a tetrahedron is ideally adaptable to a curved interface ^[15]. Shen et al. ^[14] reported a tetrahedron-based inhomogeneous MC solver that is mainly applied in regular domains. Furthermore, Jia et al. ^[16] developed a tetrahedron-based MC (TMC) simulator that is suitable for deposition of photon energy in complicated domains with an adaptive tetrahedron mesh. The distance threshold is introduced to avoid photon deposition errors caused by confused photon transportation adjacent to the mesh boundary ^[16,17]. In earlier documented TMC, the escape boundary condition (BC) is applied to computational surfaces. Although the escape BC is better than the reflecting boundary condition, this approach is suitable only for the treatment of skin surrounded by air ^[18]. An approach that addresses tissue BC should be developed to overcome this problem.

Simple geometric settings of blood vessel have been widely used in laser transportation. However, tortuosity and buckling occur frequently in a patient-specific PWS vessel structure in a clinical setting, significantly affecting the energy distribution and the rupture of the vessel ^[4,19]. An anatomically realistic vessel geometry should be established to study the error of laser transportation in simplified geometric model of the vasculature. The dorsal skin chamber (DSC) model ^[20,21] is an invaluable in vivo technique in studying light propagation, thermal transfer and temperature response in blood vessels. The observed blood vessels in the DSC model are nearly parallel to the skin surface, similar with that of PWS vessels ^[20]. Such characteristic allows high-quality 3D vessel reconstruction, providing convenience for the study of curvature-influenced laser energy deposition.

In this study, the extended BC is developed for TMC to overcome the drawback of escape BC. Outside of the tetrahedral region, model photons are propagated in laterally infinite tissue layers, but without recording the local energy deposition. A TMC with extended BC (TMCE) solver is then presented in this study. The applicability of TMCE in skin optics is validated by comparing its results with those of GMC. The influence of overall and mostly deposited region on light propagation is discussed to study the difference on the boundary adaptability of VMC and TMCE. Skin models with real vessels are reconstructed from the DSC model. The effect of vessel geometry simplification is investigated by comparing the reconstructed vessel with the real cylindrical vessel via TMCE. Additionally, the contribution of geometric curvature to energy deposition is statistically analyzed by TMCE on the reconstructed blood vessels.

2.   Materials and methods

The fundamental quantity in transport theory is the radiance J (r, s), which denotes the power flux density in a specific direction s within a unit solid angle dω. The laser radiative transport equation is given by

Where p(s, s') is the phase function of a photon to be scattered from direction s' into s, ds is an infinitesimal path length, and dω' is the elementary solid angle about the direction s'.

The main problem with which transport theory has to deal is the evaluation of the diffuse radiance, which is difficult to solve. The Monte Carlo simulation is a statistical approach based on the average of multiple photons, not solving the transport equation explicitly. MC simulation is an effective and accurate method to predict the laser propagation in skin tissues.

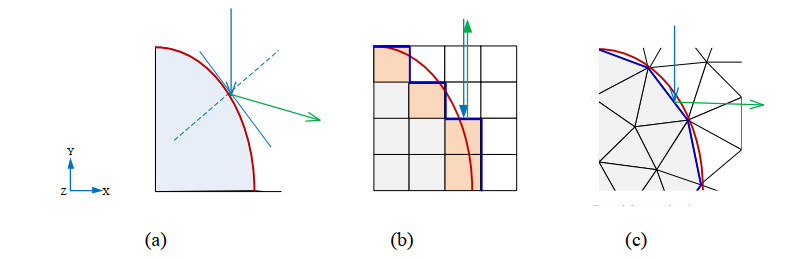
Law of light transportation is highly related to tissue interface in bio-optic MC simulation. Taking an ellipse boundary as an example, Figure 1 displays the effect on photon reflections of different implementations in GMC, VMC, and TMCE. GMC provides a non-discretized, mathematically defined geometry (Figure 1a). The computation domain in VMC is represented by a three-order matrix of hexahedron voxels (Figure 1b). The curved interface (tissue boundary) is expected to cross the grid cells, resulting in interface cells ^[9,11,22] (Figure 1b). The light greatly deviates from the real direction after reflection and refraction across the artificial boundary caused by the interface cells (Figure 1b). In this work, tetrahedra are generated along the interface, leading to a polygonal approximation to match the real interface (Figure 1c). The photon randomly propagates into a series of tetrahedra and repeatedly interacts with triangular surfaces until it loses all its weight or escapes the object.

2.1.   Photon-surface interaction in TMCE

The most challenging task required to trace a photon through complex heterogeneous structures is to identify the interaction of photon and the surface. Figure 2 shows the diagram of photon-surface interactions. Given location P and unit direction U of a photon in one tetrahedral mesh, the photon path can be described as

A free photon step size t', which determines the distance between adjacent laser-tissue events, that is, absorption and scattering, can be described ^[5]. Then, the four triangular surfaces of the tetrahedron which the photon locates in are checked to identify a possible photon-triangle interaction. For each triangle with its own inward N, we have

where Q is a point on the plane, and d is a scalar defined specialized by the plane function. The intersection point between the plane of the triangle and the photon path can be obtained by representing Q by P' in Eq. (2) as

After calculating t on the four triangles, the smallest positive t (t_s) is compared with t'. If t_s > t', then the photon transports within the current tetrahedron (Figure 2a); otherwise, the photon hits the triangle of t_s (Figure 2b). Reflection or refraction occurs when the photon propagates to the tissue interface. The photon continues to transport until the step size is covered.

Extended BC was adopted in this paper ^[18]. In extended BC, photons are launched in accordance with the profile of laser beam intensity and propagate in laterally infinite tissue layers (Figure 3). When hitting a boundary of the object, the photon has a 50% probability of refracting (escaping) the computational domain. Photons exiting the domain are propagated further in semi-infinite tissue layers until they return (Figure 3a), escape into the air (Figure 3b), or lose all their energy outside the domain (Figure 3c).

A uniform mesh with average interval sizes of Δx = Δy = Δz = 5 μm was conducted in VMC with 1.34 × 10⁵ cells in the region of blood vessel.

2.2.   Implementation of TMCE

Figure 4 shows the flowchart of TMCE. The rules of TMCE are similar to those described in ^[5]. The major difference is outlined in purple, which involves the photon-surface interaction that was introduced in Section 2.1. In TMCE, given a location (tetrahedron) and the direction of a photon in the boundary mesh of epidermis (Figure 6), a free step size of the photon can be computed according to the local optical parameters. Then, the four triangular surfaces of the tetrahedron will be examined to identify a possible photon-triangle interaction. This process can be repeated until the photon dies or escapes the object. In each cycle prior to the photon being moved, the program will check whether the photon will hit one of the triangles (Figure 2). If the photon passes through a boundary triangle, the extended BC will be implemented (Figure 3) and the program will launch a new photon if there are more.

2.3.   Blood vessel reconstruction

The DSC model was adopted to obtain images of real blood vessels ^[21]. The animal study adhered to the Guide for the Care and Use of Laboratory Animals, which was published by the US National Institutes of Health (NIH Publication No. 85-23, revised 1996) and approved by the Institutional Animal Care and Use Committee of Zhejiang Sci-Tech University (No. 20200304). In the DSC model, the approximate parallelism of the blood vessel with the skin surface in the observation chamber was fully considered to perform the 3D reconstruction (Figure 5). After a snapshot of the skin image was taken by a CCD camera (DP71, Olympus, Japan) (Figure 5a), the main blood vessels were transformed to a binary image (Figure 5b), and the skeleton and contour lines of the blood vessels were extracted from the 2D image (Figure 5c). The lofting operation in the software Solidworks was used to generate the blood vessels. The loft tool in Solidworks creates a shape (the blood vessel in this paper) by making transitions between multiple profiles (multiple cross-sections of the blood vessel) and guides curves (skeleton of the blood vessel) thus to create complex geometry (the curved blood vessel). The information of different cross-sections can be calculated by the extracted contour lines and skeleton of the blood vessels. After a smooth operation was completed (Figure 5d), the 3D model of blood vessel geometry was generated according to the extracted information ^[23] (Figure 5e). Coincidence rates of the projection of the reconstructed vessel and the original 2D vessel image are more than 96%, which verifies the rationality of this method. In this paper, twenty-five vessels were reconstructed from fifteen rats. Hence, we obtain 25 images representing each blood vessels.

2.4.   Statistical analyses

Skewness and kurtosis were adopted to analyze the differences in energy distribution by the different models. Skewness is measure of the asymmetry of the probability distribution of energy deposition in blood vessels, which can be quantified as a representation of the extent to which a given energy distribution varies from a normal distribution. The skewness of random variable X is the third standardized moment

where μ is the mean, σ is the standard deviation, E is the expectation operator.

Kurtosis is a statistical measure that defines how heavily the tails of the laser energy distribution differ from the tails of a normal distribution. The kurtosis is the fourth standardized moment, defined as

where μ is the mean, σ is the standard deviation, E is the expectation operator.

In this paper, the relationship of Gaussian curvature (GC) and mean curvature (MeC) with energy deposition were assessed to analyze the influence of vessel geometry. The principal curvatures (k₁ and k₂) were determined by using an open-source code in MATLAB language ^[24]. GC and MeC were derived from the principal curvatures as indicated in the following equations:

Correlation analyses were performed by taking deposited energy as the dependent parameter and GC or MeC as the independent parameters. For each pair, Pearson's correlation factor and its p value were calculated with a confidence level α = 0.05.

3.   Results and discussion

The two-layered skin model adopted in this paper contains the epidermis, the dermis, and the blood vessels (Figure 6). A 1.5 mm × 1.5 mm × 1.0 mm computational domain of the skin with a reconstructed blood vessel buried at a depth of 0.5 mm was used. The thicknesses of the epidermis and the dermis were set respectively as H_e = 60 μm and H_d = 940 μm based on statistical average values ^[1]. A spherical photon beam incident perpendicularly on the center of epidermis (Figure 6). In TMCE method, the tetrahedron mesh is generated by the commercial software GAMBIT 2.4. The body-fitted tetrahedra are generated along the vessel-tissue interface (vessel wall), which is efficient in increasing accuracy because no interface tetrahedra exist.

Among the three kind of MC methods mentioned in this manuscript, the GMC method gives a non-discretized, analytically defined geometry. Although contain some approximations, the mesh-based MC as VMC and TMCE methods expand the implementation of MC method. Except for the effect of MC method, the building of a real blood vessel is also regarded as an important factor of the laser-tissue simulation. In this paper, two kind of blood vessel modelling are proposed: reconstructed blood vessel and the related simplified blood vessel. In order to study the effect of vessel curvature of the reconstructed blood vessel, the standard deviation of the Gaussian curvature (stdGC) of a single vessel in the DSC model was adopted, which ranges from 10 to 80 in statistics. Figure 7 shows the distribution of stdGC of 25 blood vessels reconstructed in this paper. The stdGC presents normal distribution and the value between 10 and 80 accounts to 96%. The blood vessels were divided into three groups according to the value of stdGC: six of small stdGC (0 ≤ stdGC < 30 mm^-2), eleven of medium stdGC (30 mm^-2 ≤ stdGC < 50 mm^-2), and eight of large stdGC (stdGC ≥ 50 mm^-2). Three typical vessels (with a diameter of 100 ± 10 μm) of small, medium, and large stdGC were selected to analyze energy deposition (Figure 8). Fig 8a-c shows the reconstructed blood vessels. As shown in Figure 8d-f, the simplified cylindrical vessel was built to coincide approximately with the reconstructed vessel in position for convenience of model comparison. The diameter of the related cylindrical vessel was chosen as its volume equals to the volume of the related reconstructed vessel. The slope and the position of the cylindrical vessel was chosen as the most overset area exists when the cylindrical vessel and the related reconstructed vessel oversets.

The vessel construction method and the MC algorithms are considered important factors in simulation. In this section, three computational models: VMC with a simplified vessel (a straight cylinder), TMCE with a simplified vessel, and TMCE with a real vessel (reconstructed vessel) were made by combining blood vessel geometries with different MC methods. For simplicity, the three models are named as Models A, B, and C, respectively. By comparing model A with model B, we can obtain the error of different mesh-based method. On the other hand, by comparing model B with model C, we can analyze the effect of different vessel construction method. A uniform mesh with average interval sizes of Δx = Δy = Δz = 5 μm was conducted in VMC. Spatial discretization steps in TMC were 50 and 10 μm in the dermis and blood vessel, respectively. Thus, the three models shared almost the same mesh number (1.2-1.4×10⁵) in the vascular region, providing convenience in comparing the different algorithms.

3.1.   Validation of TMCE

The energy deposition along the skin depth in the center axis was compared with the GMC method ^[25] to validate the accuracy of the TMCE and TMC method. Two discrete blood vessels with a diameter of 120 μm and depths of 250 and 500 μm were considered (Figure 9a). The skin was irradiated by a 585 nm laser with an incident energy density of 1 J/cm² and a spot diameter of 1 mm, for the convenience of comparison with the reference ^[8]. Optical properties of blood, epidermis and dermis in 585 nm wavelength are presented in Table 1, which are assumed to be constant in space and time. Figure 10 shows that the energy deposition along the skin depth predicted by TMCE was in accordance with that by GMC.

To further compare TMC and TMCE in boundary adaptability, the smaller computational domain of 0.75 mm × 0.75 mm × 1.0 mm with the same blood vessel geometry was considered (Figure 9b). The spot diameter of laser beam in Figure 6b is 0.5 mm. Deposition errors in the annular cylinder close to the inner wall of the superficial vessel was segmented by Δr of 5 μm and θ of 1° (Figure 9c). Each 1° annular cylinder is one statistical unit of the circumferential distribution of energy deposition.

The deposition in the 1° annular cylinder computed by GMC, VMC, TMC and TMCE was collected. The relative error K_VMC, K_TMC and K_TMCE of VMC, TMC and TMCE are calculated with GMC as a benchmark, as follows:

where E is the photon deposition in each 1° annular cylinder.

Figure 11 presents the relative error distribution in each 1° annular cylinder. From Figure 11a we can see a K_VMC up to 60% observed at 120°-170° and 190°-260°, whereas K_TMC and K_TMCE maintained less than 12% and 10%, respectively, and not sensitive to angles. When reducing the computation domain, the top K_VMC slightly increased to 64%. K_TMC increased up to 15% at 120°-350°, because the escape BC adopted in TMC resulted in more loss of photon weight when the blood vessel got nearer to the boundary of the domain. the computation domain reduced. On the contrary, K_TMCE steady almost unchanged and kept in 10%, showing better spatial adaptability of computation domain.

3.2.   Overall deposition in the blood vessel

Table 2 shows the overall difference regarding energy deposition in the blood vessel in three models. Differences between the three models are inapparent: average difference of mean, standard deviation, skewness, and kurtosis ^[26] are all less than 2%. The histogram of the three models of blood vessel with stdGC = 41.3 mm^-2 are shown in Figure 12. Photon energy exhibits a bimodal characteristic. The high peak in the low deposition region is caused by the reflection and recycle of the photon that escaped from the computational region. No apparent difference in the histogram is observed among the three models. Overall deposition in the blood shows a slight difference, but distribution detail may have a large difference. Hence, the main part of deposition in blood vessels should be studied.

3.3.   Accuracy and Computational cost of model A, B and C

The accuracy and computation time should be compromised to provide a comprehensive evaluation of the three models. Firstly, the effect of different models on the computational precision was studied. Blood vessel geometry shown in Figure 8c and f were used to compare the three models. Moreover, GMC simulation with blood vessel geometry in Figure 8f was performed to provide a benchmark.

The laser energy deposited along the vessel main axis (z = 0.5 mm) was shown in Figure 13. In the region covered by the laser spot, the deposited energy has a relatively uniform distribution in GMC, whereas more energy deposited in the central region of Model A (marked as the brown circle). On the other hand, distribution of energy deposition in Model B was in consistence with that of GMC. Although the reconstructed blood vessel used in Model C has a high value of stdGC, the energy distribution characteristic agrees with that of GMC.

To further compare the accuracy of the three models, photon deposition distribution in the central cross-section of the vascular region in the blood vessel is shown in Figure 14. More energy deposits at the top half of the vessel than the bottom half, because the top half faces the photon initial direction. From Figure 14a we can see the photon that transmits to the vessel from the top half should be mostly deposited near the vessel wall, forming the crescent of high deposition region. In Model A, a zigzag appears across the vessel boundary. The results computed by TMCE show a much better crescent shape (Figure 14b-c). The result of Model B agrees with that in GMC, illustrating the accurately capture of the crescent by TMCE. Although the vessel geometry are not identical, the crescent captured by Model C were approximately agreement with that in GMC. This finding is attributed to the well adaptability of Model C.

To the pulsed dye laser with wavelength of 585 nm or 595 nm, the damage of vascular lesions mainly concentrates in rupture ^[21]. The energy deposition above 450 J/cm³ was taken as the benchmark of hemorrhage because the top half part of the vessel, which faces the photon initial direction, often collects enough energy for vessel rupture at E_h = 450 J/cm^{3 [21]}. The volume ratio (VR) was introduced as the volume ratio between mostly deposited volume (E > E_h) and the whole volume in blood vessel. VR is important because its value is closely related to the thermal damage of the target vessel ^[21]. Figure 15 shows the energy deposition in the mostly deposited vessel region obtained by the three models. Mean value, standard deviation and VR were performed on the 25 blood vessels and was averaged into three groups as small, median and large stdGC. The volume ratio of mostly deposited energy decreased from Model A to Model C then Model B. For the vessel group with large-stdGC, the relative difference between Models A and B is 39%, which is much larger than that between Models C and B (10%). For the vessel group with small stdGC, the difference drops to 9% and 5%, respectively. The results indicate that the poor adaptability of the curved tissue interface in VMC leads to a high energy deposition error, which is not recommended in the computation. To models B and C which are based on TMCE, the error is not negligible after simplifying the vessel to a cylinder in TMCE. This effect would be much more apparent in a more curved vessel. Instead of a cylinder-shaped vessel, a real vessel contains the whole curvature information. Thus, to blood vessels with high stdGC, only model C is recommended because the cylinder-shaped vessel of model B leads to unneglected errors by loss of curvature information to real blood vessel. In the following section, a statistical analysis between energy deposition and geometric factors of model C can be performed.

The time cost of the three models were studied to provide a comprehensive evaluation of the three models. Considering the different mesh element used in VMC and TMCE, the averaged mesh volume was used to compare the computation time in the three models. The Fig. 8c and f are chosen as the computational model and the photon number is 10⁶. As illustrated in Figure 16, among the three models, a smaller mesh volume results in more computation time on judgement of photon transport in grids. The time consumed in Model B is approximately 1.5 times than that in Model A. The reason may be that the time cost in mesh judgement in TMCE is more than that in VMC. The difference in time cost between Model B and Model C is small and can be ignored, illustrating that calculation do not increase due to the reconstructed blood vessel. Overall, the influence of time cost is not apparent. Model C is the recommended model under comprehensive consideration of the accuracy and computation time of the three models.

3.4.   Statistical analysis of Model C

A statistical analysis was conducted on the surface of each blood vessel by Model C. Distance factor d_ctr was introduced to consider the effect of the laser beam, as follows:

where (x₀, y₀, z₀) is the center point of the computational domain, and the d₀ is a small number set to 10^-3. Independent geometry parameters were set as the product of MeC and d_ctr and the product of GC and d_ctr:

Pearson's correlation coefficients and p values between independent factors and energy deposition are shown in Table 3. The results confirm that the two parameters influence energy deposition in the vessel wall. GC and MeC appear negatively correlated with the deposition. We define E_max as the maximum deposited energy among all the cells in the blood vessel. The E/E_max is the ratio between energy deposition in each cell and E_max. Scatter plot of E/E_max versus GC and MeC for the vessel with stdGC of 41.3 mm^-2 was taken as an example to provide a full view (Figure 17). Each point in Figure 17 represents a value of E/E_max in a certain cell in the blood vessel. Cells with E/E_max above 0.6 have large variation of GC(-1000 to 700) and MeC (-500 to -30). MeC exhibits a much stronger correlation with the deposition than GC because of a much larger absolute value of slope of the fitted curve (marked as dashed line). The characteristic of MC with the laser energy deposition can provide a view in predicting photon-thermal behavior of PWS vessels with large mean curvatures.

4.   Conclusions

In this work, we developed a TMCE method, which is a flexible, accurate approach for predicting light propagation in skin tissues. The quantification of relative error distribution by TMCE, TMC and VMC was performed in the inner part of vascular wall when taking GMC as a benchmark. The maximum relative error of VMC stays above 60% in the large or small domains. Peak value of blood vessel shows that K_TMCE kept in 10% after the computation domain reduced, whereas the high value of K_TMC increases from 10% to 15%. Comparison between VMC and TMCE on cylindrical or reconstructed blood vessels shows neglected differences in the overall distribution of energy deposition of the three models. However, in the highly deposited region, bad adaptability of the curved tissue interface in VMC leads to more energy deposition error than replacing the reconstructed blood vessel with a cylinder-shaped vessel. This effect would be more apparent in a more curved vessel. An additional outcome of the work is the statistical significance of mean curvature on energy deposition, which indicates the potential of mean curvature in predicting laser-induced behavior of PWS vessels.

Acknowledgments

This work was supported by Natural Science Foundation of Zhejiang Province (LZ15E090002); the National Natural Science Foundation of China (51727811); Science Foundation of Zhejiang Sci-Tech University (ZSTU) (19022101-Y, 2020Q012); and Key Research and Development Program of Zhejiang Province (No. 2019C03117).

Conflict of interest

The authors declare no conflict of interest.