1. Introduction
Many differential equations have been proposed (see [8,11,13], [17]-[19], [21]-[22], [24,27] and references therein) to model the dynamic changes of substrate concentration and product one in enzyme-catalyzed reactions. Among those models, a typical form ([7]) is the following skeletal system
|
{˙x=v−V1(x,y)−V3(x),˙y=q(V1(x,y)−V2(y)),
|
(1)
|
where x and y denote the concentrations of the substrate and the product respectively, v and q are both positive constants, V1(x,y) and V2(y) denote the enzyme reaction rate and the output rate of the product respectively and satisfy that
|
V1(0,y)=0, ∂V1/∂x>0, ∂V1/∂y>0, V2(y)≥0, ∀x,y>0,
|
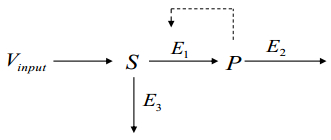
and V3(x) denotes the branched-enzyme reaction rate. Figure 1 shows the scheme of the enzyme-catalyzed reaction which comprises a branched network from the substrate. In Figure 1, S and P represent the substrate and product, respectively, and E1,E2 and E3 are the three enzymes.
The case that V3(x)≡0 in system (1), which represents an unbranched reaction, has been discussed extensively in [1,6,7,9,20]. Recently, more efforts were made to the case that V3(x)≢0. One of the efforts ([12,23]) is made for V1(x,y)=xmyn,V2(y)=y and V3(x)=lx and v=1, with which system (1) reduces to
|
{˙x=1−xmyn−lx,˙y=q(xmyn−y),
|
called the multi-molecular reaction model sometimes, where m,n≥1 are integers and l≥0 is real. All local bifurcations of this system such as saddle-node bifurcation, Hopf bifurcation and Bogdanov-Takens bifurcation were discussed in [12] and [23]. Reference [15] is concerned with the case that V1(x,y)=γxmyn, V3(x)=βx, q=1 and V2(y) is a saturated reaction rate, i.e., V2(y)=v2y/(μ2+y), with which (1) reduces to
|
{˙x=v−γxmyn−βx,˙y=γxmyn−v2yμ2+y,
|
where v,γ>0,μ2,v2 and β≥0. Results on existence and nonexistence of periodic solutions on Hopf bifurcation were obtained in [15] with n=1 and β=0. When V2(y) and V3(x) are both saturated reaction rates, system (1) was considered in [16] as
|
{˙x=v−V1(x,y)−v3xu3+x,˙y=q(V1(x,y)−v2yu2+y)
|
with V1(x,y)=v1x(1+x)(1+y)2/[L+(1+x)2(1+y)2], where L is the allosteric constant of E1. Varying the parameter v2 but fixing the other parameters, Liu ([16]) investigated numerically how the enzyme saturation affects the emergence of dynamical behaviors such as the change from a stable oscillatory state to a divergent state. Later, Davidson and Liu ([3]) discussed the saddle-node bifurcation, Hopf bifurcation and the global bifurcation corresponding to the appearance of homoclinic orbit. When V2(y) and V3(x) are both saturated reaction rates, system (1) was also considered in [4] as
|
{˙x=v−v1xy−v3xu3+x,˙y=q(v1xy−v2yu2+y)
|
(2)
|
with V1(x,y)=v1xy. With a change of variables x=u3˜x, y=u2˜y and the time rescaling t→v−11μ−12t, system (2) can be written as
|
{˙x=a−xy−bx1+x,˙y=κy(x−c1+y),
|
(3)
|
where we still use x, y to present ˜x, ˜y and take notations a:=v−11u−13u−12v, b:=v−11u−13u−12v3, c:=v−11u−13u−12v2 and κ:=u−12qu3 for positive constants. Actually, system (3) is orbitally equivalent to the following quartic polynomial differential system
|
{˙x=(1+y){(1+x)(a−xy)−bx},˙y=κ(1+x)y{(1+y)x−c},
|
(4)
|
in the first quadrant Q+:={(x,y):x≥0,y≥0} by a time scaling dτ=(x+1)(y+1)dt. In [4] Davidson, Xu and Liu discussed the case that k=1 and a<c, where the system has at most two equilibria, giving the existence of limit cycles (by the Poincaré-Bendixson Theorem seen in [10] or [26]) and the non-existence of periodic orbits (by the Dulac Criterion seen in [10] or [26]), proving the uniqueness of limit cycles (by reducing to the form of Liénard system) with some restrictions, and illustrating with the software AUTO saddle-node bifurcation, transcritical bifurcation and Hopf bifurcation for fixed κ=1,b=1.5 and c=5. Recently, the general case that κ,a,b,c>0 was discussed in [27], where all codimension-one bifurcations such as saddle-node, transcritical and pitchfork bifurcations were investigated and the weak focus was proved to be of at most order 2.
In this paper we continue the work of [27] to give conditions for the existence of a cusp and compute the parameter curves for the Bogdanov-Takens bifurcation, which induces the appearance of homoclinic orbits and periodic orbits, indicating the tendency to steady-states or a rise of periodic oscillations for the concentrations of the substrate and product.
2. Condition for cusp
It is proved in [27] that system (4) has at most 3 equilibria, i.e., E0:(a/(b−a),0), E1:(p1,c/p1−1) and E2:(p2,c/p2−1), where
|
p1:=−12{(a−b−c+1)−[(a−b−c+1)2−4(a−c)]1/2},p2:=−12{(a−b−c+1)+[(a−b−c+1)2−4(a−c)]1/2}.
|
(5)
|
Moreover, if a=a∗:=c+(b1/2−1)2, then E1 and E2 coincide into one, i.e., the equilibrium E∗:(b1/2−1,c(b1/2+1)/(b−1)−1). There are found in [27] totally 6 bifurcation surfaces
|
TE0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b≠(c+1)2}:=4⋃i=1T(i)E0,PE0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b=(c+1)2},HE1:={(a,b,c,κ)∈R4+|κ=κ1,bc/(1+c)<a<c,0<b≤1}∪{(a,b,c,κ)∈R4+|κ=κ1,bc/(1+c)<a<c+(b1/2−1)2,1<b<(c+1)2},SNE∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2,κ≠κ∗}:=4⋃i=1SN(i)E∗,B1:={(a,b,c,κ)∈R4+|a=c},B2:={(a,b,c,κ)∈R4+|a=b},
|
which divide R4+:={(a,b,c,κ):a>0,b>0,c>0,κ>0} into 8 subregions
|
R1:={(a,b,c,κ)∈R4+|c<a<a∗,1<b<c,c>1, or b<a<a∗,c<b<(c+1)2/4,c>1},R2:={(a,b,c,κ)∈R4+|b<a<c,0<b<c}R3:={(a,b,c,κ)∈R4+|bc/(1+c)<a<b,0<b<c or bc/(1+c)<a<c,c<b<c+1},R4:={(a,b,c,κ)∈R4+|0<a<bc/(1+c),0<b<c+1 or 0<a<c,b>c+1},R5:={(a,b,c,κ)∈R4+|c<a<bc/(1+c),b>c+1},R6:={(a,b,c,κ)∈R4|c<a<b,c<b<(c+1),c>3 or bc/(1+c)<a<b,c+1<b<(c+1)2/4,c>3 or bc/(1+c)<a<a∗,(c+1)2/4<b<(c+1)2,c>3 or c<a<b,c<b<(c+1)2/4,1<c≤3 or c<a<a∗,(c+1)2/4<b<c+1,1<c≤3 or bc/(1+c)<a<c+(b1/2−1)2,(c+1)<b<(c+1)2,c≤3 or c<a<a∗,1<b<c+1,c≤1},R7:={(a,b,c,κ)∈R4+|c+(b1/2−1)2<a<b,(c+1)2/4<b<(c+1)2,c>1 or bc/(1+c)<a<b,b>(c+1)2 or c<a<b,c<b<1,c≤1 or c+(b1/2−1)2<a<b,1<b<(c+1)2,c≤1},R0:=R4+∖{PE0∪SNE∗∪TE0∪(2⋃i=1Bi)∪B∪(7⋃i=1Ri)},
|
where
|
T(1)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),0<b<c+1},T(2)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),c+1<b<(c+1)2},T(3)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b>(c+1)2},T(4)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b=c+1},SN(1)E∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2/4,c>1,κ≠κ∗},SN(2)E∗:={(a,b,c,κ)∈R4+|a=a∗, b=(c+1)2/4,c>1,κ≠κ∗},SN(3)E∗:={(a,b,c,κ)∈R4+|a=a∗, (c+1)2/4<b<(c+1)2,c>1,κ≠κ∗},SN(4)E∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2,c≤1,κ≠κ∗},κ1:=p−21{(p1+1)(c−p1)}−1c{p1(c−p1)+a},κ∗:=(c−b1/2+1)−1(b1/2−1)−2c2.
|
(6)
|
The following lemma is a summary of Theorems 1, 2 and 3 of [27].
Lemma 2.1. (ⅰ) System (4) has a saddle-node E0 if (a,b,c,κ)∈TE0∪PE0. Moreover, as (a,b,c,κ) crosses either T(1)E0 from R3 to R4, T(2)E0 from R6 to R5, or T(4)E0 from R6 to R4, a saddle E0 and a stable (resp. unstable) node E1 merge into a stable node E0 on the boundary of the first quadrant Q+ for κ<κ1(resp. κ>κ1) through a transcritical bifurcation; as (a,b,c,κ) crosses T(3)E0 from R5 to R7, a stable node E0 and a saddle E2 merge into a saddle E0 on the boundary of Q+ through a transcritical bifurcation; as (a,b,c,κ) crosses PE0 from R7 to R5, a saddle E0 changes into a stable node E0, a saddle E2 through a pitchfork bifurcation at E0 on the boundary of Q+.
(ⅱ) System (4) has a weak focus E1 of at most order 2 for (a,b,c,κ)∈HE1, which is of order ℓ exactly and produces at most ℓ limit cycles through Hopf bifurcations as (a,b,c,κ)∈H(ℓ)E1, ℓ=1,2, where H(1)E1:=HE1∖H(2)E1 and
|
H(2)E1:={(a,b,c,κ)∈HE1:2p1(p1+1)a3+{(p21+p1+1)c2+p1(2p21+p1−2)c−3p31(p1+1)}a2−(c−p1){(p31+3p21+p1+1)c2+2p21(p21+3p1+3)c+3p41(p1+1)}a+p21{(p1+2)c+p21}{c−p1(p1+1)}(c−p1)2=0}.
|
(ⅲ) System (4) has a saddle-node E∗ if (a,b,c,κ)∈SNE∗. Moreover, as (a,b,c,κ) crosses either SN(1)E∗ from R0 to R1, SN(2)E∗ from R0 to R6, or SN(3)E∗∪SN(4)E∗ from R7 to R6, a stable (resp. unstable) node E1 and a saddle E2 arise through a saddle-node bifurcation for κ<κ1(resp. κ>κ1).
The above Lemma 2.1 does not consider parameters in the set
|
B:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2,κ=κ∗},
|
(7)
|
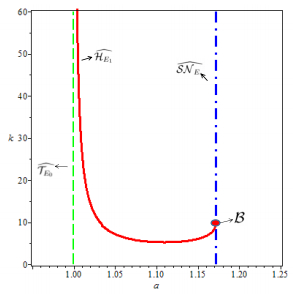
where a∗ is given below (5) and κ∗ is given in (6). B is actually the intersection of the saddle-node bifurcation surface SNE∗ and the Hopf bifurcation surface HE1, which are described by the curves ^SNE∗ and ^HE1 respectively on the section {(a,b,c,κ)∈R4+|b=2, c=1} in Figure 2. The intersection of ^SNE∗ and ^HE1 indicates B.
This paper is devoted to bifurcations in B. For (a,b,c,κ)∈B, equilibrium E∗ is degenerate with two zero eigenvalues. In the following lemma we prove that E∗ is a cusp.
Lemma 2.2. If (a,b,c,κ)∈B∖C, where
|
C:={(a,b,c,κ)∈B|c=ς(b):=14b1/2(b1/2−1){b1/2+2+(17b−12b1/2+4)1/2}},
|
then equilibrium E∗ is a cusp in system (4).
Proof. For simplicity in statements, we use the notation
For (a,b,c,κ)∈B, system (4) can be transformed into the form
|
{˙x=y+c(p2+cp+c)p3x2+1p+1xy−pc2(p+1)y2−c(p2+c)p4x3−p2+2pc+2cp2c(p+1)x2y−2p+1c2(p+1)2xy2−c2p4x4−2p2(p+1)x3y−1c2(p+1)2x2y2,˙y=−c3(p+1)p3x2−c2(p+1)p2(c−p)xy−1c−py2−(p+1)(p2+c)p5(c−p)x3−c(p2+2pc+2c)p3(c−p)x2y−2p+1p(p+1)(c−p)xy2−c4(p+1)p5(c−p)x4−2c2p3(c−p)x3y−1p(p+1)(c−p)x2y2,
|
(9)
|
by translating E∗ to the origin O and Jordanizing the linear part of system (4). For convenience, introducing new variables (x,y)↦(u,v), where u=x and v denotes the right-hand side of the first equation in (9), we change (9) into the Kukles form
|
{˙u=v,˙v=−c3(p+1)p3u2+c{(2p+2)c2−(p2+3p)c−2p3}p3(c−p)uv+c−2p−1(p+1)(c−p)v2+c3(p2+c)p4(c−p)u3−c{(p+1)(p+3)c2+p(p2−3p−3)c−p3(3p+2)}p4(p+1)(c−p)u2v−(5p2+8p+4)c+2p2(p+1)cp2(p+1)2uv2−1c2(p+1)v3−c2(c2+2p2c−p3)p5(c−p)u4+1p5(p+1)2(c−p){(p+4)(p+1)2c3+p(7p3+7p2−3p−4)c2−p3(8p2+15p+8)c−2p5(p+1)}u3v+(3p3+6p2+6p+2)c2+p(2p+1)(2p2+2p−1)c−p3(p+1)(7p+4)cp3(p+1)3(c−p)u2v2−(3p+4)c2−3p(p+2)c−2p3c3p(p+1)2(c−p)uv3−2c−3pc4(p+1)2(c−p)v4+O(|u,v|5).
|
(10)
|
Since the linear part is nilpotent, by Theorem 8.4 in [14] system (10) is conjugated to the Bogdanov-Takens normal form, i.e., the right-hand side of the second equation is a sum of terms of the form auk+buk−1v. Hence, one can use the transformation u→u, v→v−c−2p−1(p+1)(c−p)uv together with the time-rescaling dt=(1−c−2p−1(p+1)(c−p)u)dτ to change system (10) into the following
|
{˙u=v,˙v=−c3(p+1)p3u2+c{(2p+2)c2−(p2+3p)c−2p3}p3(c−p)uv+O(|u,v|3),
|
(11)
|
where the term of v2 is eliminated and terms of degree 2 are normalized. The term of u2 exists since −c3(p+1)/p3≠0. For the existence of the term of uv, we need to discuss on the quadratic equation
|
c2−p2+3p2(p+1)c−p3p+1=0,
|
(12)
|
which comes from the numerator of the coefficient of uv. Since the constant term is negative for p>0, the quadratic equation (12) has exactly one positive root
|
c=14(p+1)−1p{p+3+(17p2+22p+9)1/2},
|
which defines the function ς(b) as shown in Lemma 2.2 with the replacement (8). It implies by Theorem 8.4 of [14] that for c≠ς(b), i.e., (a,b,c,κ)∈S∖C, O is a cusp of system (11). The proof of this lemma is completed.
3. Bogdanov-Takens bifurcation
In this section we discuss in the case that (a,b,c,κ)∈B∖C, in which system (4) is of codimension 2. We choose a,κ as the bifurcation parameters and unfold the Bogdanov-Takens normal forms of codimensions 2 when (a,κ) is perturbed near the point (a∗,κ∗), where a∗ is given below (5) and κ∗ is given in (6).
Theorem 3.1. If (a,b,c,κ)∈B∖C, where B is defined in (7) and C is defined as in Lemma 2.2, then there are a neighborhood U of the point (a∗,κ∗) in the (a,κ)-parameter space and four curves
|
SN+:={(a,κ)∈U|a=a∗, κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗, κ<κ∗,c>ς(b)},SN−:={(a,κ)∈U|a=a∗, κ<κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗, κ>κ∗,c>ς(b)},H:={(a,κ)∈U|a=a∗−((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗−((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ<κ∗,c>ς(b)},L:={(a,κ)∈U|a=a∗−49/25((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗−49/25((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ<κ∗,c>ς(b)},
|
such that system (4) produces a saddle-node bifurcation near E∗ as (a,c) acrosses SN+∪SN−, a Hopf bifurcation near E∗ as (a,κ) acrosses H, and a homoclinic bifurcation near E∗ as (a,κ) acrosses L, where κ∗ and ς(b) are given in (6) and Lemma 2.2 respectively.
The above bifurcation curve H is exactly the same as HE1 given in Lemma 2.1, and the union SN+⋃SN+ is exactly the bifurcation curves SNE∗ given in Lemma 2.1.
Proof. Let p=b1/2−1 and
and consider |ε1| and |ε2| both to be sufficiently small. Expanding system (4) at E∗, we get
|
{˙x=c(p+1)pε1+(−c2(p+1)p2+cpε1)x+(−c(p+1)+(p+1)ε1)y−c(c−p)p2x2+(−c(2+3p)p+ε1)xy−p(p+1)y2+O(‖(x,y)‖3),˙y=(c3(p+1)p4+c(p+1)(c−p)p2ε2)x+(c2(p+1)p2+(p+1)(c−p)ε2)y+(c3p4+c(c−p)p2ε2)x2+(c3(2+3p)−c2p(2p+1)(c−p)p3+c(3p+2)−p(2p+1)pε2)xy+(c2(p+1)(c−p)p+p(p+1)ε2)y2+O(‖(x,y)‖3).
|
(14)
|
Introducing new variables (x,y)↦(ξ1,η1), where ξ1=x and η1 denotes the right-hand side of the first equation in (14), we change (14) into the Kukles form, whose second order truncation is the following
|
{˙ξ1=η1,˙η1=E00(ε1,ε2)+E10(ε1,ε2)ξ1+E20(ε1,ε2)ξ21+F(ξ1,ε1,ε2)η1+E02(ε1,ε2)η21,
|
(15)
|
where F(ξ1,ε1,ε2):=E01(ε1,ε2)+E11(ε1,ε2)ξ1 and Eij s (i,j=0,1,2) are given in Appendix. Notice that (a,b,c,κ)∈B∖C implies that c≠ς(b). From (12) we see that the quadratic equation has exactly one positive root c=ς(b). Thus, for c≠ς(b) we can check that
|
F(0,0,0)=0, ∂F∂ξ1(0,0,0)=E11(0,0)=(2p+2)(c2−p2+3p2(p+1)c−p3p+1)≠0.
|
By the Implicit Function Theorem, there exists a function ξ1=ξ1(ε1,ε2) defined in a small neighborhood of (ε1,ε2)=(0,0) such that ξ1(0,0)=0 and F(ξ1(ε1,ε2),ε1,ε2)=0. Thus, from the definition of F we obtain ξ1(ε1,ε2)=−E01(ε1,ε2)/E11(ε1,ε2) near (0,0). Then, we use a parameter-dependent shift
to vanish the term proportional to η2 in the equation for η2 from system (15), which leads to the following system
|
{˙ξ2=η2,˙η2=ψ1(ε1,ε2)+ψ2(ε1,ε2)ξ2+E20(ε1,ε2)ξ22+E11(ε1,ε2)ξ2η2+E02(ε1,ε2)η22,
|
(16)
|
where
|
ψ1(ε1,ε2):=E00(ε1,ε2)+E10(ε1,ε2)ξ1(ε1,ε2)+E20(ε1,ε2)ξ21(ε1,ε2),ψ2(ε1,ε2):=E10(ε1,ε2)+2ξ1(ε1,ε2)E20(ε1,ε2).
|
In order to eliminate the η22 term, one can use the transformation
|
ξ3=ξ2, η3=η2−E02(ε1,ε2)ξ2η2
|
together with the time-rescaling dt=(1−E02(ε1,ε2)ξ2)dτ to change system (16) into the following
|
{˙ξ3=η3,˙η3=ζ1(ε1,ε2)+ζ2(ε1,ε2)ξ3+˜E20(ε1,ε2)ξ23+E11(ε1,ε2)ξ3η3,
|
(17)
|
where
|
ζ1(ε1,ε2):=ψ1(ε1,ε2), ζ2(ε1,ε2):=ψ2(ε1,ε2)−ψ1(ε1,ε2)E02(ε1,ε2),˜E20(ε1,ε2):=E20(ε1,ε2)−E10(ε1,ε2)E02(ε1,ε2).
|
Further, in order to reduce coefficient of ξ23 to 1, we apply the transformation
|
u=˜E20(ε1,ε2)E211(ε1,ε2)ξ3,v=sign(E11(ε1,ε2)˜E20(ε1,ε2))˜E220(ε1,ε2)E311(ε1,ε2),
|
where ˜E20(0,0)=−c3(p+1)p3<0, and the time-scaling dt=|E11(ε1,ε2)˜E20(ε1,ε2)|dτ to system (17) and obtain
|
{˙u=v,˙v=ϕ1(ε1,ε2)+ϕ2(ε1,ε2)u+u2+ϑuv,
|
(18)
|
where ϑ=sign(E11(0,0)˜E20(0,0)),
|
ϕ1(ε1,ε2):=E411(ε1,ε2)˜E320(ε1,ε2)ζ1(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}4ε1ϕ11(ε1,ε2)p4(c−p)4ϕ212(ε1,ε2), ϕ2(ε1,ε2):=E211(ε1,ε2)˜E220(ε1,ε2)ζ2(ε1,ε2)=√2{(2p+2)c2−(p2+3p)c−2p3}ϕ21(ε1,ε2)c3/2(c−p)2(p+1)1/2pϕ3/212(ε1,ε2),
|
and polynomials ϕij s are given in the Appendix.
Let
|
μ1=ϕ1(ε1,ε2),μ2=ϕ2(ε1,ε2),
|
(19)
|
where ϕ1 and ϕ2 are defined just below (18). Clearly, ϕ1(0,0)=ϕ2(0,0)=0. Compute the Jacobian determinant of (19) at the point (0,0)
|
|∂ϕ1(ε1,ε2)∂ε1∂ϕ1(ε1,ε2)∂ε2∂ϕ2(ε1,ε2)∂ε1∂ϕ2(ε1,ε2)∂ε2|(ε1,ε2)=(0,0)=−{(2p+2)c2−(p2+3p)c−2p3}5p6c4(c−p)4(p+1)≠0,
|
(20)
|
implying that (19) is a locally invertible transformation of parameters. This transformation makes a local equivalence between system (18) and the versal unfolding system
|
{˙˜u=˜v,˙˜v=μ1+μ2˜u+˜u2+ϑ˜u˜v,
|
(21)
|
where ϑ is given in (18). As indicated in Section 7.3 of [10], system (21) has the following bifurcation curves
|
SN+:={(μ1,μ2)∈V0 | μ1=0, μ2>0},SN−:={(μ1,μ2)∈V0 | μ1=0, μ2<0},H:={(μ1,μ2)∈V0 | μ1=−μ22, μ2>0},L:={(μ1,μ2)∈V0 | μ1=−4925μ22+o(|μ2|2), μ2>0},
|
(22)
|
where V0 is a small neighborhood of (0,0) in R2.
In what follows, we present above bifurcation curves in parameters ε1 and ε2 in explicit forms. For this purpose, we need the relation between (ε1,ε2) and (μ1,μ2). Note that ϕ1 and ϕ2 defined just below (18) are Ck near the origin (0, 0)(k is an arbitrary integer). By condition (20), the well-known Implicit Function Theorem implies that there are two Ck functions
|
ε1=ω1(μ1,μ2), ε2=ω2(μ1,μ2)
|
(23)
|
in a small neighborhood of (0,0,0,0) such that ω1(0,0)=ω2(0,0)=0 and
|
μ1=ϕ1(ω1(μ1,μ2),ω2(μ1,μ2)), μ2=ϕ2(ω1(μ1,μ2),ω2(μ1,μ2)).
|
(24)
|
Substitute the second order formal Taylor expansions of ω1 and ω2 in (24) while expand ϕ1 and ϕ2 in (24) to the second order
|
ϕ1(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}4ε1/{p6c2(c−p)4(p+1)}−{(2p+2)c2−(p2+3p)c−2p3}4(24p2c4+42c4p+21c4−8p3c3−54c3p2−44c3p−36c2p4−12p3c2+27p2c2+8p5c+32cp4+16p6)ε21/{2c4p8(c−p)6(p+1)2}−{(2p+2)c2−(p2+3p)c−2p3}4ε1ε2/{(c4p4(c−p)3(p+1)}+o(|ε1,ε2|2),
|
(25)
|
|
ϕ2(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}ε1/{2c2(p3−2cp+p2+c2p+c2−2cp2)p4}−{(2p+2)c2−(p2+3p)c−2p3}ε2/c2−{(2p+2)c2−(p2+3p)c−2p3}(−243p3c3+832p3c4+513p2c4+455p4c3−594p5c2−1347p3c5−1209p2c5+165p4c4+1138p5c3−324p6c2−424p7c−200p5c4+382p6c3+512p7c2−520cp8−396c5p−48p9+108c6−48p10+384c6p3+414c6p−104cp9+264c2p8+594c6p2−672c5p4+96c6p4−136c5p5−44c4p6−76c3p7)ε21/{4c3(p+1)2(c−p)4p6}−{(2p+2)c2−(p2+3p)c−2p3}(8p2c4+23c4p+12c4+30p3c3+8c3p2−22c3p−58c2p4−85p3c2+6p2c2−8p5c+46cp4+24p6)ε1ε2/{4c4p2(p+1)(c−p)2}+(c−p)p2{(2p+2)c2−(p2+3p)c−2p3}ε22/c4+o(|ε1,ε2|2).
|
(26)
|
Then, comparing the coefficients of terms of the same degree in (24), we obtain the second order approximations
|
ε1=c2p6(c−p)4(p+1)μ1/{(2p+2)c2−(p2+3p)c−2p3}4+c2p10(c−p)6(p+1)(32p2c4+56c4p+27c4−16p3c3−79c3p2−59c3p−48c2p4−19p3c2+36p2c2+12p5c+50cp4+24p6)μ21/{2{(2p+2)c2−(p2+3p)c−2p3}8}+c2p8(c−p)5(p+1)μ1μ2/{(2p+2)c2−(p2+3p)c−2p3}5+o(|μ1,μ2|2),
|
(27)
|
|
ε2=c2p2(c−p)2(−8p5−12cp4−18cp3+8c3p2−11p2c2−9c2p+14c3p+6c3)μ1/{2{(2p+2)c2−(p2+3p)c−2p3}4}−c2μ2/{(2p+2)c2−(p2+3p)c−2p3}+c2p6(c−p)4(1314c7p2+630pc7−270p3c4+2068p3c5+612p2c5+677p4c4−1134p5c3+4387p5c4−1056p6c3−1804p7c2−3741c6p3+756c5p4+1160c3p8−2268c6p4+1176c7p3−1272c5p6−352c6p5+384c7p4−320p11+108c7−704cp10+224c2p9−2046c5p5+4258c4p6+832p7c4−1464p8c2−2289c6p2+1544p7c3−450c6p−1344cp9)μ21/{8{(2p+2)c2−(p2+3p)c−2p3}8}+c2p4(c−p)2(40p2c4+61c4p+24c4−78p3c3−158c3p2−68c3p−14c2p4+43p3c2+48p2c2+32p5c+62cp4+24p6)μ1μ2/{4{(2p+2)c2−(p2+3p)c−2p3}5}+c2p2(c−p)μ22/{(2p+2)c2−(p2+3p)c−2p3}2+o(|μ1,μ2|2).
|
(28)
|
Then we are ready to express those bifurcation curves in parameters ε1 and ε2.
For curves SN±, we need to consider μ1=0. From the first equality of (19) we see that μ1=0 if and only if ε1=0 because in the expression of ϕ1(ε1,ε2) we have ϕ11(0,0)/ϕ212(0,0)=1/p2c2(p+1)≠0. Thus, for μ1=0 we obtain from (28) that
|
ε2=−c2(2p+2)Ψ(c)μ2+O(|μ2|2),
|
(29)
|
where Ψ(c) is the same quadratic polynomial as given in (12). It follows that the inequality μ2>0 (or <0) together with the sign of Ψ(c) determines the sign of ε2. From the analysis of the quadratic equation (12) we see that Ψ(c)<0 (or >0) if 0<c<ς(b) (or c>ς(b)), where ς(b) is defined in Lemma 2.2. Hence from (22) we obtain that
|
SN+:={(ε1,ε2) | ε1=0,ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=0,ε2<0,c>ς(b)},SN−:={(ε1,ε2) | ε1=0,ε2<0,0<c<ς(b)}∪{(ε1,ε2) | ε1=0,ε2>0,c>ς(b)}.
|
For curve H, we need to consider μ1=−μ22, which is equivalent to Υ(ε1,ε2):=ϕ1(ε1,ε2)+ϕ22(ε1,ε2)=0 by (19). Clearly, Υ(0,0)=0 and
|
∂Υ∂ε1|(ε1,ε2)=(0,0)={(2p+2)Ψ(c)}4/{p6c2(c−p)4(p+1)}≠0.
|
By the Implicit Function Theorem, there exists a unique Ck function ε1=ϵ1(ε2) such that ϵ1(0)=0 and Υ(ϵ1(ε2),ε2)=0. Similarly to (27) and (28), expanding Υ at (ε1,ε2)=(0,0) and substituting with a formal expansion of ϵ1(ε2) of order 2, we obtain by comparison of coefficients that
|
ε1=ϵ1(ε2)=−p6(c−p)44(p+1)Ψ2(c)ε22+o(|ε2|2).
|
(30)
|
Further, replacing μ1 with μ1=−μ22 in (28), we get
|
ε2=−c2(2p+2)Ψ(c)μ2+o(|μ2|).
|
Similarly to (29), from (22) we obtain that
|
H:={(ε1,ε2) | ε1=−p6(c−p)44(p+1)Ψ2(c)ε22+o(|ε2|2), ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=−p6(c−p)44(p+1)Ψ2(c)ε22+o(|ε2|2), ε2<0,c>ς(b)}.
|
For curve L, we need to consider μ1=−4925μ22+o(|μ2|2), i.e., ϕ1(ε1,ε2)=−4925ϕ22(ε1,ε2)+o(|ϕ2|2). Similarly to H, we apply the Implicit Function Theorem to obtain
|
ε1=−49p6(c−p)4100(p+1)Ψ2(c)ε22+o(|ε2|2).
|
Similarly to (29), from (22) we obtain that
|
L:={(ε1,ε2) | ε1=−49p6(c−p)4100(p+1)Ψ2(c)ε22+o(|ε2|2), ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=−49p6(c−p)4100(p+1)Ψ2(c)ε22+o(|ε2|2), ε2<0,c>ς(b)}.
|
Finally, with the replacement (13) we can rewrite the above bifurcation curves SN±,H and L expressed in parameters (ε1,ε2) in expressions in the original parameters (a,b,c,κ) as shown in Theorem 3.1.
4. Conclusions
In this paper we analyzed the dynamics of system (4) near the equilibrium E∗ when parameters lie near B∖C. We proved that E∗ is a cusp when parameters lie on B∖C. We investigated the Bogdanov-Takens bifurcation near the cusp and compute in Theorem 3.1 the four bifurcation curves SN+, SN−, H and L in the practical parameters. Those bifurcation curves can be observed in Figure 3 in the case that c>1 and b=(c+1)2/4 (which implies p=(c−1)/2). They display the merge of equilibria and the rise of homoclinic orbits and periodic orbits.
More concretely, in this case,
|
a∗=(c+1)24, κ∗=8c2(c+1)(c−1)2.
|
Moreover, the four bifurcation curves divide the neighborhood U of (a∗,κ∗) into the following regions:
|
DI:={(a,κ)∈U| a<(c+1)24, κ≤8c2(c+1)(c−1)2}⋃{(a,κ)∈U| a<(c+1)24−49(c−1)6(c+1)33200(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3), κ>8c2(c+1)(c−1)2},DII:={(a,κ)∈U| (c+1)24−49(c−1)6(c+1)33200(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3)<a<(c+1)24−(c−1)6(c+1)3128(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3), κ>8c2(c+1)(c−1)2},DIII:={(a,κ)∈U| (c+1)24−(c−1)6(c+1)3128(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3)<a<(c+1)24, κ>8c2(c+1)(c−1)2},DIV:={(a,κ)∈U| a>(c+1)24}.
|
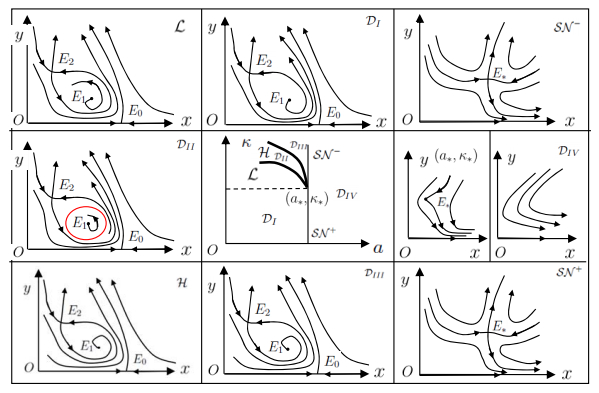
Theorem 3.1 gives dynamical behaviors of system (4) near E∗ in the first quadrant in Table 4. The coordinates of equilibria E0:(x0,0), E1:(p1,q1) and E2:(p2,q2) are given by x0:=a/(b−1) and
|
p1:=−12{(a−b−c+1)−{(a−b−c+1)2−4(a−c)}1/2},p2:=−12{(a−b−c+1)+{(a−b−c+1)2−4(a−c)}1/2}
|
as in [27]. E0 exists in the first quadrant when (a,κ)∈DI∪L∪DII∪H∪DIII but disappears when (a,κ)∈DIV (appearing in other quadrants) or (a,κ)∈SN+∪{(a∗,κ∗)}∪SN− (not existing).
Table 4. Dynamics of system (4) in various cases of parameter (a,κ).
| Parameters (a,κ) |
Equilibria |
Limit cycles and homoclinic orbits |
Region in bifurcation diagram |
| E0 |
E1 |
E2 |
E∗ |
| DI |
saddle |
unstable focus |
saddle |
|
|
DI |
| L |
saddle |
unstable focus |
saddle |
|
one homoclinic rrbit |
L |
| DII |
saddle |
unstable focus |
saddle |
|
one limit cycle |
DII |
| H |
saddle |
stable focus |
saddle |
|
|
H |
| DIII |
saddle |
stable focus |
saddle |
|
|
DIII |
| SN+ |
|
|
|
saddle-node |
|
SN+ |
| DIV |
|
|
|
|
|
DIV |
| (a∗,κ∗) |
|
|
|
cusp |
|
(a∗,κ∗) |
| SN− |
|
|
|
saddle-node |
|
SN− |
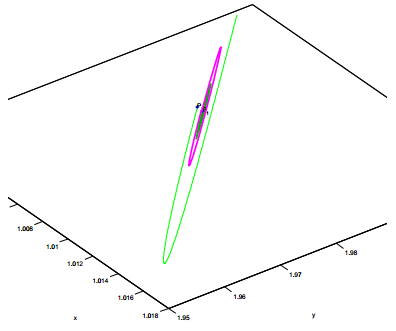
The appearance of limit cycle displays a rise of oscillatory phenomenon in system (4). Choosing parameters a=3.99999,b=4,c=3 and κ=4.495 in DII, we used the command ODE45 in the software Matlab Version R2014a to simulate the orbit initiated from (x0,y0)=(1.00432,1.98662845) numerically, which plots an attractive limit cycle in Figure 4 and shows a dynamic balance and permanence of the substrate and the product in the enzyme-catalyzed reaction. The homoclinic loop actually gives a boundary for the break of the dynamic balance and permanence.
In this paper we only considered parameters in B∖C. When parameters lie in C, higher degeneracy may happen at E∗. Although efforts have been made for higher degeneracies, for example, versal unfolding was discussed in [5] for a normal form of cusp system of codimension 3, it is still difficult to compute bifurcation curves in original parameters in the case of codimension 3. Such a computation with original parameters is indispensible for practical systems and for system (4) it will be our next work.
Appendix. Some coefficients
The functions in system (15) are
|
E00:={(2p+2)c2−(p2+3p)c−2p3}4ε1/{c2(p+1)p6(c−p)4},E10:=−{(2p+2)c2−(p2+3p)c−2p3}2ε1{(−6c3p−4c3p2−4p3c2+3p2c2+4cp4+4c4p+3c4)−(p2c2−3c3p−3c2p+cp2+2cp3−2p4)ε1−(p3c2−2cp4+p5+4c2p4−5p5c−p3c3+2p6)ε2}/{(p+1)p4c3(c−p)4},E20:={(−2c6(p+1)2(c−p)2)+(9c3p2+4c2p4−13c4p+4p5c2+6p3c3+9c5p−15p2c4−2p4c3+4p2c5−4p3c4+6c5)ε1−(2p7c−6p7c2−6p6c2−2p5c4+6p6c3+2cp8−2p4c4+6p5c3)ε2+(6p5c2−2p4c3−6p6c−6p7c+6p6c2−2p5c3+2p7+2p8)ε1ε2+(6p3c3−4p2c4−2c2p4−10p3c2−9c4p−2cp4+17c3p2−2p5c+13c3p−9p2c2−6c4)ε21}/{2c3p2(c−p)2(p+1)},E01:=−{(2p+2)c2−(p2+3p)c−2p3}{2c3ε1+(cp4−2p3c2+c3p2)ε2+(2p4−6cp3+4p2c2)ε1ε2+(12c2−6cp)ε21}/{p2(c−p)2c3},E11:={(3c3p2−8p2c4−p4c3+2c5+2c2p4+4c5p+2p2c5−5c4p+2p5c2+2p3c3−3p3c4)+(3c2p4+3c3p+p2c2+2p5c+3p2c4+3p3c2+2c4p+2cp4−4p3c3+c3p2)ε1+(5p6c2−2p7c−3p6c+7p5c2+2c2p4−p5c−5p4c3−p3c3+p3c4+p4c4−4p5c3)ε2−(5p6c−4p5c2+p4c3−5c2p4−p3c2+7p5c+p3c3+2cp4−2p7−p5−3p6)ε1ε2+(13cp2−8cp4+9c3p2−38p2c2+5cp3+10p4+10p5+19c3p+10c3−13p3c2−25c2p)ε21}/{c2(p+1)(−p+c)},E02:={(c−2p−1)+(5c3−2c2p)ε1−(3p3c2−2c3p2−cp4)ε2+(p4−cp3)ε1ε2−(2cp−c2)ε21}/{(p+1)2(c−p)2}.
|
The functions below system (18) are
|
ϕ11:=24c6p5+4c8p2−16c7p4+4c8p3−16c5p6+4p7c4+24c6p4−16c7p3−16c5p5+4c4p6+(9p4c4−16p6c3+40c3p7+68p5c4−26p3c5+3c8−6c8p+42c6p3+36c6p4−94c5p4+6c7p2−4c4p6−16c2p8−56c5p5−8c8p2+8c7p3+28c6p2−14c7p)ε1+(4c7p4+40c5p7−4c2p9−4c2p10+20c3p8+20c3p9−20c6p5+40c5p6−20c6p6−40c4p8+4c7p5−40p7c4)ε2−(40p2c5+12p4c3+32c7p2+8p5c3+12c7+92p3c5+8p6c2−32p3c4−12p6c3−28p7c2+4c5p4−88c6p2−56p4c4+36c7p+48p5c4−60c6p3+16cp8−32c6p)ε21+(12cp9−24p7c4−8c7p4−6c7p3−88c5p5−32c2p8+20cp10−24c5p4+6c6p3+2c3p7−24p6c3+36c6p5+72c4p6+96c3p8−76c2p9+36p5c4+40c6p4−44c5p6+6p7c2)ε1ε2+(8p7c−9p2c4−16p5c2+6p3c3−c2p4+11p4c4+6p3c5+10p4c3−16p5c3−18p2c5+12p3c4−9c6p2+4p6c−4p8)ε31+(−34c4p6+2c3p7+4p9−28cp9−16cp8+6p4c4+8p10−2p7c+32c2p8+32p7c2−32p6c3−14p5c3+10p6c2−6c6p4+26c5p5+12p5c4)ε21ε2+(4c3p7−c6p6+44c3p9−41c2p10−c4p6+4cp9+2c5p6−4p11+28c3p8−32c2p9+8c5p7−26c4p8+20p11c−12p7c4−p10−4p12+18cp10−6c2p8)ε1ε22,ϕ12:=(2p5c3−4p3c4+2p4c3+2p3c5+2p2c5−4p4c4)+(9c3p2+4c2p4−13c4p+4p5c2+6p3c3+9c5p−15p2c4−2p4c3+4p2c5−4p3c4+6c5)ε1+(−2p7c+6p7c2+6p6c2+2p5c4−6p6c3−2cp8+2p4c4−6p5c3)ε2+(6p3c3−4p2c4−2c2p4−10p3c2−9c4p−2cp4+17c3p2−2p5c+13c3p−9p2c2−6c4)ε21+(6p5c2−2p4c3−6p6c−6p7c+6p6c2−2p5c3+2p7+2p8)ε1ε2,ϕ21:=(6c10+12c8p5+69c8p4−77c9p3+20c7p6+9c6p4−33c7p3+18c5p6−34c6p5+45c8p2−26c7p4+102c8p3−27c9p−80c9p2+27c7p5+6c5p7+8c4p8−12c5p8−55c6p6−12c6p7+8c4p9+22c10p2−24c9p4+8c10p3+20c10p)ε1+(4p10c4+20p9c6−10p10c5−4p5c9+2p11c4−2c9p4−2p6c9+10p7c8+20p6c8+10c8p5−20p9c5+2c4p9−40p7c7−20c7p8−10c5p8−20c7p6+40c6p8+20c6p7)ε2+(−12c9+12c3p9−47c8p4+10c9p3−86c6p4−19c7p3+102c5p6−220c6p5+60c8p2+159c7p4−40c8p3+61c5p5+2c4p6−16p7c4−18c9p+3c9p2+92c7p5+12c3p8+26c5p7−14c4p8+53c8p+35c6p3−76c7p2−79c6p6)ε21+(2p5c9−34c8p5+2c3p9+19c8p4−10c9p3+151c7p6−17c5p6+39c6p5−45c7p4+26c8p3−2c3p10+3p7c4−6c9p2+23c7p5+77c5p7−26c4p8+145c5p8−85c6p6−227c6p7−31c4p9−2c9p4−103c6p8+83p7c7+51p9c5−2p10c4−4p11c3−27p6c8)ε1ε2+(−4p7c8−2p6c8−30p10c4−60p11c4+40p9c5−2p8c8+12p11c3+24c7p8+12c7p9−60p9c6+12p13c3−30p10c6+40p11c5−30p12c4−4p13c2−2p14c2−2p12c2+24p12c3−30c6p8+80p10c5+12p7c7)ε22+(−30c8+69p3c5−16p4c4−212p5c4+58p6c3+331c5p4−232c6p4+79c7p3+117c5p6−65c6p5−21c8p2−3c7p4+5c8p3+379c5p5−187c4p6+4p7c4−94c3p8+44c2p8+44c2p9+91c7p−53c8p−263c6p3+163c7p2−106c6p2−38c3p7)ε31+(36c2p10−10c8p5−199c3p9−41c8p4+9c7p6+18c2p11−166c6p4+84c7p3+165c5p6−297c6p5−18c8p2+193c7p4−48c8p3−110c3p10+164c5p5−76c4p6+47p7c4+123c7p5−78c3p8+18c2p9−208c5p7+351c4p8−219c5p8−62c6p6+79c6p7+233c4p9+12c3p7)ε21ε2+(−2p14c+c2p10−4c3p9−8c7p6+21c2p11−2p12c−72c3p10−4p13c−4c5p7+6c4p8−102c5p8+c6p6+45c6p7+118c4p9+58p9c6−114p10c5+121p11c4+102c6p8−22p7c7−212p9c5+233p10c4−138p11c3+40p12c2−70p12c3+20p13c2−14c7p8+p7c8+p6c8)ε1ε22(−176p3c4+41p4c3+769p3c5+293p2c5−388p4c4+27p5c3+28p6c2−178p5c4−58p6c3+4p7c2+20cp8+20cp9+603c5p4−192c6p4+75c7p3+127c5p5+34c4p6+72c7−234c6p−24c2p8+210c7p−616c6p3+213c7p2−658c6p2−44c3p7)ε41+(−286p5c4+154p6c3−32p7c2+136c2p10−56cp10−198c3p9−24cp9+262c5p4−32cp11−330c6p4+70c7p3+438c5p6−284c6p5+68c7p4+636c5p5−580c4p6−210p7c4+22c7p5−154c3p8+30c2p8+198c2p9+64c5p7+84c4p8−122c6p3+24c7p2−76c6p6+198c3p7)ε31ε2+(4p12+102c2p10−cp10−158c3p9−c7p6+198c2p11−64p12c−33cp11−c5p6−313c3p10−32p13c+4p7c4+8p13−6c3p8+4c2p9−57c5p7+132c4p8−126c5p8+10c6p6+26c6p7+272c4p9+4p14+16c6p8−p7c7−70p9c5+144p10c4−161p11c3+100p12c2)ε21ε22.
|









 DownLoad:
DownLoad: