1. Introduction
The brain is an organ with high energy needs. While it represents only 2% of the body weight it grabs at least 20% of its total energy needs [9]. The consumed energy can come from many forms such as glutamate, glucose, oxygen and also lactate [3]. Energy is necessary to support neural activity. Gliomas are the most frequent primary brain tumors (more than 50% of brain cancer cases according to the ICM institute). Like other cancers, they lead to alterations of cells' energy management. In particular, lactate creation, consumption, import and export of a glioma cell seem to play a key role in the cancer development [5]-[11]. Today, neuroimaging techniques allow an indirect and noninvasive measure of cerebral activity. It also enables measurement of various metabolic concentrations such as lactate and measurement of important biological parameters such as the relative cerebral blood volume (allowing relative cerebral blood flow calculations). But because energy management in healthy and tumoral cells and glioma growth can be difficult to observe and explain experimentally, we propose to use mathematical modeling to help to describe and understand cells energy changes.
To the best of our knowledge, only a few mathematical models have been proposed to study lactate fluxes in the brain and the interconnections with energy, see [3] for example. We aim herein at analyzing a model first described in [2].
Our paper is organized as follows. We first present the mathematical model proposed to describe the mechanisms of interest. We then investigate its well-posedness and derive bounds on the solutions. Indeed, such an analysis is necessary to justify how a mathematical model is well-adapted to a biological problem. We also analyze the limit model and study its steady state. Bounds on the solutions are important as they are related with the viability domain of the cell. Furthermore, as mentioned in [8], a therapeutic perspective is to have the steady state outside the viability domain where cell necrosis occurs. Additionnally, we present numerical simulations with different values of the small parameter ε and compare them with experimental data. We finally discuss our results.
2. Mathematical modeling
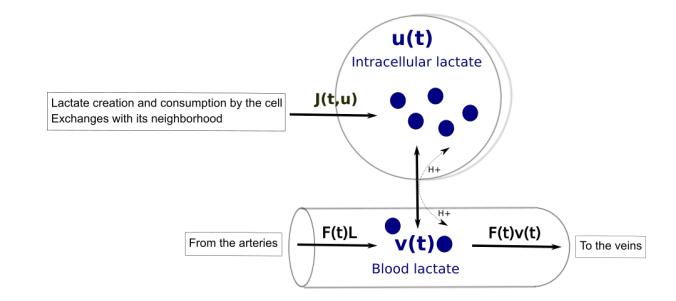
The present model is reduced in order to follow in a simpler way lacate kinetics between a cell and the capillary network in its neighborhood. It is built in vivo which means that we have to consider loss and input terms for both intracellular and capillary lactate concentrations. We denote by uε the intracellular lactate concentration and vε the capillary lactate concentration where ε stands for the volume separating the compartments. They are given in mM. One of the main parameters in the model is ε. Indeed to manage the blood flow, vessels dilate and modify their volume. We cannot model this phenomenon in a simple mathematical way. It is thus important to know how variations of their volume correlated with variations of ε impact the whole dynamics.
First, there is a lactate cotransport through the brain blood. It is taken into account by a simplified version of an equation for carrier-mediated symport. This nonlinear term depends on the maximum transport rate between the blood and the cell T>0 and the modified Michaelis-Menten positive constant for both intracellular and capillary lactate concentrations (k and k′ respectively).
Then a cell can equally produce and consume lactate, but also export surplus lactate to neighboring cells. We denote by J the balance sheet of the whole phenomenon. The function J is a nonnegative function depending on t and uε seen as a regulatory term. It is assumed to be bounded by a constant BJ and Lipschitz continuous.
Next there is a blood flow contribution to capillary lactate depending on both arterial and venous lactates. We denote by L>0 the arterial lactate concentration. We also define the blood flow F. The function F is a positive bounded continuous function (F1<F<F2) seen as a forcing term.
Finally, we have the following ODE's, for t∈R+:
|
u′ε(t)=J(t,uε(t))−T(uε(t)k+uε(t)−vε(t)k′+vε(t)),
|
(2.1)
|
|
εv′ε(t)=F(t)(L−vε(t))+T(uε(t)k+uε(t)−vε(t)k′+vε(t)).
|
(2.2)
|
The initial condition is given by :
|
(uε(0);vε(0))=(ˉu0;ˉv0)∈R+×R+.
|
The model is biologically described in [2], to which we refer the interested readers for a better understanding of this process.
3. The case ε>0
Well-posedness. Recall that an ODE system x′(t)=f(t,x(t)) on Rn, x=[x1,⋯,xn], f=[f1,⋯,fn], is called quasipositive if the condition :
is verified for all k=1,⋯,n. System (2.1)-(2.2) obviously is quasipositive. Hence solutions with nonnegative initial data (ˉu0;ˉv0) remain in (R+)2 for all positive times.
Since we have for nonnegative u1 and u2 :
|
|u1k+u1−u2k+u2|=k|u2−u1|(k+u1)(k+u2)⩽|u2−u1|k,
|
then we can rewrite (2.1)-(2.2), setting
to have ∀t∈R+ :
|
X′(t)=H(t,X(t)), X(0)=X0,
|
where H is globally Lipschitz continuous with respect to the second variable. We finally conclude, thanks to the Cauchy-Lipschitz theorem, that we have existence and uniqueness of the solution to the system ∀t∈R+.
Bounds on the solution. By means of (2.2), we have ∀t∈R+,
|
v′ε(t)⩽−F1vε(t)ε+F2Lε+Tε,
|
which implies, using Gronwall's lemma, that
|
vε(t)⩽exp(−F1tε)ˉv0+∫t0exp(−F1(t−s)ε)T+F2Lεds,
|
or equivalently,
|
vε(t)⩽exp(−F1tε)ˉv0+T+F2LF1(1−exp(−F1tε)).
|
One can see, using the above formula, that we have ∀t∈R+,
|
vε(t)⩽max(ˉv0,T+F2LF1):=Bv.
|
Theorem 3.1. We can exhibit a sufficient, but not necessary, condition to ensure a bound on uε. When it exists, let BJ∈R be such that :
and :
|
BJ<T(1−Bvk′+Bv)⇔BJ(k′+Bv)<Tk′.(C2.1)
|
In that case, we have, setting z=Bvk′+Bv+BJT and ∀t∈R+ :
|
uε(t)⩽max(kz1−z,ˉu0):=Bu.
|
(3.1)
|
Remark 1. Condition (C2.1) is related to the equation f(x)=0 with f(x)=BJ−Txk+x+TBvk′+Bv for which a positive solution exists if and only if BJ<T(1−Bvk′+Bv), i.e. (C2.1) holds. From a biological point of view, this condition means that at each time the lactate uptake by a cell (from itself or its neighborhood) cannot be larger than the lactate it can purge through the blood. Otherwise, the cell lactate concentration increase may not be limited.
Proof. Equation (2.1) gives ∀t∈R+ :
|
u′ε(t)⩽BJ+TBvBv+k′−Tuε(t)k+uε(t).
|
We set z=Bvk′+Bv+BJT and have, thanks to (C2.1) :
|
1−z=(k′+Bv)T(k′+Bv)T−Bv(T+BJ)+k′BJ(k′+Bv)T=k′T−BJ(k′+Bv)(k′+Bv)T>0.
|
Let t∈R+ be such that:
Then,
|
uε(t)(1−Bvk′+Bv−BJT)>k(Bvk′+Bv+BJT),
|
which yields
|
BJ+TBvBv+k′−Tuε(t)k+uε(t)<0,
|
hence
We finally deduce that
Remark 2. This condition on an upper bound on J is sufficient but not necessary. We can actually also consider functions J which do not satisfy (C2.1) but for which, when uε is large, we can exhibit a better upper bound satisfying (C2.1). It is thus sufficient to write that uε is bounded from above with a mild (C2.1) condition. For example, we can take J=Jtest such that, ∀(x,s)∈R+×R+ :
|
Jtest(s,x)=GJ⏟creation−LJ⏟ consumption+CJεJ+x⏟import,
|
for positive constants GJ, LJ, Cj and εJ such that GJ>LJ and GJ<LJ+Tk′k′+Bv. The second condition means that the lactate creation of the cell is smaller than its consumption and purge through the blood, so that the cell is able to manage lactate excess. Then, for x⩾CjTk′k′+Bv−GJ+LJ=Ntest, Jtest is bounded by Tk′k′+Bv and satisfies (C2.1). We conclude that, setting z=Bvk′+Bv+BJT, then u(t)⩽max(Ntest,kz1−z,ˉu0), ∀t∈R+. Even though we cannot assert that such a function J is biologically relevant, it is improbable to find relevant functions J leading to a fatal lactate increase in the cell. In fact, it is logical to expect functions decreasing in x, since, when a cell has more substrate than necessary for it to live on its own, it does not have to import or create more.
We have already proved that uε and vε are nonnegative functions. We can exhibit lower bounds by using the same method. Indeed, (2.2) gives, ∀t∈R+ :
|
v′ε(t)⩾−F2vε(t)ε+F1Lε−TεBvk′+Bv.
|
Then, if F1L−TBvk′+BvF2⩾0 and for t∈R+ such that
we have vε(t)′⩾0, so that, ∀t∈R+ :
|
vε(t)⩾min(ˉv0,F1L−TBvk′+BvF2).
|
If F1L−TBvk′+BvF2⩽0, we cannot find a positive lower bound on vε and we keep vε⩾0. Finally :
|
vε(t)⩾min(ˉv0,max(F1L−TBvk′+BvF2,0)):=Mv.
|
(3.2)
|
Similarly, ∀t∈R+ :
|
u′ε(t)⩾T(Mvk′+Mv−uεk+uε).
|
Then uε(t)⩽Mvkk′ leads to u′(t)⩾0. This shows that
|
uε(t)⩾min(ˉu0,Mvkk′):=Mu.
|
(3.3)
|
Remark 3. The upper bound Bv on vε can be derived even when the initial data ˉv0 and ˉu0 depend on ε and are bounded with respect to this parameter. To do so, we use the same method, adapting the final step so that
|
vε(t)⩽max(supˉv0ε>0,T+F2LF1).
|
The lower bounds Mv and Mu can be obtained in the same way for initial data depending on ε.
Stability of the equilibrium. For constant J and F, an equilibrium for (2.1)-(2.2) has been found in [4] :
|
ul:=k(JT+vlk′+vl)1−(JT+vlk′+vl),
|
(3.4)
|
It has also been proven that this unique stationary point is a node, hence a locally stable equilibrium. However, this equilibrium does not always exist. For existence, the parameters need to satisfy :
|
JT+LF+JF(k′+L)+J<1⇔J2+JF(L+k′)−TFk′<0.
|
(3.6)
|
Remark 4. We have already shown that vε(t)⩽L+TF=Bv, ∀t∈R+. We verify that the equilibrium vl is such that vl⩽Bv, which requires J⩽T. In fact, under (2.7), J>T implies:
|
J2+JF(L+k′)−TFk′>T2+TF(L+k′)−TFk′=T(T+FL)>0.
|
Therefore, the contraposition leads to:
|
J2+JF(L+k′)−TFk′⩽0 implies J⩽T.
|
We fix all the parameters but J. Then, we wish to rewrite this condition by giving it in terms of J. In this way, we have :
and there is an equilibrium only when J∈]Jb,Jh[, where :
|
Jb:=12(−F(L+k′)−√ΔJ),Jh:=12(−F(L+k′)+√ΔJ).
|
Knowing that J is nonnegative, there are only two possible cases :
1. 0<J<Jh with one steady-state which is a node,
2. J>Jh with no steady-state.
A therapeutic perspective is to have the steady state outside the viability domain [8]. Therefore playing on cell lactate intake could be worth exploring: a large J involves an unbounded cell lactate concentration which leads to an exit of the cell viability domain and, finally, the glioma cell death.
4. The case ε=0
We now study the limit system for ε=0, F(t):=F, J(t,x):=J constant, given ∀ t∈R+ by :
|
u′0(t)=J−T(u0(t)k+u0(t)−v0(t)k′+v0(t)),
|
(4.1)
|
|
0=F(L−v0(t))+T(u0(t)k+u0(t)−v0(t)k′+v0(t)),
|
(4.2)
|
together with the initial condition :
We first give some preliminary results and then establish bounds on the solutions and study the well-posedness of the system. We finally compare the original system (with ε>0) with this limit system (with ε=0).
Preliminaries. The function v0 given by (4.2) is defined as long as v0(t) belongs to I=]−∞,−k′[ ∪ ]−k′,+∞[:=I1 ∪ I2 and is continuous. Taking v0(0)=˜v0∈I2, then v0(t)∈I2 ∀ t∈R+. It is biologically relevant to take v0(0)=˜v0 as the positive root of (4.2) for u0(0)=ˉu0.
We define the function φc, for any constant c>0, by :
|
φc{]−c,+∞[→]−∞,T[s↦Tsc+s.
|
It is easy to see that φc is a monotone increasing function with φc(0)=0. We also define an inverse function of φc :
|
φ−1c{[0,T[→[0,+∞[z↦czT−z.
|
Furthermore, we introduce the function ψc defined by :
where ψc is a bijection from ]−c,+∞[ onto R. It can also be a bijection from R+ onto itself. Its derivative reads :
Employing (4.2), we have :
We rewrite (4.1)-(4.2) as :
|
v0(t)=ψ−1k′(FL+φk(u0(t))):=Ψ(u0(t)),
|
(4.3)
|
|
u′0(t)=J−T(u0(t)k+u0(t)−Ψ(u0(t))k′+Ψ(u0(t))):=G(t,u0(t)),
|
(4.4)
|
and set, for y∈[0,+∞[ :
A priori bounds on the solutions. Thanks to (4.4), we have :
|
G(t,0)=J+Tψ−1k′(FL)k′+ψ−1k′(FL)⩾J,
|
and the system is quasipositive : for an initial condition ˉu0⩾0, there holds u0(t)⩾0, ∀t∈R+. A fortiori, we have v0(t)=Ψ(u0(t))⩾0.
Using (4.2), we find an upper bound on v0, ∀t∈R+ :
We can also obtain an upper bound on u0 using Theorem 2.1. When it exists, we call it Bu,0.
We now rewrite (4.2) as :
|
v0(t)2+v0(t)(k′−L+TF−z)−k′(L+z)=0,
|
where z=Tu0(t)(k+u0(t))F⩽TF.
Noting that v0 is positive, ∀t∈R+, we have :
|
v0(t)=12(z+L−TF−k′+√(TF+k′−L−z)2+4k′(L+z)).
|
(4.6)
|
Well-posedness. Equation (4.4) gives :
|
u′0(t)=J−T(u0(t)k+u0(t)−Ψ(u0(t))k′+Ψ(u0(t))):=G(t,u0(t)).
|
Lemma 1. The function Ψ is Lipschitz continuous in u0, i.e. there exists KL>0 such that for all u1,u2∈[0,+∞],
Proof. Let u∈R+. We know that :
and :
|
|(Ψ−1)′(Ψ(u))|=|(φ−1k)′(ψk′(Ψ(u))−FL)ψk′(Ψ(u)))|=|Tk(T−ψk′(Ψ(u))+FL)2(F+Tk(k+Ψ(u))2)|=|Tk(Tk+F(k+Ψ(u))2)(T+φk(u))2(k+Ψ(u))2|.
|
It follows from the above that Ψ(u)=v, with :
|
0=F(L−v)+T(uk+u−vk′+v)⇒v⩽FL+T=Bv,0,v⩾0.
|
Therefore, Ψ(u)=v∈[0,Bv,0] and :
|
|Ψ′(u)|=1|(Ψ−1)′(Ψ(u))|=|(T+φk(u))2(k+Ψ(u))2Tk(Tk+F(k+Ψ(u))2)|⩽(T+Tuk+u)2(k+Ψ(u))2⩽4T2(k+Bv,0)2:=KL.
|
Consequently, G(t,u0) is Lipschitz continuous in u0. Therefore, thanks to the Cauchy-Lipschitz theorem, we have the existence and uniqueness of the solution to (4.4), ∀t∈R+. Finally we have existence and uniqueness for v0, recalling that Ψ is a bijection.
Stability of the equilibrium. As proved in [3], (4.1)-(4.2) can have at most one equilibrium given under the above parameters condition. The Jacobian of the system at this point gives the eigenvalue :
Therefore, ul is locally stable. Moreover, ∀t∈R+, v(t)=Ψ(u(t)), where Ψ is a bijective function. Setting zl=JT+vlk′+vl, we have :
|
Tulk+ul=Tkzl1−zl1−zlk=Tzl=TJT+Tvlk′+vl=F(JF+L−L)+Tvlk′+vl=F(vl−L)+Tvlk′+vl.
|
Thus :
|
Fvl+Tvlk′+vl=FL+Tulk+ul⇔vl=Ψ(ul),
|
and the stationnary point vl is locally stable.
Comparison between the original and the limit systems. We wish to bound the difference between (uε;vε) solution to (2.1)-(2.2) with F(t):=F and J(t,x):=J and (u0;v0) solution to (4.1)-(4.2), ∀t∈R+. To do so, we choose the same initial condition for uε and u0 :
We set u=uε−u0 and v=vε−v0. Using (2.1), (2.2), (4.1) and (4.2), we have, ∀ t∈R+ :
|
u′(t)=T(k′v(t)(vε(t)+k′)(v0(t)+k′)−ku(t)(uε(t)+k)(u0(t)+k)),
|
(4.7)
|
|
εv′(t)=−Fv(t)+T(ku(t)(uε(t)+k)(u0(t)+k)−k′v(t)(vε(t)+k′)(v0(t)+k′))−εv′0(t).
|
(4.8)
|
It follows from the above that, ∀ t∈R+ :
|
u′0(t)=J−T(u0(t)k+u0(t)−v0(t)k′+v0(t))∈[J−T,J+T],v0(t)⩽Bv,0,
|
Therefore, differentiating (4.2), we find :
|
Fv′0(t)=T(ku′0(t)(k+u0(t))2−k′v′0(t)(k′+v0(t))2)⇒v′0(t)(F+k′T(k′+v0(t))2)=Tku′0(t)(k+u0(t))2,
|
hence ∀ t∈R+ :
|
|v′0(t)|⩽kT(J+T)(F+k′T(k′+Bv,0)2):=γ.
|
Next, multiplying (4.7) by u(t) and (4.8) by v(t) gives, ∀ t∈R+ :
|
12ddt(u2(t))⩽Tk′|u(t)||v(t)|,
|
(4.9)
|
|
ε12ddt(v2(t))+Fv2(t)⩽Tk|u(t)||v(t)|+ε|v(t)|γ.
|
(4.10)
|
Noting that
|
Tk|u(t)||v(t)|+ε|v(t)|γ=(Tk|u(t)|2√F)(√F2|v(t)|)+(|v(t)|√F2)(2√Fεγ)⩽F2v2(t)+4T2Fk2u2(t)+4γ2Fε2
|
and
|
Tk′|u(t)||v(t)|=(Tk′|u(t)|√2√F)(√F√2|v(t)|)⩽F2v2(t)+2T2Fk′2u2(t),
|
summing (4.9) and (4.10) thus yields, ∀ t∈R+ :
|
ddt(u2(t)+εv2(t))⩽(8T2Fk2+4T2Fk′2)(u2(t)+εv2(t))+8γ2Fε2.
|
Noting finally that :
|
u2(0)=0 and u2(0)+εv2(0)=ε(ˉv0−Ψ(ˉu0))2,
|
Gronwall's lemma gives, ∀ t∈R+ :
|
u2(t)+εv2(t)⩽exp(T2tF(8k2+4k′2))(ε(ˉv0−Ψ(ˉu0))2+k2(J+T)2(F+k′T(k′+L+TF)2)22ε2(2k2+1k′2))−k2(J+T)2(F+k′T(k′+L+TF)2)22ε2(2k2+1k′2).
|
Remark 5. In the particular case \bar{v}_0 = \Psi(\bar{u}_0), we have \forall t \in [0, t_m] :
|
\begin{align*}
u^2(t)+\varepsilon v^2(t) &\leqslant (\exp \big(\frac{T^2t_m}{F}(\frac{8}{k^2}+\frac{4}{k'^2}) \big)-1)\frac{2\gamma^2\varepsilon^2}{T^2(\frac{2}{k^2}+\frac{1}{k'^2})}
\end{align*}
|
which yields that, on the finite time interval [0, t_m],
|
\begin{align} |{u(t)}|&\leqslant C_{t_m}\varepsilon, \;\;\;& |{v(t)}|&\leqslant C_{t_m}\sqrt{\varepsilon}. \end{align}
|
(4.11)
|
Remark 6. Setting v_{0}(0) = \tilde{v}_1 \in I_1 the negative root of (4.2) for u_0(t) = \bar{u}_0, we define a second solution to (4.1)-(4.2) for every t \in \mathbb{R}^+. We strongly think that we can study this degenerate system with similar mathematical tools, but this does not make sense from a biological point of view.
5. Numerical simulations and comparison with experimental data
In this section, we first present several numerical simulations with relevant values of our parameters. We also compare the numerical simulations with different values of J and \varepsilon. We finally give and study experimental data. These simulations have been done with the Matlab software.
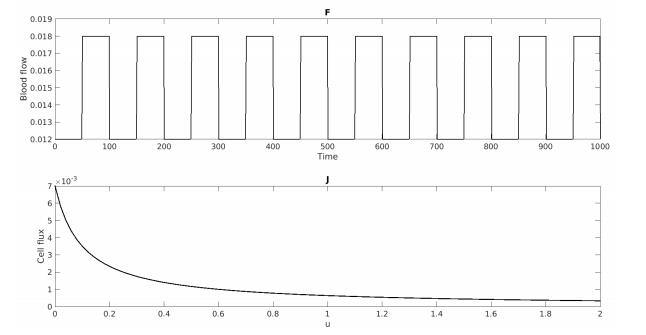
Numerical illustration with nonconstant J and F. We first consider the system given by (2.1)-(2.2). We expect that a cell manages its lactate concentration by means of its amount but not of the experiment's duration. Therefore we assume that it is biologically relevant to take a function J that does not depend of t. Besides, we expect that a cell imports more lactate when its lactate concentration is low. In other words J should be monotone decreasing in x. Under this hypothesis we choose :
|
J\left\{ \begin{align}
& {{\mathbb{R}}^{+}}\to {{\mathbb{R}}^{+}} \\
& \ \ \ x\mapsto {{G}_{J}}-{{L}_{j}}+\frac{Cj}{x+{{\varepsilon }_{j}}}, \\
\end{align} \right.
|
containing a creation term, a consumption term and an import term. This function J is a bounded and Lipschitz continuous function which enjoys the mild (C_{2.1}) condition. We also define, as given in [1] :
|
F\left\{ \begin{array}{l}
{\mathbb{R}^ + } \to {\mathbb{R}^ + }\\
t \mapsto \left\{ \begin{array}{l}
{F_0}(1 + {\alpha _f})\;\;\;{\rm{if}}\;\exists N \in\mathbb{N} /(N - 1){t_f} + {t_i}{\rm{ < }}t{\rm{ < }}N{t_f},\\
\;\;\;\;\;\;\;\;\;\;\;\;{F_0}\;\;{\rm{if}}\;\;{\rm{not}}
\end{array} \right.
\end{array} \right.
|
The parameters for these two functions are given in Table 1.
Table 1. Parameters for F and J.
| Parameter | Value | Unit |
| F_0 | 0.012 | s^{-1} |
| \alpha_f | 0.5 | 1 |
| t_i | 50 | s |
| t_f | 100 | s |
| C_J | 5.7*10^{-5} | mM^2.s^{-1} |
| \varepsilon_J | 0.001 | mM |
| G_J | 0.002 | mM.s^{-1} |
| L_J | 0.001 | mM.s^{-1} |
We also consider the parameters given in [2] and [8]. In that case, (\bar{u}_0;\bar{v}_0) = (1.15;1) and the parameters values are given in Table 2.
Table 2. Parameters values.
| Parameter | Value | Unit |
| T | 0.01 | mM.s^{-1} |
| k | 3.5 | mM |
| k' | 3.5 | mM |
| L | 0.3 | mM |
| \varepsilon | 0.001 | s^{-1} |
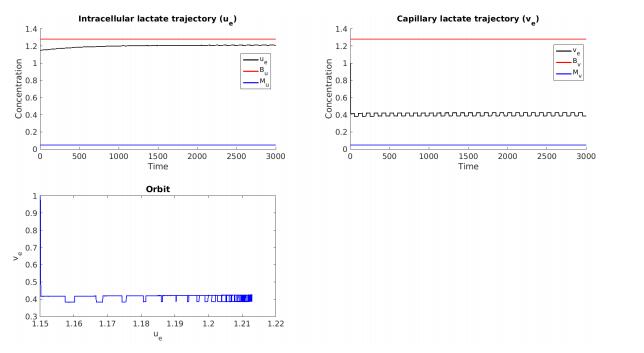
The solutions u_{\varepsilon} and v_{\varepsilon} remain nonnegative, as shown in Figure 3. Here, we have an upper bound on v_{\varepsilon} and J enjoys (C_{2.1}), so that u_{\varepsilon} has an upper bound too. Thus, the intracellular and capillary lactate concentrations match with the mathematical analysis. At the beginning, there is a dip for the capillary lactate concentration. The fluctuations on F are rapidly damped out as time grows.
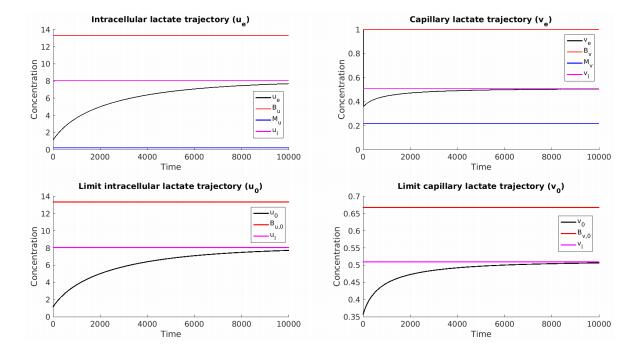
Numerical simulations with different values of J and \varepsilon. We now assume that J and F are constant in order to compare (2.1)-(2.2) with (4.1)-(4.2). The parameters values are given in Table 3, following [2] and [8], and the simulations are displayed in Figure 4.
Table 3. Parameters values.
| Parameter | Value | Unit |
| T | 0.01 | mM.s^{-1} |
| k | 3.5 | mM |
| k' | 3.5 | mM |
| L | 0.3 | mM |
| J | 0.0057 | mM.s^{-1} |
| F | 0.0272 | s^{-1} |
| \varepsilon | 0.1 | s^{-1} |
Note that, in that case, we have shown the existence of an upper bound on u and the presence of a locally stable steady state. The limit system has almost the same dynamics as the initial one. The notable difference is the presence of a hard initial dip for the dynamics of the capillary lactate with \varepsilon>0. This dip does not exist in the dynamics given by the limit system.
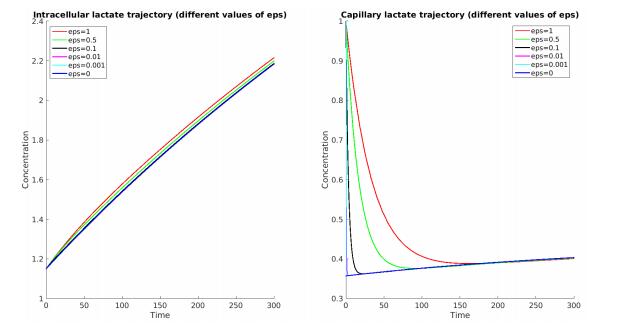
Using the parameters values given in Table 3, we perform numerical simulations with various values of \varepsilon. The results are given in Figure 5.
While the intracellular lactate trajectories seem not to differ a lot, the capillary lactate trajectories show different initial dynamics. The smaller \varepsilon is, the steeper the dip is up to \varepsilon = 0, where there is no dip.
Remark 7. An approach based on singular perturbation theory has been made on this model by Lahutte-Auboin et al. [7,8]. There, the authors give a geometrical explanation for the initial lactate dip and prove the existence of a periodic solution of the fast-slow system under a repetitive sequence of identical stimuli. In addition, our approach gives an estimate on the rate of convergence with respect to the parameters, which is usually not the case with singular perturbation theory.
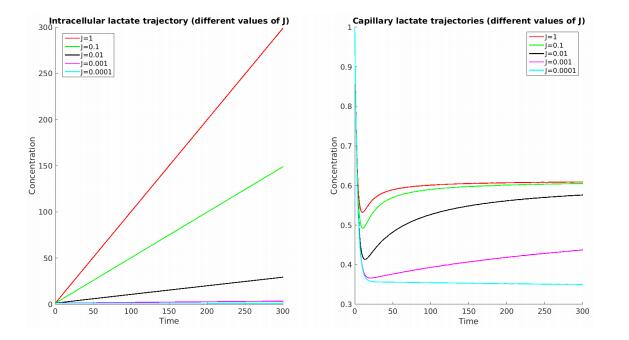
Using the parameters given in Table 3, we now test different values for J. The results are given in Figure 6.
There is a limit value of J, denoted by J_{lim}, such that there is an equilibrium only for J <J_{lim}. With these parameters values, we have :
|
J_{lim} = 0.00851 \text{ mM.s$^{-1}$}.
|
There are two types of dynamics : those with J <J_{lim} for which there is a steady state and those with J>J_{lim} for which the intracellular lactate trajectory explodes.
Experimental data. In this section we compare typical results obtained by using the model (with constant J and F) with in vivo data. This model is known to give good results when fitted to experimental data in small time variations (seconds) [2]. We want here to test its robustness on larger time variations (days).
For each five patients we have four lactate concentration measures (only three for patient 1) separated from each other by more than 80 days. Biological data were collected from patients exhibiting low grade gliomas (WHO grade 2) histologically proven, using monovoxel proton MR spectroscopy sequences performed on a same whole body 3 Tesla magnet (Verio, Siemens Ag) using specific 32 channels head coil. Raw data have been performed under the JMRUI software for appropriate quantification of metabolites, especially lactate concentration.
We are unable to distinguish between capillary lactate and intracellular lactate using imaging data. Therefore lactate concentration measures are the sum of the capillary lactate and intracellular lactate concentrations.
Because lactate concentrations variations are intrinsic and depend on lactate exchanges, we assume that it is relevant to adjust the initial values (\bar{u}_0 and \bar{v}_0) and the exchanges with neighboring cells (J) only. We give the other parameters values in Table 4.
Table 4. Parameters values.
| Parameter | Value | Unit |
| T | 0.1 | mM.d^{-1} |
| k | 3.5 | mM |
| k' | 3.5 | mM |
| L | 0.3 | mM |
| F | 0.0272 | d^{-1} |
| \varepsilon | 0.1 | d^{-1} |
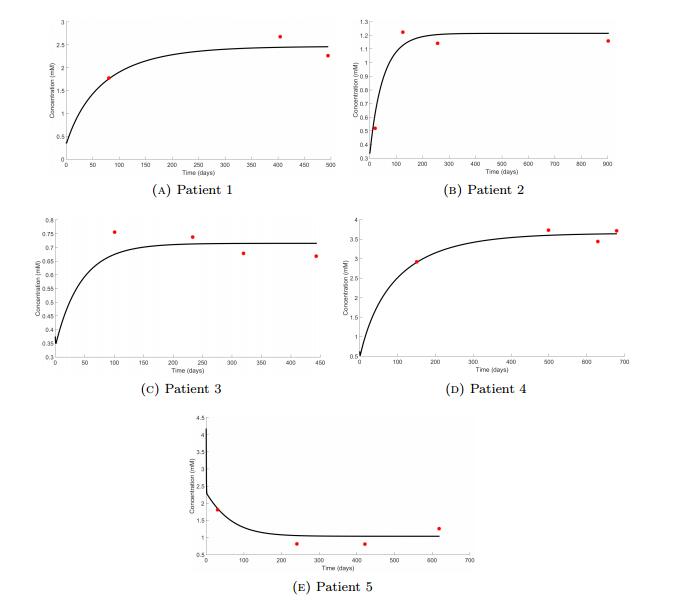
The results are given in Figure 7. Fitted values of \bar{u}_0, \bar{v}_0 and J for each patient are given in Table 5.
Table 5. Fitted values of \bar{u}_0, \bar{v}_0 and J.
| Patient | \bar{u}_0 (mM) | \bar{v}_0 (mM) | J (mM.d^{-1}) |
| 1 | 0.025 | 0.329 | 0.026 |
| 2 | 0.017 | 0.320 | 0.010 |
| 3 | 0.034 | 0.338 | 0.001 |
| 4 | 0.146 | 0.460 | 0.036 |
| 5 | 1.817 | 2.291 | 0.007 |
Our model (with constant J and F) is consistent with biological data. it is able to predict what happens after a lactate spike, when the brain sets up a huge regulation to turn back to an acceptable lactate concentration.
6. Discussion
In this study we analyze a model for lactate kinetics first given in [2]. This model is a first step in view of a better understanding of lactate dynamics in the brain. Lactate has a key role in neuroenergetics. Therefore studying its dynamics in the brain is necessary to better understand the energetic breakdown which is observed, for example in tumors. This model is known to give good results when fitted with experimental data [2], [8]. However, to the best of our knowledge, no mathematical analysis has been made to show the existence and uniqueness of the solution and conditions for bounds on the solution, but also comparisons between the original and limit systems.
In this paper, we study the original and limit systems and obtain existence, uniqueness and bounds on the solutions for the two systems. We also give a condition on J which ensures the existence of a locally stable steady state. Moreover, we give an upper estimate on the difference between the solutions of the two systems. We also give several numerical simulations, for different values of \varepsilon and J. Finally we confront the model with in vivo data.
When confronted with imaging data from NMR spectroscopy and perfusion, the model provides good results. Because there are large time variations, we cannot ensure that all the parameters remain constant in time. Therefore constant parameters are not good for explaining hard changes on the lactate concentration dynamics such as shifting from a decreasing concentration to an increasing one. Despite this, they can explain what happens after a lactate spike.
Differences in lactate dynamics suggest that there are several glioma profiles with different typical kinetics. This could indicate that non-agressive low grade gliomas show an increasing lactate concentration and then move to more agressive form (WHO Ⅱ+ to WHO Ⅲ+). At this stage the glioma will exhibit angiogenesis, modified proteins and altered transporters, which leads to fluctuating lactate kinetics [6]. This point should be considered as a critical one because of its therapeutical management consequences. Yet the patient should be referred to more agressive therapeutics such as radiotherapy or chemotherapy. Also the imaging control frequency should be restrained as well.
As already mentioned in [10], an initial dip exists in the brain lactate dynamics. This dip could be mathematically explained by the different initial values of the capillary lactate concentration between the original and limit systems. Therefore the dip can be biologically explained by compartment volume modifications.
It cannot be excluded that J stands only because the model is build to explain a local brain part dynamics. Then lactate exchanges between cells and the extracellular space have to be better studied to find a biologically relevant function J or other models with a different way to take these interactions into account. Despite this, the function J is described here with minimal assumptions. Therefore, this allows us to use this analysis with further choices for J or modified systems.
Indeed one perspective is to build more complex and suitable models for brain metabolism. Adding oxygen and glucose dynamics to this model can be the next step in view of a more accurate description of energy dynamics in the brain. It could also be interesting to build a model with different cell types (such as astrocyte and neuron), for a better understanding of the brain fuel substrate fluxes.
Acknowledgments
The authors wish to thank an anonymous referee for her/his careful reading of the paper and helpful comments.









 DownLoad:
DownLoad: