A novel approach to modelling the spatial spread of airborne diseases: an epidemic model with indirect transmission

1.   Introduction

Airborne diseases are well studied in epidemiology and public health, and still remain a serious public health concern today. Many airborne diseases are transmitted directly (host-host) and/or indirectly (host-source-host) through actions such as coughing, sneezing and sometimes vomiting ^[1]. For example, viral diseases (measles, influenza) and bacterial infections (tuberculosis) are transmitted via an airborne route. In addition, there has been evidence that airborne transmission plays a significant role in the spread of many opportunistic pathogens causing several acquired nosocomial (hospital) infections ^[2]. Some mathematical models have been used to study the transmission of airborne diseases using direct and indirect transmission pathways. Noakes et al. in ^[1] studied the transmission of airborne infections in enclosed spaces using an $SEIR$ model to show how changes to both physical environment and infection control could be a potential limitation in the spread of airborne infections. Issarow et al. in ^[3] developed a model to predict the risk of airborne infectious diseases such as tuberculosis in confined spaces using exhaled air. Several approaches including but not limited to the framework in ^[4] have been used to study the dynamics of an $SIS$ model with diffusion, ^[5] to assess the impact of heterogeneity of environment and advection on the persistence and infectious diseases eradication, and ^[6] to evaluate population migration using an $SIS$ epidemic model with diffusion. In addition, several PDE models such as ^[4,7] were also used to study the effect of diffusion. However, despite all these models and previous studies, it has largely been an open problem to evaluate the effect of diffusion on the spread of infections between one or two populations. To our knowledge none of these works has assessed the impact of diffusion using a coupled PDE-ODE $\mbox{SIR}$ model with an indirect transmission pathway.

In this paper, we consider an airborne disease as any disease caused by pathogen and transmitted through the air. Such diseases include, but are not limited to, chickenpox, influenza, measles, smallpox, and tuberculosis, among others. We focus on an indirect transmission pathways and derive fundamental quantities such as the basic reproduction number ($\mathcal{R}_0$) and the final size relation. To incorporate the limitation of the impact of diffusion among homogeneous and heterogeneous mixing population, we propose a coupled PDE-ODE model similar to the one used in ^[8] to model communication between dynamically active signaling compartments. Our model extends the models presented in ^[9] and ^[10] by incorporating diffusion of pathogens. This allows us to theoretically and numerically analyze how diffusion affects the spread of air-transmitted diseases, in which the human populations are confined to distinct spatially segretated regions. The novelty of our approach is that through a PDE-ODE system we model the spread of airborne diseases allowing for person-air-person transmission. Overall, our modeling framework provides an altenative way to describe the epidemics of airborne diseases.

The outline of this paper is as follows. In Section 2, a new coupled PDE-ODE model of epidemics is formulated, and this model is non-dimensionalized in Section 2.1. In Section 2.2, matched asymptotic expansion methods is used to reduce the dimensionless coupled PDE-ODE model into a nonlinear system of ODEs in the limit where the pathogens are diffusing very fast. In Section 3, we study the dimensionless coupled PDE-ODE model for a single population patch numerically and compare the result to that of the reduced system of ODEs. We also use the reduced system of ODEs to compute the basic reproduction number and final size relation. A similar study is performed for the case of two population patches in Section 4. In Section 5, we study the effect of patch location on the spread of infection for two population patches. The paper concludes with a brief discussion in Section 6.

2.   Model formulation

In this section, we formulate and analyze a coupled PDE-ODE model for studying the spread of airborne diseases. This model is non-dimensionalized and later reduced into a nonlinear ODE system in the limit where the diffusivity of pathogens is large.

We begin by representing human populations by localized patches with partially transmitting boundaries through which pathogens are shed into the atmosphere by infected individuals. These pathogens are assumed to diffuse and decay at a constant rate in the air (bulk region), while the spread of infection in each patch depends on the density of pathogens around the patch. Pathogens are not explicitly modeled in the patches; likewise the movement of individuals between patches is not accounted for. A susceptible individual becomes infected by coming in contact with pathogens (indirect transmission pathway). Let $\Omega \subset \mathbb{R}^2$ be our 2-D bounded domain of interest containing $m$ population patches represented by $\Omega_j$ for $j = 1, \ldots, m$, and separated by an $\mathcal{O}(1)$ distance from each other and from the boundary of the domain $\partial \Omega$. In the region $\Omega \setminus \cup_{j = 1}^{m}\, \Omega_j$ (bulk region) between the patches, the spatio-temporal density of pathogens $\mathcal{P}(\pmb{X}, T)$ satisfies the partial differential equation (PDE) given by

where $D_B > 0$ denotes the diffusion rate of pathogens in the bulk region, $\delta$ is the dimensional decay rate of pathogens, $r_j > 0$ is the dimensional shedding rate of pathogen by an infected individual in the $j^{\text{th}}$ patch, and $\partial_{n_{\pmb{X}}}$ is the outward normal derivative on the boundary of the domain $\Omega$. The dynamics of the diffusing pathogens is coupled to the population dynamics of the $j^{\text{th}}$ patch using the integro-differential system of equations given by

where $\mathcal{S}_j, \, \mathcal{I}_j$, and $\mathcal{R}_j$ denote the population of susceptible, infected, and removed individuals in the $j^{\text{th}}$ patch, respectively, with $\mathcal{N}_j(T) = \mathcal{S}_j(T) + \mathcal{I}_j(T) + \mathcal{R}_j(T)$. The parameters $\mu_j$ and $\alpha_j$ are the dimensional transmission and recovery rates, respectively, for individuals in the $j^{\text{th}}$ patch, and $p_c$ is a typical value for the density of pathogens. The integrals in (2.1c) and (2.1d) are over the boundary of the $j^{\text{th}}$ patch, and are used to account for all the pathogens around the patch. These terms show that the spread of infection within a patch depends on the density of pathogens around it. It is important to emphasize that our model does not account for pathogens in the patches. The Robin boundary condition $D_B \, \partial_{n_{\pmb{X}}} \, \mathcal{P} = -r_j \, \mathcal{I}_j$ on the boundary of the $j^{\text{th}}$ patch accounts for the amount of pathogen shed into the atmosphere by infected individuals in the patch. This condition shows that the amount of pathogens shed into the atmosphere from the $j^{\text{th}}$ patch depends on the population of infected individuals within the patch.

2.1.   Non-dimensionalization of the coupled PDE-ODE model

In this subsection, we non-dimensionalize the coupled PDE-ODE model (2.1). The dimensions of the variables and parameters of the model are given as follow:

where $[\gamma]$ represents the dimension of $\gamma$. Assuming that the patches are circular with common radius $R$, which is small relative to the length-scale $L$ of the 2-D domain $\Omega$, we introduce a small scaling parameter $\varepsilon = R/L \ll 1$ and the following dimensionless variables

In this way, $S_j, I_j$, and $R_j$ are the proportion of susceptible, infected, and removed individuals in the $j^{\text{th}}$ patch, respectively, and $P \equiv P(\pmb{x}, t)$ is the dimensionless density of the pathogens at position $\pmb{x}$ at time $t$. Upon substituting (2.3) into (2.1), we derive that the dimensionless spatio-temporal density of pathogens $P(\pmb{x}, t)$ satisfies

where $D \equiv D_B/(\delta \, L^2)$ is the effective diffusion rate of the pathogens. From the system of ODEs ((2.1c)–(2.1e)) for the population dynamics of the $j^{\text{th}}$ patch, we derive the dimensionless system

where $\Omega_{\varepsilon j} = \{ \pmb{x} : |\pmb{x}_j - \pmb{x}| < \varepsilon \}$ represents the $j^{\text{th}}$ patch of radius $\varepsilon \ll 1$ with center at $\pmb{x}_j$ and boundary $\partial \Omega_{\varepsilon j}$. It is important to remark that we have used the scaling $\text{d}S_{\pmb{X}} = L \, \text{d}s_{\pmb{x}}$ in the integrals on the boundary of the patches. Since the patches are relatively small compared to the length-scale of the domain, we assume that $\left(\mu_{j} /\delta \, L \right)$ and $r_j \left(\mathcal{N}_{j} L/ \delta \, p_c \right)$ are $\mathcal{O}(1/\varepsilon)$ in order to effectively capture the density of the pathogen shed into the atmosphere. Hence, we set

such that $\beta_j$ and $\sigma_j$ are $\mathcal{O}(1)$. This rescaling enables us to write the dimensionless transmission and shedding rates, $\beta_j$ and $\sigma_j$, respectively, as functions of the circumference of the $j^{\text{th}}$ patch. Substituting (2.6) into (2.4) and (2.5), we have that the dimensionless density of the pathogens $P(\pmb{x}, t)$ satisfies

which is coupled to the dimensionless $\mbox{SIR}$ dynamics of the $j^{\text{th}}$ patch through the integro-differential equations given by

where $\beta_j$, $\sigma_j$ and $\phi_j$ are the dimensionless transmission, shedding and recovery rates for the $j^{\text{th}}$ patch, respectively, and are given by

In the next subsection, we study the dimensionless coupled PDE-ODE model (2.7) in the limit $D = \mathcal{O}(\nu^{-1})$, where $\nu = -1/\log\varepsilon$ and $\varepsilon \ll 1$ using the method of matched asymptotic expansions, tailored to problems involving strong localized spatial perturbations ^[11,8].

2.2.   Asymptotic analysis of the dimensionless coupled PDE-ODE model

Here, the dimensionless coupled PDE-ODE model (2.7) is analyzed in the limit $D = \mathcal{O}(\nu^{-1})$, where $\nu \equiv -1/\log\varepsilon$ for $\varepsilon \ll 1$, using the method of matched asymptotic expansions. This analysis is used to reduce the coupled model into a nonlinear system of ODEs, which is then used to determine the basic reproduction number and final size relation of epidemics.

We begin our analysis by rescaling the diffusion rate of pathogens as

Substituting $D = D_0/\nu$ into (2.7a) and (2.7b), we obtain

Since the pathogens shed by infected individuals go into the air through the boundary of the patches, one would expect the density of pathogens around each patch to be high relative to the regions far away from the patches. As a result of this, we construct an inner region at an $\mathcal{O}(\varepsilon)$ neighborhood of each patch, and introduce the local variables $\pmb{y} = \varepsilon^{-1} (\pmb{x} - \pmb{x}_j)$ and $P(\pmb{x}) = Q_j(\varepsilon \pmb{y} + \pmb{x}_j)$, with $|\pmb{y}| = \rho$ for $j = 1, \ldots, m$. Upon writing (2.10a) and (2.10b) in terms of the inner variables, we obtain for $\varepsilon\ll 1$ the limiting inner problem

where $\Delta_{\rho}\equiv \partial_{\rho\rho}+\rho^{-1}\partial_\rho$ is the radially symmetric part of the Laplacian in 2-D. In this inner region, we expand $Q_j(\rho, t)$ as

Upon substituting this expansion into (2.11), and collecting terms in powers of $\nu$, we obtain the leading-order inner problem

Observe that any solution to the problem (2.13) must be a constant or a function of time, so that $Q_{0j} \equiv Q_{0j}(t)$. The next-order inner problem is given by

and its solution is readily calculated as

where $c_j$, for $j = 1, \ldots, m$, are constants to be determined. Substituting the solutions $Q_{0 j}$ and $Q_{1 j}$ into the inner expansion (2.12), and writing the resulting expression in terms of the outer variables, we obtain a two term asymptotic expansion of the inner solution

Next, from (2.4a) and (2.4b), we construct the outer problem for the density of pathogens, which is valid far away from the patches, as

where $\pmb{x}_1, \ldots, \pmb{x}_m$ are the centers of the patches. In this region, we expand the outer solution as

Substituting (2.18) into (2.17), and collecting terms in powers of $\nu$, we obtain the leading-order outer problem given by

Observe that this problem is similar to the leading-order inner problem (2.13) and any constant or function of time satisfies it. As a result of this, we chose the leading-order outer solution to be $P_0 \equiv P_0(t)$. The next order outer problem for $P_1$ is given by

Upon matching the inner solution (2.16) and the outer expansion (2.18), we obtain the following required singularity behavior for the outer solution as $\pmb{x} \longrightarrow \pmb{x}_j$:

In this way, we obtain the matching conditions

The first condition yields that $Q_{0j}(t) = P_0(t)+{\sigma_j I_j/(2\pi D_0)}$ for each $j = 1, \ldots, m$. The ODE for $P_0(t)$ is derived from a solvability condition on the problem for $P_1$. To do so, it is convenient to write the singularity behaviour of $P_1$ given in (2.22) as a delta function forcing for the PDE in (2.20). In this way, the outer problem for $P_1$ is equivalent to

Integrating (2.23) over the domain $\Omega$ and using the divergence theorem, we obtain an ODE for the leading-order density of pathogens $P_{0}(t)$ in the bulk region given by

where $|\Omega|$ denotes the area of the domain $\Omega$. This ODE is the solvability condition for the $\mathcal{O}(\nu)$ outer problem (2.23).

To solve the outer problem (2.23), we introduce the unique Neumann Green's function $G(\pmb{x}; \pmb{x}_j)$, which satisfies

where $\mathfrak{R}_j \equiv \mathfrak{R}(\pmb{x}_j)$ is the regular part of $G(\pmb{x}; \pmb{x}_j)$ at $\pmb{x} = \pmb{x}_j$. Without loss of generality, we impose $\int_{\Omega} P_1 \, \text{d}\pmb{x} = 0$, so that the spatial average of $P$ in the bulk region is $P_0$. Therefore, the solution to the outer problem (2.23) is written in terms of the Neumann Green's function $G(\pmb{x}; \pmb{x}_j)$ as

Upon substituting (2.26) into the outer expansion (2.18), we obtain a two-term asymptotic expansion of the outer solution in the bulk region as

Now, we expand (2.26) as $\pmb{x} \longrightarrow \pmb{x}_j$, and substitute the singularity behaviour of the Neumann Green's function $G(\pmb{x}, \pmb{x}_j)$ given in (2.25b) into the corresponding expansion to get

Matching the inner and outer solutions, we derive the constants $c_j$ in terms of the Neumann Green's function as

Thus, substituting (2.29) into (2.16), we derive a two-term asymptotic expansion of the inner solution $Q_j(\rho, t)$, valid in an $\mathcal{O}(\varepsilon)$ neighborhood of the $j^{\text{th}}$ patch, given by

Lastly, by substituting the inner solution (2.30) into the $\mbox{SIR}$ system in (2.7c), and evaluating the integrals over the boundary of the $j^{\text{th}}$ patch, we obtain a nonlinear system of ODEs for the leading-order density of pathogens in the bulk region coupled to the population dynamics of the $j^{\text{th}}$ patch. This system is given by

which is coupled to

Here, $\Psi_j = (\mathcal{G}\Phi)_j$ is the $j^{\text{th}}$ entry of the vector $\mathcal{G}\Phi$, with $\Phi = (\sigma_1 I_1, \ldots, \sigma_m I_m)^T$ and $\mathcal{G}$ is the Neumann Green's matrix whose entries are defined by

The function $G(\pmb{x}_j; \pmb{x}_i)$ is the Neumann Green's function satisfying (2.25) and $\mathfrak{R}_j \equiv \mathfrak{R}(\pmb{x}_j)$ is its regular part at the point $\pmb{x} = \pmb{x}_j$. In our analysis, $D_0 = \mathcal{O}(1)$ and $\nu = -1/\log\varepsilon \ll 1$. Therefore, as $\varepsilon$ tends to zero, $\nu$ also approaches zero, and so to leading-order we can neglect the $\mathcal{O}(\nu)$ terms in (2.31b). Replacing the leading-order density of pathogens $P_0$ with $p$ in (2.31), we derive the leading-order system of ODEs given by

Observe that we started with the dimensionless coupled PDE-ODE model (2.7) for studying the spread of airborne disease with indirect transmission, and arrived at the leading-order reduced system of ODEs (2.33) in the limit $D = \mathcal{O}(\nu^{-1})$. This system of ODEs also models indirect transmission of infections, even though, the terms with $\sigma_j \, I_j /(2 \pi D_0)$ in (2.33b) and (2.33c) make it look like infection is transmitted from person-to-person through direct interaction. This term does not model direct transmission; rather, it accounts for the pathogens shed by infected individuals in a patch. The density of these pathogens depend on the scaled-diffusion rate $D_0 > 0$. When the pathogens diffuse more slowly (smaller values of $D_0$), there is a significant contribution from this term. This contribution decreases as the pathogens diffuse faster (increasing $D_0$). Moreover, in the limit $D_0 \longrightarrow \infty$, this terms tends to zero and (2.33) reduces to the model for well-mixed regime given in Eq 5 of ^[10]. In Sections 3 and 4, the reduced system of ODEs (2.33) is used to compute the basic reproduction number and final size relation for one and two population patches, respectively. The effect of the spatial locations of the patches and their interaction, as characterized by the ${\mathcal O}(\nu)$ terms in (2.31), is studied in Section 5.

3.   One-patch model

In the previous section, the method of matched asymptotic expansions was used to reduce the dimensionless coupled PDE-ODE model (2.7) to the nonlinear system of ODEs (2.31), for the leading-order density of pathogens $p$ and $m$ population patches. In this section, we consider a single population patch located at the center of a unit disk, and use the dimensionless coupled model (2.7) together with the reduced system of ODEs (2.33) to study the effect of diffusion on the spread of infection in the population.

From (2.7), we derive that the density of pathogens $P(\pmb{x}, t)$ for this one-patch scenario satisfies

Here, $\Omega$ is a unit disk and $\Omega_0 \subset \Omega$ is a disk of radius $\varepsilon\ll 1$ representing the single population patch, which is located at the center of the unit disk. The density of pathogens $P$ is coupled to the $\mbox{SIR}$ dynamics of the population given by

From the reduced system of ODEs (2.33), we obtain an ODE model for a single population patch given by

To study the spread of infection in the population and the effect of diffusion on the epidemic caused by the pathogens, we solve the coupled PDE-ODE model (3.1) numerically using the commercial finite element package, FlexPDE ^[12] with several different diffusion rates of pathogens. The full PDE results are then compared with results from the reduced system of ODEs (3.2), which is valid for $D = {D_0/\nu}\gg 1$. In addition, the limiting ODE system (3.2) is analyzed using the method of Kermack-McKendrick similar to that done in ^[9,13]. To do so, the following simple lemma is needed:

Lemma 1. Let $f(t)$ be a nonnegative monotone nonincreasing continuously differentiable function such that as $t \rightarrow \infty$, $f(t) \rightarrow f_{\infty} \geq 0$, then $f^{\prime} \rightarrow 0$ as $t\to \infty$.

Upon summing the equations for $S$ and $I$ in (3.2), we obtain

This implies that $(S+I)$ decreases to a limit. It can be shown from Lemma 1 that its derivative approaches zero, so that we can conclude that $I_{ \infty} = \lim_{t\to\infty} I(t) = 0$. In addition, by integrating (3.3), we obtain

which implies that $\int_0^{\infty} I(t)dt < \infty$, where $S_{ \infty} = \lim_{t\to\infty} S(t)$ denotes the total susceptible populations remaining after the outbreak. This simple property is employed when computing the final size relation below.

3.1.   The basic reproduction number $\mathcal{R}_0$

The calculation of the basic reproduction number is done using the next generation matrix method, similar to that done in ^[14,15]. Note that there are two infectious classes $I$ and $p$ for this scenario. The Jacobian matrix $F$ for new infections evaluated at the disease free equilibrium state, DFE = $\left({S_0, 0, 0}\right)$ = $\left({N(0), 0, 0}\right)$ is given by

where the functions $\mathcal{F}_1 \equiv dI/dt$, $\mathcal{F}_2 \equiv dp/dt$ in (3.2) and $x_j = I, p$ for $j = 1, 2$. The Jacobian matrix $V$ for transfer of infections between compartments, evaluated at the disease free equilibrium point DFE is

Remark 1. In order to calculate the basic reproduction number for the model in (3.2), we use the next generation matrix method as in ^[14,15] known to be the dominant eigenvalues of $FV^{-1}$ (the spectral radius of the matrix $FV^{-1}$), and given as

Conveniently, we can decompose $\mathcal{R}_0$ as $\mathcal{R}_0 = \mathcal{R}_{\star} + \mathcal{R}_D$, where ${\mathcal{R}_{\star} = \frac{\beta N(0) \sigma }{\phi |\Omega|}}$ and ${\mathcal{R}_D = \frac{\beta N(0) \sigma }{2 \phi \pi D_0}}$.

The expression for $\mathcal{R}_0$ in (3.5) denotes the secondary infections contributed by indirect transmission ($\mathcal{R}_{\star}$) and diffusion ($\mathcal{R}_D$). The term $\mathcal{R}_{\star}$ represents the secondary infections caused indirectly through the pathogen since a single infective $I$ sheds a quantity $\sigma$ of the pathogen per unit time for a time period $1/ \phi$ and this pathogen infects $\beta N$ susceptibles. The second term $\mathcal{R}_D$ denotes the secondary infections caused by the pathogen diffusing in the bulk at the rate $D_0$ since a single infective $I$ sheds a quantity $\sigma$ of the pathogen per unit time for a time period $1/ \phi$ and this pathogen infects $\beta N$ susceptible individuals in the patch. As the diffusion rate of pathogens become asymptotically large, that is, $D_0 \to \infty$, we observe that $\mathcal{R}_D \to 0$. Therefore, in this limit, the basic reproduction number $\mathcal{R}_0$ in (3.5) can be written as

A more detailed discussion of Eq (3.6) will be given below while explaining our numerical simulations. The implication of the basic reproduction number $\mathcal{R}_0$ is summarized as follows in the readily proved result.

Theorem 1. For system (3.2), the infection dies out whenever $\mathcal{R}_0 < 1$. In contrast, an epidemic occurs whenever $\mathcal{R}_0 > 1$.

3.2.   The final size relation

The final size relation gives an estimate of the total number of infections and the epidemic size for the period of the epidemic in terms of the parameters in the model, as similar to that done in ^[16,17]. In other words, the final size relation is used to estimate the total number of disease deaths and cases from the parameters of the model. Following the approach in ^{[9,17,18,19,20,21,22,23]}, we integrate the equation for $S$ in (3.2) to get

Similarly, integrating the equation for $p(t)$ in (3.2) gives

Next, we need to show that

If the integral in the numerator of (3.9) is bounded, this relation is immediate. If the numerator is unbounded, L'Hopital's rule yields that $\lim_{t\to\infty} \int_0^t e^{- (t-s)}I(s) \, ds = \lim_{t\to\infty}I(t) = I(\infty)$, which vanishes as established above following Eq (3.3). Therefore, (3.8) yields that

By integrating (3.8), interchanging the order of integration, and then using (3.4), we get

which implies that $\int_0^{\infty}\, p(t)\, \text{d}t < \infty$. Upon substituting (3.10) into (3.7), we obtain

so that, by using (3.4), we obtain the final size relation

This implies that $S_{\infty} > 0$. In a situation where the outbreak begins with no contact with pathogen, so that $p_0 = 0$, the final size relation becomes

Equation (3.11) is referred to as the final size relation, and this gives a relationship between the basic reproduction number and the epidemic size. Note that the total number of infected population over the period of the epidemic is $N(0) - S_{\infty}$ and can also be described in terms of the attack rate $\Bigl(1- S_{\infty}/N(0) \Bigr)$ as in ^[17].

3.3.   Numerical simulation for one-patch model

Next, we present some numerical simulations of the coupled PDE-ODE model (3.1) and the reduced system of ODEs (3.2) for the case of a single population patch located at the center of a unit disk. The coupled model (3.1) is solved numerically using the commercial finite element package FlexPDE ^[12], while the reduced ODE system (3.2) is solved using the numerical ODE solver ODE45 in MATLAB ^[24]. For these models, simulations are done with different diffusion rates of pathogens in order to understand the effect of diffusion on the dynamics of the infected population. The parameters used for these simulations are shown in Table 1.

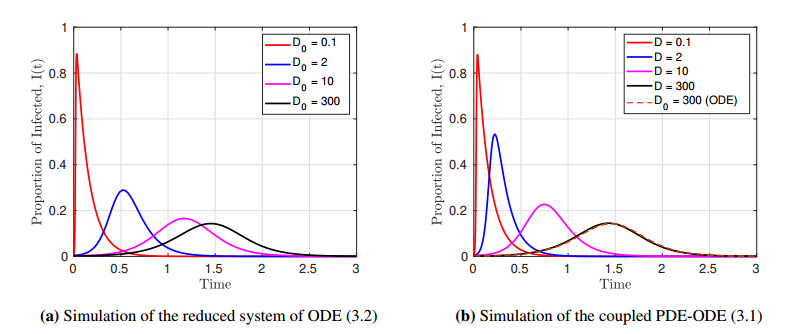
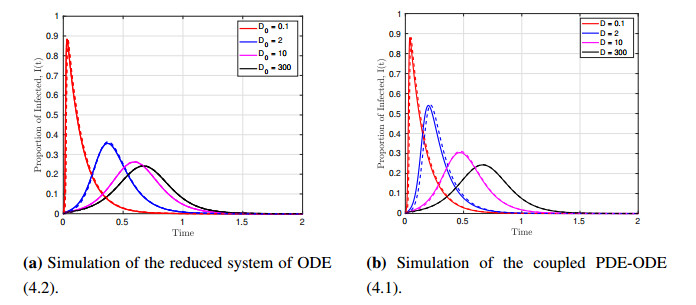
Figure 1 shows the proportion of infected over time when an epidemic begins with one infective in a total population of $250$ individuals, with susceptible, infected and recovered population given as $S(0) = 249/250$, $I(0) = 1/250$ and $R(0) = 0$, respectively. The initial density of pathogen used for both the coupled model and the reduced system of ODEs is $p(0) = P(0) = 0$, denoting that the outbreak begins with no pathogen in the air, and that the only source of pathogen into the system is the ones shed by infected individuals. We observe from this figure that the proportion of infected individuals decreases with increases in the diffusion rate of pathogen. This shows that when pathogens diffuse slowly, they cluster around the population as they are being shed. As a result, since human populations are confined in a region, this in turn leads to more infections.

However, when pathogens diffuse faster (diffusion rate increases), they diffuse away from the population as they are being shed, which in turn, reduces the density of pathogens around the patch. This effect lowers the population of infected individuals. Comparing Figure 1a and 1b, we notice that the proportion of infectives estimated by the two models are similar when $D$ and $D_0$ are small and when they are asymptotically large. Since $D = D_0/\nu$, a small value of $D_0$ implies that $D$ is also small. As a result of this, the two models would behave similar in this limit even though the reduced system of ODEs (3.2) is only valid in the limit $D = \mathcal{O}(\nu^{-1})$, where $\nu = -\log\varepsilon$, with $\varepsilon \ll 1$. The difference between the two models becomes more apparent with an increase in the diffusion rate, as the number of infectives estimated by the system of ODEs is less as compared to that of the PDE-ODE model. This is because the system of ODEs is valid in the limit $D = \mathcal{O}(\nu^{-1})$, and the spread of infection decreases as $D$ increases. Lastly, as the diffusion rates become asymptotically large, the solutions of the two models essentially coincide. This is because when $D \to \infty$, the problem becomes well-mixed, where the density of pathogen is homogeneous in space, and the coupled PDE-ODE model can be reduced to a system of ODEs. Similarly, if we take the limit of the reduced system of ODEs (3.2) as $D_0 \longrightarrow \infty$, we have the model studied in ^[9]. This suggests that the model in ^[9] can be interpreted as the well-mixed limit of the coupled PDE-ODE model (3.1).

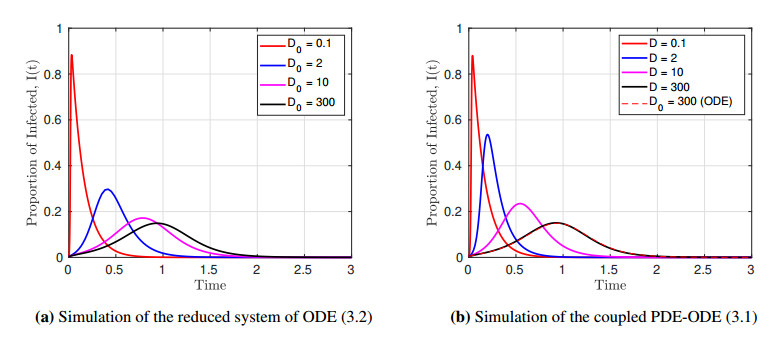
The results in Figure 2 are similar to those in Figure 1 except that the initial conditions of the pathogens is taken as $P(0) = p(0) = 1$. This models the case where there is pathogen in the air at the beginning of the outbreak. The other initial conditions are the same as those used in Figure 1. These results show how the presence of pathogens in the atmosphere at the beginning of the outbreak would affect the transmission of infection. The epidemic takes off earlier when there are pathogens in the air at the beginning of the outbreak (Figure 2) compared to when there are no pathogens at the beginning (Figure 1). When the diffusion rate is small, the model with (Figure 2) and without (Figure 1) pathogen at the beginning of the outbreak have similar estimates. This is because the pathogens are barely moving when the diffusion rate is small, and as a result, it does not make much difference whether they are present or not. As the diffusion rate of pathogens increases, there seems to be significant differences in the two solutions, since, the epidemic takes off earlier in Figure 2 as compared to Figure 1. Therefore, the presence of pathogens in the air around the population patch increases the spread of infection in the population, as expected intuitively.

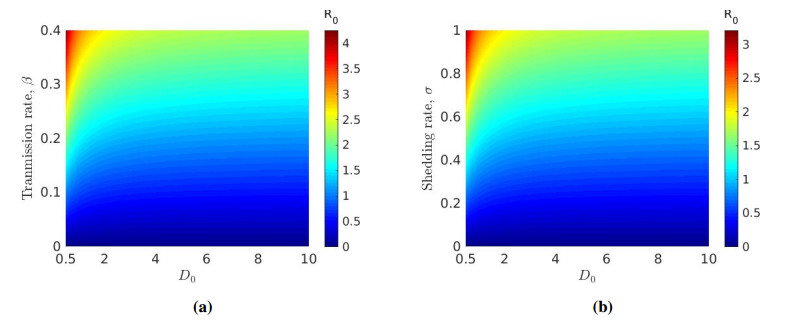
The surface plots in Figure 3 show the basic reproduction number $\mathcal{R}_0$ in (3.4) for the one-patch model (3.2) in terms of the diffusion rate of pathogens $D_0$ and the dimensionless transmission and shedding rates, $\beta$ and $\sigma$, respectively. These results show the effect of $D_0$ on the basic reproduction number, $\mathcal{R}_0$. We observe from both results in this figure that $\mathcal{R}_0$ increases as the transmission and shedding rates increase, and decreases as $D_0$ increases for a fixed value of the transmission and shedding rates. These results agree with the simulations in Figures 1 and 2, where the spread of infections decreases as the diffusion rate of pathogen increases. In Figure 3a, the largest $\mathcal{R}_0$ is obtained when $D_0$ is small and the transmission rate $\beta$ is large. This is reasonable because when pathogens diffuse slowly, it would take longer for them to diffuse away from the population, and as a result, they continue to cause infections in the population, and consequently this leads to a large basic reproduction number. Similarly, in Figure 3b, the largest $\mathcal{R}_0$ is obtained when the shedding rate of pathogen is large and $D_0$ is small, because when infected individuals shed pathogens at a high rate and the pathogens do not diffuse away from the population, they lead to more infections. When the transmission and shedding rates are low, irrespective of the diffusion rate of pathogens, the reproduction number will be less than one and the epidemic will die out.

In the next section, we perform a similar analysis for a scenario with two spatially segregated populaton patches.

4.   Two-patch model

In the previous section, we studied the effect of the diffusion rate of pathogens on the spread of infection in a single population. In this section, we consider a scenario with two population patches, and use the dimensionless coupled PDE-ODE model (2.7) and the reduced system of ODEs (2.33) with $m = 2$ to study the dynamics of infection in these populations. The patches are centered at $\pmb{x}_1 = (0.5, 0)$ and $\pmb{x}_2 = (-0.5, 0)$ in a unit disk.

For this two-patch scenario, the density of pathogen $P$ for the coupled PDE-ODE model satisfies

where $\Omega_1$ and $\Omega_2$ are the two population patches centered at $\pmb{x}_1 = (0.5, 0)$ and $\pmb{x}_2 = (-0.5, 0)$. This density of pathogen is coupled to the population dynamics of the two patches through the following ODE system:

The coupled PDE-ODE model (4.1) is solved numerically using FlexPDE ^[12] with different diffusion rates for the pathogens. The solutions are used to study the effect of diffusion on the spread of the infection caused by the pathogens within the population. From (2.33), we construct the reduced system of ODEs for the case of two patches as

with initial conditions

in a population of constant total size $N = N_1 + N_2$, where $N_1 = S_1+ I_1+ R_1 = S_{10}+I_{10}$ and $N_2 = S_2+ I_2+ R_2 = S_{20}+I_{20}.$ This system of ODEs is similar to the model studied in ^[10], in which indirect transmission of diseases with no diffusion was studied. For our model we will compute the basic reproduction number and the final size relation. The analytical approach for the Kermack-McKendrick epidemic model, as employed in ^[9] and ^[13], will be used in the analysis.

Summing the equations for $S_1$ and $I_1$, and then those for $S_2$ and $I_2$ in (4.2d), we obtain

Here, we see that $(S_1+I_1)$ and $(S_2+I_2)$ decrease to a limit, and we can show from Lemma 1 that their derivatives approach zero. Therefore, we conclude that $I_{1 \infty} = \lim_{t\to\infty} I_1(t) = 0$ and $I_{2 \infty} = \lim_{t\to\infty} I_2(t) = 0$. Next, by integrating (4.3) we get $\phi_1 \int_0^{\infty} I_1(t)dt = S_1(0) + I_1(0) - S_{1 \infty} = N_1(0) - S_{1 \infty}$, so that

which implies that $\int_0^{\infty} I_1(t)dt < \infty$. Similarly, we integrate (4.4), to obtain

Here, $S_{1 \infty} = \lim_{t\to\infty} S_1(t)$ and $S_{2 \infty} = \lim_{t\to\infty} S_2(t)$ denote the total susceptible population remaining after the outbreak in patch 1 and patch 2, respectively.

4.1.   Reproduction number $\mathcal{R}_0$

Following a similar approach to that used in Section 3.1 for the one-patch model, we construct our system of infected classes as

Using the next generation matrix approach in ^[14,15], the basic reproduction number is calculated as follows. We first introduce the three infectious classes $I_1, I_2, p$, and the Jacobian matrix of $\mathcal{F}_i = (\mathcal{F}_1, \mathcal{F}_2, \mathcal{F}_3)$, evaluated at the disease free equilibrium point DFE = $\left({S_{10}, 0, 0, S_{20}, 0, 0}\right)$ = $\left({N_1(0), 0, 0, N_2(0), 0, 0, 0}\right)$ given by

where $x_j = I_1, I_2, p$ for $j = 1, 2, 3$ and $i = 1, 2, 3$.

The Jacobian matrix of $\mathcal{V}_i = (\mathcal{V}_1, \mathcal{V}_2, \mathcal{V}_3)$, evaluated at the disease free equilibrium point DFE is

Remark 2. To calculate the basic reproduction number for the $2$-patch model in (4.7), we use the method of next generation matrix in ^[14,15] given as the dominant eigenvalues of $FV^{-1}$ (the spectral radius of the matrix $FV^{-1}$). A simple calculation yields that

where we have defined $\clubsuit$ and $\spadesuit$ by

In the well-mixed limit $D_0\gg 1$, similar to that studied for the one patch model in Section 3, the reproduction number $\mathcal{R}_0$ in (4.8) reduces to ${\mathcal{R}_0^{\infty} = \lim_{D_0 \rightarrow \infty} \mathcal{R}_0} = {\clubsuit/(\phi_1 \phi_2 |\Omega|)}$, which implies that

We observe that $\mathcal{R}_0^{\infty}$ can also be decomposed as $\mathcal{R}_0^{\infty} = \beta_1 \mathcal{R}_1 + \beta_2 \mathcal{R}_2$, where $\mathcal{R}_1 = \frac{ N_1(0) \sigma_1 }{\phi_1 |\Omega|}$ and $\mathcal{R}_2 = \frac{N_2(0) \sigma_2 }{\phi_2 |\Omega|}$.

We can interpret the large $D_0$ limiting value $\mathcal{R}_0^{\infty}$ of the reproduction number as follows. The formula for $\mathcal{R}_0^{\infty}$ in (4.9) denotes the contribution of the first and second patch. The term $\beta_1 \mathcal{R}_1$ represents the secondary infections caused indirectly through the pathogen since a single infective $I_1$ sheds a quantity $\sigma_1$ of the pathogen per unit time for a time period $1/ \phi_1$, and this pathogen infects $\beta_1 N_1$ susceptibles. The second term $\beta_2 \mathcal{R}_2$ denotes the secondary infections caused indirectly through the pathogen since a single infective $I_2$ sheds a quantity $\sigma_2$ of the pathogen per unit time for a time period $1/ \phi_2$, and this pathogen infects $\beta_2 N_2$ susceptibles.

A detailed qualitative explanation of $\mathcal{R}_0$ (for the case where $D_0 = {\mathcal O}(1)$) and $\mathcal{R}_0^{\infty}$ (for the well-mixed limit $D_0\to \infty$), will be given below when discussing our results from numerical simulations. The following easily-proved Theorem summarizes the implications of the reproduction number $\mathcal{R}_0^{\infty}$.

Theorem 2. For the well-mixed limit $D_0\to\infty$ for the system (4.2), the infection dies out whenever $\mathcal{R}_0^{\infty} < 1$, while an epidemic occurs whenever $\mathcal{R}_0^{\infty} > 1$.

4.2.   The final size relation

Following the same approach as in subsection 3.2, we integrate the equations for $S_1$ and $S_2$ in (4.2d) to get

and

Similarly, integrating the equation for $p$ in (4.2a), we obtain

Next, we need to show that

If the integral in the numerators of the two expressions in (4.13) are bounded, the result is immediate. Alternatively, if these integrals are unbounded, then by L'Hopital's rule these two limits reduce to $\lim_{t\to\infty}I_1(t)$ and $\lim_{t\to\infty}I_2(t) = 0$, which vanish since $I_1(\infty) = I_2(\infty) = 0$ as was shown above following (4.4) (see also ^[9]). As a result, (4.12) yields that

Next, upon integrating (4.12), interchanging the order of integration, and then using (4.5) and (4.6), we get

which implies that $\int_0^{\infty}\, p(t) \, \text{d}t < \infty$.

We then substitute (4.14) into (4.10) and (4.11) to get

and

which yields the final size relation

and

These expressions can be written by using $\mathcal{R}_1 = \frac{ N_1(0) \sigma_1 }{\phi_1 |\Omega|}$ and $\mathcal{R}_2 = \frac{N_2(0) \sigma_2 }{\phi_2 |\Omega|}$, as

and

where we used (4.3), which implies $S_{1 \infty} > 0$ and $S_{2 \infty} > 0$. In the case where the outbreak begins with no contact with pathogen, so that $p_0 = 0$, the final size relation for patch $1$ and $2$ can be written as

In the well-mixed limit of asymptotically large diffusion in which $D_0 \rightarrow \infty$, the final size relation (4.15) becomes

This result can be written in matrix form as

Note that the total number of infected populations in patch $1$ and $2$ over the period of the epidemic are respectively $N_1 - S_{1\infty}$ and $N_2 (0) - S_{2\infty}$, and can be described in terms of the attack rate $\Bigl(1- S_{1\infty}/N_1 (0) \Bigr)$ and $\Bigl(1- S_{2\infty}/N_2 (0) \Bigr)$ as in ^[17].

4.3.   Numerical simulation for two-patch model

Here, we present numerical simulations of the dimensional coupled PDE-ODE model (4.1) and the reduced system of ODEs (4.2) for the case of two population patches. Our goal is to study the spread of infection between and within these populations. For the coupled PDE-ODE model, our patches are centered at $\pmb{x}_1 = (0.5, 0)$ and $\pmb{x}_2 = (-0.5, 0)$ for patches 1 and 2, respectively.

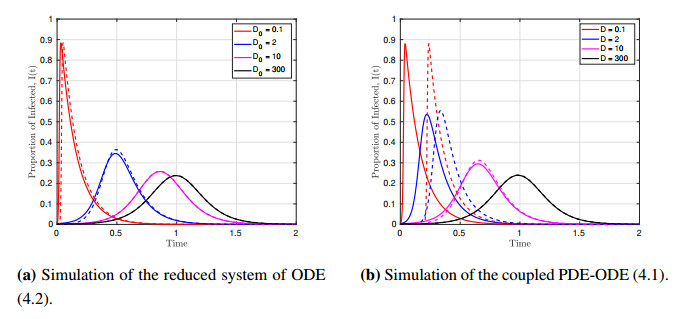
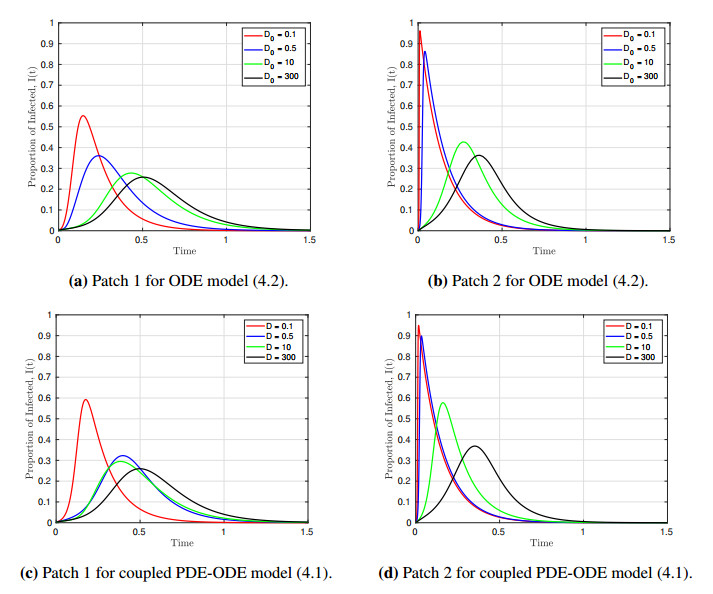
The results in Figure 4 show the proportion of infected individuals for the two patches in the case where the outbreak begins with no pathogen in the air ($P(0) = p(0) = 0$), only one infected individual in patch 1 ($I_1(0) = 1/250$), and no infections in patch 2 ($I_2(0) = 0$). The population patches are assumed to be identical with parameters as given in Table 2.

Figures 4a and 4b show the result obtained from the reduced system of ODEs (4.2) and the coupled PDE-ODE model (4.1) respectively, for different diffusion rates.

Similar to the results for a single population patch, epidemic take-off is delayed, and epidemic size decreases as the diffusion rate increases. When the diffusion rate is small, there is a delay in the epidemic take-off time in patch 2, and this delay decreases as the diffusion rate increases. The observed delays are due to the time it takes the pathogens shed in patch 1 to diffuse to patch 2, since there are no pathogens in the air, and no infections in patch 2 at the beginning of the epidemic. As the diffusion rate increases, the time it takes the pathogens to diffuse from patch 1 to patch 2 decreases, thereby decreasing the delay in epidemic take-off in the second population. In the limit where the diffusion rate becomes asymptotically large, the epidemics starts at approximately the same time in the two population patches for both models. Observe that the delay in epidemic take-off time in the second population is more obvious in the results from the coupled PDE-ODE model in Figure 4b than those of the reduced system of ODEs in Figure 4a. This is because the system of ODEs is valid in the limit where the diffusion rate of the pathogens $D = \mathcal{O}(\nu^{-1})$, where $\nu = -1/\log\varepsilon$ with $\varepsilon \ll 1$. In this limit, the pathogens are already diffusing fast enough to reduce the time it takes them to travel from patch 1 to patch 2. This reduces the delay in take-off time of the epidemic in patch 2. As $D, D_0 \to \infty$, the system becomes well-mixed, and the predictions for the two model agree ($D = D_0 = 300$).

When there is a pathogen at the beginning of the outbreak ($P(0) = p(0) = 1$), with only one infected individual in patch 1 $(I_1(0) = 1/250)$ and no infectives in patch 2 $(I_2(0) = 0)$, the epidemics start in the two patches at approximately the same time for both models, irrespective of the diffusion rate of pathogens. This occurs simply because there are pathogens in the air close to the second patch at time $t = 0$, which cause infections to spread into the population immediately. These results are shown in Figure 5. The parameters and initial conditions used are the same as those used for the results in Figure 4 except for the initial density of pathogen $p(0) = P(0) = 1$.

For a scenario with two distinct patches where the transmission of infections and shedding of pathogens are done at different rates (a more realistic scenario), the reduced system of ODEs (4.2) predicts slightly different results from the coupled PDE-ODE model (4.1). These results are shown in Figure 6. The dimensional transmission and shedding rates in patch 1 are $\mu_1 = 0.3$ and $r_1 = 0.1$, respectively, while in patch 2 are $\mu_2 = 1.2$ and $r_2 = 1$ respectively (their dimensionless equivalents can be computed with (2.8)). Figures 6a and 6b show the proportion of infected individuals in patches 1 and 2, respectively, obtained using the reduced system of ODEs (4.2) with different values of $D_0$, while Figures 6c and 6d show similar results for the coupled PDE-ODE model (4.1). We observe from these figures that even though there are no infections in patch 2 when the outbreak begins, there are still more infections occurring in patch 2 than in patch 1. This occurs simply because patch 2 has a higher shedding and transmission rate. Higher shedding and transmission rates imply more pathogens are shed and transmitted faster in patch 2 than in patch 1.

When the diffusion rate is small or asymptotically large, the estimates from the two models agree qualitatively. However, this is not the case for intermediate diffusion rates. For these rates, the coupled PDE-ODE model shows no significant difference in the epidemic take-off times in patch 1 for different values of $D$, although, the maximum number of proportion of infectives at a given time is different (see the results for $D = 0.5$ and $D = 10$ in Figure 6c). This is due to the fact that the transmission and shedding of pathogens are done at higher rates in patch 2 relative to patch 1. The pathogens shed in patch 2 diffuse to patch 1, thereby causing the epidemic in patch 1 to occur earlier than one would have expected if the populations were identical or the patches are farther away from each other. As the distance between the two patches increases, the effect of the pathogens shed in patch 2 on the population in patch 1 decreases. This qualitative effect is discussed in detail in Section 5, where we study the effect of patch locations on the spread of infections.

5.   Effect of patch location on the spread of infection

So far, we have studied the effect of the diffusion rate of pathogens on the spread of infections within and between populations, and we have not considered the effect of the location of the patches. In this section, we study the effect of patch location on the dynamics of infections by analyzing the two-term (extended model) reduced system of ODEs, as given in (2.31), which involves the Neumann Green's matrix characterizing the spatial interaction between patches. This extended ODE system is then used to compute the basic reproduction number and the final size relation, which now depends on the locations of the patches. In addition, we present some numerical simulations for two patches equally-placed on a ring of radius $r$, with $0 < r < 1$, concentric within a unit disk, and we study how the proportion of infected individuals changes as the distance between the patch locations is varied.

5.1.   Effect of patch location on the basic reproduction number

In our analysis below we assume that our domain is a unit disk and that the patches are equally-placed on a ring of radius $r$, with $0 < r < 1$, which is concentric within the disk. Here, we derive an expression for the basic reproduction number using (2.31), while following the analytical framework used in Section 4. From the reduced system of ODEs (2.31), we construct our infectious classes for $m$ patches as

Here, $\Psi_j = (\mathcal{G}\Phi)_j$ is the $j^{\text{th}}$ entry of the vector $\mathcal{G}\Phi$, with $\Phi = (\sigma_1 I_1, \ldots\sigma_m I_m)^T$, and $\mathcal{G}$ is the Neumann Green's matrix defined in (2.32). The resulting ODE system is an $(m+1)$ dimensional system of equations for the infected classes $I_1, \ldots, I_m$, and the pathogens $p$. At the disease free equilibrium state, we construct the Jacobian matrix $F$ for the new infections as

where the functions $\mathcal{F}_j \equiv I'_j$ for $j = 1, \ldots, m$, and $\mathcal{F}_{m+1} \equiv p'$ are as given in (5.1), $x_j \equiv I_j$ for $j = 1, \ldots, m$, and $x_{m+1} \equiv p$. Similarly, from (5.1), we construct the Jacobian matrix $V$ for the transfer of infections between compartments, evaluated at the disease free equilibrium state as

For the case of two population patches, the Jacobian matrices (5.2) and (5.3) reduce to

Upon calculating the inverse of the matrix $V$, and then multiplying by the matrix $F$ from the left, we construct our next generational matrix as

The dominant eigenvalue of the next generational matrix is our desired basic reproduction number. From a computation of the eigenvalues of (5.4), we derive a two term asymptotic expansion for the basic reproduction number given by

where $\mathcal{R}^0 \equiv \mathcal{R}_0$ is the leading-order basic reproduction number given in (4.8), and the $\mathcal{O}(\nu)$ term $\mathcal{R}^{1}$ is given by

where the quantities $\blacktriangle$, $\blacktriangledown$ and $\blacksquare$, are defined by

Here, the variables $\spadesuit$ and $\clubsuit$ are as defined in (4.8), and $\Psi_j$ for $j = 1, 2$ are as defined in (2.31). Since there are only two patches, we can use (2.31) to construct $\Psi_1$ and $\Psi_2$ explicitly as

where $\mathfrak{R}_j \equiv \mathfrak{R}(\pmb{x}_j)$ is the regular part of the Neumann Green's function $G(\pmb{x}_i; \pmb{x}_j)$ at $\pmb{x} = \pmb{x}_j$. Upon differentiating $\Psi_1$ and $\Psi_2$, with respect to $I_1$ and $I_2$, we obtain

To evaluate these derivatives explicitly, as are needed in (5.7), we must determine the Neumann Green's function $G(\pmb{x}_i; \pmb{x}_j)$ and its regular part $\mathfrak{R}_j$, as obtained by solving (2.25) in the unit disk. These results are well-known (see Eq (4.3) of ^[26]), and we have

Since the patches are symmetrically located on a ring of radius $r$, with $0 < r < 1$, we can take their centers as $\pmb{x}_1 = (r, 0)$ and $\pmb{x}_2 = (-r, 0)$ for patch 1 and 2, respectively, so that, $|\pmb{x}_1| = |\pmb{x}_2| = r$. Substituting $\pmb{x}_1$ and $\pmb{x}_2$ into (5.9), we conclude that

Upon substituting (5.10) into (5.8), and then using (5.8) in (5.7), we obtain

where $\clubsuit$ and $\spadesuit$ are given by

Therefore, the $\mathcal{O}(\nu)$ term in the basic reproduction number $(5.5)$ can be computed by substituting (5.12) and (5.11) into (5.6). By using the leading-order basic reproduction number $\mathcal{R}^0$, as given in (4.8), together with $\mathcal{R}^1$ in (5.5), we arrive at an explicit two term asymptotic expansion for the basic reproduction $\mathcal{R}$, which depends on the locations of the patches. Notice that the dependence on the location comes into $\mathcal{R}$ through only the $\mathcal{O}(\nu)$ term, which involves the Green's function.

5.2.   Effect of patch location on the final size relation

In the previous subsection, for a special two-patch configuration where the patches are equally spaced on a ring concentric within the disk, we derived a two-term asymptotic formula for the basic reproduction number. In this subsection, we study the effect of patch location on the final size of the epidemic.

From (2.31), a two term asymptotic expansion of the reduced system of ODEs for the case of two population patches is given by

where $p(t)$ is the leading-order density of pathogens in the air, $S_j, I_j, R_j$ are the susceptible, infected, and removed, respectively, in the $j^{\text{th}}$ patch for $j = 1, 2$. Here, $\Psi_1 = \sigma_1 I_1 \, \mathfrak{R}_1 + \sigma_2 I_2\, G(\pmb{x}_1;\pmb{x}_2)$ and $\Psi_2 = \sigma_1 I_1 \, G(\pmb{x}_2;\pmb{x}_1) + \sigma_2 I_2 \mathfrak{R}_2$, and $G(\pmb{x}_1;\pmb{x}_2) = G(\pmb{x}_1;\pmb{x}_1)$ is the Neumann Green's function and $\mathfrak{R}_1 = \mathfrak{R}_2$ is it regular part at the points $\pmb{x}_1$ and $\pmb{x}_2$. This system of ODEs depends on the locations of the patches, and the dependence arises from the $\mathcal{O}(\nu)$ terms.

Following the same approach as in subsection (4.2), we integrate the $S_1$ and $S_2$ equations in (5.13d) to obtain

and

The integrals of $\Psi_1$ and $\Psi_2$ are given by

and

Similarly, the integral of (5.13a) is given by (4.14). Upon substituting (4.14) into (5.14) and (5.15), and assuming that the outbreak begins with no epidemic ($p_0 = 0$), the final size relation is given by

and

which can be written as

where $\mathcal{R}_1 = \sigma_1 N_1(0)/(\phi_1 |\Omega|)$ and $\mathcal{R}_2 = \sigma_2 N_2(0)/(\phi_2 |\Omega|)$. Upon writing (5.16) in matrix form, we have

where the matrices $\mathbb{A}$, $\mathbb{B}$, and $\mathbb{C}$ are defined by

In this way, we have derived a two term expansion of the final size relation that depends on the location of the patches. Similar to the basic reproduction number (5.5), the dependence on the location comes into this result at the $\mathcal{O}(\nu)$ term through the Green's function and its regular part. The explanation of the final size follows from subsecion 4.2.

5.3.   Numerical simulation for two patch model with effect of patch location

Next, we present some surface plots of the basic reproduction number $\mathcal{R}$ in (5.5) and its $\mathcal{O}(\nu)$ correction term $\mathcal{R}^1$, defined in (5.6), with respect to the location of the patches. Our plots are for different values of the dimensionless transmission rates $\beta_1$ and $\beta_2$ for patches 1 and 2, respectively. In addition, we show some numerical simulations of the reduced system of ODEs (5.13) and the coupled PDE-ODE model (4.1) for two patches. The system of ODEs is solved using the MATLAB numerical ODE solver ODE45 ^[24], while the PDE is solved using FlexPDE ^[12]. Our goal is to numerically study the effect of patch location on the spread of infections and the final epidemic size.

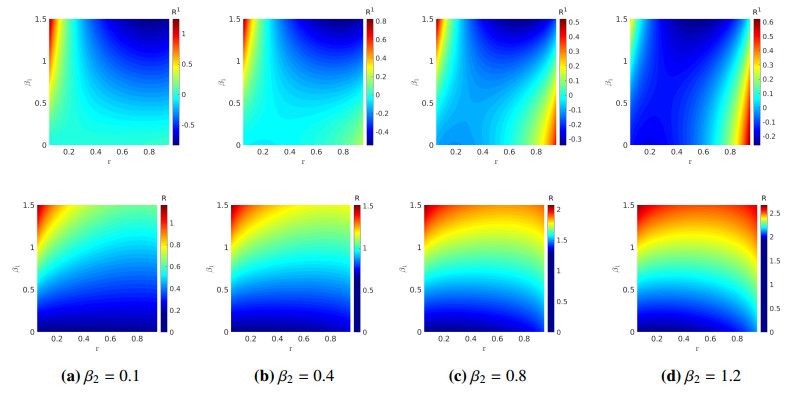
Figure 7 shows the surface plot of the $\mathcal{O}(\nu)$ term of the basic reproduction number, $\mathcal{R}^1$ (5.6) (first row), and the basic reproduction number $\mathcal{R}$ (5.5) (second row) with respect to the location of the patches and the transmission rates of the two patches. For each of the results in this figure, the transmission rate $\beta_1$ (vertical axis) is plotted against the distance of the patches from the center of the unit disk (horizontal axis). A fixed value of $\beta_2$ is used for each column, with the value increasing from left to right ($\beta_2 = 0.1, \, 0.4, \, 0.8, \, 1.2$). Since $r$ is the distance from the center of each patch to the center of the unit disk, for each value of $r$, the distance between the centers of the two patches is $2r$. The $\mathcal{O}(\nu)$ term $\mathcal{R}^1$ shows how the leading-order basic reproduction number $\mathcal{R}^0 \equiv \mathcal{R}_0$ (4.9) is perturbed by the locations of the patches. Note that we have omitted the surface plots of $\mathcal{R}^0$ from this figure because it is independent on the location of the patches.

The first row of Figure 7 shows that $\mathcal{R}^1$ may increase or decrease $\mathcal{R}$ depending on the location of the patches and the transmission rates. When the transmission rate in patch 2 is $\beta_2 = 0.1$ (Figures 7e), we observe that $\mathcal{R}^1$ has high values when $r$ is small and $\beta_1$ is high. In this case, where the two patches are close to each other, the infection is transmitted at a high rate in patch 1. As the distance between the two patches increases ($r$ increases), the value of $\mathcal{R}^1$ decreases for all values of $\beta_1$ and it attains negative values for some values of $\beta_1$. For this range, $\mathcal{R}^1$ decreases the leading-order basic reproduction number $\mathcal{R}^0$. These figures show that for all values of $\beta_2$, there are more infections ($\mathcal{R}$ and $\mathcal{R}^1$ high) when the two patches are closer to each other ($r$ small), as compared to when they are farther apart ($r$ large). In addition, as the transmission rate $\beta_2$ increases (from left to right in Figure 7), the surface plot of $\mathcal{R}^1$ in the $r, \beta_1$ parameter space changes, and the effect of the reflecting boundary of the unit disk becomes apparent. For each value of $\beta_2$, the corresponding effect of $\mathcal{R}^1$ on the overall basic reproduction number $\mathcal{R}$ is shown in the second row of Figure 7. When $\beta_2 = 1.2$, we observe that higher values of $\mathcal{R}^1$ occur for smaller values of $r$ (when the two patches are close to each other) and for values of $r$ close to 1 (when the patches are close to the boundary of the disk). When the patches become closer to the reflecting boundary of the unit disk, they see a reflection of themselves through the boundary. This leads to a feedback-effect whereby the reflection of pathogen from the boundary returns back to the patches. This boundary effect, as evident in the surface plot of the basic reproduction number $\mathcal{R}$ in Figure 7h, leads to a higher level of infections.

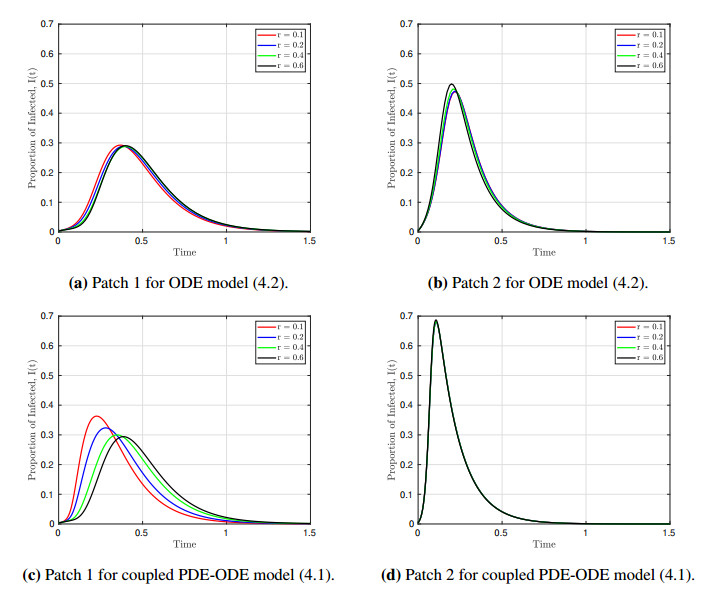
The numerical simulations of the coupled PDE-ODE model (4.1) and the reduced system of ODEs (5.13) for two patches in the unit disk are shown in Figure 8. For a fixed diffusion rate of pathogens, these two models are solved numerically for different locations of the patches. The location of each patch is given in terms of the parameter $r$, which measures the distance between the center of the patch and the center of the unit disk. Both patches have the same parameters except for the transmission rates of infection, and the shedding rate of pathogens (see Table 2). In addition, both patches have one infective at the beginning of the outbreak, and the density of pathogens in the air is fixed at $p(0) = P(0) = 1$.

Figures 8a and 8b show the results obtained from the reduced system of ODEs (5.13) for patches 1 and 2, respectively, while Figures 8c and 8d show similar results for the coupled PDE-ODE model (4.1). For each radius $r$, the epidemic in patch 2 (right column of Figure 8) is more than that in patch 1 for both models, owing to the fact that patch 2 has higher transmission and shedding rates than patch 1 (see Table 2 for the parameters). As the radius of the ring (on which the patches are located) increases, that is, as the distance between the centers of the two patches increases, the size of the epidemic in patch 1 decreases, while there seems to be no significant difference in the size of the epidemic in patch 2. Since the shedding rate of pathogens in patch 2 is larger than that of patch 1, the density of pathogens in the air around patch 2 at each point in time is higher than those around patch 1. As a result, when the two patches are closer to each other, the pathogens shed from patch 2 can easily diffuse to patch 1, and lead to more infections in the population. This effect depends on the proximity of the two patches, and it weakens as the patches move farther away from each other. This explains why infections in patch 1 decrease as the distance in the two patches increases. This observation is more prominent in the results obtained from the PDE-ODE model than in the the system of ODEs. This is due to the fact that the ODE system is valid in the limit $D \gg \mathcal{O}(\nu^{-1})$, with $\nu = -1/\log\varepsilon$ and $\varepsilon \ll 1$. In this regime where the pathogens are diffusing fast, spatial gradients in the pathogen density are smoothed out, and as a result the proximity of patch 2 to patch 1 seems to have no significant effect on the epidemic in patch 2.

However, as both patches move closer to the boundary of the domain, they receive signals of pathogens that is of equal strength as their shedding rates from the boundary (since the boundary is reflecting). In this way, there is an increasing infection in both patches as they move closer to the boundary. This observation is noticeable in the patch 2 dynamics shown in Figures (8(b)) and (8(d)), due to its high shedding rate. Specifically, it is more apparent in Figure 8b than in Figure 8d because the system of ODEs used to obtain Figure 8b are only valid in the limit where the pathogens are diffusing very fast. We observe from these simulations that the estimates and predictions of both models qualitatively agree, even though the ODE model is only valid in the limit $D \gg \mathcal{O}(\nu^{-1})$.

6.   Discussions

We developed and analyzed a coupled PDE-ODE model for studying the spread of airborne diseases with indirect transmission. This model improves previously developed epidemic models for indirect transmission ^[9,10] by incorporating the movement of pathogens, which is modeled with linear diffusion. Human populations are modeled as circular patches, that are small relative to the length scale of the domain, where each patch has an $\mbox{SIR}$ dynamics for the population of susceptible, infected, and removed, respectively. The diffusion of pathogens is restricted to the region outside the patches, while human movement is not considered. In our model, a susceptible individual becomes infected only by coming in contact with the pathogens (indirect transmission), and the spread of infection within a patch depends on the density of pathogens around the patch. In the limit $D = \mathcal{O}(\nu^{-1})$ with $\nu = -1/\log\varepsilon$ and $\varepsilon \ll 1$ (when the pathogens are diffusing fast), the coupled PDE-ODE model is reduced to a nonlinear system of ODEs. This system of ODEs was then analyzed and used to compute the basic reproduction number and the final size relation. Furthermore, the full PDE-ODE model and the reduced system of ODEs were solved numerically, and their results agreed qualitatively.

The numerical simulations for both the coupled model and the reduced system of ODEs predicted a decrease in the epidemic as the diffusion rate of pathogens increases, and the two models agreed in the limit $D, D_0 \to \infty$. When pathogens are diffusing slowly, it takes longer for them to diffuse away from the patches after shedding, and as a result, more infections occur. On the other hand, when the diffusion rate is high, pathogens diffuse away from the patches immediately after shedding, which thereby reduces infections. When there are two patches, where infection starts from only one of the patches with the other patch being disease free, and with no pathogens in the air, our models predict a delay in epidemic take-off time in the second population when pathogens diffuse slowly. This occurs as a result of the time required for pathogens to diffuse from the infected patch to the other patch. As the diffusion rate increases, the delay in epidemic take-off time decreases. The results of our model seem consistent with other previous results ^{[4,27,28,29,30,31]}, where human populations were modeled with a PDE approach. Furthermore, we studied the effect of patch location on the spread of infection. Our models predicted more infections when the two patches are close to each other, and less infections when when the patches are farther apart.

In our model, we have assumed that the amount of pathogens in a patch can be accounted for by knowing the density of pathogens around the patch, and individuals do not move between patches. This assumption may not be true for all real-life scenarios as the amount of pathogens in a patch may be different from the density around the patch. Also, people may move between cities and towns. Our model can be extended to incorporate human mobility between patches. This can be achieved by allowing both humans and pathogens to diffuse in the bulk region, or by using the approach of meta population dynamics, in which individuals are transferred from one patch to another without modeling their movement explicitly, or by using Lagrangian method to keep track of individuals' place of residence at different time. In addition to this, we can allow for infections to be transmitted in the bulk region when a susceptible individual comes in contact with the diffusing pathogens. This would lead to a reaction-diffusion type model in the bulk region. Furthermore, similar models (indirect and/or direct transmission model) can be developed for other diseases such as malaria, where the mosquitoes diffuse in the bulk region and human populations are modeled with patches. Mosquito reservoirs can also be incorporated into the modeling framework, where an ODE system is used to describe the mosquito life cycle from egg to adult.

Notwithstanding all of these limitations and assumptions, we believe that our proposed novel approach to modeling airborne diseases, where the movement of pathogens is explicitly modeled with linear diffusion, will significantly contribute to knowledge and may be seen as a better approach. Our analysis and full numerical computations suggest that disease dynamics can be adequately studied with our more tractable reduced ODE model, instead of the more intricate PDE-ODE coupled model. The presence of the parameter $D_0$ in the reduced ODE system makes it easier to study the effect of diffusion on disease transmission. Furthermore, the extended system of ODEs, which includes weak spatial effects through a Green's interaction matrix, allowed us to study the effect of patch location on disease dynamics. Including this spatial information encoded in the Green's matrix allows for characterizing the effect of the spatial distribution of patches on disease transmission between spatially segregated populations.

Acknowledgments

Fred Brauer and Michael Ward gratefully acknowledge the support from the NSERC Discovery Grant program under OGPIN 203901-99 and 81541, respectively.

Conflict of interest

All authors declare no conflict of interest in this paper.