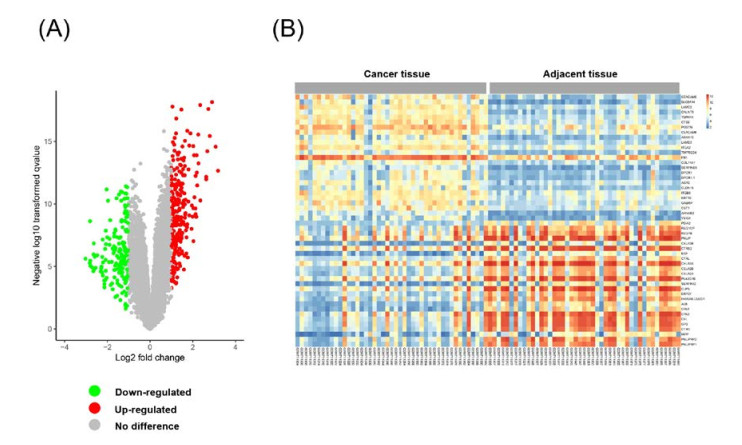
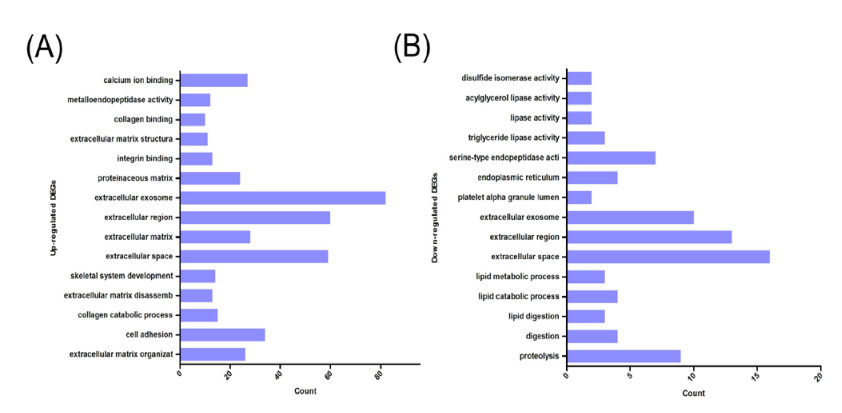
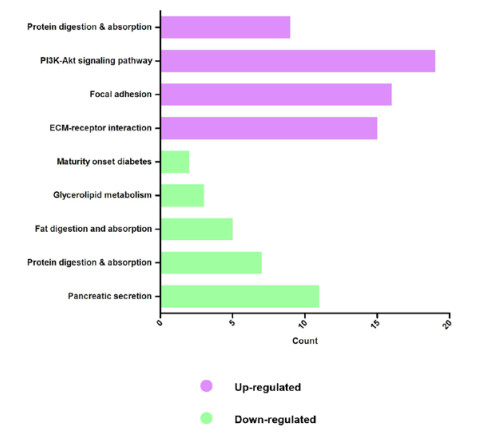
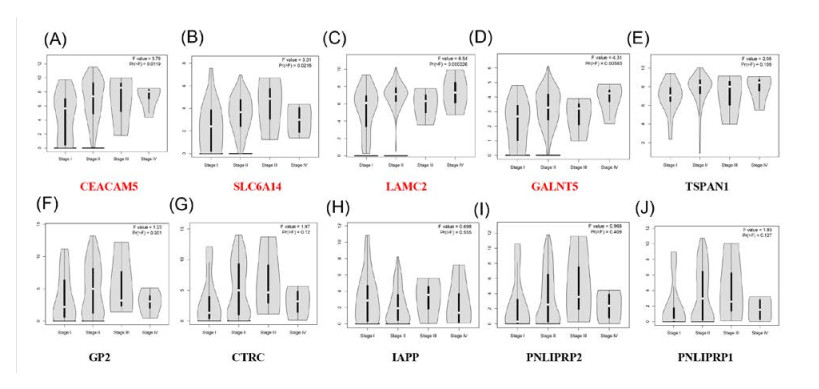
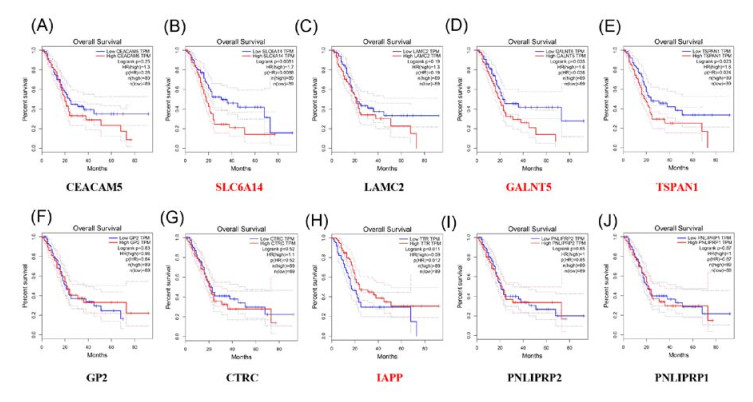
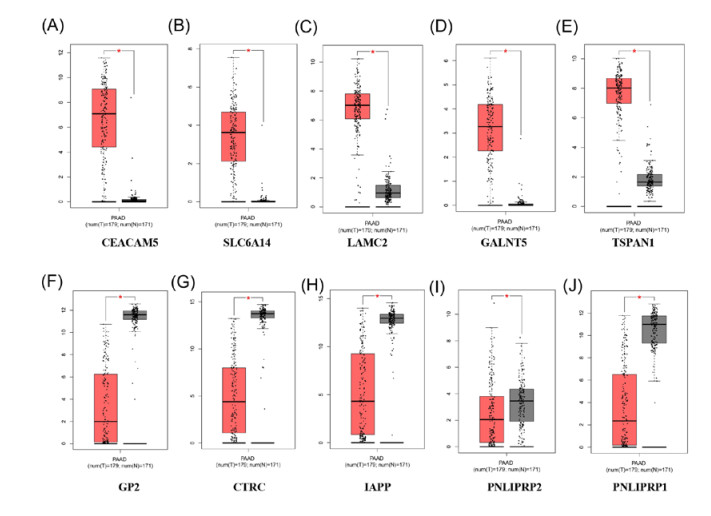
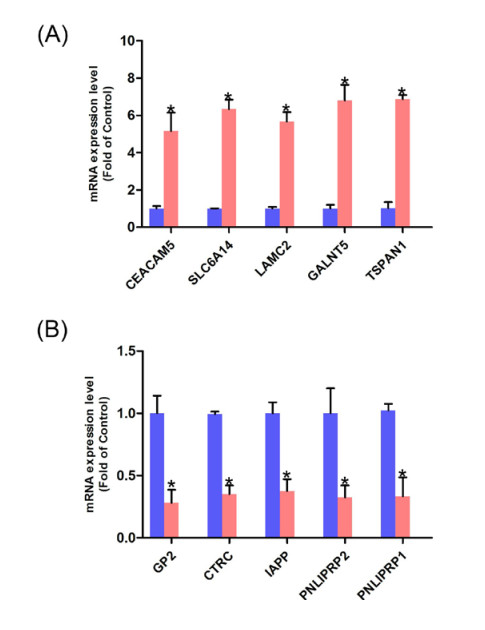
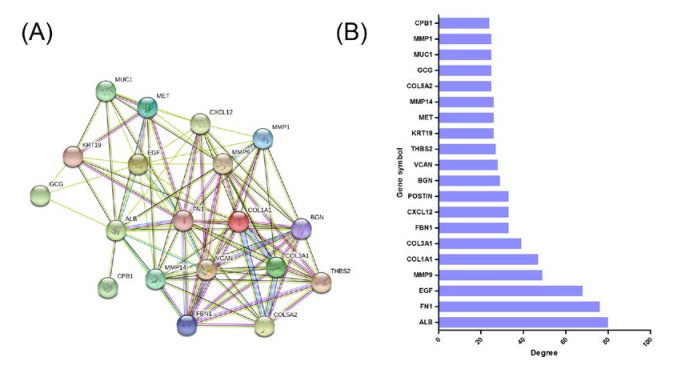
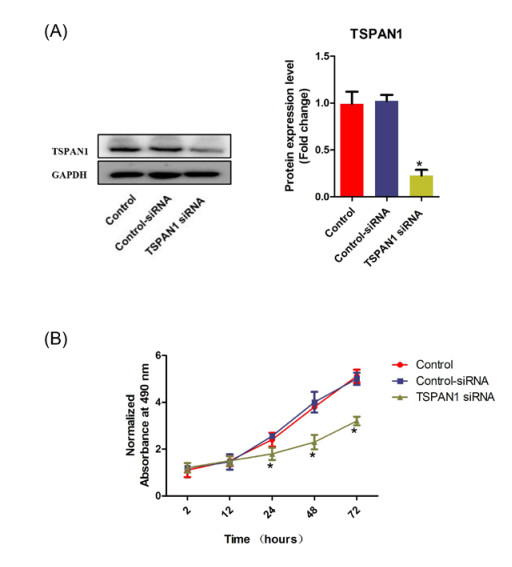
Pancreatic ductal adenocarcinoma (PAAD) is one of the most common malignant tumors in digestive system. To find the new therapeutic targets and explore potential mechanisms underlying PAAD, the bioinformatics has been performed in our study. The PAAD gene expression profile GSE28735 was chosen to analyze the differentially expressed genes (DEGs) between PAAD carcinoma tissues and normal adjacent tissues from 45 patients with PAAD. Gene ontology (GO) and Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway analysis were performed using Database for Annotation, Visualization and Integrated Discovery (DAVID). Moreover, a protein-protein interaction (PPI) network was also constructed to help us screen the top 20 hub genes in this profile and demonstrated the underlying interactions among them. The Gene Expression Profiling Interactive Analysis (GEPIA) was further performed in order to valid the mRNA levels of top5 up-regulated and top5 down-regualted DEGs, apart from exploring their association with survival rate as well as tumor stage. Finally, Q-PCR was further employed to valid the top5 up-regulated and top5 down-regulated genes in patients with PAAD. In our study, there were a total of 444 DEGs captured (271 up-regulated genes and 173 down-regulated genes). Among these DEGs, the top5 up-regulated genes were CEACAM5, SLC6A14, LAMC2, GALNT5 and TSPAN1 while the top5 down-regulated genes were GP2, CTRC, IAPP, PNLIPRP2 and PNLIPRP1. GO analysis disclosed that the DEGs were predominantly enriched in cell adhesion, lipid metabolism, integrin binding, proteolysis and calcium ion binding. KEGG analysis disclosed that the enriched pathway included pancreatic secretion, protein digestion and absorption, fat digestion and absorption, ECM-receptor interaction, focal adhesion and PI3K-Akt signaling pathway. Survival analysis unveiled that the high expression levels of SLC6A14, GALNT5 and TSPAN1 may correlate with the poor prognosis while high expression levels of IAPP may contribute to a better prognosis in patients with PAAD. Additionally, the levels of CEACAM5, SLC6A14, LAMC2 and GALNT5 were also associated with tumor stage. Furthermore, according to the connectivity degree of these DEGs, we selected the top20 hub genes, namely ALB, FN1, EGF, MMP9, COL1A1, COL3A1, FBN1, CXCL12, POSTIN, BGN, VCAN, THBS2, KRT19, MET, MMP14, COL5A2, GCG, MUC1, MMP1 and CPB1, which were expected to be promising therapeutic targets in PAAD. Collectively, our bioinformatics analysis showed that DEGs and hub genes may be defined as new biomarkers for diagnosis and for guiding the therapeutic strategies of PAAD.
1.
Introduction
Social networks contain a wealth of sensitive information, encompassing attributes of linked nodes, node labels, and graph structural features. Attackers can exploit active or passive attack models to dissect and discover this sensitive information [1]. Weighted social networks refer to networks where edges between nodes carry weights or strength values. In social networks, edge weights can depict communication frequencies related to sensitive information, prices of business transactions, and the intimacy of relationships [2]. Weighted social networks, crucial for fields such as social media analysis, social network analysis, health, and recommendation systems, enable optimization of marketing and promotion strategies through user relationships and interaction intensities.
However, due to the public or shared nature of connection and interaction information between nodes in weighted social networks, privacy leakage issues emerge. Some potential privacy leakage problems include:
1) Sensitive information leakage: Connection and interaction information between nodes in weighted social networks may involve sensitive information, such as users' personal preferences, sexual orientation, political tendencies, etc. If this information is made public or shared, it could adversely affect user privacy.
2) Individual behavior analysis: Connection and interaction information in weighted social networks can be used to analyze user behavior patterns and trends, such as which users interact frequently or are interested in specific topics. Misuse of this information could pose a potential threat to users' personal privacy.
3) Social engineering attacks: Connection and interaction information in weighted social networks can be exploited for social engineering attacks, such as deception, inducing users to click on links, providing phishing websites, etc. These attacks may lead to information leakage or financial losses for users.
4) Anti-privacy analysis attacks: Connection and interaction information in weighted social networks can be used for anti-privacy analysis attacks, such as identifying users' identities and whereabouts by associating nodes across different social networks. These attacks may expose user privacy and threaten personal security.
Therefore, in the design and implementation of weighted social networks, appropriate measures are needed to manage and protect user privacy. The research challenge in privacy protection for weighted social networks lies in determining suitable noise addition strategies to maintain data utility and accuracy while ensuring privacy. To protect sensitive information in weighted social networks, this paper proposes a social network differential privacy protection algorithm based on density clustering. This algorithm aims to protect user privacy by adding noise to the edge weights of the network. However, in the process of differential privacy protection, adding noise may lead to a decrease in the model's accuracy performance. Inspired by [3], this paper introduces the Differential Privacy Protection based on Density Clustering (DCDP) algorithm. It adds noise to the edge weights of the network at random sampling frequencies to meet differential privacy requirements, reducing the amount of added noise. Additionally, privacy budget parameters are calculated based on the size of sub-cluster edge weights, ensuring more uniform noise addition.
We employed the OPTICS density clustering algorithm to enhance the accuracy performance of the model, combining it with differential privacy protection. Our goal was to achieve higher protection effectiveness and analytical accuracy. Experimental analysis indicates that the proposed algorithm can achieve differential privacy protection for weighted social networks and is applicable to large-scale social networks. The major contributions of this paper are as follows:
1) Random sampling frequency noise addition: The algorithm uses random sampling frequencies to add noise to network edge weights, meeting differential privacy requirements. This approach reduces the amount of added noise, consequently improving data accuracy and utility.
2) Dynamic adjustment of privacy budget parameters: Addressing the issue of uneven privacy protection in weighted social networks, the algorithm designs new differential privacy budgets based on edge weights. This enables the dynamic adjustment of privacy budget parameters according to the size of sub-cluster edge weights, ensuring a more even addition of noise.
3) Theoretical proof of ε-differential privacy: The DCDP algorithm is theoretically proven to satisfy ε-differential privacy. Experimental results, utilizing common utility metrics in social networks such as average relative error and the proportion of unchanged shortest paths, validate that the DCDP algorithm effectively protects the privacy of weighted social networks.
2.
Related work
Dwork et al. [4] first proposed the differential privacy protection model in 2006 to address privacy concerns in data sharing. In the process of data sharing, data holders may inadvertently disclose sensitive information, posing a threat to individual privacy. Differential privacy protection techniques achieve privacy by perturbing the original data with noise before releasing it, making it difficult for attackers to accurately infer specific individual information and thus preserving the privacy of the data. Depending on the order of noise addition, differential privacy protection models can be divided into two types: 1) Adding noise to the original data before releasing it. While this method provides high protection, the data's availability is low. 2) Transforming, compressing, or otherwise modifying the original data before adding random noise and finally releasing the data. Although this method results in accuracy loss, it reduces errors compared to the first method while enhancing data utility. Differential privacy serves as a standard for quantifying privacy risk and has been widely used in statistical estimation, data publishing, data mining, and machine learning [5].
In the protection of edge weights in differential privacy, the common approach is to modify the network structure by adding random noise to the edge weights to achieve privacy protection. The fundamental idea is to introduce random perturbations into the network, blurring the specific values of edge weights, thus safeguarding user privacy while preserving the network's basic structure and functionality.
Traditional privacy protection algorithms face challenges in handling the complexity and randomness of noise in weighted social networks. To address these issues, researchers have proposed a series of innovative methods. Ning et al. [6] proposed a privacy protection algorithm for weighted graphs in the Internet of Things (IoT), but excessive noise affected data utility. To address this, Lan et al. [7] introduced the LWSPA (Less Weighted Social Privacy Algorithm). This algorithm, based on the random perturbation of the differential privacy model, splits the triplets in the query result set, achieving strong protection for both edges and edge weights. However, because the LWSPA algorithm directly injects Laplace noise into the query result vector set for privacy protection, the high error reduces data utility. To address the low data utility issue, Wang et al. [8], combining bucket merging and consistency inference, designed the MB-CI (Merging Barrels and Consistency Inference) privacy protection algorithm. This algorithm reduces the amount of added noise while maintaining the unchanged shortest paths in the network. Huang et al. [9], combining clustering and randomization algorithms, designed a privacy protection method based on the differential privacy model called PBCN (Privacy Preserving approach Based on Clustering and Noise). This method achieves a balance between data availability and privacy protection level, while improving the utility of processed data. Xu et al. [10] proposed a non-interactive query data publishing method based on the differential privacy model. Using histogram statistics and the non-interactive differential privacy query model as a foundation, social relationships are divided into sub-communities and noise is injected, achieving privacy protection and enhancing data utility.
As the scale of social networks increases, privacy protection for large-scale social networks becomes complex and time-consuming. To address this issue, Wang et al. [11] proposed a Large-scale Social Network Data Release Algorithm based on Random Projection and Differential Privacy (RP-DP). This algorithm utilizes random projection to reduce the dimensionality of the adjacency matrix of the social network graph and introduces Gaussian noise into the reduced matrix to generate the matrix ready for release. Other researchers have also proposed a series of algorithms, such as the clustering method based on sequence perception and local density by Qian et al. [12], the DP-LTOD scheme by Xu et al. [13], and the DRS-S algorithm by Kang [14], all providing varying degrees of protection for users at different levels.
However, existing methods commonly face a challenge where a uniform privacy budget leads to imbalances in the degree of privacy protection. To tackle this challenge, Liu et al. [15] introduced a Dynamic Differential Privacy Algorithm (DDPA) for the dynamic release of social network data. DDPA introduces Laplace noise into edge weights and dynamically identifies changing edge weight information with increasing iteration counts, thereby enhancing privacy protection budgets. Subsequently, Liu et al. [16], based on the Markov Cluster Algorithm (MCL), proposed a dynamic ε Social Network Differential Privacy Protection Algorithm (MDPA). This method adds appropriate noise to each cluster, addressing the issue of imbalanced privacy protection in weighted social networks. Yuan et al. [3], using the Spectral Clustering algorithm and the differential privacy model, presented the SCDP algorithm (Differential Privacy Protection based on Spectral Clustering). This algorithm calculates privacy budget parameters based on the edge weights of social networks to control the amount of added noise. Chen et al. [17] proposed a Density Exploration and Reconstruction (DER) method, adding noise to regions based on their density, effectively resolving the issue of excessive noise due to sparse edges in social networks. Long et al. [18] introduced a Dynamic Differential Privacy Algorithm for Social Networks based on Local Communities (DDPLA), balancing data utility and the level of privacy protection by dynamically generating privacy budgets for different communities.
The purpose of graph clustering is to cluster large and complex graphs into different clusters and then add noise to well-defined clusters with distinctive features to protect the privacy of the graph. Zhang et al. [19] proposed the DSNPP algorithm (Density for Social Network Privacy-Preserving), which employs density clustering on nodes to obtain clusters of various shapes. Techniques such as generalization and insertion of real nodes are then utilized to protect the privacy of node information and relationships between nodes. However, existing locally differentially private graph analysis methods overlook nodes affected by noise to different extents, leading to suboptimal clustering results. Hou et al. [20] introduced the Wdt-SCAN algorithm, designing a degree vector encoding model to represent social relationship graphs, reducing noise due to sparsity and achieving high-quality clustering. Lei et al.'s DWT-DP algorithm [21] employed an adaptive privacy budget allocation strategy, extending the lifecycle of privacy budgets and reducing noise injection.
Addressing the privacy protection issue in weighted social networks, this paper proposes the Density-based Clustering for Differential Privacy (DCDP) algorithm based on OPTICS. This algorithm utilizes the OPTICS clustering algorithm to partition the weight matrix of the social network into multiple sub-clusters. Subsequently, Laplace noise satisfying differential privacy is added to the edge weights of these sub-clusters to achieve privacy protection. Experimental results demonstrate that the DCDP algorithm can effectively achieve differential privacy protection for weighted social networks in large-scale social networks.
3.
Related theories
Weighted social network: This paper utilizes the triplet G = (V, E, W) to represent a weighted social network, where V = {v1, v2, …, vn} denotes the set of network nodes, E = {e = (vi, vj)|vi, vj ∈ V, i ≠ j} represents the set of network edges, and W denotes the set of weights. The weight matrix is employed to depict the weight information of the weighted social network graph. The weight matrix is an n × n matrix, where the element in the ith row and jth column represents the weight value between nodes vi and vj. If there is no connection between two nodes, the corresponding weight value is 0. Using the weight matrix, it becomes convenient to mathematically represent and compute operations on the weighted social network.
t-Distributed stochastic neighbor embedding: t-SNE is a non-linear method for dimensionality reduction, particularly effective in mapping high-dimensional data to a lower-dimensional space. It preserves the relative distances between data points, facilitating visualization and clustering. In comparison to linear dimensionality reduction algorithms like Principal Component Analysis (PCA), t-SNE excels in retaining the original structure of the data while capturing local similarities and non-linear relationships more effectively. With t-SNE dimensionality reduction, the data's dimension decreases, and the computational complexity of similarity and distance calculations is reduced, thereby accelerating the clustering speed of the OPTICS algorithm.
Ordering points to identify the clustering structure: OPTICS is a density-based clustering algorithm designed to automatically discover clusters of arbitrary shapes. It does not require a predefined number of clusters and utilizes density connections and reachability distance graphs to autonomously identify clustering structures within a dataset. OPTICS is effective in handling high-dimensional and noisy data. Social network data often exhibits high-dimensional feature spaces and includes numerous outliers and noise. The OPTICS clustering method, employing variable density clustering techniques, can discover clusters of various shapes and sizes in high-dimensional spaces, demonstrating robustness to noise and outliers.
In the DCDP algorithm, the OPTICS algorithm is employed to cluster the reduced-weight matrix. Its purpose is to group similar nodes into the same cluster, facilitating differential privacy protection. During clustering, the OPTICS algorithm assigns similar nodes to the same cluster, minimizing distances within the cluster and maximizing distances between different clusters.
The ε-differential privacy model: (ε-differential privacy [22]) If a randomized algorithm M satisfies ε-differential privacy, then for any adjacent datasets D and D', and any output set S, the algorithm M satisfies the following condition: Pr[M(D)∈S]≤eϵPr[M(D')∈S], then the algorithm M can achieve ε-differential privacy protection. Here, ε is a non-negative real number, and it controls the degree of difference between adjacent datasets. The smaller ε is, the smaller the difference, and the higher the level of privacy protection. In simple terms, differential privacy defines a privacy mechanism in which each input dataset D is transformed into a perturbed dataset D' to minimize the difference between the outputs M(D) and M(D'), while ensuring that the privacy budget does not exceed ε.
(Global sensitivity [22]) In a function f:Dn→R, where D is the domain and R is the range for two datasets x,y∈Dn, that differ by at most one element. The global sensitivity of the function f is the maximum difference over all possible datasets x,y∈Dn, the definition of the global sensitivity is given by Eq (1).
where |x−y|1 represents the norm of x and y, indicating the number of differing elements between them. Global sensitivity signifies an upper bound on the impact of an individual's information in the dataset for the given function.
(Laplace Mechanism [22]) Suppose f is a query function, x is the input dataset, Δf is the global sensitivity of f, and ε is the privacy budget. The Laplace Mechanism outputs a privacy-preserving query result by adding noise from the Laplace distribution Lap(Δf/ε) to f(x), it can be represented by Eq (2).
where Lap(b) represents the Laplace distribution with parameter b, and its probability density function is: 12bexp(−|x|b). It can be observed that the magnitude of added noise is inversely proportional to ε. The larger the edge weight within a cluster, the stronger the protection needed. Therefore, smaller ε values should be allocated for such cases.
(Composite differential privacy [22]) Let f1,f2,…,fm be m query functions, x be the input dataset, and ε be the privacy budget. Composite Differential Privacy defines the privacy protection for the joint query function f(x)=(f1(x),f2(x),…,fm(x)). It requires that for any adjacent input datasets x and x', and any output set S⊆Range(f), the inequality (3) must be satisfied. For
it is said to satisfy composite differential privacy.
Node differential privacy and edge differential privacy: Node differential privacy refers to the scenario where adding or removing a node in the graph has a negligible impact on the query results. Node differential privacy can protect the confidentiality of node attributes, preventing attackers from inferring the presence of nodes in the network, thus providing strong privacy protection. When a node is randomly added or deleted, the worst-case scenario is that the node is connected to all remaining nodes in the graph, indicating that the query sensitivity of node differential privacy is relatively high. Edge differential privacy, on the other hand, pertains to the scenario where adding or removing edges between any two nodes in the graph has a negligible impact on the query results. Edge differential privacy focuses on protecting the privacy of edge attributes, such as cooperation, trade, trust, etc., with relatively lower query sensitivity.
The query sensitivity caused by changes in nodes is directly proportional to the size of the graph. For large-scale network graphs, the sensitivity of node differential privacy is often higher than that of edge differential privacy. Consequently, the added noise is larger, making it challenging to ensure sufficient data utility. While node differential privacy can provide stronger privacy protection, edge differential privacy already meets the practical requirements of most applications, especially in large-scale social networks. Therefore, edge differential privacy has more extensive applications [23]. This paper focuses on the differential privacy protection of edge weights in social networks.
4.
Proposed method
4.1. Scenario description
In the field of social networks, the application of differential privacy technology is crucial. Social network platforms host vast amounts of user personal information, interaction history, and social relationship data, aiming to provide personalized content and enrich social experiences. However, this data encompasses highly sensitive information, including personal preferences, social circles, accurate geographical locations, etc. Once leaked, it may lead to privacy infringements and misuse risks. In this context, social network platforms urgently need to adopt differential privacy technology to protect users' privacy information. However, social network data not only includes interactions, relationships, and information from different users but also involves weight information, such as certain users contributing more to the platform's content or certain information having a more significant impact on user privacy, making the application of differential privacy technology complex and challenging.
In the social network scenario, applying differential privacy technology involves a series of challenges and trade-offs. First, to ensure that privacy protection is fair and balanced, excessive privacy protection should not be applied to specific users or data points, to maintain the overall functionality of the social network. Moreover, weight information in social network data is often very sensitive, such as users' social influence, trustworthiness, etc. Leaking or misusing this information may pose a severe threat to user privacy and security. Therefore, in differential privacy protection, moderate noise needs to be added to weight information. However, excessive noise addition may lead to data blur, making it challenging to meet the needs of social network analysis and personalized recommendations. Thus, a balance between privacy protection and data usability is necessary to ensure that users continue to enjoy a high-quality social network experience.
In this scenario, the application of differential privacy technology aims to balance the level of privacy protection among social network users while ensuring effective protection of sensitive weight information in the social network. This helps maintain user privacy, ensuring they can continue to benefit from social network analysis and personalized services while considering the trade-off between privacy protection and data usability.
For large-scale social networks, direct clustering analysis of nodes and edges would consume considerable time and resources. To reduce noise addition to important weight information and decrease the time spent on clustering analysis, this paper proposes a differential privacy protection algorithm, DCDP, based on OPTICS density clustering. The algorithm aims to achieve privacy protection and effective clustering analysis of social network data. To address the issue of excessive noise addition affecting data utility in privacy protection for social network weights and the imbalance caused by using a unified privacy parameter for global privacy, inspired by references [3] and [16], the proposed DCDP algorithm designs new privacy budget parameters. These parameters are computed based on the size of sub-cluster edge weights to determine the amount of noise to be added. Due to the non-uniform use of the privacy parameter ε and the use of the properties of combined differential privacy, the DCDP algorithm is proven to satisfy ε-differential privacy.
4.2. Method design
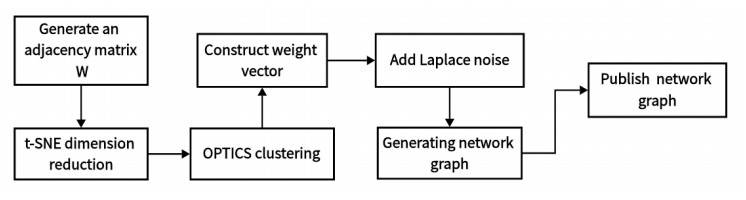
Figure 1 is the flow chart of DCDP algorithm. To mitigate the increased error caused by noise addition, we have incorporated a random sampling frequency design into the DCDP algorithm. By introducing noise through random sampling to the edge weights of clustered sub-clusters, we can effectively control the amount of noise, thereby balancing the relationship between privacy protection and data utility. This design allows for minimizing the impact on data while ensuring privacy protection. Furthermore, to ensure the balance of privacy protection, we innovatively designed a new method for calculating privacy budgets. Considering that weight information in social network data may have varying degrees of impact on user privacy, we dynamically calculate privacy budget parameters based on the size of sub-cluster edge weights. This differential privacy protection approach treats different weight information more delicately, avoiding a one-size-fits-all scenario and further enhancing the accuracy and fairness of privacy protection. Finally, to validate the privacy protection effectiveness of the DCDP algorithm, we employed the composition theorem in differential privacy for proof. Through the composition theorem, we can demonstrate that the DCDP algorithm globally satisfies the ε-differential privacy standard, providing theoretical support for its feasibility in privacy protection for social network data.
The specific steps of the DCDP algorithm include initially generating the adjacency matrix W for the social network graph. Subsequently, t-SNE is utilized to reduce the dimensionality of the weight matrix, significantly reducing the clustering time complexity. Next, the OPTICS clustering algorithm is employed to cluster the social network into different sub-clusters. Based on this, a weight vector satisfying ε-differential privacy is constructed. Random sampling frequency is then used to randomly add noise following a Laplace distribution to the edge weights. Finally, a weight social network graph satisfying ε-differential privacy is generated, and the privacy-protected social network graph is released. The following outlines the definitions of the random sampling frequency Si and privacy budget used in this study.
4.3. Sampling frequency
The DCDP algorithm addresses the challenge of reduced data utility caused by adding Laplace noise to a weighted social network. This algorithm protects data privacy by clustering the weighted social network graph into clusters with similar characteristics and utilizing the weight sum Si of each cluster as the sampling frequency. It randomly selects edge weights within each cluster for privacy protection, adding Laplace noise to satisfy the requirements of differential privacy.
The use of random sampling frequency for noise addition ensures that the perturbed data closely approximates the original data. It reduces the amount of added noise, diminishes randomness, and minimizes the impact of noise on the data. This approach enhances data utility, credibility, and availability. For smaller clusters, a smaller sampling frequency is employed, further reducing the noise added and improving data availability. Inspired by previous work [3], we define the sampling frequency Si by Eq (4).
where v1 represents the total number of edge vectors in subclusters, and v2 represents the total number of edge vectors in the dataset.
The sampling frequency is set based on the sparsity level of the dataset. If the dataset is relatively sparse, it is advisable to increase the sampling frequency appropriately to ensure that the perturbed dataset retains a certain level of utility. Conversely, reducing the sampling frequency is recommended to minimize the amount of added noise. This adjustment is made to strike a balance between preserving data utility and reducing the impact of noise, adapting to the sparsity characteristics of the dataset.
4.4. Differential privacy budget
In the context of a weighted social network, the edge weight reflects the closeness between nodes. Consequently, it is essential to allocate an appropriate privacy parameter ε based on the magnitude of edge weights to achieve a more balanced privacy protection. To enhance data usability, the DCDP algorithm computes a privacy parameter ε′ for each clustering cluster, considering the sampling frequency and differential privacy parameter ε.
Typically, edges with larger weights require stronger protection. Therefore, the maximum edge weight within a subcluster is used as a factor. The mean reflects the central tendency of the data, while the standard deviation indicates its level of dispersion. Drawing inspiration from literature [16], we define the privacy parameter ε' used in this paper by Eq (5).
In the formula: Value represents the maximum weight; ¯value denotes the average weight; δ is the standard deviation; ε signifies the initial privacy budget.
This approach allows for the protection of data privacy while minimizing disturbance to the data, thereby improving accuracy and usability. Next, each edge weight between pairs of nodes within this clustering cluster undergoes random perturbation using Laplace noise to achieve the goal of differential privacy protection.
4.5. DCDP algorithm basic flow
The specific steps of the proposed DCDP algorithm are outlined in Algorithm 1. Algorithm 2 presents the pseudocode for the DCDP algorithm, with detailed step descriptions as follows.
The algorithm incorporates random sampling frequencies and differential privacy parameter ε to calculate ε' for each subcluster after clustering. Laplace mechanism noise, compliant with differential privacy, is then added to each subcluster, ultimately resulting in a weighted social network graph that satisfies differential privacy protection.
4.6. Privacy analysis of the algorithm
As each subcluster uses a different privacy budget, we demonstrate that the DCDP algorithm satisfies ε-differential privacy using the composition theorem in differential privacy. According to the definition of differential privacy, considering two social network datasets, G1 and G2, differing by at most one edge, and a privacy algorithm K with Range(K) as the range of values, if the algorithm K, applied to datasets G1 and G2, satisfies the following inequality (6) for any output result M(M⊂Range(K)), then the K algorithm satisfies ε-differential privacy.
Theorem 1. The DCDP algorithm satisfies ε-differential privacy.
Proof. Let m ∈ M, where M has the same dimension as X. According to the conditional probability:
According to K(G1)−K(G2)≤Wmax,
Due to m ∈M, it can be inferred that P[K(G1)∈M]P[K(G2)∈M]⩽eε, thus, the DCDP algorithm satisfies compositional differential privacy.
Proof completed.
5.
Experiment and result analysis
5.1. Experimental setup
We conducted experiments on two weighted social network datasets, PolBooks and Lesmis. The evaluation of the DCDP algorithm's accuracy and feasibility was based on the average relative error and the ratio of unchanged shortest paths. Under the same privacy parameters, the experiment compared the DCDP algorithm with the LWSPA algorithm using random perturbation, the DWT-DP algorithm employing a modular adaptive privacy budget allocation strategy, the PBCN algorithm combining clustering and randomization, and the DCDP algorithm on the PolBooks and LesMis datasets.
As the DCDP algorithm calculates privacy parameters based on the edge weights of clustering clusters and adds noise with a random sampling frequency, resulting in a smaller amount of noise added, it effectively ensures the accuracy of the data. The experimental results demonstrate that the DCDP algorithm provides a more balanced differential privacy protection. The term "Laplace" refers to an algorithm that directly adds noise.
5.1.1. Experimental environment
The experimental environment utilized an AMD Ryzen 7 5800H with Radeon Graphics, operating at 3.20 GHz with 16.0 GB of memory. The operating system was Microsoft Windows 11, and the programming tool used was PyCharm, implemented using Python.
5.1.2. Experimental datasets
The datasets used in the experiment are presented in Table 1. The Polbooks dataset [24] is a graph dataset used to study the relationships between U.S. political books and their authors. Its purpose is to assist in better understanding and analyzing the relationships between various perspectives and factions within the U.S. political system. Each node represents a political book, and each edge represents the strength of the relationship between two authors. The LesMis dataset [25] is a graph dataset about the relationships between characters in the French novel "Les Misérables". Each node represents a character in the novel, and each edge signifies a relationship between two characters. The Karate [26] network is an unweighted graph, and the Demo is a randomly generated graph. Using a random number generator, edge weights are randomly assigned within the range [1,10] as integer values for the edges.
5.2. Efficiency analysis
The experiment tested the execution time of the DCDP algorithm on four social network datasets. The experimental results are the averages of five trials, as shown in Figure 2.
Our purpose of the experiment was to test the impact of variations in the privacy budget parameter ε and the minimum sample size m during the OPTICS clustering algorithm phase on the execution time of the DCDP algorithm. The values of m in Figure 1(a) to 1(c) are 5, 10, and 20, respectively, and ε takes values of 0.05, 0.1, 1, and 5. From the experimental results, it can be observed that when m is fixed, the execution time of the DCDP algorithm is relatively unaffected by an increase in ε. Comparing cases with fixed ε values, smaller values of the minimum sample size m lead to more points being considered as core points, resulting in the formation of more clusters. This sensitivity increases the algorithm's computational requirements for identifying cluster boundaries. As the value of m increases, the number of clusters in the network graph decreases, and the execution time slightly decreases. When the dataset size of the social network graph becomes larger, the execution time increases. The experimental results indicate that the execution time is primarily influenced by the number of nodes and edges in the dataset.
5.3. Data accuracy analysis
The Average Relative Error (ARE) is a metric used to assess the degree of difference between two numerical sequences. It represents the average relative error between predicted values and true values. In this study, ARE is employed to evaluate the accuracy of the data, indicating the average relative error across all edge weights. A lower ARE value implies closer proximity between predicted and true values, indicating higher prediction accuracy. The formula for calculating ARE is determined by Eq (7).
here, n represents the number of edge weights, yi denotes the true edge weight, and ^yi is the predicted edge weight. Smaller ARE values indicate higher algorithm accuracy.
In order to balance privacy and data utility, the privacy parameter ε in the experiments is set within the range of 0.05 to 10. We evaluated the error of the DCDP algorithm under different privacy parameters and compares it with traditional social network differential privacy protection algorithms, including the direct addition of Laplace noise, MDPA algorithm, LWSPA algorithm, and PBCN algorithm. The experimental results are illustrated in Figures 3 and 4.
Figures 3 and 4 present the experimental results of the average relative error for the LWSPA algorithm, DWT-DP algorithm, PBCN algorithm, and DCDP algorithm as the privacy budget ε varies. As ε increases, the average relative error decreases and approaches 0. Comparatively, the DCDP algorithm performs better, followed by the PBCN algorithm. Analyzing the experimental results in Figures 1 and 2, as ε increases, the added noise to the data decreases, leading to a reduction in the average relative error. The increase in ε allows for more noise addition, alleviating data distortion and improving data accuracy and quality. Traditional social network differential privacy protection algorithms that directly add Laplace noise to edge weights introduce significant errors between true values and noise. The LWSPA algorithm, injecting Laplace noise directly into the query result vector set, results in higher errors and reduced data utility. The DWT-DP algorithm, employing an adaptive privacy budget allocation strategy, reduces noise addition and better maintains data utility. The PBCN algorithm, combining clustering and randomization algorithms, achieves a balance between privacy protection and data utility. The DCDP algorithm, incorporating random sampling probability and privacy parameters calculated based on edge weights, adds noise conforming to differential privacy protection. It effectively minimizes the impact of errors while ensuring data privacy, thereby enhancing data analysis accuracy.
Through experiments on Lesmis and Polbooks datasets, the DCDP algorithm outperforms other algorithms with a smaller average relative error under the same privacy parameters. In conclusion, the proposed DCDP effectively reduces errors, ensuring data accuracy.
5.4. Data utility analysis
KSP (K-shortest paths preservation) is an indicator used to assess the level of protection of the differential privacy mechanism for the preservation of shortest paths [7]. KSP measures the preservation level of K shortest paths in a network topology, representing the proportion of unchanged shortest paths from the source node to the target node. The formula for calculating KSP is determined by Eq (8). It indicates the ratio of the number of paths that remain unchanged to the total number of paths, ensuring privacy protection. In a network, a higher proportion of unchanged shortest paths suggests that the impact of the differential privacy protection mechanism on the network is smaller.
In the formula, Np represents the total number of reachable shortest paths, and N'p represents the number of unchanged shortest paths after privacy protection. The KSP metric has a range of [0, 1], with a higher value indicating better protection performance, i.e., a higher proportion of unchanged shortest paths. The experimental results are shown in Figures 5 and 6:
Figures 5 and 6 show the proportion of the unchanged shortest paths for various algorithms under different privacy parameters on the Lesmis and Polbooks datasets. Overall, with the increase in ε, the shortest paths of DCDP algorithm and other comparative algorithms tend to stabilize and eventually remain unchanged. Among the compared algorithms, LWSPA algorithm performs the worst, and DCDP algorithm is slightly better than the PBCN algorithm. Analyzing the experimental results on the two weighted social network datasets, the LWSPA algorithm directly adds noise to the dataset, resulting in a greater impact on the data. The DCDP algorithm adopts a differential privacy protection algorithm based on OPTICS clustering, allocates privacy budget for each subcluster, and then performs differential privacy protection for each edge weight in each subcluster. Compared with the method of directly adding noise to the original data and the PBCN algorithm, this approach can better target protect data privacy while minimizing the impact on data analysis.
Through the comparison of experimental results on the Polbooks and LesMis datasets under the same privacy parameters, it is evident that DCDP has the best performance, better protecting the practicality of the data. In both datasets, when the privacy parameter ε of DCDP is greater than 0.05, the proportion of unchanged shortest paths stabilizes at around 98%, indicating that the DCDP algorithm improves the privacy protection effect of the data.
From the above experimental results, it can be concluded that the DCDP algorithm, compared with existing similar algorithms, can better ensure the accuracy and practicality of the data while effectively protecting privacy information.
6.
Discussion, conclusions, limitations, and future research
In addressing the challenges of excessive noise addition and uneven privacy protection for weighted social networks, we propose a differential privacy algorithm, DCDP, based on density clustering within the differential privacy model. DCDP introduces random sampling frequencies to add privacy protection algorithms to network edge weights, incorporating Laplace-distributed noise that satisfies differential privacy. Theoretical analysis and experimental results demonstrate that this algorithm can reduce the errors introduced by noise addition, maintain unchanged shortest paths, and enhance the accuracy and practicality of published data. The experimental results on real social network datasets indicate that the DCDP algorithm effectively protects the privacy of weighted social networks.
In future work, we will focus on two aspects: First, the DCDP algorithm mainly focuses on privacy protection for the entire dataset, lacking differential protection for variations among different data elements. We will consider researching more fine-grained privacy protection algorithms, such as protecting individual data elements like nodes, edges, etc., to enhance the precision of privacy protection. Additionally, we will explore the integration of other privacy protection technologies, such as homomorphic encryption, to enhance the algorithm's privacy protection capabilities. Second, due to the relatively low efficiency of differential privacy algorithms in handling large-scale network data, significant computational resources are required. We will aim to improve the algorithm's efficiency and scalability, enabling widespread applications in practical scenarios.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant 61862007.
Conflict of interest
The authors declare there are no conflicts of interest.









 DownLoad:
DownLoad: