1. Introduction
Pseudomonas aeruginosa is one of the most common pathogens found in health care settings. It is responsible for severe infections of compromised epithelial surfaces, including acute and chronic respiratory infections and severe burns. The vast majority of patients with a Pseudomonas lung infection have a serious underlying medical condition, such as neutropenia, obstructive pulmonary disease or cystic fibrosis [1,2].
The ability of P. aeruginosa to inhabit and adapt to different environments is largely due to its very large repertoire of regulatory proteins, of which two-component regulatory systems (TCS) make up one of the largest families. These systems control practically all aspects of cellular function and multiple systems regulate various aspects of virulence, one facet of which is direct cytotoxicity to the host epithelium. P. aeruginosa secretes several enzymes that contribute to the death of host epithelial cells, including type 3 secreted ExoS, ExoT and ExoU, and type 2 secreted ExoA, and various proteases, lipases and phospholipases, as well as others [3,4]. For example, strain PA14, used extensively here, is quite cytotoxic to epithelial cells largely due to a mutation in LadS [5] that leads to an upregulation in type 3 secreted cytotoxins, such as the acutely toxic ExoU, which accounts for much of this strain's cytotoxicity [6].
In the classical TCS, a membrane-bound sensor detects a ligand (signal), often externally and frequently uncharacterized, autophosphorylates at the cytoplasmic side of the membrane and then transfers the phosphate to a cytoplasmic response regulator, which in turn initiates a response, usually through the alteration of gene transcription. P. aeruginosa has 64 sensor kinases and 72 response regulators [7]. A few TCS have been characterized for their contribution to virulence or virulence-related phenotypes, particularly GacA-GacS, CbrA-CbrB, and PhoP-PhoQ, but relatively few have been shown to have direct contributions to cytotoxicity [7,8,9]. The vast majority of TCS remain uncharacterized and it is likely that many of these contribute some role to virulence. Here, we performed a survey study in which P. aeruginosa TCS mutants were screened for their altered ability to cause death to cultured lung epithelial cells, and selected regulators were subsequently examined in greater detail.
2. Materials and methods
2.1. Bacterial strains and growth
For the cytotoxicity screen, all available strain PA14 transposon mutants in sensor kinases or response regulators were obtained from the Harvard University mutant library [10]. We also examined P. aeruginosa strain PAO1 transposon mutants, including the fleS and fleR mutants from a mini-Tn5-lux library [11] and the fliC mutant from the University Washington library [12]. P. aeruginosa strain PAO1 mutants phoQ, phoP, and phoQ complemented with pucP::phoQ+ (phoQ+) [9,13,14], and fleR, fleS, and fleS complemented with pUCP::fleS+ (fleS+) were described previously [9,13,14]. All strains were grown in Luria-Bertani broth (LB) or Basal Medium 2 [BM2; comprising 7 mM (NH4)2SO4, 40 mM K2PO4, 22 mM KH2PO4, 20 mM glucose, 2 mM MgSO4, 40 μM FeSO4] at 37 °C overnight with agitation and containing applicable antibiotics: 15 μg/ml gentamicin for strain PA14 transposon mutants and the phoP and phoQ mutants in strain PAO1, 30 μg/ml tetracycline for other strain PAO1 transposon mutants, and 300 μg/ml carbenicillin for the phoQ+ complemented strain. For interaction assays, strains and mutants were grown to log phase [optical density at 600 nm, (OD600) of ∼0.5] in LB without antibiotics. Growth was measured automatically every 20 minutes by assessing turbidity at OD620 in a TECAN Spectrafluor Plus.
2.2. Complementation of the wspR mutant
For the complementation of wspR in PA14, the mini-Tn7 system was used [15,16] whereby the mini-transposon Tn7 is inserted at a single attTn7 site on the P. aeruginosa chromosome. A 1.4 kb DNA fragment containing the wspR gene was amplified with primers 3702F (5′-TGGCGGAGGTATTCGATTAG-3′) and 3702R (5′-TCGCGGTTTACTTCGACCAG-3′) and cloned into TOPO Zero-Blunt cloning vector (Invitrogen) and then into the pBBR1MCS vector. The endonuclease EcoRV was used to move the wspR gene fragment into a pUC18TminiTn7T-Tet plasmid to create pUC18TminiTn7T-Tet-wspR+. This vector was constructed by removing the tetracycline resistance gene from pFTc1 (AY712950) using the restriction enzyme SacI and ligating it into the EcoRV site of pUC18TminiTn7T (AY599226). The plasmid pUC18TminiTn7T-Tet-wspR+ was then co-electroporated with the helper plasmid pTNS2 into electrocompetent PA14 wspR mutant cells. Positive clones containing the complementing gene were selected on LB plus 50 µg/ml of tetracycline. The insertions were checked by PCR using the primers PTN7R and PglmS-down as described previously [15,16].
2.3. Cytotoxicity assays
The SV40-transformed, immortalized 16HBE14o-human bronchial epithelial cell line (HBE cells) was a gift from Dr. D. Gruenert (University of California, San Francisco, CA) [17]. These cells were grown as monolayers in minimal essential medium (MEM) with Earle's salts containing 10% fetal bovine serum (FBS) and 2 mM L-glutamine with phenol red (Gibco). HBE cells were seeded into 96-well tissue-culture treated plates and grown to confluence at 37 °C and 5% CO2 in minimal essential medium (MEM) containing 10% FBS and 2 mM L-glutamine with phenol red (Gibco). The monolayer was washed with MEM containing 1% FBS and 2 mM L-glutamine then rested for a minimum of 30 min in the same medium. Bacteria were grown to logarithmic phase in LB at 37 °C with agitation, numbers estimated using OD600 measurements, washed in PBS, and then resuspended in MEM containing 1% FBS and 2 mM L-glutamine. The HBE monolayer was infected at a multiplicity of infection (MOI) of 2 for 8-10 h (strain PA14) or at an MOI of 50 to 100 for 16-20 hr (strain PAO1), due to differences in the virulence of these strains. The HBE cells and bacteria were co-incubated at 37 °C and 5% CO2. After centrifugation to remove bacteria, media was collected and stored at 4 °C. Cytotoxicity was measured by the release of cytosolic lactate dehydrogenase (LDH) from epithelial cells into the media using a colorimetric kit (Roche Applied Sciences). The percentage cytotoxicity of the mutants was calculated from the ratio of cytotoxicity in the mutants to that of an uninfected control (0% lysis) and a 1% Triton X-100 lysis positive control (100% lysis).
Alterations in the expression of specific toxins were determined by quantitative real-time polymerase chain reaction (qRT-PCR) [18] using optimized primers, a list of which can be obtained from the authors.
2.4. Biofilm and motility assays
Static microtitre biofilm assays were performed as previously described [19,20]. After overnight incubation at 37 °C without agitation in LB, media and non-adhered cells were discarded and the wells washed with deionized H2O. Surface-attached (biofilm) bacteria were stained with 0.1% crystal violet for 20 min, then washed again with deionized water. Crystal violet bound to the attached cells was dissolved with ethanol and the biofilm quantified by absorbance at 600 nm.
Flagellum-based swimming motility was analyzed by inoculating 1 μl of overnight culture into plates containing LB solidified with 0.25% agar and the in-agar swim zone diameter was measured after overnight incubation at 37 °C. Type IV pilus mediated twitching motility was assessed by inoculating 1 μl of an overnight culture through to the plastic surface of a thinly poured 1% agar LB plate and, after overnight incubation at 37 °C, measuring the diameter of the twitch zone that formed at the interface between the plastic surface and the agar. Swarming motility was carried out on BM2-glucose plates containing 0.5% agar and, in place of (NH4)2SO4, 0.1% casamino acids for strain PA14 and 0.5% casamino acids for strain PAO1. One μl of overnight culture was inoculated onto the surface of swarm plates that were then incubated at 37 °C overnight.
2.5. Adherence to epithelial cells
HBE cells and bacteria for infection were prepared as described above for the cytotoxicity assay. Bacteria were added to the HBE monolayers at MOI 50 and co-incubated at 37 °C and 5% CO2. After 1 hour, the media was removed and the monolayer washed thrice with PBS to remove any un-adhered bacteria [21]. The monolayer was lysed with 2% triton X-100 in PBS and removed and immediately diluted for plating onto LB agar as the adhered fraction. The inoculum was also plated to estimate total bacteria. Adherence was assessed as a percentage of adhered compared to total bacteria.
3. Results
3.1. Cytotoxicity profiles of PA14 two-component system mutants
P. aeruginosa causes both acute opportunistic lung infections as well as chronic lung infections in humans. In such infections, there is often considerable damage to the epithelium of the lung mediated by a variety of toxins and secreted enzymes [1,2]. Two-component regulatory systems (TCS) provide Pseudomonas with the ability to rapidly adjust to changing conditions in the host and other environments, and in this regard likely control many aspects of P. aeruginosa cellular life and virulence. One aspect of P. aeruginosa virulence is cytotoxicity towards host cells, including epithelial cells, through injected or secreted toxins. To measure this cytotoxic effect, human bronchial epithelial (HBE) cells were grown to confluence in culture and infected with P. aeruginosa strain PA14 at a MOI of 2 for 8 hours. At this time, necrosis of the HBE cells, as assessed by microscopy, was starting to become apparent as indicated by the emergence of lesions in the monolayer (data not shown). Cytotoxicity was quantitatively assessed by measuring the release of cytosolic lactate dehydrogenase (LDH) using a colorimetric assay, background subtracted for the release by untreated HBEs, and compared to a Triton X-100 lysis control. In all, 50 sensor kinases, 50 response regulators, 5 hybrid sensor/regulators, and 4 other TCS regulator mutants from the Harvard University strain PA14 transposon library were screened for cytotoxicity to HBE cells (Table S1). The ability to grow under co-culturing conditions was assessed spectrophotometrically at the end of the incubation time (data not shown); only one mutant (PA2571) was found to have a growth defect under these conditions and was therefore excluded.
Mutants in 13 regulators (11 response regulators and 2 other regulators), 10 sensor kinases and one sensor/regulator hybrid demonstrated substantial (>15%) alterations in their ability to cause lysis of epithelial cells compared to WT (Table 1). Of those causing increased cytotoxicity by 17-58%, eight were sensor kinases (including one hybrid) and 5 were response regulators, but intriguingly there were only 2 well studied cognate pairs, GacAS and CbrAB. Conversely, the TCS regulators that suppressed cytotoxicity were less balanced with 8 response regulators and only 3 sensor kinases, including one cognate triad, FleQRS. Thus there were many instances where only a single TCS component could be shown to have an effect on cytotoxicity (e.g. PhoQ but not PhoP; PA3044 but not PA3045; PilR but not PilS), which indicated that they were cross-talking with other TCS components. Other TCS components were either orphans (no adjacent senor kinase or response regulator), perhaps also acting through cross talk to another TCS component, or in a few instances the mutant in the second component was not available. Interestingly there was one instance (WspR-WspE) where the sensor kinase and response regulator mutants had opposite effects, although for the Wsp system there are substantial doubts as to whether these represent a cognate pair. Intriguingly there were only 2 un-annotated TCS components identified in the collection to have toxicity phenotypes, and both led to increased cytotoxicity.
Overall, we demonstrated an effect on cytotoxicity of TCS components with known involvement in type IV pili (pilG, pilH, pilR) and flagella-mediated motility (fleQ, fleS, fleR), virulence (gacS, gacA, phoQ, algR, cbrA, mifS, algR), cyclic-di-GMP signaling (wspR, rocA1, fleQ, wspE), and metabolism (cbrAB, dctB, ntrBC, fpvR). In particular, the well-known virulence regulator AlgR of the AlgR-FimS TCS, showed a 67% decrease in cytotoxicity. This role for AlgR joins a wide range of other functions in several aspects of P. aeruginosa virulence, including regulation of T3SS [22,23], likely explaining its cytotoxicity phenotype, alginate and LPS biosynthesis, biofilm formation, hydrogen cyanide production [24,25], and twitching and swarming motilities [7,19], as well as regulation of virulence in murine models [26]. A mutant in the sensor kinase-encoding gene dctB (PA5165) showed only 13% of the cytotoxicity of WT (Table 1). The DctB-DctD two-component system has been identified in P. aeruginosa as having a role in C4-dicarboxylate transport [27,28,29], however intriguingly the dctD mutant had no cytotoxicity defect. Conversely, the probable sensor kinase PA2882 (139% cytotoxicity of WT) has weak homology to the binding domain found in sensors of C4-dicarboxylates.
Table 1. Effect of strain PA14 mutations in two-component regulatory system kinases and response regulators on cytotoxicity towards human bronchial epithelial cells. Shown are those mutants that demonstrated >15% change in cytotoxicity compared to WT. In general 3 or more experiments were performed assessing cytotoxicity (measured as LDH release after 8 hours of infection); results are expressed as the mean ± standard error expressed as a percentage of cytotoxicity caused by WT.
| PA14 locus ID |
PAO1 homolog |
Gene name |
Description |
Mean % of WT ± standard error |
| Mutants with increased cytotoxicity |
| PA14_07840 |
PA0601 |
agtR |
Two-component response regulator; contains a CheY-like receiver domain; amine uptake |
119.9 ± 4.2 |
| PA14_52260 |
PA0928 |
gacS |
Sensor/response regulator hybrid; multi-host virulence through regulation of small regulatory RNAs RsmZ and RsmY |
134.3 ± 4.7 |
| PA14_49170 |
PA1180 |
phoQ |
Two-component sensor kinase PhoQ |
121.1 ± 5.7‡ |
| PA14_45590 |
PA1458 |
|
Probable two-component sensor kinase; putative homolog of E. coli chemotaxis regulator CheA |
144.3 ± 6.3 |
| PA14_33780 |
PA2388 |
fpvR |
Probable Fe2+-dicitrate sensor kinase |
121.6 ± 7.9 |
| PA14_30650 |
PA2586 |
gacA |
Response regulator; multi-host virulence through regulation of small regulatory RNAs RsmZ and RsmY |
144.7 ± 15.8 |
| PA14_26810 |
PA2882 |
|
Probable two-component sensor kinase; has binding domain homologous to that found in sensors of C4-dicarboxylates |
139.3 ± 15.7 |
| PA14_16470 |
PA3704 |
wspE |
CheA-type sensor kinase; c-di-GMP regulation |
134.5 ± 10.4 |
| PA14_62530 |
PA4725 |
cbrA |
Two-component sensor kinase; required for carbon-nitrogen balance and control of catabolite repression |
158.8 ± 9.1 |
| PA14_62540 |
PA4726 |
cbrB |
Two-component response regulator; required for carbon-nitrogen balance and control of catabolite repression |
140.8 ± 9.7 |
| PA14_67680 |
PA5125 |
ntrC |
Two-component response regulator; regulates use of carbon and nitrogen |
122.6 ± 4.1 |
| PA14_67670 |
PA5124 |
ntrB |
Two-component sensor kinase; regulates use of carbon and nitrogen |
117.1 ± 5.8 |
| PA14_70790 |
PA5364 |
|
Probable two-component response regulator |
130.4 ± 9.1 |
| PA14_72740 |
PA5512 |
mifS |
Two-component sensor kinase; regulates biofilm development |
119.6 ± 13.2 |
| Mutants with decreased cytotoxicity |
| PA14_05320 |
PA0408 |
pilG |
Type IV pilus response regulator; required for pilus extension and twitching motility |
28.8 ± 4.4 |
| PA14_05330 |
PA0409 |
pilH |
Type IV pilus response regulator; required for pilus retraction |
25.8 ± 1.5 |
| PA14_50220 |
PA1097 |
fleQ |
Flagella major transcriptional regulator; cyclic-di-GMP responsive; potential FleSR modulator |
77.6 ± 12.7 |
| PA14_50200 |
PA1098 |
fleS |
Two-component sensor kinase; required for hook and basal body protein biosynthesis for flagellum assembly |
20.6 ± 6.7‡ |
| PA14_50180 |
PA1099 |
fleR |
Two-component response regulator; required for hook and basal body protein biosynthesis for flagellum assembly |
12.3 ± 0.8‡ |
| PA14_16500 |
PA3702 |
wspR |
Two-component response regulator with GGDEF domain; c-di-GMP regulation |
16.8 ± 3.7 |
| PA14_12780 |
PA3948 |
rocA |
Two-component response regulator; cyclic-di-GMP regulation |
53.2 ± 0.9 |
| PA14_60260 |
PA4547 |
pilR |
Two-component response regulator; required for pilus expression and therefore for type IV pilus biosynthesis |
14.6 ± 4.5 |
| PA14_68230 |
PA5165 |
dctB |
Two-component sensor kinase; regulates a C4-dicarboxylate transport system with DctD |
14.9 ± 3.5 |
| PA14_69470 |
PA5261 |
algR |
Alginate biosynthesis regulatory protein |
33.2 ± 11.7 |
| ‡ Mutants are listed in order of the PAO1 homolog. |
To determine the possible mechanisms underlying altered cytotoxicity, we assessed the regulation by selected TCS components of several known virulence factors (elastase, type 3 secretion, lipase, exotoxin A), each of which are known to exert independent cytotoxic effects on host cells (Table 2). Furthermore, we assessed whether there was a defect in adherence to host epithelial cells that might impact on cytotoxicity (Table 3). Overall these studies demonstrated the altered expression of exotoxin A (fleS), type 3 secretion (fleQ, fleR, and fleS) and elastase genes (fleQ, fleR, and fleS), as well as defects in adherence (fleS, fliC, pilB, wspR). We concluded that generally speaking there was no single mechanism operating in the mutants, and that selected TCS regulators were able to influence multiple mechanisms of cytotoxicity.
3.2. A regulator of flagellum biosynthesis affected cytotoxicity, biofilm formation and motility
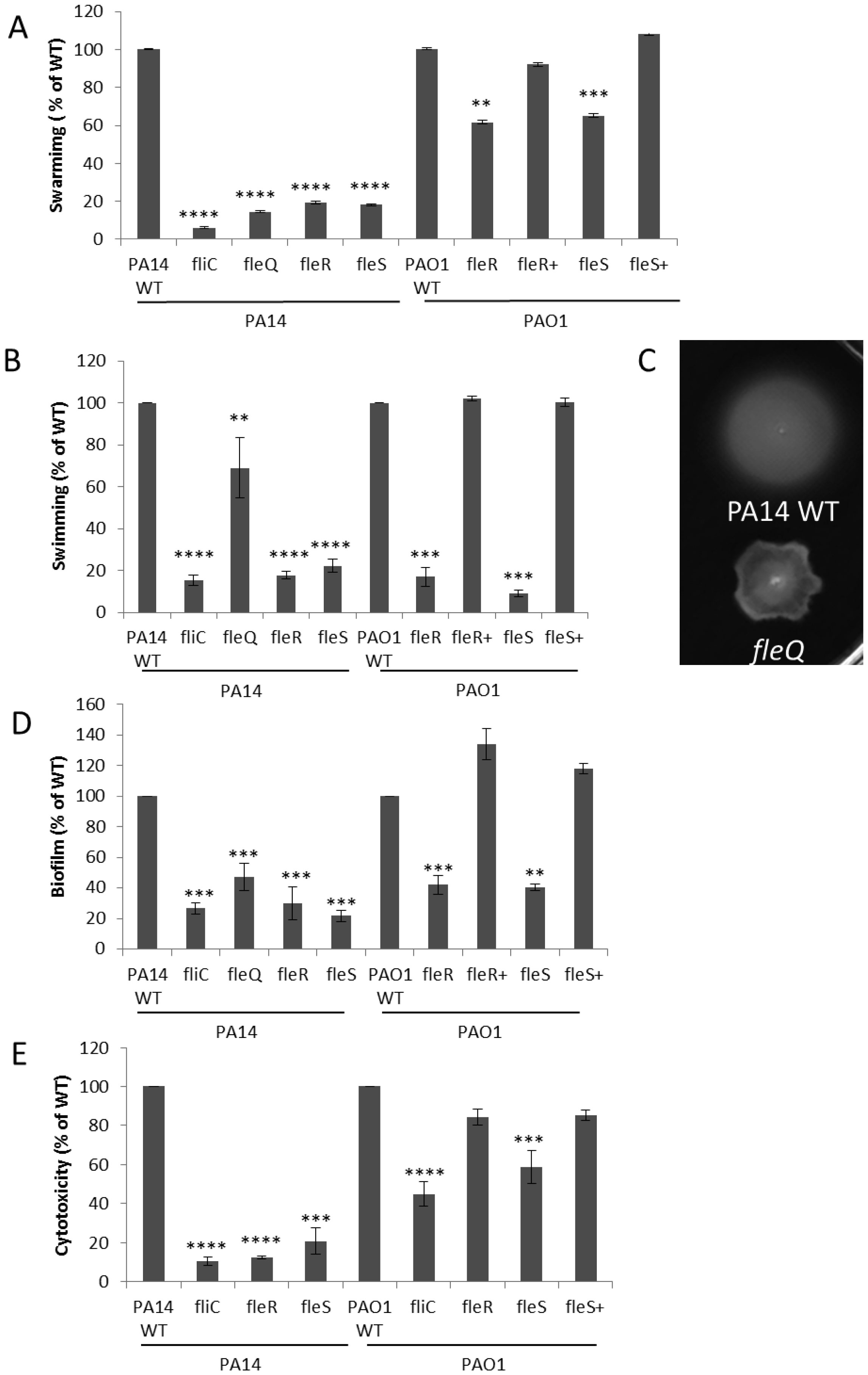
A decrease in cytotoxicity was demonstrated for mutants in the flagella-regulating TCS, FleS-FleR (21% and 12% of WT respectively) (Table 1). The FleS-FleR system controls the expression of genes encoding the basal body, hook and filament proteins in flagellum biogenesis. Neither fleS nor fleR mutants produce flagella and both have major swimming [30] and swarming (PA14 only; Figure 1A) deficiencies, as confirmed here by comparison to the control non-flagellated mutant, fliC (Figure 1B).
The bacterial flagellum is exported via a system that is ancestrally related to the T3SS [31,32] which in P. aeruginosa is responsible for secreting four known virulence effectors, ExoT, ExoY, ExoS, and ExoU [1], the latter of which is strongly cytotoxic and is expressed in strain PA14. To investigate potential overlaps between flagella and T3SS, qPCR was performed on the fleQ, fleR, and fleS mutants, revealing 1.9-fold to 3.5-fold decreases in the expression of exsA, the master T3SS regulator (Table 2). Therefore the fleQRS system likely plays a role in regulating the T3SS, which in turn has an impact on cytotoxicity.
In addition to their overlapping effects on the T3SS, flagella are involved in adherence and motility. Flagella as well as pili are required for biofilm formation [20] and swarming motility [33]. Similar to the trends shown for swimming and cytotoxicity, fleR and fleS mutants demonstrated approximately 4-fold reductions in biofilm formation (Figure 1D). Both mutants also demonstrated substantial deficiencies in swarming (Figure 1A), consistent with the known role that FleRS plays in controlling flagella expression [34]. Given the known role of flagella in adherence to surfaces, we could demonstrate that the fleS mutant had a major defect in adherence to HBE cells (Table 3); surprisingly, the fleR mutant demonstrated only a marginal defect while the upstream fleQ mutant had a strong but more modest decrease in adherence (Table 3) despite its major effect on adherence to mucin [35].
Mutants in both fleR and fleS and their complemented counterparts were available in strain PAO1 and have previously been published by this lab [14]. Strain PAO1 is less virulent and far less cytotoxic than strain PA14, and correspondingly the disruption of fleS in strain PA14 resulted in a more substantial reduction in cytotoxicity compared to WT (20.6%) than in PAO1 [58%; although this could be complemented to 85% of WT (Figure 1E)]. In contrast to its effect in strain PA14, the fleR PAO1 mutant showed very little change in cytotoxicity. Sequence alignment demonstrated 100% identity (comparing strains PA14 and PAO1) in the amino acid sequences for FleR, and a single threonine to proline substitution at the N-terminus in FleS. As with strain PA14, both fleR and fleS PAO1 mutants demonstrated downregulation of the T3SS (exsA; Table 2) and like PA14, only the fleS mutant showed a substantial adherence deficiency. These data further supported the conclusions that one basis for the reduced virulence observed in PAO1 might be altered regulation in the two different strain backgrounds. Consistent with the concept of differential regulation in these two strains, a phoQ mutant in strain PAO1 was substantially less cytotoxic [9] but the same mutant showed increased cytotoxicity in strain PA14 (Table 1). Similarly a dctB mutant showed no deficiency in strain PAO1 (data not shown) but a substantial decrease in cytotoxicity in strain PA14 (Table 1).
Table 2. Regulation of selected known virulence genes in mutants compared to the WT. The effects of various mutations on expression of lipC (lipase C), toxA (exotoxin A), exsA (master regulator of T3SS), compared to the control (pilS) were detected by qRT-PCR. Shown is the mean ± standard error. Student's t-test where *p < 0.05, **p < 0.01, ***p < 0.001, and ****p < 0.0001.
| Mutant |
Fold change compared to WT |
| PA14 |
lipC |
toxA |
exsA |
lasB |
| fleQ |
−1.54 ± 0.17 |
1.29 ± 0.12 |
−1.89 ± 0.10**** |
−1.89 ± 0.24*** |
| fleR |
1.10 ± 0.03 |
1.45 ± 0.21 |
−2.16 ± 0.09*** |
−1.33 ± 0.15*** |
| fleS |
−1.57 ± 0.10 |
−3.36 ± 0.28*** |
−2.74 ± 0.48**** |
−2.25 ± 0.23*** |
| pilS |
−1.03 ± 0.05 |
1.55 ± 0.39 |
−1.42 ± 0.22 |
−1.7 ± 0.36 |
| PAO1 |
|
|
|
|
| fleR |
−1.13 ± 0.28 |
−1.45 ± 0.02 |
−2.7 ± 0.89** |
−2.42 ± 1.64 |
| fleS |
1.15 ± 0.27 |
−1.45 ± 0.47 |
−3.49 ± 0.37*** |
−2.84 ± 0.66** |
FleQ is upstream of FleRS and has been proposed to act in a regulatory cascade with FleR in controlling motility and adhesion in P. aeruginosa. The fleQ mutant demonstrated a more modest reduction in cytotoxicity compared to either fleR or fleS (22% vs. 79-88%). Intriguingly although FleQ has been termed a master flagella regulator [35], mutation of fleQ had only a modest effect on swimming, consistent with its more modest decrease in cytotoxicity compared to the fleR and fleS mutants. Indeed the swimming phenotype observed was unusual (Figure 1C), displaying an uneven spread through the medium. Conversely, a mutant in the probable sensor PA1458 [33], which has been suggested to be a homolog of E. coli chemotaxis regulator CheA and is expressed in a FleQ dependent manner [34], demonstrated considerably higher cytotoxicity (144% of WT). This transposon mutant also displayed deficiencies in swimming and swarming motilities, but not in biofilm formation [19].
3.3. Mutants in type IV pili demonstrated decreased cytotoxicity
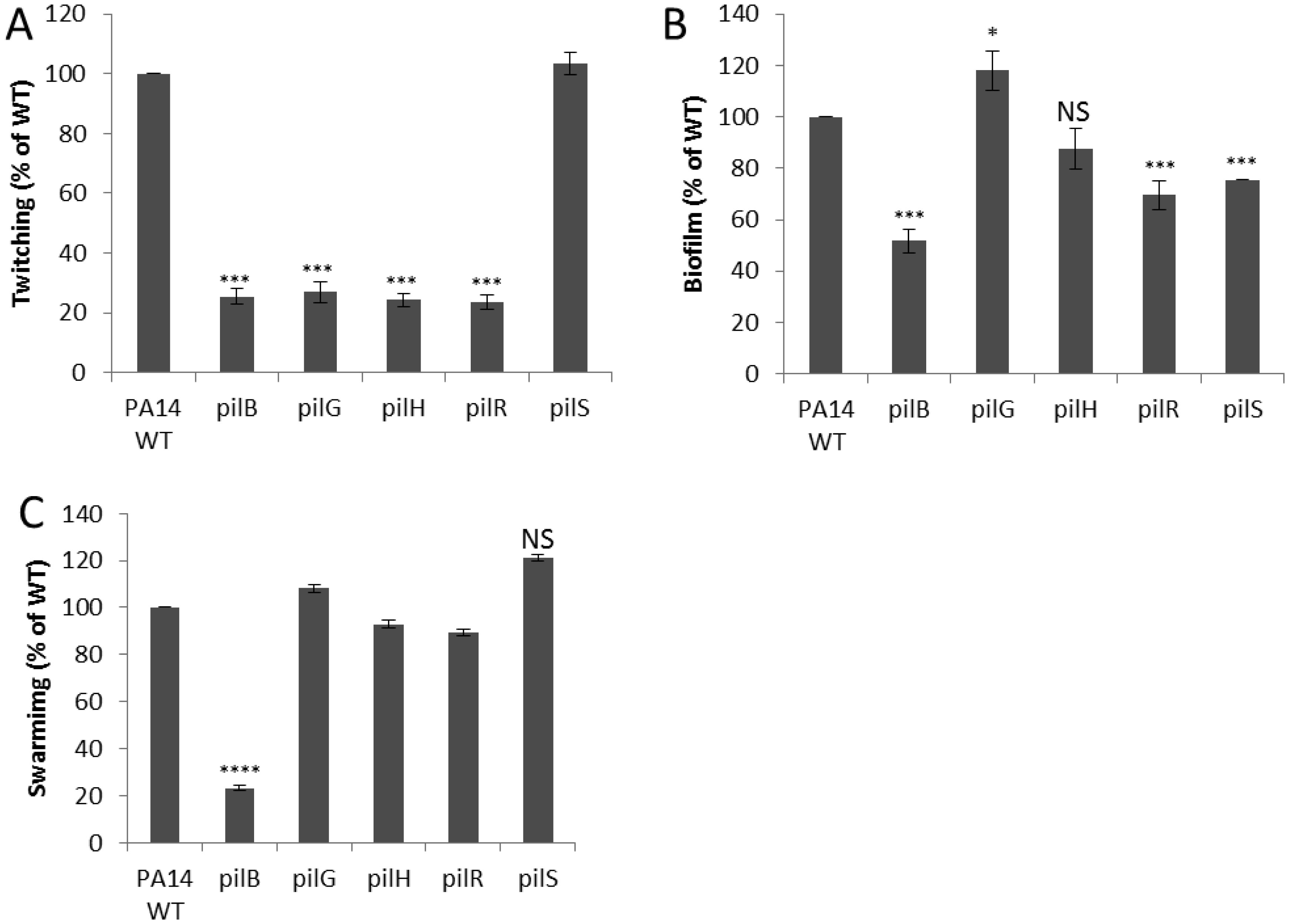
The PilS-PilR two-component system controls the transcription of pilA which encodes the type IV pilin subunit [36]. Bacterial pili are responsible for adherence to surfaces, twitching motility and biofilm formation. A pilR response regulator mutant demonstrated only 15% of the cytotoxicity of WT, while a mutant in the sensor kinase pilS showed no differences. Such a difference could indicate either that the sensor kinase PilS negatively regulated PilR, or that PilR cross-talked with a second sensor kinase. The pilGHIJKL-chpABCDE chemosensory gene cluster also contributes to the biogenesis of type IV pili, as well as to the direction and pattern of twitching motility, which are known to be essential for non-opsonic phagocytosis [37], initial attachment to inert surfaces, biofilm formation, and pathogenesis in many models [20,38,39,40,41]. The type IV pilus regulators, pilG and pilH demonstrated respectively 29% and 26% of the cytotoxicity of WT. Consistent with these cytotoxicity data, the pilG, pilH, and pilR mutants, but not the pilS mutant, were deficient in twitching motility (Figure 2A). In contrast, regarding biofilm formation there was a different trend (Figure 2B) since both pilR and pilS mutants demonstrated reductions in biofilm formation, while the pilG mutant demonstrated a small increase in biofilm formation. Conversely swarming motility, which requires type IV pili [19,33], was not affected by any of these regulators, but was affected in the non-piliated control mutant, pilB (Figure 2C). None of the pilus regulators tested had a statistically significant defect in adherence to HBE cells, in contrast to the pilB mutant that was very deficient (Table 3). This indicates that the observed cytotoxicity defects in these regulator mutants likely related to their differential ability to interact with epithelial cells rather than the presence or absence of pili per se.
3.4. Cytotoxicity was affected by the Wsp chemosensory regulators that affect c-di-GMP
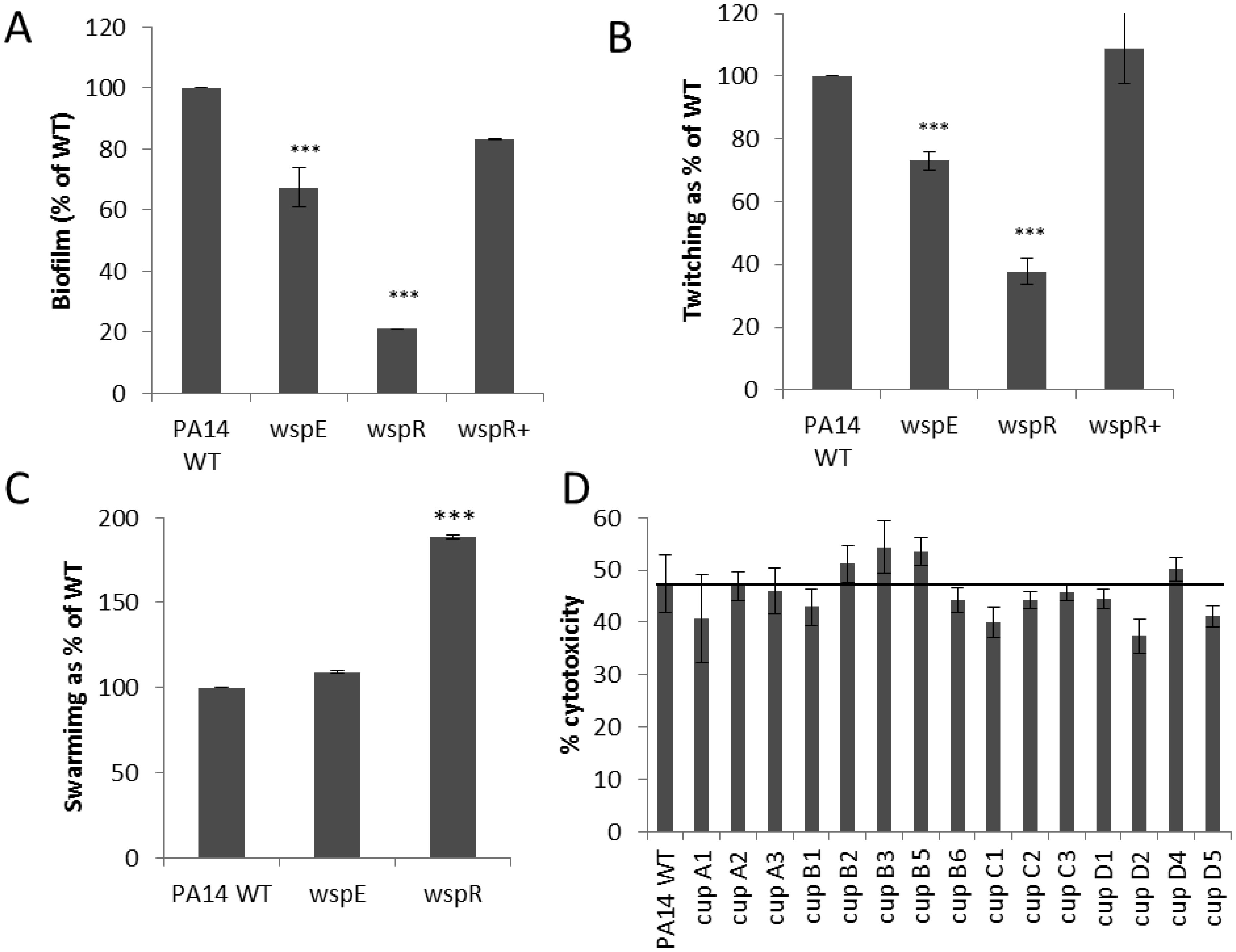
The Wsp chemosensory-type two component regulator is involved in cyclic-di-GMP (c-di-GMP) signaling networks. Instead of the DNA-binding domain of classic two-component regulators, WspR contains an enzymatic GGDEF diguanylate cyclase domain [40,42]. A mutant in the wspR response regulator displayed only 16.8% of the cytotoxicity of the WT, while a mutant in its cognate CheA-type sensor kinase WspE demonstrated a strongly increased cytotoxicity to 134% of WT (Table 1; N.B. another CheA homolog PA1458 also had a strong increase in cytotoxicity as described above). Analysis of known toxin secretion pathways by qPCR demonstrated a 2-fold increase in the type 3 secretion gene pscD for the wspE mutant which may explain its increased cytotoxic ability.
C-di-GMP has been proposed to affect functions related to the switch between the motile, single cell state and the surface-associated multicellular biofilm state [43]. The levels of c-di-GMP are regulated by GGDEF domain-containing diguanylate cyclases (e.g. WspR) and EAL-domain containing c-di-GMP phosphodiesterases [40,42]. Increased levels of c-di-GMP have been associated with increased matrix production and biofilm formation while low levels of c-di-GMP downregulate matrix production and promote a planktonic lifestyle [40]. For this reason, the ability of the Wsp mutants to form biofilms and mediate various motilities was tested. The wspR mutant was nearly completely impaired in biofilm formation, while wspE reduced biofilm formation to two thirds of WT (Figure 3A). Similarly a wspR mutant was severely impaired in twitching, while wspE led to only a modest defect in twitching (Figure 3B). Both the twitching and biofilm deficiencies of wspR could be restored to WT levels through complementation. The opposite effects of wspR and wspE mutants on cytotoxicity, but similar effects on twitching and biofilm formation indicated that these properties are differentially regulated. There was no effect on swarming for wspE, but wspR demonstrated a substantial increase (188% of WT). Swimming was unaffected (data not shown) and only the wspR mutant was deficient in adherence to HBE cells (Table 3).
Table 3. Adherence of TCS mutants to HBE cells after 1 hour. Student's t-test where *p < 0.05, **p < 0.01, ***p < 0.001, and ****p < 0.0001 compared to wildtype.
| Strain |
% Adhered ± SEM |
| PA14 WT |
7.6 ± 1.6 |
| algR |
0.3 ± 0.2* |
| cbrA |
2.0 ± 0.4* |
| cbrB |
2.8 ± 0.6 |
| dctB |
0.3 ± 0.2* |
| fleQ |
1.1 ± 0.4* |
| fleR |
2.5 ± 1.0* |
| fleS |
0.2 ± 0.1**** |
| fliC |
0.5 ± 0.4* |
| fpvR |
1.7 ± 0.4* |
| gacA |
4.1 ± 1.1 |
| gacS |
6.6 ± 1.7 |
| mifS |
2.5 ± 1.2 |
| ntrB |
1.6 ± 1.3* |
| ntrC |
1.1 ± 0.1* |
| phoQ |
2.6 ± 0.4 |
| pilB |
1.8 ± 0.5* |
| pilG |
6.7 ± 1.4 |
| pilH |
2.7 ± 0.7* |
| pilR |
0.3 ± 0.1* |
| pilS |
8.1 ± 1.2 |
| rocA1 |
1.7 ± 0.6* |
| wspE |
7.6 ± 2.7 |
| wspR |
0.5 ± 0.2** |
| PA1458 |
4.4 ± 0.4 |
| PA2282 |
2.7 ± 0.7 |
| PA5364 |
2.9 ± 1.6 |
| PAO1 WT |
8.4 ± 1.4 |
| fleS |
0.5 ± 0.2* |
| flesR |
10.0 ± 1.2 |
Signaling via the Wsp chemosensory system (WspABCDEF) results in the activation of the WspR regulator causing the upregulation of adhesion factors, including the cupA gene cluster (one of five Cup fimbrial clusters in P. aeruginosa) [42,44] that was previously demonstrated to have a role in biofilm formation [39]. However individual mutants in Cup fimbria genes showed no major alterations in cytotoxicity (Figure 3D), indicating that cytotoxicity was related to other aspects of c-di-GMP regulation. It is possible that the twitching, biofilm and adherence deficiencies of wspR indicated that the Wsp chemosensory system plays a role in regulating type IV pili.
In addition, a rocA1 (also called sadA) response regulator mutant also showed modestly decreased cytotoxicity (53% of WT), although mutants in its neighboring genes rocR (sensor kinase) rocS (encoding an EAL domain) showed no effects, indicating that its effect on cytotoxicity might be independent of c-di-GMP signalling. Alternatively it is possible that other c-di-GMP producing proteins can be regulated directly or indirectly by rocA1 and thus c-di-GMP could still be involved.
4. Conclusions
P. aeruginosa is able to cause severe infections at any compromised epithelial site. The pathogenesis and the outcome of such an infection are influenced by the host immune response and the virulence factors of the infectious organism. These virulence factors are controlled in part by bacterial TCSs that can rapidly adjust bacterial physiology to changing medium conditions. Here we performed an initial survey study to demonstrate TCS regulation of cytotoxicity was quite broad. Thus, TCS mutants of P. aeruginosa strain PA14 were co-cultured with lung epithelial cells with the purpose of uncovering which TCSs were involved in the necrotic killing of these epithelial cells. In particular, the genes influencing cytotoxicity in PA14 seemed to be grouped into several themes: control of carbon and nitrogen utilization (dctB, cbrAB, ntrBC), motility and adherence (pilG, pilH, pilR, fleQ, fleR, fleS), and c-di-GMP signaling (wspR, wspE, rocA1).
Several of the TCS mutants that demonstrated reduced cytotoxicity were involved in adherence or motility either directly, as for the flagella and pilus regulators, or indirectly, such as the regulators of c-di-GMP, a bacterial secondary messenger known to reciprocally regulate adherence and motility [43]. The observation that adherence and motility are involved in various aspects of virulence such as cytotoxicity is well known, however the data here highlight the importance of strain variations when studying the contribution of TCSs to cytotoxicity. This cytotoxicity screen was performed in strain PA14 due to the availability of a reliable and quite comprehensive PA14 transposon mutant library [10]. A few genes, where mutants were available, were also analyzed in the considerably less toxic strain PAO1. Genes directly involved in the adherence of PAO1 or PA14 (e.g. flagellum and pilus synthesis/function) largely showed decreased cytotoxicity. In contrast, the comparison of PA14 and PAO1 mutants in phoQ (Table 1, Table S1) and fleR (Figure 1E) demonstrated a large variability in the control of cytotoxicity by these regulatory systems between the two strain backgrounds. This discrepancy might be in a large part a result of differences in the T3SS, due to the high cytotoxic capability of ExoU that is present only in strain PA14 [45]. Our own studies have shown that cytotoxicity in the PAO1 background is only partly due to the T3SS, and likely works through other toxic enzymes such as lipases and proteases, as indicated by the large reduction in the cytotoxicity of mutants in these exoenzymes in PAO1 [21]. Nonetheless, few TCSs were analyzed in PAO1 due to the limited availability of reliable mutants in that strain at the time the screen was performed (there were numerous anecdotal reports [46,47] and our own lab's experience that mutants of this library had become cross contaminated). It would thus be interesting to expand the screen into PAO1, as reliable mutants become available, to see which other TCSs show substantial differences in this strain background.
A key finding here was that not all predicted sensor/regulator pairs demonstrated equivalent changes in cytotoxicity. For example, mutants of pilR, dctB and phoQ demonstrated a change in cytotoxicity to HBE cells compared to the WT, yet their cognate partners, pilS, dctD and phoP, did not. TCSs can have very substantial regulons, and different systems might have some overlap with others [7,8,9]. It is conceivable that some TCSs might play more of a global regulatory role, whereby, for example, a sensor controls a large regulon by phosphorylating its cognate response regulator as well as other response regulators, or phosphorylates an adapter protein which relays signals between regulatory networks. Certainly, cytotoxicity appears to be regulated by many systems (Table 1). Indeed we previously demonstrated that CbrA regulated susceptibility to 3 antibiotics and persistence and virulence in animal models, independently of its adjacent TCS partner CbrB, although these TCS partners jointly regulated several other properties including cytotoxicity, biofilm formation, swarming motility and catabolite repression [8]. Intriguingly although chronic infections are associated with high biofilm capacity and low cytotoxicity while acute infections are the opposite, we identified TCS regulators that regulated both elements in the same direction indicating that these processes can be coordinately regulated. Comparisons of RNA-Seq performed on different mutants known to regulate cytotoxicity could help to describe the disparate signaling networks that in turn might enable identification of potential therapeutic targets.
The use of transposon libraries carries with it the strong potential for phenotypes to be incorrectly assigned to a particular gene due to a polar effect of the transposon on expression of a downstream gene or genes within an operon. As TCS sensors and regulators are quite often transcribed together in an operon, complementation studies of fleS, fleR, and wspR were performed in part to address the possibility of polar effects in these systems. Despite this, some polar effects can be difficult to identify. For example, in P. aeruginosa the disruption of phoP has been shown to exert a polar effect on downstream phoQ due to an overlap in the genes, but only the targeted mutation of phoQ results in a major phenotypic difference [13,48]. As not all of the TCSs studied here were chosen for further analysis, it is possible that in a few cases polar effects on downstream genes led to the observed cytotoxicity phenotype.
Although in vitro studies are often used to predict the effect of a mutation or substance in a host system, increased toxicity towards host cells does not always equate with increased virulence in vivo. For example, deletion of cbrA demonstrated an increase in in vitro cytotoxicity but a decrease in pathogenesis in a murine acute lung infection model [49]. Cell cultures do not accurately reflect the complexity of the host environment with its multitude of different cell types and secreted mediators. In addition, particularly with an opportunistic pathogen such as P. aeruginosa, the pathogenesis of any given mutant might be markedly altered in one in vivo infection model but not in another (e.g. acute lung vs. chronic lung). Due to this, it is possible that many TCS components screened in this study that demonstrated no observed change in cytotoxicity may indeed contribute to virulence in an in vivo model. Notwithstanding, it is far too costly and time consuming for broad in vivo screens to be practical, meaning that for now, molecular methods must be pursued.
Overall the regulation of cytotoxicity, motility and biofilm formation is very complex and highly interlinked. Two component regulators play a special role, likely related to their special ability to rapidly transduce environmental signals into altered bacterial lifestyles.
Acknowledgements
This work was supported by grants from the Canadian Institutes for Health Research and Cystic Fibrosis Canada (CFC) (No.2585). REWH holds a Canada Research Chair and a UBC Killam Professorship. ATYY received studentships from the CFC and the Natural Sciences and Engineering Research Council of Canada (NSERC). EBMB was a recipient of a scholarship from CFC. The group of JO is supported through the German Excellence Initiative and the BioInterface (BIF) Programme of the Karlsruher Institute of Technology (KIT) in the Helmholtz Association.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: