Modeling and simulation of some cell dispersion problems by a nonparametric method

1.   Introduction

In the past decades, great attention has been paid by many researchers to SIR epidemic models ^{[1,2,3,4,5,6,7]}, in which total host population is divided into three classes called susceptible ($ S $), infective ($ I $) and removed ($ R $), and the immunity that is obtained upon recovery is assumed to be permanent. In ^[8], for herpes viral infections, considering the fact of recovered individuals may relapse with reactivation of latent infection and reenter the infective class, Tudor proposed the following SIRI epidemic model:

where $ S(t), I(t) $ and $ R(t) $ represent the number of susceptible individuals, infectious individuals and recovered individuals at time $ t $, respectively. Assumptions made in the system (1.1) are homogeneous mixing and constant population size. The parameter $ A $ is the constant birth rate, $ \mu $ is the natural death rate, $ \beta $ is the contact rate, and $ \gamma $ is the recovery rate from the infective class. It is assumed that an individual in the recovered class can revert to the infective class with a constant rate $ \delta $. Here $ \delta > 0 $ implies that the recovered individuals would lose the immunity, and $ \delta = 0 $ implies that the recovered individuals acquire permanent immunity.

We note that in system (1.1), the total population size is assumed to be constant. In reality, demographic features which allow the population size to vary should be incorporated into epidemiological models in some cases. For a relatively long-lasting disease or a disease with high death rate, the assumption of logistic growth input of the susceptible seems more reasonable ^[9]. In ^[10], Gao and Hethcote investigated a SIRS model with the standard incidence rate, and considered a demographic structure with density-dependent restricted population growth by the logistic equation. In ^[11], Li et al. studied a SIR epidemic model with logistic growth and saturated treatment, and the existence of the stable limit cycles was obtained. Rencently, there are growing interests in epidemiological models with demographic structures of logistic type ^{[12,13,14,15,16]}.

It is worth noting that in the above models, the transmission coefficient is assumed to be constant, and the infected person has the same infectivity during their periodic infection. However, laboratory studies suggest that the infectivity of infectious individuals be different at the differential age of infection ^[17,18]. Further, it was reported in ^[19,20] that, age-structure of a population is an important factor which affects the dynamics of disease transmission. In ^[21], Magal et al. discussed an infection-age model of disease transmission, where both the infectiousness and the removal rate depend on the infection age. In ^[22], an age structured SIRS epidemic model with age of recovery is studied, and the existence of a local Hopf bifurcation is proved under certain conditions. In ^[23], Chen et al. considered an SIR epidemic model with infection age and saturated incidence, and established a threshold dynamics by applying the fluctuation lemma and Lyapunov functional.

Motivated by the works of Chen et al. ^[23], Gao and Hethcote^[10], and Tudor ^[8], in the present paper, we are concerned with the effects of logistic growth and age of infection on the transmission dynamics of infectious diseases. To this end, we consider the following differential equation system:

with the boundary condition

and the initial condition

where $ \mathscr{X} = \mathbb{R}^+\times L_{+}^1(0, \infty) \times \mathbb{R}^+ $, $ L_+^1(0, \infty) $ is the set of all integrable functions from $ (0, \infty) $ into $ \mathbb{R}^+ = [0, \infty) $. In system (1.2), $ S(t) $ represents the number of susceptible individuals at time $ t $, $ i(a, t) $ represents the density of infected individuals with infection age $ a $ at time $ t $, and $ R(t) $ is the number of individuals who have been infected and temporarily recovered at time $ t $. All parameters in system (1.2) are positive constants, and their definitions are listed in Table 1.

In the sequel, we further make the following assumption:

Assumption 1.1 $ \beta(a)\in L_+^\infty((0, +\infty), \mathbb{R}) $, moreover

For convenience, we assume that

where $ e^{-(\mu+ \gamma)a} $ is the probability of infected individual to survive to age $ a $ and $ \tau > 0 $, $ \beta^* > 0 $.

The organization of this paper is as follows. In Section 2, we formulate system (1.2) as an abstract non-densely defined Cauchy problem. In Section 3, we study the existence of feasible equilibria of system (1.2). In Section 4, the linearized equation and the characteristic equation of system (1.2) at the interior equilibrium are investigated, respectively. In Section 5, by analyzing corresponding characteristic equation, we discuss the existence of Hopf bifurcation. In Section 6, numerical examples are carried out to illustrate the theoretical results, and sensitivity analysis on several important parameters is carried out.

2.   Transformation of the Cauchy problem

In this section, we formulate system (1.2) as an abstract non-densely defined Cauchy problem.

Firstly, we normalize $ \tau $ in (1.2) by the timescaling and age-scaling

and consider the following distribution

Dropping the hat notation, system (1.2) becomes

with the boundary condition $ i(0, t) = \tau\left[S(t)\int_{0}^{\infty} \beta(a)i(a, t){\rm d}a+\delta R(t)\right], $ and the initial condition $ S(0) = S^0\geq 0, i(0, \cdot) = i_0(a)\in L^1((0, +\infty), \mathbb{R}), R(0) = R^0\geq 0 $, where the new function $ \beta(a) $ is defined by

and

here $ \tau\geq 0, \beta^* > 0. $

Define

where

then the first and the third equations of system (2.1) can be rewritten as follows

where

and

here

Let

Accordingly, system (2.1) is equivalent to the following system:

where

and

We now consider the following Banach space

with the norm

Define the linear operator $ L_\tau: D(L_\tau) \rightarrow X $ by

with $ D(L_\tau) = \{0_{\mathbb{R}^3}\}\times W^{1, 1}((0, +\infty), \mathbb{R}^3)\subset X $, and the operator $ F: \overline{D(L_\tau)} \rightarrow X $ by

Therefore, the linear operator $ L_\tau $ is non-densely defined due to

Letting $ x(t) = \left( $$\begin{array}{c} 0_{\mathbb{R}^3} \\ w(\cdot, t) \\ \end{array}$$ \right), $ system (2.3) is transformed into the following non-densely defined abstract Cauchy problem

Based on the results in ^[24] and ^[25], the global existence, uniqueness and positivity of solutions of system (2.4) are obtained.

3.   Existence of feasible equilibria

In this section, we study the existence of feasible equilibria of system (2.4).

Define the threshold parameter $ \mathfrak{R}_0 $ by

Suppose that $ \bar{x}(a) = \left( $$\begin{array}{c} 0_{\mathbb{R}^3} \\ \bar{w}(a) \\ \end{array}$$ \right)\in X_0 $ is a equilibrium of system (2.4). Then we have

which is equivalent to

By direct calculation, we obtain

where $ \bar{S} = \int_0^{+\infty}u_1(a, t){\rm d}a, \bar{R} = \int_0^{+\infty}u_2(a, t){\rm d}a $. From (3.1), it is easy to show that

Integrating Eq (3.2), we get

and

We derive from the first and second equations of Eq (3.1) that

This, together with (3.4), yields

On substituting (3.6) into (3.3), we obtain that

It follows from (3.5) that

We therefore follows from (3.6) and (3.8) that

On substituting (3.7)–(3.9) into (3.2), we get

Based on the discussions above, we have the following result.

Lemma 3.1. System (2.4) always has the equilibrium

In addition, if $ \mathfrak{R}_0 > 1 $, there exists a unique positive equilibrium

Correspondingly, for system (1.2), we have the following result.

Theorem 3.1. System (1.2) always has a disease-free steady state $ E_0(K, 0, 0) $. If $ \mathfrak{R}_0 > 1 $, system (1.2) has a unique endemic steady state $ E^*(S^*, i^*(a), R^*) $, where

4.   Characteristic equation

In this section, we investivate the linearized equation of (2.4) around the positive equilibrium $ \bar{x}^*(a) $, and the characteristic equation of (2.4) at $ \bar{x}^*(a) $, respectively.

Making the change of variable $ y(t): = x(t)-\bar{x}^*(a) $, system (2.4) becomes

Accordingly, the linearized equation of system (4.1) around the origin is

where

with

After that, system (4.1) can be rewritten as

where the linear operator $ \mathscr{L}: = L_\tau+\tau DF(\bar{x}^*(a)) $ and

satisfying $ \mathscr{F}(0) = 0, D\mathscr{F}(0) = 0 $.

In the following, we give the characteristic equation of (2.4) at the positive equilibrium. By means of the method used in ^[26], we obtain the following lemma.

Lemma 4.1. Let $ \lambda\in\Omega = \{ \lambda\in\mathbb{C}:{\rm Re}(\lambda) > -\mu\tau\}, \lambda\in\rho(L_{\tau}) $ and

with $ \left( $$\begin{array}{c} \alpha \\ \psi \\ \end{array}$$ \right)\in X $ and $ \left( $$\begin{array}{c} 0_{\mathbb{R}^3} \\ \varphi \end{array}$$ \right)\in D(L_\tau) $, where $ L_\tau $ is a Hille-Yosida operator and

Let $ L_0 $ be the part of $ L_\tau $ in $ \overline{D(L_\tau)} $, that is $ L_0: = D(L_0)\subset X \rightarrow X. $ For $ \left( $$\begin{array}{c} 0_{\mathbb{R}^3} \\ \varphi \end{array}$$ \right)\in D(L_0) $, we have

where $ \hat{L_0}(\varphi) = -\varphi'-\tau Q\varphi $ with $ D(\hat{L_0}) = \{\varphi\in W^{1, 1}((0, +\infty), \mathbb{R}^3):\varphi(0) = 0\} $.

Note that $ \tau DF(\bar{x}^*): D(L_\tau)\subset X \rightarrow X $ is a compact bounded linear operator. It follows from (4.4) that

Therefore

By using the perturbation results of ^[35], we get

Hence, we have the following result.

Lemma 4.2. The linear operator $ \mathscr{L}_\tau $ is a Hille-Yosida operator, and its part $ (\mathscr{L}_\tau)_0 $ in $ \overline{D(\mathscr{L}_\tau)} $ satisfies

Set $ \lambda\in \Omega $. Since $ \lambda I-L_\tau $ is invertible, it follows that $ \lambda I-\mathscr{L}_\tau $ is invertible if and only if $ I-\tau D F(\bar{x}^*)(\lambda I-L_\tau)^{-1} $ is invertible, and

We now consider

which yields

It is easy to show that

Taking the formula of $ DB(\bar{w}^*) $ into consideration, we obtain

where

and

From (4.5), whenever $ \Delta(\lambda) $ is invertible, we have

Using a similar argument as in ^[27], it is easy to verify the following result.

Lemma 4.3. The following results hold

(i) $ \sigma(\mathscr{L}_\tau)\cap \Omega = \sigma_p(\mathscr{L}_\tau)\cap \Omega = \{ \lambda\in\Omega:\det(\Delta(\lambda)) = 0\} $;

(ii) If $ \lambda\in \rho(\mathscr{L}_\tau)\cap \Omega $, we have the formula for resolvent

where

with $ \Delta(\lambda) $ and $ \mathcal {K}(\lambda, \psi) $ given by (4.6) and (4.7).

Under Assumption 1.1, it therefore follows from (4.7) that

From (4.6), we obtain the characteristic equation of system (2.4) at the positive equilibrium $ \bar{x}^*(a) $ as follows:

where

here

Letting $ \lambda = \tau\zeta $, then

It is easy to show that

5.   Existence of Hopf bifurcation

In this section, by applying Hopf bifurcation theory ^[26], we are concerned with the existence of Hopf bifurcation for the Cauchy problem (2.4) by regarding $ \tau $ as the bifurcation parameter.

From (4.11), we have

For any $ \tau\geq 0 $, if $ \mathscr{R}_0 > 1 $, it is easy to show that

Therefore, $ \zeta = 0 $ is not an eigenvalue of Eq (5.1). Furthermore, when $ \tau = 0, $ Eq (5.1) reduces to

A direct calculation shows that

and

Hence, by Routh-Hurwitz criterion, when $ \tau = 0, $ we see that the equilibrium $ \bar{x}^*(a) $ is locally asymptotically stable if $ \mathscr{R}_0 > 1 $; and $ \bar{x}^*(a) $ is unstable if $ \mathscr{R}_0 < 1 $.

Substituting $ \zeta = \rm{i} \omega(\omega > 0 $) into Eq (5.1) and separating the real and imaginary parts, one obtains that

Squaring and adding the two equations of (5.3), it follows that

where

Letting $ z = \omega^2 $, Eq (5.4) can be written as

Denote

and define

By a similar argument as in ^[28], we have the following result.

Lemma 5.1. ^[28]. For the polynomial equation (5.6), the following results hold true:

(i) If $ h_0 < 0 $, then Eq (5.6) has at least one positive root.

(ii) If $ h_0\geq0 $ and $ \Delta < 0 $, then Eq (5.6) has no positive root.

(iii) If $ h_0\geq0 $ and $ \Delta\geq0 $, then Eq (5.6) has at least one positive root if one of $ z_1^* > 0 $ and $ h(z_1^*)\leq 0 $.

Noting that

without loss of generality, we may assume that Eq (5.6) has two positive roots denoted respectively as $ z_1 $ and $ z_2 $. Then Eq (5.4) has two positive roots $ \omega_{k} = \sqrt{z_k}(k = 1, 2). $ Further, from (5.3), we have

where $ k = 1, 2;j = 0, 1, \cdots, $ and

Based on the above discussion, we have the following result.

Theorem 5.1. Let Assumption 1.1 and $ \mathscr{R}_0 > 1 $ hold. If $ \omega_{k} $ is a positive root of Eq (5.4) and $ q_1\neq0 $, then

Therefore $ \zeta = {\rm i} \omega_{k} $ is a simple root of Eq (5.1).

Proof. It follows from (5.1) that

and

Suppose that $ \frac{ \rm{d}g(\zeta)}{ \rm{d}\zeta}\Big|_{\zeta = {\rm i} \omega_{k}} = 0, $ then

Separating the real and imaginary parts in Eq (5.8), we obtain

Squaring and adding the two equations of (5.9), we derive that

which mean that

Since $ \omega_{k} > 0 $, it follows that

which leads to a contradiction. Hence, we have

Let $ \zeta(\tau) = \alpha(\tau)+{\rm i} \omega(\tau) $ be a root of Eq (5.1) satisfying $ \alpha(\tau_k^{(j)}) = 0, \omega(\tau_k^{(j)}) = \omega_{k} $, where

Lemma 5.2. Let Assumption 1.1 and $ \mathscr{R}_0 > 1 $ hold. If $ z_k = \omega_k^2, h'(z_k)\neq 0 $ and $ q_1\neq0 $, then

and $ {\rm{d}{\rm Re}\zeta(\tau)}/{\rm{d}\tau} $ and $ h'(z_k) $ have the same sign.

Proof. Differentiating the two sides of Eq (5.1) with respect to $ \tau $, we get

On substituting $ \zeta = {\rm i} \omega_k $ into Eq (5.1), by calculating, we have

A direct calculation shows that

From Eq (5.4), we get

It therefore follows that

Since $ z_k > 0, $ we conclude that $ {\rm Re}[{\rm{d}\zeta(\tau)}/{\rm{d}\tau}] $ and $ h'(z_k) $ have the same sign.

Noting that when $ \tau = 0 $, the equilibrium $ x^*(a) $ of (2.4) is locally asymptotically stable if $ \mathscr{R}_0 > 1 $, from what has been discussed above, we have the following results.

Theorem 5.2. Let $ \tau_k^{(j)} $ and $ \omega_0, \tau_0 $ be defined by (5.7) and (5.10), respectively. If Assumption 1.1 and $ \mathscr{R}_0 > 1 $, $ q_1\neq 0 $ hold.

(i) the endemic steady state $ E^* $ of system (1.2) is locally asymptotically stable for all $ \tau\geq0 $ if $ h_0\geq 0 $ and $ \Delta\leq 0. $

(ii) the endemic steady state $ E^* $ is asymptotically stable for $ \tau\in[0, \tau_0) $ if $ h_0 < 0 $ or $ h_0\geq 0, \Delta > 0, z_1^* > 0 $ and $ h(z_1^*)\leq 0 $.

(iii) system (1.2) undergoes a Hopf bifurcation at endemic steady state $ E^* $ when $ \tau = \tau_k^{(j)} \ (j = 0, 1, 2, \cdots) $ if the conditions as stated in (ii) are satisfied and $ h'(z_k)\neq 0. $

6.   Numerical simulations

In this section, numerical simulations will be given to illustrate the theoretical results in Section 5. Further, sensitivity analysis is used to quantify the range of variability in threshold parameter and to identify the key factors giving rise to threshold parameter, which is helpful to design treatment strategies.

6.1.   Dynamics of system (1.2)

In this section, we give a numerical example to illustrate the main results in Section 5.

Based on the research works of tuberculosis ^[29,30,32], parameter values of system (1.2) are summarized in Table 2, and the maximum infection age is $ 60 $. Denote the numbers of infected individuals at time $ t $ as $ I(t) = \int_0^{100}{i(t, a)}{\rm d}a $, and

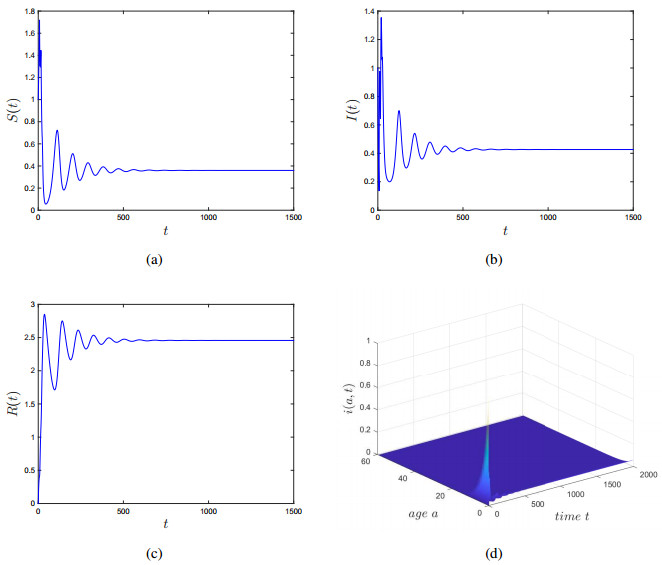
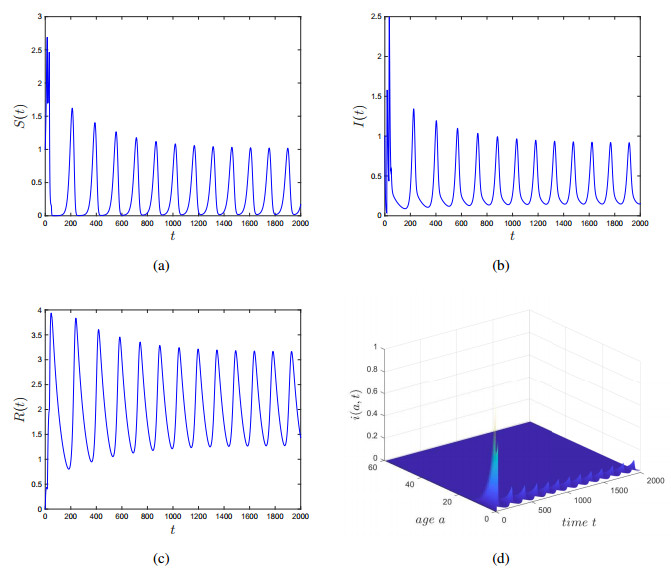
By calculation, we have $ \mathscr{R}_0 = 8.2379 > 1, h_0 = -1.1989 \times 10^{-7} < 0 $ and $ h'(z_k) = 2.7846 \times 10^{-4}\; > \; 0 $. In this case, system (1.2) has an endemic steady state $ E^*(0.6070, 0.0879\tau{e^{-0.3143\tau a}}, 3.4534) $. By calculation, we obtain $ \omega_0 = 0.0565 $ and $ \tau_0 = 14.3556 $. By Theorem 5.1, we see that the endemic steady state $ E^* $ is locally asymptotically stable if $ \tau\in[0, \tau_0) $ and is unstable if $ \tau > \tau_0 $. Further, system (1.2) undergoes a Hopf bifurcation at $ E^* $ when $ \tau = \tau_0 $. Numerical simulation illustrates the result above (see, Figures 1 and 2).

Remark. From Figure 1, we see that when the bifurcation parameter $ \tau $ is less than the critical value $ \tau_0 $, the endemic steady state $ E^* $ of system (1.2) is locally asymptotically stable. From Figure 2, we observe that $ E^* $ losses its stability and Hopf bifurcation occurs when $ \tau $ crosses $ \tau_0 $ to the right $ (\tau > \tau_0) $. This implies that the age, i.e., infection period $ \tau $ is the key factor that causes the endemic steady state $ E^* $ to become unstable and the appearance of Hopf bifurcation.

6.2.   Sensitivity analysis

Sensitivity analysis is used to quantify the range of variables in threshold parameter and identify the key factors giving rise to threshold parameter. In ^[33,34], Latin hypercube sampling (LHS) is found to be a more efficient statistical sampling technique which has been introduced to the field of disease modelling. LHS allows an un-biased estimate of the threshold parameter, with the advantage that it requires fewer samples than simple random sampling to achieve the same accuracy.

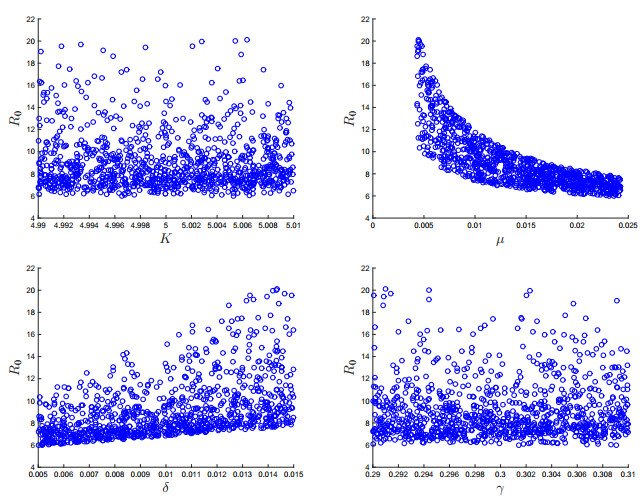
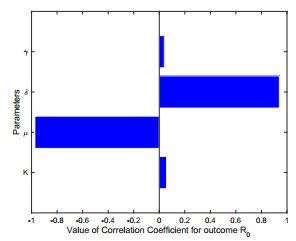
By analysis of the sample derived from Latin hypercube sampling, we can obtain large efficient data in respect to different parameters of $ {\mathscr{R}_0} $. Figure 3 shows the scatter plots of $ {\mathscr{R}_0} $ in respect to $ K $, $ \mu $, $ \delta $ and $ \gamma $, which implies that $ \delta $ is a positively correlative variable with $ {\mathscr{R}_0} $, while $ \mu $ is a negatively correlative variable. But the correlation between $ K $, $ \gamma $ and $ {\mathscr{R}_0} $ is not clear. In ^[34], Marino et al. mentioned that Partial Rank Correlation Coefficients (PRCCs) provide a measure of the strength of a linear association between the parameters and the threshold parameter. Furthermore, PRCCs are useful for identifying the most important parameters. The positive or negative of PRCCs respectively denote the positive or negative correlation with the threshold parameter, and the sizes of PRCCs measure the strength of the correlation. As can been seen in Figure 4, $ K $, $ \delta $ and $ \gamma $ are positively correlative variables with $ {\mathscr{R}_0} $ while $ \mu $ is negatively correlative variables.

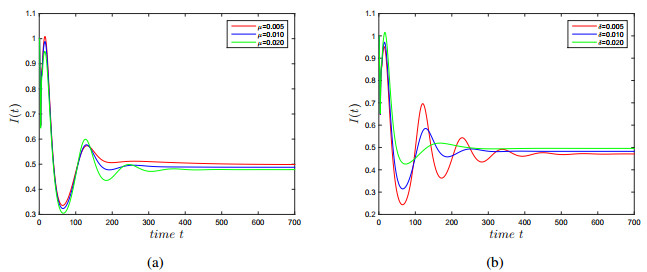
By selecting different parameter values, we can explore the influence of the parameters $ \mu $ and $ \delta $ on the numbers of infected individuals at time $ t $, which is denoted as $ I(t) $. As shown in Figure 5, increasing the natural death rate $ \mu $ and decreasing the rate at which recovered individuals return to the infective class will have a positive impact on $ I(t) $ to some extent, which means that the influence of $ \mu $ and $ \delta $ on $ I(t) $ is consistent with that on $ {\mathscr{R}_0} $.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. 11871316, 11801340), the Natural Science Foundation of Shanxi Province (Nos. 201801D121006, 201801D221007).

Conflict of interest

The authors declare that they have no competing interests.