A new approach to the problem of characterizing the dynamic behavior of nonlinear biosystems in the presence of model uncertainty using the notion of slow invariant manifold is proposed. The problem of interest is addressed within the context of singular partial differential equations (PDE) theory, and in particular, through a system of singular quasi-linear invariance PDEs for which a general set of conditions for solvability is provided. Within the class of analytic solutions, this set of conditions guarantees the existence and uniqueness of a locally analytic
solution which represents the system's slow invariant manifold exponentially attracting all dynamic trajectories in the absence of model uncertainty. An exact reduced-order model is then obtained through the restriction of the original biosystem dynamics on the slow manifold. The analyticity property of the solution to the invariance PDEs enables the development of a series solution method that can be easily implemented using MAPLE leading to polynomial approximations up to the desired degree of accuracy. Furthermore, the aforementioned attractivity property and the transition towards the above manifold is analyzed and characterized in the presence of model uncertainty. Finally, examples of certain immobilized enzyme bioreactors are considered to elucidate aspects of the proposed context of analysis.
1.
Introduction
Solar power integration to the power grid is significantly increasing in many countries [1]. Strong government policies towards greener power grid and other technological and economic factors have accelerated the growth of renewable energy generation. The growth of solar PV in 2017 was unprecedented; solar PV accounted for the 27% of overall renewables growth, followed by hydropower (22%) and bioenergy (12%) [2,3]. A large proportion of future electricity demand must be satisfied by renewable energy due to the global warming effects of conventional thermal generation. Costs of solar PV panels have reduced by more than 75% over the last decade [2]. This will continue to reduce further due to the strong focus on reducing the costs of manufacturing PV modules. Reductions in costs involve the use of thinner wafers, manufacturing wafers without ingot slicing, use of microinverters and use of multijunction solar cells [2]. Moreover, the conversion efficiency can also be increased up to 30–50%, especially by using multijunction solar cells [2].
The integration of renewable energy mostly depends on the system characteristics and further integration of renewable energy would require various types of system enhancements with an additional cost. With a large proportion of solar power in the power grid, system reliability will be drastically reduced. Large battery storage systems [4] or pump storage power plants are required to enhance the system reliability for the addition of more solar power. Accurate and reliable solar power forecasts can be used to overcome the above issues. In addition, solar power forecasting helps system control engineers to efficiently dispatch hydro and thermal power plants, manage the spinning reserves and transmission line constraints.
Solar power generation depends on seasonal changes, weather parameters, intra-hour variability and the technology used. Weather parameters such as direct irradiance, diffuse irradiance, wind speed, temperature, humidity and cloud cover can be used to model the solar power generation [5]. Thus, forecasted weather parameters can be used to obtain future solar power generation using the developed model. This is called point forecasting. Statistical methods such as regression models and Machine Learning (ML) methods can be used for modeling solar power generation.
Modeling complex and nonlinear systems using ML is a popular research field. Support Vector Machine (SVM) is a supervised ML algorithm which is used for solving classification and regression problems. SVM regression models are used to model the relationship between weather parameters and solar power generation [6,7,8,9,10,11,12,13,14]. Yang et al. [8] proposed a hybrid model consists of classification, training and forecasting stages. A self-organizing map (SOM) and learning vector quantization (LVQ) networks are used to classify the historical solar power generation data into different weather conditions e.g., rainy, sunny, etc. Then, several support vector regression (SVR) models are trained for different diurnal variations and weather conditions. In the forecasting stage, the most suitable SVR model is selected by the fuzzy inference method. Li et al. [9] have proposed SVR and Neural Network (NN) models for solar power forecasting. Time, historical power information and meteorological forecasts are used as inputs to the models. In [6,12], authors have proposed weather classification approaches with SVR forecasting. Days are classified into four categories: clear sky, cloudy, foggy and rainy. Separate SVR models are used to forecast solar power generation in each category. Fentis et al. [11] have compared feed-forward NN and SVM forecasting results using Root Mean Square Error (RMSE), Mean Square Error (MSE) and Mean Absolute Error (MAE). SVM model outperforms the NN model by a slight margin. Bouzerdoum et al. [13] have proposed a hybrid model consists of the SVM model and a seasonal Auto-Regressive Integrated Moving Average (ARIMA) method. In [14], authors have proposed a hybrid forecasting model combining Wavelet Transform (WT), Particle Swarm Optimization (PSO) and SVM for day-ahead power generation forecasting of a solar PV system. The parameters of the SVM are optimized and fine-tuned by PSO to achieve a higher forecasting accuracy.
In [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35], various types of NNs are proposed for solar power forecasting. Deep learning NNs such as Deep Belief Network (DBN), Long Short-Term Memory (LSTM) and Auto encoder-based LSTM are used to model solar power generation using weather parameters [22]. In [15,20], a modified Levenberg-Marquardt learning algorithm and Bayesian learning technique are used to determine the initial weights of multilayer perceptron NN instead of contrastive divergence method [36] used in [22]. Weather classification can be incorporated with NNs to improve the forecasting accuracy [19,23,24,31,33]. Separate NN models for different weather categories are trained to provide future solar power generation in each weather condition. Weather conditions can be categorized as cloudy, sunny, foggy, etc. [24]. A comparison of different learning rules and activation functions used in the multi-layer perceptron forecasting model is done in [21]. PSO techniques are used to update weights of feedforward NN in [26]. Two Numerical Weather Prediction (NWP) sources are used to improve the reliability and accuracy of a NN model in [27]. In [30], a one-hour-ahead solar power forecasting model is proposed using a combination of WT and artificial intelligence (AI) techniques. A novel PV power forecasting model based on NN is proposed in [32], considering aerosol index data as an additional input parameter. NNs consists of many hidden layers and hidden neurons (extreme learning machines) are used to model solar power generation in [35].
Similarity search-based models are proposed in [37,38,39]. The solar power forecasting is done by searching historically similar weather conditions and mapping the respective power generation values into the given NWP data. Authors have proposed a novel and efficient approaches for time series database search, similarity evaluation and assembling of similar clusters to an overall forecast.
Ensemble models integrate two or more ML techniques to provide a better forecast [5,40,41,42,43,44,45]. In [40], several forecasting models were implemented for predicting short term i.e., one hour ahead solar PV output. They include ARIMA, SVM, ANN, Adaptive Neuro-Fuzzy Inference System (ANFIS), and the combination models using Genetic Algorithm (GA). In [41], an ensemble model is proposed using auto-regressive, radial basis function (RBF) and forward NN models. The forward NN and RBF are trained using PSO to improve forecasting performance. In [5], an ensemble consists of seven ML techniques (decision tree, gradient boosting, K-nearest neighbors (KNN) with uniform weights, KNN with distance-based weights, Lasso, Random forests (RFs) and ridge) is proposed. Haque et al. [44] have proposed an ensemble algorithm that uses a combination of WT and fuzzy ARTMAP (FA) network. WT is used for data filtering and the ensemble model is optimized by a Firefly (FF) algorithm. In [45], an RF model is used as an ensemble learning method to combine the forecasts generated by SVMs.
Probabilistic models based on higher-order Markov chain and Bayesian methods are proposed in [46,47] respectively. An Intelligent solar power forecasting model based on Fuzzy logic is proposed in [48]. The forecasting model is applied for different types of days such as clear, hazy, partly cloudy and cloudy. Solar irradiance forecasting is a crucial factor in solar power forecasting. In [49], authors have proposed a corrective algorithm for improving the accuracy of global horizontal irradiation. An ANN is used to improve solar irradiance forecasts which are obtained from numerical weather prediction. In addition, descriptive reviews on available solar power forecasting methods can be found in [50,51].
According to the present literature, ensemble models show better forecasting performance than single machine learning methods [5,6,8,12,19,23,24,40,41,42,43,44,45]. Ensemble models are implemented in two different ways. One way is to cluster the dataset and apply a separate ML technique to each cluster [6,8,12,19,23,24,42]. The second method is to use different ML techniques on the same dataset and to derive more accurate forecasts by agammaegating the ML results [5,40,41,43,44,45]. In this paper, the authors have combined the above two approaches to provide a more accurate solar power forecast. Cloud cover data are used to cluster the dataset and ensembles consist of three ML techniques (RF, SVM, DBN) are used to model the solar power generation separately for each cluster. Moreover, it can be observed that the previously proposed ensemble models lack deep learning techniques such as DBNs, LSTM networks, etc. [5,40,41,42,43,44,45]. This limitation is addressed in this work by integrating a DBN to the proposed ensemble model. The results of three case studies are used to design the proposed ensemble model. This research extends the previous work proposed by the same authors in [52]. The proposed RF, SVM and DBN models in [52] are utilized in this work to implement stacking and averaging ensemble models. Then, by combining these two ensembling approaches, a generalized ensemble model is proposed. The proposed solar power generation model is applied to different clusters of the dataset to precisely capture the relationship between solar power generation and weather parameters. The accuracy of the proposed solar power forecasting model is compared with that of single machine learning techniques and several models present in literature.
Forecasted weather parameters are used as inputs to the proposed ensemble model. The weather parameters can be forecasted using NWP and have shown good accuracy in the short-term [53]. The forecasting horizon can be varied. However, for long-term forecasting, there will be a large error in the NWP. In this work, all the error terms are presented without the NWP error.
The paper is organized as follows. The design and implementation of the proposed ensemble model and several related case studies are described in Section 2. Section 3 presents a discussion on the outcomes of the proposed model. Section 4 concludes the paper.
2.
Implementation
The implementation procedure of the proposed ensemble model is explained in this section. Results of three case studies are analyzed to design the forecasting model which can predict the solar power generation with minimum forecasting error. The dataset explained in section 2.1 is used for training and validating the forecasting models implemented in case studies. Section 2.2 explains the feature selection procedure which is used to identify the most relevant weather parameters that affect the solar power generation. The performance measure is described in section 2.3. Brief descriptions of three ML algorithms which are used to build the ensemble model are given in section 2.4. In Section 2.5, case studies and results are presented. Feature selection and ensemble design are done by R programming language which is widely used for statistical computing. R Studio, free and open-source software is used as the development environment.
2.1. Dataset
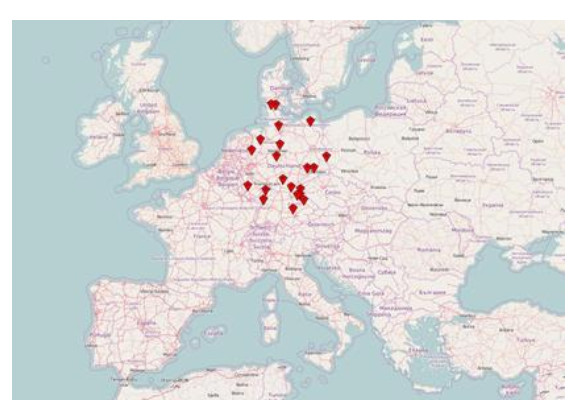
The data set of 21 German Photovoltaic (PV) facilities has been used in this study [22]. The nominal capacity of PV facilities ranges between 100 kW and 8500 kW i.e., the PV facilities range from rooftop solar arrays to solar farms. Historical NWP data and respective solar power outputs for 990 days are recorded in a three-hour resolution for each facility. The PV facilities are distributed throughout Germany as shown in Figure 1. The data set is normalized to improve the training performance of the DBN. Min-max normalization is used to normalize the weather parameters between 0 and 1. Solar power generation data are normalized by dividing the measured output power by the nominal output capacity of the corresponding PV facility. This helps to compare the forecasting accuracy without considering the PV capacity. All the observations are shuffled and 0.75 and 0.25 proportions of that are selected for training and testing, respectively.
2.2. Feature selection
The dataset contains more than 30 weather parameters. Therefore, to reduce the complexity of the ML algorithms, most important weather parameters should be identified. Feature selection algorithms such as Boruta can be used to identify the strong correlations between solar power generation and weather parameters [54]. In feature selection, Boruta expands the given dataset with permuted copies of all independent features. Then, the data in those permuted copies are shuffled to remove the dependencies with the target variable. These shuffled permuted copies are called shadow features. After that, an RF classifier is applied on the combined dataset and Boruta applies a feature importance measure such as mean decrease in accuracy to evaluate the importance of each variable. Finally, the classification algorithm stops either when all features get confirmed or rejected or it reaches a defined limit of RF iterations. Table 1 shows the most important weather parameters according to the Boruta algorithm. All the features with importance equal to or greater than 5 are selected as inputs to the ensemble model.
2.3. Performance measure
RMSE is used to evaluate the forecasting performance of the proposed ensemble models. It is the standard deviation of the prediction errors as shown in Eq 1. In RMSE calculation, the errors are squared before they are averaged. Therefore, the RMSE increases significantly when there are large prediction errors. Thus, RMSE is a more useful performance measure than MAE especially when large prediction errors are undesirable.
where N is the total number of predictions, x|n is the nth predicted value and xn is the nth actual value.
2.4. Machine learning techniques used to build the ensemble models
ML algorithms can be used to model ill-defined and complex systems (for e.g., solar PV facility) without considering the unknown nonlinear relationships within the system. Three ML algorithms i.e., DBN, SVM, and RF explained in [52] are used in this work to implement the proposed ensemble models. Moreover, the design parameters of each algorithm are explained in detail in [52].
2.4.1. Support vector machine regression
In SVR, the model inputs i.e. forecasted weather parameters are mapped to a high dimensional feature space using a Kernel function such as polynomial or Gaussian. Then, a linear regression function is computed which has at most ε deviation from the actual model outputs for all the training data. At the same time, the linear regression function should be kept as flat as possible. A symmetrical loss function is used to train the SVR model. Hence, a flexible cylinder of a minimal radius is symmetrically wrapped around the regression function to ignore the absolute values of errors less than ε.
The Kernel function of the SVR model is selected as Laplace which is a general-purpose Kernel used in both classification and regression applications. The cost of violation of constraints and the ε are obtained using the trial and error method and found to be 10 and 0.1 respectively.
2.4.2. Deep belief network
DBN is a type of deep neural network which comprises of multiple hidden layers. Multiple Restricted Boltzmann Machines (RBMs) are stacked to build the DBN. Firstly, greedy layer-wise training is done sequentially starting from the bottom layer (input layer). Each RBM layer learns a higher data representation of the preceding layer. This pre-training procedure allows better initialization of the weights of all the layers. Gibbs sampling based Contrastive Divergence (CD) method [36] is used for this initial pre-training process of stacked RBMs. Then, the weights are fine-tuned to improve DBN accuracy. The optimal values of the weights are calculated in this fine-tuning process which is generally done using the back-propagation method. In this study, two hidden layers are integrated to the DBN. The number of neurons per each layer is obtained using the trial and error method. The most appropriate number of neurons for the first and second hidden layers is found to be 7 and 4 respectively. The Sigmoid activation function is used in the RBMs. The number of training epochs is selected as 1500.
2.4.3. Random forest regression
RF is an ensemble learning method which can be used for both regression and classification problems. It provides predictions by agammaegating decisions from a set of base models such as decision trees or SVMs. A technique called bootstrap agammaegation (bagging) is used to train each base model on a different data sample in which the sampling is done with replacement. In this work, decision trees are used as the base models in the RF. The cross-validation method is used as the resampling method and the number of resampling iterations is selected as 10.
2.5. Ensemble models
Two basic ensemble models have implemented in this work i.e., stacking ensemble and averaging ensemble. In subsections 2.5.1 and 2.5.2, brief descriptions of stacking and averaging ensembles are given.
2.5.1. Stacking ensemble
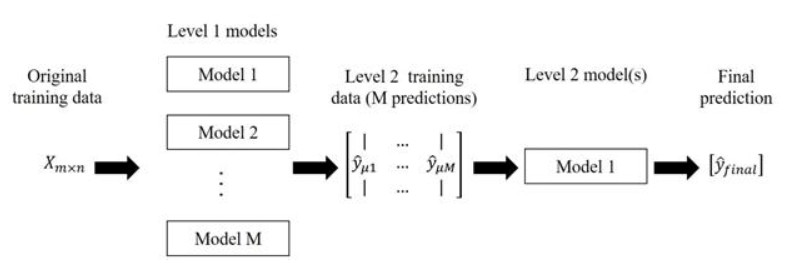
In the stacking ensemble, ML algorithms are stacked in a way such that the outputs of one-layer are considered as inputs of the following layer. This can be schematically illustrated as in Figure 2. The input training dataset X consists of m observations and n features. Then, an M number of ML models are trained using X. Each single ML algorithm provides prediction y which are then cast into a second-level training dataset consists of m observations and M features. The main contribution of the second-layer ML model is to minimize the regression error of the preceding ML models. In other words, a second regression model is trained to learn the error that first regression models have made. The integration of the estimated errors to the outputs of the first layer models can provide an improved prediction.
2.5.2. Averaging ensemble
In averaging ensemble model, the layer 2 model illustrated in Figure 2 is replaced with Eq 2.
where a1,a2,…,aM are the weights assigned to the outputs of layer 1.
The contribution of each ML method residing in layer 1 is weighted proportionally to the trust or performance of the member.
2.6. Case studies and results
Three case studies are conducted to find out the most accurate way of modeling solar power generation using ensemble forecasting techniques. Stacking and averaging based ensemble learning methods are used in this work. In the first case study, the ensemble models are used to forecast solar power generation without clustering the dataset. In case study 2, weather type classification is applied on the dataset and an ensemble model is implemented on the clustered dataset for forecasting solar power generation. In case study 3, the results of case studies 1 and 2 are analyzed to identify the contributions and limitations of the weather classification approach. Then, a new ensemble model is implemented incorporating the benefits of weather classification while eliminating the limitations.
2.6.1. Solar power forecasting using ensemble models without weather classification approach
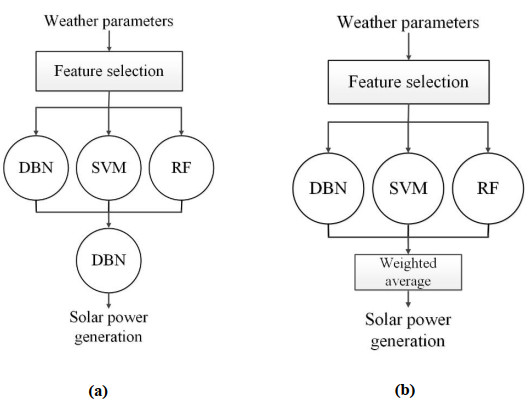
DBN, SVM, and RF algorithms are used to build the stacking and averaging ensemble models. Figure 3 illustrates the ensemble models. In the stacking model, filtered weather parameters are given to the three ML algorithms as inputs. The three outputs i.e. solar power forecasts of DBN, SVM, and RF models are used as inputs to another DBN which provides the final output i.e., the forecasted solar power generation. The average RMSE of predictions given by this model is 0.0636. Furthermore, authors have used SVM and RF models as the second layer of the stacking model and it is found that the respective average RMSE values are 0.0701 and 0.0687. Hence, the forecasting error is minimum with the DBN model. The second ensemble is a simple model which provides the weighted average of DBN, SVM and RF forecasts as the solar power generation. The most suitable weights for each single ML technique are determined by the trial and error method. The weights providing the lowest RMSE are selected. In this problem, weights of DBN, SVM, and RF are found to be 5, 3 and 8 respectively.
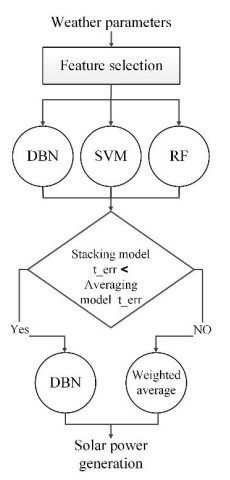
When considering a generalized ensemble model applicable for any PV facility, the ensemble model i.e., either stacking or averaging model providing the minimum training error (t_err) should be assigned to the respective PV facility. Figure 4 illustrates this generalized ensemble model.
Solar PV output mainly depends on both direct and diffuse solar irradiance i.e., the total solar irradiance received by the tilted solar panel. If the tilted irradiance is zero (for e.g., in nighttime), the solar panel output will be zero. Therefore, if the total irradiance is zero, the solar PV output is set as zero without utilizing the forecasting model. This nighttime filter will decrease the forecasting error and the computational time in the testing stage. Thus, the forecasting accuracy and the computational efficiency of the ensemble model will be increased.
The Ensemble models shown in Figures 3 and 4 are used to predict solar power output of 21 solar facilities located in Germany. The RMSE values of solar power predictions for different PV facilities are tabulated in Table 2. In addition, the RMSEs of DBN, SVM, and RF predictions are shown in Table 2 allowing comparison between single and ensemble ML techniques.
2.6.2. Solar power forecasting using ensemble models with weather classification approach
The stacking and averaging ensembles explained in section 2.5.1 are used in this case study as well. In addition, training data set, feature selection, nighttime filter, and the performance measure remains the same for this section. In weather classification approach, the dataset is clustered to train and test each cluster separately.
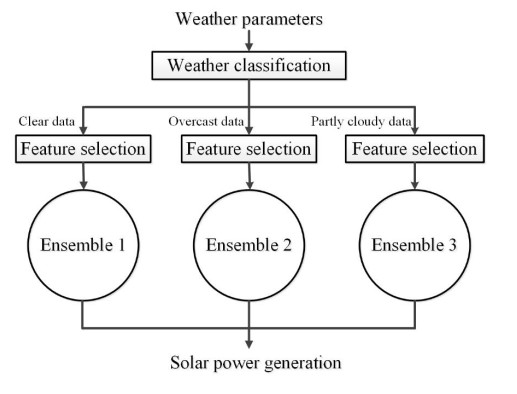
The dataset is clustered into three categories based on the cloud cover data. Then, three generalized ensemble models are trained for these three categories separately. In other words, for each weather condition, a separate generalized ensemble model (Figure 4) is assigned. The clustering process is done using the below rules.
● Clear (Sunny) - cloud cover between 0 and 0.25
● Overcast (Cloudy) - cloud cover between 0.75 and 1
● Partly cloudy - cloud cover between 0.25 and 0.75
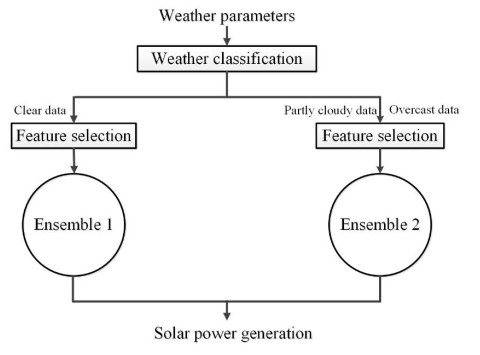
The average number of clear, overcast and partly cloudy observations in the dataset is 1400, 3260 and 1356 i.e., 23.27%, 54.19% and 22.54%, respectively. The ensemble model with weather classification is illustrated in Figure 5 in which ensembles 1, 2 and 3 are three generalized ensemble models. The RMSE values of solar power predictions of stacking and averaging ensembles with weather classification are shown in Table 3. However, the ensemble model with weather classification approach may require further modifications according to the forecasting errors of each cluster.
2.6.3. Design a new ensemble model by identifying the contributions and limitations of weather classification
The results of case studies 1 and 2 can be used to evaluate the contributions and limitations of the weather classification approach. However, the results of case study 1 are not categorized w.r.t different weather conditions. Hence, RMSE values shown in the fifth and sixth columns of Table 2 are categorized according to the respective weather conditions and then tabulated in Table 4.
Tables 3 and 4 show that the RMSE of the predictions in clear weather situation is less when cloud classification is applied. In other words, the forecasting error is less in clear weather condition if the clear ensemble i.e. ensemble 1 is trained only by clear data. But the error values are higher when partly cloudy and overcast models are trained separately by the data of each weather category. Therefore, a modification is required to acquire the forecasting performance improvement in the clear weather condition and reduce the forecasting errors in partly cloudy and overcast weather conditions. By comparing Tables 3 and 4 results, it can be observed that when the stacking and weighted average ensemble models are is trained with the whole dataset, the forecasting performance is better in overcast and partly cloudy weather situations. A new ensemble is developed considering these facts. Figure 6 illustrates the modified ensemble model. Ensembles 1 and 2 illustrated in Figure 6 are two generalized ensemble models. Ensemble 1 is trained using only clear weather data and it is used to forecast solar power generation in clear weather conditions. On the other hand, ensemble 2 is trained by the whole dataset and it is used to forecast solar power generation in partly cloudy and overcast weather conditions. Table 5 shows the RMSE values of predictions of the modified ensemble model illustrated in Figure 6.
3.
Discussion
In this section, the results obtained from the case studies are discussed in detail. Section 3.1 analyzes the results obtained from case study 1 which is conducted without clustering the dataset. Then, the results of the weather classification approach are discussed in section 3.2. The benefits of weather classification approach and the percentage error reductions of the proposed ensemble w.r.t single ML techniques are presented in section 3.3.
3.1. Solar power forecasting using ensemble models without weather classification approach
The results of case study 1 show that the SVM model has a better forecasting ability than RF and DBN models. Thus, predictions having the lowest average RMSE of 0.0637, the SVM model is the most suitable forecasting model in the single ML method's category. However, the average RMSE of RF is also very close to that of SVM. Even though DBN model predictions have the largest average RMSE, it provides the lowest RMSE values for PV10 and PV11 plants. These results show that it is difficult to specify a forecasting technique in common for all PV facilities to obtain solar power forecasts with the highest accuracy. It can be observed that the stacking ensemble method provides better results for 1, 2, 4, 8, 9, 12, 14, 16, 21 PV plants and the weighted average method provides better results for the remaining PV plants. Both the stacking method and the weighted average method gives approximately equal average RMSE values for all 21 PV facilities. The generalized model RMSE is the minimum of RMSE of either stacking model or weighted average model. Generalized ensemble model without weather classification reduces the average RMSE by 7.4%, 4.77%, and 4.93% w.r.t DBN, SVM and RF models respectively.
3.2. Solar power forecasting using ensemble models with weather classification approach
The results of case study 2 show that the average RMSEs of stacking and averaging ensembles are 0.0647 and 0.0639 respectively. It can be clearly observed that these error values are larger than those of the case study 1. Therefore, the weather type clustering approach does not improve the forecasting accuracy. Instead, it increases the forecasting error. To identify the most effective way of applying weather type classification, the results of case study 1 should be categorized into different weather conditions. Hence, case study 3 is conducted to find out the most effective method of clustering dataset.
3.3. Ensemble forecasting with partial weather classification approach
As can be seen in Table 4, the forecasting performance is higher in overcast weather situations than partly cloudy and clear weather conditions. This can happen due to two reasons. Firstly, the number of overcast observations in the dataset is more than twice as the partly cloudy or clear data and the error is obviously get reduced when the data set is large. Secondly, the variation of cloud cover is not rapid in overcast weather. Although there is a smaller number of clear weather data, the forecasting performance is high for clear weather conditions, as there are no rapid changes in the sky when the sky is clear. Forecast error depends on the variability of solar irradiance [55]. Variability is the largest in partly cloudy conditions and that is the main reason for the differences in forecast error. The forecasting error is high for partly cloudy weather conditions. This may happen due to two reasons. When the sky is partly cloudy, the cloud cover can rapidly change, unlike in clear or overcast weather conditions and that can greatly affect the accuracy of solar forecasting. Secondly, the number of observations available for this weather category is less when compared to the overcast weather condition.
In case study 3, a new modified ensemble model with partial weather classification is implemented according to the results presented in Tables 3 and 4. The average RMSE of the ensemble implemented in case study 3 is 0.0591 which is less than that of the generalized ensemble without weather classification (0.0608). Thus, it shows approximately 3% reduction in the forecasting error.
Compared to single DBN, SVM and RF models without cloud classification, this new ensemble model with cloud classification reduces RMSE error by 10.49%, 7.78%, and 7.95% respectively. In addition, the results of the proposed model can be compared with the available literature which uses the same dataset for training the forecasting models [22,38]. The RMSE error reductions compared to the work presented in [22] and [38] are 20.64% and 27.58% respectively.
4.
Conclusions
This paper proposes a novel ensemble model for solar power forecasting. The results show that the proposed ensemble model performs better than single machine learning techniques. In this study, the used training data set mostly consists of cloudy weather data i.e. more than half of the total observations belong to the overcast range. Therefore, the performance increase due to the weather classification is somewhat small (approximately 3% error reduction). The forecasting accuracy will further be increased for tropical countries because of the large proportion of clear data in the dataset. In other words, if clear data contribute to the higher proportion of the dataset, the reduction of RMSE from sunny solar predictions increases and hence, the forecasting ability of the ensemble will be increased. The ensemble can be improved by adding more machine learning algorithms such as convolutional neural networks, LSTMs, etc. It should be noted that the error terms do not incorporate NWP errors. Therefore, in the real-world application, the error terms may increase further. The longer the forecasting horizon the larger the forecasting error. Even though the model is trained using data having the 3-hour resolution, the solar power forecasts can be generated for any time period resolution as it depends on the resolution of forecasted weather parameters. It can be concluded that the combination of weather classification approach and ensemble learning technique provides more accurate solar power generation forecasts than conventional single ML techniques.
Conflicts of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: