Diffusion-limited tumour growth: Simulations and analysis

Dear Editorial Board Members,

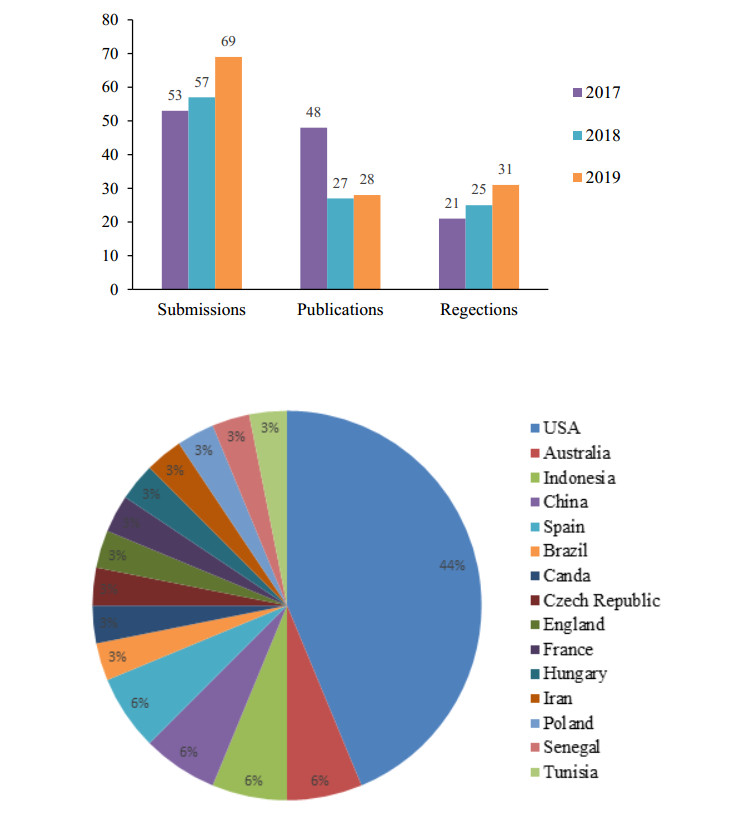
It is my pleasure to share with you the year-end report for AIMS Environmental Science. The journal continues to improve its quality as indicated by steady increases in the number of manuscripts received and the number of articles published over the past three years (Figure 1). We have received 69 submissions with 28 published online. The most downloaded and cited papers are listed in Tables 1 and 2. The top read article received more than 11390 downloads.

Figure 1.  Manuscript statistics.

DownLoad: Full-Size Img PowerPoint

Table 1.  The top 10 articles with most pdf download: (By December 31th 2019).

Title	Usages
Quantifying the local-scale ecosystem services provided by urban treed streetscapes in Bolzano, Italy	11390
Feasibility study of a solar photovoltaic water pumping system for rural Ethiopia	2021
Biophilic architecture: a review of the rationale and outcomes	2016
Low temperature selective catalytic reduction of NOx with NH3 over Mn-based catalyst: A review	1834
Remote sensing of agricultural drought monitoring: A state of art review	1808
Challenges and opportunities in municipal solid waste management in Mozambique: a review in the light of nexus thinking	1643
Nitrate pollution of groundwater by pit latrines in developing countries	1524
Assessment of repeated harvests on mercury and arsenic phytoextraction in a multi-contaminated industrial soil	1506
Urban agriculture in the transition to low carbon cities through urban greening	1463
A state-and-transition simulation modeling approach for estimating the historical range of variability	1438

---

 | Show Table

DownLoad: CSV

Table 2.  The top 10 articles with most cited: (By December 31th 2019).

Title	Number
Biophilic architecture: a review of the rationale and outcomes	21
Traffic-related air pollution and brain development	19
Enhancing water flux of thin-film nanocomposite (TFN) membrane by incorporation of bimodal silica nanoparticles	15
Quantifying the local-scale ecosystem services provided by urban treed streetscapes in Bolzano, Italy	14
Nitrate pollution of groundwater by pit latrines in developing countries	13
The mechanism of kaolin clay flocculation by a cation-independent bioflocculant produced by Chryseobacterium daeguense W6	12
An integrated approach to modeling changes in land use, land cover, and disturbance and their impact on ecosystem carbon dynamics: a case study in the Sierra Nevada Mountains of California	11
Climate change and land management impact rangeland condition and sage-grouse habitat in southeastern Oregon	11
Catalytic hydrothermal liquefaction (HTL) of biomass for bio-crude production using Ni/HZSM-5 catalysts	11
Influence of everyday activities and presence of people in common indoor environments on exposure to airborne fungi	10

---

 | Show Table

DownLoad: CSV

I would like to thank all the board members for serving on the Editorial Board and their dedication and contribution to the journal, especially to the editors for two special issues: Impacts of Microplastics in the Urban Environment Conference and Green built environment. The goal in 2020 is to solicit more manuscripts and increase paper citations. We will try our best to reduce the processing time and supply with a better experience for publication. To recognize the contribution of the Editorial Board members and authors during the years, we will continue to offer that (1) for authors invited, the article processing charge (APC) is automatically waived; (2) each editorial board member is entitled for some waivers. I am looking forward to continuing working with you to make the AIMS Environmental Science a sustainable and impactful journal. Please don’t hesitate to send me e-mails if you have new ideas and suggestions to help us to achieve this goal.

Yifeng Wang, Ph.D.

Editor in Chief, AIMS Environmental Science