Nomenclature
ρ Air density (kg/m3)
RT Blade radius (m)
λ Tip-speed ratio
CT(λ) Torque coefficient
Vτ Wind speed (m/s)
R Rotor resistance (Ω)
Rs Load resistance (Ω)
Ls Load inductance (H)
p Pole pair
Ld d-axis rotor inductance (H)
Lq q-axis rotor inductance (H)
id d-axis rotor current (A)
iq q-axis rotor current (A)
Jh Moment of inertia (kg-m2)
ϕm permanent magnet flux (Wb)
ωh Shaft speed (rad/s)
τwt wind torque (N-m)
τem electro-magnetic torque (N-m)
Abbreviations
2-DOF Two degree of freedom
ALS Automatic loop-shaping
AQFT Automated quantitative feedback theory
AWPS Autonomous wind power system
CAD Computer aided design
CSD Control system design
GA Genetic Algorithm
HFG High frequency gain
MAQFT Modified automated Quantitative feedback theory
MMQFT Multi-model Quantitative feedback theory
PFL Partial feedback linearization
PMSG Permanent magnet synchronous generator
QFT Quantitative feedback theory
1. Introduction
Quantitative feedback theory (QFT) [1,2,3,4], is a robust control system design (CSD) approach which employs system output as an feedback variable to achieve the desired dynamic performance in presence of plant uncertainties and disturbances. In general, QFT is well applicable for handling uncertainty in frequency domain. Ever since its inception, QFT is applied to solve various real time CSD problems [2,3,5,6]. Although QFT was intially applied to different to various single input - single output (linear time variant, time invariant and nonlinear) systems, its extension to multiple input - multiple output (linear and nonlinear) systems is presented in [5,7,8].
It is well known that for adequate implementation of QFT, system gain-phase loop-shaping is imperative and can be performed either manually or automatically. On this line many computer aided design (CAD) tools are developed to perform manual loop shaping like the pioneer Air Force Institute of Technology CAD tool [2,9,10], QFT control toolbox by European space agency author's group [11,12], QFT MATLAB toolbox [13,7] and Qsyn [14]. Despite its simplicity in design, the method primarily depends on the trial and error approach which indeed results in the system performance highly dependent on the designer. Further, the complexity increases profoundly for unstable and non-minimum phase uncertain systems in order to fulfil all the necessary performance specifications resulting in the need for automatic loop shaping (ALS) methods.
Concerning the attempts in developing the ALS methods, Gera and Horowitz proposed design of QFT robust controller based on iterative procedure to derive the shape of a nominal loop transfer function (L(jω)=G(jω)P(jω)) using Bode's gain phase integral [15]. However, the method requires a rational function approximation and straight line approximations leading to an underperforming CSD. Although Ballance and Gawthrop simplified the Bode's gain-phase integral iteration process, the possibility to address satisfactorily the specifications pertaining to noise rejection and stability is not well appreciable [16]. A method to approximate uncertain plant frequency responses using the nonlinear programming method is demonstrated in [17]. Approximation of templates based on the aforementioned method results in over bounding rectangles. To confront the issue of overbounding, linear programming based ALS using a series of linear approximations reported in [18] fails to define the QFT nonlinear bounds with linear inequalities. This drawback has been overcome by transforming the nonconvex closed loop bounds into linear inequalities by considering zeros alone as the optimization variables [19].
In addition, the authors, Garcia-sanz and Guillen [20], Garcia-sanz and Oses [21], and Garcia-sanz and Molins [22], have proposed the evolutionary and Genetic algorithm (GA) based ALS. Unlike the aforesaid methods, a phase independent controller is developed using the least square type algorithm [23]. Similarly, the application of particle swarm optimization, hybrid optimization (interval consistency and hull consistency), teaching learning-based optimization algorithm, flower pollination algorithm and convex concave optimization methods are presented in [24,8,25,26,27] respectively. In spite of these many efforts, a simple design methodology to devise a controller with an overall satisfactory performance is still left unattended. With this motivation, an attempt to formulate a controller structure exhibiting the characteristics of descending modular trace within the close vicinity of the universal bound is addressed.
In this paper, a modified fitness function is formulated by considering the suitable cost function terms in order to accurately capture the desired descending modular trace close-packed to the universal bound. The minimization of the cost function is accomplished by the application of GA. The suitability and superiority of the proposed QFT based controller is demonstrated by applying it to an uncertain autonomous wind power system (AWPS). Numerical simulations are performed on MATLAB platform and results revealing the improved performance of the developed controller in comparison to the state-of-the-art methods are included. Finally, an exhaustive comparative analysis proving the proposed controller's improved performance with that of other well- established methods is carried out and the corresponding results are presented.
2. System description and QFT design procedure
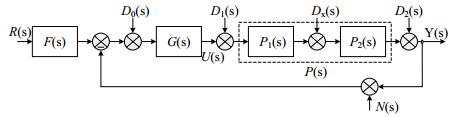
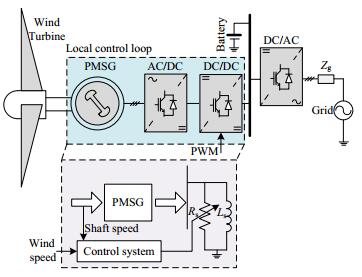
A permanent magnet synchronous generator (PMSG) -based AWPS shown in Figure 1 is considered as the test system to demonstrate the applicability and suitability of the proposed QFT based robust controller under stochastic wind speeds [28,29,30,31]. Assuming that the other system components excluding those within the local control loop as highlighted in Figure 1 works as intended, with suitable assumptions, the chopper equivalent circuit is obtained [28]. Neglecting the dynamics of power electronic converters, dynamics pertaining to the aerodynamic model of wind turbine and PMSG are accounted. The aerodynamic torque is given as,
The dynamic model of PMSG with chopper equivalent variable resistance Rs in synchronous reference frame is given as,
|
diddt=−(R+Rs)(Ld+Ls)id+p(Lq−Ls)(Ld+Ls)iqωhdiqdt=−(R+Rs)(Lq+Ls)iq−p(Ld+Ls)(Lq+Ls)idωh+pϕmdωhdt=−1Jhτwt−τemJhτem=p[(Ld−Lq)idiq−ϕmiq]
|
(2)
|
2.1. QFT Description
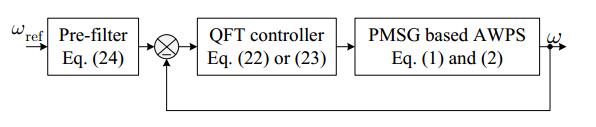
In real environment, the conventional control system fails to meet the necessary design specifications owing to its incapability to handle the uncertainties and disturbances that are inevitable in any practical operating conditions. In order to attribute to these requirements, a highly robust CSD is essential. A two degree of freedom (2DOF) control structure shown in Figure 2 is used to design the robust controller and pre-filter in QFT framework [23]. Where P(s) represents transfer function of the uncertain plant with P∈{p}, p representing the family of possible uncertain plants. The rationale behind the design of controller G(s) and pre-filter F(s) is to achieve robust stability and to meet the following performance specifications :Generally closed loop performance specifications are converted into frequency domain functions γk(ω) that are represented as transfer functions of robust stability and performance specifications, |Tk(jω)| so that: |Tk(jω)| ≤ γk(ω), k=1...7
2.1.1. Robust Stability
|
|T1(jω))|=|UD1|=|YD0|=|YN|=|L(jω))1+L(jω))|=|Y(jω)F(jω))R(jω)|≤γ1(ω)
|
(3)
|
2.1.2. Plant Output Disturbance
|
|T2(jω))|=|YD2|=|11+L(jω)|≤γ2(ω)
|
(4)
|
2.1.3. Plant Input Disturbance
|
|T3(jω))|=|YD1|=|P(jω)1+L(jω))|≤γ3(ω))
|
(5)
|
2.1.4. Robust Disturbance Rejection
|
|T4(jω)|=|YDX|=|P2(jω)1+L(jω)|≤γ4(ω)
|
(6)
|
2.1.5. Control Effort Attenuation
|
|T5(jω)|=|UDx|=|G(jω)P2(jω)1+L(jω)|≤γ5(ω)
|
(7)
|
2.1.6. Control Effort Attenuation
|
|T6(jω)|=|UN|=|UD2|=|G(jω)1+L(jω)|=|U(jω)R(jω)F(jω)|≤γ6(ω)
|
(8)
|
2.1.7. Reference Tracking
|
γ7L(ω)≤|T7(jω)|=|YR|=|F(jω)L(jω)1+L(jω)|≤γ7U(ω)
|
(9)
|
2.2. Step-by-Step QFT based Controller Design
The necessary procedure to be followed in the process of designing a QFT controller is comprehensively described below :
Step 1: Select the uncertain plant and define it's uncertainty range
Step 2: Establish the performance specifications
Step 3: Generate the template for an uncertain plant P(s)∈p, and select the frequency array ωi,i=1,...l. At each frequency obtain the variations of the plant parameters using the Nichols chart.
Step 4: Compute the QFT bounds by selecting the nominal plant such that the template points fulfils the performance specifications and are stable at every frequency for ωi,i=1,...l. Further compute the worst case bounds from the intersection of all the performance bounds at every frequency for ωi,i=1,...l.
Step 5: Perform the loop shaping G(s) using the Nichols chart until the worst case bounds for every frequency are satisfied and a stable point for the closed loop nominal system is reached.
Step 6: Design the Pre-filters F(s) using same principle of loop-shaping in order to enable the output to track the reference input.
2.3. High Frequency Gain
Reduction of high frequency noises at the sensor output and plant disturbances is desired to utilise the feedback benefits and is achieved by reducing high frequency gain (HFG) expressed as follows
where r represents the excess poles in G(s)
3. Automated QFT design
With this background the proposed design procedure of the automated QFT controller is presented in this Section. First, the problem statement formulation is discussed. Second, the modified fitness function evaluation is carried out.
3.1. Problem Statement
The critical design specifications such as reducing HFG there by maximizing the feedback benefits along with the minimization of cost of feedback are translated into a mathematical formulation given as,
|
G(x,jω)=KGnz∏i=1(jω+zi)np∏k=1(jω+pk)
|
(11)
|
where x=[KG,p1....pnp,z1....znz], KG, pk ((k=1....np)) and zi ((i=1...nz)) represents the real space parameters, gain, real poles and zeros respectively.
3.2. Fitness Function Formulation
In general, fitness function defined as combining an expression of constraints and objectives ideally defines quality of controller and its estimated behaviour. Hence it is very vital to formulate an effective fitness function and its coefficients which translates all the requisite CSD specifications into a mathematical expression. As a first step the controller excess gain-band width area on ω expressed as an integral form is given as,
|
A(ω1,ω2)=ω2∫ω1ln|G(jω)|dω
|
(12)
|
The foregoing assumptions permit the computation of the definite integral of (12) in terms of zi,pi,KG,ω1andω2 as follows (illustrated here for a proper controller, (nz=np):
|
A(ω1,ω2)=[ln(K2G)(ω2−ω1)+nz∑i=1(ω2ln[ω22+z2iω22+p2i]−ω1ln[ω21+z2iω21+p2i]+2zi tan−1(ω2zi)−2pi tan−1(ω2pi)+2zi tan−1(ω1zi)−2pi tan−1(ω1pi))
|
(13)
|
Finally, the controller gain-bandwidth area measure is used to form an augmented cost function. As an outcome, the formulated fitness function is given as,
|
J(x)=a0 k2G+a1nz∑i=1(pi−zi)4+1pizi+a2 A(ω1,ω2)+a3 V(x)+a4 nz∑i=1tan−1(pi−zipizi)
|
(14)
|
In the above cost function, the first two terms corresponds to high frequency gain and lead ratios respectively while the third and fourth terms refers to constraint pertaining to the area and the penalty respectively. The third term in (14) facilitates the tight control of gain at any frequency of interest. Thus, helps in diminishing the over-design at low frequencies. Similarly, additional terms can be included in order to cater other frequency ranges as well.
In general the nominal loop transmission should satisfy the bounds of intersection and are described as a function q with lower and upper parts, ql and qu respectively, such that,
|
Lmqu(∠L0(x,jωi),ωi)≤LmL0(x,jωi)i∈ILmL0(x,jωi)≤Lmql(∠L0(x,jωi),ωi)
|
(15)
|
where L0=GP0, I represents the frequency array points of interest, Lm indicates log10 magnitude, and P0 is the nominal plant. Further, the lower and upper bound violation limits are given by,
|
θx,i=∠L0(x,ωi)Vu(x,ωi)=max{logqu(θx,i,ωi)−logL0(x,ωi),0}Vl(x,ωi)=max{logL0(x,ωi)−logql(θx,i,ωi),0}
|
(16)
|
|
Vω(x,ωi)={min {Vu(x,ωi),Vl(x,ωi)},if qu(θx,i,ωi)≥ql(θx,i,ωi)max{Vu(x,ωi),Vl(x,ωi)},otherwise
|
(17)
|
Thus, the penalty function V(x) to penalise the unfeasible solutions that do not fulfil the performance specifications and assist in comprehending the degree of disparity of each bound at frequency ωi is given by,
It is worth noting that despite the addition of the prominent and wide spread terms into the fitness function, the inclusion of the proposed fifth term greatly aids in obtaining the desired descending modular plot of the controller. The inherent characteristics of the proposed term results in impelling the locus of the closed loop transmission L0(s) as much as nearer to the Universal bound while exhibiting descending phase response. The so formulated fitness function helps in realising a well-nigh controller that performs well against real time system uncertainties and disturbances.
4. Application and results
The proposed QFT based robust controller and pre-filter design steps as applied to an PMSG-based AWPS is discussed in this Section. The transfer function model of PMSG based AWPS is represented as an uncertain system given by,
where, the uncertainty of plant parameter is 6≤k≤20, 0.01≤T≤0.09, ξ=0.8. The nominal plant parameters are k = 20 and T = 0.09.
4.1. Template Generation
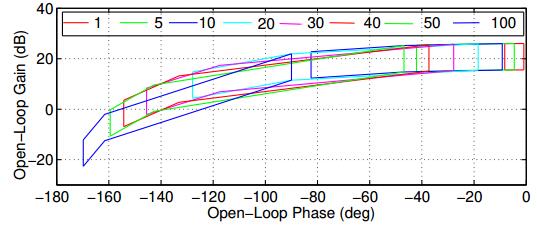
Templates are the pictorial representation of the uncertain plant's magnitude and phase response at fixed frequency. The sketch of the templates for the frequency vector ω=[151020304050100] rad/s shown in Figure 3.
4.2. Computation of Bounds
The edge point templates are used to obtain QFT bounds. Stability margins and performance specifications are transformed to frequency domain in order to represent the QFT bounds in Nichols chart. The computation of QFT bounds is accomplished by considering the quadratic inequalities and the closed loop robust stability margins are given as,
|
|L(jω)1+L(jω)|≤γ1∀P∈{p}
|
(20)
|
In this case, γ1=1.2=1.6 dB results in a gain margin and phase margin of 5.26483 dB and 49.24860 respectively.
The upper and lower reference tracking bounds for the considered AWPS are given by,
|
HU(s)=16.67s+400s2+36s+400HL(s)=12000s3+80s2+1900s+12000
|
(21)
|
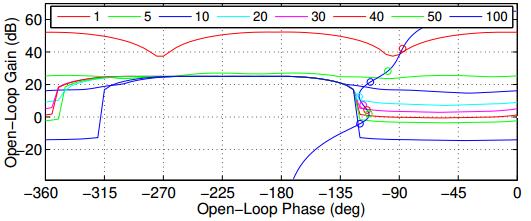
Further, all the stability and tracking bounds are grouped to calculate the worst case possibilities and are pictorially depicted in Figure 4.
4.3. Loop Shaping
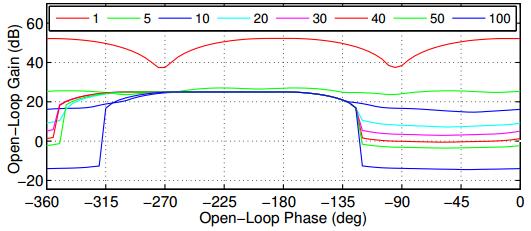
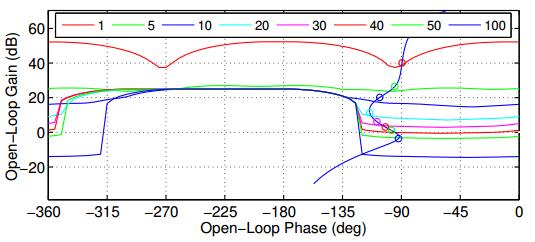
The existing and proposed ALS methodology based control structures formulated using GA are respectively given by,
|
G1(s)=15.701(s+42.29)(s+38.43)(s+10.42)(s+354)(s+134)(s+0.01765)
|
(22)
|
|
G2(s)=5.7074(s+53.06)(s+23.58)(s+13.63)(s+125.1)(s+109.6)(s+0.07097)
|
(23)
|
It is evident from Figure 5 and Figure 6 that the open loop phase of L0(s) is closer to the universal bound for the proposed controller between the frequency 10 to 100 rad/s. In addition, performance comparison of existing and proposed controllers in terms of HFG and cost value is tabulated in Table 1. With the application of proposed controller, the HFG is reduced to a value of 63.65% as compared to the application of method described in [22]. Thus, the sensitivity of proposed controller to high frequency noise is minimum and requires reduced control effort. The reduced cost function value attests the lesser feedback cost requirement of the proposed controller.
Table 1. Performance Comparison of the Proposed Controller with [22].
| Performance index | [22] | Proposed method |
| FG | 15.701 | 5.7074 |
| J(x) | 1.2286×105 | 1.0622×104 |
4.4. Pre-filter Design
The design of pre-filter is performed using the same procedure as that of loop-shaping and obtained transfer function is given as,
|
F(s)=17.614×10−6s3+0.00156s2+0.087s+1
|
(24)
|
The corresponding block diagram representation of developed system with proposed subsystems is shown in Figure 7.
5. Performance evaluation
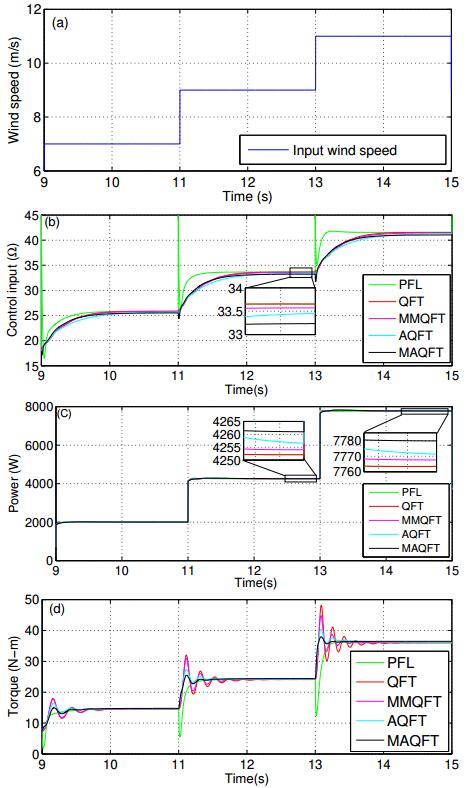
The maximum power tracking capability of the proposed controller under step change in wind speed and stochastic variation is tested and a comparative evaluation is performed against the following methods: feedback linearization [29], QFT [28], multi-model QFT [28], GA based automated QFT [22] through MATLAB simulations. The PMSG and wind turbine parameters employed for the simulation are shown in Table 2. The input wind velocity template depicts step variations at t = 11 s and 13 s is shown in Figure 8(a). The corresponding variations in the control input, extracted power and the rotor torque are shown in Figure 8(b), 8(c) and 8(d) respectively. It is observed that the proposed controller requires the minimum control input while operating as desired. Also, it noteworthy that the proposed controller facilitates in extracting the maximum power corresponding to a given wind velocity in comparison to other well established techniques. It is highly desired to have a smooth torque variation
Table 2. System parameters.
| Wind turbine parameters | PMSG parameters |
| RT =2.5 m, ρ=1.25 kgm−3 | P=3, R=3.3 Ω, Ls=0.08 H, Rs=80 Ω |
| Jh=0.0552 kg−m2 | ϕm=0.4382 Wb, Lq=Ld=0.04156 H |
owing to the associated mechanical structure. Among the other available methods, a smooth torque variation with an improved performance is witnessed with the application of the developed controller. Further the key observations proving the proposed controllers competency is enlisted in Table 3.
Table 3. Performance comparison of controllers for step variation in wind speed.
| Parameter | Wind profile | PFL | QFT | MMQFT | AQFT | MAQFT |
| Control input (Ω) | 7 m/s | 27 | 25.9 | 25.82 | 25.72 | 25.52 |
| 7 ⇒ 9 m/s | 33.65 + 33.63 % | 33.65 | 33.55 | 33.45 | 33.24 |
| 9 ⇒ 11 m/s | 41.55 + 17.83 % | 41.55 | 41.41 | 41.3 | 41 |
| Electromagnetic torque (N-m) | 7 m/s | 14.7 ± 0.15 % | 14.59 | 14.598 | 14.65 | 14.755 |
| 7 ⇒ 9 m/s | 24 - 75 % | 24.1 + 32.78 % | 24.16 + 28.31 % | 24.23 + 13 % | 24.42 + 4.42 % |
| 9 ⇒ 11 m/s | 36 -65.67 % | 36 + 34.03 % | 36.1 + 23.96 % | 36.3 + 11.57 % | 36.5 + 4.11 % |
| Power extracted (W) | 7 m/s | 2000.54 | 2000.65 | 2001.02 | 2002.3 | 2004.75 |
| 7 ⇒ 9 m/s | 4252 | 4252 | 4254 | 4256.6 | 4261 |
| 9 ⇒ 11 m/s | 7763 | 7763 | 7767.6 | 7772.2 | 7780 |
+ Overshoot;
- Decay;
± Oscillatory |
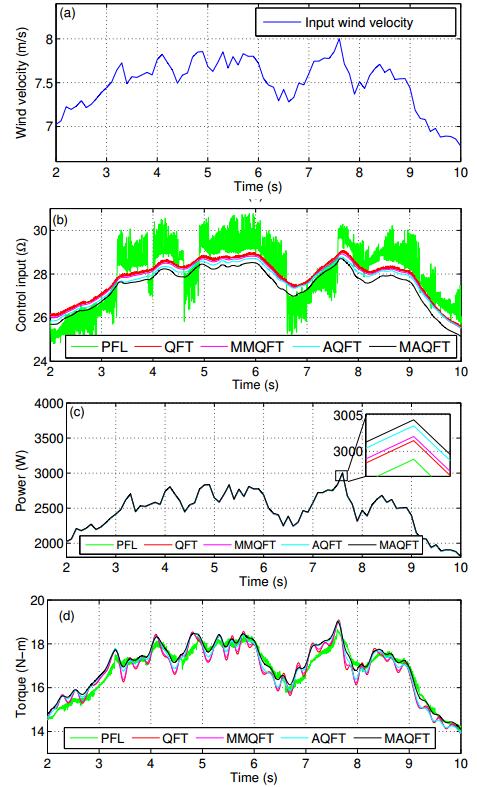
Owing to the inherent variability in the wind power generation, a stochastic wind profile is consider as the second test case. The corresponding results are shown in Figure 9. It is evident from the result figures that the proposed controller outperforms the other available CSD methods from various control system perspectives.
6. Conclusion
This paper presented a modified fitness function based automated robust controller using GA in QFT framework to extract the maximum power from PMSG based AWPS. The prominent features of the proposed controller are as follows.
1. It absolutely exhibits the highly desired decreasing modular plot and descending phase response.
2. Addition of a simple arc tangent function helps in shifting the loop-shaping curve closer to the universal bound intern significantly reducing the gain at high frequencies.
3. The usage of GA leads to the effortless acquisition of the controller parameters.
The applicability and feasibility of the developed controller is verified through extensive simulations and the results attesting its improved performance against well established methods are presented.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: