The Role Of Time Delays, Slow Processes And Chaos In Modulating The Cell-Cycle Clock

1.   Introduction

Digital topology with interesting applications has been a popular topic in computer science and mathematics for several decades. Many researchers such as Rosenfeld [21,22], Kong [18,17], Kopperman [19], Boxer, Herman [14], Kovalevsky [20], Bertrand and Malgouyres would like to obtain some information about digital objects using topology and algebraic topology.

The first study in this area was done by Rosenfeld [21] at the end of 1970s. He introduced the concept of continuity of a function from a digital image to another digital image. Later Boxer [1] presents a continuous function, a retraction, and a homotopy from the digital viewpoint. Boxer et al. [7] calculate the simplicial homology groups of some special digital surfaces and compute their Euler characteristics.

Ege and Karaca [9] introduce the universal coefficient theorem and the Eilenberg-Steenrod axioms for digital simplicial homology groups. They also obtain some results on the Künneth formula and the Hurewicz theorem in digital images. Ege and Karaca [10] investigate the digital simplicial cohomology groups and especially define the cup product. For other significant studies, see [13,12,16].

Karaca and Cinar [15] construct the digital singular cohomology groups of the digital images equipped with Khalimsky topology. Then they examine the Eilenberg- Steenrod axioms, the universal coefficient theorem, and the Künneth formula for a cohomology theory. They also introduce a cup product and give general properties of this new operation. Cinar and Karaca [8] calculate the digital homology groups of various digital surfaces and give some results related to Euler characteristics for some digital connected surfaces.

This paper is organized as follows: First, some information about the digital topology is given in the section of preliminaries. In the next section, we define the smash product for digital images. Then, we show that this product has some properties such as associativity, distributivity, and commutativity. Finally, we investigate a suspension and a cone for any digital image and give some examples.

2.   Preliminaries

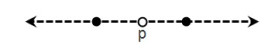
Let $\mathbb{Z}^n$ be the set of lattice points in the $n$-dimensional Euclidean space. We call that $(X,\kappa)$ is a digital image where $X$ is a finite subset of $\mathbb{Z}^n$ and $\kappa$ is an adjacency relation for the members of $X$. Adjacency relations on $\mathbb{Z}^n$ are defined as follows: Two points $p = (p_1,p_2,\ldots,p_n)$ and $q = (q_1,q_2,\ldots,q_n)$ in $\mathbb{Z}^n$ are called $c_l$-adjacent [2] for $1\leq l\leq n$ if there are at most $l$ indices $i$ such that $|p_i-q_i| = 1$ and for all other indices $i$ such that $|p_i-q_i|\neq 1$, $p_i = q_i$. It is easy to see that $c_1 = 2$ (see Figure 1) in $\mathbb{Z}$,

$c_1 = 4$ and $c_2 = 8$ (see Figure 2) in $\mathbb{Z}^2$,

and $c_1 = 6$, $c_2 = 18$ and $c_3 = 26$ (see Figure 3) in $\mathbb{Z}^3$.

A $\kappa$-neighbor of $p$ in $\mathbb{Z}^n$ is a point of $\mathbb{Z}^n$ which is $\kappa$-adjacent to $p$. A digital image $X$ is $\kappa$-connected [14] if and only if for each distinct points $x,y\in X$, there exists a set $\{a_0,a_1,\ldots,a_r\}$ of points of $X$ such that $x = a_0$, $y = a_r$, and $a_i$ and $a_{i+1}$ are $\kappa$-adjacent where $i\in\{0,1,\ldots,r-1\}$. A $\kappa$-component of a digital image $X$ is a maximal $\kappa$-connected subset of $X$. Let $a,b \in \mathbb{Z}$ with $a<b$. A digital interval [1] is defined as follows:

where $2$-adjacency relation is assumed.

In a digital image $(X,\kappa)$, a digital $\kappa$-path [3] from $x$ to $y$ is a $(2, \kappa)$-continuous function $f:[0,m]_{\mathbb{Z}}\rightarrow X$ such that $f(0) = x$ and $f(m) = y$ where $x,y\in X$. Let $f:(X,\kappa)\rightarrow (Y,\lambda)$ be a function. If the image under $f$ of every $\kappa$-connected subset of $X$ is $\kappa$-connected, then $f$ is called $(\kappa,\lambda)$-continuous [2].

A function $f:(X,\kappa)\rightarrow (Y,\lambda)$ is $(\kappa,\lambda)$-continuous [22,2] if and only if for any $\kappa$-adjacent points $a,b\in X$, the points $f(a)$ and $f(b)$ are equal or $\lambda$-adjacent. A function $f:(X,\kappa)\rightarrow (Y,\lambda)$ is an isomorphism [4] if $f$ is a $(\kappa,\lambda)$-continuous bijection and $f^{-1}$ is $(\lambda,\kappa)$-continuous.

Definition 2.1. [2] Suppose that $f, \ g:(X,\kappa)\rightarrow (Y,\lambda)$ are $(\kappa,\lambda)$-continuous maps. If there exist a positive integer $m$ and a function

with the following conditions, then $F$ is called a digital $(\kappa,\lambda)$-homotopy between $f$ and $g$, and we say that $f$ and $g$ are digitally $(\kappa,\lambda)$-homotopic in $Y$, denoted by $f\simeq_{(\kappa,\lambda)}g$.

(ⅰ) For all $x\in X$, $F(x,0) = f(x)$ and $F(x,m) = g(x)$.

(ⅱ) For all $x\in X$, $F_x:[0,m]\rightarrow Y$ defined by $F_x(t) = F(x,t)$ is $(2,\lambda)$-continuous.

(ⅲ) For all $t\in[0,m]_{\mathbb{Z}}$, $F_t:X\rightarrow Y$ defined by $F_t(x) = F(x,t)$ is $(\kappa,\lambda)$-continuous.

A digital image $(X, \kappa)$ is $\kappa$-contractible [1] if the identity map on $X$ is $(\kappa, \kappa)$-homotopic to a constant map on $X$.

A $(\kappa,\lambda)$-continuous map $f:X\rightarrow Y$ is $(\kappa,\lambda)$-homotopy equivalence [3] if there exists a $(\lambda,\kappa)$-continuous map $g:Y\rightarrow X$ such that

where $1_X$ and $1_Y$ are the identity maps on $X$ and $Y$, respectively. Moreover, we say that $X$ and $Y$ have the same $(\kappa,\lambda)$-homotopy type.

For the cartesian product of two digital images $X_1$ and $X_2$, the adjacency relation [6] is defined as follows: Two points $x_i,y_i\in(X_i,\kappa_i)$, $(x_0,y_0)$ and $(x_1,y_1)$ are $k_{*}(\kappa_1,\kappa_2)$-adjacent in $X_1\times X_2$ if and only if one of the following is satisfied:

$\bullet$ $x_0 = x_1$ and $y_0 = y_1$; or

$\bullet$ $x_0 = x_1$ and $y_0$ and $y_1$ are $\kappa_1$-adjacent; or

$\bullet$ $x_0$ and $x_1$ are $\kappa_0$-adjacent and $y_0 = y_1$; or

$\bullet$ $x_0$ and $x_1$ are $\kappa_0$-adjacent and $y_0$ and $y_1$ are $\kappa_1$-adjacent.

Definition 2.2. [3] A $(\kappa,\lambda)$-continuous surjection $f:X\rightarrow Y$ is $(\kappa,\lambda)$-shy if

$\bullet$ for each $y\in Y$, $f^{-1}(\{y\})$ is $\kappa$-connected, and

$\bullet$ for each $y_0,y_1 \in Y$, if $y_0$ and $y_1$ are $\lambda$-adjacent, then $f^{-1}(\{y_0,y_1\})$ is $\kappa$-connected.

Theorem 2.3. [5] For a continuous surjection $f(X,\kappa)\rightarrow (Y,\lambda)$, if $f$ is an isomorphism, then $f$ is shy. On the other hand, if $f$ is shy and injective, then $f$ is an isomorphism.

The wedge of two digital images $(X,\kappa)$ and $(Y,\lambda)$, denoted by $X\vee Y$, is the union of the digital images $(X^{'},\mu)$ and $(Y^{'},\mu)$, where [4]

$\bullet$ $X^{'}$ and $Y^{'}$ have a single point $p$;

$\bullet$ If $x\in X^{'}$ and $y \in Y^{'}$ are $\mu$-adjacent, then either $x = p$ or $y = p$;

$\bullet$ $(X^{'},\mu)$ and $(X,\kappa)$ are isomorphic; and

$\bullet$ $(Y^{'},\mu)$ and $(Y,\lambda)$ are isomorphic.

Theorem 2.4. [5] Two continuous surjections

are shy maps if and only if $f\times g:(A\times B, k_{*}(\alpha,\beta))\rightarrow (C\times D,k_{*}(\gamma,\delta))$ is a shy map.

Sphere-like digital images is defined as follows [4]:

where $0_n$ is the origin point of $\mathbb{Z}^n$. For $n = 0$ and $n = 1$, the sphere-like digital images are shown in Figure 4.

3.   The digital smash product

In this section, we define the digital smash product which has some important relations with a digital homotopy theory.

Definition 3.1. Let $(X,\kappa)$ and $(Y,\lambda)$ be two digital images. The digital smash product $X \wedge Y$ is defined to be the quotient digital image $(X\times Y)/(X\vee Y)$ with the adjacency relation $k_{*}(\kappa,\lambda)$, where $X\vee Y$ is regarded as a subset of $X\times Y$.

Before giving some properties of the digital smash product, we prove some theorems which will be used later.

Theorem 3.2. Let $X_a$ and $Y_a$ be digital images for each element $a$ of an index set $A$. For each $a\in A$, if $f_a\simeq_{(\kappa, \lambda)} g_a:X_a\rightarrow Y_a$ then

where $n$ is the cardinality of the set $A$.

Proof. Let $F_a:X_a \times [0,m]_{\mathbb{Z}} \rightarrow Y_a$ be a digital $(\kappa,\lambda)$-homotopy between $f_a$ and $g_a$, where $[0,m]_{\mathbb{Z}}$ is a digital interval. Then

defined by

is a digital continuous function, where $t$ is an element of $[0,m]_{\mathbb{Z}}$ since the functions $F_a$ are digital continuous for each element $a\in A$. Therefore $F$ is a digital $(\kappa^n,\lambda^n)$-homotopy between $\prod_{a\in A} f_a$ and $\prod_{a\in A} g_a$.

Theorem 3.3. If each $f_a:X_a\rightarrow Y_a$ is a digital $(\kappa,\lambda)$-homotopy equivalence for all $a\in A$, then $\prod_{a\in A} f_a$ is a digital $(\kappa^n,\lambda^n)$-homotopy equivalence, where $n$ is the cardinality of the set $A$.

Proof. Let $g_a: Y_a\rightarrow X_a$ be a $(\lambda,\kappa)$-homotopy inverse to $f_a$, for each $a\in A$. Then we obtain the following relations:

So we conclude that $\prod_{a\in A} f_a$ is a digital $(\kappa^n,\lambda^n)$-homotopy equivalence.

Theorem 3.4. Let $(X,\kappa)$, $(Y,\lambda)$ and $(Z,\sigma)$ be digital images. If $p:(X,\kappa)\rightarrow (Y, \lambda)$ is a $(\kappa,\lambda)-$shy map and $(Z, \sigma)$ is a $\sigma$-connected digital image, then

is a $(\kappa\times\sigma, \lambda\times\sigma)$-shy map, where $1_Z:(Z,\sigma)\rightarrow (Z,\sigma)$ is an identity function.

Proof. Since $(Z, \sigma)$ is a $\sigma$-connected digital image, then for $y\in Y$ and $z \in Z$, we have

Thus, for each $y \in Y$ and $z\in Z$, $(p\times 1_Z)^{-1}(y,z)$ is $\kappa$-connected by the definition of the adjacency of the cartesian product of digital images. Moreover, the map $1_Z$ preserves the connectivity, that is, for every $z_0,z_1 \in Z$ such that $z_0$ and $z_1$ are $\sigma$-adjacent, $1_Z(\{z_0,z_1\}) = \{z_0,z_1\}$ is $\sigma$-connected. It is easy to see that

Hence for each $y_0,y_1 \in Y$ and $z_0,z_1 \in Z$, $(p\times 1_Z)^{-1}(\{y_0,y_1\},\{z_0,z_1\})$ is a $k_{*}(\kappa,\sigma)$-connected using the definition of the adjacency of the Cartesian product of digital images.

Theorem 3.5. Let $A$ and $B$ be digital subsets of $(X,\kappa)$ and $(Y,\lambda)$, respectively. If $f,g:(X,A)\rightarrow (Y,B)$ are $(\kappa,\lambda)$-continuous functions such that $f\simeq_{(\kappa,\lambda)}g$, then the induced maps $\bar{f},\bar{g}:(X/A,\kappa) \rightarrow (Y/B, \lambda)$ are digitally $(\kappa,\lambda)$-homotopic.

Proof. Let $F:(X\times I, A\times I) \rightarrow (Y,B)$ be a digital $(\kappa,\lambda)$-homotopy between $f$ and $g$ where $I = [0,m]_{\mathbb{Z}}$. It is clear that $F$ induces a digital function $\bar{F}: (X/A)\times I \rightarrow Y/B$ such that the following square diagram is commutative, where $p$ and $q$ are shy maps:

Since $q \circ F$ is digitally continuous, $p\times 1$ is a shy map and $\bar{F}(p\times 1) = q\circ F$, $\bar{F}$ is a digital continuous map. Hence $\bar{F}$ is a digital $(\kappa,\lambda)$-homotopy map between $\bar{f}$ and $\bar{g}$.

We are ready to present some properties of the digital smash product. The following theorem gives a relation between the digital smash product and the digital homotopy.

Theorem 3.6. Given digital images $(X,\kappa)$, $(Y,\lambda)$, $(A,\sigma)$, $(B,\alpha)$ and two digital functions $f:X \rightarrow A$ and $g:Y\rightarrow B$, there exists a function $f\wedge g:X\wedge Y\rightarrow A\wedge B$ with the following properties:

$(i)$ If $h:A\rightarrow C$, $k:B\rightarrow D$ are digital functions, then

$(ii)$ If $f\simeq_{(\kappa,\sigma)} f^{'}:X\rightarrow A$ and $g\simeq_{(\lambda,\alpha)} g^{'}:Y \rightarrow B$, then

Proof. The digital function $f\times g: X\times Y \rightarrow A\times B$ has the property that

Hence $f\times g$ induces a digital function $f\wedge g: X\wedge Y \rightarrow A\wedge B$ and property $(i)$ is obvious. As for $(ii)$, the digital homotopy $F$ between $f\times g$ and $f^{'}\times g^{'}$ can be constructed as follows: We know that

By Theorem 3.2, we have

$F$ is a digital homotopy of functions of pairs from $(X\times Y, X\vee Y)$ to $(A\times B, A\vee B)$. Consequently a digital homotopy between $f\wedge g$ and $f^{'} \wedge g^{'}$ is induced by Theorem 3.5.

Theorem 3.7. If $f$ and $g$ are digital homotopy equivalences, then $f\wedge g$ is a digital homotopy equivalence.

Proof. Let $f:(X,\kappa)\rightarrow (Y,\lambda)$ be a $(\kappa,\lambda)$-homotopy equivalence. Then there exists a $(\lambda,\kappa)$-continuous function $f^{'}:(Y,\lambda)\rightarrow (X,\kappa)$ such that

Moreover, let $g:(A,\sigma)\rightarrow (B,\alpha)$ be a $(\sigma,\alpha)$-homotopy equivalence. Then there is a $(\alpha,\sigma)$-continuous function $g^{'}:(B,\alpha)\rightarrow (A,\sigma)$ such that

By Theorem 3.6, there exist digital functions

such that

and

So $f\wedge g$ is a digital homotopy equivalence.

The following theorem shows that the digital smash product is associative.

Theorem 3.8. Let $(X,\kappa)$, $(Y,\lambda)$ and $(Z,\sigma)$ be digital images. $(X\wedge Y)\wedge Z$ is digitally isomorphic to $X\wedge (Y \wedge Z)$.

Proof. Consider the following diagram:

where $p$ represents for the digital shy maps of the form $X\times Y \rightarrow X\wedge Y$. By Theorem 3.4, $p\times 1$ and $1\times p$ are digital shy maps. $1:X\times Y\times Z\rightarrow X\times Y\times Z$ induces functions

These functions are clearly injections. By Theorem 2.3, $f$ is a digital isomorphism.

The next theorem gives the distributivity property for the digital smash product.

Theorem 3.9. Let $(X,\kappa)$, $(Y,\lambda)$ and $(Z,\sigma)$ be digital images. $(X\vee Y)\wedge Z$ is digitally isomorphic to $(X\wedge Z)\vee (Y \wedge Z)$.

Proof. Suppose that $p$ represents for the digital shy maps of the form $X\times Y \rightarrow X\wedge Y$ and $q$ stands for the digital shy maps of the form $X\times Y \rightarrow X\vee Y$. We may obtain the following diagram:

From Theorem 2.4, $p\times p$ is a digital shy map and by Theorem 3.4, $q\wedge 1$ is also a digital shy map. The function $m:(X\times Y)\times Z \rightarrow (X\times Z)\times (Y\times Z)$ induces a digital function

Obviously $f$ is a one-to-one function. By Theorem 2.3, $f$ is a digital isomorphism.

Theorem 3.10. Let $(X,\kappa)$ and $(Y,\lambda)$ be digital images. $X\wedge Y$ is digitally isomorphic to $Y \wedge X$.

Proof. If we suppose that $g$ stands for the digital shy maps $Y\times X \rightarrow Y\wedge X$ and $p$ represents for the digital shy maps of the form $X\times Y \rightarrow X\wedge Y$, we get the following diagram:

The switching map $u:X\times Y \rightarrow Y\times X$ induces a digital shy map $f:X\wedge Y \rightarrow Y\wedge X$. Additionally, $f$ is a one-to-one. Hence, $f$ is a digital isomorphism from Theorem 2.3.

Definition 3.11. The digital suspension of a digital image $X$, denoted by $sX$, is defined to be $X\wedge S_1$.

Example 1. Choose a digital image $X = S_0$. Then we get the following digital images in Figure 5.

Theorem 3.12. Let $x_0$ be the base point of a digital image $X$. Then $sX$ is digitally isomorphic to the quotient digital image

where the cardinality of $[a,b]_{\mathbb{Z}}$ is equal to $8$.

Proof. The function

is a digital shy map defined by $\theta(t_i) = c_i \ \text{mod} \ 8$, where $c_i \in S_1$ and $i\in \{0,1,\ldots,7\}$. Hence if $p:X\times S_1 \rightarrow X\wedge S_1$ is a digital shy map, then the digital function

is also a digital shy map, and its effect is to identify together points of

The digital composite function $p\circ(1\times \theta )$ induces a digital isomorphism

Definition 3.13. The digital cone of a digital image $X$, denoted by $cX$, is defined to be $X\wedge I$, where $I = [0,1]_{\mathbb{Z}}$.

Example 2. Take a digital image $X = S_0$. Then we have the following digital images in Figure 6.

Theorem 3.14. For any digital image $(X,\kappa)$, the digital cone $cX$ is a contractible digital image.

Proof. Since $I = [0,1]_{\mathbb{Z}}$ is digitally contractible to the point $\{0\}$,

is obviously a single point.

Corollary 1. For $m\in \mathbb{N}$, $S_m\wedge I$ is equal to $S_m\wedge S_0$, where $I = [0,1]_{\mathbb{Z}}$ is the digital interval and $S_0$ is a digital $0$-sphere.

Proof. Since $S_0$ and $I$ consist of two points, we get the required result.

4.   The open problem

For each $m,n\geq 0$, can we prove that digital $(m+n)$-sphere $S_{m+n}$ is isomorphic to $S_m\wedge S_n$?

5.   Conclusion and future works

This paper introduces some notions such as the smash product, the suspension, and the cone for digital images. Since they are significant topics related to homotopy, homology, and cohomology groups in algebraic topology, we believe that the results in the paper can be useful for future studies in digital topology.

Acknowledgments

We would like to express our gratitude to the anonymous referees for their helpful suggestions and corrections.