Centralized solution in max-min fuzzy relation inequalities

1.   Introduction

Throughout this article, we only consider simple, undirected, and finite graphs and assume that all graphs are connected. Suppose $\mathscr{G}$ is a graph with the vertex set $V_(\mathscr{G}) = \{v_{1}, \; v_{2}, \cdot \cdot \cdot, \; v_{n}\}$ and the edge set $E_(\mathscr{G}) = \{e_{1}, \; e_{2}, \cdot \cdot \cdot, \; e_{m}\}$. The adjacency matrix $A(\mathscr{G})$ is a $0-1 n \times n$ matrix indexed by the vertices of $\mathscr{G}$ and defined by $a_ij = 1$ if and only if $v_{s}v_{t} \in E_{\mathscr{G}}$. For more notation, one refer to ^[1].

The Laplacian matrix of graph $\mathscr{G}$ is defined as $L(\mathscr{G}) = D(\mathscr{G}) - A(\mathscr{G})$, and assume that the eigenvalues of $L(\mathscr{G})$ are labeled $0 \leq \mu_{1} < \mu_{2} < \cdot \cdot \cdot < \mu_{n}$.

The normalized Laplacian matrix is given by

The distance, $d_{ij} = d_{\mathscr{G}}(v_s, v_t)$, between vertices us and ut of $\mathscr{G}$ is the length of the shortest $u_{s}$, $u_{t}$-path in $\mathscr{G}$. The Wiener index ^[2,3] is the sum of the distances of any two vertices in the graph $\mathscr{G}$, that is

In 1947, the distance-based invariant first appeared in chemistry ^[2,3] and began to the applied to mathematics 30 years later [5]. Nowadays, the Wiener index is widely used in mathematics ^[6,7,8] and chemistry ^[9,10,11].

In a simple graph $\mathscr{G}$, the degree, $d_{ij} = d_{\mathscr{G}}(v_i)$, of a vertex $v_{i}$ is the number of edges at $v_{i}$. The Gutman index ^[12] of the simple graph $\mathscr{G}$ is expressed by

Klein and Randic initially outlined the concepts associated with the resistance distance of the graph. Assume that each edge is replaced by a unit resistor, and we use rst to denote the resistance distance between two vertices s and t. Similar to the Wiener index, the Kirchhoff index ^[13,14] of graph $\mathscr{G}$ is expressed as the sum of the resistance distances between each two vertices, that is

In 2007, Chen and Zhang ^[15] defined the multiplicative degree-Kirchhoff index ^[16,17], that is

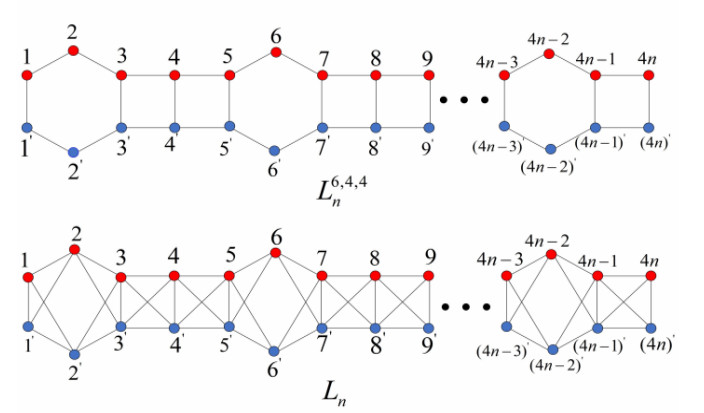
Phenyl is a conjugated hydrocarbon, and $L_{n}^{6, 4, 4}$ denote a linear chain, containing $n$ hexagons and $2n-1$ squares, as shown in Figure 1.

With the rapid changes of the times, organic chemistry has also developed rapidly, which has led to a growing interest in polycyclic aromatic compounds.

In 1985, the computational method and procedure of the matrix decomposition theorem were proposed by Yang ^[18]. This led to the solution of some problems in graph networks and allowed the unprecedented development of self-homogeneous linear hydrocarbon chains. For example, in 2021, X.L. Ma ^[20] got the normalized Laplacian spectrum of linear phenylene, and the linear phenylene containing it has $n$ hexagons and $n-1$ squares. L. Lan ^[21] explored linear phenylene with $n$ hexagons and $n$ squares. Umar Ali ^[22] analyzed the strong prism of a graph $G$, which is the strong product of the complete graph of order $2$, and X.Y. Geng ^[23] obtained the Laplacian spectrum of $L_{n}^{6, 4, 4}$, which contains $n$ hexagons and $2n-1$ squares. J.B. Liu ^[24] derived the Kirchhoff index and complexity of $O_{n}$, which denoting linear octagonal-quadrilateral networks. C. Liu ^[25] got the Laplacian spectrum and Kirchhoff index of $L_n$, and $L_n$ has $t$ hexagons and $3t+1$ quadrangles.

Inspired by these recent works, we try to investigate the Laplacians and the normalized Laplaceians for graph transformations on phenyl dicyclobutadieno derivatives.

The various sections of this article are as follows: In Section 2, we proposed some concepts and lemmas and used them in subsequent articles. In Section 3 and Section 4, we acquired the Laplacian matrix and the normalized Laplacian matrix, then we made sure the Kirchoff index, the multiplicative degree-Kirchoff index, and the complexity of $L_n$. In Section 5, we obtained conclusions based on the calculations in this paper.

2.   Preliminary works

In this article, graph $L_n$ and graph $L_{n}^{6, 4, 4}$ are portrayed in Figure $1$. Define the characteristic polynomial of matrix $U$ of order $n$ as $P_{U}(x) = det(xI-U)$.

It is easy to understand that $\pi = (1, 1')(2, 2')\cdots\big((4n), (4n)'\big)$ is an automorphism. Let $V_{1} = \{u_{1}, u_{2}, \cdots, u_{4n+1}, v_{1}, \cdots, v_{4n}\}, \; V_{2} = \{u'_{1}, u'_{2}, \cdots, u'_{4n}, v'_{1}, \cdots, v'_{4n+1}\}$, $|V(L_{n})| = 8n$ and $|E(L_{n})| = 19n-4$. Thus, the (normalized) Laplacians matrix can be expressed in the form of a block matrix, that is

where $L_{V_{s}V_{t}}$ and $\mathcal{L}_{V_{s}V_{t}}$ are a submatrix consisting of rows corresponding to the vertices in $V_s$ and columns corresponding to the vertices in $V_t$, $s, t = 0, 1, 2$. Let

then

and $Q'$ is the transposition of $Q$.

$L_{A} = L_{V_{1}V_{1}}+L_{V_{1}V_{2}}$, $L_{S} = L_{V_{1}V_{1}}-L_{V_{1}V_{2}}$, $\mathcal{L}_{A} = \mathcal{L}_{V_{1}V_{1}}+\mathcal{L}_{V_{1}V_{2}}$, $\mathcal{L}_{S} = \mathcal{L}_{V_{1}V_{1}}-\mathcal{L}_{V_{1}V_{2}}$

Lemma 2.1. ^[20] If $\mathscr{G}$ is a graph and suppose that $L_{A}(\mathscr{G}), L_{S}(\mathscr{G}), L_{A}(\mathscr{G})$, and $L_{S}(\mathscr{G})$ are determined as above, then

Lemma 2.2. ^[26] With the extensive study of the Kirchhoff index, Gutman and Mohar proposed an algorithm based on the relation between the Kirchhoff index and the Laplacian eigenvalues, namely

and the eigenvalues of $L(\mathscr{G})$ are $0 = \xi_{1} < \xi_{2} \geq \cdots \geq \xi_{n}(n\geq2)$.

Lemma 2.3. ^[14] Suppose that the eigenvalues of $L(\mathscr{G})$ are $\xi_1 \leq \xi_2 \leq \cdots \leq \xi_n$, then its multiplicative degree-Kirchhoff index can be denoted by

Lemma 2.4. ^[1] The number of spanning trees in $\mathscr{G}$ can also be called the complexity of $\mathscr{G}$. If $\mathscr{G}$ is a graph with $|V_\mathscr{G}| = n$ and $|E_\mathscr{G}| = m$. Let $\lambda_i(i = 2, 3, \cdots, n)$ be the eigenvalues of $L(\mathscr{G})$. Then the complexity of $\mathscr{G}$ is

3.   Kirchhoff index of $L_n$

In this section, the main objective is to find out the Kirchhoff index of $L_n$. Then, combining the definition of the Laplacian matrix and Eq (1.1), we can write these block matrices as follows:

and

Hence,

and

Assume that $0\leq \alpha_1 < \alpha_2\leq \alpha_3 \leq \cdots \leq \alpha_{4n}$ are the roots of $P_{L_{A}}(x) = 0$, and $0 \leq \beta_1 \leq \beta_2 \leq \beta_3 \leq \cdots \leq \beta_{4n}$ are the roots of $P_{L_{S}}(x) = 0$. By Lemma 2.2, we immediately have

Obviously, $\sum_{j = 1}^{4n}\frac{1}{\beta_{j}}$ can be obtained according to $L_{S}$.

Next, we focus on computing $\sum_{i = 1}^{4n}\frac{1}{\alpha_{i}}$. Let

Based on Vieta's theorem of $P_{L_{A}}(x)$, we can exactly get the following equation:

For the sake of convenience, let $M_s$ be used to express the $s-th$ order principal minors of matrix $A$, and $m_s = detM_s$ is recorded. We can get $m_1 = 2, m_2 = 4, m_3 = 8$.

And

by further induction, we have

In this way, we can get two theorems.

Theorem 3.1. $(-1)^{4n-1}a_{4n-1} = (4n)2^{4n-1}$.

Proof. Due to the sum of all the principal minors of order $4n-1$ of $L_A$ is $(-1)^{4n-1}a_{4n-1}$,

where

Let $m_0 = 1, det U_0 = 1$, because of the symmetry of matrix $L_A$, then $det U_{4n-s} = det M_{4n-s}$. Hence

as desired. □

Theorem 3.2. $(-1)^{4n-2}a_{4n-2} = \frac{(4n-1)(4n)(4n+1)2^{4n-1}}{3}$.

Proof. Since the $(-1)^{4n-2}a_{4n-2}$ is the tatal of all the principal minors of order $4n-2$ of $L_A$, we have

where

and

Therefore, we can have

The proof is over. □

From the results of Theorem 3.1 and Theorem 3.2, we can get

where the eigenvalues of $L_A$ are $0 \leq \alpha_1 < \alpha_2 \leq \alpha_3 \leq \cdots \leq \alpha_{4n}$.

Lemma 3.3. Suppose $L_{n}^{6, 4, 4}$ be the dicyclobutadieno derivative of phenylenes and the graph $L_n$ be obtained from the transformation of the graph $L_{n}^{6, 4, 4}$.

Proof. Substituting Eqs (3.5) and (3.6) into (3.4), the Kirchhoff index of $L_n$ can be expressed

The result is as desired. □

The Kirchhoff index of $L_n$ from $L_1$ to $L_{12}$ is shown in Table 1.

Next, we will further consider the Wiener index of $L_n$.

Lemma 3.4. Let $L_{n}^{6, 4, 4}$ be the dicyclobutadieno derivative of [n]phenylenes, and the graph $L_n$ be obtained from the transformation of the graph $L_{n}^{6, 4, 4}$, then

Proof. Consider $d_{st}$ for all vertices. For the sake of convenience, we divide the vertices of the graph into the following five categories:

Case 1. Vertex $1$ of $L_n$:

Case 2. Vertex $4j-3(j = 1, 2, \cdots, n)$ of $L_n$, $i = 4j-3$:

Case 3. Vertex $4j-2(j = 1, 2, \cdots, n)$ of $L_n$, $i = 4j-2$:

Case 4. Vertex $4j-1(j = 1, 2, \cdots, n)$ of $L_n$, $i = 4j-1$:

Case 5. Vertex $4j(j = 1, 2, \cdots, n)$ of $L_n$, $i = 4j$:

Hence, we have

Consider the above results of the Kirchhoff index and the Wiener index. We can get following equation when $n$ tends to infinity:

The result is as desired. □

4.   Multiplicative degree-Kirchhoff index and complexity of $L_n$

In this section, we use the eigenvalues of the normalized Laplacian matrix to determine the multiplicative degree-Kirchhoff index of $L_n$. Besides, we calculate the complexity of $L_n$. Then

and

Therefore,

and

Assume that the roots of $P_{L_{A}}(x) = 0$ are $0\leq \xi_1 < \xi_2\leq \xi_3 \leq \cdots \leq \alpha_{4n}$, and $0 \leq \gamma_1 \leq \gamma_2 \leq \gamma_3 \leq \cdots \leq \gamma_{4n}$ are the roots of $P_{L_{S}}(x) = 0$. By Lemma 2.3, we can get

Since $\mathcal{L}_{s}$ is a diagonal matrix. Obviously, its diagonal elements $1, \frac{4}{3}$ and $\frac{6}{5}$ correspond to the eigenvalues of $\mathcal{L}_{s}$, respectively. Then, it can be clearly obtained as

Let

$\frac{1}{\xi_{2}}, \frac{1}{\xi_{3}}, \cdot\cdot\cdot, \frac{1}{\xi_{4n+1}}$are the roots of the following equation

Based on the Vieta' s theorem of $P_{L_{A}}(x)$, we can get

Similarly, we can get another two interesting facts.

Theorem 4.1. $(-1)^{4n-1}b_{4n-1} = \frac{25}{9}(38n-8)(\frac{4}{125})^{n}$.

Proof. Let $s_p = detF_p$, then we have $s_1 = \frac{2}{3}, s_2 = \frac{1}{3}, s_3 = \frac{2}{15}, s_4 = \frac{4}{75}$, and

After further simplification, the transformation form of the above formula is obtained.

Similarly, we have $t_1 = \frac{2}{3}, t_2 = \frac{4}{15}, t_3 = \frac{2}{15}, t_4 = \frac{4}{75}$, and

Therefore, the transformation form of the above formula is obtained.

Since the $(-1)^{4n-1}b_{4n-1}$ is the total of all the principal minors of order $4n-1$ of $L_{A}$, we have

The proof of Theorem 4.1 completed. □

Theorem 4.2. $(-1)^{4n-2}b_{4n-2} = \frac{1}{3240}(14520n^3+4599n^2-1496n+3)(\frac{4}{125})^{n}$.

Proof. We observe that the sum of all the principal minors of order $4n$ in $\mathcal{L}_{A}$ is $(-1)^{4n-2}b_{4n-2}$, then

By Eq (4.8), we know that the result of $det\mathcal{L}_{A}[s, t]$ will change with the values of $s$ and $t$. Then we can get the following twenty cases:

Case 1. $i = 4s$, $j = 4t$, $1\leq{s} < t\leq{n}$,

Case 2. $i = 4s$, $j = 4t+1$, $1\leq{s}\leq t\leq{n-1}$,

Case 3. $i = 4s$, $j = 4t+2$, $1\leq{s}\leq t\leq{n-1}$,

Case 4. $i = 4s$, $j = 4t+3$, $1\leq{s}\leq t\leq{n-1}$,

Case 5. $i\equiv 0$, $j = 4n$, $1\leq{s}\leq t$,

Case 6. $i = 4s+1$, $j = 4t$, $1\leq{s} < t\leq{n}$,

Case 7. $i = 4s+1$, $j = 4t+1$, $1\leq{s} < t\leq{n-1}$,

Case 8. $i = 4s+1$, $j = 4t+2$, $1\leq{s} < t\leq{n-1}$,

Case 9. $i = 4s+1$, $j = 4t+3$, $0\leq{s} \leq t\leq{n-1}$,

Case 10. $i\equiv 1$, $j = 4n+1$, $0\leq{s} \leq{n}$,

Case 11. $i = 4s+2$, $j = 4t$, $0\leq{s} < t \leq{n}$,

Case 12. $i = 4s+2$, $j = 4t+1$, $0\leq{s} < t \leq{n-1}$,

Case 13. $i = 4s+2$, $j = 4t+2$, $0\leq{s} < t \leq{n-1}$,

Case 14. $i = 4s+2$, $j = 4t+3$, $0\leq{s}\leq t \leq{n-1}$,

Case 15. $i\equiv 2$, $j = 4t+3$, $0\leq{s} \leq{n-1}$,

Case 16. $i = 4s+3$, $j = 4t$, $0\leq{s} < t \leq{n}$,

Case 17. $i = 4s+3$, $j = 4t+1$, $0\leq{s} < t \leq{n-1}$,

Case 18. $i = 4s+3$, $j = 4t+2$, $0\leq{s} < t \leq{n-1}$,

Case 19. $i = 4s+3$, $j = 4t+3$, $0\leq{s} < t \leq{n-1}$,

Case 20. $i\equiv 3$, $j = 4t$, $0\leq{s} \leq{n-1}$,

Therefore, we can get

where

Hence

The proof of Theorem 4.2 completed. □

Let $0 \leq \xi_1 \leq \xi_2 \leq \xi_3 \leq \cdots \leq \xi_{3n+2}$ are the eigenvalues of $\mathscr{L}_{A}$. We can get the following exact equation:

Theorem 4.3. Set $L_{n}^{6, 4, 4}$ be the derivative [n]pheylenes, and the expression of the multiplicative degree-Kirchhoff index is

Proof. Together with Eq.(4.7) and Theorems 4.1 and 4.2, one can get

The result as desired. □

The multiplicative degree-Kirchhoff indices of $L_n$ from $L_1$ to $L_{12}$, see Table 2.

Then we want to calculate the Gutman index of $L_n$.

Theorem 4.4. Suppose that $L_{n}^{6, 4, 4}$ is the dicyclobutadieno derivative of [n]phenylenes and the graph $L_{n}$ is obtained from the transformation of the graph $L_{n}^{6, 4, 4}$, then

Proof. Consider $d_{ij}$ for all vertices. We divide the vertices of $L_n$ into the following four categories.

Case 1. Vertex $4i-2(i = 1, 2, \cdots, n)$ of $L_{n}$:

Case 2. Vertex $4i-1(i = 1, 2, \cdots, n)$ of $L_{n}$:

Case 3. Vertex $4i(i = 1, 2, \cdots, n)$ of $L_{n}$:

Case 4. Vertex $4i-3(i = 1, 2, \cdots, n)$ of $L_{n}$:

According to Eq.(1.3), the Gutman index of $L_n$ is

Therefore, combining with $Kf^{*}(L_n)$ and $Gut(L_n)$, we have

The result as desired.□

Finally, we want to know the complexity of $L_n$.

Theorem 4.5. For the graph $L_n$, we have

Proof. Based on Lemma 2.4, we can get

Note that

Hence,

The proof is over. □

Thus, we can get the complexity of $L_n$ from $W_1$ to $W_{8}$ which are listed in Table 3.

5.   Conclusions

In this paper, the linear chain network with $n$ hexagons and $2n-1$ squares is considered. We have devoted ourselves to calculating the (multiplicative degree) Kirchhoff index, Wiener index, Gutman index, and complexity. In the meantime, we deduced that the ratio of the (multiplicative degree) Kirchhoff index to the (Gutman) Wiener index is nearly a quarter when $n$ tends to infinity. These rules also apply to some other graphs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by the Anhui Provincial Natural Science Research Major Project (No. 2022AH040317) and the Anhui Provincial 2023 Action Project for Cultivating Young and Middle Aged Teachers in Universities (No. DTR2023095).

Conflict of interest

No potential conflicts of interest were reported by the authors.