Improved results on sampled-data synchronization control for chaotic Lur'e systems

1.   Introduction

Because of the universal existence of predation in nature, predator-prey models, especially delayed predator-prey models, have been a research topic in the field of population dynamics. In order to research mutual relationship between biological populations and regulating internal development, a great number of predator-prey models have been established. By studying the various dynamic behaviors of predator-prey models, we find that the parameters have a significant effect on the population density of organisms under certain environmental conditions. In recent years, there have been numerous research results on predator-prey models, and many excellent achievements have been presented. For instance, Enatsu et al. ^[1] explored the effects of cooperative hunting and maturation delay on the coexistence of predator-prey. Majumdar et al. ^[2] analyzed the equilibrium points and local bifurcations of the non-delayed prey-predator model, as well as the local and global stability of the interior equilibrium point in the presence of delay. Gao and Li. ^[3] discussed the Hopf bifurcation of a symbiotic predator-prey model with double time delay. Yan et al. ^[4] analyzed how nonlocal prey competition can trigger spatially inhomogeneous Hopf bifurcation and Turing instability, and its impacts on the amplitude of periodic solutions and the risk of species extinction. For more detailed studies, one can see ^[5,6,7].

In 2023, Pal et al. ^[8] put forward the following predator-prey model:

where $u_1(t)$, $u_2(t)$, $u_3(t)$ represent the densities of prey, intermediate predators, and top predators at any time $t > 0$. $\gamma$ denotes the intrinsic growth rate of the prey species in the absence of predators, and $d$ is the density-related mortality rate, $a_1$ is the capture rate of prey species by intermediate predators, $m$ is the half saturation constant, $\bar{\lambda}_1$ represents the respective gain in intermediate predator density for prey and top predators, being $\bar{\lambda}_1$ is between $0$ and $1$, $\bar{\lambda}_2$ stands for the proportional constant between the growth rate of the top predator and the response of the function, $\xi_1$–$\xi_3$ represent the natural mortality of intermediate predators, the coefficient of intraspecies competition of intermediate predators, and the natural mortality of top predators, respectively, $\beta$ and $\beta_0$ represent per capita regeneration rate and density-dependent intensity, $\varpi_1$–$\varpi_4$ are all fear parameters, $\varpi_1$ and $\varpi_2$ are the effects of fear on the reproduction ability and intraspecies competition of prey populations, $\varpi_3$ is the changes in the behavior of intermediate predators due to the presence of apex predators, and $\varpi_4$ is the impacts of predators$^{, }$ fear of top predators on intraspecies competition among intermediate predators. For a more detailed explanation of system (1.1), see ^[8]. Pal et al. ^[8] examined how fear responses influence population reproduction and foraging behavior in a three-species food chain model, and affect the system's stability of model (1.1). In numerous instances, the introduction of time delay in predator-prey models is necessary because the time delays in population development have an effect on the density of prey and predators. Based on this consideration, we can build a more suitable delayed predator-prey model, since the density of prey $u_1(t)$ not only depends on the current but also the past density of intermediate predators. In addition, the density of intermediate predator and top predators also depend on the current density and past density of top predators. Assuming that the density of prey is affected by the self-feedback time from $u_1$ to $u_1$, the density of intermediate predators is affected by the self-feedback time from $u_2$ to $u_2$, and the density of top predators is affected by the self-feedback time from $u_3$ to $u_3$. In many cases, the self-feedback time for $u_1$–$u_3$ is different. For the sake of mathematical simplification, we assume that all the self-feedback time for $u_1$–$u_3$ is similar, then, we can adjust the model (1.1) as follows:

where $\theta\geq0$ represents the time delay, and all other parameters are positive real numbers. Many studies indicate that delay is a key factor affecting the dynamic characteristics of various differential systems. In a variety of examples, delay leads to loss of stability and appearance of bifurcation, and trigger chaotic behavior and so forth ^[9,10,11]. Among these phenomena, delay-induced Hopf bifurcation is a significant dynamic feature. In biology, delay-induced Hopf bifurcation effectively describes the equilibrium relationship between biological population densities. Therefore, we argue that the in-depth study of delay-induced Hopf bifurcation in predator-prey models holds crucial theoretical value. Inspired by the viewpoint mentioned above, we are going to examine the delay-induced Hopf bifurcation and its control for model (1.2). Specifically, we aim to assess the following essential issues: (1) Analyze the characteristics of the solution of system (1.2), such as non-negativity, existence, uniqueness, and boundedness. (2) Investigate the occurrence of the Hopf bifurcation phenomenon and stability of the system (1.2). (3) Design three disparate controllers to adjust the stability region of the system and control the time of bifurcation onset in model (1.2).

The crux prominent points in this study are described as follows: (i) Based on past research achievements, a new delay-independent bifurcation and stability criterion for system (1.2) is established. (ii) By employing various controllers, both the stability domain and the time of bifurcation onset in system (1.2) can be effectively managed. (iii) The study explores how time delay influences the control of Hopf bifurcation phenomena and the stabilization of predator and prey densities in model (1.2)

The structure of this article is arranged as follows: The properties of the solution for system (1.2), which include existence and uniqueness, non-negativity, and boundedness of the solution are presented in Section $2$. Section $3$ focuses on the bifurcation behavior and stability of the system (1.2). Section $4$ addresses the control problem of the bifurcation phenomenon in system (1.2) by developing a practical hybrid delayed feedback controller that incorporates parameter perturbation with delay and state feedback. Section $5$ selects a rational hybrid delayed feedback controller to solve the bifurcation control issue in the system (1.2) by means of combining parametric perturbation with delay feedback and state feedback. Section $6$ manages the control problem of the bifurcation phenomenon in system (1.2) by devising a practical extended hybrid delayed feedback controller, which includes parameter perturbation with delay and state feedback. Section $7$ presents simulation results obtained using Matlab software to confirm the critical findings. A conclusion is provided in Section $8$.

2.   Well-posedness of solution

In this section, we are about to construct a reasonable function to discuss the well-posedness of solutions to model (1.2) (including boundedness, existence, uniqueness, and non-negativity) by utilizing fixed point theory and inequality technique.

Theorem 2.1. Let $\Omega = \{(u_1, u_2, u_3)\in R^3: \max\{|u_1|, |u_2|, |u_3|\}\leq {\mathcal{U}}\}$, where ${\mathcal{U}} > 0$ indicates a constant. For $(u_{10}, u_{20}, u_{30})\in \Omega$, system (1.2) under the initial value $(u_{10}, u_{20}, u_{30})$ owns a unique solution $U = (u_1, u_2, u_3)\in \Omega.$

Proof. Set

where

For arbitrary $U, \tilde{U}\in\Omega$, we obtain

where

Let

From (2.3), we get

Thus, $f(U)$ satisfies the Lipschitz condition for $U$. Applying the fixed point theorem, one can readily conclude that Theorem 2.1 is accurate.

Theorem 2.2. Each solution to model (1.2) beginning with $R_{+}^3$ is non-negative.

Proof. Based on the first equation of system (1.2), we can obtain

then

which results in

Then one derives

Thus

By the same method, we know

Hence, Theorem 2.2 holds true.

Theorem 2.3. If $\theta = 0$ and $\bar{\lambda}_1a_1 < \xi_1, \bar{\lambda}_2 < 1, \eta < \xi_3$, therefore, all solutions of system (1.2) initialized at $R_{+}^3$ are uniformly bounded.

Proof. Let

Then

where where

According to Eq (2.15), we obtain

Consequently, the solutions to the system (1.2) are uniformly bounded.

3.   Exploration of bifurcation of model (1.2)

In this section, we intend to explore the issues of bifurcation and stability of the model (1.2). To start, we suppose that $F(u_{1\star}, u_{2\star}, u_{3\star})$ is the equilibrium point of model (1.2), then $u_{1\star}$–$u_{3\star}$ adhere to the following requirement:

Let

Insert system (3.2) into system (1.2) and we obtain the linear system of model (1.2) at $F(u_{1\star}, u_{2\star}, u_{3\star})$:

where

The characteristic equation for system (3.3) takes the following expression:

which results in

where

If $\theta = 0$. Equation (3.6) changes to

If

is satisfied, then the three roots $\lambda_1$–$\lambda_3$ of Eq (3.8) have negative real parts. Thus the equilibrium point $F(u_{1\star}, u_{2\star}, u_{1\star})$ of system (1.2) under $\theta = 0$ is locally asymptotically stable.

Presume that $\lambda = i\nu$ is the root of Eq (3.6), then Eq (3.6) turns into

which produces

where

and

It follows from (3.10) that

Because of $\cos^2\nu\theta +\sin^2\nu\theta = 1$, we can get

So

Hence, the result is as follows:

where

Let

Suppose that

Due to $({\mathcal{Q}}_2)$, we know $\Upsilon_1(0) = -G_6 < 0$, given that $\lim_{\nu \to \infty}\Upsilon_1(\nu) > 0$, we can conclude that Eq (3.17) has at least one positive real root. Therefore, Eq (3.6) has at least one pair of purely roots. Without loss of generality, we can postulate that Eq (3.17) has twelve positive real roots (say $\nu _j, j = 1, 2, 3, \cdots, 12$). In light of (3.10), one gets

where $j = 1, 2, 3\cdots, 12; n = 0, 1, 2, \cdots$;

Assume ${\theta _0} = {\min _{\{ j = 1, 2, 3, \cdots, 12;n = 0, 1, 2, \cdots \} }}\{ \theta _j^{(n)}\}$ and suppose that when $\theta = {\theta _0}$, Eq (3.6) has a pair of imaginary roots $\pm i\nu _0$. In the next step, the assumption presented is:

where

Suppose that $\lambda(\theta) = \varrho_1(\theta)+i\varrho_2(\theta)$ is the root of Eq (3.6) at $\theta = \theta_0$ such that $\epsilon_1(\theta_0) = 0$, $\epsilon_2(\theta_0) = \nu_0$, then $Re\left(\frac{d\lambda}{d\theta}\right)\Big|_{\theta = \theta = \theta_0, \nu = \nu_0} > 0.$

Proof. Using Eq (3.6), we can gain

It means that

where

Hence

Through this assumption $({\mathcal{Q}}_3)$, we obtain

The proof is concluded. Based on the discussion above, the following result can be easily obtained.

Theorem 3.1. Assume that $({\mathcal{Q}}_1)$–$({\mathcal{Q}}_3)$ are valid, then the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of model (3.1) is locally asymptotically stable state if $\theta \in [0, \theta _{0})$. Moreover, model (3.1) exhibits a cluster of Hopf bifurcations around the equilibrium point $F(u_{1\ast}, u_{2\ast}, u_{3\ast})$ when $\theta = \theta _{0}.$

4.   Regulation of bifurcation in model (1.2) through hybrid controller 1

In this portion, we will study the time of Hopf bifurcation onset in system (1.2) by utilizing a sensible hybrid controller, containing parameter perturbation with delay and state feedback. Building on the concepts from ^[13,14], we propose the following controlled predator-prey model:

where $\eta_1, \eta_2$ indicate control parameters. System (4.1) shares the same equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ as that in system (1.2). Let

The linear system of system (4.1) near $F(u_{1\star}, u_{2\star}, u_{2\star})$ can be represented as follows:

where

The characteristic equation of system (4.3) is given by the following expression:

which leads to

where

If $\theta = 0,$ then Eq (4.6) simplifies to

Thus, all roots of Eq (4.8) have negative real parts if and only if

is satisfied, then the three roots $\lambda_1$–$\lambda_3$ of Eq (4.8) have negative real parts. Thus the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of system (4.1) with $\theta = 0$ is locally asymptotically stable.

Assume that $\lambda = i\nu^{\ast}$ is the root of Eq (4.6), then Eq (4.6) becomes:

From Eq (4.10), we can deduce that

where

and

This means that

On account of $\cos^2\nu^{\ast}\theta +\sin^2\nu^{\ast}\theta = 1$, from (4.14), it can be concluded that

Thus, the following conclusions can be drawn

where

Let

Suppose that

If $({\mathcal{Q}}_5)$ remains, then $\Upsilon_2(0) = -V_6 < 0$, since $\lim_{\nu^{\ast} \to \infty}\Upsilon_2(\nu^{\ast}) > 0$, then the Eq (4.16) possesses at least one positive real root. Consequently, Eq (4.6) has at least one pair of purely imaginary roots. Without loss of generality, we can assume that Eq (4.16) has twelve positive real roots (say $\nu^{\ast} _j, j = 1, 2, 3, \cdots, 12$). Relying on (4.14), we know

where $j = 1, 2, 3, \cdots, 12; k = 0, 1, 2, \cdots$. Assume $\theta _\ast = \min_{\{j = 1, 2, 3, \cdots, 12; k = 0, 1, 2, \cdots\}}\{\theta _{j}^{(k)}\}$ and suppose that when $\theta = \theta_\ast$, Eq (4.6) has a pair of imaginary roots $\pm i\nu^{\ast} _0$.

Next, we present the following assumption:

where

Lemma 4.1. Suppose that $\lambda(\theta) = \bar{\varrho}_1(\theta)+i\bar{\varrho}_2(\theta)$ is the root of Eq (4.6) at $\theta = \theta_\ast$ such that $\bar{\varrho}_1(\theta_\ast) = 0$, $\bar{\varrho}_2(\theta_\ast) = \nu_0^{\ast}$, then $Re\left(\frac{d\lambda}{d\theta}\right)\Big|_{\theta = \theta_\star, \nu = \nu_0^{\ast}} > 0.$

Proof. It follows from Eq (4.6) that

we can get

It means that

where

Hence

Through this assumption $({\mathcal{Q}}_6)$, we obtain

The proof is concluded. Based on the discussion above, the following result can be easily obtained

Theorem 4.1. Assuming that $({\mathcal{Q}}_4)$–$({\mathcal{Q}}_6)$ is valid, then the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of model (4.1) is locally asymptotically stable if $\theta \in [0, \theta _{\ast})$; moreover, model (4.1) exhibits a cluster of Hopf bifurcations around the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ when $\theta = \theta _{\ast}.$

Remark 4.1. In this paper, the purpose of control is to adjust the stability domain and the time of onset of Hopf bifurcation. In this section, we enlarge (or reduce) some parameter values of model (1.2) and add (or reduce) a suitable parameter perturbation with delay to adjust the density of top predators and then achieve our control objectives. In the third equation, $\eta_1$ and $\eta_2$ are feedback gain parameters. If $\eta_1 > 0(<0)$, the density of top predators increases (decreases) and if $\eta_2 > 0(<0)$, parameter perturbation increases (decreases). In a biological sense, we realize the balance of biological populations (the densities of prey, intermediate predators, and top predators) via this hybrid controller. Of course, we can add this control to other equations of model (1.2), but whether the control goal can be achieved will be explored it via mathematical analysis and computer simulation.

5.   Regulation of bifurcation in model (1.2) through hybrid controller 2

In this segment, we will study the Hopf bifurcation problem of system (1.2) through the use of a reasonable hybrid controller that combines parameter perturbation with delay and state feedback. Based on the ideas presented in ^[13,14], we develop the following controlled predator-prey model:

where $\rho_1, \rho_2$ indicate control parameters. System (5.1) shares the same equilibrium point as that in system (1.2). Let

The linear system of system (5.1) near $F(u_{1\star}, u_{2\star}, u_{2\star})$ can be described as:

where

The characteristic equation of system (5.3) owns the following expression:

which leads to

where

If $\theta = 0,$ then Eq (5.6) becomes

Thus, all roots of Eq (5.8) have negative real parts if and only if

is fulfilled, then the three roots $\lambda_1$–$\lambda_3$ of Eq (5.8) have negative real parts. Thus the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of system (5.1) with $\theta = 0$ is locally asymptotically stable.

Assume that $\lambda = i\nu^{\tau}$ is the root of Eq (5.8), then Eq (5.6) becomes:

It follows from Eq (5.10) that

where

and

So there is

In view of $\cos^2\nu^{\tau}\theta +\sin^2\nu^{\tau}\theta = 1$, it follows from (5.14) that

therefore, results can be obtained as follows:

where

Let

Assume that

If $({\mathcal{Q}}_8)$ holds, then $\Upsilon_3(0) = -R_6 < 0$, since $\lim_{\nu^{\tau} \to \infty}\Upsilon_2(\nu^{\tau}) > 0$, then we know that Eq (5.16) has at least one positive real root. Therefore, Eq (5.6) has at least one pair of pure roots. Without loss of generality, we can assume that Eq (5.16) has twelve positive real roots (say $\nu^{\tau} _j, j = 1, 2, 3, \cdots, 12$). Relying on (5.14), we know

where $j = 1, 2, 3, \cdots, 12; w = 0, 1, 2, \cdots$. Assume $\theta _\star = \min_{\{j = 1, 2, 3, \cdots, 12; w = 0, 1, 2, \cdots\}}\{\theta _{j}^{(w)}\}$ and suppose that when $\theta = \theta_\star$, Eq (5.6) has a pair of imaginary roots $\pm i\nu^{\tau} _0$.

Next, we present the following assumption:

where

Lemma 5.1. Suppose that $\lambda(\theta) = \upsilon_1(\theta)+i\upsilon_2(\theta)$ is the root of Eq (4.6) at $\theta = \theta_\star$ such that $\upsilon_1(\theta_\star) = 0$, $\upsilon_2(\theta_\star) = \nu_0^{\tau}$, then $Re\left(\frac{d\lambda}{d\theta}\right)\Big|_{\theta = \theta_\star, \nu = \nu_0^{\tau}} > 0.$

Proof. It follows from Eq (5.6) that

we can get

It means that

where

Hence

By the assumption $({\mathcal{Q}}_9)$, we get

which ends the proof. According to the above discussion, the following outcome is easily derived.

Theorem 5.1. Suppose that $({\mathcal{Q}}_7)$–$({\mathcal{Q}}_9)$ hold, then the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of model (5.1) is locally asymptotically stable if $\theta \in [0, \theta _{\star})$, and model (5.1) generates a cluster of Hopf bifurcations around the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ when $\theta = \theta _{\star}.$

6.   Controlling bifurcation in model (1.2) with an extended delayed feedback controller

In this segment, we will investigate the Hopf bifurcation issue of system (1.2) using a reasonable hybrid controller that encompasses parameter perturbation with delay and state feedback. In accordance with the notion in ^[15], we construct the controlled predator-prey model as follows:

where $\delta_1$–$\delta_6$ represent control parameters. System (6.1) shares the same equilibrium point as that in system (1.2). Let

The linear system of system (1.3) near $E(u_{1\star}, u_{2\star}, u_{3\star})$ can be demonstrated as below:

where

The characteristic equation of system (6.3) takes the following form:

which leads to:

where

If $\theta = 0,$ then Eq (6.6) becomes

Hence, the necessary and sufficient condition for all roots of Eq (6.8) to have negative real parts is

Then, three roots $\lambda_1$–$\lambda_3$ of Eq (6.8) that have negative real parts. As a result, the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of system (1.2) with $\theta = 0$ is locally asymptotically stable.

It is assumed that $\lambda = i\nu^{\mu}$ is the root of Eq (6.6) and one obtains

Next, referring to Eq (6.10), we obtain

From Eq (6.11), we are able to derive

Owing to $\sin^2\nu^{\mu}\theta = \pm\sqrt{1-\cos^2\nu^{\mu}\theta},$ Eq (6.12) can be modified to

Thus, the results can be summarized as

where

Square each side of Eq (6.14) to achieve the result presented below.

where

Based on Eq (6.16), we can obtain the representation as presented below for $\cos\nu^{\mu}$. Suppose that

where $f_1(\nu^{\mu})$ is a function that varies with $\nu^{\mu}$. We can derive the expression for $\sin\nu^{\mu}$. Assume that

where $f_2(\nu^{\mu})$ denotes a function with respect to $\nu^{\mu}$. Referring to Eqs (6.18) and (6.19), we can determine

By using a computer, we can obtain the roots of Eq (6.20). We denote the root of (6.20) as $\nu^{\mu\ast}$, then

where $j = 1, 2, \cdots; n = 0, 1, 2, \cdots$.

Let $\theta _\ast = \min_{\{n = 1, 2, \cdots\}}\{\theta _{\ast}^{(n)}\}$ and suppose that when $\theta = \theta_\ast$, Eq (6.8) possesses a pair of imaginary roots $\pm i\nu^{\mu\ast} _0$.

As the next step, we put forward the following assumption:

where

Lemma 6.1. Suppose that $\lambda(\theta) = \bar{\upsilon}_1(\theta)+i\bar{\upsilon}_2(\theta)$ is the root of Eq (6.6) at $\theta = \theta_{0\ast}$ such that $\bar{\upsilon}_1(\theta_{0\ast}) = 0$, $\bar{\upsilon}_2(\theta_{0\ast}) = \nu^{\mu\ast} _0$, then $Re\left(\frac{d\lambda}{d\theta}\right)\Big|_{\theta = \theta_{0\ast}, \nu = \nu^{\mu\ast} _0} > 0.$

Proof. As derived from Eq (6.6), it follows that

we can get

which signifies

where

Hence

Under the assumption $({\mathcal{Q}}_{11})$, we derive

which wraps up the proof. Following the preceding analysis, the subsequent result is straightforwardly reached.

Theorem 6.1. Assuming that conditions $({\mathcal{Q}}_{10})$ and $({\mathcal{Q}}_{11})$ hold, then the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$ of model (6.1) is locally asymptotically stable state for $\theta \in [0, \theta_{0\ast})$. Additionally, when $\theta = \theta_{0\ast}$, model (6.1) exhibits a cluster of Hopf bifurcations around the equilibrium point $F(u_{1\star}, u_{2\star}, u_{3\star})$.

Remark 6.1. Pal et al.^[8] revealed the complex impact of fear-induced responses on the stability and behavior of multi-species food web systems. In this article, we develop a more realistic delayed predator-prey system model and investigate the bifurcation behavior and hybrid controller design based on this model. On a theoretical level, these research methods enhance the understanding of bifurcation theory for delayed differential equations. From a biological perspective, the findings of this study are significant for managing the densities of predator and prey populations. Consequently, we believe that this paper has a certain innovation to some degree.

Remark 6.2. Based on the existing literature methods and according to the biological implication of this predator-prey model, we can add the parameter perturbation with delay and state feedback artificially to adjust the densities of prey, intermediate predators, and top predators and achieve our control objectives. Thus, these control techniques have practical significance in biology.

Remark 6.3. Although the form of hybrid controller I and hybrid controller II are same, we add this controller to the third equation of model (1.2) and to the second equation of model (1.2), respectively. Then, we obtain two different delay critical valus to generate Hopf bifurcation. In order to illustrate the different control techniques, we give three different controllers in this paper. We apply these controllers to achieve the control of stability domain and Hopf bifurcation.

Remark 6.4. Based on the biological implication, we introduce one delay into model (1). Even though there is only one difference to model (1), the introduction of delay will lead to a great change to the model. In this paper, the Hopf bifurcation and its control issue are our research topic. By exploring the delay-induced Hopf bifurcation of this predator-prey, we can effectively control the balance among the densities of prey, intermediate predators, and top predators.

Remark 6.5. In this paper, we mainly show the effect of delay on the stability domain and the time of onset of Hopf bifurcation of model (1.2). For different controllers, we can choose different control parameter values to achieve our control objectives. For this problem, we can continue the discussion in the near future.

Remark 6.6. For example, corresponding to the predator-prey model (1.2), we can assume that $u_1(t)$ stands for the density of mice, $u_2(t)$ stands for the density of bobcats, and $u_3(t)$ represent the density of wolves. For controller I, we can adjust the value of per capita regeneration rate ($\beta$), the proportional constant between the growth rate of wolves and the response of the function ($\bar{\lambda}_2$), and the natural mortality of wolves ($\xi_3$) (for ($\beta, \bar{\lambda}_2, \xi_3$, the same multiple is enlarged) and add the small perturbation to change the density of wolves to obtain control. The small perturbation is also a function of time $t$, and the density of wolves will also change with delayed feedback term. Then we can obtain the control model (4.1) from model (1.2). Based on this viewpoint, we think that this designed controller is suitable. By choosing the suitable control parameters, we can effectively adjust the time of Hopf bifurcation onset to ensure the balance of biological populations (mice, bobcats, and wolves). Based on this viewpoint, we think that this control design has important biological significance. For other controllers, we can explain them in a similar way.

Remark 6.7. In the three controlled predator-prey models (4.1), (5.1), and (6.1), we use three different hybrid controllers that contain parameter perturbation with delay and state feedback, and then we obtain three controlled predator-prey models. For controlled model (4.1), we add this hybrid controller to the third equation of model (1.2) in order to change the density of top predators and then adjust the stability domain and onset of Hopf bifurcation of system (1.2). For the controlled model (5.1), we add this hybrid controller to the second equation of model (1.2) in order to change the density of intermediate predators, and then adjust the stability domain and onset of Hopf bifurcation of system (1.2). For the controlled model (6.1), we add this hybrid controller to the three equations of model (1.2) in order to change the densities of preys, intermediate predators, and top predators, and then adjust the stability domain and onset of Hopf bifurcation of system (1.2). In actual biological systems, this is possible (see Remark 6.6). To evaluate whether these controllers are reasonable in the actual system and whether they are practical or not, we will carry out theoretical analysis via the stability and Hopf bifurcation theory and computer simulations. It is not feasible to add controllers at will.

Remark 6.8. For three different controllers, the conclusions of three controlled systems (4.1), (5.1) and (6.1) are different since the delay critical values $\delta_{\ast}, \theta_{\ast0}, \theta_{0}$ are different under different parameter conditions. When implementing control in ecosystems, we can control the growth rate and mortality rate of predators via killing predators to add the mortality rate of predators and foster predators to increase their growth rate artificially.

7.   Matlab simulation outcomes

In this section, we will use Matlab 2021 software to carry out numerical simulation.

Example 7.1. Take into account the predator-prey model, which contains a delay:

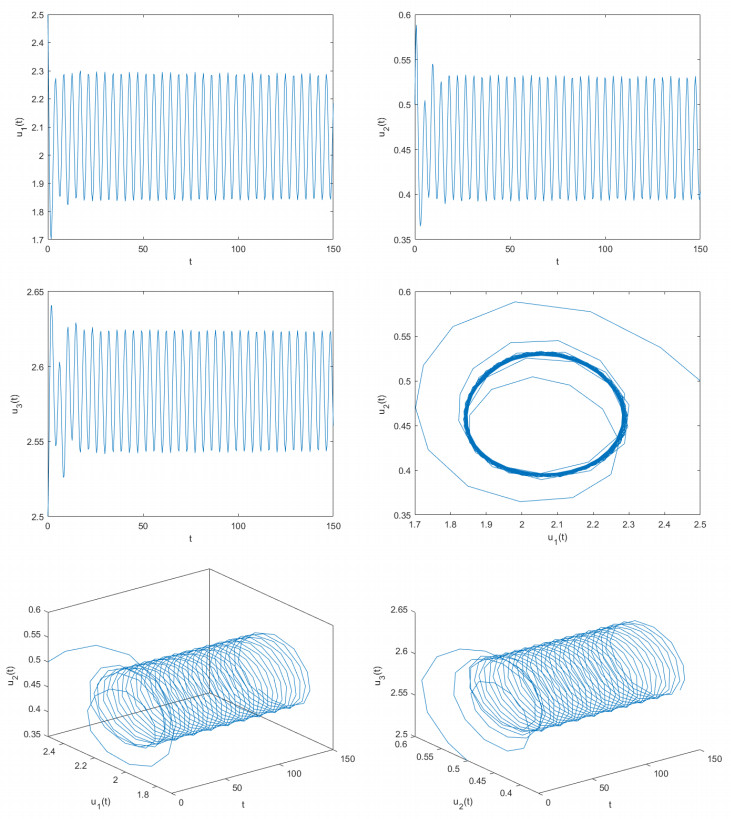
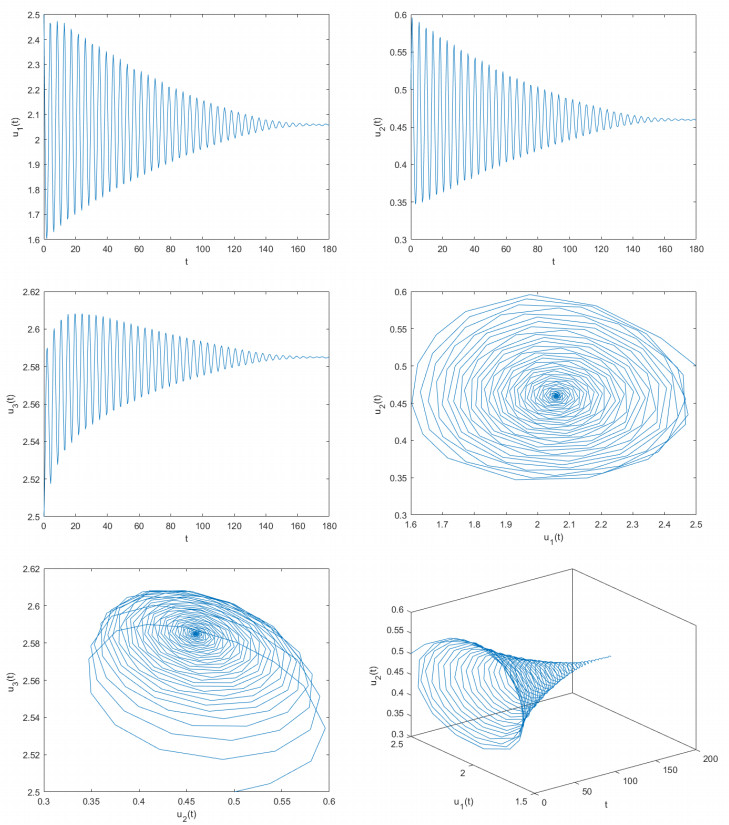
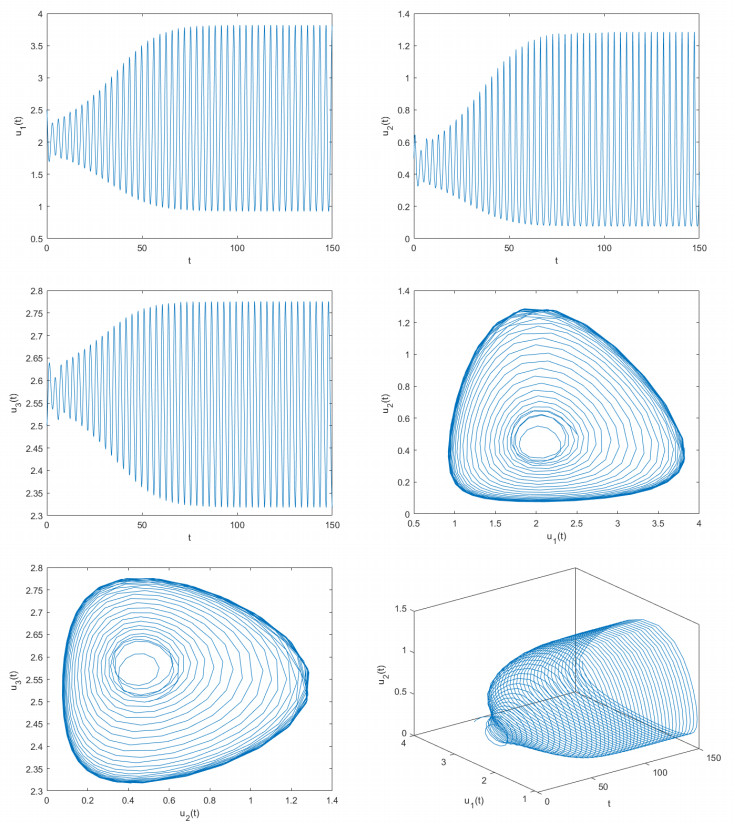
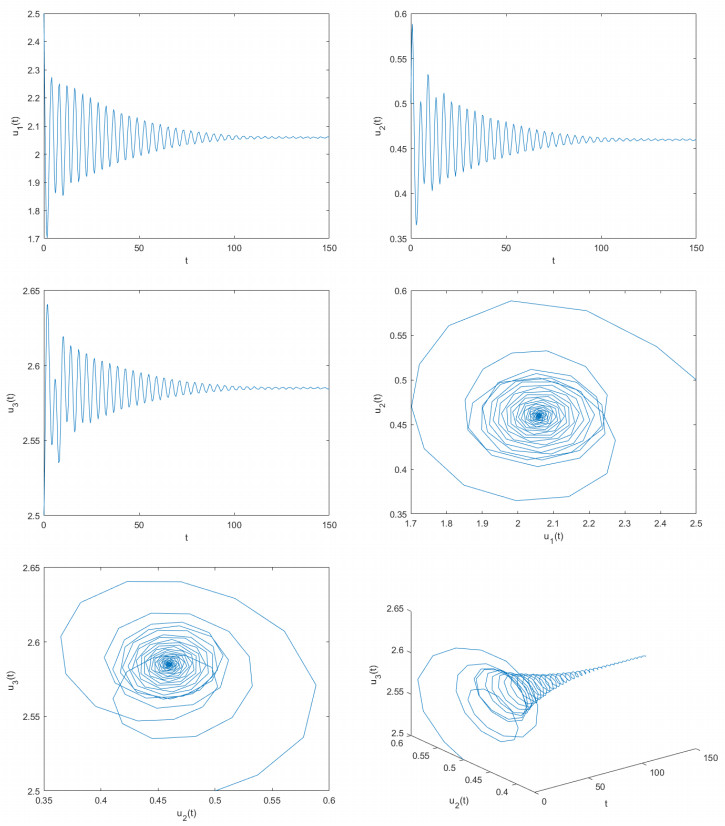
where $\gamma = 2, d = 0.3, m = 3, \varpi_1 = 0.5, \varpi_2 = 0.5, \varpi_3 = 0.1, \varpi_4 = 0.5, a_1 = 12, a_2 = 1, \lambda_1 = 0.7, \lambda_2 = 0.3, \xi_1 = 0.1, \xi_2 = 0.03, \xi_3 = 0.3, \beta_0 = 2, \beta_1 = 1.$ Obviously, model (7.1) possesses a unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$. It is simple to demonstrate that the conditions $({\mathcal{Q}}_1)$–$({\mathcal{Q}}_3)$ of Theorem 3.1 are satisfied. With the help of computational software, one can obtain that $\theta_{0}\approx5.1$. To assess the correctness of the results derived from Theorem 3.1, we pick two unequal delay values. One is $\theta = 4.8$ and the other is $\theta = 5.3.$ If $\theta = 4.8 < \theta_{0}\approx5.1$, we derive the computer simulation diagrams depicted in Figure 1. As depicted in Figure 1, it is clear that $u_1\rightarrow2.0589, u_2\rightarrow0.4597, u_3\rightarrow2.5849$ when $t\rightarrow +\infty.$ In other words, the unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$ of model (7.1) sustains a locally asymptotically stable status. As $\theta = 5.3 > \theta_{0}\approx5.1$, we acquire the computer simulation diagrams illustrated in Figure 2. As depicted in Figure 2, we can see that $u_1$ is going to maintain periodic quavering level around the value $2.0589$, $u_2$ is about to keep periodic quavering level around the value $0.4597$, and $u_3$ will hold periodic quavering level around the value $2.5849$. In other words, a set of periodic solutions (namely, Hopf bifurcations) arise in the vicinity of the positive equilibrium point $F(2.0589, 0.4597, 2.5849)$.

Example 7.2. Take into account the following controlled predator-prey model:

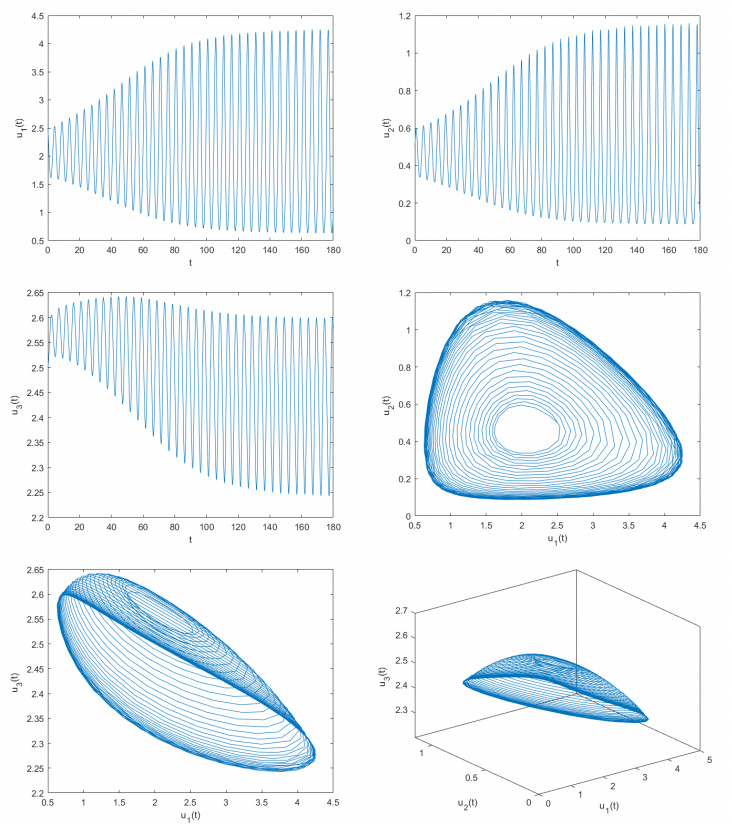
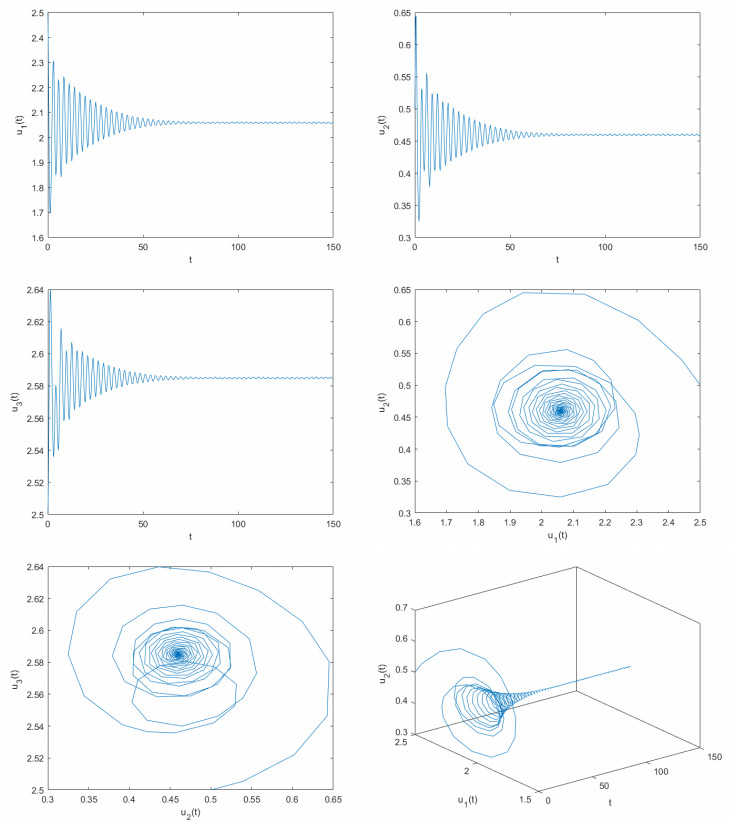
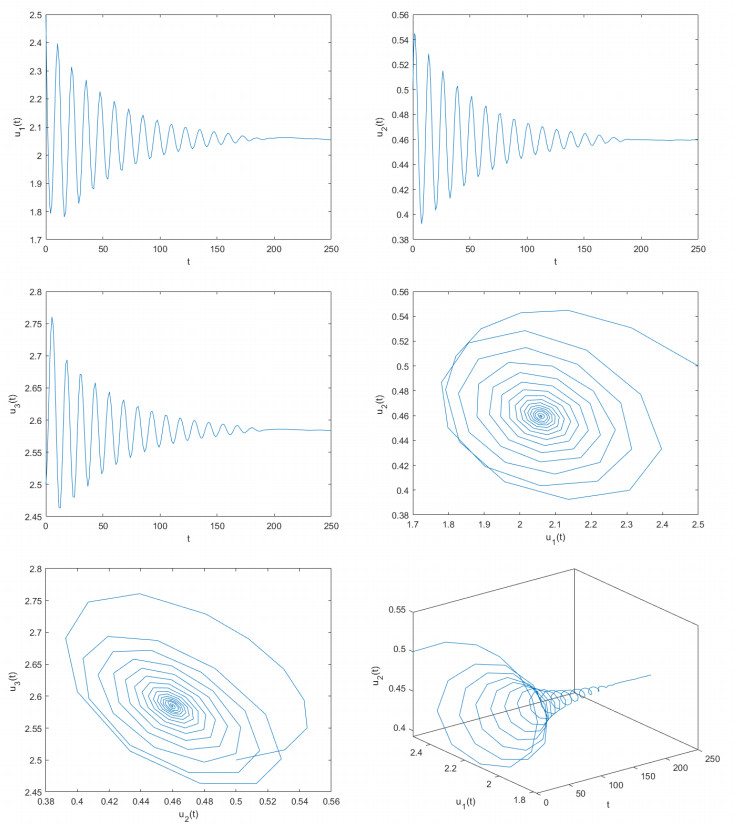
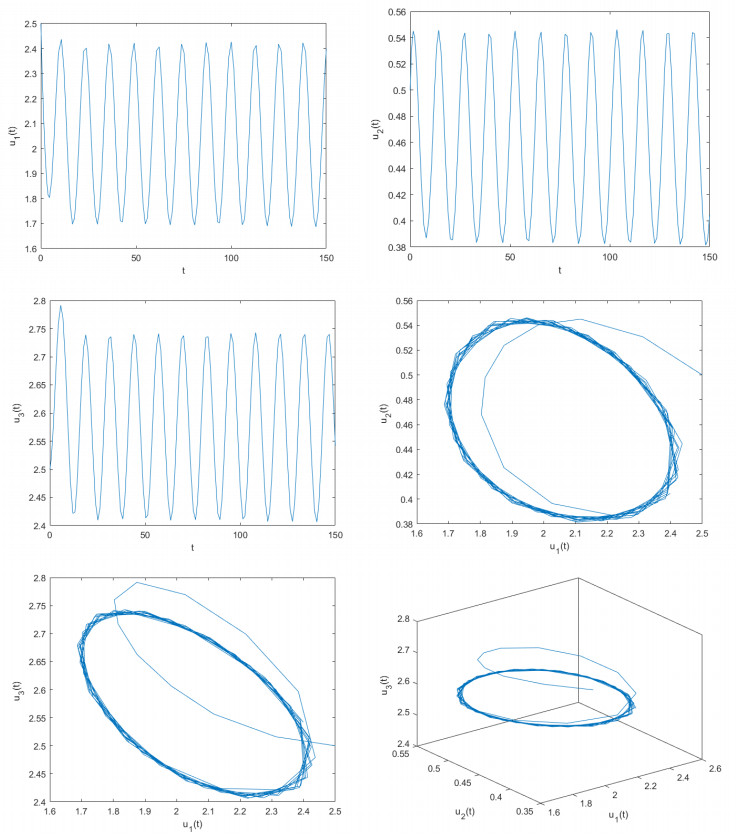
where $\gamma = 2, d = 0.3, m = 3, \varpi_1 = 0.5, \varpi_2 = 0.5, \varpi_3 = 0.1, \varpi_4 = 0.5, a_1 = 12, a_2 = 1, \lambda_1 = 0.7, \lambda_2 = 0.3, \xi_1 = 0.1, \xi_2 = 0.03, \xi_3 = 0.3, \beta_0 = 2,$ and $\beta_1 = 1$. Let $\eta_1 = 0.4$ and $\eta_2 = 0.5$. Obviously, model (7.2) possesses a unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$. It is simple to demonstrate that the conditions $({\mathcal{Q}}_4)$–$({\mathcal{Q}}_6)$ of Theorem 3.2 are satisfied. With the help of computational software, one can acquire that $\delta_{\star}\approx0.9$. To assess the correctness of the results derived from Theorem 3.2, we pick two unequal delay values. One is $\theta = 0.8$ and the other is $\theta = 1.10.$ If $\delta = 0.8 < \delta_{\ast}\approx0.9$, we derive the computer simulation diagrams depicted in Figure 3. As depicted in Figure 3, it is clear that $u_1\rightarrow2.0589, u_2\rightarrow0.4597, u_3\rightarrow2.5849$ when $t\rightarrow +\infty.$ In other words, the unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$ of model (7.2) sustains a locally asymptotically stable status. As $\theta = 5.3 > \theta_{0}\approx5.1$, we acquire the computer simulation diagrams illustrated in Figure 4. As depicted in Figure 4, we can see that $u_1$ is going to maintain a periodic quavering level around the value $2.0589$, $u_2$ will keep a periodic quavering level around the value $0.4597$, and $u_3$ will hold a periodic quavering level around the value $2.5849$. In other words, a set of periodic solutions (namely, Hopf bifurcations) arise in the vicinity of the positive equilibrium point $F(2.0589, 0.4597, 2.5849)$.

Example 7.3. Take into account the following controlled predator-prey model:

where $\gamma = 2, d = 0.3, m = 3, \varpi_1 = 0.5, \varpi_2 = 0.5, \varpi_3 = 0.1, \varpi_4 = 0.5, a_1 = 12, a_2 = 1, \lambda_1 = 0.7, \lambda_2 = 0.3, \xi_1 = 0.1, \xi_2 = 0.03, \xi_3 = 0.3, \beta_0 = 2,$ and $\beta_1 = 1.$ Let $\varsigma_1 = 0.4$ and $\varsigma_2 = 0.5.$ Obviously, model (7.3) possesses a unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$. It is simple to demonstrate that the conditions $({\mathcal{Q}}_7)$–$({\mathcal{Q}}_9)$ of Theorem 5.1 are satisfied. With the help of computational software, one can acquire that $\theta_{\ast0}\approx3.3$. To assess the correctness of the results derived from Theorem 5.1, we pick two unequal delay values. One is $\theta = 3.1$ and the other is $\theta = 3.8$. If $\theta = 3.1 < \theta_{\ast0}\approx3.3$, we derive the computer simulation diagrams depicted in Figure 5. As depicted in Figure 5, it is clear that $u_1\rightarrow2.0589, u_2\rightarrow0.4597, u_3\rightarrow2.5849$ when $t\rightarrow +\infty.$ In other words, the unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$ of model (7.3) sustains a locally asymptotically stable status. As $\theta = 3.8 > \theta_{\ast0}\approx3.3$, we acquire the computer simulation diagrams illustrated in Figure 6. As depicted in Figure 5, we can see that $u_1$ will maintain a periodic quavering level around the value $2.0589$, $u_2$ will keep a periodic quavering level around the value $0.4597$, and $u_3$ will hold a periodic quavering level around the value $2.5849$. In other words, a set of periodic solutions (namely, Hopf bifurcations) arise in the vicinity of the positive equilibrium point $F(2.0589, 0.4597, 2.5849)$.

Example 7.4. Take into account the predator-prey model, which contains a delay:

where $\gamma = 2, d = 0.3, m = 3, \varpi_1 = 0.5, \varpi_2 = 0.5, \varpi_3 = 0.1, \varpi_4 = 0.5, a_1 = 12, a_2 = 1, \lambda_1 = 0.7, \lambda_2 = 0.3, \xi_1 = 0.1, \xi_2 = 0.03, \xi_3 = 0.3, \beta_0 = 2,$ and $\beta_1 = 1.$ Let $\delta_1 = 0.6, \delta_2 = 0.-0.3, \delta_3 = 0.3, \delta_4 = -0.3, \delta_5 = 0.4,$ and $\delta_6 = 0.5.$ Obviously, model (7.4) possesses a unique positive equilibrium point $E(2.0589, 0.4597, 2.5849)$. It is simple to demonstrate that the conditions $({\mathcal{Q}}_{10})$ and $({\mathcal{Q}}_{11})$ of Theorem 6.1 are satisfied. With the help of computational software, one can obtain that $\theta_{0}\approx1.450.$ To assess the correctness of the results derived from Theorem 6.1, we pick two unequal delay values. One is $\theta = 1.4$ and the other is $\theta = 1.510.$ If $\theta = 1.40 < \theta_{0}\approx1.450$, we derive the computer simulation diagrams depicted in Figure 7. As depicted in Figure 7, it is clear that $u_1\rightarrow2.0589, u_2\rightarrow0.4597, u_3\rightarrow2.5849$ when $t\rightarrow +\infty$. In other words, the unique positive equilibrium point $F(2.0589, 0.4597, 2.5849)$ of model (7.4) sustains a locally asymptotically stable status. As $\theta = 1.510 > \theta_{0}\approx1.450$, we obtain the computer simulation diagrams illustrated in Figure 8. As depicted in Figure 8, we can see that $u_1$ will maintain a periodic quavering level around the value $2.0589$, $u_2$ will keep a periodic quavering level around the value $0.4597$, and $u_3$ will hold a periodic quavering level around the value $2.5849$. In other words, a set of periodic solutions (namely, Hopf bifurcations) arise in the vicinity of the positive equilibrium point $F(2.0589, 0.4597, 2.5849)$.

Remark 7.1. On the basis of the computer simulation graphics in Examples 7.1 and 7.2, one can clearly observe that the bifurcation values of models (7.1) and (7.2) are $\theta_0 \approx 5.1$ and $\theta _{\ast} \approx 0.9$, which indicates that we can diminish the stability region and cut down the time to bifurcation in model (7.1) by implementing the formulated hybrid controller. On the basis of the computer simulation graphics in Examples 7.3 and 7.4, one can readily observe that the bifurcation values of models (7.3) and (7.4) are $\theta _{\star} \approx 1.45$, $\theta_{0\ast} \approx 3.3$, which indicates that we can enhance the stability region and prolong the time of bifurcation onset in model (7.1) by implementing the formulated hybrid controller.

Remark 7.2. Compared with the work of Zhao et al. ^[16], although the controller design in this paper is similar, since different controllers are added to different equations, then achieved control effects are different. For example, in ^[16], the stability domain is enlarged and the onset of Hopf bifurcation is postponed; in this paper, the stability domain is narrowed and the onset of Hopf bifurcation is advanced. In addition, the controller design in the Section 6 of this paper is also different from that in ^[16]. Also, the exploration methods on the boundedness of the solution in this paper are different from that in ^[16]. Based on this viewpoint, we think that this paper presents some novelties.

8.   Conclusions

For a long time, predator-prey models have played an important role in biology and attracted great interest from both mathematical and biological fields. From a mathematical standpoint, how to reveal the effect of time delay on the dynamics of predator-prey models is a vital theme. This paper introduces a new delayed predator-prey model and provides a detailed analysis on its peculiarities, including the non-negativity, existence, uniqueness, and boundedness of the solutions, as well as the Hopf bifurcation issue. We derive the sufficient conditions on the stability and bifurcation of the model. By applying various mixed delay feedback controllers, we have successfully adjusted the stability region and the time of bifurcation onset of this model. The findings of this study hold significant theoretical value in balancing the concentrations of predators and preys. Moreover, this research approach can also be applied to explore bifurcation control issues in other complex differential models. Recently, several works have focused on the stability and Hopf bifurcation control of fractional-order dynamical models. We also plan to explore Hopf bifurcation in a fractional-order version of this model in the near future.

Author contributions

Jinting Lin: Conceptualization, formal analysis, investigation, methodology, software, writing original draft, writing-review & editing; Changjin Xu: Conceptualization, formal analysis, investigation, methodology, software, writing-original draft, writing-review & editing; Yiya Xu: Formal analysis, investigation, software, writing-review & editing; Yingyan Zhao: Conceptualization, formal analysis, investigation, methodology, writing-original draft, writing-review & editing; Yicheng Pang: Conceptualization, investigation, methodology, writing-review & editing; Zixin Liu: Conceptualization, investigation, methodology, writing-review & editing; Jianwei Shen: Conceptualization, investigation, methodology, writing-review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work is supported by National Natural Science Foundation of China (No.12261015) and Innovative Exploration and New Academic talent Project of Guizhou University of Finance and Economics (No.2024XSXMA03).

The authors would like to thank the referees and the editor for helpful suggestions incorporated into this paper.

Conflict of interest

The authors declare no conflict of interest.