Monotone iterative and quasilinearization method for a nonlinear integral impulsive differential equation

Yan Li; Zihan Rui; Bing Hu; Yan Li; Zihan Rui; Bing Hu

doi:10.3934/math.2025002

AIMS Mathematics

2025, Volume 10, Issue 1: 21-37. doi: 10.3934/math.2025002

Previous Article Next Article

Research article Topical Sections

Monotone iterative and quasilinearization method for a nonlinear integral impulsive differential equation

School of Mathematical Sciences, Zhejiang University of Technology, Hangzhou 310023, China

Received: 06 October 2024 Revised: 09 December 2024 Accepted: 23 December 2024 Published: 02 January 2025
MSC : 34B05, 34B37

In this paper, we discuss the existence and approximation of solution sequences for a class of nonlinear ordinary differential equations with an impulsive integral condition. Our major methods were the monotone iterative and quasilinearization techniques. Interestingly, many new results could be obtained, which were different from the functional differential equation.

Keywords:

Citation: Yan Li, Zihan Rui, Bing Hu. Monotone iterative and quasilinearization method for a nonlinear integral impulsive differential equation[J]. AIMS Mathematics, 2025, 10(1): 21-37. doi: 10.3934/math.2025002

Related Papers:

[1]	Zeliha Korpinar, Mustafa Inc, Dumitru Baleanu . On the fractional model of Fokker-Planck equations with two different operator. AIMS Mathematics, 2020, 5(1): 236-248. doi: 10.3934/math.2020015
[2]	Ali Khalouta, Abdelouahab Kadem . A new computational for approximate analytical solutions of nonlinear time-fractional wave-like equations with variable coefficients. AIMS Mathematics, 2020, 5(1): 1-14. doi: 10.3934/math.2020001
[3]	Hayman Thabet, Subhash Kendre, James Peters . Travelling wave solutions for fractional Korteweg-de Vries equations via an approximate-analytical method. AIMS Mathematics, 2019, 4(4): 1203-1222. doi: 10.3934/math.2019.4.1203
[4]	Xingang Zhang, Zhe Liu, Ling Ding, Bo Tang . Global solutions to a nonlinear Fokker-Planck equation. AIMS Mathematics, 2023, 8(7): 16115-16126. doi: 10.3934/math.2023822
[5]	Musawa Yahya Almusawa, Hassan Almusawa . Numerical analysis of the fractional nonlinear waves of fifth-order KdV and Kawahara equations under Caputo operator. AIMS Mathematics, 2024, 9(11): 31898-31925. doi: 10.3934/math.20241533
[6]	Zahra Pirouzeh, Mohammad Hadi Noori Skandari, Kamele Nassiri Pirbazari, Stanford Shateyi . A pseudo-spectral approach for optimal control problems of variable-order fractional integro-differential equations. AIMS Mathematics, 2024, 9(9): 23692-23710. doi: 10.3934/math.20241151
[7]	Amjid Ali, Teruya Minamoto, Rasool Shah, Kamsing Nonlaopon . A novel numerical method for solution of fractional partial differential equations involving the $\psi$ -Caputo fractional derivative. AIMS Mathematics, 2023, 8(1): 2137-2153. doi: 10.3934/math.2023110
[8]	Shu-Nan Li, Bing-Yang Cao . Anomalies of Lévy-based thermal transport from the Lévy-Fokker-Planck equation. AIMS Mathematics, 2021, 6(7): 6868-6881. doi: 10.3934/math.2021402
[9]	Krunal B. Kachhia, Jyotindra C. Prajapati . Generalized iterative method for the solution of linear and nonlinear fractional differential equations with composite fractional derivative operator. AIMS Mathematics, 2020, 5(4): 2888-2898. doi: 10.3934/math.2020186
[10]	Ramzi B. Albadarneh, Iqbal Batiha, A. K. Alomari, Nedal Tahat . Numerical approach for approximating the Caputo fractional-order derivative operator. AIMS Mathematics, 2021, 6(11): 12743-12756. doi: 10.3934/math.2021735

Abstract

1. Introduction

The ordinary differential equations (ODEs) and partial differential equations (PDEs) are widely used to represent physical phenomena in mathematical language in science and technology. The mathematical form of the physical phenomena easily explains the whole scenario of the phenomena and makes them openly understandable and investigated straightforwardly. Initially, these phenomena were not only modeled accurately by using integer-order differential equations but later on fractional differential equations have over come the deficiencies and comparatively provide the best and adequate modelling of the given problems. Fractional order ODEs and PDEs describe some phenomena more accurately than non-fractional order ODES and PDEs and have numerous applications in applied sciences. It is shown that the fractional-order ODEs and PDEs are non-local and imply that the next state of a system depends on its current state and its previous states. Therefore, the fractional-order derivatives and integration have numerous applications such as the nonlinear oscillation of earth quack is molded with fractional-order derivatives ^[1], chaos theory ^[2], fractional diabetes model ^[3], fractional order Covid-19 Model ^[4], optics ^[5], fractional model of cancer chemotherapy ^[6], effect of fractional order on ferromagnetic fluid ^[7], the fractional-order fluid dynamic traffic model ^[2], signal processing phenomena ^[9], electrodynamics ^[10], fractional model for the dynamics of Hepatitis B Virus ^[11], fractional model for tuberculosis ^[12], fractional-order pine wilt disease model ^[13], and some others references therein ^{[14,15,16,17,18]}.

The Korteweg-De Vries (KdV) equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. KdV can be solved by means of the inverse scattering transform. The mathematical theory behind the KdV equation is a topic of active research. The KdV equation was first introduced by Boussinesq (1877) and rediscovered by Diederik Korteweg and Gustav de Vries (1895) ^[19].

Among these applications, we have considered Fokker-Planck equations of fractional order of the general from

$\begin{equation} \psi_t^{\delta}(\vartheta, \tau) = L\left(\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau)\right)+N \psi_{\vartheta \vartheta}(\vartheta, \tau), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(1.1)

with initial source

$\psi (\vartheta, 0) = \hbar(\vartheta).$

The Fokker-Planck equation (1.1) was introduced by Fokker and Planck to describe the brownian motion of partiles ^[20]. The Fokker-Plank equation represents the change in probability of a random function in time and space, which explain solute transport. Many phenomena, such as wave propagation, continuous random walk, charge carrier transport in amorphous semiconductors, anomalous diffusion, the motion of ribosomes along mRNA and pattern formation, polymeric networks are modelled by PDEs of both time and space fractional order ^[21].

Gorge Adomian was the first who proposed Adomian Decomposition Method (ADM) 1980. The crucial aspect of the method is employment of the "Adomian polynomials" which allow for solution convergence of the nonlinear portion of the equation, without simply linearizing the system. ADM is a type of method that uses a decomposition technique to generate approximation and even accurate solutions for non-linear systems with valid initial data. ADM have been used effectively for the solution of partial differential equations (PDE's) and fractional partial differential equations (FPDE's). In recent years, more and more researchers have applied this method to solving non-linear systems ^[24]. ADM is preferred over other techniques because of its simple implementation for wide range of nonlinear systems, including ordinary and partial differential equations with fractional derivatives. Moreover, ADM can easily handle the solutions of nonlinear fractional problems which is not the case with other techniques. It can be extended easily for higher dimensions problems.

The targeted solutions of fractional order ODEs and PDEs are also the main research focus of the mathematicians. There are many techniques that have been used for the solutions of fractional order Fokker-Planck equations such as Generalized finite differences method (GFDM) ^[22], radial basis functions finite difference (RBF-FD) ^[23], adomian decomposition method ^[25], homotopy perturbation transform method ^[26], iterative Laplace transform method ^[27], residual power method ^[28], finite element method ^[29], fractional variational iteration method ^[30], fractional reduced differential transform method ^[31].

In this article, we have implemented new approximate analytical method (NAAM) for the solution these type Fokker-Planck equations of fractional order. The NAAM is a analytical procedure which provide series form solution. The NAAM technique is easy and straight forward approach. The obtained results are fastly convergent towards the exact solution of each problem. The graphical analysis of NAAM solutions are demonstrated which has good agreement with exact solution of the problems.The remaining paper is systematized as Section 2, shows Preliminary concepts. In Section 3, signifies Procedure of NAAM. Section 4, we explained the implementation of NAAM on Fokker-Planck equations. Section 5, we summarized the obtained results.

2. Preliminaries and basic concepts

In this section, the related definitions and preliminary concepts of fractional calculus and the procedure of the NAAM are presented.

2.1. Riemann-Liouuille integral operator ^[32]

The Riemann-Liouuille fractional partial integral denoted by $I_{\tau}^{\delta},$ where, $\delta\in N, \delta \geq0$ , which is define as under

$\begin{equation} I_{\tau}^{\delta}\psi(\vartheta, \tau) = \left\{ \begin{array}{c c} \frac{1}{\Gamma(\delta)}\int_{0}^{\tau}\psi(\vartheta, \tau)d\tau, \ \ \vartheta, \tau > 0, \\ \psi(\vartheta, \tau), \ \ \vartheta = 0, \tau > 0, \end{array} \right. \end{equation}$

(2.1)

where, $\Gamma$ is represent gamma function.

2.2. Some properties of Riemann-Liouuille fractional partial integral

Let $\delta, \beta \in R, \setminus N, \ \ \delta, \gamma > 0, \rho > -1,$ then for the function $\psi(\vartheta, \tau)$ the operator $I_{\tau}^{\delta}$ has the following properties.

$\begin{equation} \left\{ \begin{array}{c c} I_{\tau}^{\delta}\psi(\vartheta, \tau) I_t^{\gamma}\psi(\vartheta, \tau) = I_{\tau}^{\delta+\gamma}\psi(\vartheta, \tau), \\ I_{\tau}^{\delta}\psi(\vartheta, \tau) I_{\tau}^{\gamma}\psi(\vartheta, \tau) = I_{\tau}^{\gamma}\psi(\vartheta, \tau)I_{\tau}^{\delta}\psi(\vartheta, \tau), \\ I_{\tau}^{\delta}\tau^{\rho} = \frac{\Gamma(\rho+1)}{\Gamma(\delta+\rho+1)}\tau^{\delta+\rho}. \end{array} \right. \end{equation}$

(2.2)

2.3. Caputo operator of fractional partial derivative ^[36]

$\begin{equation} D_{\tau}^\delta \psi(\vartheta, \tau) = \frac{ \partial^{\delta}\psi(\vartheta, \tau)}{\partial {\tau}^{\delta}} = \left\{ \begin{array}{c c} I^{n-\delta}[\frac{ \partial^{\delta}{\psi(\vartheta, \tau)}}{\partial {\tau}^{\delta}}], \ \ n-1 < \delta < n, \ \ n\in N, \\ \frac{ \partial^{\delta}\psi(\vartheta, \tau)}{\partial {\tau}^{\delta}}, \ \ \ n = \delta. \end{array} \right. \end{equation}$

(2.3)

2.4. Theorem ^[36]

Let $\vartheta, \tau \in R, \ \tau > 0,$ and $m-1 < \rho < m\in N,$ then

$\begin{equation} \begin{split} &I_{\tau}^{\delta} D_{\tau}^\delta \psi(\vartheta, \tau) = \psi(\vartheta, \tau)-\sum\limits_{k = 0}^{m-1}\frac{\tau^k}{k!}\frac{\partial^k \psi(\vartheta, 0^{+}) }{\partial \tau^k}, \\ &D_{\tau}^\vartheta I_{\tau}^{\vartheta} \psi(\vartheta, \tau) = \psi(\vartheta, \tau). \end{split} \end{equation}$

(2.4)

2.5. Theorem

If there exists a constant $0 < \gamma < 1 such that:$

$\begin{equation} ||u_{n+1}(\vartheta, \tau)||\leq\gamma||u_{n}(\vartheta, \tau)||, \ \ n\in N, \ \ \vartheta\in \mathrm{I}\subset\mathbb{R}, \ \ 0\leq t < R, \end{equation}$

(2.5)

then the sequence of approximate solution converges to the exact solution.

Proof. See ^[35].

3. NAAM procedure for the solution of problems^[37]

Here, we have analyzed the analytical procedure for the solution of fractional order Fokker-Planck equations by introducing approximate analytical method.

Consider a general form of Fokker-Planck equation as

(3.1)

with initial source

$\psi (\vartheta, 0) = \hbar(\vartheta),$

where $L, N$ are linear and non-linear operator respectively.

Before computational procedure, we have defined some mandatory procedural results below.

3.1. Lemma ^[37]

For $L\psi(\vartheta, \tau) = \sum_{0}^{\infty}\gamma^k L\psi_k(\vartheta, \tau),$ the linear term $L\psi (\vartheta, \tau)$ satisfy the following property

$\begin{equation} L\psi (\vartheta, \tau) = \left(L\sum\limits_{k = 0}^{\infty}\gamma^k \psi_k(\vartheta, \tau)\right) = \sum\limits_{k = 0}^{\infty}\left(\gamma^k L \psi_k(\vartheta, \tau)\right). \end{equation}$

(3.2)

3.2. Theorem ^[37]

The nonlinear operator $N\psi(\vartheta, \tau),$ for the parameter $\lambda,$ we define $\psi_{\lambda}(\vartheta, \tau) = \sum_{0}^{\infty}\lambda^k \psi_k(\vartheta, \tau),$ compensate the following property

$\begin{equation} N\left( \psi_\lambda\right) = N\left(\sum\limits_{0}^{\infty}\lambda^k \psi_k(\vartheta, \tau)\right) = \sum\limits_{0}^{\infty}\left[\frac{1}{n!}\frac{d^n}{d\lambda^n}\left[N\left(\sum\limits_{0}^{\infty}\lambda^k \psi_k(\vartheta, \tau)\right)\right]_{\lambda = 0}\right]\lambda^n. \end{equation}$

(3.3)

3.3. Definition ^[1]

The polynomial $\chi_n = \chi_n(\psi_0, \psi_1, \cdots, \psi_n),$ can be calculated as

$\begin{equation} \chi_n(\psi_0, \psi_1, \cdots, \psi_n) = \frac{1}{n!}\frac{d^n}{d\lambda^n}\left[\aleph\left(\sum\limits_{0}^{\infty}\lambda^k \psi_k(\vartheta, \tau)\right)\right]_{\lambda = 0} \end{equation}$

(3.4)

3.4. Definition ^[31]

For $\chi_n = \chi_n(\psi_0, \psi_1, \cdots, \psi_n),$ the non-linear term $N\left(\psi_\lambda\right),$ with using definition (3.4), is represented as

$\begin{equation} N\left( \psi_\lambda\right) = \sum\limits_{0}^{\infty}\lambda^k \chi_k \end{equation}$

(3.5)

3.5. The existence and uniqueness of NAAM ^[37]

The following result briefly explain the exitance of NAAM.

Theorem

Let $N\left(\psi_\lambda\right), \psi(\vartheta, \tau)$ are define for $\epsilon-1 < \delta < \epsilon$ , in (3.1). The Fokker-Planck model (3.1), the unique solution is given as

$\begin{equation} \psi(\vartheta, \tau) = \psi(\vartheta, 0)+\sum\limits_{k = 1}^{\infty}\left[L_{\tau}^{-\delta}(\psi_{(k-1)})+\chi_{(k-1)t}^{-\delta}\right], \end{equation}$

(3.6)

where, $L_{\tau}^{-\delta}(\psi_{(k-1)})$ and $\chi_{(k-1)\tau}^{-\delta}$ represent the fractional partial integral of order $\delta$ for $L(\psi_{k-1})$ and $\chi_{(k-1)}$ with respect to $\tau$ .

Proof. The solution of Fokker-Planck equation $\psi(\vartheta, \tau),$ is obtained by substituting the following expansion

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(3.7)

To numerate the Eq (3.1), we can investigate as

$\begin{equation} \psi_{\tau\lambda} ^{\delta}(\vartheta, \tau) = \lambda[L (\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau))+N \psi_{\vartheta \vartheta}(\vartheta, \tau)], \ \ \lambda \in (0, 1], \end{equation}$

(3.8)

along with initial sources

$\begin{equation} \psi(\vartheta, 0) = \hbar (\vartheta). \end{equation}$

(3.9)

Additionally, the solution of Eq (3.6) is estimated as

$\begin{equation} \psi_{\lambda}(\vartheta, \tau) = \sum\limits_{0}^{\infty}\lambda^k\psi_{\lambda}(\vartheta, \tau), \end{equation}$

(3.10)

using the Caupto-Riemann property on Eq (3.8), we have

$\begin{equation} \psi_{\lambda} (\vartheta, \tau) = \psi (\vartheta, 0)+\lambda[L (\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau))+N \psi_{\vartheta \vartheta}(\vartheta, \tau)], \end{equation}$

(3.11)

assuming Eq (3.9), the initial source, Eq (3.11), become as

$\begin{equation} \psi_{\lambda} (\vartheta, \tau) = \hbar (\vartheta)+\lambda[L (\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau))+N \psi_{\vartheta \vartheta}(\vartheta, \tau)]. \end{equation}$

(3.12)

By substituting, Eq (3.10), in Eq (3.12), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty}\lambda^{k} \psi_{\lambda}(\vartheta, \tau) = \hbar (\vartheta)+ \lambda I_{t}^{\delta }\left[L\left(\sum\limits_{k = 0}^{\infty}\lambda^{k} (\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau))\right)+N\left( \sum\limits_{k = 0}^{\infty}\lambda^{k} \psi_{\vartheta \vartheta}(\vartheta, \tau)\right)\right], \end{equation}$

(3.13)

with the help of Theorem (3.4), and Lemma (3.1), the Eq (3.13) become as

$\begin{equation} \sum\limits_{k = 0}^{\infty}\lambda^{k} \psi_{\lambda}(\vartheta, \tau) = \hbar (\vartheta)+ \lambda I_{t}^{\delta }\left[L\left(\sum\limits_{k = 0}^{\infty}\lambda^{k} (\psi_{\vartheta} (\vartheta, \tau)+\psi_{\vartheta \vartheta} (\vartheta, \tau))\right)\right]+\lambda I_{t}^{\delta }\left[N\left( \sum\limits_{k = 0}^{\infty}\lambda^{k} \chi_n \right)\right], \end{equation}$

(3.14)

the iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (3.14), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = \hbar(\vartheta), \\ \psi_1(\vartheta, \tau) = L_{\tau}^{-\delta}\psi_0+\chi_{\tau 0}^{-\delta}, \\ \psi_k(\vartheta, \tau) = L_{\tau}^{-\delta}\psi_{(k-1)}+\chi_{\tau(k-1)}^{-\delta}, \ \ k = 2, 3, \cdots \end{array} \right. \end{equation}$

(3.15)

4. NAAM implementation and results discussion ^[37]

In this section, we have tested the validity and applicability of NAAM by solving some Fokker-Planck equations.

Problem 4.1. Consider a Fokker-Planck equation of time fractional order in the form ^[36]:

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right)+\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi (\vartheta, \tau)\right) = 0, \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.1)

with initial source

$\psi(\vartheta, 0) = \vartheta^2,$

for special value $\delta = 1,$ the exact form solution is

$\psi(\vartheta, \tau) = \vartheta^2 \exp^{\frac{\tau}{2}}.$

To investigate the solution of the Fokker-Planck equation (21), we compare it with the Eq (6), we get

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi (\vartheta, \tau)\right), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.2)

the genral NAAM solution of Eq (4.1), is assume as

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(4.3)

For investigating the approximate solution of Eq (4.2), we process as

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \lambda\left[\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi (\vartheta, \tau)\right)\right], \ \ \ \ \delta \in (0, 1], \end{equation}$

(4.4)

where the initial condition is given as

$\begin{equation} \psi(\vartheta, 0) = \vartheta^2. \end{equation}$

(4.5)

The assume solution of Eq (4.4), is in the form

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau). \end{equation}$

(4.6)

Using the Caupto-Riemann property on Eq (3.8), we have

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \psi(\vartheta, 0)+ \lambda I_t^{\delta}\left[\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi (\vartheta, \tau)\right)\right], \end{equation}$

(4.7)

assuming the initial condition (3.5), Eq (4.6), become as

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \vartheta^2+ \lambda I_t^{\delta}\left[\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi (\vartheta, \tau)\right)\right], \end{equation}$

(4.8)

by substituting Eq (3.10), in Eq (4.8), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau) = \vartheta^2+ \lambda I_t^{\delta}\left[ \sum\limits_{k = 0}^{\infty} \lambda^k (\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi_k (\vartheta, \tau)\right))- \sum\limits_{k = 0}^{\infty} \lambda^k\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi_k (\vartheta, \tau)\right)\right], \end{equation}$

(4.9)

the iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (4.9), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = \vartheta^2, \\ \psi_1(\vartheta, \tau) = I_t^{\delta}\left[\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi_0 (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi_0 (\vartheta, \tau)\right)\right], \\ \psi_k(\vartheta, \tau) = I_t^{\delta}\left[\frac{\partial}{\partial \vartheta}\left(\frac{\vartheta}{6} \psi_{k-1} (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{12} \psi_{k-1} (\vartheta, \tau)\right)\right]. \end{array} \right. \end{equation}$

(4.10)

Consequently, we get

$\begin{equation} \psi_0(\vartheta, \tau) = \vartheta^2, \end{equation}$

(4.11)

$\begin{equation} \psi_1(\vartheta, \tau) = \vartheta^2 \frac{t^\delta}{2 \Gamma(\delta+1)}, \end{equation}$

(4.12)

$\begin{equation} \psi_2(\vartheta, \tau) = \vartheta^2 \frac{t^{2\delta}}{8 \Gamma(2\delta+1)}, \end{equation}$

(4.13)

$\begin{equation} \psi_3(\vartheta, \tau) = \vartheta^2 \frac{t^{3\delta}}{8 \Gamma(3\delta+1)}, \end{equation}$

(4.14)

$\vdots.$

The NAAM solution is

$\begin{equation} \psi(\vartheta, \tau) = \psi_0(\vartheta, \tau)+ \psi_1(\vartheta, \tau)+ \psi_2(\vartheta, \tau)+ \psi_3(\vartheta, \tau)+\cdots, \end{equation}$

(4.15)

subsisting Eqs (4.11)–(4.14), in Eq (4.15), we get

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2+ \vartheta^2 \frac{t^\delta}{2 \Gamma(\delta+1)}+\vartheta^2 \frac{t^{2\delta}}{8 \Gamma(2\delta+1)}+\vartheta^2 \frac{t^{3\delta}}{8 \Gamma(3\delta+1)}+\cdots, \end{equation}$

(4.16)

Specifically for $\delta = 1,$ the solution converted to

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2+ \vartheta^2 \frac{t}{2 \Gamma(2)}+\vartheta^2 \frac{t^{2}}{8 \Gamma(3)}+\vartheta^2 \frac{t^{3}}{8 \Gamma(4)}+\cdots, \end{equation}$

(4.17)

which converge to exact solution as

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2 \exp^{\frac{\tau}{2}}. \end{equation}$

(4.18)

Problem 4.2.

Consider a Fokker-Planck equation of time fractional order in the form ^[36];

$\begin{equation} \frac{\partial}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right)+\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right) = 0, \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.19)

with initial source

$\begin{equation} \psi(\vartheta, 0) = \vartheta, \end{equation}$

(4.20)

for special value $\delta = 1,$ the exact form solution is

$\psi(\vartheta, \tau) = \vartheta \exp^{\tau}.$

To investigate the solution of the Fokker-Planck equation (4.19), we compare it with the Eq (3.1), we get

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = -\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.21)

the general NAAM solution of Eq (4.19), is assume as

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(4.22)

For investigating the approximate solution of Eq (4.20), we process as

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \lambda\left[-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right)\right], \ \ \ \ \delta \in (0, 1], \end{equation}$

(4.23)

where the initial condition is given as

$\begin{equation} \psi(\vartheta, 0) = \vartheta. \end{equation}$

(4.24)

The assume solution of Eq (4.23), is in the form

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau). \end{equation}$

(4.25)

Using the Caupto-Riemann property on Eq (4.23), we have

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \psi(\vartheta, 0)+ \lambda I_t^{\delta}\left[-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right)\right], \end{equation}$

(4.26)

assuming the initial condition (4.20), Eq (4.26), become as

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \vartheta+ \lambda I_t^{\delta}\left[-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right)\right], \end{equation}$

(4.27)

by substituting Eq (4.25), in Eq (4.27), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau) = \vartheta+ \lambda I_t^{\delta}\left[ \sum\limits_{k = 0}^{\infty} \lambda^k (-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi (\vartheta, \tau)\right))+ \sum\limits_{k = 0}^{\infty} \lambda^k\frac{\partial^2}{\partial \vartheta^2}\left(\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi (\vartheta, \tau)\right)\right)\right], \end{equation}$

(4.28)

the iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (4.28), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = \vartheta, \\ \psi_1(\vartheta, \tau) = I_t^{\delta}\left[-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi_0 (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi_0 (\vartheta, \tau)\right)\right], \\ \psi_k(\vartheta, \tau) = I_t^{\delta}\left[-\frac{\partial}{\partial \vartheta}\left(\vartheta \psi_{k-1} (\vartheta, \tau)\right)+\frac{\partial^2}{\partial \vartheta^2}\left(\frac{{\vartheta}^2}{2} \psi_{k-1} (\vartheta, \tau)\right)\right]. \end{array} \right. \end{equation}$

(4.29)

Consequently, we get

$\begin{equation} \psi_0(\vartheta, \tau) = \vartheta, \end{equation}$

(4.30)

$\begin{equation} \psi_1(\vartheta, \tau) = \vartheta \frac{t^\delta}{\Gamma(\delta+1)}, \end{equation}$

(4.31)

$\begin{equation} \psi_2(\vartheta, \tau) = \vartheta \frac{t^{2\delta}}{ \Gamma(2\delta+1)}, \end{equation}$

(4.32)

$\begin{equation} \psi_3(\vartheta, \tau) = \vartheta \frac{t^{3\delta}}{ \Gamma(3\delta+1)}, \end{equation}$

(4.33)

$\vdots$

The NAAM solution is

$\begin{equation} \psi(\vartheta, \tau) = \psi_0(\vartheta, \tau)+ \psi_1(\vartheta, \tau)+ \psi_2(\vartheta, \tau)+ \psi_3(\vartheta, \tau)+\cdots, \end{equation}$

(4.34)

subsisting Eqs (4.30)–(4.33), in Eq (4.34), we get

$\begin{equation} \psi(\vartheta, \tau) = \vartheta+ \vartheta \frac{t^\delta}{ \Gamma(\delta+1)}+\vartheta \frac{t^{2\delta}}{ \Gamma(2\delta+1)}+\vartheta \frac{t^{3\delta}}{\Gamma(3\delta+1)}+\cdots. \end{equation}$

(4.35)

Specifically for $\delta = 1,$ the solution converted to

$\begin{equation} \psi(\vartheta, \tau) = \vartheta+ \vartheta \frac{t}{ \Gamma(2)}+\vartheta \frac{t^{2}}{ \Gamma(3)}+\vartheta \frac{t^{3}}{ \Gamma(4)}+\cdots, \end{equation}$

(4.36)

which converge to exact solution as

$\begin{equation} \psi(\vartheta, \tau) = \vartheta \exp^{\tau}. \end{equation}$

(4.37)

Problem 4.3.

Consider a Fokker-Planck equation of time fractional order in the form ^[36];

$\begin{equation} \frac{\partial}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right)+\frac{\partial}{\partial \vartheta}\left(\frac{4}{\vartheta} \psi^2 (\vartheta, \tau)\right)-\frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi (\vartheta, \tau)\right)-\frac{\partial^2}{\partial \vartheta^2}\left( \psi^2 (\vartheta, \tau)\right) = 0, \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.38)

where initial condition, given as

$\begin{equation} \psi(\vartheta, 0) = \vartheta^2. \end{equation}$

(4.39)

For special value $\delta = 1,$ the exact form solution is

$\psi(\vartheta, \tau) = \vartheta^2 \exp^{\tau}.$

To investigate the solution of the Fokker-Planck equation (4.38), we compare it with the Eq (3.1), we get

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi (\vartheta, \tau)\right)+N \left(\psi (\vartheta, \tau)\right), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.40)

where, the non-linear term $N \left(\psi (\vartheta, \tau)\right) = \frac{\partial^2}{\partial \vartheta^2}\left(\psi^2 (\vartheta, \tau)\right)- \frac{\partial}{\partial \vartheta}\left(\frac{4}{\vartheta} \psi^2 (\vartheta, \tau)\right).$

The general NAAM solution of Eq (4.38), is assume as

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(4.41)

For investigating the approximate solution of Eq (4.40), we process as

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \lambda\left[\frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi (\vartheta, \tau)\right)+N \left(\psi (\vartheta, \tau)\right)\right], \ \ \ \ \delta \in (0, 1], \end{equation}$

(4.42)

The assume solution of Eq (4.42), is in the form

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau). \end{equation}$

(4.43)

Using the Caupto-Riemann property on Eq (4.42), we have

(4.44)

assuming the initial condition 4.39, Eq (4.44), become as

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \vartheta^2+ \lambda I_t^{\delta}\left[\frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi (\vartheta, \tau)\right)+N \left(\psi (\vartheta, \tau)\right)\right], \end{equation}$

(4.45)

by substituting Eq (4.43), in Eq (4.45), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau) = \vartheta^2+ \lambda I_t^{\delta}\left[ \sum\limits_{k = 0}^{\infty} \lambda^k (\frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi (\vartheta, \tau)\right))+ \sum\limits_{k = 0}^{\infty} \lambda^k (N \left(\psi (\vartheta, \tau)\right))\right], \end{equation}$

(4.46)

the nonlinear operator $N \left(\psi (\vartheta, \tau)\right)$ is evaluated by using definition (3.4).

The iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (4.46), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = \vartheta^2, \\ \psi_1(\vartheta, \tau) = L_{\tau}^{\frac{\partial}{\partial \vartheta}}\left(\frac{{\vartheta}}{3} \psi_0 (\vartheta, \tau)\right)+\chi_{\tau 0}^{-\delta}, \\ \psi_k(\vartheta, \tau) = L_{\tau}^{-\delta}\frac{\partial}{\partial \vartheta}\left(\frac{{\vartheta}}{3} \psi_{k-1} (\vartheta, \tau)\right)+\chi_{\tau(k-1)}^{-\delta}, \ \ k = 2, 3, \cdots. \end{array} \right. \end{equation}$

(4.47)

Consequently, we get

$\begin{equation} \psi_0(\vartheta, \tau) = \vartheta^2, \end{equation}$

(4.48)

$\begin{equation} \psi_1(\vartheta, \tau) = \vartheta^2 \frac{t^\delta}{\Gamma(\delta+1)}, \end{equation}$

(4.49)

$\begin{equation} \psi_2(\vartheta, \tau) = \vartheta^2 \frac{t^{2\delta}}{ \Gamma(2\delta+1)}, \end{equation}$

(4.50)

$\begin{equation} \psi_3(\vartheta, \tau) = \vartheta^2 \frac{t^{3\delta}}{ \Gamma(3\delta+1)}, \end{equation}$

(4.51)

$\vdots.$

The NAAM solution is

$\begin{equation} \psi(\vartheta, \tau) = \psi_0(\vartheta, \tau)+ \psi_1(\vartheta, \tau)+ \psi_2(\vartheta, \tau)+ \psi_3(\vartheta, \tau)+\cdots, \end{equation}$

(4.52)

subsisting Eqs (4.48)–(4.51), in Eq (4.52), we get

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2+ \vartheta^{2} \frac{t^\delta}{ \Gamma(\delta+1)}+\vartheta^2 \frac{t^{2\delta}}{ \Gamma(2\delta+1)}+\vartheta^2 \frac{t^{3\delta}}{\Gamma(3\delta+1)}+\cdots. \end{equation}$

(4.53)

Specifically for $\delta = 1,$ the solution converted to

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2+ \vartheta^{2} \frac{t}{ \Gamma(2)}+\vartheta^2 \frac{t^{2}}{ \Gamma(3)}+\vartheta^2 \frac{t^{3}}{ \Gamma(4)}+\cdots \end{equation}$

(4.54)

which converge to exact solution as

$\begin{equation} \psi(\vartheta, \tau) = \vartheta^2 \exp^{\tau}. \end{equation}$

(4.55)

Problem 4.4.

Consider a Fokker-Planck equation of time fractional order in the form ^[36];

$\begin{equation} \frac{\partial}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right)-\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)-\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau) = 0, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.56)

with initial source

$\begin{equation} \psi(\vartheta, 0) = \vartheta, \end{equation}$

(4.57)

for special value $\delta = 1,$ the exact form solution is

$\psi(\vartheta, \tau) = \vartheta +\tau.$

To investigate the solution of the Fokker-Planck equation (4.56), we compare it with the Eq (3.1), we get

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.58)

the general NAAM solution of Eq (4.58), is assume as

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(4.59)

For investigating the approximate solution of Eq (4.59), we process as

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \lambda\left[\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \ \ \ \ \delta \in (0, 1], \end{equation}$

(4.60)

where initial condition, given as

$\begin{equation} \psi(\vartheta, 0) = \vartheta. \end{equation}$

(4.61)

The assume solution of Eq (4.60), is in the form

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau). \end{equation}$

(4.62)

Using the Caupto-Riemann property on Eq (4.60), we have

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \psi(\vartheta, 0)+ \lambda I_t^{\delta}\left[\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \end{equation}$

(4.63)

assuming the initial condition (4.57), Eq (4.63), become as

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \vartheta+ \lambda I_t^{\delta}\left[\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \end{equation}$

(4.64)

by substituting Eq (4.62), in Eq (4.64), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau) = \vartheta^2+ \lambda I_t^{\delta}\left[ \sum\limits_{k = 0}^{\infty} \lambda^k (\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau))+ \sum\limits_{k = 0}^{\infty} \lambda^k (\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau))\right], \end{equation}$

(4.65)

the iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (4.65), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = \vartheta, \\ \psi_1(\vartheta, \tau) = I_{\tau}^{-\delta}\left[\frac{\partial}{\partial \vartheta} \psi_0 (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi_0 (\vartheta, \tau)\right], \\ \psi_k(\vartheta, \tau) = I_{\tau}^{-\delta}\left[\frac{\partial}{\partial \vartheta} \psi_{k-1} (\vartheta, \tau)+\frac{\partial^2}{\partial \vartheta^2} \psi_{k-1} (\vartheta, \tau)\right], \ \ k = 2, 3, \cdots \end{array} \right. \end{equation}$

(4.66)

Consequently, we get

$\begin{equation} \psi_0(\vartheta, \tau) = \vartheta, \end{equation}$

(4.67)

$\begin{equation} \psi_1(\vartheta, \tau) = \frac{t^\delta}{\Gamma(\delta+1)}, \end{equation}$

(4.68)

$\begin{equation} \psi_2(\vartheta, \tau) = 0, \end{equation}$

(4.69)

$\begin{equation} \psi_3(\vartheta, \tau) = 0, \end{equation}$

(4.70)

$\vdots.$

The NAAM solution is

$\begin{equation} \psi(\vartheta, \tau) = \psi_0(\vartheta, \tau)+ \psi_1(\vartheta, \tau)+ \psi_2(\vartheta, \tau)+ \psi_3(\vartheta, \tau)+\cdots, \end{equation}$

(4.71)

subsisting Eqs (4.67)–(4.70), in Eq (4.71), we get

$\begin{equation} \psi(\vartheta, \tau) = \vartheta+ \frac{t^\delta}{ \Gamma(\delta+1)}+0+0+\cdots. \end{equation}$

(4.72)

Specifically for $\delta = 1,$ the solution converted to

$\begin{equation} \psi(\vartheta, \tau) = \vartheta+ \frac{\tau}{ \Gamma(2)}, \end{equation}$

(4.73)

which converge to exact solution as

$\begin{equation} \psi(\vartheta, \tau) = \vartheta +\tau. \end{equation}$

(4.74)

Problem 4.5.

Consider a Fokker-Planck equation of time fractional order in the form ^[36];

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right)-(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)-(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau) = 0, \ \ \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.75)

with initial source

$\begin{equation} \psi(\vartheta, 0) = 1+\vartheta, \end{equation}$

(4.76)

for special value $\delta = 1,$ the exact form solution is

$\psi(\vartheta, \tau) = \exp^\tau(1+\vartheta).$

To investigate the solution of the Fokker-Planck equation (4.75), we compare it with the Eq (3.1), we get

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = (1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau), \ \ \vartheta, \tau > 0, \ \delta \in (0, 1], \end{equation}$

(4.77)

the general NAAM solution of Eq (4.75), is assume as

$\begin{equation} \psi(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty}\psi_k(\vartheta, \tau). \end{equation}$

(4.78)

For investigating the approximate solution of Eq (4.77), we process as

$\begin{equation} \frac{\partial^\delta}{\partial \tau^{\delta}}\left( \psi (\vartheta, \tau)\right) = \lambda\left[(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \ \ \ \ \delta \in (0, 1], \end{equation}$

(4.79)

where initial condition, given as

$\begin{equation} \psi(\vartheta, 0) = \vartheta+1. \end{equation}$

(4.80)

The assume solution of Eq (4.79), is in the form

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau). \end{equation}$

(4.81)

Using the Caupto-Riemann property on Eq (4.79), we have

$\begin{equation} \psi_\lambda(\vartheta, \tau) = \psi(\vartheta, 0)+ \lambda I_t^{\delta}\left[(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \end{equation}$

(4.82)

assuming the initial condition, Eq (4.82), become as

$\begin{equation} \psi_\lambda(\vartheta, \tau) = 1+\vartheta+ \lambda I_t^{\delta}\left[(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau)\right], \end{equation}$

(4.83)

by substituting Eq (4.81), in Eq (4.83), we get

$\begin{equation} \sum\limits_{k = 0}^{\infty} \lambda^k \psi_k(\vartheta, \tau) = 1+\vartheta+ \lambda I_t^{\delta}\left[ \sum\limits_{k = 0}^{\infty} \lambda^k ((1-\vartheta)\frac{\partial}{\partial \vartheta} \psi (\vartheta, \tau))+ \sum\limits_{k = 0}^{\infty} \lambda^k ((e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi (\vartheta, \tau))\right], \end{equation}$

(4.84)

the iterative scheme is obtained by comparing the identical power of $\lambda$ in Eq (4.84), as

$\begin{equation} \left\{ \begin{array}{c c} \psi_0(\vartheta, \tau) = 1+\vartheta, \\ \psi_1(\vartheta, \tau) = I_{\tau}^{-\delta}\left[(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi_0 (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi_0 (\vartheta, \tau)\right], \\ \psi_k(\vartheta, \tau) = I_{\tau}^{-\delta}\left[(1-\vartheta)\frac{\partial}{\partial \vartheta} \psi_{k-1} (\vartheta, \tau)+(e^{\tau} \vartheta^2)\frac{\partial^2}{\partial \vartheta^2} \psi_{k-1} (\vartheta, \tau)\right], \ \ k = 2, 3, \cdots \end{array} \right. \end{equation}$

(4.85)

Consequently, we get

$\begin{equation} \psi_0(\vartheta, \tau) = 1+\vartheta, \end{equation}$

(4.86)

$\begin{equation} \psi_1(\vartheta, \tau) = (1+\vartheta)\frac{\tau^\delta}{\Gamma(\delta+1)}, \end{equation}$

(4.87)

$\begin{equation} \psi_2(\vartheta, \tau) = (1+\vartheta)\frac{\tau^{2\delta}}{\Gamma(2\delta+1)}, \end{equation}$

(4.88)

$\begin{equation} \psi_3(\vartheta, \tau) = (1+\vartheta)\frac{\tau^{3\delta}}{\Gamma(3\delta+1)}, \end{equation}$

(4.89)

$\vdots.$

The NAAM solution is

$\begin{equation} \psi(\vartheta, \tau) = \psi_0(\vartheta, \tau)+ \psi_1(\vartheta, \tau)+ \psi_2(\vartheta, \tau)+ \psi_3(\vartheta, \tau)+\cdots, \end{equation}$

(4.90)

subsisting Eqs (4.86)–(4.89), in Eq (4.90), we get

$\begin{equation} \psi(\vartheta, \tau) = 1+\vartheta+ (1+\vartheta) \frac{t^\delta}{ \Gamma(\delta+1)}+(1+\vartheta)\frac{\tau^{2\delta}}{\Gamma(2\delta+1)}+(1+\vartheta)\frac{\tau^{3\delta}}{\Gamma(3\delta+1)}+\cdots. \end{equation}$

(4.91)

Specifically for $\delta = 1,$ the solution converted to

$\begin{equation} \psi(\vartheta, \tau) = 1+ \vartheta+ (1+ \vartheta) \frac{\tau}{ \Gamma(2)}+(1+ \vartheta) \frac{\tau^2}{ \Gamma(3)}+(1+ \vartheta) \frac{\tau^3}{ \Gamma(4)}+\cdots, \end{equation}$

(4.92)

which converge to exact solution as

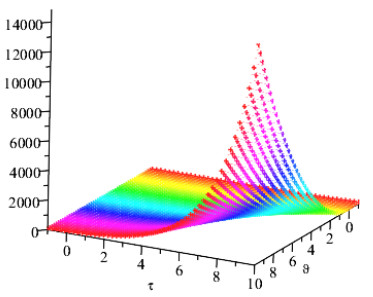
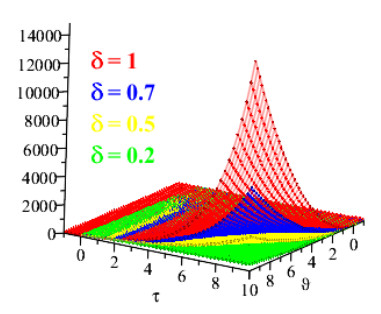
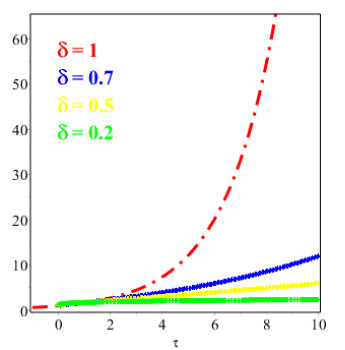
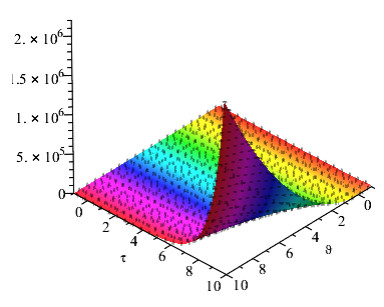
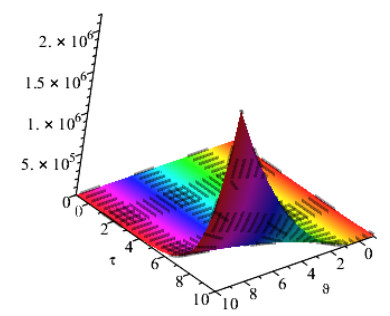
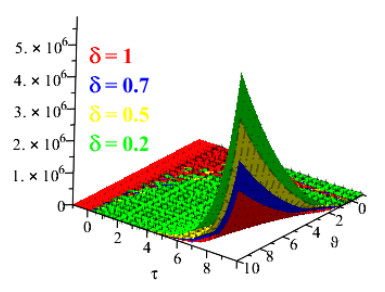
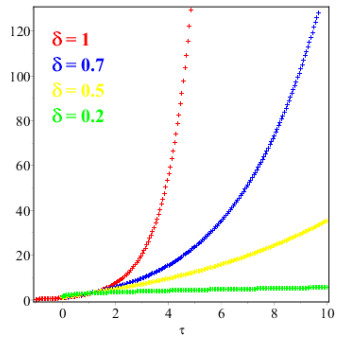
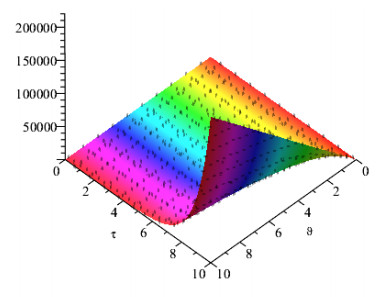
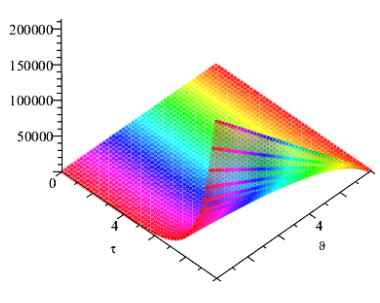
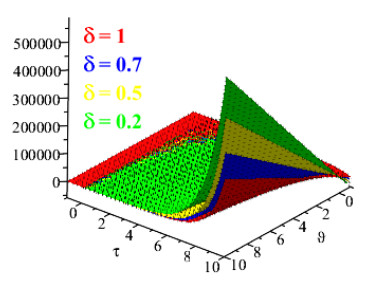
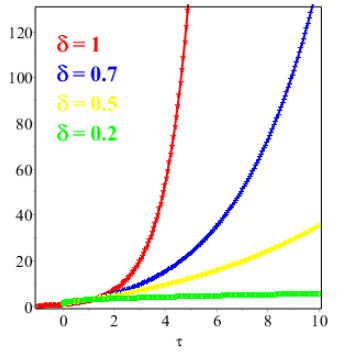
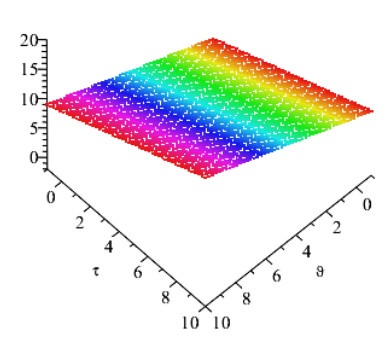
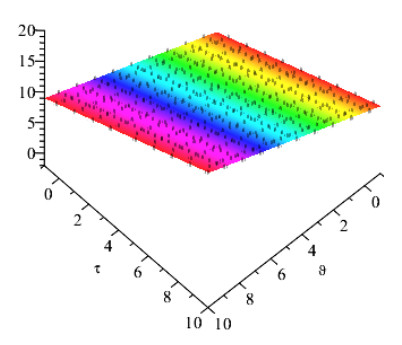
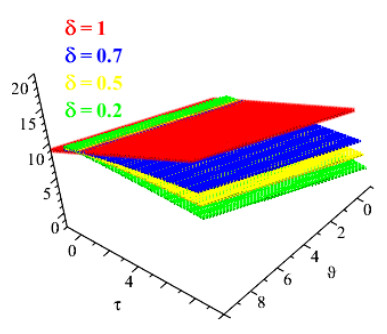
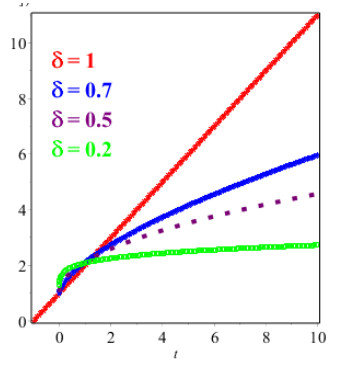
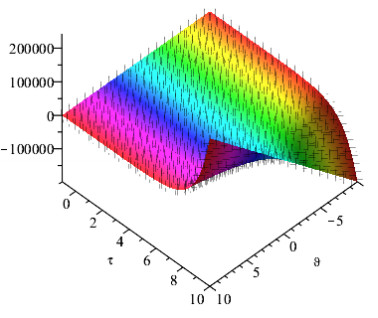
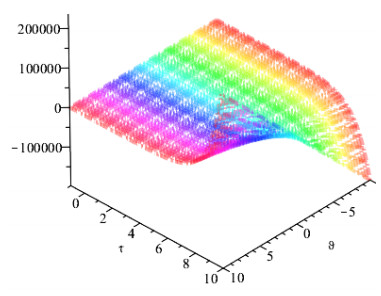
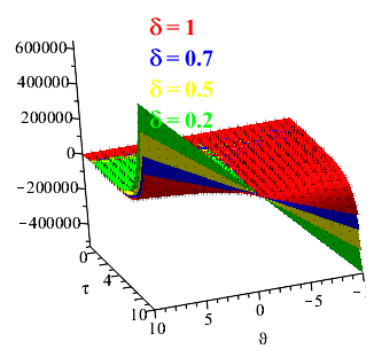
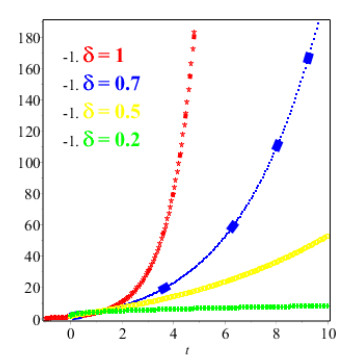
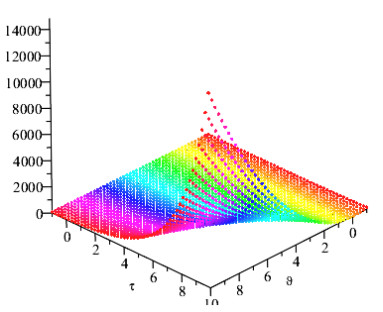
$\begin{equation} \psi(\vartheta, \tau) = \exp^\tau(1+\vartheta). \end{equation}$

(4.93)

Figures 1 and 2 show the comparison of exact and NAAM solutions while Figures 3 and 4 represent the 2D and 3D solutions graphs respectively of Problem 4.1 at different fractional orders. Figures 5 and 6 show the comparison of exact and NAAM solutions while Figures 7 and 8 represent the 2D and 3D solutions graphs respectively of Problem 4.2 at different fractional orders. Figures 9 and 10 show the comparison of exact and NAAM solutions while Figures 11 and 12 represent the 2D and 3D solutions graphs respectively of Problem 4.3 at different fractional orders. Figures 13 and 14 show the comparison of exact and NAAM solutions while Figures 15 and 16 represent the 2D and 3D solutions graphs respectively of Problem 4.4 at different fractional orders. Figures 17 and 18 show the comparison of exact and NAAM solutions while Figures 19 and 20 represent the 2D and 3D solutions graphs respectively of Problem 4.5 at different fractional orders. Table 1, display the solutions comparison of NAAM with HPM, ADM and exact solutions of Problem 4.2. Table 2, display the solutions comparison of NAAM with HPM, ADM and exact solutions of Problem 4.3. Table 3, display the solutions comparison of NAAM with HPM, ADM and exact solutions of Problem 4.4. Table 4, display the solutions comparison of NAAM with HPM, ADM and exact solutions of Problem 4.5.

Figure 1. Exact solution graph of Problem 4.1.

DownLoad: Full-Size Img PowerPoint

Figure 2. NAAM solution graph of Problem 4.1.

DownLoad: Full-Size Img PowerPoint

Figure 3. 3D fractional order solution graphs of Problem 4.1.

DownLoad: Full-Size Img PowerPoint

Figure 4. 2D fractional order solution graph of Problem 4.1.

DownLoad: Full-Size Img PowerPoint

Figure 5. Exact solution graph of Problem 4.2.

DownLoad: Full-Size Img PowerPoint

Figure 6. NAAM solution graph of Problem 4.2.

DownLoad: Full-Size Img PowerPoint

Figure 7. 3D Fractional order solution graphs of Problem 4.2.

DownLoad: Full-Size Img PowerPoint

Figure 8. 2D Fractional order solution graph of Problem 4.2.

DownLoad: Full-Size Img PowerPoint

Figure 9. Exact solution graph of Problem 4.3.

DownLoad: Full-Size Img PowerPoint

Figure 10. NAAM solution graph of Problem 4.3.

DownLoad: Full-Size Img PowerPoint

Figure 11. 3D fractional order solution graphs of Problem 4.3.

DownLoad: Full-Size Img PowerPoint

Figure 12. 2D fractional order solution graph of Problem 4.3.

DownLoad: Full-Size Img PowerPoint

Figure 13. Exact solution graph of Problem 4.4.

DownLoad: Full-Size Img PowerPoint

Figure 14. NAAM solution graph of Problem 4.4.

DownLoad: Full-Size Img PowerPoint

Figure 15. 3D Fractional order solution graphs of Problem 4.4.

DownLoad: Full-Size Img PowerPoint

Figure 16. 2D Fractional order solution graph of Problem 4.4.

DownLoad: Full-Size Img PowerPoint

Figure 17. Exact solution graph of Problem: 4.5.

DownLoad: Full-Size Img PowerPoint

Figure 18. NAAM solution graph of Problem 4.5.

DownLoad: Full-Size Img PowerPoint

Figure 19. 3D Fractional order solution graphs of Problem 4.5.

DownLoad: Full-Size Img PowerPoint

Figure 20. 2D Fractional order solution graph of Problem 4.5.

DownLoad: Full-Size Img PowerPoint

Table 1. Comparison study for solution of Problem 4.2.

${\tau}$	$\vartheta$	NAAM	HPM ^[33]	ADM ^[34]	Exact
0.2	0.25	0.305333	0.305333	0.305333	0.305351
0.2	0.50	0.610667	0.610667	0.610667	0.610701
0.2	0.75	0.916000	0.916000	0.916000	0.916052
0.2	1.00	1.221333	1.221333	1.221333	1.221403
0.4	0.25	0.372667	0.372667	0.372667	0.372956
0.4	0.50	0.745333	0.745333	0.745333	0.745912
0.4	0.75	1.118000	1.118000	1.118000	1.118869
0.4	1.00	1.490667	1.490667	1.490667	1.491825
0.6	0.25	0.454000	0.454000	0.454000	0.455530
0.6	0.50	0.908000	0.908000	0.908000	0.911059
0.6	0.75	1.362000	1.362000	1.362000	1.366589
0.6	1.00	1.816000	1.816000	1.816000	1.822119

| Show Table

DownLoad: CSV

Table 2. Comparison study for solution of Problem 4.3.

${\tau}$	$\vartheta$	NAAM	HPM ^[33]	ADM ^[34]	Exact
0.2	0.25	0.076333	0.076333	0.076333	0.076338
	0.50	0.305333	0.305333	0.305333	0.305351
	0.75	0.687000	0.687000	0.687000	0.687039
	1.00	1.221333	1.221333	1.221333	1.221403
0.4	0.25	0.093167	0.093167	0.093167	0.093239
	0.50	0.372667	0.372667	0.372667	0.372956
	0.75	0.838500	0.838500	0.838500	0.839151
	1.00	1.490667	1.490667	1.490667	1.491825
0.6	0.25	0.113500	0.113500	0.11350	0 0.113882
	0.50	0.454000	0.454000	0.454000	0.455530
	0.75	1.021500	1.021500	1.021500	1.024942
	1.00	1.816000	1.816000	1.816000	1.822119

| Show Table

DownLoad: CSV

5. Conclusions

In these research notes, we have applied an analytical procedure known as the new approximate analytical method (NAAM). The NAAM provides power series solutions in the form of convergent series with fractional derivatives. It is more powerful than other analytical methods due to its less computational work. It provides the fractional order solution directly using the Caputo-Riemann property. We have tested some Fokker-Planck equations in linear and non-linear cases. The series form solution and graphical representation reflect the applicability and validity. The main advantage of NAAM is that it significantly minimises the numerical computations required to find an analytical solution with fractional order. The fractional order solutions are also found and verified by 3D and 2D representation. Overall, the NAAM provides series form solution with fractional order, which have good agreement with the exact solutions of the problems.

Acknowledgements

Researchers Supporting Project number (RSP-2021/401), King Saud University, Riyadh, Saudi Arabia. This research was funded by National Science, Research and Innovation Fund (NSRF), and King Mongkut's University of Technology North Bangkok with Contract no. KMUTNB-FF-65-24.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	G. C. Wu, D. Q. Zeng, D. Baleanu, Fractional impulsive differential equations: Exact solutions, integral equations and short memory case, Fract. Calc. Appl. Anal., 22 (2019), 180–192. https://doi.org/10.1515/fca-2019-0012 doi: 10.1515/fca-2019-0012
[2]	V. Slyn'ko, C.Tunç, Stability of abstract linear switched impulsive differential equations, Automatica, 107 (2019), 433–441. https://doi.org/10.1016/j.automatica.2019.06.001 doi: 10.1016/j.automatica.2019.06.001
[3]	M. Akhmet, Differential equations on time scales through impulsive differential equations, In: Almost periodicity, chaos, and asymptotic equivalence, Springer, Cham, 27 (2020), 201–222. https://doi.org/10.1007/978-3-030-20572-0_9
[4]	X. Yang, D.Peng, X. Lv, X. Li, Recent progress in impulsive control systems, Math. Comput. Simulat., 155 (2019), 244–268. https://doi.org/10.1016/j.matcom.2018.05.003 doi: 10.1016/j.matcom.2018.05.003
[5]	M. Benchohra, J. Henderson, S. Ntouyas, Impulsive differential equations and inclusions, New York: Hindawi Publishing Corporation, 2006.
[6]	A. M. Samoilenko, N. A. Perestyuk, Impulsive differential equations, World scientific, 1995. https://doi.org/10.1142/2892
[7]	H. M. Ahmed, M. M. El-Borai, H. M. El-Owaidy, A. S. Ghanem, Impulsive Hilfer fractional differential equations, Adv. Differ. Equ., 2018 (2018), 226. https://doi.org/10.1186/s13662-018-1679-7 doi: 10.1186/s13662-018-1679-7
[8]	N. Mshary, H. M. Ahmed, A. S. Ghanem, Existence and controllability of nonlinear evolution equation involving Hilfer fractional derivative with noise and impulsive effect via Rosenblatt process and Poisson jumps, AIMS Mathematics, 9 (2024), 9746–9769. https://doi.org/10.3934/math.2024477 doi: 10.3934/math.2024477
[9]	X. Zhang, P. Chen, Y. Li, Monotone iterative method for retarded evolution equations involving nonlocal and impulsive conditions, Electron. J. Differ. Equ., 2020 (2020), 68–25. https://doi.org/10.58997/ejde.2020.68 doi: 10.58997/ejde.2020.68
[10]	K. Jeet, N. Sukavanam, D. Bahuguna, Monotone iterative technique for nonlocal impulsive finite delay differential equations of fractional order, Differ. Equ. Dyn. Syst., 30 (2019), 801–816. https://doi.org/10.1007/s12591-019-00498-4 doi: 10.1007/s12591-019-00498-4
[11]	Y. Guo, X. B. Shu, Q. Yin, Existence of solutions for first-order Hamiltonian random impulsive differential equations with Dirichlet boundary conditions, DCDS-B, 27 (2022), 4455–4471. https://doi.org/10.3934/dcdsb.2021236 doi: 10.3934/dcdsb.2021236
[12]	B. Ahmad, J. J. Nieto, N. Shahzad, Generalized quasilinearization method for mixed boundary value problems, Appl. Math. Comput., 133 (2002), 423–429. https://doi.org/10.1016/S0096-3003(01)00243-0 doi: 10.1016/S0096-3003(01)00243-0
[13]	B. Ahmad, A. Alsaedi, An extended method of quasilinearization for nonlinear impulsive differential equations with a nonlinear three-point boundary condition, Electron. J. Qual. Theory Differ. Equ., 2007 (2007), 1–19. https://doi.org/10.14232/ejqtde.2007.1.1 doi: 10.14232/ejqtde.2007.1.1
[14]	B. Hu, Z. Wang, M. Xu, D. Wang, Quasilinearization method for an impulsive integro-differential system with delay, Math. Biosci. Eng., 19 (2022), 612–623. https://doi.org/10.3934/mbe.2022027 doi: 10.3934/mbe.2022027
[15]	K. D. Kucche, A. D. Mali, Initial time difference quasilinearization method for fractional differential equations involving generalized Hilfer fractional derivative, Comput. Appl. Math., 39 (2020), 31. https://doi.org/10.1007/s40314-019-1004-4 doi: 10.1007/s40314-019-1004-4
[16]	P. Wang, C. Li, J. Zhang, T. Li, Quasilinearization method for first-order impulsive integro-differential equations, Electron. J. Differ. Equ., 2019 (2019), 46.
[17]	Y. Yin, Monotone iterative technique and quasilinearization for some anti-periodic problems, Nonlinear World, 3 (1996), 253–266.
[18]	B. Ahmad, J. J. Nieto, Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions, Nonlinear Anal.-Theor., 69 (2008), 3291–3298. https://doi.org/10.1016/j.na.2007.09.018 doi: 10.1016/j.na.2007.09.018
[19]	A. Zada, S. Ali, Y. Li, Ulam-type stability for a class of implicit fractional differential equations with non-instantaneous integral impulses and boundary condition, Adv. Differ. Equ., 2017 (2017), 317. https://doi.org/10.1186/s13662-017-1376-y doi: 10.1186/s13662-017-1376-y
[20]	A. Fernandez, S. Ali, A. Zada, On non-instantaneous impulsive fractional differential equations and their equivalent integral equations, Math. Method. Appl. Sci., 44 (2021), 13979–13988. https://doi.org/10.1002/mma.7669 doi: 10.1002/mma.7669
[21]	X. M. Zhang, A new method for searching the integral solution of system of Riemann–Liouville fractional differential equations with non-instantaneous impulses, J. Comput. Appl. Math., 388 (2021), 113307. https://doi.org/10.1016/j.cam.2020.113307 doi: 10.1016/j.cam.2020.113307
[22]	J. Tariboon, Boundary value problems for first order functional differential equations with impulsive integral conditions, J. Comput. Appl. Math., 234 (2010), 2411–2419. https://doi.org/10.1016/j.cam.2010.03.007 doi: 10.1016/j.cam.2010.03.007
[23]	Z. He, X. He, Monotone iterative technique for impulsive integro-differential equations with periodic boundary conditions, Comput. Math. Appl., 48 (2004), 73–84. https://doi.org/10.1016/j.camwa.2004.01.005 doi: 10.1016/j.camwa.2004.01.005
[24]	X. Hao, L. Liu, Mild solution of semilinear impulsive integro-differential evolution equation in Banach spaces, Math. Method. Appl. Sci., 40 (2017), 4832–4841. https://doi.org/10.1002/mma.4350 doi: 10.1002/mma.4350
[25]	B. Li, H. Gou, Monotone iterative method for the periodic boundary value problems of impulsive evolution equations in Banach spaces, Chaos Soliton. Fract., 110 (2018), 209–215. https://doi.org/10.1016/j.chaos.2018.03.027 doi: 10.1016/j.chaos.2018.03.027
[26]	Z. Luo, J. J. Nieto, New results for the periodic boundary value problem for impulsive integro-differential equations, Nonlinear Anal.-Theor., 70 (2009), 2248–2260. https://doi.org/10.1016/j.na.2008.03.004 doi: 10.1016/j.na.2008.03.004
[27]	V. Lakshmikantham, D. D. Bainov, P. S. Simeonov, Theory of impulsive differential equations, World scientific, 1989. https://doi.org/10.1142/0906

This article has been cited by:

1.	Muhammad Imran Liaqat, Adnan Khan, Hafiz Muhammad Anjum, Gregory Abe-I-Kpeng, Emad E. Mahmoud, S. A. Edalatpanah, A Novel Efficient Approach for Solving Nonlinear Caputo Fractional Differential Equations, 2024, 2024, 1687-9120, 10.1155/2024/1971059
2.	Yufeng Zhang, Lizhen Wang, Application of Laplace Adomian decomposition method for fractional Fokker-Planck equation and time fractional coupled Boussinesq-Burger equations, 2024, 41, 0264-4401, 793, 10.1108/EC-06-2023-0275
3.	Qasim Khan, Anthony Suen, Hassan Khan, Application of an efficient analytical technique based on Aboodh transformation to solve linear and non-linear dynamical systems of integro-differential equations, 2024, 11, 26668181, 100848, 10.1016/j.padiff.2024.100848
4.	Zareen A. Khan, Muhammad Bilal Riaz, Muhammad Imran Liaqat, Ali Akgül, Goutam Saha, A novel technique using integral transforms and residual functions for nonlinear partial fractional differential equations involving Caputo derivatives, 2024, 19, 1932-6203, e0313860, 10.1371/journal.pone.0313860
5.	Saad. Z. Rida, Anas. A. M. Arafa, Hussein. S. Hussein, Ismail Gad Ameen, Marwa. M. M. Mostafa, Application of Second Kind Shifted Chebyshev Residual Power Series Method for Solving Time-Fractional Fokker Planck Models, 2025, 11, 2349-5103, 10.1007/s40819-025-01908-8

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(820) PDF downloads(123) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Monotone iterative and quasilinearization method for a nonlinear integral impulsive differential equation

Related Papers:

Abstract

1. Introduction

2. Preliminaries and basic concepts

2.1. Riemann-Liouuille integral operator [32]

2.2. Some properties of Riemann-Liouuille fractional partial integral

2.3. Caputo operator of fractional partial derivative [36]

2.4. Theorem [36]

2.5. Theorem

3. NAAM procedure for the solution of problems[37]

3.1. Lemma [37]

3.2. Theorem [37]

3.3. Definition [1]

3.4. Definition [31]

3.5. The existence and uniqueness of NAAM [37]

4. NAAM implementation and results discussion [37]

5. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Preliminaries and basic concepts

2.1. Riemann-Liouuille integral operator [32]

2.2. Some properties of Riemann-Liouuille fractional partial integral

2.3. Caputo operator of fractional partial derivative [36]

2.4. Theorem [36]

2.5. Theorem

3. NAAM procedure for the solution of problems[37]

3.1. Lemma [37]

3.2. Theorem [37]

3.3. Definition [1]

3.4. Definition [31]

3.5. The existence and uniqueness of NAAM [37]

4. NAAM implementation and results discussion [37]

5. Conclusions

Acknowledgements

Conflict of interest

References

2.1. Riemann-Liouuille integral operator ^[32]

2.3. Caputo operator of fractional partial derivative ^[36]

2.4. Theorem ^[36]

3. NAAM procedure for the solution of problems^[37]

3.1. Lemma ^[37]

3.2. Theorem ^[37]

3.3. Definition ^[1]

3.4. Definition ^[31]

3.5. The existence and uniqueness of NAAM ^[37]

4. NAAM implementation and results discussion ^[37]

2.1. Riemann-Liouuille integral operator ^[32]

2.3. Caputo operator of fractional partial derivative ^[36]

2.4. Theorem ^[36]

3. NAAM procedure for the solution of problems^[37]

3.1. Lemma ^[37]

3.2. Theorem ^[37]

3.3. Definition ^[1]

3.4. Definition ^[31]

3.5. The existence and uniqueness of NAAM ^[37]

4. NAAM implementation and results discussion ^[37]